Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Article
  • Published:

The organization of strong links in complex networks

Nature Physics volume 8, pages 429–436 (2012)Cite this article

Subjects

Abstract

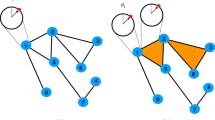
Many complex systems reveal a small-world topology, which allows simultaneously local and global efficiency in the interaction between system constituents. Here, we report the results of a comprehensive study that investigates the relation between the clustering properties in such small-world systems and the strength of interactions between its constituents, quantified by the link weight. For brain, gene, social and language networks, we find a local integrative weight organization in which strong links preferentially occur between nodes with overlapping neighbourhoods; we relate this to global robustness of the clustering to removal of the weakest links. Furthermore, we identify local learning rules that establish integrative networks and improve network traffic in response to past traffic failures. Our findings identify a general organization for complex systems that strikes a balance between efficient local and global communication in their strong interactions, while allowing for robust, exploratory development of weak interactions.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Figure 1: Link clustering in real-world networks reveals preferential placement of strong links with respect to the neighbourhood overlap of the corresponding end nodes.
Figure 2: The robustness of clustering to the loss of their weakest or strongest links in small-world networks and its correlation to link clustering.
Figure 3: Link clustering and pruning analysis for neutral, dispersive, and integrative weight organizations.
Figure 4: Summary plot of M versus R C L for all the networks analysed in the present study.
Figure 5: The cohesive nature of weak links is grounded in their random organization.
Figure 6: Adaptive implementation of integrative and dispersive weight organization.

Similar content being viewed by others

References

  1. Watts, D. J. & Strogatz, S. H. Collective dynamics of ‘small-world’ networks. Nature 393, 440–442 (1998).

    Article  ADS  Google Scholar 

  2. Amaral, L. A., Scala, A., Barthelemy, M. & Stanley, H. E. Classes of small-world networks. Proc. Natl Acad. Sci. USA 97, 11149–11152 (2000).

    Article  ADS  Google Scholar 

  3. Dorogovtsev, S. N. & Mendes, J. F. F. Evolution of Networks: From Biological Nets to the Internet and WWW. (University Press, 2003).

    Book  Google Scholar 

  4. Strogatz, S. H. Exploring complex networks. Nature 410, 268–276 (2001).

    Article  ADS  Google Scholar 

  5. Latora, V. & Marchiori, M. Efficient behavior of small-world networks. Phys. Rev. Lett. 87, 198701 (2001).

    Article  ADS  Google Scholar 

  6. Petermann, T. & De Los, R. P. Physical realizability of small-world networks. Phys. Rev. E 73, 026114 (2006).

    Article  ADS  Google Scholar 

  7. Achard, S. & Bullmore, E. Efficiency and cost of economical brain functional networks. PLoS Comput. Biol. 3, e17 (2007).

    Article  ADS  Google Scholar 

  8. Yu, S., Huang, D., Singer, W. & Nikolic, D. A small world of neuronal synchrony. Cereb. Cortex 18, 2891–2901 (2008).

    Article  Google Scholar 

  9. Hagmann, P. et al. Mapping the structural core of human cerebral cortex. PLoS. Biol. 6, e159 (2008).

    Article  Google Scholar 

  10. Sporns, O. & Honey, C. J. Small worlds inside big brains. Proc. Natl Acad. Sci. USA 103, 19219–19220 (2006).

    ADS  Google Scholar 

  11. Sporns, O. Small-world connectivity, motif composition, and complexity of fractal neuronal connections. Biosystems 85, 55–64 (2006).

    Article  Google Scholar 

  12. Eguiluz, V. M., Chialvo, D. R., Cecchi, G. A., Baliki, M. & Apkarian, A. V. Scale-free brain functional networks. Phys. Rev. Lett. 94, 018102 (2005).

    Article  ADS  Google Scholar 

  13. Bassett, D. S., Meyer-Lindenberg, A., Achard, S., Duke, T. & Bullmore, E. Adaptive reconfiguration of fractal small-world human brain functional networks. Proc. Natl Acad. Sci. USA 103, 19518–19523 (2006).

    Article  ADS  Google Scholar 

  14. Beggs, J. M. & Plenz, D. Neuronal avalanches in neocortical circuits. J. Neurosci. 23, 11167–11177 (2003).

    Article  Google Scholar 

  15. Petermann, T. et al. Spontaneous cortical activity in awake monkeys composed of neuronal avalanches. Proc. Natl Acad. Sci. USA 106, 15921–15926 (2009).

    Article  ADS  Google Scholar 

  16. Pajevic, S. & Plenz, D. Efficient network reconstruction from dynamical cascades identifies small-world topology from neuronal avalanches. PLoS Comput. Biol. 5, e1000271 (2008).

    Article  MathSciNet  Google Scholar 

  17. Barrat, A., Barthelemy, M. & Vespignani, A. Weighted evolving networks: Coupling topology and weight dynamics. Phys. Rev. Lett. 92, 228701 (2004).

    Article  ADS  Google Scholar 

  18. Barrat, A., Barthelemy, M., Pastor-Satorras, R. & Vespignani, A. The architecture of complex weighted networks. Proc. Natl Acad. Sci. USA 101, 3747–3752 (2004).

    Article  ADS  Google Scholar 

  19. Bianconi, G. Emergence of weight-topology correlations in complex scale-free networks. Europhys. Lett. 71, 1029–1035 (2005).

    Article  ADS  Google Scholar 

  20. Serrano, M. A., Boguna, M. & Pastor-Satorras, R. Correlations in weighted networks. Phys. Rev. E 74, 055101 (2006).

    Article  ADS  Google Scholar 

  21. Restrepo, J. G., Ott, E. & Hunt, B. R. Weighted percolation on directed networks. Phys. Rev. Lett. 100, 058701 (2008).

    Article  ADS  Google Scholar 

  22. Restrepo, J. G., Ott, E. & Hunt, B. R. Characterizing the dynamical importance of network nodes and links. Phys. Rev. Lett. 97, 094102 (2006).

    Article  ADS  Google Scholar 

  23. Csermely, P. Weak Links: The Universal Key to the Stability of Networks and Complex Systems (Springer, 2006).

    Google Scholar 

  24. Granovetter, M. S. The strength of weak ties. Am. J. Soc. 78, 1360–1380 (1973).

    Article  Google Scholar 

  25. Davis, J. Clustering and structural balance in graphs. Hum. Relations 20, 181–187 (1967).

    Article  Google Scholar 

  26. Onnela, J. P. et al. Structure and tie strengths in mobile communication networks. Proc. Natl Acad. Sci. USA 104, 7332–7336 (2007).

    Article  ADS  Google Scholar 

  27. Radicchi, F., Castellano, C., Cecconi, F., Loreto, V. & Parisi, D. Defining and identifying communities in networks. Proc. Natl Acad. Sci. USA 101, 2658–2663 (2004).

    Article  ADS  Google Scholar 

  28. Serrano, M. A. & Boguna, M. Clustering in complex networks. I. General formalism. Phys. Rev. E 74, 056114 (2006).

    Article  ADS  MathSciNet  Google Scholar 

  29. Gregoretti, F., Belcastro, V., di Bernardo, D. & Oliva, G. A parallel implementation of the network identification by multiple regression (NIR) algorithm to reverse-engineer regulatory gene networks. PLoS ONE 5, e10179 (2010).

    Article  ADS  Google Scholar 

  30. Albert, R., Jeong, H. & Barabasi, A. L. Error and attack tolerance of complex networks. Nature 406, 378–382 (2000).

    Article  ADS  Google Scholar 

  31. Garas, A., Argyrakis, P. & Shavlin, S. The structural role of weak and strong links in a financial market network. Eur. Phys. J. B. 63, 265–271 (2008).

    Article  ADS  Google Scholar 

  32. Ozik, J., Hunt, B. R. & Ott, E. Growing networks with geographical attachment preference: Emergence of small worlds. Phys. Rev. E 69, 026108 (2004).

    Article  ADS  Google Scholar 

  33. Newman, M. E. & Watts, D. J. Scaling and percolation in the small-world network model. Phys. Rev. E 60, 7332–7342 (1999).

    Article  ADS  Google Scholar 

  34. Barrat, A., Barthelemy, M. & Vespignani, A. Modeling the evolution of weighted networks. Phys. Rev. E 70, 066149 (2004).

    Article  ADS  Google Scholar 

  35. Yook, S. H., Jeong, H., Barabasi, A. L. & Tu, Y. Weighted evolving networks. Phys. Rev. Lett. 86, 5835–5838 (2001).

    Article  ADS  Google Scholar 

  36. Kumpula, J. M., Onnela, J. P., Saramaki, J., Kaski, K. & Kertesz, J. Emergence of communities in weighted networks. Phys. Rev. Lett. 99, 228701 (2007).

    Article  ADS  Google Scholar 

  37. Wang, S., Szalay, M. S., Zhang, C. & Csermely, P. Learning and innovative elements of strategy adoption rules expand cooperative network topologies. PLoS ONE 3, e1917 (2008).

    Article  ADS  Google Scholar 

  38. Girvan, M. & Newman, M. E. Community structure in social and biological networks. Proc. Natl Acad. Sci. USA 99, 7821–7826 (2002).

    Article  ADS  MathSciNet  Google Scholar 

  39. Sutton, R. S. & Barto, A. G. Reinforcement Learning: An Introduction (MIT Press, 1998).

    MATH  Google Scholar 

  40. Schultz, W., Dayan, P. & Montague, P. R. A neural substrate of prediction and reward. Science 275, 1593–1599 (1997).

    Article  Google Scholar 

  41. Maslov, S. & Sneppen, K. Specificity and stability in topology of protein networks. Science 296, 910–913 (2002).

    Article  ADS  Google Scholar 

Download references

Acknowledgements

We thank M. Boguna and members of the Section on Critical Brain Dynamics, NIMH, NIH, for constructive comments during this work. We also thank S. Yu for providing some of the monkey data and J. Alstott for Matlab implementation of one of the social network models. This work was supported by the NIH Intramural Research Program of the NIMH and the DCB/CIT.

Author information

Authors and Affiliations

  1. Division of Computational Bioscience, Mathematical and Statistical Computing Laboratory, Center for Information Technology, National Institutes of Health, Bethesda, Maryland 20892, USA

    Sinisa Pajevic

  2. Section on Critical Brain Dynamics, Laboratory of Systems Neuroscience, National Institute of Mental Health, Bethesda, Maryland 20892, USA

    Dietmar Plenz

Authors
  1. Sinisa Pajevic
    View author publications

    Search author on:PubMed Google Scholar

  2. Dietmar Plenz
    View author publications

    Search author on:PubMed Google Scholar

Contributions

S.P. did analysis. S.P. and D.P. discussed, commented upon and wrote the manuscript.

Corresponding author

Correspondence to Sinisa Pajevic.

Ethics declarations

Competing interests

The authors declare no competing financial interests.

Supplementary information

Supplementary Information

Supplementary Information (PDF 1674 kb)

Rights and permissions

Reprints and permissions

About this article

Cite this article

Pajevic, S., Plenz, D. The organization of strong links in complex networks. Nature Phys 8, 429–436 (2012). https://doi.org/10.1038/nphys2257

Download citation

  • Received:

  • Accepted:

  • Published:

  • Issue date:

  • DOI: https://doi.org/10.1038/nphys2257

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing