Abstract
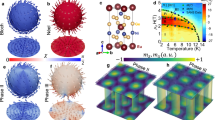
Topological spin textures are a spectacular manifestation of the chirality of the magnetic nanostructures protected by topology. Most known skyrmion systems are restricted to a topological charge of one, require an external magnetic field for stabilization, and are only reported in a few materials. Here, we investigate the possibility that the Kitaev anisotropic-exchange interaction stabilizes a higher-order skyrmion crystal in the insulating van der Waals magnet NiI2. We unveil and explain the incommensurate static and dynamic magnetic correlations across three temperature-driven magnetic phases of this compound using neutron scattering measurements, simulations, and modeling. Our parameter optimisation yields a minimal Kitaev-Heisenberg Hamiltonian for NiI2 which reproduces the experimentally observed magnetic excitations. Monte Carlo simulations for this model predict the emergence of the higher-order skyrmion crystal but neutron diffraction and optical experiments in the candidate intermediate temperature regime are inconclusive. We discuss possible deviations from the Kitaev-Heisenberg model that explains our results and conclude that NiI2, in addition to multiferroic properties in the bulk and few-layer limits, is a Kitaev bulk material proximate to the finite temperature higher-order skyrmion crystal phase.
Similar content being viewed by others
Data availability
The data that supports the findings of this study are available from the corresponding authors upon reasonable request.
Code availability
The codes that support the findings of this study are available from the corresponding authors upon reasonable request.
References
Fert, A., Reyren, N. & Cros, V. Magnetic skyrmions: advances in physics and potential applications. Nat. Rev. Mater. 2, 17031 (2017).
Nagaosa, N. & Tokura, Y. Topological properties and dynamics of magnetic skyrmions. Nat. Nanotechnol. 8, 899 (2013).
Parkin, S. & Yang, S.-H. Memory on the racetrack. Nat. Nanotechnol. 10, 195 (2015).
Muhlbauer, S. et al. Skyrmion lattice in a chiral magnet. Science 323, 915 (2009).
Rößler, U. K., Bogdanov, A. N. & Pfleiderer, C. Spontaneous skyrmion ground states in magnetic metals. Nature 442, 797 (2006).
Wang, Z., Su, Y., Lin, S.-Z. & Batista, C. D. Meron, skyrmion, and vortex crystals in centrosymmetric tetragonal magnets. Phys. Rev. B 103, 104408 (2021).
Gao, S. et al. Fractional antiferromagnetic skyrmion lattice induced by anisotropic couplings. Nature 586, 37 (2020).
Ozawa, R., Hayami, S. & Motome, Y. Zero-field skyrmions with a high topological number in itinerant magnets. Phys. Rev. Lett. 118, 147205 (2017).
Tang, J. et al. Magnetic skyrmion bundles and their current-driven dynamics. Nat. Nanotechnol. 16, 1086 (2021).
Göbel, B., Mertig, I. & Tretiakov, O. A. Beyond skyrmions: review and perspectives of alternative magnetic quasiparticles. Phys. Rep. 895, 1 (2021).
Amoroso, D., Barone, P. & Picozzi, S. Spontaneous skyrmionic lattice from anisotropic symmetric exchange in a ni-halide monolayer. Nat. Commun. 11, 5784 (2020).
Zhang, X., Zhou, Y. & Ezawa, M. High-topological-number magnetic skyrmions and topologically protected dissipative structure. Phys. Rev. B 93, 024415 (2016).
Batista, C. D., Lin, S.-Z., Hayami, S. & Kamiya, Y. Frustration and chiral orderings in correlated electron systems. Rep. Prog. Phys. 79, 084504 (2016).
Hirschberger, M. et al. Skyrmion phase and competing magnetic orders on a breathing kagomé lattice. Nat. Commun. 10, 5831 (2019).
Lin, S.-Z. & Hayami, S. Ginzburg-landau theory for skyrmions in inversion-symmetric magnets with competing interactions. Phys. Rev. B 93, 064430 (2016).
Hayami, S., Lin, S.-Z. & Batista, C. D. Bubble and skyrmion crystals in frustrated magnets with easy-axis anisotropy. Phys. Rev. B 93, 184413 (2016).
Hayami, S. & Motome, Y. Noncoplanar multiple-q spin textures by itinerant frustration: Effects of single-ion anisotropy and bond-dependent anisotropy. Phys. Rev. B 103, 054422 (2021).
Hayami, S., Ozawa, R. & Motome, Y. Effective bilinear-biquadratic model for noncoplanar ordering in itinerant magnets. Phys. Rev. B 95, 224424 (2017).
Yu, X. Z. et al. Biskyrmion states and their current-driven motion in a layered manganite. Nat. Commun. 5, 3198 (2014).
Leonov, A. O. & Mostovoy, M. Multiply periodic states and isolated skyrmions in an anisotropic frustrated magnet. Nat. Commun. 6, 8275 (2015).
McGuire, M. Crystal and magnetic structures in layered, transition metal dihalides and trihalides. Crystals 7, 121 (2017).
Kim, J. et al. Spin and lattice dynamics of the two-dimensional van der waals ferromagnet cri3. npj Quantum Mater. 9, 55 (2024).
Kuindersma, S., Sanchez, J. & Haas, C. Magnetic and structural investigations on NiI2 and CoI2. Phys. B+C. 111, 231 (1981).
Ju, H. et al. Possible persistence of multiferroic order down to bilayer limit of van der waals material NiI2. Nano Lett. 21, 5126 (2021).
Kurumaji, T. et al. Magnetoelectric responses induced by domain rearrangement and spin structural change in triangular-lattice helimagnets NiI2 and CoI2. Phys. Rev. B 87, 014429 (2013).
Son, S. et al. Multiferroic-enabled magnetic-excitons in 2D quantum-entangled van der waals antiferromagnet NiI2. Adv. Mater. 34, (2022).
Song, Q. et al. Evidence for a single-layer van der waals multiferroic. Nature 602, 601 (2022).
Bai, X. et al. Hybridized quadrupolar excitations in the spin-anisotropic frustrated magnet FeI2. Nat. Phys. 17, 467 (2021).
Kim, C. et al. Bond-dependent anisotropy and magnon decay in cobalt-based kitaev triangular antiferromagnet. Nat. Phys. 19, 1624 (2023).
Stavropoulos, P. P., Pereira, D. & Kee, H.-Y. Microscopic mechanism for a higher-spin kitaev model. Phys. Rev. Lett. 123, 037203 (2019).
Li, X. et al. Realistic spin model for multiferroic NiI2. Phys. Rev. Lett. 131, 036701 (2023).
Scheie, A. et al. Spin wave hamiltonian and anomalous scattering in NiPS3. Phys. Rev. B 108, 104402 (2023).
Stock, C. et al. Neutron-scattering measurement of incommensurate short-range order in single crystals of the S = 1 triangular antiferromagnet NiGa2S4. Phys. Rev. Lett. 105, 037402 (2010).
Wildes, A. R. et al. Magnetic dynamics of NiPS3. Phys. Rev. B 106, 174422 (2022).
Gao, B. et al. Spin waves and dirac magnons in a honeycomb-lattice zigzag antiferromagnet \({{\rm{BaNi}}}_{2}{({{\rm{AsO}}}_{4})}_{2}\). Phys. Rev. B 104, 214432 (2021).
Litvin, D. The luttinger-tisza method. Physica 77, 205 (1974).
Paddison, J. A. Scattering signatures of bond-dependent magnetic interactions. Phys. Rev. Lett. 125, 247202 (2020).
Dahlbom, D. et al. Geometric integration of classical spin dynamics via a mean-field schrödinger equation. Phys. Rev. B 106, 054423 (2022).
Yambe, R. & Hayami, S. Skyrmion crystals in centrosymmetric itinerant magnets without horizontal mirror plane. Sci. Rep. 11, 11184 (2021).
Okubo, T., Chung, S. & Kawamura, H. Multiple-q states and the skyrmion lattice of the triangular-lattice heisenberg antiferromagnet under magnetic fields. Phys. Rev. Lett. 108, 017206 (2012).
Cheong, S.-W. & Mostovoy, M. Multiferroics: a magnetic twist for ferroelectricity. Nat. Mater. 6, 13 (2007).
Gordon, E. E., Derakhshan, S., Thompson, C. M. & Whangbo, M.-H. Spin-density wave as a superposition of two magnetic states of opposite chirality and its implications. Inorg. Chem. 57, 9782 (2018).
Kenzelmann, M. et al. Field dependence of magnetic ordering in kagomé-staircase compound Ni3V2O8. Phys. Rev. B 74, 014429 (2006).
Niermann, D. et al. Domain dynamics in the multiferroic phase of MnWO4. Phys. Rev. B 89, 134412 (2014).
Granroth, G. E. et al. SEQUOIA: a newly operating chopper spectrometer at the SNS. J. Phys.: Conf. Ser. 251, 012058 (2010).
Arnold, O. et al. Mantid-data analysis and visualization package for neutron scattering and μsr experiments. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 764, 156 (2014).
Ewings, R. et al. Horace : Software for the analysis of data from single crystal spectroscopy experiments at time-of-flight neutron instruments. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 834, 132 (2016).
Itoh, S. et al. High resolution chopper spectrometer HRC at J - PARC. Nucl. Instrum. Methods Phys. Res. Sect. A Accele. Spectrometers Detect. Assoc. Equip. 631, 90 (2011).
Cao, H. et al. Demand, a dimensional extreme magnetic neutron diffractometer at the high flux isotope reactor. Crystals 9, (2019).
Dahlbom, D. et al. Sunny.jl: A julia package for spin dynamics. arXiv: 2501.13095v2 (2025).
Lane, H. et al. Kernel polynomial method for linear spin wave theory. SciPost Phys. 17, 145 (2024).
Acknowledgements
The authors thank Cristian Batista and Jong-Seok Lee for their fruitful discussion and constructive comments. The authors also thank Maxim Avdeev for his help with powder neutron diffraction measurement at ECHIDNA, ANSTO. The work at SNU was supported by the Leading Researcher Program of the National Research Foundation of Korea (Grant No. 2020R1A3B2079357) and the National Research Foundation of Korea (Grant No. RS-2020-NR049405). The work of O.V. and M.M. was supported by the U.S. National Science Foundation through Grant Nos. NSF-DMR-1750186 and NSF-DMR-2309083. S.M. acknowledges support from the Center for Nonlinear Studies at Los Alamos National Laboratory. The work of Y.K. and S.-J.K. was supported by the Pioneer Research Center Program through the National Research Foundation of Korea, funded by the Ministry of Science, ICT & Future Planning (NRF-2022M3C1A3091988). Part of this research was conducted at the High-Flux Isotope Reactor and Spallation Neutron Source, a DOE Office of Science User Facility operated by the Oak Ridge National Laboratory. The beam time was allocated to SEQUOIA on proposal numbers IPTS-27591 and 29888. The beam time was allocated to DEMAND on proposal numbers IPTS-33254. Another neutron experiment was performed at the Materials and Life Science Experimental Facility of the J-PARC Center under a user program 2022BU1201. One of the authors (J.-G.P.) acknowledges the hospitality of the Indian Institute of Science, where the manuscript was finalised, and the financial support of the Infosys Foundation.
Author information
Authors and Affiliations
Contributions
J.G.P. initiated and supervised the project. Y.L., Y.K., and S.J.K. grew the single crystal. C.K. aligned the sample for measurements. C.K., O.V., P.P., Y.A., W.C., M.B.S., A.I.K., S.I., S.A., T.M., M.M., and J.G.P. performed the INS measurement. C.K., Y.H. and M.M. performed the single-crystal neutron diffraction measurement. C.K. analyzed the data and performed Landau-Lifshitz dynamics and linear spin-wave calculations. S.M. contributed to the data fitting using the Bayesian optimization. C.K., M.M., and J.G.P. wrote the manuscript with input from all co-authors.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Kim, C., Vilella, O., Lee, Y. et al. Kitaev interaction and proximate higher-order skyrmion crystal in the triangular lattice van der Waals antiferromagnet NiI2. npj Quantum Mater. (2026). https://doi.org/10.1038/s41535-026-00851-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41535-026-00851-1