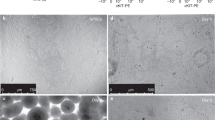
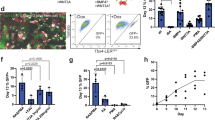
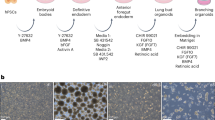
Abstract
Directed differentiation of human induced pluripotent stem cells (iPSCs) into anterior foregut endoderm (AFE) and lung progenitors (LPs) has wide-ranging implications for lung developmental biology, disease modeling, and regenerative medicine. We expand on a previously developed mathematical modeling framework and apply it to the directed differentiation of AFE into LPs. A model-based approach guides experimental design, followed by a multistage model inference process: maximum likelihood estimation based on in vitro data and identifiability analyses to eliminate unidentifiable candidates, thereby guiding model selection. To the authors’ knowledge, this is the first mathematical model of the population dynamics of directed differentiation of AFE into LPs. The model suggests that the overall dynamics are primarily driven by AFE proliferation and differentiation into LPs. In silico experiments predict that daily media change nearly doubles LP yields compared to cultures without media replenishment. Moreover, the model suggests that higher split ratios on day 10 enhance yield per input cell, a measure of differentiation efficiency, by 26%. This work provides a blueprint for refining iPSC-based lung lineage differentiation protocols by combining empirical data and mathematical modeling.
Similar content being viewed by others
Data availability
All data and code used to generate the results in this manuscript are available through https://github.com/amostof/inSilicoAFEPaper.
Code availability
All data and code used to generate the results in this manuscript are available through https://github.com/amostof/inSilicoAFEPaper.
References
Hawkins, F. et al. Prospective isolation of nkx2-1–expressing human lung progenitors derived from pluripotent stem cells. J. Clin. Investig. 127, 2277–2294 (2017).
McCauley, K. B. et al. Efficient derivation of functional human airway epithelium from pluripotent stem cells via temporal regulation of Wnt signaling. Cell Stem Cell 20, 844–857 (2017).
Spence, J. R. et al. Directing differentiation of pluripotent stem cells toward somatic progenitors and functional tissue units. FASEB J. 25, 3775–3785 (2011).
Green, M. D. et al. Generation of anterior foregut endoderm from human embryonic and induced pluripotent stem cells. Nat. Biotechnol. 29, 267–272 (2011).
Jacob, A. et al. Differentiation of human pluripotent stem cells into functional lung alveolar epithelial cells. Cell Stem Cell 21, 472–488 (2017).
Jacob, A. et al. Derivation of self-renewing lung alveolar epithelial type ii cells from human pluripotent stem cells. Nat. Protoc. 14, 3303–3332 (2019).
Yuan, H. et al. Scalable expansion of human pluripotent stem cells under suspension culture condition with human platelet lysate supplementation. Front. Cell Dev, Biol. 11, 1280682 (2023).
Venkatesan, M. et al. Recombinant production of growth factors for application in cell culture. Iscience 25, 105054 (2022).
Möller, J. & Pörtner, R. Digital twins for tissue culture techniques-concepts, expectations, and state of the art. Processes 9, 447 (2021).
Villaverde, A. F., Pathirana, D., Fröhlich, F., Hasenauer, J. & Banga, J. R. A protocol for dynamic model calibration. Brief. Bioinforma. 23, bbab387 (2022).
Geris, L., Lambrechts, T., Carlier, A. & Papantoniou, I. The future is digital: in silico tissue engineering. Curr. Opin. Biomed. Eng. 6, 92–98 (2018).
Hurley, K. et al. Reconstructed single-cell fate trajectories define lineage plasticity windows during differentiation of human PSC-derived distal lung progenitors. Cell Stem Cell 26, 593–608 (2020).
Engle, S. J. & Vincent, F. Small molecule screening in human induced pluripotent stem cell-derived terminal cell types. J. Biol. Chem. 289, 4562–4570 (2014).
Bock, C. et al. Reference maps of human ES and IPS cell variation enable high-throughput characterization of pluripotent cell lines. Cell 144, 439–452 (2011).
Varghese, B., Ling, Z. & Ren, X. Reconstructing the pulmonary niche with stem cells: a lung story. Stem Cell Res. Ther. 13, 161 (2022).
Mostofinejad, A. et al. In silico model development and optimization of in vitro lung cell population growth. PLOS ONE 19, 1–27 (2024).
Mostofinejad, A. et al. In silico modeling of directed differentiation of induced pluripotent stem cells to definitive endoderm. PLOS Comput. Biol. 21, 1–30 (2025).
Lavielle, M.Mixed Effects Models for the Population Approach: Models, Tasks, Methods and Tools, 1st edn. https://doi.org/10.1201/b17203 (Chapman and Hall/CRC, 2014).
Walter, E. Identifiability of Parametric Models (Elsevier, 2014).
Salmaniw, Y. & Browning, A. P. Structural identifiability of linear-in-parameter parabolic PDEs through auxiliary elliptic operators. J. Math. Biol. 91, 4 (2025).
Simpson, M. J., Browning, A. P., Warne, D. J., Maclaren, O. J. & Baker, R. E. Parameter identifiability and model selection for sigmoid population growth models. J. Theor. Biol. 535, 110998 (2022).
Dong, R., Goodbrake, C., Harrington, H. A. & Pogudin, G. Differential elimination for dynamical models via projections with applications to structural identifiability. J. Applied Algebra Geometry 7, 194–235 (2023).
Rackauckas, C. & Nie, Q. Differentialequations.jl–a performant and feature-rich ecosystem for solving differential equations in Julia.J. Open Research Software 5, 15 (2017).
Bezanson, J., Edelman, A., Karpinski, S. & Shah, V. B. Julia: A fresh approach to numerical computing. SIAM Rev. 59, 65–98 (2017).
Vallat, R. Pingouin: statistics in python. J. Open Source Softw. 3, 1026 (2018).
Stein, M. Large sample properties of simulations using Latin hypercube sampling. Technometrics 29, 143–151 (1987).
Moles, C. G., Mendes, P. & Banga, J. R. Parameter estimation in biochemical pathways: a comparison of global optimization methods. Genome Res. 13, 2467–2474 (2003).
Gábor, A. & Banga, J. R. Robust and efficient parameter estimation in dynamic models of biological systems. BMC Syst. Biol. 9, 74 (2015).
Wieland, F.-G., Hauber, A. L., Rosenblatt, M., T”nsing, C. & Timmer, J. On structural and practical identifiability. Opin. Syst. Biol 25, 60–69 (2021).
Raue, A., Karlsson, J., Saccomani, M. P., Jirstrand, M. & Timmer, J. Comparison of approaches for parameter identifiability analysis of biological systems. Bioinformatics 30, 1440–1448 (2014).
VandenHeuvel, D. J. Profilelikelihood.jl (2023).
Simpson, M. J. & Maclaren, O. J. Profile-wise analysis: a profile likelihood-based workflow for identifiability analysis, estimation, and prediction with mechanistic mathematical models. PLoS Comput. Biol. 19, e1011515 (2023).
Farshidfar, S. S. et al. Towards a validated musculoskeletal knee model to estimate tibiofemoral kinematics and ligament strains: comparison of different anterolateral augmentation procedures combined with isolated ACL reconstructions. Biomed. Eng. OnLine 22, 31 (2023).
El Wajeh, M. et al. Can the Kuznetsov model replicate and predict cancer growth in humans?. Bull. Math. Biol. 84, 130 (2022).
Sobol, I. M. Sensitivity analysis for non-linear mathematical models. Math. Model. Comput. Exp. 1, 407–414 (1993).
Bates, D. et al. Juliastats/glm.jl: v1.9.0. https://doi.org/10.5281/zenodo.8345558 (2023).
Liu, Q. et al. Advances in the application of bone morphogenetic proteins and their derived peptides in bone defect repair. Compos. Part B: Eng. 262, 110805 (2023).
Fernandes, R., Barbosa-Matos, C., Borges-Pereira, C., Carvalho, A. L. R. T. d & Costa, S. Glycogen synthase kinase-3 inhibition by chir99021 promotes alveolar epithelial cell proliferation and lung regeneration in the lipopolysaccharide-induced acute lung injury mouse model. Int. J. Mol. Sci. 25, 1279 (2024).
Wilson, H. K., Canfield, S. G., Hjortness, M. K., Palecek, S. P. & Shusta, E. V. Exploring the effects of cell seeding density on the differentiation of human pluripotent stem cells to brain microvascular endothelial cells. Fluids Barriers CNS 12, 1–12 (2015).
McBeath, R., Pirone, D. M., Nelson, C. M., Bhadriraju, K. & Chen, C. S. Cell shape, cytoskeletal tension, and rhoa regulate stem cell lineage commitment. Dev. cell 6, 483–495 (2004).
Peerani, R. et al. Niche-mediated control of human embryonic stem cell self-renewal and differentiation. EMBO J. 26, 4744–4755 (2007).
Huang, H., Ye, K. & Jin, S. Cell seeding strategy influences metabolism and differentiation potency of human induced pluripotent stem cells into pancreatic progenitors. Biotechnol. J. 20, e70022 (2025).
Ptasinski, V. et al. Modeling fibrotic alveolar transitional cells with pluripotent stem cell-derived alveolar organoids. Life Sci. Alliance 6 (2023).
Burridge, P. W., Holmström, A. & Wu, J. C. Chemically defined culture and cardiomyocyte differentiation of human pluripotent stem cells. Curr. Protoc. Hum. Genet. 87, 21–3 (2015).
Stephens, P. A., Sutherland, W. J. & Freckleton, R. P. What is the Allee effect? Oikos 87, 185–190 (1999).
Masters, J. R. & Stacey, G. N. Changing medium and passaging cell lines. Nat. Protoc. 2, 2276–2284 (2007).
Hong, P., Boyd, D., Beyea, S. D. & Bezuhly, M. Enhancement of bone consolidation in mandibular distraction osteogenesis: a contemporary review of experimental studies involving adjuvant therapies. J. Plast. Reconstruct. Aesthetic Surg. 66, 883–895 (2013).
Sharow, K. A., Temkin, B. & Asson-Batres, M. A. Retinoic acid stability in stem cell cultures. Int. J. Dev. Biol. 56, 273–278 (2012).
Charlebois, D. A. & Balázsi, G. Modeling cell population dynamics. In Silico Biol. 13, 21–39 (2019).
Longmire, T. A. et al. Efficient derivation of purified lung and thyroid progenitors from embryonic stem cells. Cell Stem Cell 10, 398–411 (2012).
Huang, S. X. et al. Efficient generation of lung and airway epithelial cells from human pluripotent stem cells. Nat. Biotechnol. 32, 84 (2014).
Suzuki, S. et al. Differentiation of human pluripotent stem cells into functional airway basal stem cells. STAR Protoc. 2, 100683 (2021).
Myers, P. J., Lee, S. H. & Lazzara, M. J. Mechanistic and data-driven models of cell signaling: Tools for fundamental discovery and rational design of therapy. Curr. Opin. Syst. Biol. 28, 100349 (2021).
Pir, P. & Le Novère, N.Mathematical Models of Pluripotent Stem Cells: At the Dawn of Predictive Regenerative Medicine, 331–350 (Springer New York, 2016).
Ingalls, B. P. Mathematical Modeling in Systems Biology: an Introduction (MIT Press, 2013).
Nishimura, H. et al. Kinetics of glut1 and glut4 glucose transporters expressed in Xenopus oocytes. J. Biol. Chem. 268, 8514–8520 (1993).
Fujii, S. & Beutler, E. High glucose concentrations partially release hexokinase from inhibition by glucose 6-phosphate. Proc. Natl. Acad. Sci. 82, 1552–1554 (1985).
Zhang, B. et al. Cooperative transport mechanism of human monocarboxylate transporter 2. Nat. Commun. 11, 2429 (2020).
Coy, R. et al. Combining in silico and in vitro models to inform cell seeding strategies in tissue engineering. J. R. Soc. Interface 17, 20190801 (2020).
Osiecki, M. J., McElwain, S. D. & Lott, W. B. Modelling mesenchymal stromal cell growth in a packed bed bioreactor with a gas permeable wall. PLoS ONE 13, e0202079 (2018).
Mehrian, M. et al. Maximizing neotissue growth kinetics in a perfusion bioreactor: an in silico strategy using model reduction and Bayesian optimization. Biotechnol. Bioeng. 115, 617–629 (2018).
Marciniak-Czochra, A., Stiehl, T., Ho, A. D., Jäger, W. & Wagner, W. Modeling of asymmetric cell division in hematopoietic stem cells—regulation of self-renewal is essential for efficient repopulation. Stem Cells Dev. 18, 377–386 (2009).
Wodarz, D. Effect of cellular de-differentiation on the dynamics and evolution of tissue and tumor cells in mathematical models with feedback regulation. J. Theor. Biol. 448, 86–93 (2018).
Duchesne, R., Guillemin, A., Crauste, F. & Gandrillon, O. Calibration, selection and identifiability analysis of a mathematical model of the in vitro erythropoiesis in normal and perturbed contexts. In Silico Biol. 13, 55–69 (2019).
Hossain, M. S., Bergstrom, D. & Chen, X. Modelling and simulation of the chondrocyte cell growth, glucose consumption and lactate production within a porous tissue scaffold inside a perfusion bioreactor. Biotechnol. Rep. 5, 55–62 (2015).
Kalami Yazdi, A., Nadjafikhah, M. & Distefano III, J. Combos2: an algorithm to the input–output equations of dynamic biosystems via Gaussian elimination. J. Taibah Univ. Sci. 14, 896–907 (2020).
Raue, A., Becker, V., Klingmüller, U. & Timmer, J. Identifiability and observability analysis for experimental design in nonlinear dynamical models. Chaos: Interdiscip. J. Nonlinear Sci. 20, 045105 (2010).
Storn, R. & Price, K. Differential evolution–a simple and efficient heuristic for global optimization over continuous spaces. J. Glob. Optim. 11, 341–359 (1997).
Price, K., Storn, R. M. & Lampinen, J. A. Differential Evolution: a Practical Approach to Global Optimization (Springer Science & Business Media, 2006).
Feldt, R. Blackboxoptim.jl. https://github.com/robertfeldt/BlackBoxOptim.jl (2018).
Das, S. & Suganthan, P. N. Differential evolution: a survey of the state-of-the-art. IEEE Trans. Evolut. Comput. 15, 4–31 (2010).
Mashwani, W. K. Enhanced versions of differential evolution: state-of-the-art survey. Int. J. Comput. Sci. Math. 5, 107–126 (2014).
Nelder, J. A. & Mead, R. A simplex method for function minimization. Comput. J. 7, 308–313 (1965).
Johnson, S. G. The NLopt nonlinear-optimization package. https://github.com/stevengj/nlopt (2007).
Wright, S., Nocedal, J. et al. Numerical optimization. Springe. Sci. 35, 7 (1999).
Kingma, D. P. & Ba, J. Adam: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR) (2015).
Stoica, P. & Selen, Y. Model-order selection: a review of information criterion rules. IEEE Signal Process. Mag. 21, 36–47 (2004).
Pawitan, Y. In All Likelihood: Statistical Modelling and Inference Using Likelihood (Oxford University Press, 2001).
Hastie, T., Tibshirani, R. & Friedman, J. The Elements of Statistical Learning: Data Mining, Inference, and Prediction. 2nd edn (Springer, 2009).
Daume, S., Kofler, S., Kager, J., Kroll, P. & Herwig, C. Generic workflow for the setup of mechanistic process models. In Pörtner, R. (ed.) Animal Cell Biotechnology: Methods and Protocols, vol. 2095 of Methods in Molecular Biology, 189–211 (Humana, 2020).
Zhang, X.-Y., Trame, M. N., Lesko, L. J. & Schmidt, S. Sobol sensitivity analysis: a tool to guide the development and evaluation of systems pharmacology models. CPT: Pharmacomet. Syst. Pharmacol. 4, 69–79 (2015).
Brinson, D. Figure 1. Experimental protocol and the lineage models. https://BioRender.com/2uyml6l (2025).
Acknowledgements
This study is funded in part by a Collaborative Health Research Project (CHRP) grant provided by the Canadian Institutes of Health Research in partnership with the Natural Sciences and Engineering Research Council (158270 to C.H.A. and T.W.). The study is also supported by the New Frontiers in Research Fund Transformation stream (NFRFT-2020-00787 to T.W., C.H.A., G.K., and NFRFT-2022-00447 to C.H.A.), and the University of Toronto’s Medicine by Design initiative, which receives funding from the Canada First Research Excellence Fund (to C.A. and T.W.).
Author information
Authors and Affiliations
Contributions
C.A., D.R., T.W., and G.K. designed and supervised the research. A.M. and D.B. performed research and analyzed data. A.M., D.R., and D.B. took the lead in writing the manuscript. All authors provided critical feedback and helped shape the research and the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Mostofinejad, A., Romero, D.A., Brinson, D. et al. In silico modeling of anterior foregut endoderm differentiation towards lung epithelial progenitors. npj Syst Biol Appl (2026). https://doi.org/10.1038/s41540-026-00650-1
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41540-026-00650-1