Abstract
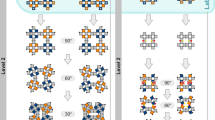
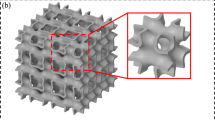
Micro-architected structures are increasingly valued for their light weight and tunable mechanical properties; this class of material includes sheet structures like the Schöen gyroid and beam lattices like the octet. For design purposes, it is critical to understand how to tune the relative density (RD) to obtain desired mechanical properties. This study investigates the mechanical response of Ti-6Al-4V gyroid structures, spanning a broad range of RDs (0.03–0.90), unit cell sizes (1–4 cm), and sheet thicknesses (0.2–7.8 mm). Results demonstrate that the classical Gibson-Ashby power law scaling between RD and modulus and yield stress does not adequately capture the response over a wide range of RDs, nor does it extrapolate correctly to the fully dense solid. Analytical models, in concert with experimental results and high-fidelity finite element calculations, show that the deviation from Gibson-Ashby reflects a transition from structure-dominated to material-dominated behavior. Distinctions are drawn between scaling relationships and property-porosity models, and an analytical model is proposed to better capture the evolution of mechanical properties with RD. These observations are mirrored in other architected topologies, like the octet, and highlight the importance of understanding the relationship between mechanical properties and geometry for design purposes.
Similar content being viewed by others
Data availability
The datasets generated and analyzed during the current study are available from the corresponding author upon reasonable request.
References
Ashby, M. Multi-objective optimization in material design and selection. Acta Mater.48, 359–369 (2000).
Ashby, M. F. The properties of foams and lattices. Philos. Trans. Royal Soc. A: Math., Phys. Eng. Sci.364, 15–30 (2006).
Meza, L. R. et al. Reexamining the mechanical property space of three-dimensional lattice architectures. Acta Mater.140, 424–432 (2017).
Al-Ketan, O., Rowshan, R. & Al-Rub, R. K. A. Topology-mechanical property relationship of 3d printed strut, skeletal, and sheet based periodic metallic cellular materials. Addit. Manuf.19, 167–183 (2018).
Yan, C. et al. Evaluation of light-weight alsi10mg periodic cellular lattice structures fabricated via direct metal laser sintering. J. Mater. Process. Technol.214, 856–864 (2014).
Yan, C., Hao, L., Hussein, A. & Young, P. Ti-6al-4v triply periodic minimal surface structures for bone implants fabricated via selective laser melting. J. Mech. Behav. Biomed. Mater.51, 61–73 (2015).
Yang, L. et al. Mechanical response of a triply periodic minimal surface cellular structures manufactured by selective laser melting. Int. J. Mech. Sci.148, 149–157 (2018).
Yang, E. et al. Effect of geometry on the mechanical properties of ti-6al-4v gyroid structures fabricated via slm: A numerical study. Mater. Des.184, 108165 (2019).
Fu, J. et al. Improved light-weighting potential of ss316l triply periodic minimal surface shell lattices by micro laser powder bed fusion. Mater. Des.222, 111018 (2022).
Qiu, N., Wan, Y., Shen, Y. & Fang, J. Experimental and numerical studies on mechanical properties of tpms structures. Int. J. Mech. Sci.261, 108657 (2024).
Ríos, I. et al. Compressive behavior of 316l stainless steel lattice structures for additive manufacturing: Experimental characterization and numerical modeling. Biomimetics10, 680 (2025).
Samudin, I. M. et al. Stress strain curve analysis of sheet based tpms structures in quasi static compression test: A review. J. Mater. Res. Technol.36, 5757–5796 (2025).
Miao, X., Hu, J., Xu, Y., Su, J. & Jing, Y. Review on mechanical properties of metal lattice structures. Compos. Struct.342, 118267 (2024).
Pabst, W., Gregorová, E. & Tichá, G. Elasticity of porous ceramics–a critical study of modulus- porosity relations. J. Eur. Ceram. Soc.26, 1085–1097 (2006).
Choren, J. A., Heinrich, S. M. & Silver-Thorn, M. B. Young’s modulus and volume porosity relationships for additive manufacturing applications. J. Mater. Sci.48, 5103–5112 (2013).
Rice, R. Comparison of physical property-porosity behaviour with minimum solid area models. J. Mater. Sci.31, 1509–1528 (1996).
Rice, R. Evaluation and extension of physical property-porosity models based on minimum solid area. J. Mater. Sci.31, 102–118 (1996).
Pabst, W. & Gregorova, E. Minimum solid area models for the effective properties of porous materials-a refutation. Ceramics-Silikáty59, 244–249 (2015).
Stefaniuk, D. & Kachanov, M. Voigt-reuss and hashin-shtrikman bounds revisited. Int. J. Eng. Sci.191, 103903 (2023).
Zhao, Y., Tandon, G. & Weng, G. Elastic moduli for a class of porous materials. Acta Mech.76, 105–131 (1989).
Messner, M. C., Barham, M. I., Kumar, M. & Barton, N. R. Wave propagation in equivalent continuums representing truss lattice materials. Int. J. Solids Struct.73, 55–66 (2015).
Carlton, H. D. et al. Mapping local deformation behavior in single cell metal lattice structures. Acta Mater.129, 239–250 (2017).
Carlton, H. D., Volkoff-Shoemaker, N. A., Messner, M. C., Barton, N. R. & Kumar, M. Incorporating defects into model predictions of metal lattice-structured materials. Mater. Sci. Eng., A832, 142427 (2022).
Zimmerman, B. K. et al. Solid face sheets enable lattice metamaterials to withstand high-amplitude impulsive loading without yielding. Int. J. Impact Eng195, 105130 (2025).
Ataee, A., Li, Y., Brandt, M. & Wen, C. Ultrahigh-strength titanium gyroid scaffolds manufactured by selective laser melting (slm) for bone implant applications. Acta Mater.158, 354–368 (2018).
Jones, A., Leary, M., Bateman, S. & Easton, M. Investigating mechanical properties of additively manufactured multimaterial gyroids: The effect of proportion, scale and shape. Addit. Manuf.76, 103784 (2023).
Maconachie, T. et al. The effect of topology on the quasi-static and dynamic behaviour of slm alsi10mg lattice structures. Int. J. Adv. Manuf. Technol.118, 4085–4104 (2022).
Maskery, I. et al. Insights into the mechanical properties of several triply periodic minimal surface lattice structures made by polymer additive manufacturing. Polymer152, 62–71 (2018).
Mazur, M. et al. Deformation and failure behaviour of ti-6al-4v lattice structures manufactured by selective laser melting (slm). Int. J. Adv. Manuf. Technol.84, 1391–1411 (2016).
Mishra, A. K., Chavan, H. & Kumar, A. Effect of cell size and wall thickness on the compression performance of triply periodic minimal surface based alsi10mg lattice structures. Thin-Walled Struct.193, 111214 (2023).
Ahmad, A. Study on the benefits of lattice structures within the framework of high-performance structural design: a case study (2024).
Al-Ketan, O. & Abu Al-Rub, R. K. Multifunctional mechanical metamaterials based on triply periodic minimal surface lattices. Adv. Eng. Mater.21, 1900524 (2019).
Schoen, A. H. Infinite periodic minimal surfaces without self-intersections, vol. 5541 (National Aeronautics and Space Administration, 1970).
Vrancken, B., Thijs, L., Kruth, J.-P. & Van Humbeeck, J. Heat treatment of ti6al4v produced by selective laser melting: Microstructure and mechanical properties. J. Alloy. Compd.541, 177–185 (2012).
DebRoy, T. et al. Additive manufacturing of metallic components-process, structure and properties. Prog. Mater Sci.92, 112–224 (2018).
Mulay, R., Moore, J., Florando, J., Barton, N. & Kumar, M. Microstructure and mechanical properties of ti-6al-4v: Mill-annealed versus direct metal laser melted alloys. Mater. Sci. Eng., A666, 43–47 (2016).
Noble, C. R. et al. Ale3d: An arbitrary lagrangian-eulerian multi-physics code. Tech. Rep., Lawrence Livermore National Lab.(LLNL), Livermore, CA (United States) (2017).
Steinberg, D. J. et al.Equation of state and strength properties of selected materials (Lawrence Livermore National Laboratory Livermore, 1996).
Johnson, G. R. A constitutive model and data for metals subjected to large strains, high strain rates and high temperatures. In Proceedings of the 7th International Symposium on Ballistics, The Hague, Netherlands, 1983 (1983).
Johnson, G. R. & Cook, W. H. Fracture characteristics of three metals subjected to various strains, strain rates, temperatures and pressures. Eng. Fract. Mech.21, 31–48 (1985).
Ashby, M. F. & Gibson, L. J. Cellular solids: Structure and properties. Press Syndicate of the University of Cambridge, Cambridge 175–231 (1997).
Deshpande, V., Ashby, M. & Fleck, N. Foam topology: bending versus stretching dominated architectures. Acta Mater.49, 1035–1040 (2001).
Boccaccini, A. R. & Fan, Z. A new approach for the young’s modulus-porosity correlation of ceramic materials. Ceram. Int.23, 239–245 (1997).
Zhong, H. et al. The gibson-ashby model for additively manufactured metal lattice materials: Its theoretical basis, limitations and new insights from remedies. Curr. Opin. Solid State Mater. Sci.27, 101081 (2023).
Hashin, Z. & Shtrikman, S. A variational approach to the theory of the elastic behaviour of multiphase materials. J. Mech. Phys. Solids11, 127–140 (1963).
Al-Ketan, O. et al. Microarchitected stretching-dominated mechanical metamaterials with minimal surface topologies. Adv. Eng. Mater.20, 1800029 (2018).
Acknowledgements
This work was performed under the auspices of the US Department of Energy by Lawrence Livermore National Laboratory under Contract DE-AC52-07NA27344 (LLNL-JRNL-2012804).
Funding
No funding to declare.
Author information
Authors and Affiliations
Contributions
BKZ: Conceptualization, Methodology, Data Curation, Writing—Original Draft, Writing—Review & Editing, Formal Analysis. HDC: Conceptualization, Methodology, Data Curation, Writing - Original Draft, Writing—Review & Editing, Investigation. JL: Conceptualization, Methodology, Data Curation, Writing—Original Draft, Writing—Review & Editing, Formal Analysis, Investigation. JK: Investigation, Data Curation, Visualization, Writing—Review & Editing. JSB: Investigation, Data Curation. MK: Conceptualization, Methodology, Writing—Review & Editing, Funding Acquisition, Supervision, Project Administration.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary Information
Below is the link to the electronic supplementary material.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Zimmerman, B.K., Carlton, H.D., Lind, J. et al. Investigating property-porosity relationships for micro-architected lattice structures. Sci Rep (2026). https://doi.org/10.1038/s41598-026-35262-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41598-026-35262-6