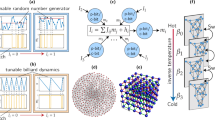
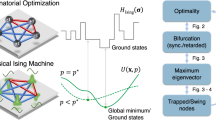
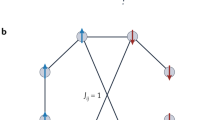
Abstract
Oscillator Ising machines (OIMs) and probabilistic bit (p-bit) platforms have emerged as promising non-Von Neumann paradigms for tackling hard computational problems. While OIMs realize gradient-flow dynamics, p-bit platforms operate through stochastic sampling. Although traditionally viewed as distinct approaches, this work presents a theoretically grounded framework for configuring OIMs as p-bit engines. We demonstrate that this functionality can be enabled through a novel interplay between first- and second harmonic injection to the oscillators. Our work identifies new synergies between the two methods and broadens the scope of applications for OIMs beyond combinatorial optimization problems to those that entail stochastic sampling. We further show that the proposed approach can be applied to other analog dynamical systems, such as the Dynamical Ising Machine.
Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Code availability
The codes associated with this manuscript are available from the corresponding author upon request.
References
Wang, T., Wu, L., Nobel, P. & Roychowdhury, J. Solving combinatorial optimisation problems using oscillator based ising machines. Nat. Comput. 20, 287–306 (2021).
Mohseni, N., McMahon, P. L. & Byrnes, T. Ising machines as hardware solvers of combinatorial optimization problems. Nat. Rev. Phys. 4, 363–379 (2022).
Lucas, A. Ising formulations of many np problems. Front. Phys. 2, 5 (2014).
Hamerly, R. et al. Experimental investigation of performance differences between coherent ising machines and a quantum annealer. Sci. Adv. 5, eaau0823 (2019).
Honjo, T. et al. 100,000-spin coherent ising machine. Sci. Adv. 7, eabh0952 (2021).
Litvinenko, A., Khymyn, R., Ovcharov, R. & Åkerman, J. A 50-spin surface acoustic wave ising machine. Commun. Phys. 8, 1–11 (2025).
Mallick, A., Bashar, M., Truesdell, D., Calhoun, B. & Shukla, N. Overcoming the accuracy vs. performance trade-off in oscillator ising machines. In Proc. International Electron Devices Meeting (IEDM) 40–2 (IEEE, 2021).
Moy, W. et al. A 1,968-node coupled ring oscillator circuit for combinatorial optimization problem solving. Nat. Electron. 5, 310–317 (2022).
Bashar, M. K. et al. Experimental demonstration of a reconfigurable coupled oscillator platform to solve the max-cut problem. IEEE J. Explor. Solid State Comput. Devices Circuits 6, 116–121 (2020).
Vaidya, J., Surya Kanthi, R. & Shukla, N. Creating electronic oscillator-based Ising machines without external injection locking. Sci. Rep. 12, 981 (2022).
Maher, O. et al. A CMOS-compatible oscillation-based VO2 Ising machine solver. Nat. Commun. 15, 3334 (2024).
Cılasun, H. et al. A coupled-oscillator-based Ising chip for combinatorial optimization. Nat. Electron. 8, 537–546 (2025).
Litvinenko, A. et al. A spinwave Ising machine. Commun. Phys. 6, 227 (2023).
King, A. D. et al. Coherent quantum annealing in a programmable 2,000 qubit Ising chain. Nat. Phys. 18, 1324–1328 (2022).
Bashar, M. K., Lin, Z. & Shukla, N. Stability of oscillator Ising machines: not all solutions are created equal. J. Appl. Phys. 134, 144901 (2023).
Cheng, Y., Khairul Bashar, M., Shukla, N. & Lin, Z. A control theoretic analysis of oscillator Ising machines. Chaos 34, https://doi.org/10.1063/5.0195464 (2024).
Allibhoy, A., Montanari, A. N., Pasqualetti, F. & Motter, A. E. Global optimization through heterogeneous oscillator Ising machines. Preprint at https://doi.org/10.48550/arXiv.2505.17027 (2025).
Camsari, K. Y., Sutton, B. M. & Datta, S. P-bits for probabilistic spin logic. Appl. Phys. Rev. 6, 011305 (2019).
Camsari, K. Y., Faria, R., Sutton, B. M. & Datta, S. Stochastic p-bits for invertible logic. Phys. Rev. X 7, 031014 (2017).
Aadit, N. A. et al. Massively parallel probabilistic computing with sparse Ising machines. Nat. Electron. 5, 460–468 (2022).
Chowdhury, S. et al. A full-stack view of probabilistic computing with p-bits: devices, architectures, and algorithms. IEEE J. Explor. Solid State Comput. Devices Circuits 9, 1–11 (2023).
Whitehead, W., Nelson, Z., Camsari, K. Y. & Theogarajan, L. CMOS-compatible Ising and Potts annealing using single-photon avalanche diodes. Nat. Electron. 6, 1009–1019 (2023).
Duffee, C. et al. An integrated-circuit-based probabilistic computer that uses voltage-controlled magnetic tunnel junctions as its entropy source. Nat Electron 8, 784–793 (2025).
Borders, W. A. et al. Integer factorization using stochastic magnetic tunnel junctions. Nature 573, 390–393 (2019).
Singh, N. S. et al. CMOS plus stochastic nanomagnets enabling heterogeneous computers for probabilistic inference and learning. Nat. Commun. 15, 2685 (2024).
Si, J. et al. Energy-efficient superparamagnetic Ising machine and its application to traveling salesman problems. Nat. Commun. 15, 3457 (2024).
Jhonsa, J. et al. A CMOS probabilistic computing chip with in-situ hardware aware learning. Preprint at https://doi.org/10.48550/arXiv.2504.14070 (2025).
Böhm, F., Alonso-Urquijo, D., Verschaffelt, G. & Van der Sande, G. Noise-injected analog ising machines enable ultrafast statistical sampling and machine learning. Nat. Commun. 13, 5847 (2022).
Lee, K., Chowdhury, S. & Camsari, K. Y. Noise-augmented chaotic ising machines for combinatorial optimization and sampling. Commun. Phys. 8, 35 (2025).
Faria, R., Camsari, K. Y. & Datta, S. Low-barrier nanomagnets as p-bits for spin logic. IEEE Magn. Lett. 8, 1–5 (2017).
Adler, R. A study of locking phenomena in oscillators. Proc. IRE 34, 351–357 (2006).
Bhansali, P. & Roychowdhury, J. Gen-adler: the generalized Adler’s equation for injection locking analysis in oscillators. In Proc. Asia and South Pacific Design Automation Conference 522–527 (IEEE, 2009).
Box, G. E. P., Jenkins, G. M., Reinsel, G. C. & Ljung, G. M. Time Series Analysis: Forecasting and Control 5th edn (John Wiley & Sons, 2015).
Ekanayake, E. & Shukla, N. Different paths, same destination: designing physics-inspired dynamical systems with engineered stability to minimize the Ising Hamiltonian. Phys. Rev. Appl. 24, 024008 (2025).
Goto, H., Tatsumura, K. & Dixon, A. R. Combinatorial optimization by simulating adiabatic bifurcations in nonlinear hamiltonian systems. Sci. Adv. 5, eaav2372 (2019).
Niazi, S. et al. Training deep Boltzmann networks with sparse Ising machines. Nat. Electron. 7, 610–619 (2024).
Bashar, M. K. & Shukla, N. Designing Ising machines with higher order spin interactions and their application in solving combinatorial optimization. Sci. Rep. 13, 9558 (2023).
Kleyko, D. et al. Efficient optimization with higher-order Ising machines. Nat. Commun. 14, 6033 (2023).
Duffee, C. et al. Extended-variable probabilistic computing with p-dits. Preprint at https://doi.org/10.48550/arXiv.2506.00269 (2025).
Honari-Latifpour, M. & Miri, M.-A. Optical potts machine through networks of three-photon down-conversion oscillators. Nanophotonics 9, 4199–4205 (2020).
Berloff, N. & Cummins, J. Vector ising spin annealer for minimizing Ising Hamiltonians. Commun. Phys. 8, 225 (2025).
Mallick, A., Bashar, M. K., Lin, Z. & Shukla, N. Computational models based on synchronized oscillators for solving combinatorial optimization problems. Phys. Rev. Appl. 17, 064064 (2022).
Delacour, C. Haverkort, B. Sabo, F. Azemard, N. & Todri-Sanial, A. Lagrange oscillatory neural networks for constraint satisfaction and optimization, NCE 5, 044004 (2025).
Ercsey-Ravasz, M. & Toroczkai, Z. Optimization hardness as transient chaos in an analog approach to constraint satisfaction. Nat. Phys. 7, 966–970 (2011).
Acknowledgements
We gratefully acknowledge Prof. Kerem Camsari for providing valuable insights on the sampling properties of p-bits. This material is based upon work supported in part by ARO award W911NF-24-1-0228 and National Science Foundation grants (#2422333, #2433871).
Author information
Authors and Affiliations
Contributions
E. M. Hasantha Ekanayake: Conceptualization (equal); Formal analysis (equal); Software (equal); Writing—original draft (equal); Writing—review and editing (equal). Nikhat Khan: Conceptualization (equal); Validation (equal); Software (equal); Writing—original draft (equal); Writing—review and editing (equal). Nikhil Shukla: Conceptualization (equal); Funding acquisition (lead); Supervision (lead); Validation (equal); Writing—review and editing (equal).
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Corentin Delacour, Jérémie Laydevant, and the other anonymous reviewer(s) for their contribution to the peer review of this work.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ekanayake, E.M.H., Khan, N. & Shukla, N. Configuring oscillator Ising machines as P-bit engines. Commun Phys (2026). https://doi.org/10.1038/s42005-026-02492-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-026-02492-z