Abstract
Anderson localization, arising from wave interference in disordered systems, profoundly hinders energy transport, yet its impact on radiative heat flux in many-body thermophotonic systems remains unclear. Here, we demonstrate a three-order-of-magnitude suppression of radiative heat transfer, resulting in ultralow radiative heat transfer, in a one-dimensional quasiperiodic chain of plasmonic nanoparticles. This suppression in radiative heat transfer is directly correlated with mode localization, as revealed by the mode decomposition of the transmission coefficient, which serves as evidence of Anderson localization. Furthermore, we elucidate the dependence of radiative thermal conductance reduction on interparticle spacing and material damping rates, uncovering the interplay between intrinsic Ohmic losses, mode localization, and long-range many-body interactions. Our findings advance the understanding of wave-mediated thermal transport in disordered photonic structures and suggest strategies for tailoring nanoscale heat management via engineered disorder.

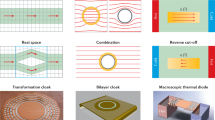
Similar content being viewed by others
Data availability
The data that support the findings of this study are available from the corresponding author upon request.
Code availability
The codes that support the findings in this study are available from the corresponding author upon request.
References
Yu, S., Qiu, C.-W., Chong, Y., Torquato, S. & Park, N. Engineered disorder in photonics. Nat. Rev. Mater. 6, 226 (2021).
Anderson, P. W. Absence of diffusion in certain random lattices. Phys. Rev. 109, 1492 (1958).
De Raedt, H., Lagendijk, A. & de Vries, P. Transverse localization of light. Phys. Rev. Lett. 62, 47 (1989).
Schwartz, T., Bartal, G., Fishman, S. & Segev, M. Transport and anderson localization in disordered two-dimensional photonic lattices. Nature 446, 52 (2007).
Yamilov, A. et al. Anderson localization of electromagnetic waves in three dimensions. Nat. Phys. 19, 1308 (2023).
Condat, C. & Kirkpatrick, T. Resonant scattering and anderson localization of acoustic waves. Phys. Rev. B 36, 6782 (1987).
Arregui, G., Lanzillotti-Kimura, N. D., Sotomayor-Torres, C. M. & García, P. D. Anderson photon-phonon colocalization in certain random superlattices. Phys. Rev. Lett. 122, 043903 (2019).
Hu, Y., Xu, Y., Yan, K., Xiao, W.-H. & Chen, X. Exactly solvable mobility edges for phonons in one-dimensional quasiperiodic chains. Nano Lett. 25, 2219 (2025).
Hu, H., Strybulevych, A., Page, J., Skipetrov, S. E. & van Tiggelen, B. A. Localization of ultrasound in a three-dimensional elastic network. Nat. Phys. 4, 945 (2008).
Amir, A., Krich, J. J., Vitelli, V., Oreg, Y. & Imry, Y. Emergent percolation length and localization in random elastic networks. Phys. Rev. X 3, 021017 (2013).
Abraham, A. J., Malkov, S., Ljubetic, F. A., Durey, M. & Sáenz, P. J. Anderson localization of walking droplets. Phys. Rev. X 14, 031047 (2024).
Lahini, Y. et al. Anderson localization and nonlinearity in one-dimensional disordered photonic lattices. Phys. Rev. Lett. 100, 013906 (2008).
Leonetti, M., Karbasi, S., Mafi, A. & Conti, C. Observation of migrating transverse anderson localizations of light in nonlocal media. Phys. Rev. Lett. 112, 193902 (2014).
Shi, W.-B. et al. Strong localization of surface plasmon polaritons with engineered disorder. Nano Lett. 18, 1896 (2018).
Conley, G. M., Burresi, M., Pratesi, F., Vynck, K. & Wiersma, D. S. Light transport and localization in two-dimensional correlated disorder. Phys. Rev. Lett. 112, 143901 (2014).
Lahini, Y. et al. Observation of a localization transition in quasiperiodic photonic lattices. Phys. Rev. Lett. 103, 013901 (2009).
Levi, L. et al. Disorder-enhanced transport in photonic quasicrystals. Science 332, 1541 (2011).
Jeon, S.-Y., Kwon, H. & Hur, K. Intrinsic photonic wave localization in a three-dimensional icosahedral quasicrystal. Nat. Phys. 13, 363 (2017).
Liu, J. et al. Random nanolasing in the anderson localized regime. Nat. Nanotechnol. 9, 285 (2014).
Hsu, C. W., Goetschy, A., Bromberg, Y., Stone, A. D. & Cao, H. Broadband coherent enhancement of transmission and absorption in disordered media. Phys. Rev. Lett. 115, 223901 (2015).
Yang, Y. et al. Tunable plasmonic system based on disordered palladium nanoparticles and its application to optical hydrogen sensors. ACS Mater. Lett. 7, 804 (2025).
Yang, X. et al. Hot spot engineering in hierarchical plasmonic nanostructures. Small 19, 2205659 (2023).
Howell, J. R., Mengüç, M. P., Daun, K., and Siegel, R. Thermal Radiation Heat Transfer (CRC press, 2020).
Ottens, R. et al. Near-field radiative heat transfer between macroscopic planar surfaces. Phys. Rev. Lett. 107, 014301 (2011).
Song, B. et al. Radiative heat conductances between dielectric and metallic parallel plates with nanoscale gaps. Nat. Nanotechnol. 11, 509 (2016).
Narayanaswamy, A. & Chen, G. Thermal near-field radiative transfer between two spheres. Phys. Rev. B 77, 075125 (2008).
Manjavacas, A. & García de Abajo, F. J. Radiative heat transfer between neighboring particles. Phys. Rev. B 86, 075466 (2012).
Yu, R., Manjavacas, A. & García de Abajo, F. J. Ultrafast radiative heat transfer. Nat. Commun. 8, 2 (2017).
Ramirez, F. V., Shen, S. & McGaughey, A. J. Near-field radiative heat transfer in graphene plasmonic nanodisk dimers. Phys. Rev. B 96, 165427 (2017).
Hu, Y., Li, H., Zhu, Y. & Yang, Y. Enhanced near-field radiative heat transport between graphene metasurfaces with symmetric nanopatterns. Phys. Rev. Appl. 14, 044054 (2020).
Cuevas, J. C. & García-Vidal, F. J. Radiative heat transfer. ACS Photonics 5, 3896 (2018).
Jouhara, H. et al. Waste heat recovery technologies and applications. Therm. Sci. Eng. Prog. 6, 268 (2018).
Zhao, B., Santhanam, P., Chen, K., Buddhiraju, S. & Fan, S. Near-field thermophotonic systems for low-grade waste-heat recovery. Nano Lett. 18, 5224 (2018).
Ahmed, S., Li, Z., Javed, M. S. & Ma, T. A review on the integration of radiative cooling and solar energy harvesting. Mater. Today Energy 21, 100776 (2021).
Fan, D. et al. Near-perfect photon utilization in an air-bridge thermophotovoltaic cell. Nature 586, 237 (2020).
Ben-Abdallah, P. & Biehs, S.-A. Phase-change radiative thermal diode. Appl. Phys. Lett. 103, 191907 (2013).
Fiorino, A. et al. A thermal diode based on nanoscale thermal radiation. ACS Nano 12, 5774 (2018).
Guo, C., Zhao, B., Huang, D. & Fan, S. Radiative thermal router based on tunable magnetic weyl semimetals. ACS Photonics 7, 3257 (2020).
Biehs, S.-A. et al. Near-field radiative heat transfer in many-body systems. Rev. Mod. Phys. 93, 025009 (2021).
Liu, Z. et al. Topological thermal transport. Nat. Rev. Phys. 6, 554 (2024).
Zhu, L., Guo, Y. & Fan, S. Theory of many-body radiative heat transfer without the constraint of reciprocity. Phys. Rev. B 97, 094302 (2018).
Zheng, C. et al. Molding broadband dispersion in twisted trilayer hyperbolic polaritonic surfaces. ACS Nano 16, 13241 (2022).
Ben-Abdallah, P. et al. Heat superdiffusion in plasmonic nanostructure networks. Phys. Rev. Lett. 111, 174301 (2013).
Latella, I., Biehs, S.-A., Messina, R., Rodriguez, A. W. & Ben-Abdallah, P. Ballistic near-field heat transport in dense many-body systems. Phys. Rev. B 97, 035423 (2018).
Tervo, E., Francoeur, M., Cola, B. & Zhang, Z. Thermal radiation in systems of many dipoles. Phys. Rev. B 100, 205422 (2019).
Kathmann, C., Messina, R., Ben-Abdallah, P. & Biehs, S.-A. Limitations of kinetic theory to describe near-field heat exchanges in many-body systems. Phys. Rev. B 98, 115434 (2018).
Hu, Y., Yan, K. & Chen, X. Emergent mobility edges and intermediate phases in one-dimensional quasiperiodic plasmonic chains. Phys. Rev. Res. 6, 013322 (2024).
Freire-Fernández, F., Park, S.-M., Tan, M. J. & Odom, T. W. Plasmonic lattice lasers. Nat. Rev. Mater. 10, 604 (2025).
Kraus, Y. E., Lahini, Y., Ringel, Z., Verbin, M. & Zilberberg, O. Topological states and adiabatic pumping in quasicrystals. Phys. Rev. Lett. 109, 106402 (2012).
Yan, Q. et al. Near-field imaging of synthetic dimensional integrated plasmonic topological harper nanochains. Nat. Commun. 16, 2592 (2025).
Liu, M. et al. Evolution and nonreciprocity of loss-induced topological phase singularity pairs. Phys. Rev. Lett. 127, 266101 (2021).
Palik, E. et al. Coupled surface magnetoplasmon-optic-phonon polariton modes on insb. Phys. Rev. B 13, 2497 (1976).
Moncada-Villa, E. & Cuevas, J. Near-field radiative heat transfer between one-dimensional magnetophotonic crystals. Phys. Rev. B 103, 075432 (2021).
Law, S., Liu, R., and Wasserman, D., Doped semiconductors with band-edge plasma frequencies. J. Vac. Sci. Technol. B 32, 052601 (2014).
Biddle, J. & Das Sarma, S. Predicted mobility edges in one-dimensional incommensurate optical lattices: an exactly solvable model of anderson localization. Phys. Rev. Lett. 104, 070601 (2010).
Zundel, L., Cuartero-González, A., Sanders, S., Fernández-Domínguez, A. I. & Manjavacas, A. Green tensor analysis of lattice resonances in periodic arrays of nanoparticles. ACS Photonics 9, 540 (2022).
Novotny, L. & Hecht, B. Principles of Nano-optics (Cambridge University Press, 2012).
Messina, R., Tschikin, M., Biehs, S.-A. & Ben-Abdallah, P. Fluctuation-electrodynamic theory and dynamics of heat transfer in systems of multiple dipoles. Phys. Rev. Bondensed Matter Mater. Phys. 88, 104307 (2013).
Chen, X., Liu, Y. & Duan, W. Thermal engineering in lowimensional quantum devices: A tutorial review of nonequilibrium green’s function methods. Small Methods 2, 1700343 (2018).
Chen, X., Xu, Y., Wang, J. & Guo, H. Valley filtering effect of phonons in graphene with a grain boundary. Phys. Rev. B 99, 064302 (2019).
Yan, K. et al. Giant tunneling magnetoresistance based on spin-valley-mismatched ferromagnetic metals. Phys. Rev. Lett. 134, 036302 (2025).
Ashida, Y., Gong, Z. & Ueda, M. Non-hermitian physics. Adv. Phys. 69, 249 (2020).
Ott, A., An, Z., Kittel, A. & Biehs, S.-A. Thermal near-field energy density and local density of states in topological one-dimensional su-schrieffer-heeger chains and two-dimensional su-schrieffer-heeger lattices of plasmonic nanoparticles. Phys. Rev. B 104, 165407 (2021).
Yang, S. et al. Non-hermitian thermophotonic funneling via nonreciprocal surface waves. Phys. Rev. Lett. 134, 196901 (2025).
Asheichyk, K. & Krüger, M. Radiative heat transfer with a cylindrical waveguide decays logarithmically slow. Phys. Rev. Lett. 129, 170605 (2022).
Wang, J. & Genack, A. Z. Transport through modes in random media. Nature 471, 345 (2011).
Skipetrov, S. E. & Sokolov, I. M. Absence of anderson localization of light in a random ensemble of point scatterers. Phys. Rev. Lett. 112, 023905 (2014).
Li, X., Li, X. & Das Sarma, S. Mobility edges in one-dimensional bichromatic incommensurate potentials. Phys. Rev. B 96, 085119 (2017).
Acknowledgements
We gratefully acknowledge financial support from the Shenzhen Science and Technology Program (grant nos. RCYX20221008092848063, JCYJ20241202123733043, and JCYJ20241202123506009) and the National Natural Science Foundation of China (grant nos. 12574256 and 12447144).
Author information
Authors and Affiliations
Contributions
Y.H. contributed to conceptualization, methodology, data analysis, visualization, writing, and manuscript revision. K.Y. and W.-H.X. contributed to the discussions of the results. X.C. led the project and contributed to project administration, supervision, writing review and editing, and funding acquisition. All authors reviewed and approved the final manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Physics thanks Ilkka Tittonen, Philippe Ben-Abdallah, and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Hu, Y., Yan, K., Xiao, WH. et al. Ultralow radiative heat flux by Anderson localization in quasiperiodic plasmonic chains. Commun Phys (2026). https://doi.org/10.1038/s42005-026-02506-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s42005-026-02506-w