Skip to main content

Thank you for visiting nature.com. You are using a browser version with limited support for CSS. To obtain the best experience, we recommend you use a more up to date browser (or turn off compatibility mode in Internet Explorer). In the meantime, to ensure continued support, we are displaying the site without styles and JavaScript.

  • Review Article
  • Published:

Artificial gauge fields in photonics

Nature Reviews Physics volume 7, pages 606–620 (2025)Cite this article

Subjects

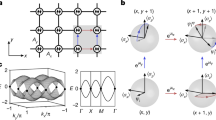
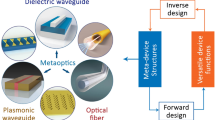
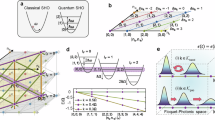
Abstract

Structured photonic systems, from photonic crystals to metamaterials and metasurfaces, provide a broad platform for photonic gauge fields. This artificial version of the real gauge fields in electrodynamics can induce a range of exotic functionalities in many branches of optical physics, enabling the manipulation of light and its interactions with various photonic structures in new and interesting ways. In this Review, we provide a viewpoint on how the concept of artificial gauge fields can connect seemingly unrelated optical effects. Artificial gauge fields in photonics can be either vectorial or scalar, Abelian or non-Abelian, real or complex. They apply not only to conventional real and momentum spaces, but also to spaces spanned by other synthetic dimensions, and are applicable to both semiclassical and quantum systems. In this Review, leveraging the wide applicability of the artificial gauge field, we connect different optical branches, including topological photonics, non-Abelian physics and non-Hermitian photonics. We discuss the current progress and next steps of research on optical gauge fields as well as their potential for future applications.

Key points

  • Artificial gauge fields, stimulated by concepts of topology, singularity, non-Hermiticity and non-Abelian character, have become a unifying framework that permeates and connects diverse branches of photonics.

  • Artificial gauge fields bridge vibrant fields of research in optics and photonics across both classical and quantum systems.

  • Artificial gauge fields provide a versatile platform to explore fundamental physics and develop advanced photonic devices, which may include integrated photonic circuits.

This is a preview of subscription content, access via your institution

Access options

Buy this article

  • Purchase on SpringerLink
  • Instant access to the full article PDF.

USD 39.95

Prices may be subject to local taxes which are calculated during checkout

Fig. 1: Artificial gauge fields in photonics.
Fig. 2: Scalar gauge potentials.
Fig. 3: Vector gauge potentials.
Fig. 4: Non-Abelian gauge fields.
Fig. 5: Complex gauge potentials.
Fig. 6: Artificial gauge fields for photons.

Similar content being viewed by others

References

  1. Yang, C. N. in Selected Papers of Chen Ning Yang II, 78–92 (World Scientific, 2013).

  2. Aidelsburger, M., Nascimbene, S. & Goldman, N. Artificial gauge fields in materials and engineered systems. C. R. Phys. 19, 394–432 (2018).

    ADS  Google Scholar 

  3. Aharonov, Y. & Bohm, D. Significance of electromagnetic potentials in the quantum theory. Phys. Rev. 115, 485–491 (1959).

    ADS  MathSciNet  Google Scholar 

  4. Wu, T. T. & Yang, C. N. Concept of nonintegrable phase factors and global formulation of gauge fields. Phys. Rev. D 12, 3845–3857 (1975).

    ADS  MathSciNet  Google Scholar 

  5. Madison, K. W., Chevy, F., Wohlleben, W. & Dalibard, J. Vortex formation in a stirred Bose–Einstein condensate. Phys. Rev. Lett. 84, 806–809 (2000).

    ADS  Google Scholar 

  6. Lin, Y. J., Compton, R. L., Jiménez-García, K., Porto, J. V. & Spielman, I. B. Synthetic magnetic fields for ultracold neutral atoms. Nature 462, 628–632 (2009).

    ADS  Google Scholar 

  7. Fang, K., Yu, Z. & Fan, S. Realizing effective magnetic field for photons by controlling the phase of dynamic modulation. Nat. Photon. 6, 782–787 (2012).

    ADS  Google Scholar 

  8. Rechtsman, M. C. et al. Photonic floquet topological insulators. Nature 496, 196–200 (2013). Experimental realizations of photonic Floquet topological insulators.

    ADS  Google Scholar 

  9. Fang, K. J. et al. Generalized non-reciprocity in an optomechanical circuit via synthetic magnetism and reservoir engineering. Nat. Phys. 13, 465–471 (2017).

    Google Scholar 

  10. Süsstrunk, R. & Huber, S. D. Observation of phononic helical edge states in a mechanical topological insulator. Science 349, 47–50 (2015).

    ADS  Google Scholar 

  11. Xiao, M., Chen, W.-J., He, W.-Y. & Chan, C. T. Synthetic gauge flux and Weyl points in acoustic systems. Nat. Phys. 11, 920–924 (2015).

    Google Scholar 

  12. Lee, C. H. et al. Topolectrical circuits. Commun. Phys. 1, 39 (2018).

    Google Scholar 

  13. Pendry, J. B., Schurig, D. & Smith, D. R. Controlling electromagnetic fields. Science 312, 1780–1782 (2006). Introducing the concept of transformation optics, providing a blueprint for designing materials that can precisely control the path of electromagnetic fields.

    ADS  MathSciNet  Google Scholar 

  14. Miri, M. A., Heinrich, M., El-Ganainy, R. & Christodoulides, D. N. Supersymmetric optical structures. Phys. Rev. Lett. 110, 233902 (2013).

    ADS  Google Scholar 

  15. Lu, L., Joannopoulos, J. D. & Soljačić, M. Topological photonics. Nat. Photon. 8, 821–829 (2014).

    ADS  Google Scholar 

  16. Ozawa, T. et al. Topological photonics. Rev. Mod. Phys. 91, 015006 (2019). Comprehensive review of recent advances in topological photonics.

    ADS  MathSciNet  Google Scholar 

  17. Zhang, X., Zangeneh-Nejad, F., Chen, Z.-G., Lu, M.-H. & Christensen, J. A second wave of topological phenomena in photonics and acoustics. Nature 618, 687–697 (2023).

    ADS  Google Scholar 

  18. Yang, Y. et al. Non-Abelian physics in light and sound. Science 383, 844 (2024).

    MathSciNet  Google Scholar 

  19. Feng, L., El-Ganainy, R. & Ge, L. Non-Hermitian photonics based on parity–time symmetry. Nat. Photon. 11, 752–762 (2017).

    ADS  Google Scholar 

  20. El-Ganainy, R. et al. Non-Hermitian physics and PT symmetry. Nat. Phys. 14, 11–19 (2018).

    Google Scholar 

  21. Özdemir, S. K., Rotter, S., Nori, F. & Yang, L. Parity–time symmetry and exceptional points in photonics. Nat. Mater. 18, 783–798 (2019).

    ADS  Google Scholar 

  22. Miri, M.-A. & Alù, A. Exceptional points in optics and photonics. Science 363, eaar7709 (2019).

    MathSciNet  Google Scholar 

  23. Yao, S. Y. & Wang, Z. Edge states and topological invariants of non-Hermitian systems. Phys. Rev. Lett. 121, 086803 (2018). Extension of topological band theory to non-Hermitian system.

    ADS  Google Scholar 

  24. Zhang, X., Zhang, T., Lu, M.-H. & Chen, Y.-F. A review on non-Hermitian skin effect. Adv. Phys.: X 7, 2109431 (2022).

    Google Scholar 

  25. Clark, L. W., Schine, N., Baum, C., Jia, N. Y. & Simon, J. Observation of Laughlin states made of light. Nature 582, 41–45 (2020).

    ADS  Google Scholar 

  26. Deng, J. F. et al. Observing the quantum topology of light. Science 378, 966–971 (2022). Experimental observation of quantum topological properties of light.

    ADS  Google Scholar 

  27. Huang, K. Fundamental Forces of Nature: The Story of Gauge Fields (World Scientific, 2007).

  28. Bloch, F. Uber die Quantenmechanik der Elektronen in Kristallgittern. Z. Phys. A 52, 555–600 (1928).

    Google Scholar 

  29. Zener, C. A theory of the electrical breakdown of solid dielectrics. Proc. R. Soc. Lond. A 145, 523–529 (1934).

    ADS  Google Scholar 

  30. Peschel, U., Pertsch, T. & Lederer, F. Optical Bloch oscillations in waveguide arrays. Opt. Lett. 23, 1701–1703 (1998).

    ADS  Google Scholar 

  31. Block, A. et al. Bloch oscillations in plasmonic waveguide arrays. Nat. Commun. 5, 3843 (2014).

    ADS  Google Scholar 

  32. Liu, W., Neshev, D. N., Miroshnichenko, A. E., Shadrivov, I. V. & Kivshar, Y. S. Bouncing plasmonic waves in half-parabolic potentials. Phys. Rev. A 84, 063805 (2011).

    ADS  Google Scholar 

  33. Levy, U. et al. Inhomogenous dielectric metamaterials with space-variant polarizability. Phys. Rev. Lett. 98, 243901 (2007).

    ADS  Google Scholar 

  34. Staliunas, K. & Masoller, C. Subdiffractive light in bi-periodic arrays of modulated fibers. Opt. Express 14, 10669–10677 (2006).

    ADS  Google Scholar 

  35. Pyrialakos, G. G. et al. Bimorphic Floquet topological insulators. Nat. Mater. 21, 634–639 (2022).

    ADS  Google Scholar 

  36. Hwang, M.-S., Kim, H.-R. & Park, H.-G. Topological manipulation for advancing nanophotonics. npj Nanophoton. 1, 32 (2024).

    Google Scholar 

  37. Peterson, C. W. et al. Trapped fractional charges at bulk defects in topological insulators. Nature 589, 376–380 (2021).

    ADS  Google Scholar 

  38. Liu, Y. et al. Bulk-disclination correspondence in topological crystalline insulators. Nature 589, 381–385 (2021).

    ADS  Google Scholar 

  39. Hu, Z. et al. Topological orbital angular momentum extraction and twofold protection of vortex transport. Nat. Photon. 19, 162–169 (2025).

    ADS  Google Scholar 

  40. Yang, Z., Lustig, E., Lumer, Y. & Segev, M. Photonic Floquet topological insulators in a fractal lattice. Light Sci. Appl. 9, 128 (2020).

    ADS  Google Scholar 

  41. Biesenthal, T. et al. Fractal photonic topological insulators. Science 376, 1114–1119 (2022).

    ADS  Google Scholar 

  42. Miri, M. A., Heinrich, M. & Christodoulides, D. N. SUSY-inspired one-dimensional transformation optics. Optica 1, 89–95 (2014).

    ADS  Google Scholar 

  43. Yim, J. et al. Broadband continuous supersymmetric transformation: a new paradigm for transformation optics. eLight 2, 16 (2022).

    Google Scholar 

  44. Hokmabadi, M. P., Nye, N. S., El-Ganainy, R., Christodoulides, D. N. & Khajavikhan, M. Supersymmetric laser arrays. Science 363, 623–626 (2019).

    ADS  Google Scholar 

  45. Heinrich, M. et al. Supersymmetric mode converters. Nat. Commun. 5, 3698 (2014).

    ADS  Google Scholar 

  46. Liu, X. et al. Perfect excitation of topological states by supersymmetric waveguides. Phys. Rev. Lett. 132, 016601 (2024).

    ADS  Google Scholar 

  47. Vonklitzing, K., Dorda, G. & Pepper, M. New method for high-accuracy determination of the fine-structure constant based on quantized hall resistance. Phys. Rev. Lett. 45, 494–497 (1980).

    ADS  Google Scholar 

  48. Onoda, M., Murakami, S. & Nagaosa, N. Hall effect of light. Phys. Rev. Lett. 93, 083901 (2004).

    ADS  Google Scholar 

  49. Haldane, F. D. M. & Raghu, S. Possible realization of directional optical waveguides in photonic crystals with broken time-reversal symmetry. Phys. Rev. Lett. 100, 013904 (2008).

    ADS  Google Scholar 

  50. Wang, Z., Chong, Y. D., Joannopoulos, J. D. & Soljacic, M. Observation of unidirectional backscattering-immune topological electromagnetic states. Nature 461, 772–775 (2009).

    ADS  Google Scholar 

  51. Rechtsman, M. C. et al. Strain induced pseudomagnetic field and photonic Landau levels in dielectric structures. Nat. Photon. 7, 153–158 (2013).

    ADS  Google Scholar 

  52. Yang, Z., Gao, F., Yang, Y. & Zhang, B. Strain-induced gauge field and Landau levels in acoustic structures. Phys. Rev. Lett. 118, 194301 (2017).

    ADS  Google Scholar 

  53. Huang, Z. T. et al. Pattern-tunable synthetic gauge fields in topological photonic graphene. Nanophotonics 11, 1297–1308 (2022).

    Google Scholar 

  54. Hafezi, M., Mittal, S., Fan, J., Migdall, A. & Taylor, J. M. Imaging topological edge states in silicon photonics. Nat. Photon. 7, 1001–1005 (2013).

    ADS  Google Scholar 

  55. Wu, L. H. & Hu, X. Scheme for achieving a topological photonic crystal by using dielectric material. Phys. Rev. Lett. 114, 223901 (2015).

    ADS  Google Scholar 

  56. Dong, J. W., Chen, X. D., Zhu, H. Y., Wang, Y. & Zhang, X. Valley photonic crystals for control of spin and topology. Nat. Mater. 16, 298–302 (2017).

    ADS  Google Scholar 

  57. Gao, F. et al. Topologically protected refraction of robust kink states in valley photonic crystals. Nat. Phys. 14, 140–144 (2018).

    Google Scholar 

  58. Fang, K., Yu, Z. & Fan, S. Photonic Aharonov–Bohm effect based on dynamic modulation. Phys. Rev. Lett. 108, 153901 (2012).

    ADS  Google Scholar 

  59. Luo, H. K. et al. Guiding Trojan light beams via Lagrange points. Nat. Phys. 20, 95–100 (2024).

    Google Scholar 

  60. Celi, A. et al. Synthetic gauge fields in synthetic dimensions. Phys. Rev. Lett. 112, 043001 (2014).

    ADS  Google Scholar 

  61. Yu, D. et al. Comprehensive review on developments of synthetic dimensions. Photon. Insights 4, R06–R06 (2025).

    Google Scholar 

  62. Yuan, L., Shi, Y. & Fan, S. Photonic gauge potential in a system with a synthetic frequency dimension. Opt. Lett. 41, 741 (2016).

    ADS  Google Scholar 

  63. Lustig, E. et al. Photonic topological insulator in synthetic dimensions. Nature 567, 356–360 (2019).

    ADS  Google Scholar 

  64. Wimmer, M., Price, H. M., Carusotto, I. & Peschel, U. Experimental measurement of the Berry curvature from anomalous transport. Nat. Phys. 13, 545–550 (2017).

    Google Scholar 

  65. Luo, X. W. et al. Synthetic lattice enabled all-optical devices based on orbital angular momentum of light. Nat. Commun. 8, 16097 (2017).

    ADS  Google Scholar 

  66. Dutt, A. et al. A single photonic cavity with two independent physical synthetic dimensions. Science 367, 59–64 (2020). Exploration of higher-dimensional physics using synthetic dimensions.

    ADS  Google Scholar 

  67. Citro, R. & Aidelsburger, M. Thouless pumping and topology. Nat. Rev. Phys. 5, 87–101 (2023).

    Google Scholar 

  68. Zilberberg, O. et al. Photonic topological boundary pumping as a probe of 4D quantum Hall physics. Nature 553, 59–62 (2018).

    ADS  Google Scholar 

  69. Wang, Q., Xiao, M., Liu, H., Zhu, S. N. & Chan, C. T. Optical interface states protected by synthetic Weyl points. Phys. Rev. X 7, 031032 (2017).

    Google Scholar 

  70. Song, W. et al. Bound-extended mode transition in type-II synthetic photonic Weyl heterostructures. Phys. Rev. Lett. 132, 143801 (2024).

    ADS  Google Scholar 

  71. Ozawa, T., Price, H. M., Goldman, N., Zilberberg, O. & Carusotto, I. Synthetic dimensions in integrated photonics: from optical isolation to four-dimensional quantum Hall physics. Phys. Rev. A 93, 043827 (2016).

    ADS  Google Scholar 

  72. Ma, S. et al. Linked Weyl surfaces and Weyl arcs in photonic metamaterials. Science 373, 572–576 (2021).

    ADS  Google Scholar 

  73. Yang, Y. et al. Demonstration of negative refraction induced by synthetic gauge fields. Sci. Adv. 7, eabj2062 (2021).

    ADS  Google Scholar 

  74. Lumer, Y. et al. Light guiding by artificial gauge fields. Nat. Photon. 13, 339–345 (2019). Illustrating how artificial gauge fields can be used to control light in photonic structures.

    ADS  Google Scholar 

  75. Pilozzi, L., Leykam, D., Chen, Z. & Conti, C. Topological photonic crystal fibers and ring resonators. Opt. Lett. 45, 1415–1418 (2020).

    ADS  Google Scholar 

  76. Zhu, B. et al. Topological photonic crystal fibre. Preprint at https://arxiv.org/abs/2501.15107 (2025).

  77. Niu, Q. et al. Realization of a Dirac-vortex topological photonic crystal fiber. Preprint at https://arxiv.org/abs/2503.04194 (2025).

  78. Song, W. et al. Subwavelength self-imaging in cascaded waveguide arrays. Adv. Photon. 2, 036001 (2020).

    ADS  Google Scholar 

  79. Pendry, J. B. Negative refraction makes a perfect lens. Phys. Rev. Lett. 85, 3966 (2000).

    ADS  Google Scholar 

  80. Ye, H. et al. Reconfigurable refraction manipulation at synthetic temporal interfaces with scalar and vector gauge potentials. Proc. Natl Acad. Sci. USA 120, e2300860120 (2023).

    MathSciNet  Google Scholar 

  81. Wang, S. L. et al. High-order dynamic localization and tunable temporal cloaking in ac-electric-field driven synthetic lattices. Nat. Commun. 13, 7653 (2022).

    ADS  Google Scholar 

  82. Wang, S. et al. Photonic Floquet Landau–Zener tunneling and temporal beam splitters. Sci. Adv. 9, eadh0415 (2023).

    Google Scholar 

  83. Yang, Y. et al. Synthesis and observation of non-Abelian gauge fields in real space. Science 365, 1021–1025 (2019). Realizing the synthesis and observation of non-Abelian gauge fields in real space.

    ADS  MathSciNet  Google Scholar 

  84. Arnold, V. Lectures and Problems: A Gift to Young Mathematicians (American Math Society (translated from Russian), 2015).

  85. Yang, C. N. & Mills, R. L. Conservation of isotopic spin and isotopic gauge invariance. Phys. Rev. 96, 191–195 (1954).

    ADS  MathSciNet  Google Scholar 

  86. Chen, Y. et al. Non-Abelian gauge field optics. Nat. Commun. 10, 3125 (2019).

    ADS  Google Scholar 

  87. Polimeno, L. et al. Experimental investigation of a non-Abelian gauge field in 2D perovskite photonic platform. Optica 8, 1442–1447 (2021).

    ADS  Google Scholar 

  88. Lovett, S. et al. Observation of Zitterbewegung in photonic microcavities. Light Sci. Appl. 12, 126 (2023).

    ADS  Google Scholar 

  89. Ye, W. et al. Photonic Hall effect and helical Zitterbewegung in a synthetic Weyl system. Light Sci. Appl. 8, 49 (2019).

    ADS  Google Scholar 

  90. Wu, J. et al. Non-Abelian gauge fields in circuit systems. Nat. Electron. 5, 635–642 (2022).

    Google Scholar 

  91. Terças, H., Flayac, H., Solnyshkov, D. D. & Malpuech, G. Non-Abelian gauge fields in photonic cavities and photonic superfluids. Phys. Rev. Lett. 112, 066402 (2014).

    ADS  Google Scholar 

  92. Whittaker, C. E. et al. Optical analogue of Dresselhaus spin–orbit interaction in photonic graphene. Nat. Photon. 15, 193–196 (2021).

    ADS  Google Scholar 

  93. Brosco, V., Pilozzi, L., Fazio, R. & Conti, C. Non-Abelian Thouless pumping in a photonic lattice. Phys. Rev. A 103, 063518 (2021).

    ADS  MathSciNet  Google Scholar 

  94. Yan, Q. et al. Non-Abelian gauge field in optics. Adv. Opt. Photon. 15, 907–976 (2023).

    Google Scholar 

  95. Cheng, D. L., Wang, K. & Fan, S. H. Artificial non-Abelian lattice gauge fields for photons in the synthetic frequency dimension. Phys. Rev. Lett. 130, 083601 (2023).

    ADS  MathSciNet  Google Scholar 

  96. Cheng, D. et al. Non-Abelian lattice gauge fields in photonic synthetic frequency dimensions. Nature 637, 52–56 (2025).

    ADS  Google Scholar 

  97. Wong, B. T. T., Yang, S., Pang, Z. & Yang, Y. Synthetic non-Abelian electric fields and spin–orbit coupling in photonic synthetic dimensions. Phys. Rev. Lett. 134, 163803 (2025).

    ADS  MathSciNet  Google Scholar 

  98. Dong, Z. et al. Temporal multilayer structures in discrete physical systems towards arbitrary-dimensional non-Abelian Aharonov–Bohm interferences. Nat. Commun. 15, 7392 (2024).

    ADS  Google Scholar 

  99. Pang, Z., Abdelghani, O., Soljačić, M. & Yang, Y. Topological quantum walk in synthetic non-Abelian gauge fields. Preprint at https://arxiv.org/abs/2412.03043 (2024).

  100. Pancharatnam, S. The propagation of light in absorbing biaxial crystals. Proc. Indian Acad. Sci. A 42, 86–109 (1955).

    Google Scholar 

  101. Bender, C. M. & Boettcher, S. Real spectra in non-Hermitian Hamiltonians having PT symmetry. Phys. Rev. Lett. 80, 5243 (1998).

    ADS  MathSciNet  Google Scholar 

  102. Li, A. D. et al. Exceptional points and non-Hermitian photonics at the nanoscale. Nat. Nanotechnol. 18, 706–720 (2023).

    ADS  Google Scholar 

  103. Ding, K., Fang, C. & Ma, G. C. Non-Hermitian topology and exceptional-point geometries. Nat. Rev. Phys. 4, 745–760 (2022).

    Google Scholar 

  104. Wang, C. Q. et al. Non-Hermitian optics and photonics: from classical to quantum. Adv. Opt. Photon. 15, 442–523 (2023).

    Google Scholar 

  105. Doppler, J. et al. Dynamically encircling an exceptional point for asymmetric mode switching. Nature 537, 76–79 (2016). Encircling an exceptional point for asymmetric mode switching.

    ADS  Google Scholar 

  106. Nasari, H. et al. Observation of chiral state transfer without encircling an exceptional point. Nature 605, 256–261 (2022).

    ADS  Google Scholar 

  107. Song, W. G. et al. Breakup and recovery of topological zero modes in finite non-Hermitian optical lattices. Phys. Rev. Lett. 123, 165701 (2019).

    ADS  Google Scholar 

  108. Li, A. D. et al. Hamiltonian hopping for efficient chiral mode switching in encircling exceptional points. Phys. Rev. Lett. 125, 187403 (2020).

    ADS  Google Scholar 

  109. Schumer, A. et al. Topological modes in a laser cavity through exceptional state transfer. Science 375, 884–888 (2022).

    ADS  Google Scholar 

  110. Zhen, B. et al. Spawning rings of exceptional points out of Dirac cones. Nature 525, 354–358 (2015).

    ADS  Google Scholar 

  111. Zhou, H. et al. Observation of bulk Fermi arc and polarization half charge from paired exceptional points. Science 359, 1009–1012 (2018).

    ADS  MathSciNet  Google Scholar 

  112. Cerjan, A. et al. Experimental realization of a Weyl exceptional ring. Nat. Photon. 13, 623–628 (2019).

    ADS  Google Scholar 

  113. Song, W. et al. Observation of Weyl interface states in non-Hermitian synthetic photonic systems. Phys. Rev. Lett. 130, 043803 (2023).

    ADS  Google Scholar 

  114. Zhang, X., Ding, K., Zhou, X., Xu, J. & Jin, D. Experimental observation of an exceptional surface in synthetic dimensions with magnon polaritons. Phys. Rev. Lett. 123, 237202 (2019).

    ADS  Google Scholar 

  115. Hatano, N. & Nelson, D. R. Localization transitions in non-Hermitian quantum mechanics. Phys. Rev. Lett. 77, 570–573 (1996).

    ADS  Google Scholar 

  116. Sun, C.-P. High-order adiabatic approximation for non-Hermitian quantum system and complexification of Berry’s phase. Phys. Scr. 48, 393 (1993).

    ADS  Google Scholar 

  117. Longhi, S., Gatti, D. & Valle, G. D. Non-Hermitian transparency and one-way transport in low dimensional lattices by an imaginary gauge field. Phys. Rev. B 92, 094204 (2015).

    ADS  Google Scholar 

  118. Okuma, N., Kawabata, K., Shiozaki, K. & Sato, M. Topological origin of non-Hermitian skin effects. Phys. Rev. Lett. 124, 086801 (2020).

    ADS  MathSciNet  Google Scholar 

  119. Zhang, K., Yang, Z. S. & Fang, C. Correspondence between winding numbers and skin modes in non-Hermitian systems. Phys. Rev. Lett. 125, 126402 (2020).

    ADS  MathSciNet  Google Scholar 

  120. Borgnia, D. S., Kruchkov, A. J. & Slager, R. J. Non-Hermitian boundary modes and topology. Phys. Rev. Lett. 124, 056802 (2020).

    ADS  MathSciNet  Google Scholar 

  121. Weidemann, S. et al. Topological funneling of light. Science 368, 311–314 (2020). Experimental realization of the non-Hermitian skin effect.

    ADS  MathSciNet  Google Scholar 

  122. Xiao, L. et al. Non-Hermitian bulk boundary correspondence in quantum dynamics. Nat. Phys. 16, 761–766 (2020).

    Google Scholar 

  123. Xin, H. R. et al. Manipulating the non-Hermitian skin effect in optical ring resonators. Phys. Rev. B 107, 165401 (2023).

    ADS  Google Scholar 

  124. Longhi, S. Non-Hermitian gauged topological laser arrays. Ann. Phys. 530, 1800023 (2018).

    MathSciNet  Google Scholar 

  125. Teo, W. X., Zhu, W. W. & Gong, J. B. Tunable two-dimensional laser arrays with zero-phase locking. Phys. Rev. B 105, L201402 (2022).

    ADS  Google Scholar 

  126. Liu, Y. G. N. et al. Complex skin modes in non-Hermitian coupled laser arrays. Light Sci. Appl. 11, 336 (2022).

    ADS  Google Scholar 

  127. Gao, Z. H. et al. Two dimensional reconfigurable non-Hermitian gauged laser array. Phys. Rev. Lett. 130, 263801 (2023).

    ADS  Google Scholar 

  128. Yi, Y. F. & Yang, Z. S. Non-Hermitian skin modes induced by on-site dissipations and chiral tunneling effect. Phys. Rev. Lett. 125, 186802 (2020).

    ADS  MathSciNet  Google Scholar 

  129. Lin, Z. K., Ding, L., Ke, S. L. & Li, X. Steering non-Hermitian skin modes by synthetic gauge fields in optical ring resonators. Opt. Lett. 46, 3512–3515 (2021).

    ADS  Google Scholar 

  130. Li, Y., Lu, C., Zhang, S. & Liu, Y.-C. Loss-induced Floquet non-Hermitian skin effect. Phys. Rev. B 108, L220301 (2023).

    ADS  Google Scholar 

  131. Sun, Y. et al. Photonic Floquet skin-topological effect. Phys. Rev. Lett. 132, 063804 (2023).

    ADS  Google Scholar 

  132. Lin, Z. et al. Observation of topological transition in Floquet non-Hermitian skin effects in silicon photonics. Phys. Rev. Lett. 133, 073803 (2024).

    ADS  Google Scholar 

  133. Wang, K., Dutt, A., Wojcik, C. C. & Fan, S. Topological complex energy braiding of non-Hermitian bands. Nature 598, 59–64 (2021).

    ADS  Google Scholar 

  134. Patil, Y. S. S. et al. Measuring the knot of non-Hermitian degeneracies and non-commuting braids. Nature 607, 271–275 (2022).

    ADS  Google Scholar 

  135. Parto, M., Leefmans, C., Williams, J., Nori, F. & Marandi, A. Non-Abelian effects in dissipative photonic topological lattices. Nat. Commun. 14, 1440 (2023).

    ADS  Google Scholar 

  136. Pang, Z., Wong, B. T. T., Hu, J. & Yang, Y. Synthetic non-Abelian gauge fields for non-Hermitian systems. Phys. Rev. Lett. 132, 043804 (2024).

    ADS  MathSciNet  Google Scholar 

  137. Shen, J. T. & Fan, S. H. Strongly correlated two-photon transport in a one-dimensional waveguide coupled to a two-level system. Phys. Rev. Lett. 98, 153003 (2007).

    ADS  Google Scholar 

  138. Wang, C. et al. Realization of fractional quantum Hall state with interacting photons. Science 384, 579–584 (2024). Realizing the optical simulation of fractional quantum Hall physics.

    ADS  MathSciNet  Google Scholar 

  139. Blais, A., Grimsmo, A. L., Girvin, S. M. & Wallraff, A. Circuit quantum electrodynamics. Rev. Mod. Phys. 93, 025005 (2021).

    ADS  MathSciNet  Google Scholar 

  140. Schine, N., Ryou, A., Gromov, A., Sommer, A. & Simon, J. Synthetic landau levels for photons. Nature 534, 671–675 (2016).

    ADS  Google Scholar 

  141. Corman, L. Light turned into exotic Laughlin matter. Nature 582, 37–38 (2020).

    ADS  Google Scholar 

  142. Lim, H. T., Togan, E., Kroner, M., Miguel-Sanchez, J. & Imamoglu, A. Electrically tunable artificial gauge potential for polaritons. Nat. Commun. 8, 14540 (2017).

    ADS  Google Scholar 

  143. Knüppel, P. et al. Nonlinear optics in the fractional quantum Hall regime. Nature 572, 91–94 (2019).

    ADS  Google Scholar 

  144. Ke, Y. G., Poshakinskiy, A. V., Lee, C. H., Kivshar, Y. S. & Poddubny, A. N. Inelastic scattering of photon pairs in qubit arrays with subradiant states. Phys. Rev. Lett. 123, 253601 (2019).

    ADS  Google Scholar 

  145. Ke, Y. G., Huang, J. X., Liu, W. J., Kivshar, Y. S. & Lee, C. H. Topological inverse band theory in waveguide quantum electrodynamics. Phys. Rev. Lett. 131, 103604 (2023).

    ADS  Google Scholar 

  146. Ke, Y. G. et al. Radiative topological biphoton states in modulated qubit arrays. Phys. Rev. Res. 2, 033190 (2020).

    Google Scholar 

  147. Poshakinskiy, A. V. et al. Quantum Hall phases emerging from atom–photon interactions. npj Quantum Inf. 7, 3435 (2021).

    Google Scholar 

  148. Roushan, P. et al. Chiral ground-state currents of interacting photons in a synthetic magnetic field. Nat. Phys. 13, 146–151 (2017).

    Google Scholar 

  149. Walter, A.-S. et al. Quantization and its breakdown in a Hubbard–Thouless pump. Nat. Phys. 19, 1471–1475 (2023).

    Google Scholar 

  150. Ke, Y. & Lee, C. Topological quantum tango. Nat. Phys. 19, 1387–1388 (2023).

    Google Scholar 

  151. Song, W. et al. Dispersionless coupling among optical waveguides by artificial gauge field. Phys. Rev. Lett. 129, 053901 (2022). Introducing artificial gauge fields into photonic chips for broadband optical coupling.

    ADS  Google Scholar 

  152. Feng, X. et al. Non-Hermitian hybrid silicon photonic switching. Nat. Photon. 19, 264–270 (2025).

    ADS  Google Scholar 

  153. Dai, T. et al. A programmable topological photonic chip. Nat. Mater. 23, 928–936 (2024).

    ADS  Google Scholar 

  154. Lin, Z. et al. Ultrabroadband low-crosstalk dense lithium niobate waveguides by Floquet engineering. Phys. Rev. Appl. 20, 054005 (2023).

    ADS  Google Scholar 

  155. Zhao, W. et al. Landau rainbow induced by artificial gauge fields. Phys. Rev. Lett. 133, 233801 (2024).

    ADS  Google Scholar 

  156. Descheemaeker, L., Ginis, V., Viaene, S. & Tassin, P. Optical force enhancement using an imaginary vector potential for photons. Phys. Rev. Lett. 119, 137402 (2017).

    ADS  Google Scholar 

  157. Mittal, S., Goldschmidt, E. A. & Hafezi, M. A topological source of quantum light. Nature 561, 502–506 (2018).

    ADS  Google Scholar 

  158. Blanco-Redondo, A., Bell, B., Oren, D., Eggleton, B. J. & Segev, M. Topological protection of biphoton states. Science 362, 568–571 (2018).

    ADS  MathSciNet  Google Scholar 

  159. Tambasco, J.-L. et al. Quantum interference of topological states of light. Sci. Adv. 4, 3187 (2018).

    ADS  Google Scholar 

  160. Wang, Z. et al. Artificial-gauge-field-based inverse design for wideband-flat power splitter and microring resonator. Adv. Photon. Nexus 4, 016001 (2025).

    Google Scholar 

  161. Pilozzi, L., Farrelly, F. A., Marcucci, G. & Conti, C. Machine learning inverse problem for topological photonics. Commun. Phys. 1, 57 (2018).

    Google Scholar 

  162. Xia, S. et al. Deep-learning-empowered synthetic dimension dynamics: morphing of light into topological modes. Adv. Photon. 6, 026005 (2024).

    ADS  Google Scholar 

Download references

Acknowledgements

The authors thank all their collaborators on the topic of artificial gauge fields and related work. W.S. and T.L. acknowledge funding from the National Key R&D Program of China (2023YFA1407700, 2022YFA1404301) and National Natural Science Foundation of China (nos. 12522421, 12204233, 12174186, 62288101, 92250304 and 62325504). W.L. is supported by Outstanding Young Researcher Scheme of Hunan Province (2024JJ2056). S.Z. acknowledges support from the Quantum Science Center of Guangdong–Hong Kong–Macau Great Bay Area, New Cornerstone Science Foundation and the Hong Kong Research Grant Council (STG3/E-704/23-N, AoE/P-701/20, 17315522).

Author information

Authors and Affiliations

  1. National Laboratory of Solid State Microstructures, Key Laboratory of Intelligent Optical Sensing and Manipulations, Jiangsu Key Laboratory of Artificial Functional Materials, Collaborative innovation center of advanced microstructures, College of Engineering and Applied Sciences, Nanjing University, Nanjing, China

    Wange Song, Zhiyuan Lin, Xuanyu Liu, Shengjie Wu, Chen Chen, Shining Zhu & Tao Li

  2. New Cornerstone Science Laboratory, Department of Physics, University of Hong Kong, Hong Kong, China

    Wange Song, Yi Yang & Shuang Zhang

  3. HK Institute of Quantum Science and Technology, University of Hong Kong, Hong Kong, China

    Yi Yang

  4. Institute of Quantum Precision Measurement, State Key Laboratory of Radio Frequency Heterogeneous Integration, College of Physics and Optoelectronic Engineering, Shenzhen University, Shenzhen, China

    Yongguan Ke & Chaohong Lee

  5. Laboratory of Quantum Engineering and Quantum Metrology, School of Physics and Astronomy, Sun Yat-Sen University (Zhuhai Campus), Zhuhai, China

    Yongguan Ke

  6. Quantum Science Center of Guangdong–Hong Kong–Macao Greater Bay Area, Shenzhen, China

    Chaohong Lee & Shuang Zhang

  7. Nanhu Laser Laboratory and Hunan Provincial Key Laboratory of Novel Nano-Optoelectronic Information Materials and Devices, College for Advanced Interdisciplinary Studies, National University of Defense Technology, Changsha, P. R. China

    Wei Liu

  8. Nonlinear Physics Center, Research School of Physics, Australian National University, Canberra, Australian Capital Territory, Australia

    Yuri Kivshar

  9. Department of Electronic and Electrical Engineering, University of Hong Kong, Hong Kong, China

    Shuang Zhang

  10. Materials Innovation Institute for Life Sciences and Energy (MILES), HKU-SIRI, Shenzhen, China

    Shuang Zhang

  11. State Key Laboratory of Optical Quantum Materials, The University of Hong Kong, Hong Kong, China

    Shuang Zhang

Authors
  1. Wange Song
    View author publications

    Search author on:PubMed Google Scholar

  2. Yi Yang
    View author publications

    Search author on:PubMed Google Scholar

  3. Zhiyuan Lin
    View author publications

    Search author on:PubMed Google Scholar

  4. Xuanyu Liu
    View author publications

    Search author on:PubMed Google Scholar

  5. Shengjie Wu
    View author publications

    Search author on:PubMed Google Scholar

  6. Chen Chen
    View author publications

    Search author on:PubMed Google Scholar

  7. Yongguan Ke
    View author publications

    Search author on:PubMed Google Scholar

  8. Chaohong Lee
    View author publications

    Search author on:PubMed Google Scholar

  9. Wei Liu
    View author publications

    Search author on:PubMed Google Scholar

  10. Shining Zhu
    View author publications

    Search author on:PubMed Google Scholar

  11. Yuri Kivshar
    View author publications

    Search author on:PubMed Google Scholar

  12. Tao Li
    View author publications

    Search author on:PubMed Google Scholar

  13. Shuang Zhang
    View author publications

    Search author on:PubMed Google Scholar

Contributions

All authors researched data for the article. All authors contributed substantially to discussion of the content. All authors wrote the article. W.S., W.L., Y.K., T.L. and S.Zhang reviewed and/or edited the manuscript before submission.

Corresponding authors

Correspondence to Wange Song, Wei Liu, Yuri Kivshar, Tao Li or Shuang Zhang.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Reviews Physics thanks the anonymous reviewers for their contribution to the peer review of this work.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Rights and permissions

Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.

Reprints and permissions

About this article

Check for updates. Verify currency and authenticity via CrossMark

Cite this article

Song, W., Yang, Y., Lin, Z. et al. Artificial gauge fields in photonics. Nat Rev Phys 7, 606–620 (2025). https://doi.org/10.1038/s42254-025-00869-7

Download citation

  • Accepted:

  • Published:

  • Version of record:

  • Issue date:

  • DOI: https://doi.org/10.1038/s42254-025-00869-7

This article is cited by

Search

Advanced search

Quick links

Nature Briefing

Sign up for the Nature Briefing newsletter — what matters in science, free to your inbox daily.

Get the most important science stories of the day, free in your inbox. Sign up for Nature Briefing