Abstract
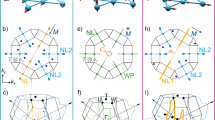
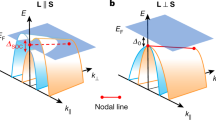
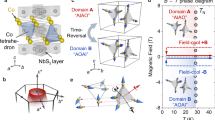
Magnetic nodal line semimetals, defined by twofold degenerate gapless crossings along extended momentum paths, offer significant potential for spintronics and future information technologies. Despite their potential, these systems are rare in nature, with only few examples known to date. Here, using spin- and angle-resolved photoemission spectroscopy and density functional theory-based calculations, we classify ferromagnetic hexagonal close-packed (hcp) cobalt as a prototypical system exhibiting these properties. We demonstrate that manifolds of magnetic gapless nodal rings enclosing the Γ and K points in the kz = 0 plane, and magnetic nodal lines spanning the entire A-L path in the \({k}_{z}=\frac{\pi }{c}\) plane, coexist and dominate the fermiology of this elemental system. These mirror-protected bulk crossing points are associated with surface states, both of which exhibit controllable spin textures. This work is the first identification of cobalt as a simple, yet highly tunable and rich topological platform for exploring and manipulating spin-polarised Weyl-like nodal lines at room temperature.
Similar content being viewed by others
Data availability
Data are available from the authors upon reasonable request.
References
Sánchez-Barriga, J., Clark, O. J. & Rader, O.Angle-resolved photoemission of topological materials, vol. 4, 334–369 (Elsevier, Netherlands, 2024), 2nd edn. https://www.sciencedirect.com/science/article/pii/B9780323908009002742.
Kim, K. et al. Large anomalous hall current induced by topological nodal lines in a ferromagnetic van der waals semimetal. Nat. Mater. 17, 794–799 (2018).
Burkov, A. A. Anomalous hall effect in weyl metals. Phys. Rev. Lett. 113, 187202 (2014).
Chang, G. et al. Room-temperature magnetic topological weyl fermion and nodal line semimetal states in half-metallic heusler co2tix (x=si, ge, or sn). Sci. Rep. 6, 38839 (2016).
Kim, Y., Wieder, B. J., Kane, C. L. & Rappe, A. M. Dirac line nodes in inversion-symmetric crystals. Phys. Rev. Lett. 115, 036806 (2015).
Fang, C., Chen, Y., Kee, H.-Y. & Fu, L. Topological nodal line semimetals with and without spin-orbital coupling. Phys. Rev. B 92, 081201 (2015).
Bzdušek, T., Wu, Q., Rüegg, A., Sigrist, M. & Soluyanov, A. A. Nodal-chain metals. Nature 538, 75–78 (2016).
Bi, R., Yan, Z., Lu, L. & Wang, Z. Nodal-knot semimetals. Phys. Rev. B 96, 201305 (2017).
Fu, B. B. et al. Dirac nodal surfaces and nodal lines in zrsis. Sci. Adv. 5, eaau6459 (2019).
Chang, T.-R. et al. Realization of a type-ii nodal-line semimetal in mg3bi2. Adv. Sci. 6, 1800897 (2019).
Bian, G. et al. Topological nodal-line fermions in spin-orbit metal pbtase2. Nat. Commun. 7, 10556 (2016).
Yu, R., Weng, H., Fang, Z., Dai, X. & Hu, X. Topological node-line semimetal and dirac semimetal state in antiperovskite \({{{\rm{cu}}}}_{3}{{\rm{PdN}}}\). Phys. Rev. Lett. 115, 036807 (2015).
Xie, L. S. et al. A new form of ca3p2 with a ring of dirac nodes. APL Mater. 3, 083602 (2015).
Xu, Q., Yu, R., Fang, Z., Dai, X. & Weng, H. Topological nodal line semimetals in the cap3 family of materials. Phys. Rev. B 95, 045136 (2017).
Wu, H. et al. Nonsymmorphic symmetry-protected band crossings in a square-net metal ptpb4. npj Quantum Mater. 7, 31 (2022).
Yang, S.-Y. et al. Symmetry demanded topological nodal-line materials. Adv. Phys.: X 3, 1414631 (2018).
Ekahana, S. A. et al. Observation of nodal line in non-symmorphic topological semimetal inbi. N. J. Phys. 19, 065007 (2017).
Wu, Y. et al. Dirac node arcs in ptsn4. Nat. Phys. 12, 667–671 (2016).
Li, S. et al. Nonsymmorphic-symmetry-protected hourglass dirac loop, nodal line, and dirac point in bulk and monolayer X3site6 (x = ta, nb). Phys. Rev. B 97, 045131 (2018).
Schoop, L. M. et al. Dirac cone protected by non-symmorphic symmetry and three-dimensional dirac line node in zrsis. Nat. Commun. 7, 11696 (2016).
Neupane, M. et al. Observation of topological nodal fermion semimetal phase in zrsis. Phys. Rev. B 93, 201104 (2016).
Chen, C. et al. Dirac line nodes and effect of spin-orbit coupling in the nonsymmorphic critical semimetals mSiS(m = Hf, Zr). Phys. Rev. B 95, 125126 (2017).
Topp, A. et al. Surface floating 2d bands in layered nonsymmorphic semimetals: Zrsis and related compounds. Phys. Rev. X 7, 041073 (2017).
Hosen, M. M. et al. Tunability of the topological nodal-line semimetal phase in ZrSix-type materials (x = S, Se, Te). Phys. Rev. B 95, 161101 (2017).
Wang, X. et al. Quantum electronics: Evidence of both surface and bulk dirac bands and anisotropic nonsaturating magnetoresistance in zrsis (adv. electron. mater. 10/2016). Adv. Electron. Mater. 2, 10 (2016).
Yen, Y. et al. Dirac nodal line and rashba spin-split surface states in nonsymmorphic zrgete. N. J. Phys. 23, 103019 (2021).
Cheng, Z. et al. Visualizing dirac nodal-line band structure of topological semimetal zrgese by arpes. APL Mater. 7, 051105 (2019).
Wang, Y. et al. Spectroscopic evidence for the realization of a genuine topological nodal-line semimetal in lasbte. Phys. Rev. B 103, 125131 (2021).
Lou, R. et al. Emergence of topological bands on the surface of zrsnte crystal. Phys. Rev. B 93, 241104 (2016).
Hirschmann, M. M., Leonhardt, A., Kilic, B., Fabini, D. H. & Schnyder, A. P. Symmetry-enforced band crossings in tetragonal materials: Dirac and weyl degeneracies on points, lines, and planes. Phys. Rev. Mater. 5, 054202 (2021).
Xie, Y.-M. et al. Kramers nodal line metals. Nat. Commun. 12, 3064 (2021).
Zhang, Y. et al. Kramers nodal lines and weyl fermions in smalsi. Commun. Phys. 6, 134 (2023).
Seo, J. et al. Colossal angular magnetoresistance in ferrimagnetic nodal-line semiconductors. Nature 599, 576–581 (2021).
Li, Y. Magnetic quadratic nodal lines in half-metallic anode material tif3: A first-principles study. Phys. B: Condens. Matter 686, 416083 (2024).
Yang, X. P. et al. A topological hund nodal line antiferromagnet. Nat. Commun. 15, 7052 (2024).
Jeon, S., Oh, Y.-T. & Kim, Y. Ferromagnetic nodal-line metal in monolayer h-inc. Phys. Rev. B 100, 035406 (2019).
Jin, L. et al. Ferromagnetic two-dimensional metal-chlorides mcl (m = sc, y, and la): Candidates for weyl nodal line semimetals with small spin-orbit coupling gaps. Appl. Surf. Sci. 520, 146376 (2020).
Schröter, N. B. M. et al. Weyl fermions, fermi arcs, and minority-spin carriers in ferromagnetic cos2. Sci. Adv. 6, eabd5000 (2020).
Robredo, I. et al. Theoretical study of topological properties of ferromagnetic pyrite cos2. J. Phys. D: Appl. Phys. 55, 304004 (2022).
Belopolski, I. et al. Discovery of topological weyl fermion lines and drumhead surface states in a room temperature magnet. Science 365, 1278–1281 (2019).
Sánchez-Barriga, J. et al. Strength of correlation effects in the electronic structure of iron. Phys. Rev. Lett. 103, 267203 (2009).
Sánchez-Barriga, J. et al. Quantitative determination of spin-dependent quasiparticle lifetimes and electronic correlations in hcp cobalt. Phys. Rev. B 82, 104414 (2010).
Sánchez-Barriga, J. et al. Effects of spin-dependent quasiparticle renormalization in fe, co, and ni photoemission spectra:an experimental and theoretical study. Phys. Rev. B 85, 205109 (2012).
Sánchez-Barriga, J., Ovsyannikov, R. & Fink, J. Strong spin dependence of correlation effects in ni due to stoner excitations. Phys. Rev. Lett. 121, 267201 (2018).
Campbell, B. J., Stokes, H. T., Perez-Mato, J. M. & Rodríguez-Carvajal, J. Introducing a unified magnetic space-group symbol. Acta Crystallogr. Sect. A 78, 99–106 (2022).
Zhang, L. & Wang, K. Pure zirconium: Type ii nodal line and nodal surface states. Front. Chem. 8, 585753 (2020).
Chan, Y.-H., Chiu, C.-K., Chou, M. Y. & Schnyder, A. P. Topological semi-metals with line nodes and drumhead surface states. Phys. Rev. B 93, 205132 (2016).
Fritzsche, H., Kohlhepp, J. & Gradmann, U. Epitaxial strain and magnetic anisotropy in ultrathin co films on w(110). Phys. Rev. B 51, 15933–15941 (1995).
Kleibert, A., Senz, V., Bansmann, J. & Oppeneer, P. M. Thickness dependence and magnetocrystalline anisotropy of the x-ray transverse magneto-optical kerr effect at the Co2p edges of ultrathin co films on w(110). Phys. Rev. B 72, 144404 (2005).
Mulazzi, M. et al. Fermi surface of co(0001) and initial-state linewidths determined by soft x-ray angle-resolved photoemission spectroscopy. Phys. Rev. B 80, 241106 (2009).
Damascelli, A. Probing the Electronic Structure of Complex Systems by ARPES. Phys. Scr. 2004, T109 61 (2004).
Hosen, M. M. et al. Experimental observation of drumhead surface states in sras3. Sci. Rep. 10, 2776 (2020).
Muechler, L. et al. Modular arithmetic with nodal lines: Drumhead surface states in zrsite. Phys. Rev. X 10, 011026 (2020).
Monastra, S. et al. Quenching of majority-channel quasiparticle excitations in cobalt. Phys. Rev. Lett. 88, 236402 (2002).
Zhang, J. et al. Topological band crossings in hexagonal materials. Phys. Rev. Mater. 2, 074201 (2018).
Feng, B. et al. Experimental realization of two-dimensional dirac nodal line fermions in monolayer cu2si. Nat. Commun. 8, 1007 (2017).
Yang, T., Jin, L., Liu, Y., Zhang, X. & Wang, X. Spin-polarized type-ii nodal loop and nodal surface states in hexagonal compounds xtio2 (x = li, na, k, rb). Phys. Rev. B 103, 235140 (2021).
Xu, H., Xi, H. & Gao, Y.-C. Hexagonal zr3x (x = al, ga, in) metals: High dynamic stability, nodal loop, and perfect nodal surface states. Front. Chem. 8, 608398 (2020).
Lin, P., Fang, F., Zhang, L., Li, Y. & Wang, K. Various nodal lines in p63/mmc-type tite topological metal and its (001) surface state. Front. Chem. 9, 755350 (2021).
Zhang, X., Jin, L., Dai, X. & Liu, G. Highly anisotropic type-ii nodal line state in pure titanium metal. Appl. Phys. Lett. 112, 122403 (2018).
Pradhan, S. et al. Topological nodal line features in nise semimetal: Insights from electronic transport and density functional theory studies. Phys. Rev. B 110, 195153 (2024).
Gosálbez-Martínez, D., Souza, I. & Vanderbilt, D. Chiral degeneracies and fermi-surface chern numbers in bcc fe. Phys. Rev. B 92, 085138 (2015).
Gosálbez-Martínez, D., Autès, G. & Yazyev, O. V. Topological fermi-arc surface resonances in bcc iron. Phys. Rev. B 102, 035419 (2020).
Grechnev, A. et al. Theory of bulk and surface quasiparticle spectra for fe, co, and ni. Phys. Rev. B 76, 035107 (2007).
Eastman, D. E., Himpsel, F. J. & Knapp, J. A. Experimental exchange-split energy-band dispersions for fe, co, and ni. Phys. Rev. Lett. 44, 95–98 (1980).
Nayak, A. K. et al. Resolving the topological classification of bismuth with topological defects. Sci. Adv. 5, eaax6996 (2019).
Schindler, F. et al. Higher-order topology in bismuth. Nat. Phys. 14, 918–924 (2018).
Hsieh, D. et al. Observation of unconventional quantum spin textures in topological insulators. Science 323, 919–922 (2009).
Clark, O. J. et al. Observation of a giant mass enhancement in the ultrafast electron dynamics of a topological semimetal. Commun. Phys. 4, 165 (2021).
Hossain, M. S. et al. A hybrid topological quantum state in an elemental solid. Nature 628, 527–533 (2024).
Yan, B. et al. Topological states on the gold surface. Nat. Commun. 6, 10167 (2015).
Agapito, L. A., Kioussis, N., Goddard, W. A. & Ong, N. P. Novel family of chiral-based topological insulators: Elemental tellurium under strain. Phys. Rev. Lett. 110, 176401 (2013).
Bradlyn, B. et al. Topological quantum chemistry. Nature 547, 298–305 (2017).
Vergniory, M. G. et al. A complete catalogue of high-quality topological materials. Nature 566, 480–485 (2019).
Vergniory, M. G. et al. All topological bands of all nonmagnetic stoichiometric materials. Science 376, eabg9094 (2022).
Sánchez-Barriga, J. et al. Photoemission of Bi2Se3 with Circularly Polarized Light: Probe of Spin Polarization or Means for Spin Manipulation? Phys. Rev. X 4, 011046 (2014).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Hafner, J. Ab initio molecular dynamics for liquid metals. Phys. Rev. B 47, 558–561 (1993).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized Gradient Approximation Made Simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Dudarev, S. L., Botton, G. A., Savrasov, S. Y., Humphreys, C. J. & Sutton, A. P. Electron-energy-loss spectra and the structural stability of nickel oxide: An lsda+u study. Phys. Rev. B 57, 1505–1509 (1998).
Moon, R. M. Distribution of magnetic moment in hexagonal cobalt. Phys. Rev. 136, A195–A202 (1964).
Černý, M., Pokluda, J., Šob, M., Friák, M. & Šandera, P. Ab initio calculations of elastic and magnetic properties of fe, co, ni, and cr crystals under isotropic deformation. Phys. Rev. B 67, 035116 (2003).
Iraola, M. et al. IrRep: Symmetry eigenvalues and irreducible representations of ab initio band structures. Comput. Phys. Commun. 272, 108226 (2022).
Mostofi, A. A. et al. An updated version of wannier90: A tool for obtaining maximally-localised wannier functions. Comput. Phys. Commun. 185, 2309–2310 (2014).
Wu, Q., Zhang, S., Song, H.-F., Troyer, M. & Soluyanov, A. A. WannierTools: An open-source software package for novel topological materials. Comput. Phys. Commun. 224, 405–416 (2018).
Acknowledgements
J.S.-B. Acknowledges financial support from the Impuls- und Vernetzungsfonds der Helmholtz-Gemeinschaft under grant No. HRSF-0067. M.G.V. and M.G.-D. Thank support to PID2022-142008NB-I00 project funded by MICIU/AEI/10.13039/501100011033 and FEDER, UE, Canada Excellence Research Chairs Program for Topological Quantum Matter, NSERC Quantum Alliance France-Canada and to Diputación Foral de Gipuzkoa Programa Mujeres y Ciencia. This work was supported by the Deutsche Forschungsge-meinschaft (DFG) through QUAST-FOR5249 and the Würzburg-Dresden Cluster of Excellence on Complexity and Topology in Quantum Matter, ct.qmat (EXC 2147, Project ID 390858490). IMDEA team acknowledges support from the Spanish AEI PID2024-157112OB-C53 (HYBRID-OS: HYPERFAN) and from the Comunidad de Madrid through projects TEC-2024/TEC-380 (Mag4TIC-CM).
Funding
Open Access funding enabled and organized by Projekt DEAL.
Author information
Authors and Affiliations
Contributions
O.J.C., J.F. and J.S.-B. grew the Co films and performed the photoemission experiments. M.G.-D. and M.G.V. performed the theoretical calculations. O.J.C. and J.S.-B. analysed the data. O.J.C. and J.S.-B. wrote the manuscript with significant contribution from M. G.-D, and further input from J.F., O.R., R.M. and M.G.V. O.J.C. and J.S.B. conceived the project and were responsible for overall project planning and direction.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Materials thanks Qi Jiang and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Clark, O.J., Garcia-Diez, M., Fink, J. et al. Manifold of magnetic nodal lines in an elemental ferromagnet. Commun Mater (2026). https://doi.org/10.1038/s43246-026-01072-6
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43246-026-01072-6