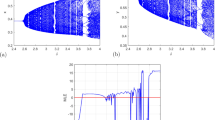
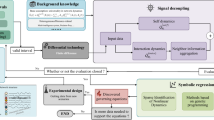
Abstract
Ecological systems often exhibit complex nonlinear dynamics like oscillations, chaos, and regime shifts. Universal dynamic equations have shown promise in modeling complex dynamics by combining known functional forms with neural networks that represent unknown relationships. However, these methods do not yet accommodate the forms of uncertainty common to ecological datasets. To address this limitation, we developed state-space universal dynamic equations by combining universal difference and differential equations with a state-space modeling framework, accounting for uncertainty. We tested this framework on three simulated and two empirical case studies and found that this method can recover nonlinear biological interactions that produce complex behaviors including chaos and regime shifts. Their forecasting performance is context-dependent, with the best performance on chaotic and oscillating time series. This innovative approach leveraging both ecological theory and data-driven machine learning offers a promising new way to make accurate and useful predictions of ecosystem change.
Similar content being viewed by others
Data availability
The data used in this paper were obtained from two publicly accessible data repositories: The Jornada Experimental Range LTER (https://doi.org/10.6073/pasta/63bfa45df4858db674bf37b52ee5ff44) and the RAM Legacy Stock Assessment Database https://doi.org/10.17616/R34D2X.
Code availability
Software to implement the State-space universal dynamic equation method presented in this papers has been published by the authors on the Julia programming language registry (https://github.com/JuliaRegistries/General) and on GitHub (https://github.com/Jack-H-Buckner/UniversalDiffEq.jl).
References
Suding, K. N. & Hobbs, R. J. Threshold models in restoration and conservation: a developing framework. Trends Ecol. Evol. 24, 271–279 (2009).
Perretti, C. T., Sugihara, G. & Munch, S. B. Nonparametric forecasting outperforms parametric methods for a simulated multispecies system. Ecology 94, 794–800 (2013).
Arroyo-Esquivel, J., Klausmeier, C. A. & Litchman, E. Using neural ordinary differential equations to predict complex ecological dynamics from population density data. J. R. Soc. Interface 21, 20230604 (2024).
Bonnaffé, W., Sheldon, B. C. & Coulson, T. Neural ordinary differential equations for ecological and evolutionary time-series analysis. Methods Ecol. Evol. 12, 1301–1315 (2021).
Rackauckas, C. et al. Universal differential equations for scientific machine learning. Preprint at. http://arxiv.org/abs/2001.04385 (2021).
Cheridito, P., Jentzen, A. & Rossmannek, F. Efficient approximation of high-dimensional functions with neural networks. IEEE Trans. Neural Netw. Learn. Syst. 33, 3079–3093 (2022).
Bonnaffé, W. & Coulson, T. Fast fitting of neural ordinary differential equations by Bayesian neural gradient matching to infer ecological interactions from time-series data. Methods Ecol. Evol. 14, 1543–1563 (2023).
Vaswani, A. et al. Attention is all you need. Preprint at. http://arxiv.org/abs/1706.03762 (2023).
Hochreiter, S. & Schmidhuber, J. Long short-term memory. Neural Comput. 9, 1735–1780 (1997).
Turan, E. M. & Jäschke, J. Multiple shooting for training neural differential equations on time series. IEEE Control Syst. Lett. 6, 1897–1902 (2022).
Auger-Méthé, M. et al. A guide to state–space modeling of ecological time series. Ecol. Monogr. 91, e01470 (2021).
Hastings, A. & Powell, T. Chaos in a three-species food chain. Ecology 72, 896–903 (1991).
RAM Legacy Stock Assessment Database. RAM Legacy Stock Assessment Database v4 Zenodo https://doi.org/10.5281/ZENODO.2542919 (2018).
Christensen, E. et al. Quadrat-based monitoring of desert grassland vegetation at the Jornada Experimental Range, New Mexico, 1915–2016. Ecology 102, e03530 (2021).
Medeiros, L. P., Sorenson, D. K., Johnson, B. J., Palkovacs, E. P. & Munch, S. B. Revealing unseen dynamical regimes of ecosystems from population time-series data. Proc. Natl. Acad. Sci. USA. 122, e2416637122 (2025).
Munch, S. B., Rogers, T. L. & Sugihara, G. Recent developments in empirical dynamic modelling. Methods Ecol. Evol. 14, 732–745 (2023).
Munch, S. & Rogers, T. GPEDM: Gaussian process regression for empirical dynamic modeling. https://tanyalrogers.github.io/GPEDM/reference/GPEDM-package.html (2024).
Holmes, E., E., Ward, E., J. & Wills, K. MARSS: multivariate autoregressive state-space models for analyzing time-series data. R J. 4, 11 (2012).
Ellner, S. P., Seifu, Y. & Smith, R. H. Fitting population dynamics models to time-series data by gradient matching. Ecology 83, 2256–2270 (2002).
Rosenzweig, M. L. & MacArthur, R. H. Graphical representation and stability conditions of predator-prey interactions. Am. Nat. 97, 209–223 (1963).
Wan, E. A. & Van Der Merwe, R. The unscented Kalman filter for nonlinear estimation. in Proc. IEEE 2000 Adaptive Systems for Signal Processing, Communications, and Control Symposium (Cat. No.00EX373) 153–158. https://doi.org/10.1109/ASSPCC.2000.882463 (IEEE, 2000).
Estes, J. A. & Duggins, D. O. Sea otters and kelp forests in Alaska: generality and variation in a community ecological paradigm. Ecol. Monogr. 65, 75–100 (1995).
Konar, B. & Estes, J. A. The stability of boundary regions between kelp beds and deforested areas. Ecology 84, 174–185 (2003).
Rogers-Bennett, L. & Catton, C. A. Marine heat wave and multiple stressors tip bull kelp forest to sea urchin barrens. Sci. Rep. 9, 15050 (2019).
Harrold, C. & Reed, D. C. Food availability, sea urchin grazing, and kelp forest community structure. Ecology 66, 1160–1169 (1985).
Wilen, J. E. Common property resources and the dynamics of overexploitation: the case of the North Pacific Fur Seal. Mar. Resour. Econ. 33, 217–243 (2018).
Smith, V. L. On models of commercial fishing. J. Polit. Econ. 77, 181–198 (1969).
Free, C. M. et al. Harvest control rules used in US federal fisheries management and implications for climate resilience. Fish Fish. https://doi.org/10.1111/faf.12724 (2022).
Walters, C. J. & Hilborn, R. Adaptive control of fishing systems. J. Fish. Res. Board Can. 33, 145–159 (1976).
Pacific Fisheries Management Council. Pacific Coast Goundfish Fishery Management Plan, 159 (NOAA Fisheries, Pacific Fisheries Management Council, 2019).
Dick, E. J. & He, X. Status of Cowcod (Sebastes Levis) in 2019 (NOAA Fisheries, 2019).
Field, J. C., Beyer, S. G. & He, X. Status of the Chilipepper Rockfish, Sebastes Goodei, in the California Current for 2015 (NOAA Fisheries, 2015).
Briske, D. D., Fuhlendorf, S. D. & Smeins, F. E. State-and-transition models, thresholds, and rangeland health: a synthesis of ecological concepts and perspectives. Rangel. Ecol. Manag. 58, 1–10 (2005).
Briske, D. D., Fuhlendorf, S. D. & Smeins, F. E. Vegetation dynamics on rangelands: a critique of the current paradigms. J. Appl. Ecol. 40, 601–614 (2003).
Schlesinger, W. H. et al. Biological feedbacks in global desertification. Science 247, 1043–1048 (1990).
D’Odorico, P. et al. Vegetation–microclimate feedbacks in woodland–grassland ecotones. Glob. Ecol. Biogeogr. 22, 364–379 (2013).
Christensen, E. M., James, D. K., Randall, R. M. & Bestelmeyer, B. T. Abrupt transitions in a southwest USA desert grassland related to the Pacific Decadal Oscillation. Ecology 104, e4065 (2023).
Treven, L., Wenk, P., Dörfler, F. & Krause, A. Distributional gradient matching for learning uncertain neural dynamics models. Preprint at. https://doi.org/10.48550/arXiv.2106.11609 (2021).
Boettiger, C., Ross, N. & Hastings, A. Early warning signals: the charted and uncharted territories. Theor. Ecol. 6, 255–264 (2013).
Scheffer, M. et al. Early-warning signals for critical transitions. Nature 461, 53–59 (2009).
Tilman, A. R., Krueger, E. H., McManus, L. C. & Watson, J. R. Maintaining human wellbeing as socio-environmental systems undergo regime shifts. Ecol. Econ. 221, 108194 (2024).
Dandekar, R. et al. Bayesian neural ordinary differential equations. Preprint at. http://arxiv.org/abs/2012.07244 (2022).
Doucet, A., Godsill, S. & Andrieu, C. On sequential Monte Carlo sampling methods for Bayesian filtering. in Readings In Unobserved Components Models (eds Harvey, A. C. & Proietti, T.) 418–441.https://doi.org/10.1093/oso/9780199278657.003.0022 (Oxford University PressOxford, 2005).
Langendorf, R. E. et al. Dynamic and context-dependent keystone species effects in kelp forests. Proc. Natl. Acad. Sci. USA. 122, e2413360122 (2025).
Meunier, Z. D., Hacker, S. D. & Menge, B. A. Regime shifts in rocky intertidal communities associated with a marine heatwave and disease outbreak. Nat. Ecol. Evol. 8, 1285–1297 (2024).
Watson, J. R., Kendall, B. E., Siegel, D. A. & Mitarai, S. Changing seascapes, stochastic connectivity, and marine metapopulation dynamics. Am. Nat. 180, 99–112 (2012).
Kingma, D. P. & Ba, J. Adam: a method for stochastic optimization. Preprint at. http://arxiv.org/abs/1412.6980 (2014).
Dixit, V. K. & Rackauckas, C. Optimization.jl: A Unified Optimization Package. https://doi.org/10.5281/ZENODO.7738525 (2023).
Bezanson, J., Edelman, A., Karpinski, S. & Shah, V. B. Julia: a fresh approach to numerical computing. SIAM Rev. 59, 65–98 (2017).
Innes, M. Don’t unroll adjoint: differentiating SSA-form programs. Preprint at. http://arxiv.org/abs/1810.07951 (2019).
Tsitouras, C. Runge–Kutta pairs of order 5(4) satisfying only the first column simplifying assumption. Comput. Math. Appl. 62, 770–775 (2011).
Rackauckas, C. & Nie, Q. DifferentialEquations.jl – a performant and feature-rich ecosystem for solving differential equations in Julia. JORS 5, 15 (2017).
Bhagavan, S., De Koning, B., Maddhashiya, S. & Rackauckas, C. DataInterpolations.jl: fast interpolations of 1Ddata. JOSS 9, 6917 (2024).
Stickel, J. J. Data smoothing and numerical differentiation by a regularization method. Comput. Chem. Eng. 34, 467–475 (2010).
Golub, G. H., Heath, M. & Wahba, G. Generalized cross-validation as a method for choosing a good ridge parameter. Technometrics 21, 215–223 (1979).
Harrell, F. E. Jr Hmisc. Harrell Misc. 5, 2–3 (2003).
Acknowledgements
This research was supported by the National Science Foundation awards #2233982 and #2233983 to JRW and LCM on Model Enabled Machine Learning for Predicting Ecosystem Regime Shifts. This paper is a product of the model-enabled machine learning for ecology working group, which includes the authors of the paper as well as Cheyenne Jarman, Kunal Rathore, and Emerson Arehart, all of whom provided valuable contributions to the intellectual environment that led to this paper. We would also like to thank Chris Rackauckas for help working with Julia Scientific Machine learning tools and the Hawaiʻi Institute of Marine Biology for hosting a workshop where the ideas for this project were developed.
Author information
Authors and Affiliations
Contributions
J.H.B.: Conceptualization, formal analysis, methodology, software, writing-original draft. Z.D.M.: Conceptualization, methodology, software, writing-review and editing. J.A.E.: Conceptualization, funding acquisition, software, writing-review and editing. N.F.: methodology, software, writing-review and editing. A.G.: Conceptualization, writing-review and editing. L.C.M.: Funding acquisition, project administration, writing-review and editing. JRW: Conceptualization, funding acquisition, project administration, writing-review and editing.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Communications Earth and Environment thanks the anonymous reviewers for their contribution to the peer review of this work. Primary Handling Editors: Lifen Jiang and Mengjie Wang. [A peer review file is available].
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Buckner, J.H., Meunier, Z.D., Arroyo-Esquivel, J. et al. Recovering complex ecological dynamics from time series using state-space universal dynamic equations. Commun Earth Environ (2026). https://doi.org/10.1038/s43247-025-03130-2
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s43247-025-03130-2