Main

The most efficient thermoelectrics have historically been heavily doped semiconductors because the Pauli principle restricts the heat-carrying electrons to be close to the Fermi energy1 for metals. The Wiedemann–Franz law, κe/σT = π2/3(k/e)2 = (156 μV K-1)2, where κe is the electronic contribution to κ, constrains ZT = S2σT;/κ, where S is the Seebeck coefficient (or thermoelectric power, measured in V K-1), and σ and κ are the electrical and thermal conductivities, respectively. Semiconductors have a lower density of carriers, leading to larger S values and a κ value that is dominated by phonons (κph), implying that the electrical and thermal conductivities are somewhat decoupled1. κ can be reduced by using bulk semiconductors of high atomic weight, which decreases the speed of sound. However, this strategy has not yet produced materials with ZT > 1.

For a metal or highly doped semiconductor, S is proportional to the energy derivative of the density of electronic states. In low-dimensional (nanostructured) systems the density of electronic states has sharp peaks7,8,9 and, theoretically, a high thermopower. Harnessing this electronic effect to produce high-ZT materials has had only limited success10,11. However, optimization of the phonon dynamics and heat transport physics in nanostructured systems has yielded results4,5,6. Nanostructures may be prepared with one or more dimensions smaller than the mean free path of the phonons and yet larger than that of electrons and holes. This potentially reduces κ without decreasing σ (ref. 12). Bulk silicon (Si) is a poor thermoelectric (ZT300 K ≈ 0.01; ref. 13), and this phonon physics is important for our Si nanowires, in which the electronic structure remains bulk-like.

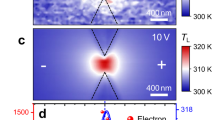
Figure 1 shows images of the devices and the Si nanowires we used for these experiments. Details related to the fabrication, calibration and experimental measurements are presented in the Supplementary Information. The platform permits four-point measurements of the electrical conductivity of the nanowires, Joule heating to establish a thermal gradient across the nanowires, and four-point thermometry to quantify that gradient10,14. The resistance of the four-point thermometry electrodes is typically two orders of magnitude smaller than the resistance of the nanowires. The measurement platform is suspended in vacuum to allow measurement of nanowire thermal conductivity15,16. For all measurements, the Si nanowires could be selectively removed using a XeF2 etch, thus allowing for measurements of the contributions to σ, S and κ from the platform and oxide substrate.

Figure 1: Scanning electron micrographs of the device used to quantitate the thermopower and electrical and thermal conductivity of Si nanowire arrays.
figure 1

a, This false-colour image of a suspended platform shows all electrical connections. The central green area is the Si nanowire array, which is not resolved at this magnification. The four-lead yellow electrodes are used for thermometry to quantify the temperature difference across the nanowire array. The thermal gradient is established with either of the two Joule heaters (the right-hand heater is coloured red). The yellow and blue electrodes are combined to carry out four-point electrical conductivity measurements on the nanowires. The grey region underlying the nanowires and the electrodes is the 150-nm-thick SiO2 insulator that is sandwiched between the top Si(100) single-crystal film from which the nanowires are fabricated, and the underlying Si wafer. The underlying Si wafer has been etched back to suspend the measurement platform, placing the background of this image out of focus. b, Low-resolution micrograph of the suspended platform. The electrical connections radiate outwards and support the device. c, High-resolution image of an array of 20-nm-wide Si nanowires with a Pt electrode.

Full size image

There are several ways to prepare Si nanowires, including materials methods for bulk production17. We wanted Si nanowires in which the dimensions, impurity doping levels, crystallographic nature, and so on, were all quantifiable and precisely controlled. We used the superlattice nanowire pattern transfer (SNAP) method18, which translates the atomic control over the layer thickness of a superlattice into control over the width and spacing of nanowires. Si nanowires made via SNAP inherit their impurity dopant concentrations directly from the single-crystal Si epilayers of the silicon-on-insulator substrates from which they are fabricated19. These epilayers were 20- or 35-nm-thick Si(100) films on 150 nm of SiO2, and were p-type impurity (boron) doped using diffusion-based doping19. Four-point probe conductivity measurements of the silicon-on-insulator films were used to extract dopant concentrations. We prepared nanowire arrays several micrometres long, with lateral width × thickness dimensions of 10 nm × 20 nm, 20 nm × 20 nm and 520 nm × 35 nm. The last approximates the bulk and, in fact, measurements on the sample obtained bulk values for S, σ and κ. Measurements of κ for our nanowires were consistent with literature values for materials grown (round) Si nanowires16.

All values of S, σ and κ reported here are normalized to individual nanowires, although each experiment used a known number of nanowires ranging from 10 to 400. The Si microwires and nanowires were prepared using the same substrates, doping methods, and so on, but different patterning methods (electron-beam lithography versus SNAP).

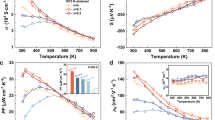
Measurements of κ and S2 for Si nanowires (and microwires) for different nanowire sizes and doping levels are presented in Fig. 2. More complete data sets, electrical conductivity data and a statistical analysis are presented in the Supplementary Information. The nanowire electrical conductivity is between 10 and 90% of the bulk, depending on nanowire dimensions. A reduced σ probably arises from surface scattering of charge carriers19. Nevertheless, all nanowires are highly doped and most exhibit metallic-like conductivity (increasing σ with decreasing T).

Figure 2: Factors contributing to ZT for various Si nanowires. All nanowires are 20 nm in height.
figure 2

a, The temperature dependence of the thermal conductivity κ, presented as κbulk / κnanowire to highlight the improvement that the reduction of κ in nanowires lends to ZT. κbulk values, which are slightly below the true bulk value for Si, are taken from an identically measured 520 nm × 35 nm-sized film. The inset scanning electron microscope micrographs show the region of the device containing the nanowires before (top) and after (bottom) the XeF2 etch to remove the nanowires. b, The temperature dependence of S2 for 20-nm-wide Si nanowires at various p-type doping concentrations (indicated on the graph). Note that the most highly doped nanowires (pink line) yield a thermopower similar to that of bulk Si doped at a lower level. For nanowires doped at slightly higher and slightly lower concentrations than the bulk, S peaks near 200 K. This is a consequence of the one-dimensional nature of the Si nanowires.

Full size image

The temperature dependence of κ for a microwire and 10- and 20-nm-wide nanowires were recorded at modest statistical resolution to establish trends. This data indicated that κ drops sharply with shrinking nanowire cross-section (Fig. 2a) and that the 10-nm-wide nanowires exhibited a κ value (0.76 ±0.15 W m-1 K-1) that was below the theoretical limit of 0.99 W m-1 K-1 for bulk Si (ref. 20). Thus, very large data sets were collected for 10- and 20-nm-wide nanowires to allow for a more precise determination of κ.

Our observed high ZT for Si nanowires (Fig. 3) occurs because κ is sharply reduced and the phonon drag component of the thermopower Sph becomes large. Below, we show that Sph increases because of a three-dimensional to one-dimensional crossover of the phonons participating in phonon drag and decreasing κ. However, we first discuss why our measured κ at 300 K for 10-nm-wide Si nanowires is less than κmin (ref. 20).

Figure 3: Temperature dependence of ZT for two different groups of nanowires.
figure 3

The cross-sectional area of the nanowires, and the p-type doping level, are given. The 20-nm-wide nanowires have a thermopower that is dominated by phonon contributions, and a ZT value ∼1 is achieved near 200 K. The smaller (10-nm-wide) nanowires have a thermopower that is dominated by electronic contributions. The ZT at 350 K is calculated using the thermal conductivity value for the 10-nm-wide nanowires at 300 K. The error bars represent 95% confidence limits.

Full size image

The derivation of κmin assumes that the minimum path length of wavelength λ phonons is λ/2 and that the phonons are described by the Debye model using bulk sound speeds with no optical modes. The λ/2 value is an order-of-magnitude estimate and is difficult to determine precisely, much like the minimum electron mean free path used to calculate the Mott–Ioffe–Regel σmin. Also, κmin is proportional to the transverse and longitudinal acoustic speeds of sound20. These are reduced in our nanowires at long wavelengths because the modes become one-dimensional. The ratio of the one-dimensional to two-dimensional longitudinal speeds of sound is [(1 + ν)(1 - 2ν)/(1 - ν)]1/2 = 0.87 where ν = 0.29 is the Poisson ratio of Si. The transverse acoustic speed goes to zero at long wavelength because ω ∝ k2d where d is the nanowire width21. Therefore, the bulk κmin estimate above is invalid for our nanowires and values smaller than κmin are attainable.

For all but the most highly doped nanowires, S peaks near 200 K (Fig. 2b). This peak is unexpected: similarly doped bulk Si exhibits a gradual decrease in S as T is reduced (green trace). For T < 100 K, a peaked S(T) is observed for metals and lightly doped semiconductors and is due to phonon drag13,22,23.

Phonon drag is generally assumed to vanish with decreasing sample dimensions because the phonon path length is limited by the sample size24,25,26. This seems to eliminate phonon drag as the reason for the peak in our nanowires. We show below that the phonon wavelengths participating in drag are of the order of or larger than the wire width. This leads to a three-dimensional to one-dimensional crossover of these modes and removes the cross-sectional wire dimensions from limiting the phonon mean path (see Fig. 4 inset). The nanowire boundaries are incorporated into the one-dimensional mode and are not an obstacle to phonon propagation. Therefore, the limiting size becomes the wire length (∼1 μm) and phonon drag ‘reappears’ at very small dimensions.

Figure 4: Thermopower calculation plotted along with experimental data (black points) from a 20-nm-wide Si nanowire p-type doped at 3 × 1019 cm-3.
figure 4

The black curve is the fitted expression for the total thermopower Se + Sph. The red curve is the phonon contribution Sph and the blue line is the electronic term Se arising from the fit. The fit has maximum error 6.1 μV K-1 and root-mean-square error 1.8 μV K-1. The experimental error bars represent 95% confidence limits and at 150, 200 and 225 K are smaller than the data points. The blue data points are experimental values for bulk wires (doping 2 × 1020 cm-3; crosses), 10-nm-wide nanowires (doping 7 × 1019 cm-3; diamonds), and 20-nm-wide wires (doping 1.3 × 1020 cm-3; triangles) where only a linear-T electronic contribution was found. This data are close to the extracted electronic contribution from the black data points (blue line) and shows that the fitted linear term is reasonable. The drop in S to 0 as T→0 occurs because the phonon mean free path reaches the sample size and the specific heat tends to 0 according to the third law of thermodynamics. The inset shows the character of a three-dimensional bulk longitudinal acoustic phonon mode (top) and a one-dimensional mode when the wavelength is larger or of the order of the width (bottom). The one-dimensional mode incorporates the existence of the boundary by transverse expansion (or compression) for longitudinal compression (or expansion). The ratio of the transverse strain to the longitudinal strain is the Poisson ratio (0.29 for Si).

Full size image

In addition, classical elasticity theory21 is valid for the phonon wavelengths considered here27, leading to thermoelastic damping21,28,29 of sound waves proportional to κ. Thus Sph is further enhanced, owing to the observed reduced thermal conductivity κ. A detailed discussion is in the Supplementary Information.

It might seem that elasticity theory leads to a contradiction because κ is proportional to the mean phonon lifetime. If the phonon lifetimes increase as stated above, then κ should also increase. But because the elasticity expression is only valid for long-wavelength modes, and κ is the average of all modes, there is no contradiction.

We now consider separately the electronic and phonon contributions to the thermopower—S = Se+Sph—for the nanowire data at T > 200 K. Charge carriers dissipate heat to the lattice through a process that first involves momentum conserving (non-dissipative) electron–phonon collisions. The phonons that contribute to phonon drag cannot have a wavelength shorter than λmin, which is determined by the size of the Fermi surface. Phonon drag is observed in metals only at low T because the Fermi surface is large and the heat carrying short-wavelength phonons have short lifetimes. At low T (<20 K), Sph ∝ T3 from the phonon specific heat (∝T3). For kT ≫ ΘDebye, the specific heat becomes constant and the number of phonons available for phonon–phonon scattering is ∝T, leading to Sph ∝ 1/T (ref. 1).

For p-type Si, the holes are near the valence band maximum. The phonon drag modes are acoustic with the largest wavevector kph = 2kFermi = 0.2 Å-1 (for impurity doping of 3 × 1019 cm-3). The shortest wavelength is λph = 2π/k = 31 Å.

Umklapp (non-momentum-conserving) phonon–phonon scattering processes determine the rate of phonon heat dissipation. The Debye energy ΘD sets the energy scale for Umklapp scattering. The number of Umklapp phonons available to dissipate the long-wavelength phonons is given by the Bose–Einstein function:

leading to a scattering rate 1/T;ph ∝ NU. When T ≫ ΘD, 1/T;ph ∝ T. Because ΘD = 640 K for Si, the full Bose–Einstein expression must be applied for T ≤ 350 K. The electronic contribution Se is estimated from the Mott formula1:

where the conductivity derivative equals the reciprocal of the energy scale over which it varies (the Fermi energy EF). Assuming hole doping occurs in the heavier Si valence band (mass 0.49), this leads to EF = 0.072 eV = 833 K and kF = 0.1 Å-1 for the number density of boron dopant atoms n = 3 × 1019 cm-3. Thus Se(T) = aT where a = 0.34 μV K-2.

The T > 200 K thermopower data of the 20-nm-wide wire (doping n = 3 × 1019 cm-3) fits:

where a, b and ΘD are varied to obtain the best fit (Fig. 4). The coefficients are a = 0.337 μV K-2, b = 22.1 μV K-1, and ΘD = 534 K. The coefficient a is almost identical to our estimate of 0.34 μV K-2. Thus phonon drag explains the observed thermopower. Consistent with measurements24 of phonon drag in bulk Si, S in our nanowires increases significantly at lighter doping. This data, plus a fit of the Fig. 4 data using the experimental ΘD = 640 K, is presented in the Supplementary Information. Rather than fitting by varying a, b and ΘD, we fixed ΘD to its known experimental value (640 K) and allowed only a and b to vary.

The phonon drag contribution to S is of the form23,30:

T;ph, the phonon lifetime, is ∝1/κ from elasticity theory. μ is the electron mobility. ZT scales as (neglecting Se):

leading to increased ZT with decreasing mobility. This is the opposite conclusion reached from when we consider only Se (ref. 7).

We have combined experiment and theory to demonstrate that semiconductor nanowires can be designed to achieve extremely large enhancements in thermoelectric efficiency, and we have shown that the temperature of maximum efficiency may be tuned by changing the doping and the nanowire size. Theory indicates that similar improvements should be achievable for other semiconductor nanowire systems because of phonon effects. These nanowire thermoelectrics may find applications related to on-chip heat recovery, cooling and power generation. Additional improvements through further optimization of nanowire size, doping and composition should be possible.

Methods Summary

Single-crystalline Si nanowires were fabricated using the SNAP process18. The nanowires were doped p-type using a boron-containing spin-on dopant (see Supplementary Information for details)19. Electron-beam lithography was used to create Ti/Pt electrodes for the electrical and heat transport measurements. The entire device was suspended using a XeF2 etch, leaving the nanowires anchored to a thin SiO island (see Supplementary Information for details). The nanowire electrical conductivity was measured by a Keithley 2400 using a four-point measurement to eliminate contact resistance. For measurement of S and κ, a temperature difference was created across the ends of the nanowires by sourcing a direct current through one of the resistive heaters. The resistance rise of each thermometer was recorded simultaneously using a lock-in measurement (Stanford Research Systems SRS-830) as the temperature was ramped upwards. The resistance of the thermometers was typically two orders of magnitude smaller than the nanowire array. For measurement of S, the thermoelectric voltage, as a response to the temperature difference, was recorded using a Keithley 2182A nanovoltmeter. A difference measurement was used to determine κ, whereby the κ value of the nanowires plus the oxide island was subtracted from the κ value of the oxide island. The thermal conductivity of the oxide island was determined by removing the nanowires with a highly selective XeF2 etch (see Supplementary Information for details).