Introduction

Chinese ancient paintings embody the national spirit and artistic achievements spanning five thousand years, owning immense artistic and historical value. Due to environmental factors or human activities, these paintings often suffer from fading and discoloration1,2,3, which greatly diminishes their aesthetic appeal and historical value. Therefore, reconstructing the colors of ancient paintings is of great importance.

Color reconstruction of ancient paintings enhances colors in backgrounds, mountains, trees, rocks, and other elements with manual or digital methods. It addresses issues of fading and discoloration while preserving structural information and content details. Manual color reconstruction requires a deep analysis of the painting’s style, content, and techniques, which is inefficient and can even damage the artwork4. As computer technology advances, the techniques for digital color reconstruction are widely used. Digital methods are easily adjustable, and they avoid direct manipulation of the original paintings, thus preventing potential damage. Digital color reconstruction techniques are based on traditional methods and deep learning methods. Traditional methods rely on model selection and parameter settings. For example, Li et al.5 used multispectral imaging to identify pigments for mural color reconstruction. However, improper model selection or parameter settings can result in suboptimal reconstructed results.

In recent years, with the advancement of artificial intelligence, deep learning has been widely applied to color reconstruction tasks6,7,8,9, enhancing the effectiveness of color reconstruction by deeply learning the characteristics of ancient paintings. Using deep learning techniques for the color reconstruction of ancient paintings typically involves constructing datasets for color reconstruction, training models to learn semantic and color features of the paintings, and ultimately applying the trained models to reconstruct colors. Color reconstruction models often use VGG as an encoder, which struggles to preserve image details. Meanwhile, inaccurate colors frequently appear in the reconstructed results due to the difficulties in accurately extracting semantic and color features. Additionally, models generally process images as a whole, resulting in suboptimal local color reconstruction. Therefore, it is crucial to preserve the structural information and content details of ancient paintings, accurately reconstruct colors, and enhance local reconstruction effects.

The CAP-VSTNet10 introduced a method by using flow-based models11 for natural image style transfer, effectively preserving content information. Inspired by this, a color reconstruction model is proposed for ancient paintings based on Dual Pooling Attention and Pixel Adaptive Convolution. This model maintains the structural integrity and content details of ancient paintings by using the flow-based model, mitigates fading and discoloration issues, reduces inaccuracies in color reconstruction, and enhances the reconstruction effects both globally and locally. The main contributions of this paper are as follows:

  • To address the issue of inaccurate colors in color reconstruction of ancient paintings, a Dual Pooling Channel Attention module (DPCA) is constructed. This module enhances the model’s ability to extract features by assigning different weights to the image channels, reducing inaccurate colors and improving the color reconstruction of ancient paintings.

  • To solve the problem of inconsistent color reconstruction due to variations in background and content, a Content Adaptive Feature Extraction module (CAFE) is constructed. This module adaptively adjusts the convolution parameters in terms of the differences in background and content, improving the overall effectiveness of color reconstruction.

  • To improve the localized color reconstruction of ancient paintings, a Contrastive Coherence Preserving Loss (CCPL) is introduced. The loss enhances the model’s focus on image localization by constraining local features, thereby improving the local color reconstruction.

Related work

The proposed method involves image style transfer, flow-based models, and color reconstruction. This section discusses related work in these three areas.

Image style transfer

Image style transfer is an important research area in computer vision. It transfers the style of a style image to a content image while preserving the content. The content of an image includes details and positions of objects, while style refers to the information such as color and brightness. Gatys6 used convolutional neural networks to extract image features, separating content and style information at the feature level. Following this, many deep learning-based methods for image style transfer emerged. To address the slow speed of style transfer, feed-forward neural networks were used to accelerate the process8,12. Research then focused on using a single model for multi-style transfer13,14, but these models only handle specific styles. Consequently, many studies15,16 aimed at universal style transfer. Li et al.17 proposed a linear transfer network for transferring any style to a content image. SANet18 added non-local self-attention to style transfer models but failed to align local features. AdaAttN7 combined SANet and AdaIN16, balancing local and global stylization effects. PhotoWCT19 replaced the upsampler operation in VGG decoders with uppooling, better preserving details in transfer results. WCT220 replaced pooling layers in VGG decoders with wavelet pooling, better preserving spatial information of content images. DPST21 and CAP-VSTNet10 introduced Matting Laplacian22 into networks to retain details in transfer results, achieving good results.

Flow-based models

Flow-based models are generative models that learn high-dimensional feature distributions with a series of reversible transformations. Dinh et al.11 first proposed NICE to model high-dimensional complex data for image generation. Real NVP23 introduced new transformation operations to reduce computation and improve image quality. Glow24 simplified the structure of Real NVP, making the model more streamlined and standardized. Flow++25 enhanced feature expression by introducing self-attention mechanisms and new coupling layers. Recently, flow-based models have been applied in image generation24,25, speech synthesis26, and other fields. BeautyGlow27 designed a flow-based model for digital makeup. ArtFlow28 used a flow-based model for artistic style transfer. CAP-VSTNet10 proposed a flow-based model for universal style transfer in images and videos.

Color reconstruction

Color reconstruction involves reconstructing color from faded or discolored images. Wan et al.29 used variational autoencoders to reconstruct details and colors in photos. Pik-Fix30 focused on reconstructing colors in degraded old photographs. JWA et al.31 used deep convolutional networks for image colorization of natural images. DDNM32 developed a zero-shot framework for colorizing grayscale natural images. Wang et al.33 built a generative adversarial network model for color reconstruction of faded and discolored murals. DC-CycleGAN34 extracted complex features of mural images to construct a model for the color reconstruction of murals. CR-ESRGAN35 addressed the fading of cultural relics by developing a color reconstruction model, but suffers from inaccurate color reconstruction. The proposed model effectively preserves structural information and content details. It adapts to different contents of ancient painting, achieving better color reconstructed results both globally and locally.

Methodology

The model is proposed for color reconstruction. In this section, the proposed model is described in detail, including the overall structure, Dual Pooling Channel Attention module (DPCA), Content Adaptive Feature Extraction module (CAFE), and loss functions.

Overall structure

It is essential to preserve the structural and detailed information of degraded ancient paintings in color reconstruction. CAP-VSTNet10 uses a flow-based model for natural image style transfer, effectively retaining content information. Inspired by this, a method for the color reconstruction of ancient paintings is proposed with a flow-based model, considering the rich details and delicate colors of ancient paintings.

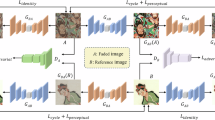
The structure of the constructed model is shown in Fig. 1, including the feature extraction module and the color reconstruction module. Firstly, the model uses the feature extraction module to obtain features from the degraded and reference images. Then, these features are fed into the color reconstruction module for color reconstruction, yielding reconstructed color features. Lastly, the reconstructed features are input back into the feature extraction module, and then the color-reconstructed image is obtained in terms of the reversibility of the flow-based model.

Fig. 1
figure 1

Structure of the proposed model.

Full size image

The feature extraction module consists of a channel expansion module, several reversible residual blocks, two Squeeze modules, and a channel refinement module. The channel expansion module increases the number of channels of the input image, thereby enhancing the model’s ability to feature representation. The reversible residual blocks are stacked to achieve a larger receptive field, thereby extracting deeper features. The Squeeze module reduces the spatial dimensions of features while increasing the number of feature channels to capture larger-scale feature information. The channel refinement module reduces the number of feature channels to eliminate redundant information. The color reconstruction module integrates Cholesky decomposition36 and WCT15 for color reconstruction, producing reconstructed features.

The forward and backward inference in reversible residual blocks are shown in Fig. 2. In the forward inference, let \(x\) be the input and \(y\) the output. The input \(x\) is split into \({x}_{1}\) and \({x}_{2}\) along the channel dimension. The transformations are formulated by (1) and (2):

$${y}_{1}={x}_{1}+F({x}_{2})$$
(1)
$${y}_{2}={x}_{2}$$
(2)

where \({y}_{1}\) and \({y}_{2}\) are the results obtained from \({x}_{1}\) and \({x}_{2}\) according to (1) and (2), respectively. These are concatenated along the channel dimension to form the output \(y\) of the reversible residual block. \(F\) is the sequential concatenation of the Dual Pooling Channel Attention module (DPCA) and the Content Adaptive Feature Extraction module (CAFE). In the backward inference, let \(y\) be the input and \(x\) the output. The input \(y\) is split into \({y}_{1}\) and \({y}_{2}\) along the channel dimension. The inverse process is formulated by (3) and (4).

$${x}_{2}={y}_{2}$$
(3)
$${x}_{1}={y}_{1}-F({x}_{2})$$
(4)
Fig. 2
figure 2

Forward and backward inference in reversible residual blocks.

Full size image

Information loss during data propagation in the model is avoided with these reversible transformations, effectively preserving the structure and details of degraded ancient paintings10,11. The DPCA is introduced into the reversible residual block, which enhances the abilities to extract features and reduces inaccurate colors in the reconstructed results. The CAFE is incorporated into the reversible residual block, dynamically adjusting convolutional parameters to ensure color consistency between the background and the content. The Contrastive Coherence Preserving Loss is introduced to constrain the local features of degraded and reconstructed paintings, which improves the local color reconstruction.

Dual pooling channel attention module

Chinese ancient paintings exhibit rich color layers. It is essential to accurately extract features of ancient paintings for color reconstruction. The Efficient Channel Attention Network (ECANet)37,38 enhances the model’s performance by calculating channel weights through local cross-channel interaction. Inspired by this, to address the issue of inaccurate colors in reconstructed results, the Dual Pooling Channel Attention (DPCA) module is constructed. This module assigns different weights to image channels, enhancing the model’s ability to extract and match image features, thereby reducing inaccurate colors, as shown in Fig. 3.

Fig. 3
figure 3

Dual Pooling Channel Attention module.

Full size image

Firstly, an average pooling (AP) is performed on the input features of size \(H\times W\times C\) to obtain features of size \(50\times 50\times C\). Then, global average pooling (GAP) is applied to these features, producing features of size \(1\times 1\times C\). After that, a convolution operation with a kernel size \(k=5\) and a Sigmoid activation function is performed to obtain the attention weights. Finally, the weights are element-wise multiplied with the input features to produce the output features. The features of images are better extracted and matched by assigning different weights to the image channels, reducing inaccurate colors in reconstructed results.

Content adaptive feature extraction module

Elements in Chinese ancient paintings, such as mountains, trees, and rocks, are often painted with different pigments and techniques from those used for backgrounds. This results in varying degrees of color degradation and makes it challenging to adaptively reconstruct colors based on the background and compositional elements. Pixel Adaptive Convolution (PAC)39 modifies the convolution kernel according to image features, allowing adaptive feature extraction based on image content. Inspired by this, to address the aforementioned problem, the Content Adaptive Feature Extraction (CAFE) module is constructed. CAFE adjusts convolution kernel parameters based on image content, better adapting to the backgrounds and compositional elements of ancient paintings, as shown in Fig. 4.

Fig. 4
figure 4

Content Adaptive Feature Extraction Module.

Full size image

CAFE consists of two convolution layers and one pixel adaptive convolution layer. When features are input into CAFE, convolution is first performed to obtain features \(f\) and \(v\). Then, \(f\) is input into the kernel function \(K\) to obtain adaptive weights. After that, the weights are multiplied by the convolution kernel \(W\) to obtain pixel-adaptive convolution parameters. Simultaneously, the convolution kernel parameters are multiplied by the feature \(v\) to obtain the output feature \(v\text{'}\). The kernel function \(K\) is formulated by (5):

$$K({f}_{({x}_{i},{y}_{i})},{f}_{({x}_{j},{y}_{j})})=\exp \left(-\frac{1}{2}{({f}_{({x}_{i},{y}_{i})}-{f}_{({x}_{j},{y}_{j})})}^{T}({f}_{({x}_{i},{y}_{i})}-{f}_{({x}_{j},{y}_{j})})\right)$$
(5)

where \({f}_{({x}_{i},{y}_{i})}\) represents the feature value at the position \(({x}_{i},{y}_{i})\) in the feature map, \(T\) denotes the matrix transpose. The module obtains adaptive weights by inputting features into the kernel function \(K\). The weights are then multiplied by the convolution kernel \(W\), enabling the adjustment of convolution kernel parameters based on image content. This obtains better color reconstruction adapted to the backgrounds and compositional elements of ancient paintings.

Loss function

The local colors of Chinese ancient paintings are rich and detailed, making it challenging to reconstruct the color of paintings accurately. The Contrastive Coherence Preserving Loss40 is introduced to enhance the model’s focus on image localization, thereby improving the reconstruction of local colors.

Total loss

The total loss of the proposed model is formulated by (6):

$${L}_{total}={\lambda }_{ccp}{L}_{ccp}+{\lambda }_{s}{L}_{s}+{\lambda }_{m}{L}_{m}+{\lambda }_{cyc}{L}_{cyc}$$
(6)

where \({L}_{ccp}\) is the contrastive coherence preserving loss, \({L}_{s}\) is the style loss, \({L}_{m}\) is the Matting Laplacian loss, \({L}_{cyc}\) is the cycle consistency loss, and \({\lambda }_{ccp}\), \({\lambda }_{s}\), \({\lambda }_{m}\), and \({\lambda }_{cyc}\) are the weights for \({L}_{ccp}\), \({L}_{s}\), \({L}_{m}\) and \({L}_{cyc}\), respectively.

Contrastive coherence preserving loss

The Contrastive Coherence Preserving Loss (CCPL)40 is introduced to enhance the model’s focus on image localization by constraining local features, thereby improving the reconstruction of local colors. To apply CCPL, initially, the degraded and reconstructed images are input into an encoder to obtain feature maps. Feature vectors are then sampled from these maps, along with their eight nearest neighboring vectors for each vector. Then the difference vectors are obtained by vector subtraction between a vector and its neighboring vectors. CCPL constraints local features by using positive and negative pairs, positive pairs consist of difference vectors from the same spatial locations in the degraded and reconstructed paintings, while negative pairs consist of vectors from different locations. CCPL operates by maximizing the mutual similarity of positive pairs while minimizing the similarity of negative pairs, thereby enhancing local coherence. The contrastive coherence preserving loss is formulated by (7):

$${L}_{ccp}=\mathop{\sum }\limits_{m=1}^{N}\left[-\,\log \left[\frac{\exp ({d}_{g}^{m}\cdot {d}_{c}^{m}/\tau )}{\exp ({d}_{g}^{m}\cdot {d}_{c}^{m}/\tau )+{\sum }_{n=1,n\ne m}^{N}\exp ({d}_{g}^{m}\cdot {d}_{c}^{n}/\tau )}\right]\right]$$
(7)

where \(N\) is the total number of difference vectors. \({d}_{g}^{m}\) and \({d}_{c}^{m}\) are the m-th difference vectors in reconstructed and degraded paintings, respectively.\({d}_{c}^{n}\) is the n-th difference vector in degraded paintings.\(\tau\) is a hyperparameter set to 0.07.

Style loss

The style loss10 is formulated by (8):

$${L}_{s}=\mathop{\sum }\limits_{i=1}^{4}{\Vert \mu ({\phi }_{i}({I}_{cs}))-\mu ({\phi }_{i}({I}_{s}))\Vert }_{2}+\mathop{\sum }\limits_{i=1}^{4}{\Vert \sigma ({\phi }_{i}({I}_{cs}))-\sigma ({\phi }_{i}({I}_{s}))\Vert }_{2}$$
(8)

where \({I}_{s}\) is the reference painting, and \({I}_{cs}\) is the color-reconstructed painting. Features of ancient paintings are extracted using the first four layers of the pre-trained VGG19 network. \({\phi }_{i}\) is the output feature map of the \(i\)-th layer of the VGG19 network. \(\mu\) and \(\sigma\) are the mean and standard deviation, respectively. \({\Vert\! \cdot \!\Vert }_{2}\) is the \({L}_{2}\)-norm. The style loss constrains the color differences between the reconstructed and reference paintings, making their color styles similar.

Matting Laplacian loss

The Matting Laplacian loss10,22 is formulated by (9):

$${L}_{m}=\frac{1}{N}\mathop{\sum }\limits_{c=1}^{3}{V}_{c}{[{I}_{cs}]}^{T}M{V}_{c}[{I}_{cs}]$$
(9)

where \(N\) is the number of image pixels. \({V}_{c}[{I}_{cs}]\) is the vectorized form of the color-reconstructed painting \({I}_{cs}\) in channel \(c\). \(T\) is the transpose of the obtained vector. \(M\) represents the Matting Laplacian matrix of the color-degraded painting. The Matting Laplacian loss constrains the pixel differences between the color-degraded and color-reconstructed paintings. This ensures better preservation of lines, brushstrokes, and other details in the color-reconstructed painting.

Cycle Consistency loss

The cycle consistency loss10 is formulated by (10):

$${L}_{cyc}={\Vert {\tilde{I}}_{C}-{I}_{C}\Vert }_{1}$$
(10)

where \({\tilde{I}}_{C}\) is the result obtained by inputting the reconstructed painting into the model, using the degraded painting as a reference. \({I}_{C}\) is the degraded painting. \({\Vert\! \cdot \!\Vert }_{1}\) is the \({L}_{1}\)-norm. The cycle consistency loss allows the model to reconstruct the input image. This constrains the features of the degraded and reference paintings, ensuring accurate color matching between them.

Experiments and results

This section will introduce the dataset, training process, comparison experiments, and ablation study, respectively.

Construction of dataset

A dataset for the color reconstruction of ancient paintings is established to train and test the proposed model. Firstly, 214 paintings are selected, including the styles of ink wash, blue and green, and light crimson from different dynasties. These paintings are then cropped into \(512\times 512\), excluding those with overly uniform colors like pure white or black. This leads to 3888 sample images. The construction process is shown in Fig. 5. 3828 samples are used as the training set, and 60 samples are used as the test set. The number of samples is detailed in Table 1, and some samples are shown in Fig. 6.

Fig. 5
figure 5

Dataset construction process.

Full size image
Table 1 Number of samples of constructed dataset
Full size table
Fig. 6: Samples of the constructed dataset.
figure 6

a The Ink wash samples. b The blue and green samples. c The light crimson samples (The first row is the degraded paintings, and the second row is the reference paintings).

Full size image

Training process

After testing, the weights for the model’s loss function are set to \({\lambda }_{ccp}=5\), \({\lambda }_{s}=1\), \({\lambda }_{m}=1500\), and \({\lambda }_{cyc}=10\). Adam optimizer is used to update the weights. The initial learning rate is set to 0.00001. The model is trained for 80,000 iterations with a batch size of 2. Training and testing are performed on a single NVIDIA RTX 3090 GPU.

The curve of the loss function of the proposed model during training is displayed in Fig. 7. The lighter line represents the raw loss function curve, while the darker line shows the smoothed curve obtained using TensorBoard. A logarithmic scale is used for the vertical axis to clearly depict the convergence trend of the loss function. Obviously, the model’s loss steadily decreases and eventually stabilizes as iterations increase. This indicates that the model converges stably, leading to effective color reconstruction of ancient paintings.

Fig. 7
figure 7

Curve of loss function changes.

Full size image

Experimental results

The color reconstructed results on the constructed dataset are shown in Fig. 8. By comparing Fig. 8a with Fig. 8c, the proposed model effectively preserves the details of compositional elements like mountains, trees, and rocks of the degraded paintings. For instance, in Fig. 8c, the boundaries of the tree are distinct in the first row, the original lines of the river are preserved in the second row, and the contours of the mountain are maintained in the third row.

Fig. 8: Color reconstructed results of the proposed model.
figure 8

a Degraded ancient paintings; b Reference paintings; c Reconstructed results (Rows 1, 2, and 3 show the reconstructed results in ink wash, blue and green, and light crimson styles, respectively).

Full size image

By comparing Fig. 8b with Fig. 8c, the model successfully transfers the color style of the reference paintings. For example, in Fig. 8c, the color of the rocks in the first row is similar to that of the reference painting, the overall greenish tint in the second row matches the reference, and the color of the mountains in the third row is similar to that of the reference painting.

In summary, the proposed model is demonstrated to be effective for color reconstruction of ancient paintings in ink wash, blue and green, and light crimson styles.

Comparison experiments

To verify the effectiveness of the proposed model, ArtFlow28, PCA-KD41, Photo-WCT242, DTP43, CAP-VSTNet10, and CCPL40 are selected for comparison. ArtFlow develops a flow-based method for natural image style transfer. PCA-KD employs knowledge distillation to construct models for natural image style transfer. PhotoWCT2 uses blockwise training and high-frequency residual skip connections for style transfer. DTP creates a model incorporating correlation and generation modules to perform style transfer on input images. CAP-VSTNet introduces a flow-based model for natural image style transfer. CCPL devises a versatile method for style transfer.

Qualitative comparison

To comprehensively evaluate the proposed model, faded ancient paintings are selected with ink wash, blue and green, and light crimson styles, respectively. Reference paintings are chosen based on the same styles, similar compositional elements, and good color preservation.

The comparative results of different models are shown in Fig. 9. In Fig. 9c, CAP-VSTNet preserves the content details well but fails to reconstruct color accurately. The color of the mountains in the third row differs significantly from the reference painting, and the color of the mountains in the upper part of the sixth row is not accurately reconstructed. In Fig. 9d, CCPL produces unsatisfactory color reconstructions. The color of the mountains in the third row deviates significantly from the reference painting, and the color of the lower-right mountain in the fifth row is not accurately reconstructed. The results of ArtFlow are similar in style to the reference paintings in Fig. 9b. However, noticeable color inconsistencies appear due to the lack of matching color and content features between input images. Details of ancient paintings are not well preserved compared to the degraded paintings, resulting in blurry details. Specifically, in Fig. 9e, significant color inconsistency appears in the upper part of the third row, and detail loss is observed in the mountains in the upper right of the fifth row. PCA-KD preserves content details in Fig. 9f, but the color still shows some differences from that of the reference paintings. For example, the first and fifth rows are overall blurry, and the colors of the mountain in the third row are not accurately reconstructed. PhotoWCT2 preserves content details but fails to reconstruct colors accurately in Fig. 9g. Incorrect colors are seen around the branches of the first row and the trees on the right side of the fifth row. The results of DTP show color deviations and unclear details in Fig. 9h. The colors of the second and third rows differ from those of the reference paintings, and the details of the tree on the right side of the fifth row are blurred.

Fig. 9: Comparison of reconstructed results using different models (Red boxes are used for comparison of details).
figure 9

a Degraded ancient paintings. b Reference paintings. c CAP-VSTNet. d CCPL. e ArtFlow. f PCA-KD. g PhotoWCT2. h DTP. i Ours (Rows 1 and 2 correspond to the style of ink wash, rows 3 and 4 correspond to the style of blue and green, and rows 5 and 6 correspond to the style of light crimson).

Full size image

In Fig. 9i, the proposed model first incorporates a Dual Pooling Channel Attention module to correct color inaccuracies. Then, a Content Adaptive Feature Extraction module is built to improve color reconstruction for different backgrounds and elements in ancient paintings. Lastly, the Contrastive Coherence Preserving Loss is introduced to enhance local color reconstruction. In conclusion, the proposed model effectively preserves painting details and improves color reconstruction, both globally and locally.

Quantitative comparison

The experimental results in Fig. 9 correspond to the quantitative metrics presented in Tables 2–4, which represent the results for ink wash, blue and green, and light crimson styles, respectively. Structural Similarity (SSIM)44 and Gram Loss10 are used as evaluation metrics. SSIM calculates the preservation of content details, while Gram Loss evaluates the color reconstructed effectiveness. A higher SSIM indicates greater structural similarity between the degraded and reconstructed paintings, while a lower Gram Loss indicates closer color style similarity between the reconstructed and reference paintings.

Table 2 Comparison of evaluation metrics (ink wash style)
Full size table
Table 3 Comparison of evaluation metrics (blue and green style)
Full size table
Table 4 Comparison of evaluation metrics (light crimson style)
Full size table

Taking the results for the ink wash style as an example, it is evident that CAP-VSTNet has relatively poor color reconstruction, resulting in a high Gram Loss. CCPL shows unsatisfactory color reconstruction and fails to effectively preserve content details, resulting in lower SSIM and higher Gram Loss compared to the proposed model. ArtFlow performs poorly in preserving the structural details of the degraded paintings, resulting in a low SSIM. PCA-KD has relatively poor color reconstruction, resulting in a high Gram Loss. PhotoWCT2 fails to reconstruct the color of the ancient paintings effectively, resulting in a high Gram Loss. DTP shows poor color reconstruction and detail loss, thus having lower SSIM and higher Gram Loss compared to the proposed model. The same conclusion can be drawn for the other two styles.

The proposed model firstly incorporates a Dual Pooling Channel Attention module to correct color inaccuracies. Secondly, a Content Adaptive Feature Extraction module is constructed to handle different backgrounds and compositional elements in ancient paintings. Lastly, the Contrastive Coherence Preserving Loss is introduced to improve local reconstruction. In conclusion, the proposed model achieves the highest SSIM and the lowest Gram Loss, achieving the best performance in color reconstruction.

Ablation study

An ablation experiment is conducted on the constructed dataset to verify the effect of the Dual-Pooling Channel Attention module (DPCA), Content-Adaptive Feature Extraction module (CAFE), and Contrastive Coherence Preserving Loss (CCPL) on the reconstructed ability of the proposed model, including both qualitative and quantitative analysis.

The results of the ablation experiments for different modules are shown in Fig. 10, Fig. 11, and Fig. 12, respectively. DPCA improves the model’s ability to match and extract image features by assigning different weights to the image channels, thereby reducing inaccurate colors. By comparing Fig. 10c with Fig. 10d, after adding the DPCA, inaccurate colors around the leaves in the reconstructed paintings are reduced. CAFE adjusts convolution kernel parameters based on the differences in background and content, enhancing color reconstruction for the background and various elements. Figure 11c and d show that, when the CAFE is added, the background color of the reconstructed painting is more similar to that of the reference painting, improving the overall color reconstruction. CCPL enhances the model’s focus on image localization by constraining local features, thereby improving the local color reconstruction. Figure 12c and d show that, after adding CCPL, the color of the stones on the right side of the painting is closer to that of the reference painting, improving local reconstruction. These comparisons demonstrate that each proposed module positively impacts the model’s performance in color reconstruction.

Fig. 10: Comparison before and after using DPCA (Red boxes are used for comparison of details).
figure 10

a Degraded ancient painting. b Reference painting. c With DPCA. d Without DPCA.

Full size image
Fig. 11: Comparison before and after using CAFE (Red boxes are used for comparison of details).
figure 11

a Degraded ancient painting. b Reference painting. c With CAFE. d Without CAFE.

Full size image
Fig. 12: Comparison before and after using CCPL (Red boxes are used for comparison of details).
figure 12

a Degraded ancient painting. b Reference painting. c With CCPL. d Without CCPL.

Full size image

The experimental results in Figs. 10–12 correspond to the quantitative metrics presented in Table 5. The DPCA focuses on prominent features by assigning weights to image channels, enhancing the model’s ability to match and extract colors. Without DPCA, the model produces noticeable incorrect colors. The CAFE improves the color reconstruction of backgrounds and various elements by adjusting convolutional kernel parameters. In the absence of CAFE, color reconstruction of the backgrounds is less accurate. The CCPL enhances the model’s ability to reconstruct local colors by constraining local features. Without CCPL, the model performs poorly in reconstructing local colors. The above analyses indicate that removing the proposed modules results in lower SSIM and higher Gram Loss compared to the proposed model, demonstrating the significance of the modules in color reconstruction.

Table 5 Evaluation metrics for the ablation study
Full size table

The proposed model firstly incorporates a Dual Pooling Channel Attention module to correct color inaccuracies. Secondly, a Content Adaptive Feature Extraction module is constructed to improve the color reconstruction of backgrounds and elements. Lastly, the Contrastive Coherence Preserving Loss is introduced to enhance local color reconstruction. In conclusion, the proposed model effectively preserves the details of ancient paintings and addresses the issues of fading and color changes. It reconstructs paintings with consistent colors, achieving better results both globally and locally.

Experiments on landscape painting dataset

To demonstrate the generalization ability of the proposed model, it is trained and tested on a landscape painting dataset45, and compared with the contrast models. This dataset contains 2192 landscape painting samples with size of \(512\times 512\), which are obtained from open-source museums. 2152 samples are used as the training set, and 40 samples are used as the test set.

The experimental results are shown in Fig. 13, with the corresponding quantitative metrics shown in Tables 6–8, which represent the results for ink wash, blue and green, and light crimson styles, respectively. Taking the results for the blue and green style as an example, CAP-VSTNet has relatively poor color reconstruction in Fig. 13c, resulting in a high Gram Loss. The results of CCPL in Fig. 13d show unsatisfactory color reconstruction and fail to effectively preserve content details, resulting in lower SSIM and higher Gram Loss compared to the proposed model. ArtFlow fails to preserve the details of the degraded paintings in Fig. 13e, resulting in blurred reconstructions with the lowest SSIM. The reconstructed colors of PCA-KD in Fig. 13f still differ from the reference paintings, resulting in a high Gram Loss. PhotoWCT2 produces unsatisfactory color reconstructions in Fig. 13g, resulting in the highest Gram Loss. The results of DTP in Fig. 13h show unclear details and poor color reconstruction, resulting in lower SSIM and higher Gram Loss compared to the proposed model. The same conclusion can be drawn for the other two styles.

Fig. 13: Reconstructed results of different models using the landscape painting dataset (Red boxes are used for comparison of details).
figure 13

a Degraded ancient paintings. b Reference paintings. c CAP-VSTNet. d CCPL. e ArtFlow. f PCA-KD. g PhotoWCT2. h DTP. i Ours (Rows 1, 2, and 3 correspond to ink wash, blue and green, and light crimson styles, respectively).

Full size image
Table 6 Comparison of evaluation metrics on the landscape painting dataset (ink wash style)
Full size table
Table 7 Comparison of evaluation metrics on the landscape painting dataset (blue and green style)
Full size table
Table 8 Comparison of evaluation metrics on the landscape painting dataset (light crimson style)
Full size table

In Fig. 13i, the proposed model effectively preserves the details of ancient paintings and produces consistent colors in the reconstructed results, leading to the highest SSIM and the lowest Gram Loss.

In conclusion, the results from both the constructed ancient painting dataset and the existing landscape painting dataset demonstrate that, the proposed model performs well in color reconstruction of paintings, proving its applicability in this domain.

Conclusion

A color reconstruction model for ancient paintings is proposed based on dual pooling attention and pixel adaptive convolution. Firstly, a Dual Pooling Channel Attention module is proposed to address inaccurate colors in reconstructed results. This module enhances the model’s ability to extract features by assigning different weights to the image channels, thereby reducing inaccurate colors. Secondly, to solve the problem of inconsistent color reconstruction due to variations in background and content, a Content Adaptive Feature Extraction module is constructed. This module dynamically adjusts the convolutional parameters based on predefined features to adaptively extract features of ancient paintings, thereby improving the overall color reconstruction of ancient paintings. Lastly, a Contrastive Coherence Preserving Loss is introduced to solve the problem of poor local color reconstruction. The loss enhances the model’s focus on image localization by constraining local features, thereby improving the local color reconstruction. Experiments are conducted on the constructed color reconstruction dataset of ancient paintings, including comparison experiments and ablation studies. The results show that the proposed model effectively preserves the structural information and content details of ancient paintings, while adapting to different backgrounds and content, achieving better color reconstruction both globally and locally. Additionally, color reconstruction experiments are performed on a landscape painting dataset, proving the effectiveness and applicability of the proposed model.