Numerical simulation of spatial wind fields in Xumishan Grottoes over complex terrain

Abstract

Windy weather frequently occurs in Northwest China, and wind erosion is a typical issue for stone carvings in the caves. In the present study, computational fluid dynamics (CFD) simulations relying on steady 3D Reynolds-averaged Navier-Stokes (RANS) equations were used to simulate the spatial wind field over complex terrain with field measurement validation. This study has the following two aims: (1) to evaluate the accuracy of wind fields simulations with the Interpolated Multiscale Profile (IMP) method over complex terrain; and (2) to provide spatial wind field data of Xumishan Grotto Zone under neutrally stratified atmospheric boundary layer (ABL) over complex terrain. Unmanned aerial vehicle (UAV) oblique photogrammetry and multirotor UAV technology provide application scenarios for the establishment of a high-precision digital model and the determination of accurate inlet boundary conditions. By compiling user-defined functions (UDF) and using the block interpolation method, this method addresses the overestimation of the inlet wind velocity caused by the large elevation difference of the inlet over complex terrain. The results show that the 3D steady RANS simulation based on the IMP method can reasonably and accurately simulate spatial wind fields over complex terrain. This study also provides spatial wind fields data for addressing stone carving erosion caused by strong winds in semi-open Grottoes.

Introduction

The Xumishan Grottoes are located in Northwest China. The Grottoes were initially built in the late period of the Northern Wei Dynasty (386–534) and were listed as a key state-level cultural site in 1982. They were located in an important passage along the ancient Silk Road. There are more than 350 stone statues in the Grottoes, of which the great Buddha statue in Cave 5 is one of the few statues of the Tang Dynasty in China.

The north-south mountain ranges and valley are formed by river erosion. The Grottoes of Xumishan are carved out of eight irregular succession hills on the north side of a valley. The Xumishan Grottoes, which are composed of valleys and hills with different elevations, are characterized by high levels of complexity.

Spatial wind fields over complex terrain have generated increasing research interest in recent years in areas including urban ventilation corridors planning^1,2, urban pollutants dispersion^3,4, and urban heat island⁵. At present, studies on wind fields mainly include field measurements^6,7,8,9, wind tunnel tests^10,11,12 and numerical simulations^13,14,15,16. Wind fields data with high reliability can be obtained by field measurements. However, due to spatial resolution limitations, traditional measurement methods cannot obtain all wind fields data within the research range, and the time and cost burdens are very high. Wind tunnel tests are flexible and can collect the characteristic parameters of wind fields under different inlet conditions. This method has the same limitation: wind tunnel data cannot capture the characteristics of the whole wind field, and wind tunnel scaling down model tests need to meet the requirements of the similarity principle¹⁷. In the past 50 years, numerical simulation has developed rapidly due to significant improvements in computer power and the development of various commercial computing software programs^18,19,20. Compared with the previous two methods, numerical simulations can obtain the spatial data of each position in the wind field. Unlike the scaling down of wind tunnel tests, numerical simulations can be performed at full size, and without the need to dedicate a significant amount of time into the physical modelling of the terrain. To study the spatial wind field, the approach relies on field measurements and wind tunnel tests can be complemented by numerical simulations. Therefore, numerical simulation has become the main method for studying spatial wind fields over complex terrain. However, the accuracy and reliability of numerical simulation largely depend on the setting of calculation parameters and the operation of software. Best guidelines for numerical simulations practices in wind engineering are used to guide modeling and calculation parameter settings^21,22,23. For these reasons, field measurements are also imperative to verify the accuracy of numerical simulations.

The scale of the meteorological research range in the ABL(Atmospheric Boundary Layer) can be divided into the macroscale, mesoscale, localscale and microscale²⁴. Mesoscale refers to the spatial scales from 10 km to 200 km, localscale refers to spatial scales range 0.1 km-50 km and microscale is under 1 km. Meteorological models such as the Numerical Weather Prediction (NWP) model are suitable for reproduce wind fields within mesoscale scale such as pollutants dispersion while computational fluid dynamics (CFD) offers a significant advantage in the microscale. The coupling method of mesoscale NWP and CFD has been also used to study the problems of urban airflow and pollutants dispersion²⁵. The NWP-CFD multiscale simulation incorporate the meteorological model with microscale wind environments, and the simplification of the geometric models in mesoscale models comes at a price as it compromises the simulation’s ability to reflect the influence of topography on the characteristics of wind flow²⁶. When dealing with case where there is a transition between the mesoscale and microscale, such as studying steady wind fields on a scale of ten of kilometers, a method to simulate mesoscale wind environments with high accuracy and affordable computation needs. Based on the existing coupling method of NWP-CFD, this paper generated geometry models with highly accurate geometries, and the multiscale simulation between CFD and CFD is used in this research.

The setting of the inlet boundary plays a key role in numerical simulation, greatly affecting the accuracy of the simulation results²⁷. At present, the general method for determining the inlet boundary is fitting the velocity profile into an empirical (logarithmic/power) law namely, the Fitted Empirical Profile (FEP).The empirical law of the velocity profile can be obtained by determining the typical aerodynamic roughness length of a uniform surface²⁸, but these values are measured on the surface of homogeneous terrain, and the problem of how to determine the roughness length and profile index of heterogeneous terrain has not been solved well. At present, wind observation towers²⁹ and field measurements are set by Doppler wind lidars^30,31 or wind tunnel tests¹¹ to obtain the velocity profile and then fit to determine the expression of the inlet boundary. As mentioned earlier, traditional weather surveys have limitations in spatial resolution and time, and wind tunnel tests are relatively expensive and complex. The rapid development of unmanned aerial vehicles (UAVs) in the field of meteorological observations provides a feasible method for the real-time acquisition of vertical profiles of the mean wind speed and direction^32,33,34. Fixed-wing UAV can indirectly obtain the wind profile by measuring the wind speed vector by a pressure sensor and the ground speed vector by GPS³⁵. Low-cost, highly maneuverable multirotor UAVs are more suitable for wind profile measurement due to their ability to hover in a specified position³⁶.

The accuracy of the digital elevation model (DEM) in the study is an important factor affecting the simulation results. In recent years, the rapid production of large-range and high-precision terrain models has mainly occurred through airborne laser measurements¹⁴, the Shuttle Radar Topography Mission (SRTM)³⁷, and the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER)³⁸, but the latest version of the SRTM and ASTER data set have a horizontal resolution of 30 m. Airborne laser measurements have a horizontal resolution of 1 m or even less, which is often down-sampled to 10 m, 30 m or 50 m for convenience. Creating a DEM with a resolution of 1 m for an area larger than a few square kilometers can be computationally heavy and is seldom used in practice. With the rapid development of UAV technology and the improvement in civilianization, UAV oblique photogrammetry has been widely applied in the field of modeling due to its flexibility, rapid acquisition of 3D data and low cost³⁹. However, oblique photogrammetry modeling is mainly applied in 3D urban modeling⁴⁰ and geological environment monitoring⁴¹with the exception of a paper discussing the performances of photogrammetry modeling for pedestrian wind simulation⁴². The potential of this technologies to be used in spatial wind fields over complex remains underutilized.

In recent years, wind fields over complex terrain have been well studied in areas such as wind urban ventilation and pollutant dispersion. Many studies of the cultural heritage wind fields have focused on the microclimate and natural ventilation inside caves^43,44,45,46, as well as the use of artificial gravel surfaces, shrub belts, and other methods to control wind-driven sand and wind erosion damage^47,48,49. The studies reported in the literature rarely focus on the question of how to provide spatial wind fields data for solving the problem of stone carving erosion caused by strong wind erosion, let alone the relationships between the local wind conditions and the wind erosion of historical stone carvings in semi-open grottoes. Moreover, with the exception of isolated hilly areas, simulations of wind fields over complex terrain verified by field measurements have received little attention²⁷. Additionally, the above application conditions focus on different wind field characteristic parameters. With the improvement in cultural relic protection, it is necessary to take the wind field into account as an integral feature of Grottoes.

The aims of this study are as follows: (1) to evaluate the accuracy of wind fields simulations with the Interpolated Multiscale Profile (IMP) method over complex terrain; and (2) to provide spatial wind field data of Xumishan Grotto Zone under neutrally stratified atmospheric boundary layer (ABL) over complex terrain. Based on the existing method of coupled NWP and CFD, the Interpolated Multiscale Profile (IMP) method is proposed to simulate wind fields over complex localscale terrain in this paper. Highly accurate point cloud data generated through unmanned aerial vehicle (UAV) oblique photogrammetry and wind vector profile estimated by multirotor UAV technology was used to establish a high-precision digital model and determine the accurate inlet boundary conditions. This study can provide theoretical support for a quantitative analysis approach to study relic wind fields and a scientific method for the conservation of historical stone carvings. By exploring the preventive protection technology of heritage sites, the study will promote the progress of the research and practice of cultural relics protection.

Site location and problem statement

The case under study is located in Northwest China, the Xumishan Grotto Zone roughly extends from 105°58'46”–105°59'21“E, 36°16'13”–36°17'18“N (Fig. 1). The stone carvings of the Xumishan Grottoes are mainly concentrated in the southern area, with Cave 5 as the center within 1 × 1 km². And due to the influence of the aerodynamic roughness length, the development of the mean velocity and turbulence properties of the ABL profile usually must consider the topographic influence 5–10 km upstream of the study area²⁷. Therefore, this paper focuses on the localscale wind fields within this range. The west side of the Xumishan Grottoes are mountains with higher altitudes, and the east side is the gradual dune slope.

Fig. 1: Topographic map of the surrounding terrain of Xumishan Grottoes.

a Top view; b Perspective view from east, where red is the Grotto Zone; c Perspective view from west.

The Xumishan Grottoes are located in the semiarid continental climate of the warm temperate plateau, where gales and sandstorms occur frequently. Wind erosion is a typical issue for stone carvings in this area⁵⁰. The deterioration of the Xumishan Grottoes is the long-term result, and wind blowing and rotary grinding are the main causes of wind erosion. Because most of the Grottoes are located in complex terrain such as cliffs, canyons and mountainous valleys, the wind field in the Grotto Zone is affected by the complex terrain.

Cave 5, which this paper focuses on, is representative of the Tang Dynasty statues in the Xumishan Grottoes. The cave where the giant Buddha is located is semi-open, 15.5 meters wide, 16.5 meters deep and 21.5 meters high (Fig. 2a). Cave 5 is located at the entrance of the valley. When air flows into the valley from the open area, it accelerates through and forms a high-speed canyon wind⁵¹. The Buddha statue and the mountain where it is located are seriously eroded by wind. The feet of the Buddha statue in the Grottoes have been eroded by strong wind into honeycomb caves (Figs. 2b and 2c).

Fig. 2: Xumishan Grottoes status.

a Buddha statue in Cave 5; b Wind erosion symptoms of mountain; c Wind erosion symptoms of Buddha foot.

Field measurements

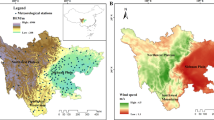
Climatological and meteorological stations for simulation comparison

To illustrate the characteristics of the local wind climate in the Xumishan Grotto Zone, meteorological data from 2020 provided by the Guyuan Observatory were selected. The Huangduobao meteorological station is located 5 kilometers northwest of Xumishan meteorological station, and the surrounding terrain is flat and without obstacles, so it can provide the prevailing wind direction in this area. The meteorological station of the Xumishan Grottoes, situated approximately 300 meters from Cave 5, provides accurate monitoring of the wind climate within the Grottoes zone (Fig. 3). Although located outside the immediate vicinity of Cave 5, this station serves as an appropriate reference site for assessing the wind climate in the Grottoes area. As illustrated in the map (Fig. 3), the station is positioned on the level ground, making it an ideal location for validating the results of the CFD simulations.

Fig. 3

Location of meteorological stations and Cave 5.

The installation of the meteorological station conforms to the ground meteorological observation specifications, and the weathervane and the wind cup are 10 m from the ground (Fig. 4).

Fig. 4

Anemometer in meteorological station of Xumishan Grottoes.

Figure 5a shows that the prevailing wind in the region is east and east-southeast all year round. Figure 5b shows that the wind near the Xumishan Grottoes meteorological station is mainly west-southwest and southwest due to the influence of the terrain. The topography has a great influence on the wind speed and direction of the wind field.

Fig. 5: Wind rose of mean wind speed (2020.1-2020.12).

a Huangduobao meteorological station; b Xumishan meteorological station.

Due to the prevailing wind direction and the location of the Huangduobao meteorological station, wind directions of 67.5°, 90°, 112.5° and 135° were selected as inflows to simulate the wind characteristics within the research area. The Huangduobao meteorological station was located upstream of the prevailing wind direction as a reference; the Xumishan Grottoes meteorological station was selected as a comparison to validate the accuracy of the simulation results. The measured data samples had to meet two requirements: First, only the 10-min average wind direction within the range of 10° of the inflow can be counted as valid sample statistics, and valid data groups of the wind direction sector must exceed twenty²⁷. Then, the averaged value and standard deviation of 10-min data within this sector are calculated. Second, the simulations of spatial wind fields are performed for neutral atmospheric conditions, which ignores the influence of the thermal effect on the wind speed. In a spatial wind field over the high complexity of the terrain, turbulence effects due to the terrain roughness are likely to be much larger than those induced by buoyancy⁵². To filter the data affected by the thermal effects, the 10-minute average wind speed of the meteorological station must be greater than a certain wind speed threshold. According to the regulations of sample processing for wind engineering, invalid data should be ignored, and valid data must be more than 98%⁵³. Then, a linear interpolation method is to interpolate the ignored data.

Selection of an appropriate threshold mean wind speed

The influence of the mountainous environment on the local wind conditions is mainly twofold, namely thermal and mechanical. On the one hand, the airflow moves vertically due to radiation and transmission from the ground surface, namely, convection. On the other hand, the horizontal airflow arises from the friction exerted by the wind against ground surface. This study focuses on the spatial wind fields of localscale complex terrain under neutrally stratified conditions, in which the thermal interaction should not be taken into consideration⁵⁴. It is important to filter the data affected by thermal effects, and make sure that the simulations are performed for isothermal conditions. The stability of the ABL Pasquill classification criteria needs to comprehensively consider meteorological data⁵⁵, such as wind speed, radiation, and cloud cover. Unfortunately, due to conditional limits, these data are not obtained in this study. A rough method of filtering the data affected by thermal effects is to set up a wind speed threshold, with the assumption that local wind are mainly affected by mechanical influence under high wind speed. The value of the threshold may affect the validation results. In order to ensure that the value of threshold can exclude the data affected by local thermal effects, it is necessary to compares the wind speed ratios of four different wind speed thresholds. The Pasquill atmospheric boundary layer stability classification criteria indicate that when wind speed is around 4 m/s, the conditions are classified as being between neutrally stratified and weakly unstable stratified states. Given the strong local wind conditions in the Xumishan Grotto Zone and the specific characteristics of the onsite observational data, the minimum wind speed threshold of 4 m/s was selected for the analysis of strong winds in order to meet the required sample size for the study. Four distinct wind speed thresholds were defined for the analysis:Uref, m = 4 m/s, Uref, m = 6 m/s, Uref, m = 8 m/s, and Uref, m = 10 m/s, as illustrated in Fig. 6.

Fig. 6: Comparison of wind speed ratios (Um/Uref, m) with different thresholds.

Comparison of wind speed ratios (Um/Uref, m) with different thresholds. Um refer to measured average wind speed of Xumishan meteorological station. Uref, m refers to measured average wind speed of Huangduobao meteorological station.

Wind speed measurements were collected at the meteorological station from January to December 2020 using anemometers (weathervane and wind cup). Data were sampled at 1 Hz and subsequently averaged over 10-minute intervals. The number of recorded samples, filtered according to the wind speed thresholds of 4 m/s, 6 m/s, 8 m/s, and 10 m/s, is presented in Table 1.

Table 1 The number of filtered record samples

The results show that the measured wind speed ratio decreases with increasing wind speed threshold. This trend is consistent with the above assumption. Under the condition of low wind speed, the flow is composed of mechanically induced flow and thermally induced flow. However, under high wind speed conditions, the thermal effect is weakened, and the mechanically induced flow becomes the main factor for air movement, which induce the decrease in the wind speed ratio. When the wind speed of the Huangduobao meteorological station is greater than 8 m/s, the value of the wind speed ratio tends to be constant. Therefore, it can be considered that when the average wind speed of the Huangduobao meteorological station is greater than 8 m/s, the measurement values that can be affected by local thermal effects were excluded.

UAV field meteorological observations

In this study, a quad rotor UAV (M210 V2, DJ, and Fig. 7) equipped with a DJI D-RTK2 global navigation satellite system, which can achieve high-precision positioning, with hover accuracy of 0.1 m in the vertical and horizontal directions. It had dimensions of 88 × 88 × 43 cm. The UAV sensor was a 2D ultrasonic anemometer (FT205, FT Technologies), which is specifically designed for UAV applications. The built-in electronic compass made it ideal for mobile platform applications. The ultrasonic sensor had a wind direction accuracy of 4° root mean square (RMS) and a resolution of 1°. The wind speed accuracy was 0.3 m/s (0–16 m/s range), ±2% (16 m/s-40 m/s range), and the resolution was 0.1 m/s. Sensors were mounted on aluminum poles 45 cm from the top of the UAV to ensure that the downwash generated by wing rotation did not disturb the accuracy of wind speed measurements. The ultrasonic sensor output data interval was 1 s. The data collected by the wind sensor were transmitted wirelessly from the receiving end installed on the UAV deck to the PC end, and the PC interface could display real-time wind speed and direction data. The maximum transmission capacity was 500 m in the view-through environment.

Fig. 7

Multirotor UAV installed with an ultrasonic anemometer.

To obtain the wind profile index α, meteorological observations were carried out up at the heights up to 300 m above ground level. The observation site was the Huangduobao meteorological station, and observations were conducted on 22 October 2020. The UAV was controlled to fly vertically while remaining stationary horizontally and hovering for 1 min at 10, 30, 50, 100, 150, 200, and 300 m above ground level. The flight was in a strong wind period above ground level within approximately 15 min, and the wind speed was measured during hovering. The applicability of UAV measure the wind speed profiles at multiple points was examined by meteorological field observations at Sakurajima⁵⁶. The observations was conducted by the UAV and Doppler lidar, and results shows that UAV can estimate the wind profile like a Doppler lidar does.

Figure 8 shows the wind profile at different heights measured by the meteorological UAV. Wind speed values measured at different heights are plotted with different symbols. The so-called “fitted profile” in Fig. 8 are obtained by least-square fit of the power law profile to the measured data. The wind profile measured by the UAV are shown by a green line, while the fitted wind profile is shown by the red line. The wind profile index α obtained by fitting was 0.26. According to the specifications of different surface categories²⁸, the surface roughness type of the Huangduobao meteorological station was determined to be the suburban type, and its wind profile gradient height was 500 m.

Fig. 8: Fitting curve of wind profile.

The error bars show the interquartile range of the 1-min wind speed data. The parameters in the box are the fitting wind profile index α and the fitting error parameters.

Numerical method

Interpolated Multiscale Profile (IMP) method

At present, the general numerical simulation is performed in one level and the inlet boundary of complex terrain is determined by fitting the velocity profile into an empirical (logarithmic/power) law namely, the Fitted Empirical Profile (FEP). To reflect the influence of topography on the characteristics of wind flow, the topographic area is usually expanded beyond the study area. The problem of excessive resource consumption caused by selecting a larger study area can be solved by simulating the higher-level and current-level.

The Interpolated Multiscale Profile (IMP) method performing numerical simulation of the wind field by simulating with the higher-level and current-level. The velocity and turbulence properties of the outlet boundary from the simulation results of the wind field at the higher-level was extracted as the inlet boundary conditions of the current-level simulation. In the current-level simulation, a power law wind profile is adopted at the inlet of the domain, and inflow turbulence characteristics are imposed using Eqs. (1)-(4):

$$U({\rm{z}})={U}_{{ref}}\left({\frac{z}{{z}_{0}}}\right)^{\alpha }$$

(1)

$${\rm{k}}({\rm{z}})={\left(U({\rm{z}}){\rm{\cdot }}{\rm{I}}({\rm{z}})\right)}^{2}$$

(2)

$${\rm{\varepsilon }}({\rm{z}})={C}_{u}^{3/4}{k}^{3/2}/({\kappa }_{v}z)$$

(3)

$${\rm{I}}\left({\rm{z}}\right)=\left\{\begin{array}{l}0.1{({z}_{b}/{z}_{G})}^{-\alpha -0.05}\;z\,\le\, {z}_{b}\\ 0.1{(z/{z}_{G})}^{-\alpha -0.05}\,\,\,{z}_{b} \,<\, z\,\le\, {z}_{G}\\ 0.1\qquad\qquad\qquad\,z \,> {z}_{G}\end{array}\right.$$

(4)

where ${z}_{0}$ and ${U}_{{ref}}$ are the standard reference height and standard reference wind speed, respectively, and are set to 10 m and 10 m/s in this paper. The fitting result for the profile index α is 0.26 according to the field test wind profile, and the gradient wind height is 400 m.

Note that the height of the computational domain in this work is not much lower than the atmospheric boundary layer height. To meet the inflow conditions required by ABL self-sustainability, the inflow turbulent kinetic energy and dissipation rate are formulated by Eqs. (3) - (4)²³. I (z) represents the turbulence intensity and is calculated according to the Architectural Institute of Japan (AIJ) load codes for buildings. ${C}_{u}$ = 0.09, and ${\kappa }_{v}$ is von Karman’s constant (${\kappa }_{v}=0.41$). ${z}_{b}$ = 15 m is the standard reference height, and ${z}_{G}$ = 400 m is the gradient height.

In traditional numerical simulation, the lowest point of the model entrance is used as the reference point to determine the inlet boundary conditions. However, this method is applicable only to the terrain where the inlet boundary has a similar elevation, such as seas or plains⁵⁷. In the cases of a large difference in the near ground elevation at the entrances of complex terrain, the wind speed at an entrance with relatively high elevation in the wind field is overestimated, and the simulation results are inaccurate. In this study, the user-defined function (UDF) program was compiled, and the method of block interpolation was adopted to determine the wind profile at each position of the inlet boundary according to:

$$U({\left(Z\right)}_{i})={U}_{{ref}}\left({\frac{{\left(Z\right)}_{i}}{{z}_{0}}}\right)^{\alpha }$$

(5)

where$\,{\left(Z\right)}_{i}$ is the actual height of each block, i = 1 to n, and n is the number of the interpolated blocks.

The accuracy of the results increases with increasing number of blocks. Taking the calculation burden and accuracy of the interpolation into consideration, the entrance boundary is divided into 100 blocks in this paper, leading to closer agreement between the modeled entrance boundary conditions in the complex mountainous region and the actual situation. The distribution of the entrance wind speed is shown in Fig. 9.

Fig. 9: Wind profile of inlet boundary.

a Traditional inlet boundary; b reasonable inlet boundary.

Due to the influence of the terrain 5–10 km upstream of the research area on the wind flow characteristics, the horizontal area of the computational domain is 10 × 10 km². The horizontal extent of the domain is sufficient to reflect the development of the approaching ABL. The maximum elevation difference within the research area is 430 m. Following the guidelines for numerical simulation setup⁵⁸, the vertical dimension of the computational domain is defined as 2 km. To reduce the calculation burden, the calculation area is divided into two areas: an outer area of 10 × 10 × 2 km³–1 km × 1 × 2 km³ and inner area of 1 × 1 × 2 km³. At the higher-level, a computational domain of 10 ×10 ×2 km³ is established. The Grotto Zone in this study is 1 × 1 km², a computational domain with the same size is established at the current-level, and the wind characteristics (including the velocity profile, turbulent kinetic energy profile and dissipation rate profile) of the higher-level simulation are used as the inlet boundary conditions of the current-level simulation (Fig. 10).

Fig. 10: Computational domains of numerical simulation.

Domain 1 is the higher-level domain. Domain 2 is the current-level domain. Dashed lines indicate interface of wind characteristics interpolated to the current-level.

A comparison between the FEP method and IMP method for CFD simulation of the wind field is presented in Fig. 11.

Fig. 11

Comparison between the FEP method and IMP method.

Geometry modeling, domain and grid

The terrain model with a horizontal resolution of 20 m within 10 km is established based on geographic information system (GIS) data. This paper focuses on the wind field in the 1 × 1 km² region centered on Cave 5 and establishes a horizontal resolution of 5 m in this area through UAV oblique photogrammetry. A DJ M210 V2 multirotor UAV with a centimeter-level navigation and positioning system and a high-performance imaging system was selected for low-altitude photogrammetry in this flight (Fig. 12). To ensure data accuracy, the flight was set with a lateral overlap rate of 75%, course overlap rate of 80%, relative flight height of 400 m and ground resolution of 10 cm. A total of 1348 original photos were obtained. The UAV flight time started at 10 am, the weather was clear, and the photo imaging effect was good.

Fig. 12

UAV oblique photography.

After the image photos required for modeling were obtained, the software Context Capture was used to complete aerial triangulation calculations (Fig. 13a). The aerial triangulation calculation of the software was automatically completed under the bundle block adjustment method and optimized based on the spatial rectangular coordinate system. The exterior orientation elements of each photo were calculated using Position and Orientation System (POS) data processing results. According to the exterior orientation elements calculated by aerial triangulation, dense surface point clouds could be obtained by intensive matching of multiview images. Due to the influence of flight factors and ground object shelter, the point cloud data produced by oblique photogrammetry will inevitably have abnormal values. And because the course must maintain a certain degree of overlap, point cloud data of different course should be accurately splicing to eliminate systematic error and random error as far as possible. The software Terra Solid was used to perform outlier culling, point cloud filtering, data splicing, and point cloud classification output to generate a DEM.

Fig. 13: UAV oblique photography image processing.

a Aerial triangulation calculation procedure; b 3D model of Xumishan Grottoes; c Digital Elevation Model of Xumishan Grottoes

To adapt to the complex mountainous terrain of the Xumishan Grottoes, boundary layer elements (prismatic cells) parallel to the walls and ground surfaces can better meet the flow of wind in the boundary layer. In the vertical direction, the grid height of the first layer near the ground is set as 0.05 m in accordance with the standard wall function requirements, so the corresponding value of y+ within the range of 30–300. The boundaries of the ground are covered with several layers of prisms, and tetrahedral unstructured grids are filled to adapt the complicated geometry. The growth factor of the grid from bottom to top is 1.2 (Fig. 14).

Fig. 14: Calculation domain grid.

a Wall boundary layer grid; b Side view; c Top, east and south vertical side surface of the domain.

To ensure the accuracy of the simulation results and to reduce the use of computing resources, three grid meshing schemes are adopted for the grid sensitivity analysis, as shown in Table 1. The wind speed ratio of the three schemes corresponding to different monitoring points in the Xumishan Grottoes is calculated and compared to determine the final grid division scheme. The wind speed ratio is defined as:

$${K}_{i}=\frac{U}{{U}_{{ref}}}$$

(6)

where ${K}_{i}$ is the wind speed ratio corresponding to the grid meshing scheme i, U is the wind speed of the monitoring point, and ${U}_{{ref}}$ is the wind speed at the Huangduobao meteorological station. Table 2.

Table 2 Meshing schemes

The comparison results of the wind speed ratios at the monitoring points of different schemes (Fig. 15) show that the simulated deviation between schemes 1 and 2 is close to 20%, while the simulated deviation between schemes 2 and 3 is less than 10%, indicating that the computational accuracy of schemes 2 and 3 is similar, and scheme 3, with the most grids has the highest calculation accuracy. Considering the current computing power and simulation accuracy, meshing scheme 2 is used in the following CFD simulation.

Fig. 15: Grid sensitivity analysis results.

a Comparison of schemes 1 and schemes 2; b Comparison of schemes 2 and schemes 3

Setting computing parameters

The roughness of the terrain in the computational domain largely determines the development of wind flow in the ABL within the region^27,59,60. In this paper, the roughness is modified in Ansys/Fluent 14.0 using the wall function and based on the roughness height ${k}_{s}$ and the roughness constant${\rm{C}}{\rm{s}}$. First, the terrain in the computational domain is subdivided according to a similar roughness(as shown in Table 3), and then the roughness value is estimated according to the updated Davenport roughness classification²⁸. The roughness ${z}_{0}$ is converted into the corresponding wall function parameters ${k}_{s}$ and ${\rm{C}}{\rm{s}}$ (see Fig. 16). The calculation formula is derived as⁶¹:

$${k}_{s}=\frac{9.793{z}_{0}}{{\rm{C}}{\rm{s}}}$$

(7)

Table 3 Classification of surface types and corresponding$\,{k}_{s}$ and ${\rm{Cs}}$

Fig. 16

Subdivision of local terrain based on roughness classification

When using CFD simulation methods to analyze turbulence models, Direct Numerical Simulation (DNS) can obtain flow information for each scale. However, a sufficient number of grids are needed to simulate all scales of flow, which canncot be achieved with the current computational performance of computers. In addition, Large Eddy Simulation (LES) is a method whereby Navier-Stokes equations are averaged in a certain spatial area to filter out small-scale vortices in the flow field and to derive the equations satisfied by large-scale vortices. This cost is at least an order of magnitude larger than that for RANS and possibly two orders of magnitude larger when including the necessary actions for verification and validation, so LES remains very computationally demanding. The RANS method averages the basic equations of a fluid and represents the pulsation components that differ from the mean by the model. RANS method undeniably has limitations in capturing the turbulent kinetic energy, and does not capture the fluctuating wind pressure on the surface of the object. While this method can balance calculation precision and calculation resources well and is the main method used in wind engineering problems for predicting mean wind speeds in high-speed areas. The high wind speed is also a crucial factor in the wind erosion damage to the cave, making it an important focus of the study⁶².

Flow in the atmospheric boundary layer (ABL) over complex terrain is inherently unsteady, and therefore, strictly speaking, an unsteady approach is needed. However, the unsteady turbulence model and the spatial-temporal varying inflow conditions are indispensable for the simulation of unsteady wind event. Considering the current computer hardware, in recent years, the simulation of a real unsteady atmospheric boundary layer flows with more than 10 millions of grid cells is not realizable^18,63. In addition, although URANS and LES is intrinsically superior, because the lack of BPGs it can even yield results that are less accurate and less reliable that those by RANS⁵⁸. Despite claims over the past decades that LES would make RANS obsolete, RANS remains widely used in in outdoor airflow simulation researches^64,65. Therefore, CFD simulations were performed with the steady RANS approach. Regarding the choice of turbulence models, the realizable k–ε turbulence model introduces a new formulation for the turbulent viscosity and a new transport equation for the dissipation rate and exhibits superior performance for the flows involving separation and recirculation, which is appropriate for high-Reynolds number flows and efficient in convergence with skewed tetrahedral grids^66,67. And this paper mainly focuses on the mean flow characteristics of the Xumishan Grottoes. Hence, the realizable k–ε model was adopted in this study based on its comprehensive performance.

The implicit solver is used for incompressible modeling through the finite-volume CFD code Fluent. The semi-implicit method for pressure linked equation (SIMPLE) algorithm is used to solve the pressure-velocity coupling. The pressure term is discretized in the second-order scheme, and the convective term and viscous term are discretized in the second-order quadratic upstream interpolation for convective kinematics (QUICK) scheme.

The convergence criterion is that the residuals stay at a relatively low value (continuity: 10⁻³, k and ε: 10⁻⁴, and x- y- and z-momentum: 10⁻⁵) and that the wind speed of key points basically does not change. The sides and top surfaces of the computational domain are free-slip boundary conditions, where the velocity components and the normal gradients of all velocity components are zero. At the outlet, a zero pressure outlet boundary is set.

Results and discussion

Comparison between the measured and simulated results

The measured wind speed ratios (K) and wind direction are compared with the simulated results obtained by the FEP and IMP methods. As mentioned in Section 4, the wind speed ratio K is the wind speed at a 10 m height of the Xumishan Grottoes meteorological station at the measurement point divided by the wind speed at the same height of the Huangduobao meteorological station at the reference point. Figures 17–20 show the colour contours of wind speed ratio at inlet wind directions of 67.5°, 90°, 112.5° and 135°. The mean and standard deviation of the measured values and wind speed ratio and wind direction are given in the Tables 4–7, as well as the simulated values. For the speed ratio K in the measurement position, the simulated values are in black, and the measured values are in red, and the wind direction standard deviation of the measured values is in red.

Fig. 17: Colour contours of the simulated wind speed ratio at 10 m height above ground for the inlet wind direction θ = 67.5°.

a FEP method; b IMP method.

Fig. 18: Colour contours of the simulated wind speed ratio at 10 m height above ground for the inlet wind direction θ = 90°.

a FEP method; b IMP method.

Fig. 19: Colour contours of the simulated wind speed ratio at 10 m height above ground for the inlet wind direction θ = 112.5°.

a FEP method; b IMP method.

Fig. 20: Colour contours of the simulated wind speed ratio at 10 m height above ground for the inlet wind direction θ = 135°.

a FEP method; b IMP method.

Table 4 Average values and standard deviations for the inlet wind direction θ = 67.5°

Table 5 Average values and standard deviations for the inlet wind direction θ = 90°

Table 6 Average values and standard deviations for the inlet wind direction θ = 112.5°

Table 7 Average values and standard deviations for the inlet wind direction θ = 135°

Figure 21a compares the measured values for wind speed ratio K and the simulated values of IMP and FEP in the four inlet wind directions (67.5°, 90°, 112.5° and 135°) that meet the requirements (as described in Section 3). For the IMP method, the numerical values are generally within 20% of the corresponding measurements, and those of the FEP method are up to 40%. Figure 21b provides the measured values of the same inflow wind direction as well as the simulated values of IMP and FEP. The maximum difference value of the FEP method is 30%, while that of the IMP method is less than 20°. The results show that compared with the traditional FEP method, the IMP method can more accurately simulate the spatial wind field of complex terrain. The inlet inflow boundary conditions of this method retain greater accuracy on the basis of the actual wind field characteristics of complex terrain, so the IMP method has certain rationality and superiority. The following discussion is based on the simulation results obtained by the IMP method.

Fig. 21: Simulation results of FEP and IMP methods.

a Wind speed ratio; b wind direction.

Simulated wind-flow patterns in the Grottoes

Based on the above validation, this part analyzes the wind-flow patterns in the Grotto Zone under different inflow conditions, focusing on the impact of terrain on the wind field in front of Xumishan Grottoes Cave 5.

Figure 22 presents the colour contours of wind speed ratio at 10 m height from the ground under different inflow wind directions. The simulation results show that the distribution of wind speed and direction near the surface is significantly different from that in flat areas due to the severe fluctuation of mountain elevation. Generally, the wind speed is larger at the ridge and smaller at the valley. Under each wind direction, the distribution of wind speed in the high wind speed area of the ridge has a certain difference. The west side of Cave 5 is a steep mountain range, to the east lies the river valley, overall form a terrain similar to “one-way open groove”. For wind directions 45° and 90°, on the windward side and the top of the mountain, because mountain block causes air currents to rise, extrusion, accelerate the phenomenon is more obvious at the top of the mountain, the top position of the wind speed ratio between 2.1 ~ 3.0; For wind directions 270°and 315°, influenced by the high mountains in the upper reaches of the northwest direction, the air flow in the coming direction is separated and the wind shadow area is generated in the lower reaches of the mountain, making the wind speed at the top of the mountain lower with the wind speed ratio between 0.3 ~ 0.9.

Fig. 22: Colour contours of the simulated wind speed ratio at 10 m height above ground for the inlet wind directions of 22.5°–360°.

a 22.5°; b 45°; c 67.5°; d 90°; e 112.5°; f 135°; g 157.5°; h 180°; i 202.5°; j 225°; k 247.5°; l 270°; m 292.5°; n 315°; o 337.5°; p 360°.

Figure 23 shows the distribution of the wind speed ratio in Cave 5 height under different inflow directions. Under different inflow wind directions, there are significant differences in the wind speed in front of the Cave 5. When the inlet wind direction is northeast, the wind speed amplification coefficient reaches the maximum value of 2.1. At this time, the inlet wind direction is basically consistent with the valley trend near Cave 5, and the airflow is less blocked. The rough cliffs on both sides of the valley are irregular, so the maximum wind speed is not in the valley center but near the entrance to the valley of the protruding topography on both sides of the hillside; this is similar to the windy ridge effect. The wind speed increases near the outer edge of the protrusion, and the leeward side wind speed decreases; thus, in the analysis of the wind field in the Grotto Zone, the influence of the local topography cannot be ignored. When the angle between the inlet wind direction and the river channel increases, the mountain barrier effect appears, and the wind speed in front of the cave decreases accordingly. When the wind direction is northwest, the blocking effect of the mountain on the northwest side result in the wind speed in front of the cave on the leeward side of the mountain reaches the lowest value, and the wind speed amplification coefficient is 0.3.

Fig. 23: Colour contours of the simulated wind speed ratio in a horizontal plane at Cave 5 height for the inlet wind directions of 22.5°–360°.

a 22.5°; b 45°; c 67.5°; d 90°; e 112.5°; f 135°; g 157.5°; h 180°; i 202.5°; j 225°; k 247.5°; l 270°; m 292.5°; n 315°; o 337.5°; p 360°.

Figure 23 also shows the wind velocity vector around the Cave 5 for the inlet wind directions of 22.5°–360°. When the flow from northeast and southwest, the wind velocity vector around the Cave 5 was similar to inlet wind directions. The relative uniform wind velocity vector illustrate wind characteristics is associated with lower turbulence. If the flow from northwest, the wind velocity vector varies greatly in the hill downstream region around the Cave 5.The significantly change of wind velocity vector indicate that turbulence increases locally. The significantly change of wind velocity vector for the northwest flow is attributed to the Cave5 located at the wake region of reversed flow close to the ground on the lee side of the hill. The wake region behind the hill where the wind speed is reduced and a maximum in turbulent kinetic energy. The genesis of wake region is due mainly to the adverse pressure gradient on the lee side of the hill.

Relationship between local wind conditions and wind erosion

The experimental investigation of wind erosion on stone carvings using a wind tunnel demonstrates that the extent of wind erosion is strongly influenced by wind speed. Moreover, the wind erosion modulus exhibits a significant increase as wind speed rises⁶².The average wind speed is a positive factor affecting the value of the wind erosion modulus. Wind erosion for stone carvings is generally relevant at high wind velocity, while the air turbulence was not considered; therefore, generally it was neglected. This means that if other factors in climatic conditions remain constant, when the inlet wind direction is northeast, the wind speed amplification coefficient of Cave 5 is 7 times greater than that of the northwest wind, and the extent of wind erosion is significantly more pronounced compared to the northwest wind. Therefore, analysis should focus to primary-harm wind direction when historical stone carvings is at the highest erodibility conditions and the most effective way to mitigate the wind erosion of the historical stones is to reduce the mean velocity around Cave 5.

Since wind speed is the most important factor affecting wind erosion of rock in cave wind environment, this paper chooses northeast wind direction (the maximum wind speed direction in front of Cave 5) and northwest wind direction (the minimum wind speed direction in front of Cave 5) as incoming wind direction to study the influence of wind environment on wind erosion.

The pressure distribution on the mountain surface is shown in Fig. 24. As can be seen from the figure, when the incoming flow is northeast, the maximum pressure on the mountain surface within the cave area appears on the windward side of the mountain and in the valley area between the two mountains. The surface pressure value near Cave 5 is 192 Pa. The sand-carrying wind impact caused by high mountain surface pressure will accelerate the wind erosion degree of the stone carvings surface. When the wind turned from east to northwest, the surface pressure distribution on the east and south sides of the mountain decreased significantly, and the pressure value reached the minimum value -150Pa at the top of the slope. After crossing the top of the mountain, the wind pressure on the leeward side gradually recovered. Cave 5 was located on the leeward side of the hill, and the surface pressure near it was 6 Pa.

Fig. 24: The pressure distribution on the mountain surface.

a 45°; b 315°.

Figure 25 shows the distribution of friction coefficient on the mountain surface. As shown in the figure, when the incoming flow is eastward, the friction coefficient of the windward side of the mountain and the ridge is relatively high. The southeastern part of the mountain where Cave 5 is located is exposed to high shear stress, and the sand-carrying wind rotational grinding results in obvious wind erosion on the mountain surface. When the incoming flow is northwest wind direction, the friction coefficient of the mountain surface reaches the maximum value at the top of the mountain, but the value is smaller than that of the northeast flow.

Fig. 25: Mountain surface friction coefficient distribution map.

a 45°; b 315°.

Finally, in order to analyze the influence of wind environment on the stone carvings in the cave area and the mountain wind erosion, the northeast direction, which is the most critical influence on the wind erosion, is selected as the incoming flow direction, and the friction coefficient and surface pressure distribution on the mountain surface are analyzed. Then, make an intuitive comparison between the obtained friction coefficient and surface pressure with the image of the current condition of the mountain and stone carving cultural relics, as shown in Fig. 26. These areas are affected by high surface pressure and shear stress under the action of strong winds, which may be the main cause of wind erosion of stone carvings.

Fig. 26: Comparison of actual mountain condition and predicted mountain wind erosion area.

a Recent images of the mountain and cave; b Average pressure distribution; c Average surface friction coefficient distribution.

Conclusions

Based on the three-dimensional steady RANS equation and localscale numerical simulation of Realizable K -ε model, the spatial wind field of the Xumishan Grottoes over complex terrain are studied in this paper. The main conclusions are summarized as follows:

• (1) CFD simulation based on the IMP method provides inflow conditions more consistent with wind characteristics for the numerical simulation of wind fields in complex terrain composed of mountains and valleys at different elevations. With the establishment of a high-precision DEM, the actual terrain characteristics are retained, the actual wind characteristics are reproduced, and the computational efficiency is improved. Compared with those of the traditional FEP method, the simulated values of the IMP method are closer to the measured values. The difference between the measured and simulated values of the IMP method is nearly 20%, and the difference between the measured and simulated values of the FEP method is 40%. The maximum difference between the simulated wind direction and the measured wind direction by the FEP method is 30%, while the comparison result by the IMP method is less than 20°. Compared with the FEP method, the IMP method is a more accurate numerical simulation.

• (2) With an increasing mean wind speed at the inlet boundary, the measured wind speed ratio presents a declining trend because under the conditions of high wind speed, the thermal effect is weakened, and the mechanical effect becomes the main factor of air movement. Since only mechanical turbulence is simulated in CFD, the results of numerical simulation methods become more consistent as the threshold increases. When the wind speed of the Huangduobao meteorological station is greater than 8 m/s, the value of the wind speed ratio tends to be constant. Therefore, it can be considered that the measurement values that could be affected by local thermal effects were excluded and it is recommended to adopt a relatively high wind speed threshold based on the premise of sufficient wind samples.

• (3) Compared with the wind tunnel test, CFD can obtain the wind field flow characteristics of each location in the whole domain and then analyze the influence of the local terrain on the wind field in the Grotto Zone. When the wind direction is 45°, the funnel effect of local terrain leads to an increase in wind speed in front of the cave. For the 315° wind direction, the shielding effect of the mountain leads to a significant decrease in the wind speed in front of the cave.

• (4) When the incoming flow is from the northeast, the surface pressure near Cave 5 is 192 Pa, and the friction coefficient of the mountain surface is 0.006. The wind’s blowing and grinding effects on the mountain accelerate wind erosion on the surface of the stone cultural relics, which is detrimental to their preservation.

CFD simulation based on the IMP method is feasible for studying spatial wind fields under complex localscale terrain. Urban ventilation corridor planning and urban pollutants dispersion are all based on localscale wind fields simulations. The study of this paper also provides a reference for similar scale wind field simulations.

However, in view of the diversity of influencing factors in wind fields researches on complex terrain, there are still some problems and challenges worthy of further study: (1) This paper establishes the whole terrain model based on the geographic information elevation data obtained by GIS and UAV oblique photography modeling. For small-scale terrain features, such as individual buildings and trees, the roughness of the wall function is corrected by the adjusting parameters K_S and C_S. Therefore, the effects of vegetation and architecture on microscale wind fields need to be further studied. (2) This study focuses on the impact of strong wind erosion on stone carvings in the Grottoes, so the current simulation is limited to neutral atmospheric conditions. However, in reality, the nonneutral ABL is affected by local thermal effects. Therefore, thermodynamic processes should be considered in future work. (3) In this paper, the Reynolds-averaged model is used to simulate only the time-averaged wind field under the influence of complex terrain. With the progress of CFD numerical simulation technology and improvements in computing power, more accurate equations such as LES should be used for research.