Introduction

Over eighty years ago, Rabi oscillations were proposed to describe the strong coupling and population transfer in a two-level quantum system exposed to an oscillatory driving field1. From then on, Rabi oscillation plays an essential role in abundant physical phenomena and is considered as one of the most fundamental processes in light-matter interactions with a characterized frequency given by the laser parameters as well as the energy gap and dipole between two involved electronic states. It is utilized to control the quantum state in a single quantum dot2,3,4, lay the foundation for quantum computation5, realize the coherent phase modulation of free-electron states6, observe the many-atom entangled state in an optical-clock transition7, and enhance the collective atom-light coupling8,9. With the advent of intense ultrafast laser pulses, one is able to observe the Rabi oscillation of resonant state in continuum spectra10,11, also named as Autler-Townes splitting12. Recently, by utilizing the Freeman resonance13, the femtosecond two-photon Rabi oscillations in atoms have been demonstrated14. The laser-driven transient dipole response was experimentally reconstructed15, and the breaking of the area theorem of the carrier-wave Rabi flopping16 was observed in the high-harmonic generation of atoms17.

As compared to atoms, molecules have an extra degree of vibration, which adds an additional knob to the Rabi oscillations in light-molecule interactions. Taking H2+ as an example, during its stretching or dissociation, the energy gap and the dipole between the ground (1sσg) and excited (2pσu) states vary, leading to the bond-length-dependent Rabi frequency for a given laser field. Though Rabi oscillations in atoms and solid-state systems have been extensively studied, surprisingly, only a few theoretical and experimental works reported Rabi oscillations in molecules. In 1996, the two-photon Rabi oscillation in a three-level molecular system was demonstrated in both theory and experiment18. In 1999, the Rabi oscillation among dissociative states of a Na2+ molecule was theoretically explored19 but yet lacked experimental observations yet. It is recently predicted that the laser-driven Rabi oscillation in H2+ depends on the molecular orientation, and thus the dissociative fragments present angular nodes in their angular distributions20. Generally, Rabi oscillations in a molecule inevitably couple with the nuclear motion21. However, how such a coupling determines the kinetic energy release (KER) in the dissociative fragments is still an open question.

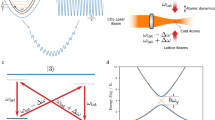
Here we unveil the importance of the dynamical Rabi coupling in strong-laser-field dissociation of H2+ and explore intriguing dissociation dynamics beyond the well-accepted resonant one-photon dissociation scenario22,23,24,25,26,27,28,29,30,31,32,33,34,35. During the dissociation, coupled with the laser field, the electron hops between the 1sσg and 2pσu states, forming the Rabi oscillations. Meanwhile, as illustrated in Fig. 1, the nuclear wave packet (NWP) may propagate alternatively along the two potential energy curves towards a larger internuclear distance monotonically, termed as the rolling process, or may propagate outwards along the 2pσu potential energy curve followed by the inward propagation in the 1sσg potential curve and then be relaunched to 2pσu state again followed by subsequent dissociation, termed as the looping process. The rolling and looping dissociation pathways lead to different KERs of the ejected protons. In the following, we first verify the role of the Rabi oscillations in strong-laser-field dissociation of H2+ and then analyze the proton energy spectra determined by the rolling and looping processes, which are afterward compared with the experimental measurements.

Fig. 1: Schematic illustration of dynamical Rabi coupling in strong-field dissociation of H2+.
figure 1

Violet and orange curves denote the potential energy curves of the electronic ground (1sσg) and excited (2pσu) states, respectively. The yellow vertical arrow between the two curves indicates the resonant one-photon transition at Rω. The two insets sketch the looping and rolling processes during the molecular dissociation, marked by the gray frame. The dashed horizontal line marks the eigenenergy of the υ = 6 vibrational state on the 1sσg potential energy curve

Full size image

Results

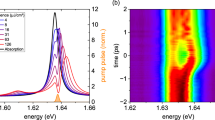
Verifying laser-driven Rabi oscillations in molecular dissociation

The dissociation of H2+ is governed by the laser coupling of the two lowest electronic states. We, therefore, simulate the two-level time-dependent Schrödinger equation (TDSE) (see “Methods”) and trace the wave function evolution to unveil the mechanism. We start from the v = 6 vibrational state on the 1sσg potential energy curve since such an NWP has the maximum population at around Rω = 3.8 to embrace the well-accepted one-photon resonant excitation26,33,34,36,37,38, as illustrated in Fig. 1. The laser pulse has four optical cycles and the central wavelength is 400 nm. Figure 2a shows the laser-intensity-dependent proton KER spectrum of the laser-dissociated H2+. The vertical integration of Fig. 2a over the region of 1.5 eV < KER < 2.5 eV gives the intensity-dependent dissociation probability, as shown by the solid red curve in Fig. 2b. In Fig. 2a, the concentrated yield of protons around 2.0 eV in the KER spectrum at weak laser intensities originates from the dissociation via the one-photon resonant transition between 1sσg and 2pσu states at around Rω = 3.826,33,34,36,37,38, termed as the resonant one-photon dissociation pathway, which is however completely suppressed at the laser intensity of 4 × 1013 W/cm2. In both Figs. 2a and 2b, one can see that the dissociation probability oscillates with the increasing laser intensity. To understand such a strong modulation of the intensity-dependent dissociation yield, we perform TDSE simulations by temporarily freezing the nuclear motion and fixing the internuclear distance to be Rω, i.e., only switching on the dipole transition at Rω. Such a treatment is analogous to perform a simulation in atomic systems. The atomic-like calculations give the population on the 2pσu state at the end of the laser pulse, as shown by the blue curve in Fig. 2b.

Fig. 2: Observing dynamical Rabi coupling using a few-cycle laser pulse.
figure 2

a The simulated KER spectra of dissociative fragments as a function of the peak intensity of a four-optical-cycle 400-nm laser pulse. Red and blue dashed curves denote the predicted KER using Eq. (3), where the molecule undergoes half-integral and integral Rabi oscillations at different internuclear distances, respectively. b Populations of the 2pσu state after the laser-H2+ interaction, i.e., the proton yield, as a function of the laser intensity. The red curve is obtained by integrating the two-dimensional map in a over the region of 1.5 eV < KER < 2.5 eV. The blue curve is numerically simulated by only switching on the transition at Rω. The black dashed curve is analytically calculated using Eq. (1). The maxima of all the curves are normalized to one for the convenience of comparison. c The dissociation yields as a function of the KER obtained by integrating the two-dimensional map in (a) within the laser intensity regions of [0, 3.7 × 1013], [3.7 × 1013, 1.5 × 1014], and [1.5 × 1014, 4 × 1014] W/cm2 corresponding to the three peaks. d Number of Rabi oscillations Nosc as a function of the laser intensity and internuclear distance. White, red, and black dashed curves denote the positions where Nosc = 1, 2, and 3, respectively. The initial state in the calculation is the v = 6 vibrational state

Full size image

In the atomic-like simulation, within the rotating wave approximation omitting the high-frequency term and reserving the near-resonance low-frequency term39, one can analytically write down the time-dependent population of the 2pσu state at a given internuclear distance Rr where Rabi oscillations occur39 as follows

$$P_u\left( {I_0,R_r,t} \right) = \frac{{E_0^2D^2\left( {R_r} \right)}}{{\omega _r^2\left( {I_0,R_r} \right)}}\sin ^2\left[ {\frac{{\omega _r\left( {I_0,R_r} \right)}}{2}t} \right]$$
(1)

where \(\omega _r\left( {I_0,R_r} \right) = \sqrt {\left[ {E_0D\left( {R_r} \right)} \right]^2 + \left[ {V_u\left( {R_r} \right) - V_g\left( {R_r} \right) - \omega } \right]^2}\) denotes the Rabi frequency as a function of the laser peak intensity I0 = E02 and the internuclear distance Rr considering the nuclear motion of H2+. According to Eq. (1), the population of the 2pσu state approaches maximum when \(\frac{{\omega _r\left( {I_0,R_r} \right)}}{2}t = \left( {n + \frac{1}{2}} \right)\pi\), with n an integer starting from 0. Thus, the number of Rabi oscillations at the end of the laser pulse is described as

$$N_{{{{\mathrm{osc}}}}}\left( {I_0,R_r} \right) = \frac{{\omega _r\left( {I_0,R_r} \right)\tau _{{{{\mathrm{eff}}}}}}}{{2\pi }} = \frac{{\omega _r\left( {I_0,R_r} \right)N_{{{{\mathrm{eff}}}}}}}{\omega }$$
(2)

where τeff = NeffT denotes the effective duration of the laser pulse for a square-of-sine-shaped envelope, which means that only the central part of the laser pulse is strong enough to induce the Rabi oscillation. Here, by setting the effective optical cycle of Neff = 1.88, the population of the 2pσu state governed by Eq. (1) as a function of the laser intensity, shown as the black curve, agrees with the other two curves in Fig. 2b. All these agreements verify the Rabi oscillation in the dissociation of H2+. Integral (half-integral) Rabi oscillations lead to the minimum (maximum) population of the 2pσu state and thus determines the yield of the protons around 2.0 eV.

KER spectra determined by rolling and looping dynamics

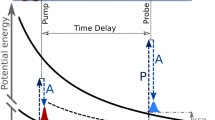
After verifying the Rabi oscillations in strong-laser-field dissociation of H2+, we now analyze how it alters the KER of the ejected protons. Compared to atoms, Rabi frequency in molecular dissociation depends on the bond length. More importantly, the bond stretching and Rabi oscillations are inevitably coupled, which challenges our understanding of the KER spectrum based on the well-accepted dissociation scenario. In Fig. 2a, in addition to the main peak located around 2.0 eV, one may see the high-energy tails above 2.5 eV guided by the red arrow and the low-energy shifts below 2.0 eV guided by the green arrow in Fig. 2c. The KER spectra labeled with different peaks in Fig. 2c are obtained from Fig. 2a by horizontally integrating over different intensity regions, i.e., [0, 3.7 × 1013], [3.7 × 1013, 1.5 × 1014] and [1.5 × 1014, 4 × 1014] W/cm2. Such unexpected characters can be understood by tracing the Rabi oscillations in the time domain. As illustrated in the insets in Fig. 1, once the H2+ is pumped to the 2pσu state from the 1sσg state, the NWP may move outwards and gain kinetic energy. Besides the direct dissociation along the 2pσu potential energy curve, this NWP may transit back to the 1sσg state at a large internuclear distance due to the Rabi oscillation. Then, the NWP continuously moves outwards along the 1sσg curve, followed either by being pumped again to the 2pσu state at a larger internuclear distance, or by decelerating and then reversing its moving direction before being transited again to the 2pσu state at a smaller internuclear distance followed by subsequent dissociation. These two scenarios are named as rolling and looping processes, respectively. The looping and rolling dissociation pathways end with protons carrying larger and smaller kinetic energies, respectively, compared to the resonant one-photon pathway.

To quantitatively understand the KERs induced by the aforementioned rolling and looping processes illustrated in Fig. 1, we formulate the KER of the dissociating NWP as

$${{{\mathrm{KER}}}} = E_v + {{\Delta }}V\left( {R_\omega } \right) - {{\Delta }}V\left( {R_r} \right) + {{\Delta }}V(R_{r^\prime }) - V_u( + \infty )$$
(3)

where Ev denotes the eigenenergy of the v = 6 vibrational state on the 1sσg potential energy curve, Rω, Rr and \(R_{r^\prime }\) denote the transition internuclear distances, ΔV(R) denotes the R-dependent energy gap between 1sσg and 2pσu states, and Vu(+∞) denotes the dissociation limit of the 2pσu state. Here, the critical internuclear distances Rr and \(R_{r^\prime }\) are determined by the nuclear motion at the most probable instant where the population of the 2pσu state achieves another maximum after the first one-photon transition from 1sσg to 2pσu states at Rω. According to Eq. (2), one may retrieve the internuclear distances Rr to accomplish integral or half-integral Rabi oscillations if the laser pulse is given. For example, the critical internuclear distances for integral Rabi oscillations (Nosc = 1, 2, and 3) are indicated as the dashed curves in Fig. 2d. Based on these critical internuclear distances, we can predict the maxima and minima of the proton yield as a function of the KER and laser intensity. For instance, considering the looping dynamics where the inward-moving NWP on the 1sσg state is assumed to undergo another one-photon transition at Rω, Eq. (3) can be written as

$${{{\mathrm{KER}}}} = E_v + {{\Delta }}V\left( {R_\omega } \right) - {{\Delta }}V\left( {R_r} \right) + {{\Delta }}V(R_\omega ) - V_u( + \infty )$$
(4)

According to the simplified formula Eq. (4), the proton KERs from the dissociation of H2+ undergoing integral or half-integral Rabi oscillations as a function of the laser intensity are plotted with blue and red dashed curves in Fig. 2a. The red and blue dashed curves precisely predict the location of the maximum and minimum proton yields, respectively. The excellent accordance between the analytical calculation and numerical simulation verifies the origin of the high-energy and low-energy protons, i.e., produced via the looping and rolling pathways ensured by the bond-length-dependent dynamical Rabi coupling.

Pulse-length-dependent Rabi oscillations

Such dynamical Rabi coupling becomes more prominent if the driving laser pulse has a longer duration since more Rabi oscillations will be involved during the stretching of the molecule. Figure 3a shows the intensity-dependent proton KER spectrum driven by a ten-optical-cycle laser pulse with a central wavelength of 400 nm. The proton yield integrated over the whole energy region as a function of laser intensity is plotted by the red curve in Fig. 3b. Note that the red curve has been normalized by its maximum. The corresponding atomic-like calculation is shown by the blue curve in Fig. 3b with the same laser parameters. The smaller modulation depth of the red curve here compared to the red one in Fig. 2b is undoubtedly attributed to the more distinct nuclear motion in a longer laser pulse. Multiple Rabi oscillations bring several looping processes, which may mix with the rolling process, resulting in complex KER distributions. The low KER distribution, guided by the black arrow in Fig. 3a, shows a clear tendency that the energy peaks shift lower monotonically with the increasing laser intensity induced by the pure rolling pathway. On the contrary, the branch having the highest KER, as guided by the yellow arrow in Fig. 3a, is due to the pure looping process. The mixture of looping and rolling processes contributes to the KER spectra between these two branches. The most prominent mixed pathway is the first-order looping pathway, meaning that there is only one looping process happening during the whole rolling process, guided by the red arrow in Fig. 3a. It should be mentioned that the mixed pathway is a sequential process of looping and rolling. However, the order of these two processes may depend on the instantaneous field strength and nuclear momentum when the NWP reaches critical internuclear distances for Rabi oscillations.

Fig. 3: Verifying rolling and looping dynamics in a multicycle laser pulse.
figure 3

a The simulated KER spectra as a function of the peak intensity of a ten-optical-cycle 400-nm laser pulse. b Populations of the 2pσu state after the laser-H2+ interaction, i.e., the proton yield, as a function of the laser intensity. The red curve is obtained by integrating the two-dimensional map in (a) over the whole KER region. The blue curve is numerically simulated by only switching on the dipole transition at Rω. The maxima of both curves are normalized to one for the convenience of comparison. c The dissociation yields as a function of the KER obtained by integrating the two-dimensional map in (a) within the laser intensity regions of [0, 1 × 1012], [5 × 1013, 9 × 1013] and [1.3 × 1014, 2 × 1014] W/cm2, corresponding to the 1st, 4th and 6th peaks, respectively. d Temporal evolution of the density distribution of χu calculated with the laser intensity I0 = 1 × 1014 W/cm2, labeled by the green dashed line in (a). The five small red arrows denote that the outward NWP undergoes five Rabi oscillations. The initial state in the calculation is the v = 6 vibration state

Full size image

As indicated in Fig. 1, the NWP must move inward in the looping process, and we now trace the propagation details of the NWP during the dissociation. In Fig. 3d, we show the wave packet propagation on the 2pσu potential energy curve driven by the ten-optical-cycle laser pulse with a peak intensity of 1 × 1014 W/cm2. The main trace of the NWP undergoes five Rabi oscillations, marked by the five small red arrows in Fig. 3d, contributing to the fifth rolling peak, guided by the vertical green dashed line in Fig. 3a, at I0 = 1 × 1014 W/cm2. Looking into the details in Fig. 3d more closely, one may observe two sub-traces denoting one pathway of moving outwards and the other of moving inwards, guided by black and red arrows, respectively. As already described in Fig. 1, for the looping process, once the NWP moves inwards on the 1sσg potential curve, it will continuously move inward even after it is relaunched to the 2pσu state until it is decelerated to rest. Such a looping process is guided by the red arrow in Fig. 3d. Generally, more intense lasers induce more Rabi oscillations. Thus, the NWP experiences more propagation along the 1sσg curve to conquer the dissociation limit, resulting in smaller kinetic energy release in the rolling process. On the contrary, in the looping processes, once the NWP propagates inwards on the 1sσg curve, it will acquire more kinetic energies after being relaunched to the 2pσu curve at a smaller internuclear distance.

The direct visualization of the dynamical Rabi coupling has been verified using laser fields with another wavelength in TDSE simulations. For any wavelength of the incident laser pulse, the initial vibrational state of H2+ is selected to meet the condition of the one-photon resonant transition. The energy gap between two electronic states at the internuclear distance where the distribution of the resonant vibrational state is maximum is equal to the one-photon energy, producing the maximum dissociation probability26.

Experimental measurements

Based on the above understanding of the rolling and looping processes, we conceive an experiment using the COLTRIMS technique (See “Methods”) to observe such scenarios. Experimentally, H2 is photoionized and the generated H2+ is afterward dissociated by the incident laser pulse. In order to compare with experimental measurements, in the following numerical simulation, the initial state is set to be the superimposed vibrational states weighted by the Frank-Condon factors, mimicking the NWP just after the single ionization of H2. Figure 4a presents the proton KER spectrum in the dissociation of H2+ driven by a ten-optical-cycle 400-nm laser pulse with different peak intensities ranging from I0 = 3.3 × 1013 W/cm2 to 1.2 × 1014 W/cm2. Here, the superimposed Frank-Condon state firstly freely propagates 6 fs to move outwards on the 1sσg potential energy curve, and then the laser pulse is introduced to generate the laser-molecule coupling mainly around the internuclear distances in favor of Rabi oscillations. Hence, the main three-peak structures at I0 = 4 × 1013, 7 × 1013, and 1.1 × 1014 W/cm2 in Fig. 4a are similar to those in Fig. 3a. The aforementioned low-energy and high-energy structures can be distinguished by two clear traces in Fig. 4a, where the low-energy rolling pathway is almost the same as the one in Fig. 3a. While different from the multi-order looping structures with higher KERs in Fig. 3a, only the first-order looping pathway is observed in Fig. 4a, which is mainly ascribed to the nuclear movement. When the NWP weighted by the Frank-Condon factors moves to the internuclear distances for effective Rabi oscillations, the NWP already obtains non-negligible velocity moving outwards. Thus, such an outward velocity makes it hard to reverse its moving direction, and thus the looping pathway is relatively suppressed. Considering that H2 can be photoionized in each optical cycle in the whole laser pulse, we freely propagate the NWP for different periods before introducing the laser pulse to dissociate H2+. Numerically, we run different simulations by freely propagating the NWPs in a range of 2,10 fs and average the KER spectrum from the 2pσu state, as shown in Fig. 4b. The looping and rolling branches are blurred in Fig. 4b due to the energy overlap in simulations using different free propagation time.

Fig. 4: Probing rolling and looping dynamics via comparing experiments with simulations.
figure 4

a The simulated KER spectra as a function of the peak intensity of a ten-optical-cycle 400-nm laser pulse. The initial state is the superimposed vibrational state weighted by Frank-Condon factors, which freely propagates 6 fs before the laser pulse acts. b Same as (a) but averaged over free propagation time of 2,10 fs of the initial state. c The experimentally measured KER spectra at different laser intensities. The white curves in (a–c) illustrate the mean values of the KER spectra at different laser intensities. d The asymmetric KER spectra obtained by integrating the signals in (b) and (c) over all laser intensities. The low- and high-energy regions partitioned by the black dashed line are labeled as rolling and looping pathways. The maxima of all the spectra are normalized to one for the convenience of comparison. e Schematic illustration of the experimental set-up

Full size image

The experimental KER spectra of the dissociative fragments of H2+ as a function of the laser intensity are shown in Fig. 4c. The white curve in Fig. 4c is the mean value of the KER spectrum as a function of the laser intensity, which is also plotted in Fig. 4a, b for comparison. The experimental results demonstrate a similar structure as the simulation results, especially the aforementioned mean-KER trace and the asymmetric KER spectra in Fig. 4d, which are horizontally integrated over the laser intensities from Fig. 4b, c. The green and blue arrows in Fig. 4d are used to divide the contribution of the nuclear looping and rolling dynamics in the experimental KER spectrum, respectively. Although the periodical oscillation is blurred in experiments due to the averaging effect, the monotonic decrease of KER with the increasing laser intensity agrees with the simulation results, verifying the looping and rolling scenarios, and hence supporting the Rabi oscillation in molecular systems.

Discussion

The Rabi oscillations in molecular dissociation demand a laser intensity between the perturbative and ionization regime. Only the one-photon dissociation pathway is noticeable in the perturbative regime, where the laser intensity is smaller than 1 × 1013 W/cm2. The perturbative theory is good enough to describe the coupling between the 1sσg and 2pσu states26. While in the ionization regime, where the laser intensity is higher than 3 × 1014 W/cm2, the laser field can ionize the majority of the H2+ molecules. Thus the ionization dynamics will influence the dissociation dynamics, and the two-level model needs to be amended. For the laser parameters we used in the theory-experiment joint study, though the peak intensity is up-limited to about 1.3 × 1014 W/cm2, the dissociation happens at the falling edge of the pulse40, where the field-induced ionization can be neglected.

In many fields where Rabi oscillations have been fully investigated, such as quantum optics and quantum dots, the external laser field is weak and has a long-time duration to maintain the high energy resolution and finely control the energy level. While in the ultrafast and strong-field community, a strong femtosecond laser pulse is often utilized to induce the Rabi oscillations and even to observe the ultrafast dynamics of atoms and molecules in femtosecond time scales at the cost of the energy resolution due to the time-energy uncertainty.

In retrospect, our explanation based on the coupling of nuclear movement and electron Rabi oscillations is fundamentally different from the conventional one-photon bond-softening scenario. Using the Floquet formalism41,42, different dissociation pathways have been well recognized22,43,44,45,46, and it is suggested that lower vibrational states can spill out the potential energy curves when a driving laser pulse becomes stronger. The Floquet formalism works well when the driving laser is a continuum wave, which unambiguously identifies the dissociation pathways from the energy point of view by paying for the loss of time information. On the contrary, we propose a fundamentally different scenario upon Rabi oscillations to explore more fruitful dynamical processes beyond the previous studies. In the Rabi oscillation scenario, H2+ may first absorb one photon and then transit from the 1sσg state to the 2pσu state. Once the accumulated population in the 2pσu state is larger than that in the 1sσg state, H2+ in the 2pσu state may emit one photon and dump to the 1sσg state, forming a complete Rabi oscillation. During the dissociation, if the NWP undergoes half-integer multiples of Rabi oscillations, the proton will end with the net-one-photon absorption, which is similar to the bond-softening scenario only from the energy point of view. However, if integer multiples of the Rabi oscillation have been accomplished, H2+ dissociates along the 1sσg curve in accordance with the net-zero-photon dissociation pathway37,47,48.

In the dissociation of H2+, the laser-driven Rabi oscillations between the two lowest electronic states during the stretching of the molecular bond alter the well-known one-photon resonant dissociation pathway and enrich the KER spectrum of dissociative fragments. Based on the analysis of the propagation of the NWP on the potential energy curves, the nuclear looping and rolling dynamics ensured by the dynamical Rabi coupling of the two lowest electronic states in a stretching H2+ are clearly identified in the TDSE simulations and further verified in experiments. The dynamical Rabi coupling is an essential step of the well-known Rabi oscillations from atoms to molecules, giving birth to a complete understanding of the laser-driven molecular dissociation, particularly the ejection of slow nuclear fragments. It also provides a time-resolved perspective to understand the ultrafast processes in molecular dissociation beyond the Floquet theorem. The electron hopping mechanism presented here is general for strong-field dynamics of a stretching molecule, which also has implications for complex molecular processes, including the nuclear-electron correlations.

Materials and methods

Quantum simulations

For H2+, the 1sσg and 2pσu potential energy curves are far from others, and these two states generally govern the dissociation. Theoretically, we study its strong-laser-field dissociation by simulating the two-level one-dimensional time-dependent Schrödinger equation (TDSE)49 with the Born-Oppenheimer approximation (atomic units are used throughout unless stated otherwise):

$$i\frac{\partial }{{\partial t}}\left( {\begin{array}{*{20}{c}} {\chi _g\left( {R,t} \right)} \\ {\chi _u\left( {R,t} \right)} \end{array}} \right) = \left( {\begin{array}{*{20}{c}} {\hat T + V_g\left( R \right)} & {D(R)E\left( t \right)} \\ {D\left( R \right)E\left( t \right)} & {\hat T + V_u\left( R \right)} \end{array}} \right)\left( {\begin{array}{*{20}{c}} {\chi _g\left( {R,t} \right)} \\ {\chi _u\left( {R,t} \right)} \end{array}} \right)$$
(5)

Here the dipole approximation and the length gauge are adopted. χg(R, t) and χu(R, t) are NWPs associated with the electron in the 1sσg and 2pσu states, respectively. Vg(R) and Vu(R) are the 1sσg and 2pσu potential energy curves, respectively, as sketched in Fig. 1. R is the internuclear distance, \(\hat T\) is the nuclear kinetic energy operator, D(R) is the R-dependent transition dipole between the two states, and E(t) is the electric field of the incident laser pulse. Molecular rotation is neglected in this model. The time and spatial steps are dt = 0.1 and dR = 0.02, respectively. R spans the range [0, 100]. The simulation box is large enough to hold all dissociating NWPs and thus no absorbing boundaries are used. The initial state is obtained using the imaginary-time propagation algorithm50, and the Crank-Nicolson method51 is adopted to propagate the NWP in real time. The laser pulse is written as E(t) = E0sin2(πt/τ)cos(ωt), where E0 is the electric field amplitude, ω is the laser frequency, and τ is the duration of the laser pulse. The laser polarization direction is parallel to the molecular axis. The initial state will be chosen according to concrete calculations. The dissociation yield is mainly attributed to the population of the 2pσu state at the end of the simulation, i.e., \(P_u = {\int} {\left| {\chi _u(R,t_{end})} \right|} ^2dR\). The KER spectra are calculated from the momentum distribution, i.e., \(\left| {\phi _u\left( {p,t_{end}} \right)} \right|^2/p\), where \(\phi _u(p,t_{end})\) denotes the Fourier transform of the position-dependent nuclear wave function. In the two-level simulation, the electron is restricted to the two bound states, and thus the ionization of H2+ is neglected. We have examined that the ionization rate is minimal compared to the dissociation rate in this theory-experiment joint work using a TDSE simulation with a model including ionization52.

Experimental details

We perform the experiment in an ultrahigh vacuum chamber of a cold target recoil ion momentum spectrometer (COLTRIMS)53,54. A linearly polarized ultraviolet laser pulse (46 fs at FWHM, 395 nm) focused into the apparatus is produced by frequency doubling the near-infrared femtosecond laser pulse delivered from a multi-pass Ti:sapphire laser system in a β-barium borate crystal. A supersonic gas beam of H2 with a driving pressure of 2.0 bar is injected into the vacuum chambers and cooled to tens of Kelvins after the adiabatic expansion through a 30-µm nozzle. The H2 target molecule is firstly ionized and subsequently dissociates into a proton (H+) and a hydrogen atom (H), where the charged proton can be accelerated with a weak (~14.7 V/cm) static electric field and detected by a time- and position-sensitive microchannel plate detector at the end of the spectrometer, as shown in Fig. 4e. The peak intensity of the laser pulse in the interaction region is adjusted by a neutral filter in the beamline, ranging from I0 = 3.3 × 1013 W/cm2 to 1.2 × 1014 W/cm2. To avoid mixing the dissociation yield of the molecules not oriented along the laser polarization, in the experiment, we select the dissociative fragments along the laser polarization within a small range, i.e., |ϕion – ϕE| < 5°, where ϕion and ϕE denote the emission direction of dissociative fragments H+ and the polarization direction of the laser pulse, respectively.