Introduction

Mechanical resonators have been researched for decades and are widely used in timing and sensing. Due to their low phase noise and inherent temperature stability, quartz crystal resonators have dominated the market of timing reference devices and high-precision sensing. In recent years, silicon-based MEMS resonators have shown enormous potential to replace quartz crystal resonators in engineering applications due to their smaller size, lower consumption, and better compatibility with semiconductor fabrication processing technology. Several recent studies have even employed silicon-based resonators to facilitate information processing and quantum science. More importantly, the scale effect makes MEMS resonators more shock-resistant than quartz crystal resonators, allowing them to operate in harsh environments. However, the temperature coefficient of frequency (TCf) of silicon is relatively larger than that of quartz crystal, which can lead to drastic frequency drifts of silicon-based MEMS resonators, degrading the performance of resonator-based devices.

A variety of temperature compensation methods have been proposed to suppress the frequency drift of silicon-based MEMS resonators. Passive compensation methods, such as doping1,2, geometry engineering3,4,5, and orientation adjustment4,6,7, can reduce the TCf of MEMS resonators to the ppm level over a wide temperature range, which can only satisfy the frequency stability requirements of consumer electronics. In contrast to passive compensation methods, active compensation approaches, such as oven control8,9, electrostatic modulation10,11,12, and electronic compensation13, employ a feedback control loop to maintain a stable output frequency. Among the active temperature-compensated MEMS resonators, oven-controlled MEMS resonators with on-chip oven structures have been demonstrated to achieve ppb-level stability, which far exceeds that of the passive compensated MEMS resonators14,15. In the on-chip oven control scheme, the MEMS resonators, heaters, and temperature sensors are manufactured on the same substrate during the process, which reduces the thermal gradient and improves the heating efficiency. For example, Thomas Kenny et al. demonstrated a dual-mode MEMS resonator with an integrated micro-oven structure and an isolation frame16. The isolation frame, along with the on-chip oven, allows the resonator to maintain a uniform temperature distribution with a power consumption of 10 mW. The on-chip oven-controlled resonator achieves frequency stability of ±5 ppb while ramping the ambient from −40 °C to 60 °C. However, the oven-controlled resonators with on-chip oven structures still suffer long warm-up times. More importantly, an on-chip oven architecture is specifically designed for one individual resonator, which offers little post-fabrication flexibility. A careful redesign of the resonator structure or even a change in the process is needed to meet the temperature control requirements17, making the on-chip oven control scheme lack versatility and hard to adapt to a general class of resonators.

Recently, nonlinearities in silicon-based MEMS resonators have been demonstrated to significantly suppress both the long-term frequency drifts11,18 due to temperature changes and short-term frequency fluctuations19,20,21 caused by thermomechanical noise22,23, transduction noise24, equipment noise25, etc. The intrinsic nonlinearities in MEMS resonators provide inspiration to realize frequency stability enhancement of resonators from the perspective of nonlinear dynamics. However, research to date has been confined to passively enhancing the frequency stability using nonlinearities, and the potential of nonlinearity-mediated frequency stabilization schemes has not been fully revealed.

Towards the objective of developing a robust and versatile temperature compensation scheme with ppb-level frequency stability when the ambient temperature changes transiently, in this work, a nonlinearity-mediated temperature compensation scheme is proposed and demonstrated. Firstly, to improve the short-term frequency stability (i.e., the performance limit of MEMS resonators), a MEMS resonator with a quality factor of 1.694 × 106 is designed. The reported quality factor surpasses that of the state-of-the-art oven-controlled MEMS resonator. Subsequently, to suppress the long-term frequency drift of the MEMS resonator both accurately and rapidly, a nonlinearity-mediated temperature system consisting of two-stage temperature control modules is designed. The first stage off-chip oven control module maintains the temperature of the resonator within ±1 m°C, utilizing the PWM-based fuzzy proportional integration differentiation (PID) control method. The second-stage nonlinear frequency drift suppression module rapidly reduces the residual frequency drift of the MEMS resonator based on its intrinsic dependence of frequency on amplitude in the Duffing nonlinear regime. The MEMS resonator under two-stage temperature compensation achieves a frequency stability of ±14 ppb over transient changes in ambient temperature. The proposed nonlinearity-mediated temperature compensation scheme does not require a redesign of the resonator structure. This novel scheme provides a general and efficient approach to improve the frequency stability of resonator-based devices, which can be easily incorporated into a variety of resonant systems.

Results

Device design and fundamental characteristics

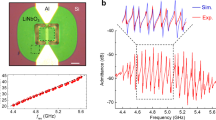
The short-term frequency stability of a MEMS resonator directly depends on its quality factor according to Robin’s formula22. We specifically designed a symmetrical MEMS resonant structure in which two identical resonators are distributed on the left and right ends of an elastic connection beam (anchor beam). As shown in Fig. 1a, the square resonator body is supported by four equally distributed rods. To reduce anchor loss, these rods are collectively attached to a suspension frame. The frame and the resonator body are then anchored to the glass substrate with the anchor beam. Both the frame and the resonator body are suspended above the glass substrate. The entire MEMS resonator structure is anchored to the glass substrate by three anchor positions, as shown in the area within the red dotted boxes in Fig. 1a. The width and the thickness of the resonator body are 600 μm and 40 μm, respectively. The widths of the rods and anchor beam are 20 μm and 40 μm, respectively. The lengths of the rods and anchor beam are 110 μm and 296 μm, respectively. During the experiments, the MEMS resonator on the left was excited and sensed by four capacitive electrodes labeled from 1 to 4. The resonator structure was fabricated based on a commercial silicon-on-glass process using (100) single-crystal silicon. As shown in the inset of Fig. 1d, the resonator was designed to exhibit a 2nd-order Lamé mode.

Fig. 1
figure 1

Experimental setup and basic characteristics of the resonator. a The left subfigure is the schematic of the MEMS resonator and the open-loop measuring circuits. The right subfigure is the schematic of the cross-section of the resonant structure, wherein the resonator processed on the silicon layer is anchored to the glass substrate through three anchor positions shown in the area within the red dotted boxes. b The linear amplitude response (blue solid line) and phase response (red solid line) of the device at an AC driving voltage of 50 mV. c Ring-down measurement. The blue dot is the experimental data, and the red solid line is the fitting result. Please see the “Materials and methods” section for more details. d Measured temperature coefficient of frequency of the 2nd Lamé mode. The inset shows the mode shape of the 2nd Lamé mode

Full size image

For a vacuum encapsulated MEMS resonator, the dominant dissipation mechanisms are anchor loss, thermomechanical loss, and Akhiezer damping, which determine the total quality factor of the MEMS resonator in the form of26

$${Q}_{{tot}}={\left(1/{Q}_{{anchor}}+1/{Q}_{{TED}}+1/{Q}_{{AKE}}\right)}^{-1}$$
(1)

The Qanchor and QTED of the designed MEMS resonator obtained utilizing finite element simulation are 7.795 × 106 and 5.939 × 108, respectively. The QAKE is calculated according to the Akhiezer limited f∙Q expression \(f\cdot {Q}_{{AKE}}=\rho {c}^{2}{c}_{D}^{2}/2\pi {\gamma }_{{eff}}^{2}\kappa T\) as27,28 4.283 × 106 where f is the resonant frequency, ρ is the density, c is the velocity of the acoustic wave, cD is the Debye velocity, γeff is the effective Grüneisen parameter, κ is the thermal conductivity, and T is the temperature. The total quality factor of the MEMS resonator can then be calculated by Eq. (1) as 2.751 × 106, which demonstrates that the quality factor of the designed device is dominated by the Akhiezer damping. The proposed resonator structure effectively improves the quality factor of the MEMS resonator close to the intrinsic limit of single-crystal silicon.

With the resonator hermetically sealed in a metal package with a pressure of less than 0.1 Pa, we characterized the dynamic responses of the resonator. The vibrational motion was actuated and detected using the electrostatic transduction method. A Zurich Instrument lock-in amplifier (HF2LI) was utilized to generate the desired alternating current (AC) driving voltage Vac, and a low noise power supply was utilized to generate the desired DC driving/detection voltages (Vd and −Vd) on the electrodes and DC voltage (V0) on the resonator body. \({V}_{d}\) and \({V}_{0}\) were maintained at 30 V and -30 V respectively, unless otherwise specified. It is worth noting that the voltage difference between electrode 4 and the resonator body was set to zero to permit the detection of only the feedthrough signal \({i}_{m}^{{\prime} }\). When the feedthrough signal \({i}_{m}^{{\prime} }\) is subtracted from the current signal \({i}_{m}\) comprising both the response signal and the feedthrough signal, a clean motion signal without feedthrough can be obtained.

Figure 1b shows the linear frequency responses of the resonator. The 2nd-order Lamé mode exhibits a resonant frequency of 5.37 MHz. By utilizing the half-power method and ring-down method (shown in Fig. 1c), the quality factor of the device at room temperature (25 °C) was calculated as 1.694 × 106 and 1.662 × 106, respectively, which is in the same order of magnitude as the theoretical value of 2.751 × 106, verifying the proposed anchor loss reduction structure. The detailed descriptions of the ring-down measurement are presented in the “Materials and methods” section. The frequency shift of the 2nd Lamé mode was measured in an environmental chamber over a temperature range from 0 °C to 80 °C, as shown in Fig. 1d. The frequency shift reaches 1347 ppm over the entire temperature range.

Duffing nonlinearity in the MEMS resonator

As the AC driving voltage increases, the response converts from linear to stiffness-hardening nonlinear (shown in Fig. 2a, b). When the MEMS resonator is driven into self-sustained oscillation in the top bifurcation (at the top bifurcation, the phase of the response \(\varphi\) is equal to \(\pi /2\)), its output frequency \(\varOmega\) can be obtained as \(\varOmega ={\omega }_{0}+3\alpha {F}_{0}^{2}/8{\gamma }^{2}{\omega }_{0}^{3}\), where \({\omega }_{0}\) is the natural frequency, \(\alpha\) is the Duffing nonlinear stiffness, \({F}_{0}\) is the driving strength, and \(Q\) is the quality factor; see “Materials and methods” section for a more detailed analysis of the derivation of the output frequency. The output frequency \(\varOmega\) of a MEMS resonator with Duffing nonlinearity exhibits a linear dependence on the square of the driving force \({F}_{0}\), provided that it is operated at its top bifurcation.

Fig. 2
figure 2

Duffing nonlinearity in the resonator. a, b The amplitude responses and phase responses of the device under different AC driving voltages. The responses convert from linear to stiffness-hardening nonlinear when the AC driving voltage increases from 50 mV to 800 mV (left to right). c The real-time oscillation amplitude (blue solid line) and oscillation frequency (red solid line) of the resonator when it generated self-sustained oscillation in a phase-locked loop. The AC driving voltage was first increased from 400 to 800 mV in steps of 50 mV and then decreased from 800 to 400 mV in steps of 50 mV. The inset shows the oscillation frequency of the device when the AC driving voltage was increased from 450 to 500 mV. The device can re-stabilize within 0.48 s. d The experimental and theoretical quadratic dependence of oscillation frequency on AC driving voltage

Full size image

Figure 2c shows the real-time frequency response of the MEMS resonator under varying AC driving voltage when it generated self-sustained oscillation at the top bifurcation utilizing a phase-locked loop (PLL). The AC driving voltage was initially increased from 400 to 800 mV in increments of 50 mV and subsequently reduced to 400 mV in 50 mV steps. The oscillation frequency varies stepwise with the AC driving voltage. As shown in the inset in Fig. 2c, the oscillation frequency can re-stabilize within 0.48 s. The red dots in Fig. 2d demonstrate the quadratic dependence of oscillation frequency on AC driving voltage extracted from the experimental data in Fig. 2c, and the black solid line in Fig. 2d is the theoretical fitting curve with a fitting coefficient R2 of 0.9997 according to Eq. (14) in the “Materials and methods” section. The amplitude-frequency (A-f) dependence of the Duffing MEMS resonator offers an approach to rapidly modulate the frequency of MEMS resonators by controlling the driving force.

Nonlinearity-mediated temperature compensation system

The overall structure of the reported oven-controlled MEMS resonator is illustrated in Fig. 3a. The MEMS resonator structure is encapsulated within a metal package. The metal package and the associated control circuits are enclosed in an aluminum case. Polyurethane insulation with a thickness of 9 mm is designed as a passive thermal insulation structure between the aluminum case and the stainless-steel case. Two polyimide (PI) heating films are, respectively, installed on the side walls of the aluminum case and on the top lid of the metal package to actively heat the chamber. The printed circuit boards below and above the metal package are two separate PID temperature control circuits. Figure 3b shows the schematic of the two-stage nonlinearity-mediated temperature compensation system. The first stage off-chip oven control module maintains the chamber temperature through active heating. Simultaneously, the second-stage nonlinear frequency drift suppression module, which we term the “amplitude-frequency (A-f) control” module, suppresses the residual frequency drift of MEMS resonator utilizing the intrinsic dependence of the frequency on the driving force in the Duffing nonlinear regime (see Fig. 2d and Eq. 14). The two modules function independently to keep the output frequency of the MEMS resonator constant.

Fig. 3
figure 3

Basic characteristics of the two-stage nonlinearity-mediated temperature compensation system. a The overall structure of the system. b Schematic of the control system. c, d The comparison of control speed and control accuracy between the conventional PID temperature control and fuzzy-PID temperature control

Full size image

In the first stage off-chip oven control module, the chamber temperature is maintained constant utilizing two separate PWM-based PID control circuits. The outer PID control circuit roughly maintains the temperature of the chamber to a fixed value by controlling the output power of the PI heating film on the aluminum case, while the inner PID control circuit is employed to achieve more precise temperature control of the MEMS resonator, utilizing the PI heating film on the top lid of the metal package. For simplicity, only one PID control loop of the oven control module is plotted in Fig. 3b. Specifically, two platinum resistors (Pt1000) are mounted on the inner wall of the aluminum case (temperature sensor of the outer PID control circuit) and inside the metal package (temperature sensor of the inner PID control circuit), respectively. The measured temperatures of the two temperature sensors are first converted to digital quantities by the analog-to-digital converter. The temperature differences (\(\Delta T\)) between the measured temperatures and the temperature setpoints (set temperature) are then separately used as the control signals of the two PID control circuits (executed by an STM 32 program), which modulate the duty cycle of the PWM wave and thus the equivalent power consumption of the PI heating films to achieve a constant temperature.

Utilizing the fuzzy-PID control algorithm, higher temperature control accuracy can be obtained with less warm-up time. As shown in the red line in Fig. 3c, d, the first stage off-chip oven control module based on fuzzy-PID control algorithm achieves a temperature stability of 1.62 mK and completes the warm-up within 8.17 min, which is respectively 26.4 percent and 53 percent lower than that of the oven control module based on the traditional PID control algorithm (blue line). During the experiments, the temperature setpoints of the outer and inner PID control circuits were 30 °C and 40 °C, respectively.

In the second-stage A-f control module, the PLL in the HF2LI lock-in amplifier is first employed to operate the MEMS resonator at the desired phase condition, thus tracking and recording the frequency variation of the MEMS resonator. During the experiments, the phase \(\varphi\) was set to π⁄2 to excite the MEMS resonator at its top bifurcation. The measured oscillation frequency is then fed to a MATLAB script to calculate the difference (\(\Delta f\)) between the measured frequency and the set frequency. Once the frequency drift exceeds the preset range, a PID controller is utilized to calculate the desired AC driving voltage required to suppress the frequency drift. The AC controller then converts the desired AC driving voltage into a digital control signal, which is fed to the lock-in amplifier to regulate the AC driving voltage, thus adjusting the output frequency of the MEMS resonator according to Eq. (14) until the frequency drift is controlled within the preset range.

Frequency stability under only off-chip oven control

The frequency stability of the MEMS resonator under only the off-chip oven control was then tested. The temperature setpoints of the outer and inner PID control circuits were set to 20 °C and 35 °C, respectively; the experiments were conducted in the commercial temperature chamber with a temperature of −10 °C. The AC driving voltage was set to 800 mV. The blue and red solid lines in Fig. 4a demonstrate the temperatures of the aluminum case (outer temperature measured by the outer temperature sensor) and the metal package (inner temperature measured by the inner temperature sensor) under the first stage oven control, respectively. After the temperature of the metal package was maintained within 35 ± 0.001 °C for 3750 s (shown in the inset of Fig. 4a), we measured the frequency shift of the MEMS resonator for 1800 s.

Fig. 4
figure 4

Performance test of the MEMS resonator under only off-chip oven control. a Temperatures of the aluminum case (blue solid line, measured by the outer temperature sensor) and the metal package (red solid line, measured by the inner temperature sensor) under the first stage oven control. The inset shows that the temperature of the metal package was maintained within 35 ± 0.001 °C after a warm-up time of 3750 s. b The frequency of the MEMS resonator was measured for a duration of 1800 s after the temperature of the resonator was maintained within 35 ± 0.001 °C. A residual frequency drift of 2104 ppb was observed. c Temperature oscillation during the warm-up of the first stage oven control. d The rapid compensation capacity of the A-f control module

Full size image

As shown in Fig. 4b, the oscillation frequency drifted downwards by 2104 ppb, which far exceeds the frequency drift over the temperature range of 35 ± 0.001 °C calculated from the TCf (±18 ppb). In addition to the residual frequency drift, oven-controlled MEMS resonators commonly require a long warm-up time to stabilize the operating temperature (on the order of minutes). Moreover, the temperature of the resonator undergoes an oscillating process during the warm-up of the oven control (shown in Fig. 4c), causing the output frequency of the MEMS resonator to oscillate (shown in the red line in Fig. 4d). The residual frequency drift as well as the long warm-up time of oven control scheme make it hard to adapt in scenarios with rapid response requirements.

Performance characterization of the MEMS resonator under nonlinearity-mediated temperature compensation

By employing the second-stage A-f control module, both the residual frequency drift and the long warm-up time of the oven-controlled MEMS resonator can be addressed. As shown in Fig. 4d, with the second-stage module being activated, the oscillation of the output frequency (167.4 ppb) caused by the temperature oscillation during the warm-up can be suppressed to within 18.6 ppb, thus significantly reducing the warm-up time required to achieve the desired frequency stability. More importantly, the residual frequency drift can be suppressed. As shown in Fig. 5a, the residual frequency drift of 2104 ppb (red line, same data as in Fig. 4b) is significantly reduced to 46.25 ppb (blue line). The inset is the zoom-in of the blue line. The frequency Allan deviation of the MEMS resonator reaches 0.09 ppb at an integration time of 289 s (dark blue dot line in Fig. 5b), which is 2660 times better than that under only the oven control (dark red dot line in Fig. 5b).

Fig. 5
figure 5

Performance characterization of the nonlinearity-mediated temperature-compensated MEMS resonator. a Comparison of the frequency drift with (dark blue) and without (dark red) the second-stage A-f control. The first stage oven control is activated in both sets of experiments. The inset is the zoom-in of the blue line. b The dark blue dot line and dark red dot line are the Allan deviation curves of the output frequency of the resonator with and without the second-stage A-f control, respectively. Both Allan deviation curves are calculated using the raw frequency data in (a). The light blue solid line is the Allan deviation curve calculated according to the output frequency of the resonator in the transiently varying ambient temperatures. c Frequency stability of the nonlinearity-mediated temperature-compensated MEMS resonator at transiently varying ambient temperatures. Subfigure (ⅰ) shows the ambient temperature. Subfigure (ⅱ) demonstrates the real-time compensated temperature of the aluminum case (outer temperature) and the metal package (inner temperature). Subfigure (ⅲ) shows the output frequency of the MEMS resonator (light blue dots) under the two-stage temperature compensation. The light red line is the real-time oscillation amplitude of the resonator, which is used as a stabilizer to suppress the residual frequency drift. It can be clearly seen that the oscillation amplitude exhibits an opposite trend to the inner temperature

Full size image

Next, we tested the performance of the nonlinearity-mediated temperature-compensated MEMS resonator at transiently varying ambient temperatures. The frequency stability over temperature was tested with the overall structure being placed in a commercial temperature chamber; see the subfigure (ⅰ) in Fig. 5c for the temperature in the temperature chamber. The ambient temperature was varied between −10 °C and 30 °C while the temperature setpoints of the outer and inner PID control circuits were set to 20 °C and 35 °C, respectively. The second-stage A-f control module was activated with the initial AC driving voltage of 800 mV. The MEMS resonator was excited to generate self-sustained oscillation at the peak amplitude utilizing the PLL.

In this ambient temperature, the temperature measured at the aluminum case (outer temperature) changed from 20 °C to 21.8 °C (light blue line in the subfigure (ⅱ) in Fig. 5c) while the temperature of the metal package (inner temperature) was maintained within ±20 m°C (light red line in the subfigure (ⅱ) in Fig. 5c). This residual temperature drift in the metal package can lead to a frequency drift of 732 ppb calculated according to the measured TCf. With the second-stage A-f control module being activated, the oscillation amplitude of the MEMS resonator was adjusted according to the drift in its output frequency. As shown in the light red line in subfigure (ⅲ) in Fig. 5c, the oscillation amplitude changes in a trend opposite to the temperature change of the metal package (light red line in subfigure (ⅱ)), which suppresses the residual frequency drift caused by the untimely temperature compensation of the first stage oven control. A final frequency stability of ±14 ppb was achieved, as shown in the light blue dots in subfigure (ⅲ) in Fig. 5c. The Allan deviation of the oscillation frequency is calculated as 0.17 ppb at an integration time of 104 s (see the light blue line in Fig. 5b). The deterioration of the Allan deviation compared to that in constant ambient temperature (dark blue line in Fig. 5b) may stem from the enhanced electromagnetic interference from the higher power consumption of the first stage oven control module at transiently varying ambient temperatures.

A performance comparison of the state-of-the-art oven-controlled MEMS resonators is illustrated in Table 1. It is worth noting that frequency stability refers to the dynamic frequency drift with temperature transient over the temperature range. Compared with the reported oven-controlled MEMS resonators, the device in this work has the highest quality factor. More importantly, the frequency stability of our off-chip oven-controlled MEMS resonator already exceeds that of most reported oven-controlled MEMS resonators in the literature and is close to the best frequency stability of the on-chip oven-controlled MEMS resonator (±5 ppb), which offers intriguing opportunities to enhance the performance of resonator-based devices without the need to redesign their structures. However, due to the limitation of the heating efficiency of the off-chip oven structure, the oven-controlled MEMS resonator prototype can only be operated in a limited temperature range, which cannot meet the requirements for industrial-grade equipment. In addition, the power consumption of the prototype is still large compared with its counterparts of oven-controlled MEMS resonators. Work is ongoing to further reduce the power consumption by utilizing a more integrated off-chip oven control system.

Table 1 Performance comparison of state-of-the-art oven-controlled MEMS resonators
Full size table

Conclusions

In this work, a nonlinearity-mediated temperature-compensated MEMS resonator is demonstrated, which consists of a MEMS resonator with intrinsic Duffing nonlinearity, an off-chip oven control module, and a nonlinear frequency drift suppression module. After the residual frequency drift of the off-chip oven-controlled MEMS resonator is suppressed utilizing its intrinsic amplitude-frequency dependence in the Duffing nonlinear regime, a frequency stability of ±14 ppb is achieved. This nonlinearity-enhanced oven control scheme simultaneously improves the frequency stability over temperature of the oven-controlled MEMS resonator and reduces the warm-up time for oven control. The temperature compensation scheme contravenes the conventional wisdom and establishes a new paradigm for the frequency stabilization of mechanical resonators. More importantly, the new paradigm can be readily incorporated into a variety of systems without the need to design auxiliary on-chip structures or change the process flow, which offers intriguing opportunities for implementing high-performance timing and sensing.

Materials and methods

Theoretical analysis

The displacement, x, of the Duffing resonator embedded in a PLL is given by

$$\ddot{x}+\gamma \dot{x}+{\omega }_{0}^{2}x+\alpha {x}^{3}={F}_{0}\cos \left({\omega }_{0}t+\phi +\delta \right),$$
(2)

where \(\gamma ={\omega }_{0}/Q\) is the linewidth, \({\omega }_{0}\) is the natural frequency, \(Q\) is the quality factor, \(\alpha\) is the Duffing nonlinearity, \({F}_{0}\) is the driving force, \(\phi\) is the phase of the motion, and \(\delta\) is the phase set point of the PLL. The method of multiple scales can be utilized to capture the dynamics of the Duffing nonlinear resonator by introducing

$${x=x}_{0}\left({T}_{0},{T}_{1},{T}_{2}\right)+\epsilon {x}_{1}\left({T}_{0},{T}_{1},{T}_{2}\right),$$
(3)

where \(\epsilon\) is the infinitesimals, \({T}_{0}=t\) is the fast time scale, and \({T}_{1}=\epsilon {T}_{0}\) is the first-order slow time scale. Time derivatives are transformed into

$$D={D}_{0}+\epsilon {D}_{1},$$
(4)
$${D}^{2}={{D}_{0}}^{2}+2\epsilon {D}_{0}{D}_{1}.$$
(5)

We substitute Eqs. (3)–(5) into Eq. (2) and collect the coefficients of the same order of \(\epsilon\) to obtain the \({\epsilon }^{0}\) and \({\epsilon }^{1}\) order equations as

$${\epsilon }^{0}:$$
$${{D}_{0}}^{2}{x}_{0}+{\omega }_{0}^{2}{x}_{0}=0,$$
(6)
$${\epsilon }^{1}:$$
$${{D}_{0}}^{2}{x}_{1}+{\omega }_{0}^{2}{x}_{1}=-{\gamma }^{{\prime} }{D}_{0}{x}_{0}-{\alpha }^{{\prime} }{x}_{0}^{3}-2{D}_{0}{D}_{1}{x}_{0}+{F}_{0}^{{\prime} }\cos \left({\omega }_{0}t+\phi +\delta \right),$$
(7)

where \(\gamma ={\epsilon \varGamma }^{{\prime} }\), \(\alpha =\epsilon {\alpha }^{{\prime} }\), and \({F}_{0}=\epsilon {F}_{0}^{{\prime} }\). From Eq. (6), we can obtain the first-order approximation of the solutions as

$${x}_{0}=A\left({T}_{1},{T}_{2}\right){{\rm{e}}}^{i{{\omega }_{0}T}_{0}}+c.c.,$$
(8)

where \(c.c.\) represents the complex conjugate of the preceding term. Substituting Eq. (8) and \(A=\frac{1}{2}a\left({T}_{1},{T}_{2}\right){e}^{i\phi \left({T}_{1},{T}_{2}\right)}\) into Eq. (7), eliminating the secular terms, and separating the real and imaginary parts, we can obtain

$$\frac{d\phi \left({T}_{1},{T}_{2}\right)}{d{T}_{1}}a=\frac{3}{8{\omega }_{0}}{\alpha }^{{\prime} }{a}^{3}-\frac{{F}_{0}^{{\prime} }}{2{\omega }_{0}}\cos \left(\delta \right),$$
(9)
$$\frac{{da}\left({T}_{1},{T}_{2}\right)}{d{T}_{1}}={-\frac{1}{2}\gamma }^{{\prime} }a+\frac{{F}_{0}^{{\prime} }}{2{\omega }_{0}}\sin \left(\delta \right),$$
(10)

where \(a\) is the steady-state amplitude. Multiplying both sides of Eqs. (9) and (10) by ϵ, we can get

$$\epsilon \frac{d\phi \left({T}_{1},{T}_{2}\right)}{d{T}_{1}}a=\frac{d\phi }{d{T}_{0}}a=\frac{3}{8{\omega }_{0}}\alpha {a}^{3}-\frac{{F}_{0}}{2{\omega }_{0}}cos \left(\delta \right),$$
(11)

and

$$\epsilon \frac{{da}\left({T}_{1},{T}_{2}\right)}{d{T}_{1}}=\frac{{da}}{d{T}_{0}}=-\frac{1}{2}\gamma a+\frac{{F}_{0}}{2{\omega }_{0}}\sin \left(\delta \right).$$
(12)

By setting \(\frac{{da}\left({T}_{1},{T}_{2}\right)}{d{T}_{1}}\) in Eq. (12) to zero, we can obtain the steady-state conditions for the amplitude. The expression of the steady-state amplitude \(a\) is derived as \(a=\frac{{F}_{0}}{\gamma {\omega }_{0}}\sin \left(\delta \right)\). Substituting the amplitude expression into Eq. (11), we can obtain the output frequency \(\varOmega\) of the nonlinear MEMS resonator as

$$\varOmega ={\omega }_{0}+\frac{d\phi }{d{T}_{0}}={\omega }_{0}+\frac{3\alpha }{8{\omega }_{0}}\frac{{F}_{0}^{2}}{{\gamma }^{2}{\omega }_{0}^{2}}{sin }^{2}\left(\delta \right)-\frac{{F}_{0}}{2{\omega }_{0}}cos \left(\delta \right).$$
(13)

When the phase set point \(\delta\) of the PLL is equal to \(\pi /2\) (corresponding to the top bifurcation point), the output frequency can be simplified as

$$\varOmega ={\omega }_{0}+\frac{3}{8}\frac{\alpha {F}_{0}^{2}}{{\gamma }^{2}{\omega }_{0}^{3}}.$$
(14)

Ring-down measurement

We conducted the ring-down measurement to characterize the quality factor of the resonator utilizing the HF2LI lock-in amplifier. The resonator was first driven into resonance at the peak amplitude of the linear response curve (with Vac = 20 mV and Vd = 20 V). After that, upon switching off the AC driving signal, the free-decaying resonance amplitude was tracked, as shown in Fig. 1c. The time constant of the demodulator was set to 100 μs to make sure that the demodulator does not influence the decay time of the resonator. Then, the exponential decay time \({\tau }_{d}\) was extracted at the amplitude of \({A}_{0}/e\), where \({A}_{0}\) is he peak amplitude and \(e\) is the Euler number. The quality factor is then calculated by

$$Q=\pi {f}_{0}{\tau }_{d},$$
(15)

where \({f}_{0}\) is the resonant frequency of the resonator.