Introduction

Individuals with methamphetamine use disorder (iMUDs) suffer devastating physical and psychological consequences [1] and rates of overdose and mortality have increased in recent years [2, 3]. The growing prevalence of this disorder, poor treatment outcomes, and high rates of relapse all necessitate a better understanding of its etiology and maintenance factors [4, 5]. In particular, decision mechanisms promoting continued use despite negative consequences remain inadequately understood.

To date, research examining decision-making in iMUDs and other stimulants has found greater impulsivity [6, 7], impaired inhibitory control, increased risk-taking [8, 9], and elevated delay-discounting compared to non-users [10, 11], which may jointly reflect an impaired ability to consider potential consequences before choices are made. This also suggests low levels of cognitive reflectiveness (i.e., the tendency to stop and “think things through” before responding [12,13,14]), although the explanatory power of reflectiveness measures in this population remains to be examined. The substance use literature has instead tended to focus on reward processing. For instance, one recent neuroimaging study in amphetamine users suggested greater anticipatory processing for large rewards (right amygdala activation) compared to non-users [15]. This exemplifies a large prior literature suggesting decision-making in these individuals may be biased toward large, immediate gains.

Computational approaches have allowed quantitative mathematical modeling of these decision-making processes. Of greatest relevance here, two broad classes of computational reinforcement learning (RL) algorithms have been used to explain choice in iMUDs (for reviews, see [16, 17]). Namely, model-free (MF) algorithms assume decision-making operates through trial-and-error action value learning based on observed outcomes (i.e., assuming no explicit future expectations). Model-based (MB) algorithms instead assume decisions are made based on expected future rewards. To date, MF explanations have received more attention in experimental studies. These tend to attribute maladaptive choice patterns to repeated positive outcomes following drug use and negative outcomes associated with withdrawal. On the other hand, MB approaches explain continued use by assuming affected individuals overweight the expected reward of use and underweight expected negative consequences [18]. Investigations focused on distinguishing these algorithms suggest a shift from reliance on MB to MF algorithms with repeated use [19, 20]; yet, the mechanisms behind this shift, and those underpinning MB deficits, remain largely unknown. In particular, multi-step planning – a paradigmatic example of MB decision-making – has received insufficient attention in empirical studies and may be crucial for understanding these impairments.

Another factor known to promote poor choice is avoidance of negative affect and the aversive interoceptive states linked to stress and withdrawal [21,22,23,24,25,26]. Here, planning could be affected by the initial discomfort expected under certain choices or might be preferentially impacted by heightened negative states. For example, some plans may not be given ample consideration if expected short-term effects are negative (e.g., expected withdrawal states), even if longer-term outcomes would be ideal (e.g., recovery). This difficulty considering distal outcomes of plans with unpleasant short-term consequences is referred to as aversive decision tree pruning (AP) and appears to be a reflexive, Pavlovian response [27]. However, potential moderators of this mechanism, such as the aversive interoceptive states discussed above, are currently unknown. The degree to which AP is relevant to iMUDs in comparison to other potentially explanatory mechanisms – such as reduced reward sensitivity or planning horizon (i.e., the overall number of future steps one considers) – has also not been thoroughly investigated.

Here we assessed multi-step planning in iMUDs during an anxiogenic interoceptive perturbation protocol involving inspiratory breathing resistance. We used computational modeling to assess behavior on a previously validated planning task and compared computational metrics of behavior (i.e., AP, planning horizon, and reward sensitivity) between task runs under conditions with and without the breathing perturbation, allowing assessment of the effect of interoceptive/somatic state anxiety. Computational measures were also examined in relation to cognitive reflectiveness and severity of drug-related consequences, withdrawal, and craving. Our primary aims were to: (1) evaluate whether aversive state induction moderated computational planning mechanisms, (2) differentiate competing hypotheses regarding which computational mechanisms were altered in iMUDs, and (3) evaluate whether differences in computational planning mechanisms may be explained by trait differences in cognitive reflectiveness and potentially predict symptom severity.

Methods

Participants

Data were collected at the Laureate Institute for Brain Research (LIBR) in Tulsa, Oklahoma. Eligible participants came from the Tulsa community, were 18–65 years old, weighed ≤250 pounds (due to equipment limitations), and did not have a history of traumatic brain injury or neurological disorders. Participants included healthy comparisons (HCs) without any diagnosed psychiatric conditions or elevated symptom levels (n = 49) and those diagnosed with amphetamine use disorder with methamphetamine as a primary drug of choice (n = 40). Participants with MUD were recruited from recovery centers in the Tulsa area within 45 days of entry into treatment. A comorbidity breakdown is shown in Supplementary Table S1.

A post-hoc power analysis confirmed that our sample size would provide 80% power to detect hypothesized group differences (i.e., lower AP in iMUDs than HCs), assuming a moderate effect size of Cohen’s d = 0.54 and a false positive rate of p < 0.05.

Ethics approval and consent to participate

This study was carried out in accordance with the Declaration of Helsinki and was granted ethical approval by the WCG Institutional Review Board (#20211403), and all methods were performed in accordance with relevant guidelines and regulations. Written informed consent was obtained from all enrolled participants before their involvement in the study.

Measures

Descriptions of all relevant measures are provided in Supplementary Materials. Measures of substance use severity (DAST: Drug Abuse Screening Test [28]), withdrawal symptoms (MAWQ: Methamphetamine Withdrawal Questionnaire [29]), and craving (DSQ: Desire for Speed Questionnaire [30]) were collected only in iMUDs. As part of a larger funded study, descriptive symptom severity data from these measures has previously been reported to characterize an overlapping sample [31; also see 32]. All analyses/results reported here in relation to computational/behavioral measures are novel.

Experiment design

Aversive state induction and sensitivity protocol

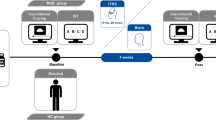
In the present study, we attempted to induce a temporary state of interoceptive/somatic anxiety by altering breathing effort. Specifically, participants were asked to breathe through a mask (Fig. 1a) with resistors that adjusted how difficult it felt to inhale (in cmH2O/L/sec), while no resistance was applied to exhalation. Before task performance, they were exposed to 6 increasing levels of resistance (i.e., 0, 10, 20, 40, 60, and 80 cmH2O/L/sec) for 60 s each and rated their anxiety immediately after each exposure on a scale from 0 = no anxiety to 10 = maximum possible anxiety one could tolerate. This “resistance sensitivity protocol” provided participants the chance to become accustomed to the resistances and allowed assessment of differences in sensitivity.

Fig. 1: Study equipment, task interface, and computational model.
figure 1

a Equipment used for anxiety induction: silicon mask with adjustable straps and single breathing port; resistors used to create resistance during inhalation and induce anxiety; two-way valve connected to the mask, which ensures that inhalations engage one port while exhalations engage the other; tube connecting two-way valve to resistor. b Graphical interface of the Planning Task. The blue button on the button box (center right) corresponds to transitions with blue arrows and the yellow button corresponds to transitions with yellow arrows. c Computational model of (1) path valuation, (2) the probability of selecting a particular action sequence, and (3) calculation of AP. Note that AP = π, NLL-discounting = 1-γG, and LL-discounting = 1-γS. d Example decision tree based on an example starting position with point values for transitions and final path points demonstrating aversive pruning. Points for the optimal path and the second-best path (indicated with thicker connecting lines) are shown in green and red, respectively. Colors of connections indicate whether the move was performed using the left (blue) button or the right (yellow) button.

Full size image

Participants also provided ratings of other secondary questions pertaining to difficulty, valence, and arousal (see Supplementary Materials). Please note that anxiety ratings in response to this series of resistance levels have previously been described in conjunction with other data gathered as part of a larger funded study [31]. However, all analyses of this data in relation to computational measures described here are novel and focused on distinct research questions.

Planning task

The behavioral task completed by participants in this study was a modified version of the Sequential Planning Task previously described and validated by Huys, Eshel [27] and used in subsequent studies [33, 34]; see Fig. 1b. Six squares are presented during the task. Specific unidirectional transitions from one square to another are allowed, each with associated point values. Transitions and point values are memorized through extensive pre-training and testing and are not shown during the task. Possible transitions include small losses (−20), small gains (+20), large losses (−70), or large gains (+140). The task structure was designed with these specific transitions and associated point values to allow clear assessment of AP behavior; i.e., in which individuals might choose to avoid paths with one or two large losses, despite a subsequent large gain that made these paths optimal overall. Starting positions vary trial-to-trial with allowable sequences of 3, 4, or 5 moves on different trials, ensuring some trials have optimal paths with large losses while other trials do not. Moves are planned during a 9 s “planning period” and then entered in sequence during a subsequent 2.5 s “response period.” Participants completed two runs of 72 trials. They also completed a post-task assessment that evaluated memory retention for the transitions and point values (see Supplementary Fig. S1 for more details). However, this post-test was only added part-way into the study to help rule out potential retention-based confounds; thus, data for this measure were not collected in all participants (available data in HCs = 46, iMUDs = 36).

Procedure

For HCs, the planning task was completed on the second visit of a larger funded study after they completed surveys and other activities on Day 1. On Day 2, after filling out initial screening questions and passing a urine drug analysis, HCs completed the task training and then performed the planning task inside an MRI scanner for their two task runs (fMRI data analysis for the larger study is in progress and will be reported elsewhere). Due to scheduling limitations with collaborating recovery homes, task training and performance for iMUDs were completed after a lunch break in a one-day study visit that began with the same surveys and other study activities that HCs performed on Day 1. Participants with MUD completed their two task runs in a mock MRI scanner designed to best match task environments for the two groups. All participants responded to a self-reported anxiety question and the State-Trait Anxiety Inventory (STAI) State Scale [35] before and after each run of the task. During one run of the task (counterbalanced order), participants were continuously exposed to a resistance level of 40 cmH2O/L/s, chosen to maintain a moderate (but tolerable) anxiety level (i.e., based on previous work using this paradigm [36] and confirmed by results of the sensitivity protocol). The other run was completed with no resistance.

Computational modeling and model fitting

Model-based behavioral analyses were performed using the computational modelling approach outlined in Lally, Huys [33] and conducted in MATLAB (R2022a). Here, the value of each action sequence is based on the expected reward at each transition. A discounting parameter 0≤γ≤1 down-weights the influence of expected wins/losses at later steps in a given sequence (higher values indicate less discounting). This parameter is separated into two independent components: (1) γS applies to paths with large-loss transitions (i.e., −70 points); and (2) γG applies to all other paths (i.e., combinations of −20, +20, and/or +140 points), reflecting a general planning horizon. The influence of path value differences on choice probability is then scaled by a reward sensitivity parameter β ≥ \(0\), referred to as RS below. As in prior work, model comparison using the Bayesian Information Criterion (BIC) confirmed that this model outperformed simpler models (i.e., that either discounted all paths equally or applied no discounting; ΔBICs ≥ 2323; see Supplementary Fig. S2). Parameter recoverability analyses were also performed to demonstrate sufficient accuracy in estimation. This was done by generating simulated behavior within the model under representative combinations of parameter values, estimating parameter values from this simulated behavior, and then evaluating the magnitude of associations between the generative and estimated values. Results of these analyses are reported in Supplementary Materials (see Supplementary Fig. S3), confirming strong recoverability in each case (rs ≥ 0.91).

To assess an individual’s propensity to avoid large-loss paths above and beyond their general planning horizon, we calculated a difference score, π=γG−γS, corresponding to their aversive pruning (AP) value. Note that, for directional consistency, we report 1−γG (NLL-discounting) and 1−γS (LL-discounting) below. See Supplementary Materials and Huys, Eshel [27], Lally, Huys [33] for details regarding model fitting and model comparison.

To assess the unique contribution of AP to overall task performance, simulations testing correlations between AP and overall points won on the task are also shown at different fixed values for RS and NLL-discounting in Supplementary Fig. S4. This confirmed that higher AP was associated with worse task performance, confirming it can be interpreted as maladaptive in this context.

Statistical analyses

Anxiety induction efficacy

All statistical analyses were performed using R Studio version 4.2.0 [37].

We first confirmed the efficacy of the anxiety induction. Specifically, we ran linear mixed effects models (LMEs; using the lmer function within the lme4 R package [38]) with anxiety level as the outcome variable, and with group (sum-coded: HCs = −1, iMUDs = 1), breathing resistance (no resistance = −1, resistance = 1), and their interaction as predictors. This was done both for self-reported anxiety across resistance levels during the sensitivity protocol (coded as a continuous variable) as well as self-reported anxiety and STAI state before and after the two task runs. We also tested the effect of anxiety induction on craving by examining DSQ scores before vs. after participants underwent the sensitivity protocol.

Computational parameters and task behavior

We then performed similar LMEs predicting each model parameter with group, resistance condition, and their interaction as predictors, while accounting for possible effects of age (centered) and sex (sum-coded: male = −1, female = 1). These models also included an interaction between resistance condition and self-reported anxiety during the task to address the hypothesis that differences in efficacy of the anxiety induction would impact task behavior. Comparable LMEs replacing model parameters with model-free behavioral metrics were also run.

Despite counterbalancing, we were also interested in assessing stability in behavioral metrics between runs and understanding potential practice effects. Thus, we carried out supplemental analyses of intraclass correlations (ICCs) for each model parameter and tested further LMEs including potential effects of run number (i.e., Run-1 vs. Run-2).

Secondary analyses of potential confounds

To rule out memory-related confounds, LMEs predicting post-task memory accuracy were run using question type (either memory of point values or transition directions), point value (−70, −20, +140, +20), and group as predictors (all categorical variables sum-coded).

As a further check, analyses of task performance (both model-based and model-free metrics) were repeated while accounting for working memory (NIH Toolbox List Sorting corrected score [39]) and accuracy on the post-task memory test. These secondary analyses could only be performed in the subset of participants for which these data were available, but helped to confirm that group differences were not explained by differences in either general cognitive ability or memory for different path values. The post-task memory metric was calculated by taking the ratio between accuracy on questions for large-loss transitions and accuracy on all other questions (i.e., mirroring apparent AP effects). Additional secondary analyses included (separate) possible effects of Group x Sex interactions, length of abstinence, days since starting treatment, medication status, specific substance use diagnoses, and continuous depression (PHQ-9: Patient Health Questionnaire [40]) and anxiety (OASIS: Overall Anxiety Severity and Impairment Scale [41]) levels.

Secondary dimensional analyses

To evaluate whether sensitivity to the anxiety induction and changes in anxiety during each task run might relate to disorder severity in iMUDs, we next ran linear models (LMs) with change in self-reported anxiety as the outcome variable, and severity, withdrawal, or craving as predictor variables (i.e., DAST, MAWQ, or DSQ, each in separate models). To assess whether change in anxiety might lead to changes in craving, the model with DSQ as a predictor also included change in DSQ from baseline to after the 80 cmH2O/L/sec resistance exposure. Baseline anxiety, age, and sex were also controlled for in each of these models.

We also examined possible associations between AP and cognitive reflectiveness as measured by the Cognitive Reflection Test-7 (CRT; [14]). Specifically, we ran an LME predicting AP from CRT scores (while including effects of resistance, age, and sex), both across all participants and in iMUDs alone. Motivated by initial results, we subsequently ran a mediation analysis testing CRT as a potential mediator of the relationship between group and AP (i.e., testing whether group differences in AP might be accounted for by differences in reflectiveness). For this test, we used the mediate function (mediation package in R [42]) with 5000 simulations. This analysis was also repeated in Supplementary Materials to account for working memory.

Supplementary exploratory analyses were also performed for other available measures in the larger study reflecting impulsivity and reward-seeking. All details of these exploratory analyses are provided in Supplementary Materials.

Results

The breathing-based aversive state induction was effective at increasing anxiety

The clinical and demographic makeup of the present sample is presented in Table 1. Self-reported anxiety after each resistance level in the sensitivity protocol is shown in the top panel of Fig. 2. Full results of models testing effects of group, resistance level, and their interaction on anxiety are reported in Supplementary Materials. Confirming prior results in an overlapping sample [31], anxiety levels increased with resistance, iMUDs had higher anxiety ratings than HCs, and anxiety increased more steeply in iMUDs than in HCs. Analogous figures and statistics for the other ratings given during the resistance sensitivity protocol (e.g., unpleasantness, difficulty, etc.) are provided in Supplementary Fig. S5 and Table S2.

Table 1 Demographic makeup of both groups (mean and SD) and statistical tests to assess sample differences.
Full size table
Fig. 2: Anxiety induction efficacy.
figure 2

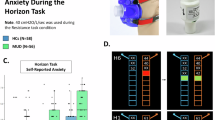
Top: Boxplots (median and quartiles) for self-reported anxiety ratings across the resistance sensitivity protocol (scale 0–10). Anxiety for iMUDs (n = 40) was higher than HCs (n = 49; F(1,101) = 14.21, p < 0.001, \({\eta }_{p}^{2}=0.12\)), and anxiety increased as a function of inspiratory resistance level (F(1,977) = 710.53, p < 0.001, \({\eta }_{p}^{2}=0.42\); b = 0.644). Bottom: Boxplots for self-reported anxiety (scale 0–10) and State-Trait Anxiety Inventory (STAI; [35]) State ratings (scale 0-80) from pre- to post-task for runs with and without the breathing resistance. Again, anxiety was generally higher in iMUDs (Fs > 14.39, ps < 0.001) and also increased with resistance level (Fs > 4.50, ps < 0.001). Stars indicate significant differences in post-hoc comparisons between groups at each resistance level (top) or time point (bottom). *p < 0.05,**p < 0.01,***p < 0.001.

Full size image

Anxiety ratings (both self-reported and from the STAI State scale) gathered before and after each run of the task are shown in Fig. 2. Full results for analogous models testing effects of group, time (i.e., pre or post), and resistance condition (and possible interactions) are reported in Supplementary Materials. Overall, results indicated the breathing resistance was effective at generating moderate anxiety.

Data characterization and quality control

Values in the present sample for each parameter in this model demonstrated sufficient normality under both resistance conditions (skew < |2|; density plots shown in Supplementary Fig. S6). In the subset of participants (HCs = 46, iMUDs = 36) who completed the post-task assessment (Supplementary Fig. S1), overall accuracy confirmed successful retention of transitions and point values (M = 87.4%, SD = 19.3%) with HCs outperforming iMUDs (t(80) = 4.95, p < 0.001; see Supplementary Materials for more details). Thus, in relevant analyses below, we confirmed whether differences in any computational measures could be accounted for by these memory differences (while noting that AP-like behavior reduces the number of times that large-loss transitions were observed during the task, which would itself be expected to lead to worse post-task memory). Based on iterative Grubbs (threshold: p < 0.01; grubbs.test function from outliers package; [43]), one HC was identified as an outlier for RS. However, this reflected plausible behavior with high task performance; thus, we retained this data point. Nonetheless, we confirmed that all results remained qualitatively identical if it was removed.

Aversive pruning was elevated in individuals with methamphetamine use disorder

Model parameter values by group and resistance condition (as well as model-free measures of behavior) are presented in Table 2 and visualized in Fig. 3. Results of the Group effect in each LME are also shown in Table 2. All other results are provided in Supplementary Table S3A. The Resistance effect was not significant in any model (Fs ≤ 3.68, ps ≥ 0.058).

Table 2 Computational model parameters and model-free task metrics by group and resistance condition.
Full size table
Fig. 3: Computational parameters and model-free metrics of behavior.
figure 3

a Raincloud plots showing distributions for each model parameter by group and resistance condition as well as individual data points connected by thin lines and group means and standard errors depicted by thick lines and confidence ribbons (iMUDs: n = 40; HCs: n = 49). Independent of resistance level, iMUDs had larger AP estimates (F(1,100) = 16.46, p < 0.001, \({\eta }_{p}^{2}=0.14\)) and larger LL-discounting estimates (F(1,100) = 13.45, p < 0.001, \({\eta }_{p}^{2}=0.12\)) than HCs. b Means and standard errors for choice accuracy, which differed by group in trials where the optimal path included large losses (OLL trials; F(1,490) = 25.30, p < 0.001, \({\eta }_{p}^{2}=0.05\)). This was driven by differences at depths 3 and 4. Stars indicate significant effects. LL large loss, NLL no large loss. *p < 0.05, **p < 0.01, ***p < 0.001.

Full size image

In the model predicting AP, there was a significant effect of group (F(1,100) = 16.46, p < 0.001, \({\eta }_{p}^{2}=0.14\)), such that iMUDs pruned more than HCs (large effect size of Cohen’s d = 0.81 in post-hoc contrasts). There was also a significant Group x Resistance interaction (F(1,90) = 5.17, p = 0.025, \({\eta }_{p}^{2}=0.05\)) indicating that iMUDs pruned more without the added resistance than with it. An effect of sex was also observed (F(1,84) = 5.98, p = 0.017, \({\eta }_{p}^{2}=0.07\)), indicating greater pruning in female participants.

For further interpretation, we subsequently analyzed LL-discounting and NLL-discounting separately. When predicting LL-discounting in analogous LMEs, there were again main effects of group and sex, such that iMUDs discounted more than HCs and that female participants discounted more than male participants (F(1,85) = 4.70, p = 0.033, \({\eta }_{p}^{2}=0.05\)). Similarly, there was a significant Group x Resistance interaction (F(1,90) = 4.84, p = 0.030, \({\eta }_{p}^{2}=0.05\)), reflecting a pattern consistent with what was found in models of AP.

Analogous LMEs predicting NLL-discounting showed no significant effects (Fs ≤ 2.38, ps ≥ 0.126), suggesting findings for AP were explained by differences in LL-discounting. In other words, the alternative (or complementary) hypothesis that iMUDs would show a shorter planning horizon in general was not supported.

Analogous LMEs predicting RS did not show any significant results. This therefore did not provide support for the alternative (or complementary) hypothesis that iMUDs would show a generally lower level of prospective reward sensitivity in planning. However, it bears mention that the notably greater RS values (numerically) in HCs (shown in Fig. 3) were significant (F(1,85) = 5.65, p = 0.020, \({\eta }_{p}^{2}=0.06\)) before accounting for group differences in state anxiety; thus, covariance between anxiety levels and group may have masked this effect.

Group differences in task performance were primarily at shorter depths

After assessing model-based behavior, we also performed complementary assessment of model-free metrics (i.e., overall points won and accuracy by path depth on trials with and without large losses on the optimal path [i.e., OLL and ONLL], respectively). Bar plots for accuracy by trial depth and resistance condition are shown in Fig. 3b. Results showed that HCs won more points than iMUDs (see Table 2) and that male participants scored higher than female participants (F(1,85) = 5.04, p = 0.027, \({\eta }_{p}^{2}=0.06\)).

When predicting percentage of correct OLL trials by path depth, there were effects of group (see Table 2), depth (F(1,437) = 158.79, p < 0.001, \({\eta }_{p}^{2}=0.27\)), and their interaction (F(1,437) = 11.84, p < 0.001, \({\eta }_{p}^{2}=0.03\)). Post-hoc contrasts showed that: (1) HCs had higher overall accuracy than iMUDs; (2) accuracy decreased as path depth increased (b = −0.102); and (3) OLL accuracy decreased more sharply in HCs (estimated marginal trend [ET] = −0.13) than iMUDs (ET = −0.07; t(437) = 3.44, p < 0.001, Cohen’s d = 0.33). Here, HCs were more accurate than iMUDs at depth 3 and depth 4 but dropped more steeply to become equivalent to iMUDs at depth 5. There was also an effect of sex (F(1,85) = 10.06, p = 0.002, \({\eta }_{p}^{2}=0.11\)), where male participants (estimated marginal mean [EMM] = 0.33) had higher OLL accuracy than female participants (EMM = 0.21; t(85) = 3.17, p = 0.002, Cohen’s d = 0.70).

Aside from the expected effect of depth on ONLL trials (with greater path depth predicting worse accuracy; F(1,437) = 215.49, p < 0.001, \({\eta }_{p}^{2}=0.33\); b = −0.132), no other significant effects were observed (Fs ≤ 2.44, ps ≥ 0.119).

Group differences were not explained by memory, anxiety/depression, or comorbidities

To address potential concerns about confounding effects of working memory capacity or long-term recall on task performance, we reran the models above predicting computational parameters when including working memory scores and accuracy on the post-task memory assessment as covariates. Results of all LMEs above were largely equivalent when including working memory and post-task memory scores as additional covariates (i.e., in the subset of participants with available data; see results in Supplementary Table S3B). In particular, observed group differences for AP remained significant.

No models testing possible effects of trait anxiety and depression (i.e., scores on the OASIS and PHQ-9, respectively) showed significant results (see Supplementary Tables S4A, B). When comparing iMUDs with and without specific comorbid substance use diagnoses, we found no differences in AP estimates between those with and without alcohol or opioid use disorders (noting that we were 80% powered to detect large effects only; \({\eta }_{p}^{2} > 0.17\)). However, we did observe that individuals with alcohol use disorder showed lower LL-discounting than those without (see Supplementary Materials for details; see Supplementary Table S1 for a full breakdown of comorbidities). However, values for both alcohol (37.5%) and non-alcohol users (62.5%) each remained numerically higher than HCs (alcohol: M = 0.41 ± 0.16; non-alcohol: M = 0.52 ± 0.14; HCs: M = 0.36 ± 0.18). No other significant differences were found for any computational parameter.

No significant effects were found when predicting model parameters with length of abstinence (days since last methamphetamine use: M = 57.25 ± 42.65), days since start of treatment (M = 30.28 ± 11.00), or medication status (n = 30 medicated; Fs ≤ 3.33, ps ≥ 0.077; see Supplementary Materials).

AP showed a negative relationship with total points won in both resistance conditions (rs ≥ |0.26|, ps ≤ 0.013), suggesting that higher pruning in iMUDs was maladaptive; all other relationships between model-based and model-free metrics were in expected directions (Fig. 4a). As further confirmation of the unique relationships between each parameter and task performance, we also tested a model that included all three parameters as joint predictors of total points won (with resistance condition as a covariate). As expected, results showed that each parameter was independently associated with performance (ps < 0.001). Namely, higher values for each discounting parameter were associated with fewer points (in thousands; bNLL = −9.29; bLL = −2.89), while greater reward sensitivity showed the expected positive association (b = 30.40). Thus, the maladaptive influence of LL-discounting (and thus AP) on points was not accounted for by differences in RS or general planning horizon (i.e., NLL-discounting).

Fig. 4: Correlations between computational measures and other measures of interest.
figure 4

a Correlations between model parameters and model-free task metrics across groups. b Inter-correlations between model parameters. c Correlations between model parameters and covariates (statistics shown for sex represent t-values from independent samples t-tests, where the negative direction indicates higher values in male participants). All relationships are shown separately for parameters under the no resistance (top) and resistance (bottom) conditions. OLL = trials in which the optimal path contains a large loss, ONLL = trials in which the optimal path does not contain a large loss. RS Reward Sensitivity, NLLd = ONLL Path Discounting Probability, LLd = OLL Path Discounting Probability, AP Aversive Pruning. *p < 0.05, **p < 0.01, ***p < 0.001.

Full size image

Inter-correlations between the three model parameters for all participants demonstrated sufficient differentiability (Fig. 4b). Exploratory relationships between model parameters and demographic variables are shown in Fig. 4c.

Supplemental analyses of intraclass correlations (ICCs; one-way, consistency) for each model parameter between runs (Supplementary Table S6) suggested that, despite condition differences, repeated task performance tended to produce moderately consistent values for each participant (ICCs: AP = 0.61; NLL-discounting = 0.48; LL-discounting = 0.66; RS = 0.48). Complementary LMEs presented in Supplementary Table S7 and Supplementary Fig. S8 also tested for potential practice effects (Run-1 vs. Run-2) on each parameter (including age, sex, and potential interactions with group as covariates). In brief, results suggested practice effects on RS (greater values in Run-2), as well as decreased NLL-discounting values from Run-1 to Run-2 in HCs but not iMUDs. No significant practice effects were observed for LL-discounting or AP (see Supplementary Materials).

Craving and withdrawal symptoms relate to both resistance sensitivity and model parameters

When restricting to iMUDs (n = 40), linear models (LMs) predicting resistance sensitivity (i.e., change in anxiety level from pre- to post-sensitivity protocol session), using DAST (drug abuse), MAWQ (withdrawal), and DSQ (craving) scores showed largely nonsignificant results (Fs ≤ 1.90, ps ≥ 0.177; details in Supplementary Materials). However, more severe MAWQ emotional symptoms were associated with greater increases in anxiety after the sensitivity protocol (F(1,35) = 9.15, p = 0.005, \({\eta }_{p}^{2}=0.21\), b = 0.602), which remained significant after correcting for four subscale comparisons. No other significant predictors of changes in anxiety ratings (measured by self-reported anxiety and STAI State) from pre- to post-task were found (Fs ≤ 3.96, ps ≥ 0.054).

In an LME predicting AP in iMUDs, including substance abuse severity (DAST), resistance, and their interaction, and accounting for age and sex, there was a significant main effect of DAST scores (F(1,36) = 12.15, p = 0.001, \({\eta }_{p}^{2}=0.25\)), indicating (surprisingly) that more severe consequences of drug use were associated with less pruning (b = −0.043; see Supplementary Fig. S10). In analogous models replacing DAST scores with each scale on the withdrawal questionnaire (MAWQ) separately, there were no effects of withdrawal symptoms found on AP (Fs ≤ 1.28, ps ≥ 0.266). In a model including baseline craving symptoms (DSQ; n = 28), there was no significant effect of craving (F(1,24) = 2.74, p = 0.111). However, changes in DSQ scores after anxiety induction, accounting for baseline craving scores and the interaction between DSQ change and resistance condition, showed a positive association with AP (F(1,23) = 8.82, p = 0.007, \({\eta }_{p}^{2}=0.28\)), indicating that an increase in craving following anxiety induction (i.e., within the pre-task resistance sensitivity protocol) was associated with more pruning (b = 0.005; Supplementary Fig. S10). There was also a significant negative effect of baseline craving on AP (F(1,23) = 5.70, p = 0.026, \({\eta }_{p}^{2}=0.20\)), indicating that higher baseline craving predicted less pruning (b = −0.002).

To understand the unexpected negative relationships between AP and either baseline craving or substance abuse severity (DSQ and DAST, respectively) scores, we looked at individual scale items as predictors in LMEs that included resistance condition only. We found that a small number of items reflecting self-control on both measures acounted for these relationships (DAST items 3, 4, 8; Fs ≥ 5.40, ps ≤ 0.026 [n = 40]; DSQ items: 2, 14, 15, 27, 30, 36; Fs ≥ 4.34, ps ≤ 0.047 [n = 28]), highlighting a context in which pruning can be adaptive within iMUDs (e.g., individuals with greater pruning were more likely to say “no” to items such as “Have you engaged in illegal activities in order to obtain drugs?” that involve possible negative immediate outcomes).

Results of analogous models testing effects of symptoms on other model parameters are in Supplementary Materials. Briefly, results found for LL-discounting matched those of AP. When predicting NLL-discounting, there was also an interaction between functional (MAWQ) withdrawal symptoms and resistance condition (p = 0.047), suggesting that anxiety induction increased the effect of withdrawal state on planning horizon.

Cognitive reflectiveness partially explained group differences in aversive pruning

An LME including CRT scores (n = 88), resistance condition, age, and sex as predictors revealed that higher reflectiveness tendencies were associated with less pruning (F(1,84) = 17.43, p < 0.001, \({\eta }_{p}^{2}=0.17\), b = −0.036). CRT scores showed a similar relationship with LL-discounting and a positive relationship with RS, but were not predictive of NLL-discounting (see Supplementary Materials).

These results suggested a potential mediation model in which greater AP in iMUDs might be explained by lower CRT scores. As shown in Fig. 5, testing this model revealed a significant indirect effect (ab = 0.063, p = 0.026, 95% CI: [0.01,0.13]), as well as a significant direct effect (c = 0.111, p = 0.024, 95% CI: [0.01,0.21]), indicating partial mediation (total effect cˊ = 0.174, p < 0.001, 95% CI: [0.09,0.25]). Thus, group differences in AP were partially accounted for by variation in reflectiveness.

Fig. 5: Mediation model indicating that cognitive reflectiveness partially accounted for group differences in aversive pruning.
figure 5

Graphical depiction of results indicating that lower cognitive reflectiveness levels (CRT scores) partially accounted for greater aversive pruning (AP) in iMUDs compared to HCs (available data: n = 89). Note that the relationship shown between group and CRT accounts for age and sex.

Full size image

We also assessed whether CRT scores related to symptom severity measures in a way that could explain pruning differences in iMUDs. In those with available data, we found that both changes in craving scores after anxiety induction and DAST scores each showed noteworthy but non-significant associations (DSQ: F(1,24) = 4.06, p = 0.055, \({\eta }_{p}^{2}=0.14\); DAST: F(1,37) = 3.54, p = 0.068, \({\eta }_{p}^{2}=0.09\)) that might be further tested in future studies with larger sample sizes. There were no relationships observed between CRT scores and withdrawal symptoms (Fs ≤ 0.43, ps ≥ 0.517).

Finally, supplementary exploration of potential relationships between model parameters and available measures of impulsivity/reward-seeking from the larger study did not reveal evidence for any relationships (Supplementary Materials).

Discussion

This study evaluated computational mechanisms of multi-step planning in individuals with methamphetamine use disorder (iMUDs) and healthy comparisons (HCs), and tested effects of an aversive interoceptive state induction. Computational measures included aversive pruning (AP; avoiding plans with large short-term losses), planning horizon (number of future steps one considers), and reward sensitivity (the degree to which planning is guided by expected reward). We observed substantially greater AP in iMUDs compared to HCs, independent of affective state, but no difference in overall planning horizon. To our knowledge, no previous study has examined this effect. Interestingly, group differences in AP were also partly mediated by cognitive reflectiveness, and greater pruning further predicted greater increases in craving in response to aversive state induction. This may be especially important given that negative affective states are known to promote vulnerability to relapse [44, 45], which our results suggest could be amplified in individuals with greater pruning tendencies.

Surprisingly, we found no evidence for greater pruning after aversive interoceptive state induction. In iMUDs, results actually suggested greater pruning at baseline. However, it should be noted that the induction protocol only generated modest changes in anxiety (i.e., ~2–3 point increases on a 10-point scale). One possibility is that effects could be accounted for by known inverted-U relationships between arousal and cognition [46], in which the induction kept iMUDs in a more alert or concentrated state, and that greater anxiety would have been necessary to produce the opposite effect.

The relationship we observed between pruning and cognitive reflectiveness suggests that those who have developed the cognitive habit of “thinking things through” before making a decision may also be less susceptible to overuse of AP. This finding may relate to previous work demonstrating deficits in other prospective cognitive processes in methamphetamine users (e.g., prospective memory performance and directed exploration [31,47,48]). It also builds on the larger body of work in computational psychiatry suggesting shifts from model-based to model-free control in substance use disorders (for reviews, see [17, 49]).

We also highlight, however, that AP should not always be seen as maladaptive. Indeed, in contexts where a decision tree is too large for exhaustive search, AP can act as a beneficial heuristic. This may also be the case when planning is constrained by internal effort costs or limited cognitive resources. In this light, cognitive reflectiveness scores in our data might be seen to index an individual’s subjective cost of internal simulation, perhaps accounting for their relationship to AP. On the other hand, one might expect the cost of internal simulation to reduce planning depth generally, as opposed to affecting AP in particular. Limitations on cognitive effort would likely promote greater randomness in choice as well (i.e., reflected by lower reward sensitivity). It should also be emphasized that, even when accounting for effects of the other parameters, higher AP in our data was associated with worse task performance (e.g., reduced overall points won), suggesting it was maladaptive in this context. Differences in performance associated with AP were also seen at the shortest planning depths (i.e., depth 3), where internal simulation would have been least costly. This suggests the greater AP in iMUDs seen here may be better explained by cognitive avoidance of thinking about plans with immediate negative outcomes, as opposed to less internal search in general or greater resource constraints (recall that working memory capacity differences also did not account for these effects).

Of potential clinical relevance, studies have demonstrated that reflectiveness can be improved with training [50,51,52,53,54,55]. Thus, this could be a targetable mechanism through which AP might be reduced. In line with our present findings, it is also possible that those with stronger cravings during aversive states (e.g., stress, withdrawal) are those who become more short-sighted during decision-making, which could, in turn, promote relapse [44, 45]. Future studies in larger samples should evaluate whether lower reflectiveness could link craving and pruning behavior, and whether interventions focused on increasing reflectiveness might reduce pruning and/or lessen chances of relapse.

Some important limitations and future directions should be considered. First, sex was imbalanced between groups, with limited sample size to support tests of possible differences. While we confirmed group differences were present for each sex separately (see Supplementary Fig. S9), future work in a balanced sample should replicate these results and investigate possible sex effects within each group. At present, the observed patterns across males and females should be interpreted with caution. Some iMUDs also had comorbid disorders, with opioid and alcohol use disorder being most prominent. These disorders have also been characterized in terms of cognitive and decision-making impairments, such as increased impulsivity [56, 57], reduced cognitive flexibility [58, 59], and reduced consideration of long-term outcomes [60,61,62]. While these comorbidities did not account for observed group differences in our analyses, our data nonetheless provide only limited evidence for specificity to MUD.

The available sample size to examine relationships between task behavior and continuous clinical measures was also limited. Nonsignificant results (e.g., with respect to depression/anxiety scores) might therefore reflect false negatives. Significant results (e.g., observed relationships to craving) should also be seen as preliminary and interpreted with caution, and replication in larger samples will be important to confirm their generalizability.

As there were some differences in the surrounding study protocol for the two groups (see Methods), we also cannot rule out that this influenced behavior. It should also be highlighted that the cross-sectional design of the present study does not allow us to differentiate whether observed effects represent pre-existing vulnerability factors or effects of substance use itself. We did not find lower pruning in those with greater length of abstinence, but studies testing a wider range of abstinence periods will be important.

Finally, the present study focused largely on planning mechanisms aimed at minimizing losses, allowing us to measure avoidance-related cognition and choice. However, possible differences with respect to small vs. large (and early vs. late) gains may not be fully captured in this task. Thus, future work in substance use disorder populations should also use tasks better optimized for detecting possible deficits in planning mechanisms in the domain of maximizing gains as opposed to minimizing losses.

In summary, we found that individuals with methamphetamine use disorder exhibited elevated aversive pruning on a multi-step planning task designed to pit large anticipated losses in the short-term against optimal positive outcomes in the long-term. This novel finding suggests a model-based impairment in the ability to consider optimal plans that require one to endure short-term aversive states. This effect has potential real-world relevance, as it mirrors difficult decisions faced by this population in which pruning could maintain use (e.g., not being able to consider the long-term benefits of abstinance due to the anticipated short-term pain of withdrawal). It also highlights a potentially novel treatment target with correlates (i.e., reflectiveness) known to improve with training. If replicated in future work, crucial next steps will require longitudinal and intervention studies designed to assess how pruning might relate to vulnerability and treatment response, and whether it can be modified in a manner that could improve clinical outcomes.