Introduction

Large earthquakes reoccur on natural faults due to the interaction between tectonic loadings and frictional resistance. The characteristic earthquake model on an isolated seismogenic zone is often used to conceptualize observations of recurring earthquakes whose magnitudes are similar, such as the moderate earthquakes in the Parkfield segment of the San Andreas fault1,2 and small repeating earthquakes3. For large subduction earthquakes, the supercycle model is required to explain the more complicated rupture behaviors on faults where multiple large earthquakes of different sizes occur in one complete supercycle4. Predicting the recurrence times of large earthquakes is challenging, even for the simple characteristic model5,6, mainly due to the unpredictable nucleation conditions7 and the uncertainties in stress states8. While we still cannot predict where and when earthquakes will start, recent advances9,10 can help us pinpoint where earthquakes might stop, thus how large they might grow.

An accessible way to assess future seismic hazard is to estimate the maximum possible earthquake magnitudes on faults as a function of elapsed time, capturing for example the possibility that a fault might not be ready to break over its whole length. Kinematically-based models11,12,13 or dynamically-based8,14,15,16,17,18,19,20 models on various fault systems, including estimates of their slip budget, have been used to infer their potential seismic moments. Specifically, fault geometric complexities21,22, such as fault bends and step-overs, have been integrated into single rupture simulations15,16,17,18 and earthquake cycle models19,20. Furthermore, complex fault systems have also been incorporated with a physics-based statistical simulator23 to reproduce seismic hazard statistics in Southern California. Both kinematically-based and dynamically-based models provide important insights on rupture segmentation and seismic hazard assessment. However, kinematically-based methods, although efficient, may overestimate the maximum magnitudes of potential earthquakes due to the lack of integration with rupture dynamics, while dynamically-based numerical simulations are too computationally expensive for efficient hazard assessment and thorough sensitivity analysis.

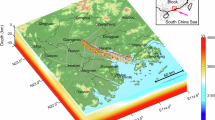
The Xianshuihe-Xiaojiang fault (XXF) is one of the longest left-lateral faults in southwest China with a spatial scale (~1100 km) comparable to the San Andreas fault in California. The deformation in the middle part of the XXF is accommodated by two branches: the mature Anninghe-Zemuhe fault (AZF) and immature Daliangshan fault (DLSF) (Fig. 1). Paleoseismic evidence shows that large earthquakes frequently occurred on the AZF in the past 500 years, including six M > 6.5 events and three M > 7.5 events24, whereas there is barely paleoseismic evidence of large events on the DLSF in the past 500 years25. The northern segment of the AZF is now thought to be close to its reoccurrence period since the last M~7.5 event in 1480 (ref. 24). However, questions persist about the elastic energy currently accumulated on the two faults and about the maximum possible earthquake magnitudes the faults can accommodate currently and in the future.

Fig. 1: Tectonic setting and fault coupling ratio on the Anninghe-Zemuhe fault (AZF) system.
figure 1

A Tectonic setting of the study area. Black solid lines indicate active faults obtained from the public Data catalog of the China Seismic Experiment Site. Red and gray triangles represent the 24 newly-developed near-field GNSS stations and existing stations used for constraining the kinematic coupling model, respectively. Cyan stars indicate historical events (M > 6.5) in the past 500 years (ref. 24). Blue vectors show the GNSS velocity in this region (“Data availability” section). ANHF: Anninghe fault; ZMHF: Zemuhe fault; DLSF: Daliang Shan fault; LJ-XJHF: Lijiang-Xiaojinhe fault; LMSF: Longmen Shan fault. Cyan vectors in the upper left inset show the block motions. Red star and ellipse represent show the epicenter and rupture extent of the 2022 Mw 6.6 Luding earthquake. B Coupling ratio on the AZF and DLSF. The fault changes from a completely locked state to a fully steady slip state as the coupling ratio varies from 1 to 0. Gray dots show the seismicity distribution that was projected onto the faults. AZF-1 to AZF-6 show the identified asperities on the AZF. Purple dots represent the near-fault cities. The topography data used in the figure is obtained from NOAA Data Catalog. The GNSS velocities on the new stations are available at Table S1. The seismic catalog data is available in Supplementary Data 1. The figure was drawn using the GMT5 software (“Code availability” section).

Full size image

Here, we combine kinematic inversions and a physics-based theoretical model based on three-dimensional (3D) dynamic fracture mechanics to show that the demonstrated fault system has already the potential to produce Mw > 7 earthquakes and the maximum possible magnitude will increase to Mw > 7.3 in 2200.

Results

Separated asperities on the Anninghe-Zemuhe fault system

Fault coupling controls the accumulation of slip deficit on faults and thus provides key constraints on the location and rupture extent of potential large earthquakes26,27,28. To obtain a high-resolution fault coupling distribution, we combine observations on 24 newly-developed near-field GNSS (Global Navigation Satellite System) stations and on previous stations around the AZF and DLSF (Fig. 1A) to estimate the long-term crustal velocities (Fig. 1 and Table S1) for the kinematic inversion of fault coupling (“Methods” section). Because the AZF has a near N-S trending that limits the applicability of the InSAR (Interferometric Synthetic Aperture Radar) technique, the near-field GNSS observations in this study can provide valuable constraints on fault coupling distribution. In the interseismic stage, viscoelastic relaxation at depth can affect crustal deformations in middle- and far-filed areas29. Ignoring this effect in the kinematic inversions results in larger slip deficits on deep fault segments to compensate, which thus leads to an overestimation of their coupling ratio30. We therefore adopt viscoelastic deformation models to infer the coupling ratio of the AZF and the DLSF. Our results further confirm that the elastic model overestimates the fault coupling on deep patches (Fig. S1). We find that the inferred geodetic slip rate on the AZF decreases from north to south, from 6.1 mm/a to 4.9 mm/a, which agrees well with geologic observations of 6.5 ± 1.0 mm/a31. The DLSF has a slip rate of 3.3–4.8 mm/a, responsible for ~40% of the sinistral motion across the fault system, which is also consistent with the geologic estimation of ~3–4 mm/a32. The fault coupling ratio on the AZF shows “string-beads-shaped” lateral variation along the strike, featuring six high-coupling asperities with spatial scales of 20–40 km (Fig. 1B). Along the DLSF with a comparable length to the AZF, we identify four high-coupling asperities. Checkerboard tests show that asperities with scales >20 km can be effectively resolved (Fig. S2), owing to the newly developed dense near-field stations (Fig. 1A), which therefore provides sufficient resolution in our inverted coupling model.

The AZF and the DLSF have different fault maturities32: the mature AZF has more continuous surface traces than the immature DLSF (Fig. 1A). Seismological33,34 and experimental34 studies show that the fault topographic roughness, representative of the fault structural maturity, may control earthquake sizes: smoother fault interfaces tend to produce larger earthquakes. Here, our results show that the AZF and the DLSF have distinct patterns of coupling ratio distributions that may also be caused by different fault maturities: the mature AZF has shorter scales of coupling heterogeneities than the immature DLSF. In addition, lacking paleoseismic evidence of large earthquakes on the immature DLSF25 is qualitatively consistent with previous studies of fault roughness33,35. If the experimental results of fault roughness in the laboratory (e.g., ref. 35) can be upscaled to natural faults, the AZF may tend to produce larger events than the DLSF, yet a conclusive comparison should also consider their accumulated slips, geological ages, tectonic loading conditions, and other relevant factors.

Spatial correlation with historical ruptures and current seismic b values

The laterally variable fault coupling is strongly related with the accumulated shear stress and rupture extents of historical earthquakes. We first can use the rupture extents of large historical earthquakes to validate the reliability of the obtained fault coupling maps. As shown in Fig. 2A, there is a strong spatial correlation between the inverted fault asperities on the AZF and the observed rupture extents of large historical earthquakes in the past ~500 years, delineated by comprehensive analysis of multi-disciplinary observations24. Three M 6.8 earthquakes, which occurred in 1952, 1489, and 1732, only ruptured single isolated asperities, whereas three M 7.5 events in 1480, 1536, and 1850 connected two adjacent asperities. If the rupture is confined within an isolated asperity, the earthquake magnitude is generally less than Mw 7, but it can reach up to Mw 7.5 if ruptures break through multiple adjacent asperities. Besides, we observe two low coupling zones, i.e., north of asperity AZF-3 and south of asperity AZF-4, that seem to be long-standing barriers as no ruptures breaking through them have been observed. The phenomenon that historical ruptures were generally impeded by low coupling areas strongly demonstrates that fault coupling controls the rupture extent and magnitude of large events. The correlation also indicates that the fault coupling may represent a long-term stable feature and thus we propose that our results based on decades of observations can be extended to at least one earthquake cycle.

Fig. 2: Spatial variation of coupling ratio, historical rupture, b value, and stress along the Anninghe-Zemuhe fault (AZF).
figure 2

A Comparison between the depth-averaged (0–15 km) coupling ratio (blue dots with gray error bars) and the rupture extent of large historical earthquakes (orange lines, ref. 24) on the AZF. The gray error bars show 1-σ uncertainty of the coupling ratio inferred from statistical analysis (“Method” section). The solid orange lines indicate historical ruptures of high reliability, whereas the dashed lines represent observations with relatively large uncertainty. AZF-1 to AZF-6 at the top of the panel show the identified asperities on the AZF. B Distribution of accumulated shear stress since 1480. C The b values along the AZF, the error bar show 1-σ uncertainty. D Comparison between recurrence intervals calculated based on the physics-based rupture theory (black line) and those inferred from geologic observations (red bars).

Full size image

We further calculate the stressing rate distribution based on the fault coupling ratio on the AZF and estimate the current accumulated shear stress on each asperity since the last large earthquakes (Fig. 2B; “Methods” section). The b value has been suggested to act as a stress meter that is inversely correlated with the stress level36,37. To compare with the calculated stress, we derive the b value in this region based on the updated earthquake catalog in the period from 2009 to 2023 and draw it along the AZF (“Methods” section). As shown in Fig. 2C, we observe two areas of low b values near asperity AZF-1 and AZF-4, indicating highly stressed conditions, which are consistent with the high shear stress on the fault accumulated since the last large events (Fig. 2B). On asperity AZF-3 and AZF-6, the b value is relatively high, revealing a relatively low-stress level due to short elapsed times on these asperities (Fig. 2B). These results highlight that the shear stress constrained by the geodetic and paleoseismic observations is qualitatively consistent with the b value based on the statistical properties of current seismicity.

Maximum possible earthquake magnitudes

The accumulated slip deficit and shear stress, combined with 3D dynamic rupture theory, allow us to assess the maximum possible earthquake magnitude on the AZF and the DLSF. In dynamic rupture theory9, rupture propagation and arrest on a fault are controlled by the accumulated elastic energy \({G}_{0}\) from tectonic loadings and the dissipation energy \({G}_{c}\) due to frictional resistance. This theory predicts that rupture accelerates when \({G}_{0} \, > \, {G}_{c}\) and decelerates when \({G}_{0} \, < \, {G}_{c}\), encapsulating a physics-based arrest criterion for dynamic ruptures: \({\int }_{{x}_{0}}^{{x}_{0}+L}(1-{G}_{c}(x)/{G}_{0}(x)){dx}=0\), where L is predicted along-strike arrest location distance from the hypocenter (located at x0). The criterion applies to each of the rupture fronts on bilateral ruptures. For the AZF (Fig. 3) and DLSF (Fig. S3), the distribution of \({G}_{0}(x)\) along strike can be derived based on the inverted coupling map and the elapsed time since the last large earthquake and \({G}_{c}(x)\) can be determined using a power-law slip-weakening friction model to fit global earthquake observations (“Methods” section).

Fig. 3: The maximum possible magnitude of earthquakes on the Anninghe-Zemuhe fault (AZF).
figure 3

A The estimated distribution of the potential energy release rate and fracture energy along strike before the 1952 M 6.8 earthquake. The top histogram shows the seismicity distribution along the strike between 2009 and 2023. The colored band accounts for uncertainties of the Gc scaling. B The maximum possible earthquake magnitude as a function of hypocenter location estimated by the 3D theory (purple symbols; vertical error bars indicate the uncertainties caused by the fitting of the Gc scaling) and by numerical simulations (blue curve) with the same Gc scaling. The thick red line marks the ruptured region of the 1952 M 6.8 earthquake. C, D Same as (A, B) but in 2023. In B and D the pink areas indicate the high-hazard regions where the maximum possible earthquake magnitudes are close to Mw 7 and the inset in (D) shows the maximum possible earthquake magnitude as a function of time until the year 2250.

Full size image

We first use this theory to estimate the maximum possible earthquake magnitude on the AZF in 1952 before the occurrence of the M 6.8 earthquake, by assuming various hypocentre locations (Fig. 3B). We find that before the 1952 event, G0 on the asperity AZF-3 is higher than Gc (Fig. 3A), and thus it is in a favorable state for ruptures. The theoretical model shows that if a rupture nucleates around asperity AZF-3 the fault has a potential to generate a Mw 7.0 event before 1952, which is consistent with the actual occurrence of the M 6.8 earthquake in 1952 (Fig. 3B). After accounting for the stress perturbation of the 1952 earthquake (“Methods” section), we assess the G0, Gc and the maximum possible earthquake magnitude in the current stress state (Fig. 3C, D). Because the 1952 earthquake has released part of the stored elastic energy, the asperity AZF-3 has less possibility to produce a Mw 7 event in its current state. But its neighboring asperities can still accommodate Mw > 7 events and their maximum magnitudes slightly increase due to the loading from the 1952 rupture. Due to the lack of direct constraints on the 1952 M 6.8 earthquake in the current model, the possibility of a future Mw 7.5 event bridging AFZ-3 and AFZ-4, similar to the 1536 M 7.5 event, cannot be excluded and thus is worthy of further investigation. On the AZF, we primarily focus on the Anninghe fault and the northern segment of the Zemuhe fault, as the shear stress on the southern segment of the Zemuhe fault is currently insufficient to accommodate large events. We also use this theory to estimate the maximum possible earthquake magnitude on the DLSF, although its coupling is less finely resolved than that of the AZF. Due to the absence of paleoseismic evidence for the DLSF, we assume that the elapsed time since the last large earthquake is either 500 or 1000 years, to obtain a lower bound estimate of the maximum possible earthquake magnitude. We find the maximum possible earthquake magnitude on the DLSF could also reach Mw 7 (Fig. S3) if the elapsed time since the last large earthquake is longer than 500 years.

To confirm these theoretical predictions, we first set a 3D dynamic rupture model with a vertical planar fault intersecting the free surface in a linear elastic medium. In the numerical model, we implement the power and exponential slip-weakening friction laws, respectively, whose coefficients are determined based on the data of global earthquakes within the relevant range of slip values (“Methods” section). These two friction laws represent two end-member regimes of thermal pressurization38 caused by the shear heating of fault zone pore fluids. The exponential friction law is also proposed in laboratory experiments39. The current shear stress on the fault has been building up since the latest large earthquake, during which the frictional strength dropped to a residual value \({\tau }_{r}\). Due to the lack of direct constraints, we need to indirectly infer \({\tau }_{r}\) value of the last big event. For the exponential friction, we assume \({\tau }_{r}\) equals the minimum dynamic strength \({\tau }_{d}\) (“Methods” section). Note that the absolute value of \({\tau }_{d}\) is irrelevant in elastic rupture dynamics on vertical planar faults9. For the power-law friction, we assume \({\tau }_{r}\) is larger than \({\tau }_{d}\), corresponding to an empirical slip of the last big event (“Methods” section). As supported by laboratory experiments of large slips39, the assumption of \({\tau }_{r}={\tau }_{d}\) for the exponential friction relies on the estimated slip of the last big event being sufficiently large. The assumption for the power friction relies on the estimated slip of the historical big event: overestimated slips lead to underestimated \({\tau }_{r}\) and thus result in underestimated potential earthquake sizes. Despite these different assumptions of shear stresses and friction laws, we find that the theoretical and numerical predictions (Figs. 3 and S12) are quantitatively consistent in different rupture scenarios within the uncertainties in fitting the Gc scaling data. Both the theory and numerical model predict that the maximum possible earthquake magnitude may increase to Mw > 7.3 on the AZF if the earthquake occurred in 2200 (Figs. 3D and S13).

We then conduct additional 3D dynamic rupture models with a curved fault as used in the coupling inversion model (red curve in Fig. 4A), characterized by a significant bending within segment AZF-4. For comparison, we also consider a model with smoothed fault trace (blue curve in Fig. 4A). Based on the current stress state of the AZF constrained in this study, we find that fault bending is not the primary factor controlling earthquake sizes on the AZF, and that the numerical simulations are quantitatively consistent with the theoretical prediction regardless of different fault geometries on the AZF (Fig. 4B, C). The explanation may be that the dominant wavelength of fault curvature on the AZF is larger than the length scales of rupture depths or seismic asperities. Consequently, the first-order rupture dynamics on the AZF can be well predicted by 3D dynamic fracture mechanics based on a planar fault. While in the future, it is necessary to consider the effects of fault complexities, such as step-overs on the DLSF, despite its observations being less constrained compared to those of the AZF.

Fig. 4: Effects of fault geometries on maximum possible magnitude of earthquakes on the Anninghe-Zemuhe fault (AZF).
figure 4

A The surface traces of curved and planar faults (legend) used in dynamic rupture simulations. B The maximum possible earthquake magnitude in 2023 as a function of hypocenter location predicted by simulations with curved and planar faults (legend in A). The simulation results are compared with the theoretical prediction. C Accumulated shear stress on curved fault (top) and superimposition of slip for four earthquake scenarios on curved (upper middle), smoothed (lower middle), and planar (bottom) faults, each assuming a different nucleation location (marked by purple stars).

Full size image

Discussion

In earthquake cycle models, small seismicity can be seen as failed initiations of potential large earthquakes40. The seismicity in asperity AZF-1 is more active than in the other asperities (Fig. 3), which implies that this asperity has more frequent chances to initiate a large event with maximum possible magnitude reaching up to Mw 7. To the north of this segment, the Mw 6.6 Luding earthquake occurred in 2022 (ref. 41), triggered many aftershocks42, and loaded this fault segment by 0.2 MPa (Fig. S4). Based on these seismic observations and our models, we suggest that asperity AZF-1 has higher seismic hazard than the other segments and is currently ready to host a Mw 7 event.

Due to the high-coupling ratio and long elapsed times, the current accumulated slip deficits on asperities AZF-1 and AZF-4 reach ~3 m, close to the coseismic slip of historical events as revealed by paleoseismic investigations43. The slip deficit on asperities AZF-5 and AZF-6 is less than 1.0 m due to the short time elapsed since their last ruptures in 1732 and 1850. The accumulated slip deficit is less than 0.5 m on asperity AZF-3 due to its recent last rupture in 1952. We estimate the recurrence intervals of big events on these asperities based on 3D dynamic rupture theory (“Methods” section): \(T=\frac{S}{{s}_{b}}\), where S and sb are the critical slip for recurred ruptures and the slip deficit rate derived from the kinematic inversion, respectively. We estimate S at any given fault point as the slip deficit value for which the point reaches the necessary condition for runaway rupture, \({G}_{0}\approx {G}_{c}\). Because G0 increases faster than Gc with the accumulated slip deficit, S can be uniquely determined (“Methods” section). Note that this estimate only gives a lower bound on the rupture time because the earthquake may nucleate later when the runaway condition is satisfied. As shown in Fig. 2D, the estimated return periods are about 500 years on these asperities, quantitatively consistent with that inferred from geological studies43,44. Two sampling sites located in the low coupling zones (Ganhaizi and Daqingliangzi) have long return periods, which is also close to our estimate on the low coupling patches.

In summary, we combine geodetic, seismological, and geological observations with physics-based models to assess the seismic hazard of the Anninghe-Zemuhe fault system. While faulting is also affected by additional complicated processes whose parameters are poorly constrained currently, such as fault zone fluids, geometric complexities, and the state of absolute stress, we demonstrated that a useful estimate of the maximum magnitude of potential earthquakes is readily available based on the accumulated slip deficit on faults and dynamic rupture models. Improved constraints on fault coupling and stress state, thanks to future developments of geodetic and seismological observations, together with advances in dynamic fracture theory and numerical simulations like the ones demonstrated here, should enable a more reliable, time-dependent evaluation of the location and magnitude of potential large earthquakes.

Methods

Inversion of fault coupling ratio

The fault coupling models of the AZF, as shown in previous studies26,27,28, may suffer from the sparsely distributed GNSS stations near the fault (Fig. 1). To better constrain the coupling ratio distribution along the AZF, we built 24 new near-fault GNSS stations in 2018 and surveyed them three times in 2019, 2020 and 2022 (Fig. 1A). In order to reduce seasonal effects, field surveys were performed at the similar time of the year (July). The occupation of each survey was larger than 72 h to ensure the stability of the observation. We solve the velocities on these new GNSS stations using the strategy shown in Diao et al.45 and combine them with the existing GNSS velocities46 for the kinematic inversion following the method of Wang and Shen46. The solved GNSS velocities and associated uncertainties on these new stations are shown in Table S1. To model the crustal deformation and invert for the fault coupling ratio, a combined 3D deformation model as shown in Eq. (1) has been widely used26,

$${V}_{{obs}}={V}_{B}+{V}_{\varepsilon }+{V}_{p}+{V}_{{blackslip}}$$
(1)

where Vobs are the observed GNSS velocities, VB and \({V}_{\varepsilon }\) the velocities due to steady state block rotation and interior strain26, respectively, Vp the postseismic viscoelastic relaxation effect of large historical earthquakes, and Vbackslip the deformation caused by fault coupling.

VP is accounted for in our model by simulating the postseismic viscoelastic effect of historical earthquakes since 1480. For this purpose, we use the PSGRN/PSCMP code47 with a layered infinite half-space model that consists of an elastic upper crust and two underlying viscoelastic layers representing the lower crust and upper mantle (Fig. S5). The elastic and viscoelastic parameters in the model are from ref. 48 and refs. 45,49, respectively. The postseismic viscoelastic relaxation effect is driven by the coseismic rupture of historical earthquakes, of which the parameters are inferred from refs. 24,50,51,52 and listed in Table S2. As shown in Fig. S6, this effect remains less than 0.5 mm/a despite different viscosities being used. Beside the viscoelastic relaxation effect due to stress loading of historical events (VP in Eq. (1)), we also consider the viscoelastic effect caused by the interseismic stress accumulation due to the fault coupling. Based on the theoretical derivation shown in ref. 53, we consider the interseismic viscoelastic effect by constructing the viscoelastic Green’s function of \(G (x,t)=[E(x)+{Vis}(x,t)H(t)]\) for slip deficit inversions (Eq. (2)), where H(t) is the Heaviside function, E(x) the elastic displacement, and Vis(x, t) the time-dependent displacement induced by the interseismic viscoelastic relaxation. Considering the long earthquake recurrence period on the AZF, we calculate \(G(x,t)\) by simulating a fully relaxed viscoelastic effect (\(t\to \infty\) using the layered viscoelastic model (Fig. S5).

VB and \({V}_{\varepsilon }\) are calculated by using an Euler vector and a strain rate tensor54 that are solved by the least square method from the GNSS velocities within each block. We divide the study area into three blocks (Model 1 in Fig. S7) based on the strategy inferred from an Euler pole clustering technique55. We also test the other block division strategy (Model 2 in Fig. S7) to investigate whether the LJ-XJHF shall be defined as the block boundary in the model. In Model 1 and Model 2 we use different coverages of GNSS stations to define the motion of blocks west of the AZF, i.e. Chuandian block and Dianzhong block in Fig. S7. Modeling results indicate that Model 2 leads to a slip rate of 9.2–5.7 mm/a along the AZF (Model 2 in Fig. S7) that is higher than the geological result of 6.5 ± 1.0 mm/a31. On the contrary, Model 1 that neglects the XJHF, generates a slip rate of AZF (6.1–4.9 mm/a) that agrees better with the geologic investigations.

After decomposing VB, Vε, and VP from the observations, the residual deformation is assumed to be caused by the fault coupling that is represented by Vbackslip. We set the fault trace based on the geologic data56 and assume the AZF to be vertical following previous studies26,27,28,57. We further subdivide the fault into discrete patches with a size of 5 × 5 km, and invert for back-slip rate utilizing a constrained least squares method45. To make the solution stable, we add an a-priori smoothing constraint in the cost function,

$${{\rm{F}}}({s}_{b})={{{\rm{||G}}}{s}_{b}-{{\rm{y||}}}}^{2}+{{{\rm{\alpha }}}}^{2}{{||}{{\rm{H}}}{s}_{b}{||}}^{2}$$
(2)

where \({s}_{b}\) is the back-slip rate vector on fault patches, G the aforementioned viscoelastic Green’s function, y the deformation component related to fault back-slip rate (in Eq. (1)), H the finite difference approximation of the Laplacian operator, and α the smoothing factor that controls the trade-off between model roughness and data misfit (Fig. S8). After obtaining the back-slip rate, we obtain the fault coupling ratio (\(r\)) by \(r=\frac{{s}_{b}}{s}\), where s is the fault slip rate. We estimate the uncertainty of the inverted slip deficit rate and coupling ratio using the statistic method53. The details are as follows: we first generate a set of Gaussian noise signals using the observation uncertainty as the standard deviation. Then, we add them to the observation data to get several sets of disturbed synthetic data. For each of the disturbed datasets, we repeat the inversion process to get the coupling ratio on each fault patch and the mean coupling ratio above 15 km. These steps were run 500 times in order to estimate the uncertainty of the parameters statistically.

Moreover, to test the effect of secondary faults within the Chuandian block (Lijiang-Xiaojinhe fault and Litang fault), we forward calculate the crustal deformation due to the motion of these secondary faults using the “buried-dislocation” model54 and associated fault slip rate58,59. As shown in Fig. S9, such effect is ~0.5 mm/a near the AZF. After removing this effect from the GNSS velocities, we re-run Model 1 to get the fault coupling distribution (Fig. S9). Not surprisingly, we find that the coupling model remains stable and the effect of these secondary faults is negligible.

Estimates of the b value

Based on the seismic records in the past 14 years (2009–2023), we update the earthquake catalog of the study area using the TomoDD code60, and obtain the precision location of more than 94400 ML > 1.5 events in this region. Based on this refined earthquake catalog (Supplementary Data 1), we estimate the b values homogeneously over space by employing the maximum-likelihood method within the ZMAP software61, with a dense spatial grid (0.03 × 0.03°) and a sampling volume of circular shape (r = 25 km). We also estimate the magnitude of completeness (Mc) on each grid using the Goodness-of-Fit test62. For a good fit to the G-R law61, we only calculate the b values on the grids where the number of events (magnitude > Mc) exceeds \({N}_{\min }\). We collect the b values on grids near the AZF (<5 km) to build the profile shown in Fig. 2C. To verify the robustness of the inferred b values, we conduct additional tests. First, we increase \({N}_{\min }\) from 30 to 60 and observe the resulting variation in the calculated b values (Fig. S10). Then, we further increase \({N}_{\min }\) to 80 and 100, but with an enlarged sampling radius r of 40 km (Fig. S11). We find that the primary features of the inferred b values are qualitatively consistent, despite low \({N}_{\min }\) values resulting in large uncertainties and high \({N}_{\min }\) values leading to a highly smoothed variation (Figs. S10, S11). In this study, we therefore choose \({N}_{\min }\) = 50 with a sampling radius r of 25 km, following ref. 37, to ensure sufficient spatial sampling while preserving spatial variations of the b values in each asperity. In addition, the frequency-magnitude distributions within selected patches also show that the estimates of the b value are robust (Fig. S10).

Scaling relations between fracture energy and slip

To constrain frictional properties on faults, we compile the datasets of global earthquakes from the literature63,64,65,66 and determine the scaling relations between fracture energy and final slip (Fig. S12A). It has been proposed that fracture energy \({G}_{c}\) increases with increasing final slip D as inferred in natural faults38,67,68 and also observed in laboratory experiments69. As a first-order approximation derived from off-fault inelastic dissipation70,71 and thermal pressurization38, the scaling relation between the fracture energy and final slip can be expressed as a power-law, \({G}_{c}\approx B{D}^{n}\), where B and n are coefficients to be determined. Alternatively, laboratory experiments39 show that the friction weakening behaviors of natural rocks can be described by an exponential slip-weakening friction, \(\tau=({\tau }_{s}-{\tau }_{d}){e}^{-D/{d}_{c}}+{\tau }_{d}\), where \(({\tau }_{s}-{\tau }_{d})\) and \({d}_{c}\) are the strength drop and the critical slip-weakening distance. For this friction, the scaling relation between fracture energy and final slip is \({G}_{c}=({\tau }_{s}-{\tau }_{d}){d}_{c}\cdot (1-(1+D/{d}_{c}){e}^{-D/{d}_{c}})\), where \(({\tau }_{s}-{\tau }_{d})\) and dc are coefficients to be determined. In this study, we separately constrain these two sets of free coefficients and use them for the seismic hazard assessment (Fig. 3). The best fitting coefficients are B = 1.8 and n = 0.85 for the power-law slip-weakening friction, and \({\tau }_{s}-{\tau }_{d}\) = 8 MPa and dc = 0.2 m for the exponential slip-weakening friction (Fig. S12A). The two friction laws are comparably consistent with the fracture energy scaling data within the range of slip values that are most relevant for this study (0.1–1 m). To do the sensitivity analysis for the theoretical models, we vary the value of B by a factor of 1.4 (Fig. 3). Note that in this study we only include the data of \({G}_{c}\) constrained by dynamic models in the literature63,64,65,66 for our fitting of friction coefficients, therefore, our constrained value of B is different from that in ref. 9, which also included the experimental data in their fitting.

Dynamic rupture simulations

We set 3D dynamic rupture simulations on a vertical planar or curved fault of 20 km width intersecting the free surface in a linear elastic and homogeneous medium. The computational domain has a size of 200 × 100 × 70 km, which is large enough to avoid contamination by waves reflected from the artificial boundaries during the rupture times. The P wave speed, S wave speed, and density of the medium of the elastic model are uniformly assumed as 5770 m/s, 3330 m/s, and 2705 g/m3 based on the parameters in the upper layers shown by Liu et al.48. As the variation of shear modulus is less than 10% within the seismogenic zone48, the specific choice of the velocity models has a secondary effect on the numerical simulations. We use the spectral element software SPECFEM3D72 for the dynamic simulation. The time step is set to 0.007 s (Table S3), meeting the Courant-Friedrichs-Lewy stability condition, a criterion widely used to ensure the stability of the numerical simulation. We set a grid size of 250 m to guarantee sufficient numerical resolution.

We use both the power and exponential slip-weakening friction laws in the numerical simulations. To confirm the theoretical model, we first use the nonlinear friction model proposed by ref. 73: \(\tau={\tau }_{d}+\left({\tau }_{s}-{\tau }_{d}\right)/{\left(1+\frac{\delta }{p{d}_{c}}\right)}^{p}\), where \(p\) is the power-law coefficient, \({\tau }_{s}\), \({\tau }_{d}\), and \({d}_{c}\) are the static strength, the dynamic strength, and the critical slip-weakening distance, respectively. In the simulations, we set \(p=1-n=0.15\), \({d}_{c}=0.01m\), and \({\tau }_{s}-{\tau }_{d}=28{MPa}\), as determined by the data of global earthquakes within the relevant range of slip values (red curve in Fig. S12A). This friction law produces a similar scaling relation as that used in the theoretical model (Fig. S12A). The initial shear stress is set as \({\tau }_{{ini}}=\varDelta {\tau }_{{accu}}+{\tau }_{r}\), where we assume that the latest large earthquakes dropped the shear stresses to the minimum strength that is corresponding to a slip of 5 m, thus we set \({\tau }_{r}={\tau }_{d}+\left({\tau }_{s}-{\tau }_{d}\right)/{\left(1+\frac{5}{p{d}_{c}}\right)}^{p}\). For the exponential slip-weakening friction law, we assume \(\tau=\left({\tau }_{s}-{\tau }_{d}\right){e}^{-\delta /{d}_{c}}+{\tau }_{d}\), where \({\tau }_{s}\) and \({\tau }_{d}\), and \({d}_{c}\) are the static strength, the dynamic strength, and the critical slip-weakening distance, respectively. The friction coefficients are also determined based on the data of observed global earthquakes by fitting the scaling of the fracture energy (blue curve in Fig. S12A), where \({\tau }_{s}-{\tau }_{d}=8{{\rm{MPa}}}\) and \({d}_{c}=0.2m\). Note that the absolute value of \({\tau }_{d}\) is not important in these two friction laws on vertical planer faults70, therefore here we artificially set \({\tau }_{d}=1.2{{\rm{MPa}}}\). In the exponential friction law, the initial shear stress is set as \({\tau }_{{ini}}=\varDelta {\tau }_{{accu}}+{\tau }_{d}\), where we assume that the latest large earthquakes dropped the shear stresses to the minimum dynamic strength \({\tau }_{d}\) and the current shear stresses built up since then. We list the key parameters used for dynamic rupture simulations in Table S3.

To estimate \(\varDelta {\tau }_{{accu}}\), we first use the coupling ratio to calculate the shear stress changes per year τ and then calculate the total accumulated shear stress based on the elapsed time \(T\) since the latest large earthquakes, Δτaccu = τT (Fig. 2B). For the simulations with stresses at the current time (Fig. 3D), we account for the stress perturbation caused by the 1952 earthquake. As there is no slip model available for that event, we use the stress change from a numerical model that produces a similar magnitude earthquake.

We use a time-dependent weakening to nucleate the ruptures, where the nucleation zone is 6 km and the nucleation speed is 1200 m/s. Rupture propagation is spontaneously controlled by the slip-weakening friction law outside the nucleation zone. In the simulations, the depth of the nucleation is 6 km and the horizontal nucleation location is varied along strike in different models to search for the maximum possible earthquake magnitude as a function of the nucleation location. For all the ruptures, we calculate the final seismic moment and compare them with the theoretical prediction (Fig. 3).

Theoretical model based on 3D dynamic fracture mechanics

The rupture arrest locations and earthquake sizes are estimated based on the theory of 3D dynamic fracture mechanics on long faults with finite rupture width9,10. The 3D theory9,10 suggests a simple criterion for determining the arrest location of dynamic ruptures by evaluating the rupture potential: \(\phi={\int }_{{x}_{0}}^{{x}_{0}+L}(1-{G}_{c}(x)/{G}_{0}(x)){dx}=0\), where \(L\) is predicted along-strike arrest location distance from the hypocenter (located at \({x}_{0}\)), \({G}_{0}(x)\) and \({G}_{c}(x)\) are the potential elastic energy and dissipated fracture energy as a function of the along-strike location \(x\), respectively. The criterion applies to each of the rupture fronts on bilateral ruptures. The potential elastic energy \({G}_{0}(x)\) is calculated based on the seismic coupling map and the elapsed time since the last M~7.5 large earthquakes. To obtain \({G}_{0}(x)\), we first estimate the total slip deficit \({D}_{a{ccu}}\) based on the elapsed time \(T\) since the latest large earthquakes, and then calculate the accumulated shear stress \(\triangle {\tau }_{{accu}}\) on fault. The density of the potential elastic energy accumulated on the seismogenic fault is defined by 0.5\(\varDelta {\tau }_{{accu}}{D}_{{accu}}\). Following previous method10, we average 0.5\(\varDelta {\tau }_{{accu}}{D}_{{accu}}\) across the seismogenic depth (i.e., \(W=20{km}\) in this paper) to obtain \({G}_{0}(x)\) along strike (Fig. 3A, C). The fracture energy \({G}_{c}\) is estimated based on potential earthquake slip D and the scaling relation \({G}_{c}\left(x\right)=B{D}^{n}\) with B = 1.8 and n = 0.85 from the best fitting of the observations. For the models in the current time (Fig. 3D), we account for the 1952 earthquake by subtracting the approximated slip of this earthquake from the total slip deficit. We then calculate the density of the potential fracture energy by using \(B{D}_{{accu}}^{n}\) and average it across the seismogenic depth to obtain \({G}_{c}(x)\) along strike. Finally, we use the criterion of rupture potential to determine the final rupture length L given an assumed nucleation location and compute the final seismic moment by integrating the released slip along the ruptured area.