Quantitative matching of forensic evidence fragments using fracture surface topography and statistical learning

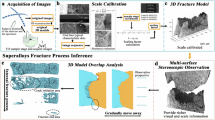
Abstract

The complex jagged trajectory of fractured surfaces of two pieces of forensic evidence is used to recognize a “match” by using comparative microscopy and tactile pattern analysis. The material intrinsic properties and microstructures, as well as the exposure history of external forces on a fragment of forensic evidence have the premise of uniqueness at a relevant microscopic length scale (about 2–3 grains for cleavage fracture), wherein the statistics of the fracture surface become non-self-affine. We utilize these unique features to quantitatively describe the microscopic aspects of fracture surfaces for forensic comparisons, employing spectral analysis of the topography mapped by three-dimensional microscopy. Multivariate statistical learning tools are used to classify articles and result in near-perfect identification of a “match” and “non-match” among candidate forensic specimens. The framework has the potential for forensic application across a broad range of fractured materials and toolmarks, of diverse texture and mechanical properties.

Introduction

Consider the example of a crime scene where investigators have found the tip of a knife or other tool that appears to have broken off from the rest of the object. Later, investigators recover a base that appears to topographically match, as indicated in Fig. 1a, b and they wish to show that the two pieces are from the same knife in order to use that evidence later at trial. To this extent, the analyst comparison relies on subjective pattern recognition methodologies. Scientific testimony used in a criminal or civil trial must be “not only relevant but reliable”, according to the Supreme Court decision Daubert v. Merrell Dow Pharmaceuticals, Inc (1993). The application of this ruling forced a reconsideration of some previously acceptable forensic evidence and a re-evaluation of the scientific validation of its premises and techniques¹. In 2009, The National Academy of Sciences issued a report² that evaluated the state of forensic science and concluded that,

Fig. 1: Association of forensic fragments and their fracture surface characteristics.

a Visual jigsaw match of the macroscopic crack trajectory at the typical examination scale. b Physical pattern match with comparative microscopy, with analyst focusing on macroscopic topological features. c 3D representation of a pair of fracture surfaces, showing detailed topographic features at the relevant comparison scale (∽20 grains), utilized in the current work. The fracture surface shows a biased orientation of the low-frequency texture in the direction of crack propagation, along the x-axis. d Height-height correlation variation with the size of the correlation window, showing the domain of the self-affine deformation and the deviation of the fracture surface characteristics at higher length scales ( >50–70 μm), which could be used for matching purposes. e For quantitative analysis of the fracture surface pairs, a series of aligned topographical images were taken, relative to a reference coordinate w.r.t. the right edge of the fractured article. A series of k = 9 topographical images with 75% overlap between successive images, rendering three fully independent sequel images on the fracture surface.

…much forensic evidence—including, for example, bite marks and firearm and toolmark identification—is introduced in criminal trials without any meaningful scientific validation, determination of error rates, or reliability testing to explain the limits of the discipline².

However, it should be noted that a considerable amount of prior work has been done to provide a quantitative and scientific basis for firearm and tool mark identification, for example, with the consecutive matching striae (CMS) method^3,4,5. The report highlighted the need to develop new methods that have meaningful scientific validation and are accompanied by statistical tools to determine error rates and the reliability of the methods. To that end, the American Association for the Advancement of Science has published reports on the state of fire investigation⁶ and latent fingerprint examination⁷.

The proposed framework focuses on fracture matching, the forensic discipline of determining whether two pieces came from the same fractured object. The fracture mechanisms leave surface marks on both surfaces that could be utilized for matching fragments. The basis for physical matching is the assumption that there is an indefinite number of matches all along the fracture surface. The irregularities of the fracture surfaces are considered to be distinctive and may be exploited to individualize or distinguish correlated pairs of fracture surfaces^8,9. Current forensic practice for fracture matching involves visually inspecting the complex jagged trajectory of fracture surfaces to recognize a match, either by an examiner or even by a layperson on a jury. The process uses comparative microscopy and tactile pattern analysis^8,10, where macro-features on a pair of fracture fragments are correlated as demonstrated in Fig. 1a, b. Previous research has supported that the observed fracture patterns in metals are unique^11,12 and that inspection via a microscope of the fracture surfaces by examiners can reliably validate matches¹³. However, experience, understanding, and judgment are needed by a forensic expert, to make reliable examination decisions using comparative microscopy and physical pattern match as indicated in Fig. 1b to identify correlated macroscopic topological features. The comparative process relies on subjective comparison without a statistical foundation, which may be flawed, as the 2009 NAS report argues:

But even with more training and experience using newer techniques, the decision of the toolmark examiner remains a subjective decision based on unarticulated standards and no statistical foundation for estimation of error rates².

Indeed, the microscopic details of the non-contiguous crack edges on the observation surface of Fig. 1a, b cannot always be directly linked to a pair of fracture surfaces, except possibly by a highly experienced examiner. There are many published studies and case reports concerning fracture or pattern matching of different materials such as rubber shoe soles, wood, glass, tape, paper, skin, fishing line, cable, and, most commonly, metal^{14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29}. However, at about one-tenth the scale of Fig. 1b, the 3D microscopic details imprinted on the topographical fracture surface of Fig. 1c carry considerable information that could provide a quantitative forensic comparison with higher evidentiary value. Forensically, glass and metal fracture surfaces have been shown to have highly stochastic fracture-branches due to the randomness of the microstructure and grain sizes^11,30, with limited prior attempts to quantitatively match two measured fracture surface topographies^13,16. It is therefore desirable to develop more objective methods using quantitative measures that can be validated with less human input for use in a criminal or civil trial.

In this work, we propose using the fractal nature of fracture surface topography and their transition to non-self-affine properties³¹ (where self-affinity means the roughness scales with the observation window) to define a suitable comparison scale. We also aim to develop supporting statistical methods for forensic fracture matching using three-dimensional (3D) topological imaging of fracture surface details. Fracture surface topography exhibits unique characteristics across various length scales, offering significant insights into damage initiation and propagation. The material microstructure controls the micro-mechanisms of fracture and the microscopic crack growth path, while the loading direction determines the macroscopic crack trajectory³². Mandelbrot et al.³¹ first demonstrated the self-affine nature of fractured surfaces, relating their roughness to the material’s resistance to fracture through the fractal dimension. This self-affine roughness has been experimentally verified for various materials (metals, ceramics, and glasses) and under static and dynamic loading conditions^{33,34,35,36,37}. A key finding is the variation of the surface descriptors when measured parallel to the crack front and along the direction of propagation³⁸. The cut-off length scale of the self-affine behavior has been suggested as a unique scale to characterize the microscale fracture process in ductile^34,39,40 and brittle/semi-brittle materials^34,41,42. Motivated by observations about the self-affine nature of fracture surfaces, we hypothesize that a randomly propagating crack will exhibit distinctive topographical details when observed from a global coordinate that does not recognize the direction of crack propagation. This work explores the existence of such distinctions at relevant length scales, which implies they can be used to individualize and distinguish paires of fracture surfaces. Our approach leverages the distinctive attributes of microscopic fracture surface features at relevant length scales, arising from the interaction of the propagating crack-tip process-zone and microstructure details, as shown in Fig. 1c. The corresponding surface roughness analysis is shown in Fig. 1d using a height-height correlation function, $\delta h(\delta {{{\bf{x}}}})=\sqrt{{\langle {[h({{{\bf{x}}}}+\delta {{{\bf{x}}}})-h({{{\bf{x}}}})]}^{2}\rangle }_{{{{\bf{x}}}}}}$, where the 〈 ⋯  〉 operator denotes averaging over the x-direction. At the small length scale of less than 10–20 μm, the roughness characteristic is self-affine (i.e. proportional to the analysis window scale). However, at larger length scales (>50–70 μm), the roughness characteristic deviates and reaches a saturation level, highlighting the individuality of the surface topography at such scale. The height-height correlation function at this transition scale, as shown in Fig. 1d, captures the uniqueness of the fracture surfaces. We use this transition scale to set the observation scales (i.e., field of view (FOV) and imaging resolution) for comparing matching and non-matching surfaces, and creating a statistical model for classification. This imaging scale should be greater than about 10-times the self-affine transition scale to avert signal aliasing. Multiple observations at different spectral topographical frequency bands (around the transition scale of fracture surface topography) can be combined into one model to improve discrimination between surfaces of the same class or from similar manufacturing processes. This statistical model can produce a likelihood ratio or log-odds ratio for classifying new surface sets, similar to methods used in fingerprint identification and bullet matching^{43,44,45,46,47,48,49}. This model can estimate misclassification probabilities and compare them to actual rates in test data. For example, in fingerprint identification, features (minutiae) on reference and latent prints are marked and scored based on their match, forming part of a probabilistic model that reports a likelihood ratio⁵⁰. Similarly, the Congruent Matching Cells approach in ballistics divides scanned cartridge breech face surfaces into cells, searches for matches, and uses this input for a statistical model to output a likelihood ratio^51,52.

After presenting an overview of the method and the study objectives, we provide an evaluation of the method and several experiments to guide choices in imaging and in the parameters for the statistical model. We also examine the general application of the framework to different modes of failure under generalized loading, mimicking mixed mode-I and mode-III loading in fracture mechanics. Finally, we discuss our results and illustrate how it may be applied in a forensic context. In the method section, we describe the sample generation and the imaging process used to create training and forensically relevant data sets. We then provide a description of the statistical model which discriminates the matching fracture surfaces from the non-matching surfaces. Supplementary materials provide additional information about the methods and materials. An R⁵³ software package to perform the model fitting and analysis, MixMatrix, and code to reproduce the analysis and figures is available⁵⁴.

Results

In this section, we demonstrate the developed framework for matching fragments and discuss some of its attributes, generalities, and limitations.

Imaging scale for comparison

When comparing characteristic features on a fractured surface, identifying the proper magnification and FOV are critical. An optical image obtained by high magnification and a small field of view will possess a visually indistinguishable characteristic. This is the range where surface roughness shows a self-affine or fractal nature as noted in Fig. 1d. In this range, the material intrinsic local fracture mechanism shows similar topographical surface features over the fractured surface (e.g. local cleavage steps and river patterns, and/or dimples and voids). On the contrary, employing lower magnifications will result in a lower power of identifying the class characteristics of the surface. However, we showed that the transition scale of the height-height correlation function captures the uniqueness of the fracture surfaces. We found that this transition scale is about 2–3 times the average grain size for the class of materials examined here and undergoes cleavage fracture. Interestingly, this scale is consistent with the average cleavage critical distance for the local stresses to reach the critical fracture stress^34,55 required for cleavage fracture initiation and typically extends to 2–3 times the grain size, or around 50–75 μm for the tested material system. This critical microstructural size scale for cleavage crack initiation is stochastic in nature as it statistically encompasses the location of the critical fracture-triggering microscopic inclusion or particle^34,56,57.

Accordingly, the surface characteristic becomes statistically unique and non-self-affine at a larger scale. This scale sets; (i) the observation FOV to be around 10-periods of such scale. And (ii) the range of wavelengths or frequencies to perform correlations on pairs of fragments. When correlating the frequency bands in the range of 5–20 mm⁻¹ (i.e. 50–200 μm wavelength) full separation and clustering can be clearly observed in Fig. 2a for matched and non-match fracture surface pairs. Furthermore, beyond this frequency range, the match and non-match correlations overlap, as noted on Fig. 2b. The identified imaging scale (which should be established for each class of materials) coupled with the statistical analysis framework provides a promising quantitative forensic comparison for a wide class of materials. However, it is crucial to acquire precise 3D topographical representations of the fracture surface without imaging artifacts for the comparison process. Two main issues may pose additional problems for the technique⁴⁹. (1) The comparison technique is well-suited for materials that exhibit cleavage fracture, which typically possesses a relatively planar fracture surface within several hundred microns. The planarity of the cleavage fracture surface ensures that the imaging depth resolution remains in the sub-micron range across the entire surface topography. However, if the fracture surface exhibits ductile tearing with large, tortuous fracture path and millimeter-scale morphological variations⁵⁸, additional mathematical treatments will be needed, similar to the comparison of cylindrical surfaces like cartridge cases^59,60. (2) Surface anomalies, such as grain fall-out and fracture surface corrosion, will reduce fracture-pair correlations among matches, making the matching and non-matching classes less distinct. In such cases, a larger image set will be necessary to maintain the same power of separation.

Fig. 2: Topography based separation.

a Scatter plot of correlations for 81 matched pairs and 648 non-matched pairs from training set K-1-1 for the 5–10 and 10–20 mm⁻¹ frequency ranges on a Fisher-z (nonlinear) axis. We see that true matches and true non-matches are distinguished in this example by features in the 5–10 and 10–20 mm⁻¹ frequency ranges. The connected points show the values of nine overlapping images from the same surface, indicating that while some individual images may not distinguish matches from non-matches, taking an ensemble of images from the surface importantly improves the ability to discriminate between the two classes in this data set. b Histograms of correlations of true matches and true non-matches for the same data set split by frequency band. Lower frequencies are well-separated, but higher frequencies begin to have more substantial overlap.

Classification performance

There are two datasets from the knives and two from the steel bars: “K-1-1” is the first set of images from the first set of knives (Supplementary Fig. 1), and the imaging is independently repeated generating additional sets of images “K-1-2”and “K-1-3” for repeat analysis. “K-2” indicates the other set of knives, whereas “S-1” and “S-2” indicate the two steel bar samples (Supplementary Fig. 2). Figure 3a shows the classifications obtained by training on each of the four datasets, represented by one of the color boxes, with all 9 images per sample and classifying on all the other sets of surfaces using the matrix-variate t distribution and a common degrees of freedom parameter, ν = 3, 5, 10, 15, 20, and 30, and prior probability of being a match of 0.5 (for example, training on the first set and testing on sets 2, 3, and 4, and continuing the same process with the other sets as the training set). The output (Supplementary Table 1) given in terms of the log-odds of being a match—log-odds larger than zero (p = 0.5) indicate classification as a match. While initially there are no false positives or false negatives, as the degrees of freedom parameter (DF or ν) increases, there is one false positive, though this probability is very close to 0.5 and all of the true positives have a probability close to 1, which suggests using a classification threshold other than 0.5 would yield perfect classification in this set of data. A different threshold can be chosen by selecting a low probability (such as 10⁻⁴) as a probability of a false alarm and using the distribution of log-odds of the true non-matches to fix that threshold conservatively by selecting an upper confidence bound of that quantile⁶¹. Using the upper 95% confidence bound for the threshold at which the false alarm probability based on the distribution of true negatives is 10⁻⁴ sets the threshold at a probability of 0.8814 for the most conservative training set at the setting of ν = 10, for example, which still results in perfect classification. Additionally, we may consider the probability in the range of 0.5 > P > 0.88 to bound the range of inconclusive decisions.

Fig. 3: Classification performance.

a Log-odds of being a match split by training set and true class membership for matrix − t distributions with 3, 5, 10, 15, 20, and 30 degrees of freedom. A log-odds ratio greater than 0 indicates greater odds of being a match than a non-match. The predictions for each training set are performed on all four sets of fracture surfaces. b Individual true match correlations for three repetitions of topographical imaging of the K-1 set of 9 knives and with 9 images per knife. The similarity among the three distributions demonstrates that similar results will be obtained upon re-imaging the same surface, which is important in forensic applications. The large dots indicate the means of the sets, and we display the covariance matrices through the 99% ellipses of concentration of their distributions.

Reproducibility of results

In order to determine the reproducibility of results for a given sample, we re-imaged one of the knife samples three times and examined the distributions of the true match image correlations in Fig. 3b. The different re-imaged sets are labeled “K-1-1”, “K-1-2”, and “K-1-3”. The means of the distributions (indicated by the large shapes) are similar and the covariance matrices, visualized using 99% confidence ellipses, are also similar. Using the two-sample Peacock test, a two-dimensional extension of the Kolmogorov-Smirnov test^62,63, there is no evidence these distributions differ significantly (H₀: distributions are the same for 1 and 2, p = 0.21; H₀ for 1 and 3, p = 0.32; H₀ for 2 and 3, p = 0.25). We conclude that the imaging and analysis processes are reproducible for the analyzed samples.

Selecting DF (ν)

The training sets do not have a sufficient number of observations in both classes to estimate ν in the MxVt model. However, the analysis in the previous section indicates it has some influence on the results. We performed a leave-one-out cross-validation (LOOCV) procedure to provide guidance about the effects of changing the parameter. For each surface in a training set, a model was trained on the set of observations excluding that surface and tested on the observations using the excluded surface. This was done for k = 9 images on training sets S-1 and S-2 and using k = 5 images (restricting to the images with only 50% overlap) and k = 3 images (restricting to the non-overlapping images) on all four training sets. The procedure was performed only on sets S-1 and S-2 for k = 9 because nine surfaces are needed to fit the model and K-1-1 and K-2 have only nine fracture pairs, while S-1 and S-2 have ten fracture pairs. Figure 4a shows the results for k = 3, 5, and 9 respectively. The parameter ν varied from 3 to 30. In all cases, the true matches and true non-matches were perfectly classified using a threshold probability of 0.5 (log-odds of 0). Higher values of ν had more separation between the classes. Using 9 images with 75% overlap had greater separation than 5 images with 50% overlap and greater separation between the identification of true matches. However, given that there is perfect classification in all cases, this finding does not provide much guidance on the selection of ν.

Fig. 4: Demonstration of model discrimination power.

a Cross-validation results for models fit using k = 3, 5, and 9 images of each surface. The cross-validation was done to provide guidance about the number of images and the choice of DF (ν). There were no false positives or false negatives in this analysis, so it did not provide any conclusive results. b Rates of false positive and false negative classifications (in %) using models trained on the four different sets of surfaces and tested on consecutive subsets of those images for k = 2, 3, …, 9. A full summary of the results is provided in Supplementary Table 1. c Distributions of the log-odds of a match using models trained on the four different sets of surfaces and tested on subsets of k consecutive images for k = 2, 3, …, 9, for a model with ν = 10. d Rates of false positive classifications (in %) using models trained on the four different sets of surfaces using only the images with at most 50% overlap and tested on subsets of k consecutive images for k = 2, 3, 4, 5 and using only the 3 non-overlapping images and tested on subsets of k consecutive images for k = 2, 3. A full summary of the results is in Supplementary Tables 2 and 3.

Required number of images for discrimination and model selection

Due to the existence of morphological disturbances in some images (e.g., grains fall out from the fracture surface or substantially large out-of-plane curvature within the range of comparisons), there is no perfect separation between all image pairs for the matches and non-matches. This can be seen in Fig. 2a where some image pairs have a correlation coefficient of less than 0.50 for the two bands of frequency analysis. To mitigate the influence of local topographical disturbances when deciding whether a pair of fragments represents a match or not, multiple observations are needed. To determine how many images are needed to optimize classification performance, we started by training models using all nine images from each base-tip pair in each training set as before. We again used the MxVt model with ν = 3, 5, 10, 15, 20, and 30, and then tested them on subsets of consecutive overlapping images of size k, for k = 2, 3, …9 with the model reduced to considering only the selected images and the training set for each model excluded from testing. A summary of the complete results is given in the Supplementary Section S.4.

In Fig. 4b, models with higher ν have higher false negative rates for all values of k. For values of k over 4, only 20 and 30 DF have false negatives (specifically, they each have one false negative result, Supplementary Table 1). Low values of the degrees of freedom parameter have false positives. All of this suggests that choosing a value near ν = 10 and k ≥ 5 images is sufficient for error-free classification in the examined sample sets. Figure 4c displays complete results for a model with ν = 10. As k increases, the typical classification results become more separated. However, even with only two images considered in the test cases for the ν = 10 model, the accuracy is very high. The worst case of a false positive is classified with only a probability of 0.8314. The worst case of a false negative is classified with a probability of 0.504. Again, this is the range of match probabilities where an inconclusive match result could be assimilated for 0.5 > P > 0.88 as noted in the classification performance section.

Percentage of imaging overlap

Guided by the results of Fig. 4c, it is apparent that we need at least 5 to 6 images for error-free discrimination in this particular example, and that performance improves with additional images. We reassessed the imaging procedure to gauge the role of the image-overlap ratio. The initial experiment involved imaging surfaces using nine images with 75% overlap between images, which provides three observations for each point on the surface, apart from the edges. However, a similar area can be imaged using 5 images with 50% overlap, which produces two observations of each point on the surface apart from the edges, or using 3 non-overlapping images, which raises the question of whether anything is gained by having an additional third image of the same area and, if so, what level of overlap is best.

We can evaluate this by providing an analysis similar to that done previously: looking at the classification results when restricted to cases with the specified overlap. We train classifiers on the same sets as before, except using 5 images with 50% overlap instead of 9 images with 75% overlap and then test the models on the other sets excluding the set used to train the model by classifying pairs of surfaces using all possible subsets of those images on the surface of sizes 2, 3, 4, and 5. When restricted to the case of 50% overlap, Fig. 4d only shows perfect classification when all four or five images are included and ν < 20. In all cases, there are no false negatives.

We perform a similar exercise in the case of the non-overlapping images. There are three non-overlapping images per surface which can be used to train the classifiers and the models can then be tested on subsets of those images on each surface of sizes 2 and 3. In the case of non-overlapping images, no model results in perfect classification. The false positives for each model are also shown in Fig. 4d. There are no false negatives in the classification decisions.

This suggests that, while having more images is generally better, using 5 images with 50% overlap appears to be sufficient if all the images are used. Imaging the entire surface with 50% overlap outperforms imaging the entire surface with 75% overlap in the sense that it works for all of the classes of model. However, if training with 9 images with 75% overlap is possible, testing on new surfaces is feasible with as few as 5 test images with an appropriate choice of the degrees of freedom parameter in the model.

Calibration of output probabilities

The models present the outputs as probabilities, therefore we need to assess how well the probabilities in the models reflect the underlying probabilities in the matching and non-matching populations. Figure 5 displays a calibration plot comparing the output probabilities for all predictions to the empirical proportions in each class with a line drawn by a local regression smoother (LOESS) for each model^64,65. These predictions can be compared to the reference line on the plot, y = x, to judge the calibration. The true matches correspond with y = 1 and the true non-matches with y = 0. The vast majority of the model classifications are correct with probabilities of being a match of either  <0.001 for non-matches or  >0.999 for matches. The relative lack of samples in the middle range makes it hard to judge the calibration. The lowest probability of a match among the true matches was 0.3709. Among the various models, the 99th percentile of the predictions for non-matches was, in the worst case, 0.1437. Only outliers overlapped in middle range. We note that our evaluation of the calibration is limited by the sample size in the experiment—with more samples and more observations with match probabilities between 0.1 and 0.9, a better evaluation of the calibration could be made.

Fig. 5: A calibration plot of all the predictions from the various models and the empirical proportions with a LOESS smoother for each model.

The lines should be compared to the diagonal reference line. Matches are indicated at y = 1 and non-matches are indicated at y = 0.

Examining the framework capabilities on a twisted-fracture knife set

All examined sets of fractured articles were tested in tension or bending. This is mode-I cleavage fracture where the crack propagation direction is normal to the loading axis. The fracture surface showed topographical features normal to the fracture surface, similar to those shown in the scanning electron microscope (SEM) image of Fig. 1b. However for a general forensic article such as a knife or a pry tool, an edge could be broken due to bending and twisting of the article. This would impose a mixed mode of loading including mode-I opening and mode-III twisting of a crack. To understand the effect of external loading mode on the generality of the proposed analysis framework, a set of nine knives from the same manufacturer similar to the previously used sets were fractured at random using the same fixture (Supplementary Fig. 1b) and forming set of twisted knives shown in Supplementary Fig. 1e. A typical twisted knife fracture topography is very different at both the macro and micro scales. At the macro-scale, the crack trajectory is no longer planer with curvilinear or twisted trajectory (Supplementary Fig. 1e). At the micro-scale, the SEM image of Fig. 6b shows twisted fracture morphology in the plane of the crack that is very different than those under mode-I loading of Fig. 6a. This unique texture would probably further enhance the individuality of the fracture surface. We will attempt to examine the validity of the analysis protocol on such general case of fractured articles. The twisted knife set was imaged using the same procedure discussed in “Sample Generation and Imaging” section and the same magnification of 20X. However, due to the excessive tortuosity of the crack path, five images (k = 5) with 75% overlap between adjacent images were employed. Using the models previously trained on the four training sets loaded in tension or bending, and restricted to 5 images and setting the degrees of freedom ν = 10. The results for this set, shown in Fig. 6c, are similar to those obtained in Fig. 3a despite the use of a different external loading of mode-I tensile cleavage fracture. The true match cases were identified with a probability exceeding 99.999% and the true non-match was identified with a probability not exceeding 0.05% for all different training sets. This suggests the scale of comparison, derived from the self-affine saturation scale of the fracture surface topography is more general and tied to the microstructure scale (grain size) for the class of materials failing by cleavage fracture (similar to hardened tool materials). This result is far more reaching with practical implications. As long as the cleavage fracture is the dominant mode of failure, a single robust training data set under simplified loading conditions for the same material class would be sufficient to help in discriminating; (i) articles that were exposed to complex external loading (i.e. mixed mode of fracture). (ii) articles from different classes of materials, but share the same grain size distributions, and (iii) articles with different grain sizes, which would only require changes of the FOV to cover 20-grains while changing the comparison frequency bands to cover the corresponding 2–4 and 4–8 grain size ranges. It is conceivable to extend these results to glassy metals, polymers and ceramics, that undergo cleavage and/or brittle or semi-brittle fracture. In such cases, the limits of the fractal scale should be examined and compared to the critical microstructure scale of the fracture surface topography, such as river and herringbone patterns. Though, additional experimental verification is needed for these classes of non-crystalline materials.

Fig. 6: Framework capabilities.

a SEM image of a typical fracture surface bent of a knife broken in bending, showing topological details normal to the imaging plane. b SEM image of a typical fracture surface of a broken knife in torsion, showing in-plane swirl textures. c Classification performance on a set of nine knives broken by twisting. The models were trained on different training bending and tensile fracture sets using five images and ν = 10.

Discussion

This paper provides a formal quantitative basis for matching metal fragments found at crime scenes. Our proposed approach combines fracture mechanics with statistics and machine learning to quantify, given a prior probability, the posterior probability that two candidate specimens are a match. Our methodology utilizes 3D spectral analysis of the fracture surface topography, mapped by white light non-contact surface profilometers. Specifically, our framework realizes the distinctive attributes for a pair of fragment surfaces when viewed at a length scale defined by the transition of fracture surface topography to become non-self-affine, and uses them to do a quantitative physical match analysis of metal fragments. Fracture surface morphology has been analyzed for many classes of materials and external loading conditions including tensile, bending and twisting of articles, and shown to be self-affine within a microscopic scale relevant to the fracture surface topography.

The transition scale of the height-height correlation function, shown in Fig. 1d is used to set the FOV and imaging resolution. For the examined class of materials, the saturation level is observed at a length scale ( >50–70 μm). Moreover, the examined class of materials has an average grain size of approximately dg = 25–35 μm. This will determine the transition scale, where the individuality and uniqueness of the fracture surfaces become apparent, to be approximately two-grain diameters. This relationship, characterized by a constant fractal dimension and related to the material average grain size, has been observed in some cleavage fracture mechanics studies. Dauskardt et al.³⁴ have examined the topography of a wide range of brittle failure of well-characterized mild steel at extremely low temperature and observed two ranges over which the fractal dimension is constant. The first range is 1–10 μm corresponding to the cleavage step. This range of cleavage steps will be non-unique as it will be found in all surfaces of the same alloy that exhibit cleavage failure. The second range is of the order of twice to three times the grain size. It is shown that the fractal dimension is constant over a range of the order of twice to three times the grain size range for transgranular cleavage fracture, about twice the grain size range for intergranular fracture, and of the order of the grain size for the quasicleavage fracture³⁴. Some fracture mechanics studies have demonstrated that cleavage failure occurs when the local stress ahead of the crack tip exceeds the fracture strength of the material over a characteristic distance, equal to about two grain diameter^34,55. This critical scale is required for cleavage crack initiation. However, it is apparent that such critical scale is also embedded in the topography of the fracture surface. When a microcrack is initiated at a hard-particle, it may be arrested if there is insufficient global driving forces to continue crack propagation⁵⁷. Accordingly, the requirement of reaching critical stress over a microstructure critical distance will be maintained for continued crack propagation until the macroscopic crack reach an unstable propagation domain, and thereby set-forth the critical fractal scale on the topography of the fracture surface. It is also important to note that the reported fractographic details are reported for mild steel, examined at extremely low temperature, below the ductile to brittle transition temperature (DTBTT) of (−95 ^oC), where fracture occurs before general yielding due to slip-induced cleavage. For the current examined alloy of AISI 440C stainless steel, a common alloy for cutlery and knives, the alloy has up to 1.2% carbon content in order to make the alloy hard and remain sharp. Such carbon content also shifts the DBTT to be above the room temperature⁶⁶. Accordingly, it is no surprise that the examined alloy in the form of rods or knives at room temperature shows similar fractal character to mild steel alloys tested below their DTBTT^34,55. The requirement of local stress ahead of a crack to exceed the fracture stress over a microstructurally significant distance⁵⁵ should be viewed in statistical terms. The characteristic dimension represents the location of the weakest link for the fracture process to occur⁵⁷. The cleavage fracture process zone is statistical in nature⁵⁶, as a finite volume of the material ahead of the crack tip should include a local defect to nucleate the cleavage crack. Such statistical argument is used to explain the large scatter in the cleavage fracture toughness data, wherein two nominally identical articles from the same material lot might show very different toughness (resistance to fracture) and failure strength values. By extension, we speculate also that such statistical differences will result in different local fracture surface topography because of the statistical randomness of the microscopic spatial location of the critical fracture-triggering particle. Susceptibility of cleavage fracture is sensitive to microstructure (grain size and carbide population), yield strength, stress state (triaxiality), and environment (temperature and radiation). Similarly, the fracture topography will exhibit unique microscopic feature signatures that exist on the entire fracture surface. We extend these parameters to generally include the material microstructure, the intrinsic material resistance to fracture, the direction of the applied load, and the statistical distribution of imperfections within the microstructure. The proposed framework’s ability to classify large sets of fracture surface pairs under various macroscopic loading conditions (both controlled and random) reinforces the foundational aspects of fracture mechanics in forensic comparisons. By leveraging the fractal nature of fracture surface topography and the statistical nature of cleavage fracture initiation, this approach establishes the critical length scale required for imaging comparisons and identifies the unique attributes of the fracture surface for forensic applications.

We exploit these distinctive features to quantitatively distinguish the microscopic features on fracture surfaces. Statistical learning tools are used to classify specimens. Using at least 5–6 images in the case of 75% image overlap or five images with 50% image overlap, we found that the matrix-variate t-distribution with 10–15 degrees of freedom, and a first-order autoregressive correlation structure to describe between-image correlation provides highly effective discrimination between matching and non-matching surface pairs. Our results show the distinctive individuality and the lack of identified discrepancies for a pair of fractured surfaces at wavelengths in the range of 2–8 grain diameters (50–200 μm, or the frequency range of 5–20 mm⁻¹ for the examined tool-steel). Near-perfect discrimination was achieved in the four training sets totaling 38 samples along with a set of 9 twisted samples, even in cases where some images on a surface had correlations that were not distinguishable from non-matching images. Challenges to this technique arise from high topographical details with a large aspect ratio that might shadow the surrounding details and might disturb one of the frequency bands. Statistical methods using two frequency bands and an extended number of base-tip image pairs yielded highly accurate match decisions. Among the range of training sample sets, this domain of distinctive individuality was found to be persistent and easily identified.

Our results suggest that for the class of materials that undergoes cleavage fracture, a single robust training data set would be needed for the identification of different classes of materials that share the same grain size distribution, but exposed to different and complex loading conditions. Furthermore, a framework is provided for performing matching of fragments with recommendations for model parameters, procedures for training models on a similar class of materials and setting the imaging scale and comparison bands as a function of the grain sizes, and procedures for testing new samples. Repeated imaging on the same surfaces consistently provided similar results. Our framework provided near-perfect matching with high confidence and so has the potential to be of significant impact, providing the ability to introduce more formality into how forensic match comparisons are conducted, through a rigorous mathematical framework. Our framework is also general enough to be applied, after suitable modifications and identification of the proper imaging scale, to a broad range of fractured materials and/or toolmarks, with diverse textures and mechanical properties. In doing so, we expect our proposed methodology and findings to help forensic scientists and practitioners place forensic decision-making on a firmer scientific footing. This can help formalize the scientific basis for conclusive matching of fragments leading to quantitative and more objective forensic decisions.

Methods

Sample generation and imaging

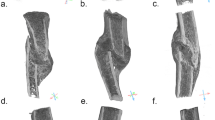
To mimic forensic articles found in a crime scene that might undergo comparative analysis, we consider two main material classes⁶⁷: sets of rectangular rods of a common tool steel material (SS-440C) fractured under control tension and bending configurations (Supplementary Fig. 2b, d), and sets of knives (Supplementary Fig. 1c, d) from the same manufacturer, fractured at random employing the fixture shown in Supplementary Fig. 1b. Figure 1a shows a typical pair of fragments, generated for this study. The average grain size for both groups was approximately dg = 25–35 μm. Four different sets of samples were established with nine specimens in the two sets of knives and ten specimens in the two sets of steel rods. To show the generalization of the approach for modes of loading, an additional set of 9-knives (Supplementary Fig. 1e) was tested by random twisting utilizing the same fixture (Supplementary Fig. 1b). The fracture surface topography would be influenced by a combination of fracture loading modes; that is mixed mode of the tensile mode-I and tearing mode-III loading as shown in the SEM images of Fig. 6b. The SEM images show subtle differences between the Modes of loading. Figure 6a shows cleaved grains in a direction normal to the imaging plane due to the pulling action (mode-I) under bending. Figure 6(b) shows swirl texture due to the combined out of plane tensile (mode-I) and in plane tearing (mode-III) loading. These topographical textures are very different and clearly show the critical role of external loading direction. Further details about sample preparations are given in Supplementary Section 1.

For clarity, we refer to the surface attached to the knife handle as the base and the surface from the tip portion of the knife as the tip and apply the same terminology to samples from the rectangular steel rods. The microscopic features of pairs of fracture surfaces were analyzed by a standard non-contact 3D optical interferometer (Zygo-NewView 6300), which provides a height resolution of 20 nm. Utilizing the results of the height-height correlations of Fig. 1d, the transition scale commences at around 50–70 μm to become non-self-affine and saturate, rendering a required imaging FOV of about 500 μm. For the examined material systems, this scale amounts to 2–3 times the grain size (consistent with the fracture process zone for cleavage fracture⁵⁵), and the FOV should cover 20–30 grain diameters. Accordingly, an optical magnification of 20X is employed, providing a 550 μm FOV and 0.55 μm/pixel resolution (Fig. 1c). Two fragments were aligned for imaging relative to their rectangular edges and their lower right corner. Image mis-registration can greatly affect the correlation estimations between a pair of images. However, the implemented procedure in this work to utilize the spectral (frequency) space is very tolerant to linear mis-registration of up to 20% of the FOV and several degrees of angular miss-registration, further elaborated in Supplementary Section 2.

A series of k-overlapping surface height 3D topographic maps were acquired from the pairs of fracture surfaces (Fig. 1e; k = 9), and quantified using Fourier transform based power spectral analysis as summarized in Fig. 7a in the image analysis step. The choice of overlap means there are three full independent sequential images on a surface. Multiple overlapping images were needed to overcome problems arising from missing grains between pairs of the fracture surface and/or the special circumstances of complex tortuous path of fracture. The effect of the number of images and overlapping ratio are further discussed in the result section. Additionally, having a super-image of stitched FOVs results in misregistration at the overlapping boundary of the stitched images, leading to an additional interfering frequency within the frequency bands of comparison⁴⁹.

Fig. 7: Flow chart summarizing our classification framework.

Steps include (a) image spectral analysis, (b) model training, and (c) classification of new objects to provide classification probabilities. For a new field-find object, an examiner would use (a) to image the object and perform (c) for object classification, using a model trained in (b) on samples of the same class to guide forensic conclusions.

Image spectral analysis and frequency correlations

From the 3D imaging of the fracture surface, the measured height distribution function h(x) is acquired to define the topography of the fracture surface at every spatial point, x on the fracture surface of a pair of fragments, shown in Fig. 7a. Each wavelength on the fracture surface has a distribution, in the frequency domain H(f), which is acquired using a Fast Fourier Transform (FFT) operator. For example, grain size has a distribution of frequencies across the spectrum rather than one specific frequency. Similarly, other microscopic fracture features have a range of spectral distributions^67,68,69. For a pair of fractured surfaces, the population of these features contains relevant information about the physical fracture processes present at each length scale (e.g. cleavage steps, dimples and voids at the sub-microscale, and river marks at scales of tens of microns). The spectral space analysis provides a straightforward segmentation of the surface topographical frequency ranges for comparison. After calculating the spectra of each pair of images, each spectrum was divided into multiple radial sectors. The segmented angular sectors for the frequency range (0^∘, 180^∘) represent the entire data set because the amplitude of H(f) exhibits inversion symmetry. The spectral array size is proportional to 2ⁿ, as this is a mathematical feature of the FFT. For the image size employed in this work, a spectral array of 1024 by 1024 is acquired, although only the upper half is utilized because of symmetry. The radial segments for comparison in the frequency domain (marked on the FFT spectral representation in Fig. 7a) are chosen to reflect the physical process scales and the corresponding wavelength, identified from the height-height correlation of Fig. 1d.

For comparison, we use the frequency amplitude, $\bar{H}({{{\boldsymbol{f}}}})$ for each surface spectral frequency. To compare the surfaces of two fragments, two-dimensional statistical correlations between their spectra are computed in banded radial frequencies, producing a similarity measure for each frequency band across the corresponding k pairs of images. As noted earlier, the increments for the bands’ frequency are determined by the scale of the image and the material microstructure, covering the transition scale of the height-height correlation of Fig. 1d. A training data set with N fracture surfaces is utilized to estimate the correlation distribution among the two selected frequency bands on all k image pairs for both the population of true matches and true non-matches fracture surfaces. For establishing a statistical match, these distributions, shown in Fig. 2 (a), form the basis for our classification and matching process strategy, following the two modules summarized in Fig. 4, (b) Model training on an initial data set, and (c) performing classification of new sample(s).

Model training/fitting

A statistical model will be developed to distinguish matching from non-matching fracture surfaces⁷⁰. Employing a training data set, the behavior of the frequency band correlations in the population of matches and non-matches has to be estimated and modeled. The proposed framework provides a separate model for each class (i.e., match and non-match). The model training process, highlighted in Fig. 4b, entails:

• 1. Choice of controlled and robustly characterized data set of fractured pairs to train the model.

• 2. Computation of the correlations for the frequency bands for the sets of k images for all N matching and N(N − 1)/2 non-matching surface pairs.

• 3. Employing the Fisher’s z transformation on the correlation data to stabilize variance⁷¹.

• 4. Fitting the models using a matrix-variate distribution (as detailed later in this section) to describe the distribution of true matches and true non-matches. The matrix-variate models account for the difference in the location of the correlations and account for the covariance of the repeated observations across the surface.

The frequency band correlations for one of the examined data sets (K-1-1) are shown in Fig. 2. The proposed method’s discrimination ability can be judged from the clear separation of matching and non-matching surfaces within two separate clusters. The data in this illustration were derived from N = 9 base-tip pairs from fractured knives. A series of k = 9 overlapping images were taken from each base and tip fracture surface, resulting in N × 2k = 162 total images (81 from the tips and 81 from the bases). Additional details are given in the Supplementary Section 2 for different data sets. In this example, image pairs for when the tip and base surfaces were from the same knife are true matches (N × k = 81 matched-pairs), while those pairs for which the tip and base surfaces were from different knives are true non-matches (N(N − 1) × k = 648 unmatched-pairs). Furthermore, there is one image-pair among the true matches in Fig. 2a which cannot be distinguished from the true non-matches and three other pairs that are ambiguous. To further improve the discrimination, considering multiple k − observations from the same surface would distinguish it from the non-matches, since the other observations on that surface are well-separated from the non-matches. In the current framework, we take the information from every pair of images and collectively based on the model, a decision is driven accounting for the fact that the images are not independent, i.e. overlapping and coming from the same fracture surface. The role of imaging repetition or overlap, may improve the signal to noise ratio. Figure 2b summarizes the correlation analysis over several ranges of frequency bands. A clear separation (lower values for the true non-matches and higher values for the true matches) can be observed for the 5–10 and 10–20 mm⁻¹ frequency-band ranges. Beyond these frequency ranges, there is some overlap, where the true match and the true non-match correlation distributions become less distinct and overlap more.

For the presented data set of k = 9 overlapping images for each fracture surface and two (or more) comparison frequencies, each comparison between a pair of fracture surfaces based on the ensemble of nine images provides a 2 × 9 matrix of correlations. Our model needs to account for the lack of independence in the images from the same specimens. Accordingly, we propose using a matrix-variate distribution^72,73 to model the densities of the matching and non-matching populations, and, specifically, a matrix-variate t distribution (MxVt) because the data for the individual comparisons are approximately elliptically distributed but have heavier tails than a normal distribution. A definition of the distribution is in the Supplementary Section 3 and the density is defined in Supplementary Equation 1.

We use matrix-variate distributions to model the relationship between the two frequency bands in each image comparison and across all the images being compared for each of the base and tip pairs (e.g. Fig. 2a). Because of the overlapping-image structure of the data source, our model allows between-image correlations in the matrix-variate model to be related according to an autoregressive model of order 1 (or AR(1)) model (implying that immediately adjacent images can be correlated). The AR(1) model implies that the mean correlations in the two frequency bands remain the same across the images on a surface in the model. The parameters of the model are estimated using an expectation-maximization (EM) algorithm developed for the matrix-variate t distribution⁷⁴.

Classification of a new object

Figure 7c sumarizes the classification procedure. Suppose the fitted model has been trained on a set of k-images per fracture surface, yielding probability density functions f₁ corresponding to the population of true matches and f₂ corresponding to the population of true non-matches. Suppose also that there is a new pair of fracture surfaces that may or may not match. First, the correlations for the k-aligned image pairs in the chosen frequency bands are computed and transformed, yielding a new observation X, which is a matrix of observations of correlations with one row for each frequency band and one column for each pair of images—here, a 2 × k matrix. Then, presuming prior probability p of being a true match and prior probability 1 − p of being a true non-match, we can find, by combining prior probabilities and the match and non-match densities from the model, the posterior probability that the two surfaces match as follows:

$$P(X\,{{\mbox{is}}} \, {{\mbox{a}}} \, {{\mbox{match}}})=\frac{p{f}_{1}(X)}{p{f}_{1}(X)+(1-p){f}_{2}(X)}.$$

(1)

Alternatively, a likelihood ratio (LR) can be calculated as f₁(X)/f₂(X), a common method in forensic applications^{43,44,45,46,47,48,49}. These LR results can then be used to express the uncertainty about the strength of evidence under different sets of assumptions⁷⁵. The likelihood ratio can be combined with prior odds (p / (1 − p)) to produce posterior odds:

$${{\mbox{Posterior}}} \, {{\mbox{Odds}}}=\frac{p}{1-p}\times LR$$

(2)

with the conversion of odds O to probability P performed by the formula P = O / (1 + O). In this paper, odds and likelihood ratios are employed and reported on the logarithmic scale. Once the posterior odds are obtained, classification decisions can be made according to the rules of evidence in setting prior probability relevant to each forensic case. For the purposes of illustrating the method, we are using an equal prior probability of being a match or non-match (i.e., p = 0.5 or a log prior ratio of 0). In an actual criminal or civil case, choosing a prior match probability would require carefully considering any other evidence or relevant information previously presented, but such considerations are beyond the scope of this paper.