Introduction

The study of chemical short-range order (CSRO) in high or medium entropy alloys (HEAs/MEAs) has attracted significant attention due to its ambiguous influence on material properties1,2,3,4,5,6,7. Researchers have proposed the occurrence and importance of CSRO in shaping the structural and mechanical characteristics of HEAs. This phenomenon, rooted in the local arrangement of atoms, is under heated debate in the community over whether it plays a pivotal role in determining the alloy’s behavior under various conditions.

The Warren–Cowley parameter is a statistical measure used to describe the CSRO in alloys8. It quantifies the deviation of the actual atomic concentration in a given shell from the bulk concentration for different atomic pairs at various distances. Its definition is given as follows:

$${\alpha }_{{ij}}^{m}=1-\frac{{P}_{{ij}}\left(m\right)}{{c}_{j}}$$
(1)

where \({\alpha }_{{ij}}^{m}\) is the Warren–Cowley parameter for an atom of type i and an atom of type j at the m-th nearest-neighbor distance, Pij(m) is the probability of finding an atom of type j at the m-th nearest-neighbor distance from an atom of type i, and cj is the concentration of type j atoms in the alloy. Positive values of this parameter indicate an aversion between atom types, while negative values denote preferential bonding; thus, this parameter provides simple and direct information on the nature of CSRO.

To comprehensively understand the effects of CSRO, its presence must first be confirmed and quantified. However, it is challenging to experimentally detect and quantify CSRO, so the existence of conflicting data in the literature regarding the effect of CSRO on mechanical properties is understandable4,5. To directly show the presence of CSRO, various measurement methods have been employed including transmission electron microscopy (TEM) and X-ray diffraction (XRD)5,9,10,11,12,13,14. Fewer studies have used other techniques, such as extended X-ray absorption fine structure (EXAFS)15 and partial pair distribution function (PDF)15. While TEM, XRD, and EXAFS provide valuable insights, their application becomes challenging when attempting to distinguish signals from elements that are adjacent on the periodic table, which is the case from the well-studied alloy CoCrNi (Co33Cr33Ni33 in at.%). Despite the high spatial resolution of TEM, its ability to unambiguously prove the presence of CSRO is also limited in this system. Diffuse diffracted intensities are commonly observed and have been attributed to CSRO in zone axes such as the 〈112〉9, but it has more recently been shown that these can be easily confounded with effects from higher-order Laue zones (HOLZ), various structural defects, thickness variations, and artifacts of sample preparation16,17.

In parallel, approaches such as nanohardness2, electrical resistivity1,18, specific heat19, and dilatometry20 have been widely used to indirectly demonstrate the presence of CSRO. Despite being widely adopted methods for conventional alloys, these indirect approaches have been applied in only a few HEAs studies to date and are currently regarded mostly as qualitative measurements of the effect of CSRO. A notable success was the study by Li et al.18, who showed that aging CoCrNi for long times below 973 K changed its electrical resistivity. The authors proposed that these changes could be due to CSRO as higher electrical resistivity saturation values were reached for lower aging temperatures. The authors showed that long heat treatments at lower temperatures did not change any of the intrinsic mechanical properties, including the twinning critical resolved shear stress. Other authors have demonstrated changes in mechanical properties upon annealing. Zhang et al.5 observed an increase in yield strength by ~25% attributed to CSRO in the annealed CoCrNi alloy. Nanoindentation analysis showed an increase from 4.07 ± 0.23 GPa in the water-quenched sample to 4.37 ± 0.58 GPa in the recrystallized sample. In the same way, Zhang et al.2 also observed shifts in the early stages of the nanoindentation curve, which were called the “pop-in loads”, which could be correlated to the aging temperature of the samples. This phenomenon was attributed to CSRO, where there is an increase in the barrier for dislocation nucleation in the early deformation of a crystal with low initial dislocation density. While all these studies show an effect of heat treatment on properties, none have been able to quantify CSRO in the CoCrNi alloy.

To overcome these gaps, the primary objective of this research is to establish a new approach to experimentally quantify the presence and type of CSRO, and to propose a mechanism by which CSRO can form and be destroyed. To do so, we chose to work with CoCrNi, since it is the most widely studied composition on this topic, together with the model binary CrNi2 (Cr33Ni66 in at.%), which was selected due to the similarity with the ternary alloy and the large body of work on this composition and its ordering reactions19,21,22,23. These compositions were produced and thermomechanically processed as described in Methods; the resulting material was cut into samples that were annealed at 1273 K for 1 h, and water quenched, producing a recrystallized microstructure. These samples from here on will be referred to as “recrystallized”. The samples were then aged at 748 K for different times up to 240 h followed by water quenching. The temperature used in the aging treatments was selected based on B. Stephan et al.22 work, which indicates that 748 K is the temperature that provides the maximum transformation kinetics in CrNi2 for the formation of the ordered oI6-CrNi2 phase (Immm space group).

Results and discussion

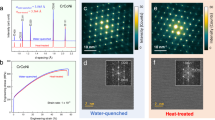
Figure 1a, b presents structural characterization results of CrNi2 and CoCrNi via synchrotron X-ray diffraction (SXRD) after varying heat treatment conditions. The emergence of extra peaks in the binary alloy corresponds to the long-range ordered oI6 phase, along with peaks of a disordered FCC phase (i.e., a solid solution), particularly for 170 and 240 h aging times. Together with the appearance of oI6 peaks, the disordered-FCC CrNi2 lattice parameter underwent a non-negligible decrease between 100 and 170 h aging, in line with what has been observed in literature23. On the other hand, no substantial differences have been observed in the CoCrNi alloy lattice parameter as a function of the aging time. Indeed, the CoCrNi alloy exclusively shows peaks associated with a disordered FCC phase, with no superlattice reflections for the oI6-ordered phase.

Fig. 1: Microstructural characterization by SXRD and TEM in both alloys under different heat treatment conditions.
figure 1

SXRD of a CrNi2 and b CoCrNi under different thermal treatment conditions. Additional SXRD peaks are detected in CrNi2 after aging for 170 and 240 h (see the inset in a, which is plotted on a log scale), indicating the presence of the long-range ordered oI6 phase. Only disordered FCC peaks are detected in CoCrNi. The triangles mark the 2nd harmonic of the main FCC peaks; they appear due to a secondary, low-intensity radiation with twice the energy of the main radiation. TEM c BF and d DF images (from circled reflections in e and f SAED patterns from the CrNi2 alloy aged for 240 h. Additional spots from the long-range ordered oI6 phase (red circles) are seen amidst the primary FCC spots. g BF-TEM image of a grain boundary of the CoCrNi sample showing the absence of coarser particles. h and i SAED of the CoCrNi alloy after aging for 240 h. No additional spots were detected beyond the disordered FCC phase. To mitigate dynamic scattering effects, all patterns were acquired using precession angles of 0.5°.

Full size image

Figure 1c–i showcases TEM images of the recrystallized and 240 h aged alloys. Figure 1c, d present bright-field (BF) and dark-field (DF) images of the CrNi2 sample after 240 h, highlighting ordered oI6 domains, while Fig. 1g reveals a grain boundary of the CoCrNi sample, also after the same aging time, without any discernible precipitates. Furthermore, Fig. 1e, f, h, i illustrate selected area electron diffraction (SAED) patterns of the same samples, clearly indicating the presence of extra spots representing the long-range ordered oI6 phase amid the disordered FCC phase spots for the binary alloy (Fig. 1e, f), and the absence of any reflections in addition to the fundamental FCC reflections for the 240 h aged CoCrNi sample (Fig. 1h and i).

EXAFS analysis was also performed on these samples. While the CrNi2 aged specimens indicate unfavorable Cr–Cr pairs in the 1st shell (averaging two neighbors instead of the four expected in the random case), this was the only trustworthy simultaneous Ni–K and Cr–K refinement. On the other hand, only single-edge and average-scatterer refinements gave reasonable bond length results for CrNi2 recrystallized and CrCoNi specimens, (Supplementary Information Fig. 1), therefore not providing any information on CSRO for comparison with the CrNi2 aged sample. Conventional EXAFS in these alloys, therefore, was not able to add conclusive information on CSRO for this alloy24.

None of the preceding techniques reveal any discernible change in the ternary alloy following aging at 748 K for up to 240 h. These same aging treatments produce precipitates of the long-range ordered oI6 phase in CrNi2 that are seen in BF and DF TEM images (Fig. 1c, d). Further, superlattice reflections from the oI6-CrNi2 phase, although weak, are clearly observed in SAED (Fig. 1e, f), and SXRD (Fig. 1a) patterns. The low oI6 superlattice scattering intensities are a consequence of the closely matched X-ray and electron scattering factors for Cr, Co, and Ni mentioned earlier. Therefore, the data displayed here shows unequivocally that long-range order is only present in the binary alloy for aging times of at least 170 h.

While CSRO is expected to precede long-range order23,25, none of the previous experiments were able to inform us about CSRO in any regard. We address this by employing high-precision differential scanning calorimetry (DSC) to provide the needed additional data. DSC measures the energy flux generated when a material transitions between different structural states. The energy produced (or absorbed) by the formation (or dissolution) of long-range ordered phases is well understood, and both the temperature and kinetics of the order–disorder transformation are well-studied in CrNi219,23. Here we investigate the energy-flux trends for the formation and destruction of CSRO. Figure 2a–f presents curves of the specific heat capacity as a function of temperature for CrNi2 after various heat treatments. Each sample was heated twice in the calorimeter from 373 to 973 K at a rate of 10 K min−1. The first heating cycle shows the thermal response of the initial sample condition, while the second heating cycle evaluates the influence of slow cooling (40 K min−1) from 973 K, thus generating a curve that is similar/comparable for all samples. DSC is a technique sensitive to sample geometry and size, leading to small variations among samples despite their similar dimensions. This sensitivity is addressed by employing the second heating cycle as a standard for comparing all conditions. As a result, the energy of each peak can be calculated with respect to the same reference condition by integrating the area in between both cycles.

Fig. 2: Specific heat variations with temperature for CrNi2 and CoCrNi after different heat treatments.
figure 2

For CrNi2 a recrystallized and followed by aging at 748 K for b 1 h, c 10 h, d 100 h, e 170 h, and f 240 h. For CoCrNi g recrystallized and followed by aging at 748 K for h 1 h, i 10 h, j 100 h, k 170 h, and l 240 h. The solid lines are for the first heating cycle and the dashed lines correspond to the second heating. The exothermic (EXO) direction is marked by an arrow.

Full size image

The various features in the specific heat capacity profiles (Fig. 2a–f) show the effect of aging time at 748 K. While an exothermic reaction is observed only in the recrystallized sample, endothermic reactions are observed for all other aging times. The magnitude of the endothermic reactions increases with aging time (see Supplementary Information Table 1). The second heating cycle curves are qualitatively identical for all samples.

The endothermic peak for the 170 and 240 h aged binary samples (Fig. 2e, f) have an onset temperature of 884 K, which is consistent with the reported dissolution temperature of the oI6 ordered phase of 89319 and 863 K26. Meanwhile, the samples aged for 1, 10, and 100 h (Fig. 2b–d) do not display clear SXRD oI6 superlattice peaks (Fig. 1a). However, they still show an endothermic peak in the same temperature range where the long-range ordered oI6 phase is dissolved in samples with longer aging times. Together, the results in Fig. 2b–f suggest that the endothermic peaks correspond precisely to the well-established ordering/disordering temperature for this binary alloy19,23.

For the ternary CoCrNi alloy, exothermic reactions are observed in both recrystallized and 1 h-aged samples. After further aging, all samples showed endothermic reactions that grew in intensity with increasing aging time, eventually saturating at around 100 h. This time scale is in good agreement with the recent electrical resistivity measurements performed by Li et al.18, which were attributed to the formation of CSRO. Together with Fig. 1b, g–i, these results clearly indicate that although no long-range order is formed in this sample, there is an endothermic reaction of small intensity occurring at the same temperature range in which long-range order is destroyed in the binary sample. Further details of the temperature ranges are provided in Supplementary Information Table 1.

An activation energy analysis was performed to give additional insight into the underlying origin of the exothermic signals in Fig. 2a, g. The activation energy for this reaction was determined to be 314 ± 14 kJ/mol for CrNi2 and 251 ± 19 kJ/mol for CoCrNi. These values are similar to each other and are close to the activation energies for self-diffusion in Co, Cr, and Ni, and for atomic diffusion in CoCrFeMnNi. This suggests that diffusion is the rate-controlling mechanism for the exothermic reactions in Fig. 2a, g. This analysis is illustrated in Supplementary Information Fig. 2, and activation energies for diffusion in relevant materials are shown in Supplementary Information Table 2.

In the case of the ternary CoCrNi alloy, the possibility of long-range order formation was unequivocally dismissed based on evidence from synchrotron measurements and TEM analyses in Fig. 1b, g–i. The reactions observed in Fig. 2g–l cannot be attributed to a transition from a paramagnetic to a ferromagnetic state because the Curie temperature is reported to be TC < 10 K27; the prospect of recrystallization was ruled out as the sample had already undergone annealing. The exothermic peaks (Fig. 2a, g) cannot be attributed to the annihilation of vacancies and defects resulting from non-equilibrium solidification. This dismissal is supported by the DSC analysis of a homogenized and water-quenched pure Ni sample with similar mass and geometry (Supplementary Information Fig. 3), which does not display an exothermic peak. It is reasonable to expect both samples to have a similar number of quenched-in vacancies given their similar melting/liquidus temperatures (1728 K for Ni and 1703 K for CrCrNi, as shown later in Fig. 6). The considerations above rule out alternative sources for the reactions observed in Fig. 2g–l, except for CSRO.

Based on these results, a comprehensive explanation of the reactions observed for CoCrNi is presented in Fig. 3. In this figure we compare DSC results for samples prepared with three different thermal treatments: the recrystallized sample (yellow), the sample aged at 748 K for 240 h in the first DSC heating cycle (green), and the second heating cycle of the same sample treatment for 240 h (gray).

Fig. 3: Schematic of the heat evolved during DSC testing (heating cycles).
figure 3

Below around 748 K, the kinetics are too slow to change the CSRO in the experimental timescale. Above 748 K, CSRO can be either created (purple shade) or destroyed (red shade), as indicated by exothermic and endothermic reactions, respectively.

Full size image

Firstly, as shown previously, CSRO takes more than 100 h at 748 K to saturate due to diffusion being the rate-controlling mechanism and 748 K being a low temperature for this material, which is further detailed in Supplementary Information Fig. 4, where the average time for atomic jumps based on the diffusivity values of this alloy is estimated. Since the DSC heating and cooling cycles are performed at 10 and 40 K min−1 respectively, the time-temperature combination induced by the test is insufficient for appreciable diffusion to occur and change the CSRO state below 748 K. Consequently, no structural changes occur in the samples, and all heat input is associated with temperature alteration. At temperatures above 748 K, we eventually enter a regime where the kinetics of vacancy diffusion becomes significant for the time scale of the experiment18. Thus, the CSRO state of the alloy will change in time towards its thermodynamic equilibrium state. Figure 3 also shows the heat flux required to only increase the sample temperature (blue line, “base Cp line”), i.e., without any reaction due to changes in the CSRO state occurring. This will be used as a baseline to describe the behavior of the three samples.

The sample aged at 748 K for 240 h (green line in Fig. 3) is initially in a CSRO state of thermal equilibrium at this temperature, which is a much higher amount of CSRO than what is initially present in the recrystallized sample. Once this temperature is reached during the DSC test, the pre-existing CSRO in the aged sample begins to dissolve with increasing temperature to stay as close to its thermodynamic equilibrium state as the kinetics of vacancy diffusion allows it, thereby explaining the endothermic peak observed in Fig. 2.

The recrystallized sample (yellow line in Fig. 3) has a CSRO deficit due to the rapid cooling, which “freezes” a high-temperature CSRO state with lower CSRO magnitude than the equilibrium state at 748 K. Consequently, as temperature is increased above 748 K, the sample initially undergoes an exothermic event to increase CSRO (shown in Fig. 3 as the purple “Creation of CSRO” region), thereby explaining the exothermic peak observed in Fig. 2g. At higher temperatures, after this exothermic reaction, the recrystallized sample experiences an upward shift above the Cp baseline (towards the endothermic direction). In this regime, CSRO is progressively destroyed with increasing temperature in order to stay as close to its thermodynamic equilibrium state as the kinetics of vacancy diffusion allow it.

Finally, consider the second heating cycle of the aged sample (gray line in Fig. 3). This sample was slowly cooled (40 K min−1) from 973 K after the first heating cycle, thereby retaining an amount of CSRO, more than the annealed and water quenched sample but less than the aged samples. Thus, this sample displays a gradual baseline shift with no evident peak.

Next, we quantitatively validate the mechanism proposed in Fig. 3 by evaluating the portion of the heat evolution involved only in the CSRO reactions and demonstrating that this quantity agrees well with results derived from atomistic simulations.

The calorimetric heat Qtotal, calculated by integrating the area under the DSC curve, is converted into enthalpy:

$${Q}_{{{{total}}}}={\int }_{{\!\!\!\!T}_{{{i}}}}^{{T}_{{{f}}}}{q{{d}}T}=\varDelta {H}_{\varDelta T}+\varDelta {H}_{{{{CSRO}}}}$$
(2)

where \(\varDelta {H}_{\varDelta T}\) is the heat absorbed by the sample when its temperature increases from \({T}_{{\rm {i}}}\) to \({T}_{{\rm {f}}}(\varDelta T={T}_{{\rm {f}}}-{T}_{{\rm {i}}})\) and \(\varDelta {H}_{{{\rm {CSRO}}}}\) is the enthalpy related to changes in the sample’s CSRO state, since the structure will be changing, the material will suffer an enthalpy change from a low-temperature state \({H}_{{{\rm {CSRO}}}}({T}_{{\rm {i}}})\) to the high-temperature state \({H}_{{{\rm {CSRO}}}}\left({T}_{{\rm {f}}}\right)\), with the \(\Delta {H}_{{{\rm {CSRO}}}}\) being the difference between these states. Thus, the DSC curves (Fig. 2) reflect the material’s intrinsic specific heat capacity (Cp) and also contribute to the formation and annihilation of CSRO. Below 748 K the alloy undergoes negligible CSRO changes due to limited kinetics, in which case the heat exchange leads purely to a temperature increase, representing the intrinsic Cp. Therefore, for Tf < 748 K:

$$\varDelta {H}_{\varDelta T}={\int }_{{\!\!\!\!T}_{{{i}}}}^{{T}_{{{f}}}}{C}_{{{p}}}{{{d}}T}$$
(3)

In practice, \(\varDelta {H}_{\varDelta T}\) is measured below 748 K and extrapolated to higher temperatures (see Supplementary Information Fig. 5a), as schematically illustrated in Fig. 3 by the blue line labeled “base Cp”. By substituting Eq. (3) back in Eq. (2) we are able to obtain a precise quantification of \(\varDelta {H}_{{{\rm {CSRO}}}}\), shown as a function of Tf by the red line in Fig. 4a for the 240 h aged sample with Ti = 748 K. We now turn to atomistic simulations to evaluate the same quantity and validate the results in Fig. 4a.

Fig. 4: Monte Carlo atomistic simulations employing a machine learning potential developed to capture CSRO in CrCoNi29.
figure 4

a Direct comparison of ΔHCSRO between simulations and experiments. The \(\varDelta {H}_{{{\rm {CSRO}}}}\) can be understood as \({H}_{{{\rm {CSRO}}}}^{{T}}-{H}_{{{\rm {CSRO}}}}^{748\,{\rm {K}}}\), or in other words, as the difference in enthalpy between the sample at a temperature T and the equilibrium state at 748 K. b Enthalpic contribution stemming from CSRO as a function of temperature (blue) and Cr–Cr Warren–Cowley parameter \({\alpha }_{{{\rm {Cr}}}-{{\rm {Cr}}}}^{m=1}\) (green) for first neighbors. At temperatures above 748 K, the figure shows the enthalpy is higher (or more positive), meaning that there is heat absorption by the system to destroy CSRO. Good agreement between the experimental and simulated values is seen only above 873 K because only at this temperature do the kinetics of the system allow the system to reach equilibrium within the experimental timescale. Below this temperature, the experimentally measured ΔHCSRO is expected to be lower than simulations because experiments do not achieve the equilibrium CSRO due to slow kinetics, while simulations always predict equilibrium values. A 4.3% error was considered for the experimental data as explained in the “Methods” section, also further details on the calculation of the experimental curve are given in Supplementary Information Fig. 6.

Full size image

To evaluate ΔHCSRO from atomistic simulations in a physically realistic manner, one must take a few precautions. The highest levels of physical fidelity require electronic-structure methods such as density-functional theory (DFT). Yet, it has been recently demonstrated that the characteristic length scale of CSRO can be as large as 25 Å28, which is exceedingly large for DFT calculations. In the absence of properly sized simulations, the calculations may underestimate CSRO28 formation. Our approach to circumvent this limitation is to employ a machine learning interatomic potential (MLP) that we have recently developed with the sole purpose of accurately capturing CSRO as learned from DFT29. MLPs allow for the simulation at the appropriate length scale for CSRO while retaining the accuracy of DFT.

The enthalpy contribution due to CSRO (HCSRO(T)) can be evaluated using Monte Carlo simulations with our MLP by subtracting the enthalpy of the thermally equilibrated alloy (i.e., with CSRO) from the enthalpy of a random solid solution (see Supplementary Information Fig. 5a for the intermediary quantities). Figure 4b shows HCSRO(T) as a function of temperature. From the definition in Eq. (2) one can evaluate ΔHCSRO directly as the change in the CSRO component of enthalpy with temperature, i.e., ΔHCSRO = HCSRO(Tf)−HCSRO(Ti).

The comparison between ΔHCSRO as evaluated from DSC and atomistic simulations, shown in Fig. 4a can be understood as follows. The Ti = 748 K temperature was chosen as the reference state for ΔHCSRO because, for the aged samples, the CSRO formation has saturated at this temperature after about 100 h. Thus, the 240 h sample is expected to have achieved CSRO equilibrium at 748 K. According to the explanation of the DSC measurements provided in Fig. 3, the CSRO state of this aged sample lags behind the equilibrium CSRO state due to the limited kinetics of vacancy diffusion. This lasts only until the end of the endothermic peak at around 873 K, at which point all three samples in Fig. 3 evolve with similar slopes. This is also supported by the diffusivity calculations presented in Supplementary Information Fig. 4 and by the measurements in ref. 18, which indicate that above 873 K, CSRO saturates in less than 5 min (DSC heating occurs at 10 K min−1). Consequently, the ΔHCSRO measured above 873 K is in great agreement with simulations (Fig. 4a, while below 873 K the ΔHCSRO from experiments is lower than simulations because the simulations always predict the equilibrium ΔHCSRO, while the experiments are limited by kinetics.

Our approach allows the quantification of the amount of “frozen-in” CSRO in a nonequilibrium sample, such as the recrystallized sample. For this purpose, we introduce the concept of an effective CSRO temperature (TCSRO), defined as the temperature at which a sample in thermodynamic equilibrium would have the same HCSRO as its nonequilibrium counterpart. While there may be configurational differences in their chemical order, these structures are equivalent energetically. This definition is offered in the same spirit as the ‘law of corresponding states’ in the pioneering work of Martin30 in the field of driven alloys. Consider as an example the recrystallized sample, an analysis of its HCSRO, further described in Supplementary Information Fig. 6c, d, leads to HCSRO = −8.9 J/g (or about −0.5 kJ/mol). By extending the experimental curve in Fig. 4a slightly, we estimate that TCSRO = 1015 K for this sample, which aligns with the expectation of a CSRO state at or below the annealing temperature of 1273 K. This effective temperature also is in agreement with Supplementary Information Fig. 4, as shown in this plot, at this temperature the average time for atomic jumps is on the order of a second or less, which is reasonable since considering a thin sample when water quenched will reach room temperature in a few seconds. This would yield \({\alpha }_{{{\rm {Cr}}}-{{\rm {Cr}}}}^{m=1}=0.17\) based on Supplementary Information Fig. 5b, which is about 70% of the value for the 240 h aged sample (0.24) for the 240 h aged sample, with a TCSRO of 748 K. Note that for a fully ordered oI6 phase, only 2 of the 12 first neighbors of each Cr atom would be other Cr atoms as shown in Supplementary Information Fig. 7, so the \({\alpha }_{{{\rm {Cr}}}-{{\rm {Cr}}}}^{m=1}\) for a fully ordered structure would be 0.5. Therefore, relative to this long-range ordered state, both samples, even in the more disordered state, are shown to have significant amounts of CSRO.

These results also help to explain variations in other physical properties reported in the literature. For example, the resistivity changes reported by Li et al.18 can be interpreted through our findings, where increased levels of CSRO lead to increased electrical resistivity. Furthermore, lower temperatures will always achieve higher CSRO levels and take longer times to achieve saturation. Finally, as mentioned previously, the time scale for achieving saturation by electrical resistivity matches the time scale observed in this study to saturate the endothermic reaction energy. Similarly, the dilatometry results reported by Andreolli et al.27 can be explained by our CSRO quantification, as the structural changes due to CSRO affect the lattice parameters and dimensional stability during thermal cycling.

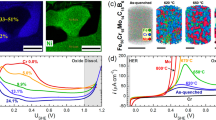
The methodology implemented here unequivocally demonstrates that samples aged for more than 100 h at 748 K possess significantly more CSRO compared to those in the recrystallized condition. This leads to an imperative question about the extent to which CSRO influences the mechanical properties of the alloy. To address this, we conducted microhardness and tensile tests complemented by in-situ synchrotron radiation, the outcomes of which are depicted in Fig. 5. The hardness tests (Fig. 5a) reveal a pronounced trend: the binary alloy’s hardness escalates with extended aging. However, notice that the hardness of the binary alloy is only noticeably different from the recrystallized state after 100 h of aging, which aligns with the specific heat capacity profiles data in Fig. 2a–f showing that the endothermic peak becomes significantly larger after 100 h. However, the ternary alloy’s hardness remains uniform across various thermal treatments, indicating no systematic changes.

Fig. 5: Analysis of the mechanical properties of CrNi2 and CoCrNi alloys under different heat treatment conditions.
figure 5

a Hardness of CrNi2 and CoCrNi under different heat treatment conditions. As the aging time increases in the binary alloy, there is an increase in hardness. In the ternary alloy, the hardness remains unchanged for all heat treatment conditions. The scale bar was created using the standard deviation. b Tensile tests of CrNi2 and CoCrNi recrystallized and aged for 240 h. In the binary alloy, an increase in ultimate tensile strength (\({\sigma }_{{{\rm {UTS}}}}\)) and yield strength (\({\sigma }_{0.2}\)) is observed after aging for 240 h. The measured grain size for each sample is shown. However, regarding strain to failure (εf), no significant changes are observed. As for the ternary alloy, the values of \({\sigma }_{{{\rm {UTS}}}}\), \({\sigma }_{0.2}\), and εf remains consistent in both recrystallized and aged conditions for 240 h. c and d Mechanical properties of the CrNi2 (c) and CoCrNi (d) for different aging times. The scale bar was created using the standard deviation for both figures (c) and (d). e Results of dislocation density analysis and tensile curves for CoCrNi alloy, using the modified Williamson–Hall method for 8 FCC Peaks (111, 200, 220, 311, 222, 400, 331, 420) in the transverse direction integration (Azimuthal range 0 ± 20°) after subtracting the instrumental broadening. The dislocation density (ρ) is determined by the slope, as a function of strain. As shown in the figure, both samples have similar capacities to accommodate dislocations at different strain levels. All error bars correspond to one standard deviation of the measured quantity.

Full size image

For tensile testing, the results are shown in Fig. 5b–d. The aged CrNi2 alloy displayed significant enhancements in ultimate tensile strength (σUTS) and yield strength (σ0.2) after 240 h aging, a state characterized by the formation of ordered oI6 precipitates, as established previously22,23,31. The ductility, measured as strain to failure (εf), did not show marked changes. Conversely, the CoCrNi alloy exhibited consistent σ0.2, σUTS, and εf across both the recrystallized and aged states for 240 h, which were all similar as indicated by a statistical one-way analysis of variance (ANOVA) analysis presented as Supplementary Information Note 1. The ANOVA analysis also indicated that the CrNi2 sample heat treated for 240 h was statistically different from the other samples, further reinforcing the observed effect of LRO on the mechanical properties of the binary alloy. This contrast underscores that while LRO order can augment the mechanical attributes of an alloy, the presence of a greater degree of CSRO need not significantly alter its strength or ductility. Given that the HEA field is expansive, it is risky to draw general conclusions from a single alloy. It is often assumed that CSRO will have an important effect on mechanical properties. While this may be true in some alloys, we show one example in the present study where CSRO has no significant effect on primary mechanical properties.

The XRD data acquired during tensile testing enabled an analysis of the dislocation density, denoted as ρ, and its variation under strain for the ternary alloy with both minimal and pronounced CSRO—specifically, the recrystallized sample versus the 240 h aged sample. This analysis, visualized in Fig. 5e, showed that both samples displayed a comparable ability to accommodate dislocations across various levels of strain, leading to nearly identical work-hardening rates. This similarity also extended to the flow stress behavior, resulting in almost indistinguishable stress-strain curves for both material states. It is worth noting, though, that some minor discrepancies on the ρ profiles were observed at the initial stages of the tensile tests; however, these should be approached with caution due to their less reliable fit, as shown in Supplementary Information Fig. 8. Additionally, throughout the testing, only FCC peaks were present, showing that the TRIP effect that is shown to happen in this alloy22 was not detected in either sample; this is probably related to the low intensity and broad peaks of the HCP phase.

The mechanical testing unequivocally shows that varying CSRO levels do not significantly influence the mechanical properties of the CoCrNi alloy. In contrast, the binary alloy’s mechanical properties are markedly enhanced by the presence of long-range ordered oI6 precipitates. To further probe the potential for forming such precipitates in the ternary alloy, we examined the effect of Co additions on the long-range order temperature for CoCrNi alloys through DFT. Our DFT calculations revealed that the formation enthalpy for the oI6-CrNi2 phase is −3.06 kJ/mol, suggesting a relatively stable-ordered structure. Conversely, the oI6-CrCo2 phase presents a formation enthalpy of 6.44 kJ/mol, indicating it is an unstable phase.

Incorporating the formation energies for Co2Cr and CALPHAD-optimized values for oI6-CrNi232 into the CALPHAD method allows for the creation of the pseudo-binary phase diagram presented in Fig. 6. The ordered phase was modeled as a solid solution of the type M2Cr, with M = Co,Ni, since Co and Ni both show similar bonding preferences, as revealed by the Monte Carlo simulations29. This phase was added to the database published by Gheno et al.33. The phase diagram, which plots the dissolution temperatures for ordered M2Cr phases, reveals a trend of decreasing dissolution temperature with increasing cobalt content. For the equiatomic CoCrNi alloy, the model predicts a dissolution temperature below 673 K, aligning with our experimental findings—even after extensive heat treatment at 748 K, a condition sufficient for precipitating the same ordered phase in the binary alloy, no ordered phase forms in the ternary alloy. Additionally, the lack of evolution in endothermic enthalpy after 100 h of treatment suggests that the alloy may have reached a state of equilibrium, at least concerning ordering. This analysis suggests that the ternary alloy is inherently less inclined to form ordered phases compared to the binary system. Nonetheless, the possibility remains that prolonged treatments at temperatures below 673 K could potentially lead to the formation of the ordered phase, albeit in a time-consuming and perhaps impractical manner.

Fig. 6: Pseudo-binary phase diagram between CrNi2 and CoCrNi endpoints, charting the dissolution temperature of the ordered M2Cr phase as a function of Co content, where M is Co or Ni.
figure 6

The diagram, calculated to match experimental evidence, indicates a dissolution temperature for the equiatomic alloy that is below 673 K.

Full size image

Through this comprehensive investigation of CSRO in the CoCrNi medium entropy alloy, we have not only validated the existence and quantified CSRO within these alloys but also introduced a practical method to assess the CSRO state in materials. Although CSRO levels varied within the CoCrNi alloy, no significant impact on mechanical properties was observed. In stark contrast, the CrNi2 alloy demonstrated substantial alterations in mechanical strength and ductility due to long-range ordering. Our study enriches the current understanding of CSRO, highlighting its intricate effects on material properties. The methodology developed herein is adaptable to other alloy systems where the effects of CSRO are still being debated, offering a new avenue for research into the delicate balance between atomic ordering and alloy performance in HEAs/MEAs.

Methods

Materials and sample preparation

The CrNi2 and equiatomic CoCrNi alloys were produced by arc melting with high-purity elements (all >99.99%) in an argon atmosphere. To ensure homogeneity, each ingot was remelted five times. The chemical composition (in at.%) for the ternary alloy was 33.58% Cr, 33.28% Co, and 33.13% Ni, and for the binary alloy, it was 35.81% Cr and 64.19% Ni, measured by energy-dispersive X-ray spectroscopy (EDS) in a scanning electron microscope (SEM). Subsequently, the melted ingots were homogenized at 1473 K for 4 h, followed by water quenching. Each ingot was hot-rolled at a temperature of 1423 K until reaching a thickness of 2 mm and cold-rolled with a 50% reduction. Finally, all samples underwent total recrystallization of the cold-rolled material, achieved through additional annealing at 1273 K for 1 h, followed by rapid water quenching. After full recrystallization, aiming to promote different degrees of CSRO, the samples underwent five different aging treatments at 748 K, as detailed in Table 1.

Table 1 List of heat treatment conditions
Full size table

With the aim of evaluating the influence of heat treatments on grain growth, a quantification analysis of grain size was conducted using the linear intercept technique, following the ASTM standard34. The samples were analyzed under recrystallized and aged conditions for 240 h for both compositions. The results for the CoCrNi alloy, in the recrystallized and aged conditions, were 26.7 ± 1.9 and 28.7 ± 1.9 µm, respectively. For the CrNi2 alloy, the values were 35.8 ± 2.5 and 41.6 ± 1.5 µm under recrystallized and aged conditions, respectively.

To further understand the impact of these changes, we applied the Hall–Petch relationship to estimate the grain size contribution to yield strength of the ternary alloy. The estimated difference in yield strength due to grain size change was <5 MPa, calculated using the values of 600 MPa m0.5 from Schneider et al.35 and 653 MPa m0.5 from Lu et al.36. The observed differences in yield strength, being within the standard deviation of our measurements, indicate that the influence of grain size on mechanical properties is insignificant. Therefore, the small variations in grain size induced by the heat treatment do not significantly affect the mechanical properties.

Characterization analysis

To understand the influence of heat treatments, both alloys were analyzed by SXRD under the six thermal treatment conditions presented in Table 1, with dimensions of 7 × 4 × 1 mm³. The analyses were conducted at the DESY beamline, operating at 87.1 keV (0.142346 Å). A LaB6 standard was used to calibrate the distance between the sample and the detector, the detector tilt angle, and the position of the beam center. A Perkin-Elmer detector with a resolution of 2048 × 2048 pixels was employed for image acquisition. Data integration was performed using the PyFAI software, with 1024 points, converting to intensity vs. two-theta (2θ). The foils for TEM observations were mechanically grinded to 50 μm. Subsequently, the precision ion polishing system mode 691 by GATAN was employed in the preparation process. The thin sections within the TEM specimens utilized for the experiments had a targeted thickness of approximately 30 nm. TEM analyses were carried out on both alloys in the recrystallized and 240 h aged samples using an FEI Tecnai F20 FEG microscope operating at 200 kV.

EXAFS analysis

EXAFS analysis was conducted at the Brazilian Synchrotron Light Laboratory (LNLS) on the extreme condition beam line (EMA)37. Measurements were acquired in transmission mode using conventional ion chambers filled with optimized mixtures of He, N2, and/or Ar gases at a total pressure of 1.5 bar. This configuration aimed to achieve 10% photon absorption in the first ion chamber and 70% photon absorption in the second one. Energy calibrations were performed by measuring metallic foils of the alloy elements Co, Cr, and Ni.

Thermal properties analysis

The specific heat at constant pressure (Cp) was measured using a Netzsch-DSC404C differential DSC in the temperature range of 373–973 K for both alloys under all thermal treatment conditions presented in Table 1. The measurements were performed on samples weighing approximately 40 mg in an Ar atmosphere, with a heating rate of 10 K min−1 and a cooling rate of 40 K·min−1, with two cycles of heating and cooling. An empty platinum crucible was used as a reference baseline, and sapphire was employed as the reference material, following the international ASTM standards38. The Cp was calculated using Netzsch Proteus® software according to the method described in the literature38. The assessment of DSC precision was carried out using a potassium chromate (K2CrO4) standard. Three runs were performed, during which the enthalpy values at the exothermic peak were determined. This procedure allowed for the calculation of the error associated with the analysis. The error in the heat capacity was estimated to be ~4.3%. The complete DSC heating and cooling curves are shown in Supplementary Information Fig. 2c, d. Also, to rule out any possibility of oxidation occurring during the heating and cooling, a thermogravimetric analysis was performed in the same sample environment as the DSC tests performed in this work in a Netzsch-STA 449 Jupiter, using the same type of sample holder, crucible and gas as performed in the main DSC analysis. These results are shown in the Supplementary Information Fig. 9.

The Kissinger method was used to calculate the activation energy in the exothermic reactions obtained in the recrystallized condition for both alloys. The Kissinger equation39 is presented below as Eq. (5)

$${ln}\left(\frac{{\beta }_{k}}{{T}_{{{p}}}^{1.95}}\right)=\frac{-Q}{R{T}_{{{p}}}}+C$$
(5)

where \({\beta }_{k}\) is the heating rate, \({T}_{{\rm {p}}}\) is the peak temperature, Q is the activation energy, and C is a constant. The activation energy was obtained from the Cp curves using the slope of the ln(\({\beta }_{k}\)/\({T}_{{\rm {p}}}^{1.95}\)) vs. 1/R\({T}_{{\rm {p}}}\) graph (according to Eq. (1)). The standard deviation of the graph was also calculated.

The energies of the exothermic and endothermic reactions were determined by numerically integrating the areas under the thermal analysis curves for both samples under all thermal treatment conditions. To determine the ΔHCSRO of the aged sample with respect to the recrystallized sample, the calculations shown in Supplementary Information Fig. 6 were performed. This difference should, in principle, be estimated as the area between both curves. However, since the DSC analysis is sensitive to the initial sample geometry, the following approach was followed to minimize the error by considering the second run as a reference state for each curve, which, since has the exact same sample geometry as their respective first run, will eliminate this error. First, the difference between both curves and their respective second runs was taken, as shown in Supplementary Information Fig. 6d, then the total area between both curves was calculated for the temperature interval between 723 and 883 K, which is taken as the ΔHCSRO. As shown in the figure, these are the temperatures where both curves behave differently. The extrapolation of the experimental ΔHCSRO curve above 923 K is given in Supplementary Information Fig. 6e.

Atomistic simulations

The temperature-dependent equilibrium chemical arrangement in CoCrNi was obtained using atom-swap Monte Carlo (MC) simulations using the Metropolis-Hasting algorithm40. Following our established methodology in ref. 28, statistics were gathered from 40 independent and size-converged MC simulations with 4000 atoms of cubic FCC supercells. Starting from chemically random configurations with Cr, Co, and Ni atoms randomly assigned to the FCC lattice, we carried out 30 atom-swap attempts per atom (60,000 total attempts). These simulations were repeated from room temperature (300 K) to the melting point (1700 K) in intervals of 100 K. The employed lattice parameters are evaluated from separate molecular dynamic simulations, where a Nosé–Hoover thermostat and barostat were employed to maintain the corresponding temperature and zero hydrostatic pressure for 10,000 steps with a step size of 2.5 fs. The initial and final structure from each simulation were relaxed (i.e., energy minimization) at fixed volume before evaluating the cohesive energies of the random and thermal equilibrium states, respectively.

All simulations were performed within the LAMMPS code41 using a Moment Tensor Potential42 we previously trained using high-fidelity ab-initio databases systematically designed to capture CSRO and its effects on phase stability and other materials properties29.

DFT and CALPHAD calculations

Density functional calculations were performed on quantum Espresso software. Relaxation calculations were performed on a set of structures: FCC and BCC pure Cr, FCC and BCC pure Ni, FCC and HCP pure Co. The CrM2 phase was calculated as well with the CrCo2 and CrNi2 compositions. Before the calculations, convergence tests were made to find adequate input parameters. The converged values of the cut-off energies were 220 and 1000 Ry for all the structures. The value of k-mesh was 20 × 20 × 20 for all the cubic pure metals, and the other structures had k-mesh values of the same magnitudes.

The energy of the converged CrCo2 structure (6.44 kJ/mol) was input into the thermodynamic assessment of the Co–Cr–Ni–Al system developed by Gheno and co-workers (−7.51 kJ/mol)33. The formation energy for the CrNi2 phase was added from the assessment performed by Chan and co-workers32. The CrM2 phase was defined as a simple substitutional solid solution with M being Co or Ni.

Mechanical properties analysis using microhardness and in-situ tensile tests with synchrotron radiation

The hardness measurements were performed using a Shimadzu H100C microhardness tester, with a load of 1.96 N and a holding time of 10 s, in all sample conditions exposed in Table 1. Twelve indentations were performed in independent locations on each sample.

The tensile tests were conducted on a sample with the gauge section dimensions of 20.28 × 1.80 × 1 mm3, in both the recrystallized and 240 h aged conditions for both alloys. The data was obtained through SXRD in conjunction with in-situ tensile tests at the DESY beamline, operating at 87.1 keV (0.142346 Å). To ensure consistent deformation conditions, the experiments were conducted at a strain rate of 10−3 s−1, with XRD patterns acquired every second, enabling real-time tracking of lattice strain evolution and deformation structures during the mechanical tests. A Perkin-Elmer detector with a resolution of 2048 × 2048 pixels was used for the image acquisition, and the data integration was performed with the PyFAI Integrate software, employing 1024 points. For the analysis of dislocation density and tensile behavior, the transverse direction integration method was utilized, covering an azimuthal range of 0° ± 20°. Using a pseudo-Voigt function, the eight face-centered cubic (FCC) crystal structure peaks (111, 200, 220, 311, 222, 400, 331, 420) were precisely fitted. Moreover, instrumental broadening was effectively removed from the obtained patterns, referencing the LaB6 pattern. The subsequent implementation of the modified Williamson-Hall method involved the measurement of full width at half maximum (β) and peak position (θ) of the identified peaks. The resulting dislocation density (ρ) was plotted against strain using the slope derived from the data.