Introduction

Precise displacement measurement is crucial to modern science and technology1,2,3,4, with numerous applications in many fields such as microscopy imaging, advanced manufacturing, and gravitational wave detection. Over decades, light has emerged as a potent tool for precision displacement metrology from classical to quantum physics5,6,7,8,9,10,11 owing to its ultra-high frequencies (typically at the level of 100 THz) and diverse degrees of interaction with matters. Recent advancements in nanophotonics and micro/nano-fabrication technologies have engendered many innovative approaches for achieving precise displacement measurement, including photonic gear12,13, polarization-encoded metasurface14,15, and super-oscillatory field16. In particular, by breaking the half-wavelength diffraction limit, a displacement resolving power of over \(\lambda /800\) (λ is the operating wavelength) has been demonstrated in experiments16.

However, in some specific scenarios, such as underwater environments, biological tissues, and complex machinery components, light is not an optimal option for displacement measurements and other activities. In contrast, sound waves are highly promising for achieving this goal, owing to their high energy transfer efficiency, minimal biological loss, and excellent object penetration17. Despite these benefits, nowadays, sound waves are rarely exploited for high-resolution displacement metrology. This awkward situation is primarily caused by the lower frequency of sound waves, usually not exceeding 100 MHz, which is six orders of magnitude lower than light. It results in limited resolving power that fails to match that achievable with light. For example, conventional displacement sensors based on ultrasound pulse-echo techniques typically offer a resolution of 100 μm at 0.35 MHz, corresponding to approximately \(\lambda /10\) resolving power. While elevating the operating frequency can enhance the resolution, this straightforward approach is impeded by constraints inherent in ultrasound transducer technology and associated costs. Meanwhile, the measurement accuracy is restricted by pivotal factors18 including echo sampling rates, electronic noise, and algorithmic processing. As such, the realization of super-resolution displacement measurement within the acoustic community remains a fundamentally challenging pursuit.

Here, we introduce an innovative method for acoustic displacement metrology that enables super-resolution measurements at low-frequency sound waves, achieved through the creation of topological pairs (TPs) in orbital meta-atoms. The concept of TPs is inspired by the Cooper pairs19 in spinful electrons that enable the development of superconducting quantum interference devices for precise magnetic field measurements20. The orbital meta-atom is engineered by artificial microstructures21,22,23 to carry two opposite orbital angular momentum (OAM) modes. We showcase that TPs are conjugately formed to generate robust interference through twisting orbital meta-atoms, physically ensured by geometric phases24,25,26 of two distinct transport pathways in mode space. Consequently, an acoustic analogue of Malus’s law is revealed to realize acoustic displacement metrology. By incorporating the configuration of screw threads in orbital meta-atoms, we design an acoustic prototype of a physical micrometer to demonstrate micron-scale displacement metrology, where displacement information is directly encoded in interference intensity. We further demonstrate experimentally an acoustic micrometer that enables a displacement resolving power of 1.2 μm at an audible frequency of 3.43 kHz, which is approximately \(\lambda /{10}^{5}\), a remarkable super-resolution more superior than state-of-the-art optical methods14,15,16. This TP-mediated mechanism significantly enhances the displacement resolution without breaking the diffraction limit or relying on deep-learning techniques and nonlinear effects27,28,29,30, while possessing superior features of simple structure, high efficiency and low cost. As the quantity of the topological charge is unlimited, the displacement resolution determined by the pitch and topological charge can theoretically reach infinity. Our work presents a novel approach to super-resolution displacement measurement and paves the way for ultra-sensitive angle and displacement metrology applications in acoustics.

Results

Model and theory of topological pairs

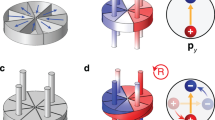
The orbital meta-atom is engineered by q groups of periodically angular supercells constituted by phase elements of “0” and “π”, enabling opposite and orthogonal OAM modes ±q (see Fig. 1a), where q is the topological charge. Empowered by the near-field coupling, these OAM modes across two meta-atoms are paired to form four TPs in general, i.e., (+q, −q), (−q, +q), (+q, +q), and (−q, −q). Like Cooper pairs with zero total spin, the first two TPs have total orbital charge of zero and are conjugate in mode space (see Fig. 1a), i.e., TP (+q, −q) and TP* (−q, +q). Meanwhile, the last two TPs exhibit total charge of ±2q. When two meta-atoms are loaded in a cylindrical waveguide (see Fig. 1b), TPs of ±2q are naturally excluded due to the subwavelength waveguide of \(R \, \ll \, \lambda\) (λ is the operating wavelength of the meta-atom) allowing only the plane wave of \(q=0\) inside it. Notably, a single meta-atom cannot support wave transport because the waveguide also forbids the OAM propagation of ±q, while two coupled meta-atoms can offer transport channels via TPs, exhibiting effects similar to those enabled by Cooper pairs in the superconductivity.

Fig. 1: Concept of TPs using orbital meta-atoms and the resulting interference effect in analogy with Malus’s law.
figure 1

a Schematic diagram of two orbital meta-atoms (left) carrying topological charges ±q, which are paired to form the conjugate TPs (right) in mode space, i.e., TP: (+q, −q) and TP* (−q, +q), where the total OAM is zero. b Illustration of the evolution process of incident plane wave passing through two orbital meta-atoms in a cylindrical waveguide, where it is gradually converted to conjugate OAM waves and then transformed back to the plane wave (see the inset). The outgoing plane waves (red and blue colors) are from two distinct routes in mode space enabled by the conjugate TPs. c By twisting one of two meta-atoms with angle of θ, such two kinds of outgoing plane waves can experience geometric phases of \({\varphi }_{{{\rm{g}}}}^{\pm}=\pm q\theta\) via conjugate TPs, enabling the generation of acoustic interference.

Full size image

Provided that a plane wave passes through these two meta-atoms, it is gradually converted to OAM modes of ±q and then transformed back to the plane wave in real space (see the inset in Fig. 1b), governed by time-reversal symmetry. This macroscopic process can be divided into two transport routes enabled by the conjugate TPs. Therefore, the outgoing plane waves are a superposition of two outputs from two distinct routes, as schematically indicated by the red and blue planes in Fig. 1b. If there is no relative variation between two meta-atoms, such two outputs are aligned with each other. However, by twisting one of the meta-atoms (e.g., the right one) with an angle θ, these two output plane waves will undergo additional geometric phases of \({\varphi }_{{{\rm{g}}}}^{\pm}=\pm q\theta\), resulting from the cyclic evolution of OAM transformation in mode space25. A phase difference \(\Delta {\varphi }_{{{{\rm{g}}}}}=2q\theta\) occurs (see Fig. 1c) and leads to an interference effect in analogy with the Malus’s law (see Supplementary Note 1), with the output intensity I given as,

$$I={\left|\frac{A}{2}{e}^{i({\varphi }_{{\rm{s}}}+{\varphi }_{{\rm{g}}}^{+})}+\frac{A}{2}{e}^{i({\varphi }_{{\rm{s}}}+{\varphi }_{{\rm{g}}}^{-})}\right|}^{2}={A}^{2}{(\cos q\theta )}^{2}={I}_{{{\max}}}\cdot \left(\frac{1+\,\cos 2q\theta }{2}\right),$$
(1)

where \({\varphi }_{{{{\rm{s}}}}}\) denotes the spatial phase, A is the initial amplitude of an incident wave, and \({I}_{\max }={A}^{2}\) represents the maximal output. Equation (1) provides a new way to achieve intrinsic q-fold augmentation of the angular resolution beyond the limitations of spin-orbital interaction12, where auxiliary optical components (e.g., wave plates and polarizers) cannot be avoided so that the whole system is still bulky even using the state-of-the-art platform of metasurfaces.

Experiments for acoustic analogue of Malus’s law

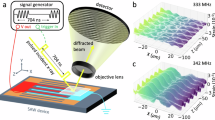
To verify the theory, two meta-atoms with thicknesses of \(h=0.5\lambda\) are placed in a tube with \(R=0.25\lambda\), where \(\lambda=100\ {{{\rm{mm}}}}\) is considered. Five cases of meta-atoms with \(q=1\) to 5 are performed by full-wave simulations (see Supplementary Note 2), which agree with the theoretical predictions via Eq. (1). Experimental investigations are proceeded by designing two phase units of “0” and “π” presented in Fig. 2a. Both units have angle widths of 45°. The unit “0” is an empty structure filled with air whereas the unit “π” is designed by a common metamaterial structure (see Supplementary Note 3). These two units are arranged into a supercell, and q groups of supercells constitute an orbital meta-atom. As the unit “π” is a resonant structure, the unit transmission and phase difference of π within the meta-atom have narrow frequency bands. As a result, this acoustic like Malus’s law can work at a relatively tight frequency range (see Supplementary Note 3). Here, two types of orbital meta-atoms with \(q=2\) and \(q=4\) are designed and fabricated using 3D printing with commercial photopolymer materials, as depicted in Fig. 2b, c. The experimental setup, primarily consisting of four modules: an impendence tube, four microphones, the meta-atom sample, and data acquisition system, is exhibited in Fig. 2d (Methods). In experiments, meta-atoms are placed closely and connected to both sides of the impendence tube with \(R=25\ {{{\rm{mm}}}}\). As the samples have a large size, mark scales with 5-degree interval are involved at the edge for controlling the twist angle (see Supplementary Note 4). Microphones are used to detect the acoustic pressure fields, which are received by data acquisition system to calculate the transmission intensity. Experimental results are shown in Fig. 2e, f, respectively for the cases of \(q=2\) and \(q=4\). The interference effect of the transmitted wave can be evidently observed, holding an oscillation period of π/q with the twist angle θ, which coincides with the theoretical results. This oscillation period proves that the angular resolution takes a q-fold magnification, making it promising for angular displacement metrology.

Fig. 2: Experimental demonstration of acoustic analogue of Malus’s law through orbital meta-atoms.
figure 2

a Topography of designed phase units of “0” and “π”. b, c Fabricated samples comprised of two orbital meta-atoms with \(q=2\) (b) and \(q=4\) (c). d Setup for interference measurement. e, f Measured (red balls) and theoretical (solid curves) acoustic intensity for the samples of \(q=2\) (e) and \(q=4\) (f). The error bars are the standard deviation of three measurements.

Full size image

Acoustic micrometer for micron-scale displacement metrology

Using orbital meta-atoms, the acoustic interferometer with q-fold magnification can be a superior tool for acoustic displacement metrology. As presented in Fig. 3a, a physical micrometer is implemented by the spiral twist of an external mechanical knob to achieve accurate displacement metrology based on the principle of spiral amplification. Inspired by that, we propose an acoustic micrometer, implemented by the spiral twist meta-atoms (Fig. 3b), to realize micron-scale displacement metrology. Two orbital meta-atoms are loaded with mutually matched screw threads with a pitch of d. When the twist angle θ is operated, a spiral twist displacement is generated, i.e.,

$$\Delta d=\theta d/2{{{\rm{\pi }}}}.$$
(2)
Fig. 3: Design and demonstration of the acoustic micrometer using spiral twist meta-atoms.
figure 3

a A physical micrometer through spiral twist of a mechanical knob. b An acoustic micrometer designed by the spiral twist meta-atoms loaded with screw threads with a pitch of d, where an interference intensity is regarded as a displacement mark. c Interference intensity versus the spiral twist displacement for the acoustic micrometer (q = 4) with d = 3 mm, 10 mm and 16 mm, where the relevant results of experiments (red balls), the ideal theory (black solid curves), the coupled-mode theory (dot curves) involving the phase distortion and practical losses in meta-atoms, and the fitting results using Eq. (3) (dash dot curves) are respectively shown in each case. The stable region (shaded area ranging from 0 to π/8) in all cases is selected as the available measurement range for the acoustic micrometer. The error bars are the standard deviation of three measurements. d Scaling formula of the acoustic micrometer (q = 4 and d = 16 mm) using logarithmically fitting (solid curve) on experimental data (red balls), which is used for micron-scale displacement metrology. The error bars are the standard deviation of one hundred measurements.

Full size image

In this way, the twisted meta-atom serves as a conventional knob, and the displacement information is encoded in the scale of interference intensity, referring to Eq. (1). Notably, the spiral twist displacement will exert an impact on the interference, as the OAM modes of ±q are evanescent waves. The growth of ∆d will reduce the coupling of two meta-atoms. Accordingly, a decay factor \({e}^{-\alpha \Delta d}\) should be considered in Eq. (1), where α is attenuation constant of the OAM waves. As a result, the effective measurement range of the acoustic micrometer should be confirmed. To portray experimentally this range, the meta-atoms with q = 4 are selected to fabricate three prototypes with different screw pitches of d = 3 mm, 10 mm, and 16 mm, and mark scales with 1.5-degree interval on these samples are designed for the twist angle control (see Supplementary Note 4). As demonstrated in Fig. 3c, the measured results match the theoretical values in the initial twist region from 0 to π/8 (see the shaded areas), while they gradually deviate with each other as the longitudinal displacement continues to rise. In fact, this discrepancy mainly results from a slight phase distortion in meta-atoms due to the inevitable losses in metamaterial units and a larger loss from viscous, thermal dissipations in the air gap enabled by the longitudinal displacement.

To confirm this claim, the coupled-mode theory is developed to analytically study the acoustic micrometer (see Supplementary Note 5). By considering empirical values for the phase distortion in the meta-atoms and acoustic losses in the air gap, the analytical results (dot curves in Fig. 3c) agree with the experimental results. Accordingly, Eq. (1) ranging from 0 to π/8 is modified as:

$$I=\frac{{I}_{{{\max}}}}{2}\left[1+\,\cos \left(\eta \cdot \frac{4q\pi }{d}\right)\right]\cdot {e}^{-\gamma \varDelta d},$$
(3)

where η is the phase distortion coefficient of the phase unit of “π” (\(\eta=1\) denotes a perfect “π” unit) and γ denotes the total damping rate in the air gap. By choosing appropriate parameters for η and γ (see Supplementary Note 5), the experimental results in measurement range are fitted by Eq. (3), as indicated by the dashed dot curves in Fig. 3c. In addition, Eq. (3) reveals that these two factors, for a small twist, have little influence on the interference. In contrast, they are gradually enlarged along with the growth of the twist displacement so that the interference feature vanishes. Based on the above discussions, the twist region from 0 to π/8 maintains a stable tendency of the interference feature in all cases, offering a robust measurement range for the acoustic micrometer.

We use the acoustic micrometer with d = 16 mm to demonstrate the micron-scale displacement metrology. The interference intensity from the sample is recorded at a twist interval of 1.5 degrees, whose precision is improved by averaging the measured values of 100 times, and this mean value can be regarded as a “mark” of the acoustic micrometer. Utilizing these marks, a relevant displacement scaling function can be derived from the numerical fitting, as an analytic formula even using Eq. (3) is not available. A logarithmic expression Δd = a + bln(I + c) is employed for the scaling formula, where a, b and c are fitting constants (see Supplementary Note 6), and a favorable fitting result is presented in Fig. 3d. This formula is an overall expression over the whole measurement range, which is used for detecting major displacements. According to this formula, the associated displacement can be directly read out from the interference intensity. To evaluate its practical capability, we twist the acoustic micrometer randomly to four different positions (P1 to P4). In each case, the interference intensity is measured repeatedly to obtain the displacement information. As illustrated in Table 1, the measured displacements via the acoustic micrometer are matched with those measured by a physical micrometer (see Supplementary Note 6), with the maximal error among these results being 0.2%, implying that the acoustic micrometer has a superior performance in practical applications.

Table 1 Displacement measurements of four random positions using acoustic micrometer
Full size table

The acoustic micrometer can be applied to the precise measurement of tiny displacements. To quantify the sensitivity, the absolute value of the slope of the interference curve is employed. The sensitivity in the ideal case of Eq. (1) is expressed as \(s=|\frac{\partial I}{\partial (\varDelta d)}|=\frac{2q\pi }{d}\,\sin (\frac{4q\pi }{d}\cdot \varDelta d)\), reaching the maximal value \({s}_{\max }=\frac{2q\pi }{d}\) at the position \(\Delta {d}_{{\rm{opt}}}=\frac{d}{8q}\). In practice, the loss and the phase distortion in the acoustic micrometer can force this position to drift away, thus changing the optimal sensitivity. Based on Eq. (3), the actual position of the maximal sensitivity is calculated as,

$$\Delta {d}_{{{{\rm{opt}}}}}^{{\prime} }=\frac{1}{\xi }\cdot \arccos \left(\xi \cdot \frac{\sqrt{2}\gamma+2\sqrt{{\gamma }^{2}+2{\xi }^{2}}}{{\gamma }^{2}+4{\xi }^{2}}\right),$$
(4)

and the maximal sensitivity is derived as,

$${s}_{\max }^{{\prime} }\approx \sqrt{2}\, \xi \left(1-\gamma \Delta {d}_{{{{\rm{opt}}}}}^{{\prime} }\right)\cdot \cos \left(\xi \Delta {d}_{{{{\rm{opt}}}}}^{{\prime} }\right),$$
(5)

where \(\xi=\frac{2\eta q\rm\pi }{d}\). According to Eqs. (4, 5), a linear region around \(\Delta {d}_{{{{\rm{opt}}}}}^{{\prime} }\) is available to realize the precision measurement. Moreover, \({s}_{\max }^{{\prime} }\) can be rewritten as \(\sqrt{2}\eta (1-\gamma \Delta {d}_{{{{\rm{opt}}}}}^{{\prime} })\cdot \cos (\xi \Delta {d}_{{{{\rm{opt}}}}}^{{\prime} })\cdot {s}_{\max }\), from which a loss-enhanced sensitivity is uncovered. In general, losses imply a sacrifice in the device performance, which is undesired yet inevitable, but here it is beneficial for improving the sensitivity. In our case, the loss varies with the twist displacement, producing an inhomogeneous loss distribution. This non-uniformity could compress the interference curve to be narrower, so that the ideal position \(\Delta {d}_{{{{\rm{opt}}}}}\) shifts to the starting point of the curve, thus enabling the enlargement of smax. From Eq. (5), the loss-enhanced sensitivity has an upper limit value of \(\sqrt{2}\) when \({\Delta d}_{{{{\rm{opt}}}}}^{{\prime} }\to 0\).

Based on Eqs. (4, 5), \({s}_{\max }^{{\prime} }\) for these samples of d = 3 mm, 10 mm, and 16 mm in Fig. 3c are 9.53 × 10−3 μm−1, 2.99 × 10−3 μm−1, and 2.20 × 10−3 μm−1 in theory, respectively (see Supplementary Note 7). Experimental results of the corresponding linear regions are shown in Fig. 4a–c, where the measured sensitivities by the linear fittings are 9.68 × 10−3 μm−1, 3.03 × 10−3 μm−1, and 2.29 × 10−3 μm−1, which are consistent with the theoretical ones. The loss-enhanced value of the sensitivity is about 1.2, which is lower than the upper limit due to a nonzero \(\Delta {d}_{{{{\rm{opt}}}}}^{{\prime} }\). A general description for \({s}_{\max }^{{\prime} }\) is given as \({s}_{\max }^{{\prime} }\cdot d\propto 2\sqrt{2}q\pi\), which indicates that these two independent degrees of freedom (q and d) in the acoustic micrometer offer great flexibility in promoting the sensitivity. Among these samples, the sensitivity of the acoustic micrometer with d = 3 mm is larger due to its shorter screw pitch. We use it to reveal the displacement resolution of the acoustic micrometer for precision measurements. Within the corresponding linear region (Fig. 4a), we select an initial position around the point denoted with a dashed box. Next, the meta-atom is slightly twisted to a new position where the associated interference intensity is changed. In virtue of the variation of intensities between these two positions, the twist displacement can be directly obtained based on the sensitivity illustrated in Fig. 4a. To eliminate the random errors referring to the irregular fluctuations in experimental measurements, the statistical average over repeated measurements is adopted, thereby reducing standard deviations to enhance the measuring precision.

Fig. 4: Resolution and precision of the acoustic micrometer.
figure 4

a-c Based on the experiments (red balls), linear regions with fitting slopes of 9.68 × 10−3 μm−1 (violet solid line), 3.03 × 10−3 μm−1 (gold solid line), and 2.29 × 10−3 μm−1 (blue solid line), respectively for acoustic micrometers (q = 4) with d = 3 mm (a), 10 mm (b), and 16 mm (c). The error bars are the standard deviation of three measurements. d–f The statistical analysis with 100 times measurements by use of the sample with d = 3 mm, depicting the displacements at two distinct positions. (d), Highly resolvable displacement of 7.5 μm with a precision of 0.5 μm. (e), Critically resolvable displacement of 1.2 μm with a precision of 0.2 μm. (f), Indistinguishable displacement of 0.3 μm with a precision of 0.1 μm.

Full size image

We repeatedly measure these two positions for 100 times by recording the interference intensities. Figure 4d showcases the corresponding histograms depicting the normalized intensity distributions at two distinct positions. Each histogram is fitted with a Gaussian function, revealing a prominent displacement of 7.5 μm between these two discernible peaks. This Gaussian fitting curve is also used to estimate the measurement precision of the acoustic micrometer by employing the error transfer function (see Supplementary Note 7). The estimated error for the measurements in Fig. 4d is calculated as σ = 0.5 μm. For a diminished displacement in Fig. 4e, the distinction between the two positions approaches a just distinguishable level, which is defined by that the peak of one histogram locates at the boundary of full width at half-maximum of the other one. In this case, a displacement of 1.2 μm with an estimated error σ = 0.2 μm is identified, signifying a remarkable resolving capability of almost \(\lambda /{10}^{5}\). As the displacement is further minimized to be 0.3 μm, the two positions in Fig. 4f become less pronounced together with a percentage error of approximately 33.3%. We argue that the resolution in Fig. 4e represents the upper limit of the resolving ability, whereas by fabricating acoustic micrometers with smaller d and higher q, more superior resolution that could be infinity in theory can be attained.

Discussion

As the presented acoustic micrometer is devised by orbital meta-atoms at subwavelength scale, it may have a limited linear region and the intrinsic ‘dead region’ due to the near-field coupling of evanescent OAM waves. In general, it is challenging for a precision measurement to simultaneously achieve high sensitivity and a wide measurement range31. For the acoustic micrometer with a fixed q, a shorter d leads to a higher sensitivity, yet bringing about a limited measurement range. In practical scenarios, d can be customized to balance these two key factors. However, by designing orbital meta-atoms that support propagating OAM modes in the waveguide32, TPs releasing from the near-field coupling can achieve a robust interference effect in the whole spiral-twist process, leading to multiple linear regions ranging from 0 to 2π. A long-range linear measurement with a high sensitivity14 could be realized by stitching these linear regions covering the full measurement cycle.

To summarize, we have demonstrated a novel acoustic displacement metrology technique using the concept of TPs within orbital meta-atoms. By leveraging the acoustic analogue of Malus’s law, this approach can produce an ultrahigh displacement resolution. As a proof of concept, we have designed and experimentally tested an acoustic micrometer capable of measuring micron-scale displacements at 3.43 kHz. A super-resolution of the displacement measurements around \(\lambda /{10}^{5}\) has been observed. By increasing the topological charge and reducing the screw pitch of the acoustic micrometer, the resolution can be further promoted and even infinite in theory. Notably, our approach offers several competitive advantages, including simple design, compact size, low cost, and high stability. These characteristics facilitate easy device fabrication and integration at ultrasound frequencies, enabling the implementation of acoustic displacement metrology in some ultrasound applications such as non-destructive testing, precision manufacturing, and biological monitoring. Moreover, the proposed concept of TPs holds potential beyond acoustics and can be applied in classical wave systems, presenting significant opportunities for developing metrological techniques in other fields, such as optics, cold atomic systems, and quantum information. We anticipate that this protocol may serve as a promising platform for further exploration of intriguing wave physics, advanced metrology techniques, and ultrasensitive sensing applications.

Methods

Numerical simulations

The pressure acoustics module in COMSOL is utilized for the full-wave simulations. The meta-atoms are put in the center of a cylindrical waveguide, and the boundaries between air and solid artificial structures are considered as the sound-hard boundary. The port settings are employed to generate plane waves in the waveguide, detecting their reflection and transmission coefficients. In addition, the coupled-mode theory is developed to analytically study the interference effect with the spiral twist. More details related to the coupled-mode theory can be found in Supplementary Note 5.

Experiments

The samples are fabricated by use of 3D printing with a commercial photopolymer material (Wenext 8200Pro). The complete testing process is carried out in the SAC-ZK100/29 impedance tube that is manufactured by Beijing Sheng An Chuang Technology Co., Ltd. Initially, white noise signals are generated via the NI USB-4431 and then it is delivered to a loudspeaker inside the impedance tube via a Yamaha PX3 power amplifier. The sound pressure signals within the impedance tube are captured by four SCA-4450 microphones and subsequently collected by the NI USB-4431 for computer-based analysis. All the testing and data processing procedures comply with the American standard of ASTM E2611-09. When samples are put into the impedance tube, the data acquisition system can automatically proceed the accurate and reliable analysis to transmitted sound signals, further giving the associated interference intensity after each twist operation.