Abstract
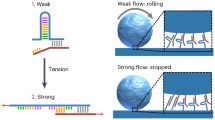
Unlike most adhesive bonds, biological catch bonds strengthen with increased tension. This characteristic is essential to specific receptor-ligand interactions, underpinning biological adhesion dynamics, cell communication, and mechanosensing. While artificial catch bonds have been conceived, the tunability of their catch behaviour is limited. Here, we present the fish-hook, a rationally designed DNA catch bond that can be finely adjusted to a wide range of catch behaviours. We develop models to design these DNA structures and experimentally validate different catch behaviours by single-molecule force spectroscopy. The fish-hook architecture supports a vast sequence-dependent behaviour space, making it a valuable tool for reprogramming biological interactions and engineering force-strengthening materials.
Similar content being viewed by others
Introduction
Cells communicate mechanically by applying tension across cell-cell and cell-environment adhesions1,2,3,4,5. The transduction of specific signals across these adhesive junctions relies on the force-dependent behaviour of the receptors and ligands. Many biochemical pathways activate as a response to external force, and the degree of this activation can vary depending on the magnitude, direction, loading period, and loading rate of mechanical strain. For example, T-cell receptor (TCR) specificity between agonists and antagonists is enhanced 4-fold when tension is applied6, focal adhesion maturation is mediated by sustained high forces and fast loading rates7, cell polarization during migration is determined by direction-dependent tension between vinculin and actin8, and E. coli avoids being flushed out by the high shear stress of urinal and intestinal tracts while retaining mobility under low shear stress9. In all these cases, measuring the dissociation constant (Kd) or lifetime in a zero-force environment (τ0) is not enough to see the full scale of biologically relevant behaviours.
In a purely hypothetical space, there are three adhesion responses to increasing force—the slip bond, which weakens (force-dependent lifetime (τF) decreases); the catch bond, which strengthens (τF increases); and the ideal bond, which is insensitive to force (τF remains constant). Given that all covalent and hydrogen bonds are slip bonds individually10, one might assume that adhesive interactions that involve a number of these slip bonds in different geometries—as is the case with receptor-ligand interactions – would also result in slip bonds, albeit with a higher τ0. However, this is not always the case. In biology, proteins demonstrate a colourful array of multi-phasic τF, including biphasic catch-slip8,9,11,12,13,14,15,16,17,18,19 and triphasic slip-ideal-slip20 or slip-catch-slip13,21 bonds. The counter-intuitive catch behaviour is vital to many cellular functions and biological behaviours. For instance, the catch bond behaviour in TCR interactions is essential in tuning their specificity, making them more sensitive to antigens presented on sessile, tension-producing cells than the unbound ones. Cells that function in environments with fluid shear, such as E. coli in the intestine and neutrophils in the bloodstream22, rely exclusively on catch bonds to facilitate rolling adhesion motility across a large range of external forces. Cell-matrix adhesion and mechanosensing involve focal adhesion proteins like integrins and vinculin, both of which exhibit catch bond character: Integrins enhance their substrate binding through a force-dependent conformation change and vinculin binds to actin in a direction-dependent catch bond3,8,13. Similarly, cadherins and downstream mechanotransduction proteins such as catenins require catch behaviour to regulate cell-cell communication and maintain tissue integrity11,23. Overall, catch bonds play a pivotal role in cell adhesion, motility, mechanosensing, communication, and organization across a wide spectrum of biological contexts.
Biological systems have evolved catch bond behaviours as adaptive solutions to many challenges, employing a variety of mechanisms9,24,25,26,27,28,29,30. Given their biological importance, designs for artificial catch bonds have been put forward in an effort to expand our molecular toolbox10,31,32,33,34,35,36,37. To create a framework for thinking about artificial catch bond designs, two very similar base-principle models were conceptualized in parallel – one from a synthetic chemistry perspective10, and one from a biomolecular perspective31. While these architectures were purely theoretical, they cemented a series of guiding principles which subsequent work32,33,35 relied upon: i.e. the interactions must have a weak state Sw, a strong state Ss, and a force-dependent interconversion between the two that biases the Sw at low force and Ss at high force12,24,38. These designs pull directly from the two-state, two-pathway model, one of the simplest theories that fit experimental data (the other being the one-state, two-pathway model) among many ways to model biological catch behaviour12,15,39,40,41.
Small-molecule mechanophores exhibiting catch bond behaviour were created by using force-dependent molecular geometry to change the impact of work on the scission point36,37. While applicable to creating self-protecting materials, breaking covalent bonds occurs at forces on the nano-Newton scale. In contrast, molecular forces in biology occur on the pico-Newton (pN) scale. Using similar principles, a protein-based artificial catch bond was created34. A protein-ligand complex (Dockerin G:Cohesin E) with two native unbinding pathways was pulled from different non-native anchor points, of which one combination produced catch behaviour. While more biologically relevant, the design methodology would only work under specific circumstances: the initial protein-ligand complex must have two existing unbinding pathways, with no predictability of whether different pulling geometry will produce catch behaviour. Around the same time as this work, a DNA-based catch bond was also created using a cryptic binding site hidden in a force-unfoldable DNA hairpin called the barrier35. While the authors showed that the barrier length can alter the catch behaviour, they stated that the tunability of the design is relatively limited due to high sensitivity to the barrier length. Given these advancements in catch bond design, it is clear that a tunable catch bond architecture that enables a variety of catch behaviours within a biologically relevant range is needed.
In this work, we present the fish-hook architecture, a highly tunable DNA catch bond. We show the conceptual design, probe the catch behaviour with single-molecule force spectroscopy (SMFS), and demonstrate its wide range of tunability both experimentally and through analytical simulation.
Results
Conceptual design of a DNA catch bond
To create a catch bond, our strategy is to design a DNA construct with two dissociation pathways of distinct mechanical strengths. By biasing towards the weak pathway at low force and the strong pathway at high force, we can effectively create the catch behaviour. To do so, we designed a force-switchable structure with two rupturable domains, nicknamed the hook and the jaw (Fig. 1a). When force is initially applied at the two points, both the hook and jaw are in the unzipping geometry and compete to unbind. If the hook opens first, the closed jaw locks it in the weak unzipping geometry. On the other hand, if the jaw opens first, the hook converts to the stronger shearing geometry. We have accomplished our goal if we can predictably control which of the two pathways is active by force. Our previous work demonstrated that the unzipping of two DNA placed in series can be preferentially controlled by force and sequence (Supplementary Fig. 1)42. Thus, we designed the jaw and hook sequences such that the τF of jaw unzipping is higher than hook unzipping at low force and vice versa at high force, intersecting each other at a crossover force (Fc) (Fig. 1b). The differential unzipping τF ensures that the hook is more likely to open at F < Fc. In contrast, the jaw is more likely to open at F > Fc, effectively creating a force-dependent bias towards the weak and strong pathways around Fc (Fig. 1c). Given that the ultimate hook dissociation in the weak and strong pathways are unzipping and shearing, respectively, the switching from the weak pathway to the strong pathway as force increases will effectively create a slip-catch-slip behaviour (Fig. 1d).
a Schematic of a two-state mechanism that allows the DNA construct to dissociate via two pathways directed by force above or below a crossover force (Fc). In the weak pathway, the closed jaw locks the hook in the unzipping geometry. In the strong pathway, the open jaw switches the hook to the shearing geometry. b The lifetimes (τF) of the hook unzipping and jaw opening are designed to intersect, enabling force-dependent pathway selection. c Below Fc, the construct follows the weak pathway, as the jaw remains closed, and thus the hook unzips. Above Fc, the jaw opens before the hook, steering the construct into the strong pathway, thereby increasing the proportion of constructs with an open jaw (Pjaw-open) as force escalates. d As the force increases, the transition from the hook unzipping to shearing creates a slip-catch-slip behaviour. e Slip bonds are characterized by a unimodal rupture force probability density function (PDF) at a specific loading rate. f In contrast, catch bonds exhibit a bimodal rupture force PDF (catch-slip-catch shown here). Here, the high rupture force population (red) corresponds to high-force slip behaviour and the low rupture force population (green) arises from the catch behaviour. For comparison, a slip-only PDF is represented by a grey dashed line. The catch behaviour shifts subpopulations from high-force to low-force ruptures (grey arrows). g Additionally, the fraction of high rupture force in the bimodal distribution increases with force ramp speed or loading rate.
Relating our system to the two-state, two-pathway model, the weak, closed-jaw conformation is Sw, while the strong, open-jaw conformation is Ss. The conversion rates between Sw and Ss are the unbinding and rebinding rates of the jaw hairpin, which are slow due to the large loop. This slow conversion rate is characteristic of the two-state model and is necessary to explain the catch-slip behaviour of FimH/mannose24, vinculin/F-actin8, and cadherins in the X-dimer configuration11. At faster conversions, the two-state model collapses to the one-state model12, which assumes a single bound state with two competing unbinding pathways12,15,39,41. The survival probabilities predicted from the one-state model fit catch-slip data collected from P- and L-selectins/PSGL-112,15 and myosin/actin43. This general framework for building an artificial catch bond aligns with the guiding principles described earlier10,31,32,33.
The force-dependent dissociation of interactions can be experimentally examined by SMFS. The rupture force distributions in a force ramp experiment provide the mechanical signatures of the bond characteristics. For a slip bond, the dissociation probability monotonically increases with force over time until the cumulative dissociation probability approaches 1, leading to a unimodal rupture force distribution (Fig. 1e). However, for a slip-catch-slip bond, the local minimum in τF creates a local maximum in dissociation probability, resulting in an additional peak in the rupture force distribution. This bimodal distribution is the first signature of a catch bond (Fig. 1f). Additionally, the force ramp speed controls the population ratio of the bimodal rupture force distribution, with higher ramp speed biasing towards more high-force ruptures (Fig. 1g). This force-dependent ratio of the two rupture force populations is a second signature of a catch bond.
Characterization of the DNA catch bond by SMFS
To implement the above strategy, we created a fish and a hook, two DNA pieces that act as receptors and ligands in this artificial catch bond. In our dual trap optical tweezers experiment, the hook was bound to one bead and the fish to the other (Fig. 2a). With this configuration, we began an approach-dwell-retract fishing pattern where the fish bead would approach the hook, dwell for a few seconds, and then retract. The fish contains a closed jaw and a single-stranded region complementary to the hook (Fig. 2a, b – regrettably, the jaw does not bite the hook). In order to show the two signatures of a catch bond (Fig. 1f, g), we designed the hook and jaw sequences by considering the ramp speed limits of our optical tweezers (max 2000 nm s−1). We used an analytical model to find τF for sequences of various lengths and CG contents, and then used Monte Carlo simulations that emulate our pulling experiments to find a set of sequence parameters that would show a clear shift towards high-force rupture population at our available ramp speeds. Further details about the model and simulation can be found in the Methods section. The construct we selected has a jaw length of 18 base pairs (bp), of which 8 are C/G (jaw 8/18); and a hook length of 9 bp, of which all 9 are C/G (hook 9/9). (Fig. 2b) This construct is predicted via the analytical model to have the slip-catch-slip τF shown in Fig. 2d with an Fc of 12.6 pN. To ensure the jaw can open fully, the loop must be at least as long as the two jaw strands combined; in our case, our jaw was 18 bp long, so the loop must be at least 36 nucleotides (nt) (Fig. 2b). We designed the poly-T section of the loop to be 42 nt long as an extra precaution.
a Schematic representation of the dual-trap optical tweezers experiment. The hook is attached to bead A, and the fish is attached to bead B via DNA handles of 2633 and 272 bp, respectively. Both handles are attached to the beads by a biotin-streptavidin linkage on the 5′ end of each handle (top inset). Bead B undergoes an oscillatory motion with a dwell period before retraction (bottom inset) to increase the fishing success rate (binding between the hook and the fish). b The construct sequence. A 9-mer polyethylene glycol (PEG) linker attaches the hook to its DNA handle to minimize nonspecific base interactions with the fish and increase flexibility. c Schematic showing the weak and strong pathways. d The expected τF of the selected construct sequence based on our analytical model, showing the overall expected slip-catch-slip behaviour resulting from transitioning from hook unzipping to hook shearing around the intersection of the jaw opening and the hook unzipping τF at Fc = 13.6 pN. The anticipated force-extension curves differ for the weak (e) and strong (f) pathways, as predicted by the extensible worm-like chain model (XWLC). In the weak pathway, we expect a singular low-force rupture event indicative of hook unzipping (e). In the strong pathway, we expect a jaw-opening transition preceding a high-force rupture event corresponding to hook shearing (f).
Once the hook successfully catches the fish, it will unbind via one of the two pathways (Fig. 2c). In the weak pathway (F < Fc), the hook unzips first, leaving a low rupture force signature characteristic of DNA unzipping (Fig. 2e). Conversely, in the strong pathway (F > Fc), the jaw opens before the hook unbinds, creating an unfolding event with a change in contour length (ΔLc) corresponding to the loop size. As the force continues to increase, the hook, now in the shearing geometry, will eventually rupture at a much higher force (Fig. 2f). The two pathways can be clearly distinguished by examining their force-extension signatures. If the system undergoes the weak pathway, the fish remains folded in the original conformation with its jaw closed. If the system undergoes the strong pathway, the jaw will remain open until the hook unbinds but will refold and revert to its initial jaw-closed conformation. Hence, the fish-hook catch interaction can be indefinitely repeated.
In the fishing experiment, we pulled every tether until it broke to ensure both a single tether interaction and a new fish-hook pair formed each time. The force-extension curves showed two distinct behaviours: a population of curves that break at low forces (10–15 pN), corresponding to hook unzipping in the weak pathway (Fig. 3a, blue traces), and another population of curves that break at high forces (30–50 pN), corresponding to hook shearing in the strong pathway (Fig. 3a, red traces). The latter is always accompanied by an additional low force (10–15 pN) unfolding event prior to rupture with a contour length difference (ΔLc) of 20.4 ± 0.3 nm, which is in excellent agreement with the theoretical ΔLc of 20.2 nm (Fig. 3b) of the jaw-opening event in the strong pathway. Additionally, the force-extension curves of the weak pathway align with the pre-rupture portion of the strong pathway, indicating both are in the jaw-closed conformation. This evidence demonstrates that the fish-hook system exhibits the two designed pathways. We used an approach-dwell-retract fishing pattern to maximize the likelihood of catching a fish on any given approach (Fig. 2a, inset). The dwell time of ~8 s allowed the 9 bp hook to find a fish reliably while also allowing any fish with open jaws from the previous pull to close their jaws, preventing any history-dependent behaviour. We tested multiple beads in multiple samples for each experimental condition.
a Experimental force-extension curves in chronological order from a medium ramp experiment, showing non-history dependent switching between strong (red) and weak (blue) rupture events for the hook9/9-jaw 8/18 construct shown in Fig. 2b. Traces end when the hook unbinds. Fishing attempts that do not yield single tethers are not shown. b The same force-extension curves in (A), but with theoretical worm-like chain curves overlaid for the two possible states (dashed lines). The distribution of ΔLc (inset) from all medium pulls with a jaw opening event, as compared with the theoretical ΔLc of 20.20 nm. c Rupture force distributions at three pulling rates compared to the Monte-Carlo simulation. The slow pulling rate has a higher proportion of hook unzipping, while the fastest pulling rate has a higher proportion of hook shearing. d Rupture force plotted against force loading rate for the three ramps, calculated at the moment of rupture. Due to the long DNA handles, each pulling speed (nm s−1) has a range of loading rates (pN s−1) obtained from the worm-like chain model. e The proportion of open-jawed constructs as a function of pulling rate compared to the simulation. Two additional catch bonds were tested in addition to the one shown in the rest of Figs. 2 and 3 (h9/9j8/18), one with an 11/11 CG content hook (h11/11j8/18; yellow; n = 101, 178, 130 for slow, medium, and fast ramp speed) and one with a 10/18 CG content jaw (h9/9j10/18; green; n = 253, 490, 187 for slow, medium, and fast ramp speed). Error bars are the 95% confidence interval of the proportion; n = 1000 for each simulated point.
Next, we examined the rupture force distribution of the fish-hook catch bond at fast (2067 nm s−1), medium (206.7 nm s−1), and slow (51.7 nm s−1) ramp speeds (Fig. 3c). In all three experimental sets, the fish-hook system exhibits the characteristic bimodal distribution of a catch bond. By checking for the presence of a jaw-opening event, we are able to determine the dissociation pathway and colour code them in the histograms, where the lower force peak is dominated by the weak hook unzipping pathway, while the high force peak is dominated by the strong hook shearing pathway. Our simulation of the system demonstrates quantitatively similar bimodal distribution as the experiment, taking into account the non-linear elasticity of the DNA handles in the optical tweezers experiment. To examine this further, we plotted rupture force as a function of the loading rate at the time of rupture, colour-coded by the identity of the pathway (Fig. 3d). As expected, the rupture forces from both pathways increase with ramp speed and loading rate. The simulated results under the same conditions overlayed well with the experimental results. The scatter distribution from each ramp speed is curved due to the non-linear elasticity of the DNA handle used in the optical tweezer experiment, where the loading rate (pN s-1) scales with the spring constant (pN nm-1) at constant ramp speeds (nm s−1).
Lastly, we examined the fraction of rupture events undergoing the strong and the weak pathways at different ramp speeds. The fraction of rupture events from the strong pathway increased from 0.33 at the low ramp speed to 0.74 at the fast ramp speed (Fig. 3e, pink). This, again is in good agreement with our simulation results indicating that higher ramp speed leads to a greater fraction of rupture events from the strong pathway (Fig. 3e), demonstrating our fish-hook system exhibits the designed catch bond behaviour. Our experimental results cover approximately 2 orders of magnitude in ramp speed, which are at the limit of our instrument (high ramp speed) and reasonable experimental time scale (low ramp speed). We additionally tested 2 other fish-hook catch bonds, one with a longer hook (Fig. 3e, yellow, CG content of 11 bp, length of 11 bp (11/11 hook)) and one with a more CG-rich jaw (Fig. 3e, green, CG content of 10 bp, length of 18 bp, (10/18 jaw)). The longer hook resulted in a higher proportion of jaw-opening at the same speeds. This makes sense because a longer hook is a stronger hook, making the jaw weaker by comparison and allowing it to open more often. The opposite is true of creating a more CG-rich jaw: if the jaw is stronger, the hook unzips more often, shifting the proportion of jaw opening events down at the same speeds. As with the original fish-hook, these trends are mirrored by the model.
Design of fish-hook catch bonds in biological ranges
The design space of the fish-hook catch bond is vast. Using the analytical model, we searched all hook/jaw sequence combinations with varying CG contents and lengths from 7–30 bp for catch behaviour. For a combination to have catch behaviour, the following conditions must be met: First, the log(τF) curves of the hook and jaw must intersect. The intersection creates the force-dependent state switching behaviour and dictates the force range (around Fc) at which it happens. Second, the log(τF) curves of the hook and jaw must intersect in the correct order: the τF of the hook must be lower than the jaw at lower force and higher than the jaw at higher force. In other words, the slope of log(τF) for the jaw must be steeper than the hook. In the opposite case, the hook would shear at low force and unzip at high force, leading to a more exaggerated slip behaviour rather than slip-catch-slip. The slope of log(τF) in hairpin unzipping is almost entirely dependent on the sequence length, rather than CG content42, thus the jaw should be longer than the hook. Third, there must exist a positively-sloped (catch) region in the overall log(τF). Even if the hook and jaw intersect correctly, the overall τF may not have a catch region for two reasons: Firstly, when the slopes of the hook and jaw are very similar, the state switching from hook unzipping to shearing occurs too gently for log(τF) to be positively sloped. Secondly, as Fc approaches 0, the difference between the shearing and unzipping log(τF) of the hook is less prominent and disappears at F = 0, thus reducing both the height and width of the catch region.
Within these bounds, we found 96645 combinations satisfying the first two conditions; of those, 54354 had a positively-sloped catch region (Supplementary Figs. 4, 5); of those, 3493 were within a biologically relevant range (we define this as τF in the catch region between 0.01–100 s and the force marking the start of catch region (Fstart) between 0-10 pN). We found τF located at Fstart and Fend (Fig. 4d) for the catch region of each construct (Fig. 4a) and calculated the force range (ΔF) and τF range (Δlog(τF)) that characterize the catch region of each construct (Fig. 4b). Both graphs (Fig. 4a, b) are colour-coded by the 2D colormap shown in the inset of Fig. 4b.
a Catch regions of fish-hook catch bonds within the biologically relevant window of 0.01 <τ < 100 s and 0 <Fstart < 10 pN, simplified to a straight line between the lowest and highest τF. The tallest and widest catch behaviours are marked with * and #, respectively. b The characteristic Δlog(τF) and ΔF parameters of the catch regions. c, d The tallest and widest catch regions from (a, b). e Jaw lengths and CG contents that create catch behaviour are shown, coloured by the number of hook sequences that form catch bonds with them. The most versatile jaw, with a 0 bp CG content and a 27 bp length of (jaw0/27), is marked by a black box. f The hook sequence space that forms catch behaviour with the most versatile jaw in (e). g, h The same as (e, f), but for the hook design space and the jaws, which catch with the most versatile hook, which has an 8 bp CG content and an 8 bp length (hook8/8). Colours in (a–d, f, h) are coded by the 2D colour bar of the (b) inset.
We see a vast diversity of behaviours even in this biologically-relevant subset of the total design space, with catch behaviour covering up to two orders of magnitude in τF and up to 8 pN in ΔF (Fig. 4b). The τF of the constructs exhibiting the greatest Δlog(τF) and ΔF are shown in Fig. 4c, d, and marked by * and #, respectively in Fig. 4a, b. One interesting feature of the design space in Fig. 4b is the abundance of quasi-ideal bonds covering the bottom of the fin-shaped distribution with relatively small changes in τF (« 1 order of magnitude). Outside of this quasi-ideal bond range, there is a distinct lack of steep catch bonds with narrow force ranges (ΔF < ~ 3 pN) to the left edge of the fin (Fig. 4b). This is because ΔF depends on how different the slopes of hook unzipping τF and jaw opening τF are. If they are very different, ΔF is very narrow – the extreme case where jaw opening is perfectly vertical and hook unzipping is perfectly horizontal would have a ΔF of 0. Since a DNA unzipping slope can only be so different from another DNA unzipping slope, DNA will never be able to probe this area of catch behaviour alone42. That said, one can imagine that by constructing the hook or jaw with biomolecular interactions other than DNA unzipping, more of this area could be covered.
Next, we explore the combinatorial sequence space of jaw and hook that creates catch bond behaviour within the biologically relevant range as defined earlier. We found that the most versatile jaw had a length of 27 bp made entirely of A/T (Fig. 4e) and can create catch behaviour with 44 unique hooks from 7–19 nt with relatively low CG content (Fig. 4f). The most versatile hook had a length of 8 bp made up entirely of C/G (Fig. 4g) and can create catch behaviour with 124 unique jaw sequences between 13–30 nt also with relatively low CG content (Fig. 4h). The fact that the most versatile lengths are near the upper and lower extremes of our search space highlights the fact that length changes the slope of the log(τF) – the steeper slope (longer sequence) the jaw has, the more hooks it pairs with; and the flatter slope (shorter sequence) the hook has (Supplementary Fig. 1), the more jaws it pairs with. CG content represents a vertical shift in log(τF), which also makes sense with the most versatile jaw/hook42: as the jaw CG content decreases or the hook CG content increases, Fc increases and a more dramatic catch behaviour is observed due to a larger difference in shearing and unzipping τF.
Discussion
The fish-hook catch bond is a physical demonstration of the power of using the well-characterized DNA duplex as a means to create interesting nanomechanical properties. Additionally, the vast design space with catch bond parameters within the biologically relevant range allows the design to interface directly with biological systems and create novel behaviours. Of course, DNA as a molecule has its limitations – there are certain areas of the catch bond parameter space that it cannot cover, such as regions of ΔF below 3 pN and above 8 pN (Fig. 4b). Additionally, DNA suffers from potential problems of nuclease degradation in biological environments. That said, because this architecture has been demonstrated to work in such a simple system as DNA, it opens up the opportunity for more complicated systems to use a similar concept: intersecting force dependent lifetimes are the only thing needed to bias a two-state molecule to be in one state at low force and the other at high force. From there, you could imagine using alternative/non-canonical oligonucleotides, protein structure, metal coordination, or even covalent bonds to create catch behaviour. Binding slip-DNA to the membrane-bound E-cadherin was recently shown to impact cell junction formation44, and researchers have been using slip-behaving tension gauge tethers (TGT) to measure and change motility and spreading for years4,45,46,47,48,49,50,51,52. What could we do with a library of tunable catch bonds instead? The fish-hook catch bond allows the design of interactions that more closely mimic biological adhesive, mechanotransduction, and mechanosensing interactions exhibiting catch bond behaviour. Our current work also builds the foundation towards rationally designing further slip-catch-slip, slip-ideal-slip, catch-slip, and perhaps even stranger multi-phasic behaviours with force-switchable DNA configurations.
Methods
DNA construction
All DNA primers and oligos were ordered from Integrated DNA Technologies (Coralville, IA, USA). Sequences used in the are shown in Supplementary Table 1. We synthesized the construct in two parts: the hook and the fish.
The hook handle was a 2633 bp PCR-amplified segment of a lambda DNA template (New England Biolabs, Whitby, ON, Canada). The forward primer had a 9-mer polyethelene glycol (PEG) linker attached to the 5′ end, which itself was attached to the single-stranded hook segment. The PEG linker prevented the hook segment from being included in amplification. The reverse primer was modified with a 5′ biotin for attachment to streptavidin-coated polystyrene beads (Bangs Laboratories, Fishers, IN, USA). The final hook construct was 2633 bp of double-stranded DNA (dsDNA) with a PEG spacer connecting the single-stranded hook on one 5′ end and a biotin on the other 5′ end.
The fish handle was 272 bp of dsDNA, similarly constructed from the lambda template with a reverse primer modified with 5′ biotin. The forward primer was unmodified but contained a cut site for digestion with BsaI (New England Biolabs, Whitby, ON, Canada). The fish was created separately from two single-stranded sequences: one containing the hook binding region and one of the jaw strands, and the other containing the complementary jaw strand and a sticky end for ligation to the handle. These sequences were annealed together at room temperature (23 °C) overnight before being ligated to the digested handle. The final fish construct was 272 bp of dsDNA with biotin on one 5′ end and the fish on the other end.
Optical trap experiment
All optical trap experiments were performed at room temperature (~23 °C). The trap buffer used in all the optical trap experiments contains 50 mM NaCl, 10 mM Tris-HCl (pH 8.0), 5 mM MgCl2, and an oxygen scavenger system using 20 mM protocatechuic acid (PCA) and 50 nM protocatechuate-3,4-dioxygenase (PCD; Sigma Aldrich, St Louis, MO, USA). The fish and hook DNA constructs were attached separately to 1 µm diameter streptavidin-coated polystyrene beads (Bang Labs, Fishers, IN, USA) by incubation at 5 ng µl−1 (hook) or 1 ng µl−1 (fish) at 4 °C for at least 30 min in TE buffer (10 mM Tris-HCl and 1 mM EDTA at pH 8.0). Prior to experiments, the beads were washed in the trap buffer and loaded into separate 500 μl syringes. The two syringes containing fish and hook beads as well as a 3rd syringe containing just the trap buffer were each connected to separate inlets of a custom microfluidics chip. This chip enables laminar flow of each input solution through a combined channel into a single outlet (Supplementary Fig. 2). The chip was made by sandwiching cut parafilm between two plasma-cleaned glass coverslips and melting in a 75 °C and 110 °C oven for ~1 min each. Optical trap experiments were conducted with a custom-built dual-trap system based on existing designs53. Traps were calibrated using power spectrum analysis with data collected at 100 kHz53. Beads are captured one at a time and moved to the working area in the centre channel (Supplementary Fig. 2). The fish bead is steered toward the hook bead until they are nearly touching, held there for ~8 s, and then retracted away. The retract speed is set to one of the three experimental speeds while the approach is made as fast as possible to save time. Data is collected at 5000 Hz using custom LabVIEW code.
Force extension curve analysis
Each retraction can result in no tethers, one tether, or multiple tethers. The trace is discarded when tethers with more than two rupture events are observed (indicating multiple tethers). If one or two rupture events are observed, the trace is manually compared to the extensible worm-like chain (XWLC) model (contour length Lc is 0.34 nm bp−1 for dsDNA and 0.451 nm nt−1 for ssDNA; persistence length Lp is 50 nm for dsDNA and 1.1 nm for ssDNA; stretch modulus S is 1200 pN for dsDNA and 800 pN for ssDNA)53,54,55,56 and removed if it does not match the expected contour (Supplementary Fig. 6). The remaining single-rupture traces (weak pathway) were fit to the XWLC model. For traces that contain a jaw opening event (strong pathway), the section before and after the jaw opening were fitted separately by XWLC. The Lc of dsDNA was used as a fitting parameter to obtain the ΔLc. To calculate the force loading rate at each rupture, the last 10% of points of each F(t) trace before rupture was fit to a 2nd-degree polynomial and the slope at the point of rupture was calculated.
Simulation parameters
All simulations were run at T = 300 K, at [Na+] = 50 mM and [Mg2+] = 5 mM. The time step of the Monte Carlo simulation was adjusted to the time it takes for the traps to move 0.01 nm away from each other; thus, as ramp speed increases, the time step decreases.
Modelling catch behaviour
We used an analytical model42 based on a literature model57 to find expected τF for DNA hairpins. The model takes into consideration the sequence-, temperature- and salt-specific nearest-neighbour energies (ΔGNN)58 and the energy of single-stranded DNA stretching (ΔGstretch) for the amount of length released as each bp opens57. Using these parameters, one can find the energy landscape as a function of extension, providing the height (ΔG‡) and width (x‡) of the energy barrier of unzipping. The work done by the trap and the resulting τF is found by:
where F is force, kB is the Boltzmann’s constant, T is temperature, and τ* is a pre-factor (4.12 × 10−5 s) that fit to literature off-rates57. We used 1000 random sequences for each combination of length (7–30 bp) and CG content (0–100%) to obtain the median τF at forces from 0–20 pN in increments of 2 pN. This coarse-graining gave us results that were closer to our experimental values than the more sequence-specific model. We used the median because the force-dependent lifetimes were not normally distributed; the median more closely represented the peak value. The log of the median τF was linearly fit against force (with R-values ranging from 0.99 to 1). These lines were used to find the intersection points for each combination. For the sequence we chose, these are shown in Fig. 2d as the hook unzipping and jaw opening lines. We then calculated the probability of jaw opening (τj) or hook unzipping (τhu):
and found the expected lifetime of the overall construct at any given force:
This equation produces the overall behaviour shown in Fig. 2d, and clearly shows the slip-catch-slip behaviour expected.
Unfolding forces at different pulling rates were found by Monte Carlo simulation using τF directly from the analytical model. The simulation begins at F = 0. For each time step, F is incremented. Instead of incrementing F linearly, we incremented it in a way that resembles our optical trap experiment. Our steering mirror moves linearly, but since the DNA handles on our construct exhibit non-linear elasticity, the force on the construct increases at a rate modellable by extensible worm-like chain (XWLC). Once F is updated, τF is updated for each of the hook and jaw via Eq. 1. The probability of the hook unzipping and the jaw opening are separately assessed according to:
If the hook unzips, the current force is recorded as the rupture force. If the jaw unzips, the simulation continues iterating in time and force, but the τF used is that of the hook shearing. To find the τF of the shearing component, we used the equation:
where τ0 is the lifetime of hook unzipping at zero force according to Eq. 1. The parameter we used for x‡ was determined with an approximation based on experimental data45,59 and should be used only as an estimate for calculating lifetime:
where l is the shear sequence length in bp. Shearing lifetime is not involved in the force-dependent biasing of the catch bond, only in the final strength of the strong state, so the level of accuracy of this model was deemed adequate. This Monte-Carlo method was also used to determine constant-force τF (Supplementary Fig. 3).
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
Code availability
Code for generating Figs. 2d–f, 3, and 4; as well as analytical and Monte-Carlo simulation code can be found at https://doi.org/10.5281/zenodo.1092922260.
References
Baum, B. & Georgiou, M. Dynamics of adherens junctions in epithelial establishment, maintenance, and remodeling. J. Cell Biol. 192, 907–917 (2011).
Friedl, P. & Mayor, R. Tuning collective cell migration by cell–cell junction regulation. Cold Spring Harb. Perspect. Biol. 9, a029199 (2017).
Wang, X. et al. Integrin molecular tension within motile focal adhesions. Biophys. J. 109, 2259–2267 (2015).
Zhao, Y., Wang, Y., Sarkar, A. & Wang, X. Keratocytes generate high integrin tension at the trailing edge to mediate rear de-adhesion during rapid cell migration. iScience 9, 502–512 (2018).
Tan, S. J. et al. Regulation and dynamics of force transmission at individual cell-matrix adhesion bonds. Sci. Adv. 6, eaax0317 (2020).
Hong, J. et al. Force-regulated in situ TCR–peptide-bound MHC class II kinetics determine functions of CD4+ T cells. J. Immunol. 195, 3557–3564 (2015).
Andreu, I. et al. The force loading rate drives cell mechanosensing through both reinforcement and cytoskeletal softening. Nat. Commun. 12, 4229 (2021).
Huang, D. L., Bax, N. A., Buckley, C. D., Weis, W. I. & Dunn, A. R. Vinculin forms a directionally asymmetric catch bond with F-actin. Science 357, 703–706 (2017).
Yakovenko, O. et al. FimH forms catch bonds that are enhanced by mechanical force due to allosteric regulation. J. Biol. Chem. 283, 11596–11605 (2008).
van Galen, M., van der Gucht, J., & Sprakel, J. chemical design model for emergent synthetic catch bonds. Front. Phys. 8, 361 (2020).
Rakshit, S., Zhang, Y., Manibog, K., Shafraz, O. & Sivasankar, S. Ideal, catch, and slip bonds in cadherin adhesion. Proc. Natl. Acad. Sci. USA 109, 18815–18820 (2012).
Evans, E., Leung, A., Heinrich, V. & Zhu, C. Mechanical switching and coupling between two dissociation pathways in a P-selectin adhesion bond. Proc. Natl. Acad. Sci. USA 101, 11281–11286 (2004).
Kong, F., García, A. J., Mould, A. P., Humphries, M. J. & Zhu, C. Demonstration of catch bonds between an integrin and its ligand. J. Cell Biol. 185, 1275–1284 (2009).
Huang, Z. et al. Direct observation of delayed fluorescence from a remarkable back-isomerization in Cy5. J. Am. Chem. Soc. 127, 8064–8066 (2005).
Sarangapani, K. K. et al. Low force decelerates l-selectin dissociation from P-selectin glycoprotein ligand-1 and endoglycan. J. Biol. Chem. 279, 2291–2298 (2004).
Yago, T. et al. Catch bonds govern adhesion through L-selectin at threshold shear. J. Cell Biol. 166, 913–923 (2004).
Liu, B., Chen, W., Evavold, B. D. & Zhu, C. Accumulation of dynamic catch bonds between TCR and agonist peptide-MHC triggers T cell signaling. Cell 157, 357–368 (2014).
Das, D. K. et al. Force-dependent transition in the T-cell receptor β-subunit allosterically regulates peptide discrimination and pMHC bond lifetime. Proc. Natl. Acad. Sci. USA 112, 1517–1522 (2015).
Li, Z. et al. Domain-specific mechanical modulation of VWF–ADAMTS13 interaction. Mol. Biol. Cell 30, 1920–1929 (2019).
Arora, N. et al. Emergence of slip-ideal-slip behavior in tip-links serve as force filters of sound in hearing. Nat. Commun. 15, 1595 (2024).
Wayman, A. M., Chen, W., McEver, R. P. & Zhu, C. Triphasic force dependence of E-selectin/ligand dissociation governs cell rolling under flow. Biophys. J. 99, 1166–1174 (2010).
Marki, A., Buscher, K., Mikulski, Z., Pries, A., Ley, K. Rolling neutrophils form tethers and slings under physiologic conditions in vivo. J. Leukoc. Biol. jlb.1AB0617-230R (2017).
Wang, A., Dunn, A. R. & Weis, W. I. Mechanism of the cadherin–catenin F-actin catch bond interaction. eLife 11, e80130 (2022).
Thomas, W. et al. Catch-bond model derived from allostery explains force-activated bacterial adhesion. Biophys. J. 90, 753–764 (2006).
Lou, J. & Zhu, C. A structure-based sliding-rebinding mechanism for catch bonds. Biophys. J. 92, 1471–1485 (2007).
Pereverzev, Y. V. & Prezhdo, O. V. Force-induced deformations and stability of biological bonds. Phys. Rev. E 73, 050902 (2006).
Pereverzev, Y. V., Prezhdo, O. V. & Sokurenko, E. V. Regulation of catch binding by allosteric transitions. J. Phys. Chem. B 114, 11866–11874 (2010).
Chen, H. & Alexander-Katz, A. Polymer-based catch-bonds. Biophys. J. 100, 174–182 (2011).
Barkan, C. O. & Bruinsma, R. F. Topology of molecular deformations induces triphasic catch bonding in selectin–ligand bonds. Proc. Natl. Acad. Sci. USA 121, e2315866121 (2024).
Chakrabarti, S., Hinczewski, M. & Thirumalai, D. Plasticity of hydrogen bond networks regulates mechanochemistry of cell adhesion complexes. Proc. Natl. Acad. Sci. USA 111, 9048–9053 (2014).
Dansuk, K. C. & Keten, S. A simple mechanical model for synthetic catch bonds. Matter 1, 911–925 (2019).
Dansuk, K. C. & Keten, S. Self-strengthening biphasic nanoparticle assemblies with intrinsic catch bonds. Nat. Commun. 12, 85 (2021).
Dansuk, K. C., Pal, S. & Keten, S. A catch bond mechanism with looped adhesive tethers for self-strengthening materials. Commun. Mater. 4, 1–10 (2023).
Liu, Z. et al. Engineering an artificial catch bond using mechanical anisotropy. Nat. Commun. 15, 3019 (2024).
van Galen, M. et al. De novo DNA-based catch bonds. Nat. Chem. 1–8 https://doi.org/10.1038/s41557-024-01571-4 (2024).
Konda, S. S. M. et al. Molecular catch bonds and the anti-Hammond effect in polymer mechanochemistry. J. Am. Chem. Soc. 135, 12722–12729 (2013).
Horst, M. et al. Mechanochemistry of pterodactylane. J. Am. Chem. Soc. 146, 884–891 (2024).
Barsegov, V. & Thirumalai, D. Dynamics of unbinding of cell adhesion molecules: transition from catch to slip bonds. Proc. Natl. Acad. Sci. USA 102, 1835–1839 (2005).
Bartolo, D., Derényi, I. & Ajdari, A. Dynamic response of adhesion complexes: beyond the single-path picture. Phys. Rev. E 65, 051910 (2002).
Thomas, W. E., Nilsson, L. M., Forero, M., Sokurenko, E. V. & Vogel, V. Shear-dependent ‘stick-and-roll’ adhesion of type 1 fimbriated Escherichia coli: stick-and-roll bacterial adhesion. Mol. Microbiol. 53, 1545–1557 (2004).
Pereverzev, Y. V., Prezhdo, O. V., Forero, M., Sokurenko, E. V. & Thomas, W. E. The two-pathway model for the catch-slip transition in biological adhesion. Biophys. J. 89, 1446–1454 (2005).
Murad, Y. & Li, I. T. S. Quantifying molecular forces with serially connected force sensors. Biophys. J. 116, 1282–1291 (2019).
Guo, B. & Guilford, W. H. Mechanics of actomyosin bonds in different nucleotide states are tuned to muscle contraction. Proc. Natl. Acad. Sci. USA 103, 9844–9849 (2006).
Schoenit, A. et al. Tuning epithelial cell–cell adhesion and collective dynamics with functional DNA-E-cadherin hybrid linkers. Nano Lett. 22, 302–310 (2022).
Liu, J. et al. Tension gauge tethers as tension threshold and duration sensors. ACS Sens. 8, 704–711 (2023).
Jo, M. H., Cottle, W. T., Ha, T. Real-time measurement of molecular tension during cell adhesion and migration using multiplexed differential analysis of tension Gauge Tethers. ACS Biomater. Sci. Eng. https://doi.org/10.1021/acsbiomaterials.8b01216 (2018).
Liu, Y. et al. DNA-based nanoparticle tension sensors reveal that T-cell receptors transmit defined pN forces to their antigens for enhanced fidelity. Proc. Natl. Acad. Sci. USA 113, 5610–5615 (2016).
Albrecht, C. et al. DNA: a programmable force sensor. Science 301, 367–370 (2003).
Wang, X. & Ha, T. Defining single molecular forces required to activate integrin and notch signaling. Science 340, 991–994 (2013).
Wang, X. et al. Constructing modular and universal single molecule tension sensor using protein G to study mechano-sensitive receptors. Sci. Rep. 6, 21584 (2016).
Liu, Y., Galior, K., Ma, V. P.-Y. & Salaita, K. Molecular tension probes for imaging forces at the cell surface. Acc. Chem. Res. 50, 2915–2924 (2017).
Rao, T. C. & Mattheyses, A. L. Tension Gauge tether probes for quantifying growth factor mediated integrin mechanics and adhesion. JoVE J. Vis. Exp. 11, e63529 (2022).
Wang, G. et al. “Calibration of a dual-trap optical tweezers for single molecule force spectroscopy study” B. Lee, Y. Su, M. Gu, X. Yuan, D. Jaque, Eds. (Beijing, China, 2015; http://proceedings.spiedigitallibrary.org/proceeding.aspx?doi=10.1117/12.2199680), p. 96720P.
Strunz, T., Oroszlan, K., Schafer, R. & Guntherodt, H.-J. Dynamic force spectroscopy of single DNA molecules. Proc. Natl. Acad. Sci. USA 96, 11277–11282 (1999).
Bosco, A., Camunas-Soler, J. & Ritort, F. Elastic properties and secondary structure formation of single-stranded DNA at monovalent and divalent salt conditions. Nucleic Acids Res. 42, 2064–2074 (2014).
Whitley, K. D., Comstock, M. J. & Chemla, Y. R. Elasticity of the transition state for oligonucleotide hybridization. Nucleic Acids Res. 45, 547–555 (2017).
Woodside, M. T. et al. Nanomechanical measurements of the sequence-dependent folding landscapes of single nucleic acid hairpins. Proc. Natl. Acad. Sci. USA 103, 6190–6195 (2006).
Huguet, J. M. et al. Single-molecule derivation of salt dependent base-pair free energies in DNA. Proc. Natl. Acad. Sci. USA 107, 15431–15436 (2010).
Marin-Gonzalez, A., Vilhena, J. G., Perez, R. & Moreno-Herrero, F. Understanding the mechanical response of double-stranded DNA and RNA under constant stretching forces using all-atom molecular dynamics. Proc. Natl. Acad. Sci. USA 114, 7049–7054 (2017).
Yang, M., Bakker, D. t.R., Li, I. T. S. UBC-SMMB/ArtificialCatchBondMY2024: Pre-Publication Data, Zenodo Release. Zenodo https://zenodo.org/doi/10.5281/zenodo.10929222 (2024).
Acknowledgements
This research was supported by the Natural Sciences and Engineering Research Council of Canada Discovery Grant (RGPIN-2017-04407, RGPIN-2024-04352, ITSL), Canada Foundation for Innovation (35492, ITSL), Canada Research Chair (CRC-2020-00143, ITSL), Michael Smith Health Research BC Scholar Award (SCH-2020-0559, ITSL).
Author information
Authors and Affiliations
Contributions
Conceptualization: M.Y., I.L. Methodology: D.B., M.Y., I.L.; Investigation: D.B., M.Y.; Visualization: M.Y., I.L.; Funding acquisition: I.L.; Supervision: I.L.; Writing – original draft: M.Y.; Writing – review & editing: M.Y., I.L., D.B.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Wendy Thomas and the other, anonymous, reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Yang, M., Bakker, D.t.R. & Li, I.T.S. Engineering tunable catch bonds with DNA. Nat Commun 15, 8828 (2024). https://doi.org/10.1038/s41467-024-52749-w
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-52749-w
This article is cited by
-
DNA catch bonds demonstrate the art of getting stuck
Nature Chemistry (2024)