Introduction

The quantum Hall (QH) effect, observed in a two-dimensional electron gas subject to a perpendicular magnetic field, realizes multiple quantum phase transitions (QPT) between distinct insulating topological states1. The magnetic field B quenches the electronic kinetic energy into disorder-broadened discrete Landau energy levels (LL). All electronic single-particle states are localized, barring those at a specific critical energy Ec near the center of each LL, which are extended2,3,4,5,6,7. When the Fermi energy lies between the extended states of two successive LLs, the system is in a distinct topological phase characterized by a quantized value of Hall resistance Rxy and vanishingly small longitudinal resistance Rxx. As the Fermi energy approaches Ec, the localization length ξ characterizing the single-particle states diverges as ξ ~ ∣E−Ec∣−γ while the slowest time-scale diverges as τ ~ ξz  ~ ∣E−Ec∣−zγ8,9. The exponent γ governs the critical divergence of the localization length as the filling fraction or magnetic field approach the critical values and z governs the divergence of the coherence length with decreasing temperatures10. From the finite-size scaling theory10,11,

$${\rm {d}}{R}_{xy}/{\rm {d}}{\nu }_{\nu={\nu }_{{\rm {c}}}}\propto {T}^{-1/z\gamma }$$
(1)

Here, ν = nh/eB, n is the areal charge-carrier density, h is the Planck constant, e is the electronic charge, and T is the temperature. One additionally defines the scaling exponent κ = 1/zγ11,12,13 that governs this temperature dependence of the slope of Rxy as well as the width of the Rxx peak at the transition. The values of these three critical exponents (of which only two are independent) have been argued to be universal, with γ ≈ 2.3, κ ≈ 0.42, and z = 1 for all IQH transitions4,10,11,14,15.

Low temperatures and high magnetic fields enhance the effective electron-electron interactions, producing a richer set of the fractional quantum Hall (FQH) phases at rational filling fractions16. The question then arises: Can IQH and FQH phase transitions be analyzed using a ‘unified’ scaling framework17? While the IQH phases originate from the topology of the single particle electronic Chern bands18, the FQH phases are crucially underlain by strong electronic interactions. These are marked by distinct electronic correlations, topological order, ground state degeneracy, and topological entanglement. The transition between FQH plateaus is driven by a proliferation of anyonic quasiparticles (characterized by quasiparticle statistics and fractional charge). This picture may suggest that the critical behavior at the transitions depends on the specifics of the topological FQH states involved and is also different from the analogous transitions in the IQH regime.

Experimental investigations of scaling in the IQH regime have reported κ varying between 0.16 ≤ κ ≤ 0.81 (Supplementary Information, Supplementary Note 13). This wide variation has been attributed to varying disorder correlation lengths with a universal critical behavior seen only in samples with short-range disorder19,20. This lack of a tight constraint on κ has hindered any claims of their universality. Similar experimental investigations of scaling laws at transitions between FQH phases are scarce21,22,23. A recent experimental study on extremely high-mobility 2D electron gas confined to GaAs quantum wells found the value of κ in the FQH regime to be non-universal, this observation being attributable to long-range disorder correlation23. Thus, despite over three decades of study, the fundamental question of the values of the critical exponents across quantum Hall transitions (integer and fractional) remains unsettled14,23,24.

This article reports the experimental observation of a surprising super universality in the scaling exponents for transitions between various IQH and FQH phases in trilayer graphene. We measure both the scaling exponent κ and the localization length exponent γ independently over several integer-to-integer, integer-to-fractional, and fractional-to-fractional Quantum Hall transitions. Contrary to the expected picture of multiple plateau-to-plateau quantum phase transitions, each with its own distinct critical properties, here we find that for all IQH and FQH plateau-to-plateau transitions (PT), κ = 0.41 ± 0.02, γ ≈ 2.4 ± 0.2, and z ≈ 1, closely aligned with the predictions of the scaling theory of localization13. Given the distinct origins of the two phenomena, this striking similarity of the critical exponents suggests a connection between the IQH and FQH effects that transcends the composite fermion (CF) framework.

We estimate the values of κ near criticality (ν ≈ νc) using three distinct approaches: (i) analyzing the critical divergence of dRxy/dν, (ii) probing the critical divergence of the inverse width of Rxx(T), and (iii) a scaling analysis of Rxy near the critical point. The localization exponent γ is obtained deep in the tails of the localized regime from the dependence of Gxx on ν. A scaling analysis of Quantum Hall transitions for fractional and integer states provides a second, independent way to extract γ.

The realizations of these quantum phase transitions in graphene-based systems are associated with a highly tunable set of parameters. These include the ability to alter electron density, which is typically unachievable in semiconductor heterostructures25, the capability to manage screening, and the option to induce band mixing by applying a displacement field D. This flexibility helps us establish that weak Landau level mixing does not significantly affect these critical exponents.

Graphene also provides a platform where the nature of disorder scattering can be controlled. This is because the electrical transport properties of high-mobility graphene devices are dominated by short-range impurity scattering, while those of low-mobility graphene devices are controlled by both short-ranged and long-ranged scattering potentials26,27. Thus, high-mobility graphene devices represent a natural candidate to investigate the universality of scaling exponents. Our comparative study between graphene devices of varying mobility shows that as long as long-range impurity scattering can be suppressed, the universality of scaling parameters persists, independent of the quantum Hall bulk phases involved.

Results

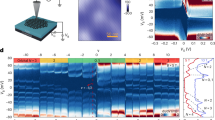
Standard dry transfer technique is used for the fabrication of dual graphite-gated hexagonal-boron-nitride (hBN) encapsulated TLG devices (Fig. 1a) (for details, see Supplementary Information, Supplementary Note 1)28. Figure 1b shows measurements of the longitudinal resistance Rxx and the transverse conductance Gxy versus the Landau level filling factor ν; the measurements were performed at B = 13 T, T = 20 mK, and D = 0 V/nm. We identify several major odd denominator FQH states by prominent dips in Rxx and corresponding plateaus in Gxy. Indications of developing ν = 3 + 1/5 and 3 + 2/7 states are also seen. Several of these FQH states are resolved at B = 4.5 T, attesting to the high quality of the device in terms of excellent homogeneity of number density and suppression of long-range scattering (Supplementary Information, Supplementary Note 6).

Fig. 1: FQH in Bernal-stacked TLG.
figure 1

a Device schematic of TLG encapsulated between two hBN and few-layer graphite flakes. b Line plots of Gxy (left-axis; solid red line) and Rxx (right-axis; solid blue line) versus ν measured at B = 13 T, T = 20 mK, and D = 0 V/nm. The dashed vertical lines mark the FQH states formed at corresponding ν, and the arrows indicate corresponding plateaus in Gxy. c Calculated band structure of Bernal stacked trilayer graphene for D = 0 V/nm. The four LLs of the NM = 0 (The MLG LLs are marked by the subscripts M, and orbital contents are given by the numbers 0) band are indicated schematically. d Calculated Landau levels as a function of energy E and B for D = 0 V/nm. The blue lines are the monolayer-like LLs, while the red lines are the bilayer-like LLs. The solid and dotted lines indicate the LLs from K and \({K}^{{\prime} }\)-valley, respectively. The solid-green line is the spin-degenerate NM = 0−↑ and NM = 0−↓ monolayer-like LLs that host the FQH states probed in this article.

Full size image

The band structure of TLG is formed of monolayer-like and bilayer-like Landau levels (Fig. 1c)—these are protected from mixing by the lattice mirror-symmetry29. The calculated LL spectrum as a function of B and energy E is shown in Fig. 1d, where blue (red) lines mark the monolayer-like (bilayer-like) LLs. For B > 8 T, the ν = 2 and ν = 3 arise from the spin-split NM = 0−↑ and NM = 0−↓ bands of the monolayer-like LLs. Here, (+ , −) refers to the two valleys, and (↑, ↓) refers to electronic spins. We confine our study to 8 T < B < 13 T to avoid Landau level-mixing at lower B and phase transitions between competing FQH states at higher B30,31,32.

Critical exponents near FQH plateau-to-plateau transitions

Figure 2a shows the T-dependence of Rxy between the IQH states ν = −2 and ν = −1. Similar data for transition between the FQH states ν = 2 + 2/3 and ν = 2 + 3/5 are shown in Fig. 2b. The critical points νc of the plateau-to-plateau transition (identified as the crossing point of the Rxy curves at different T) are indicated in the plots. The exponent κ evaluated from the peak value of dRxy/dν versus T near criticality (Fig. 2c and d) in both cases is κ = 0.41 ± 0.01. Analysis of the T-dependence of the inverse of the half-width of Rxx as ν is varied between two consecutive FQH plateaus also yields κ = 0.41 ± 0.02 (Supplementary Information, Supplementary Note 2).

Fig. 2: Scaling near ν = νc.
figure 2

Plot of Rxy versus ν for transition between the (a) IQH states ν = −2 and ν = −1 (the critical point νc = −1.5) and b the FQH states 2 + 2/3 and 2 + 3/5 (νc = 2.625). c Double logarithmic plot of ∣dRxy/dν∣ versus T for the PT ν = −2 and ν = −1 at νc. The dashed line is the fit to the data points using Eq. (1). d Same as in (c) for the PT between FQH states 2 + 2/3 and 2 + 3/5. e Scaling analysis of Rxy for the PT transition between ν = 2 + 1/3 and ν = 2 + 2/5. The inset is a plot of T versus α in a double logarithmic scale (open circles); a linear fit to the data (dotted line) yields κ = 0.40 ± 0.03. (For an error analysis, see Supplementary Information, Supplementary Note 7).

Full size image

To demonstrate the scaling properties of Rxy in the vicinity of νc, we use the following form13:

$${R}_{xy}(\nu,T)={R}_{xy}({\nu }_{{\rm {c}}}) \, f[\alpha (\nu -{\nu }_{{\rm {c}}})]$$
(2)

with α ∝ T−κ. Here, f(0) = 1, and \({f}^{{\prime} }(0) \, \ne \, 0\). This gives us a third, independent method of estimating κ. Figure 2e shows the plots of Rxy/Rxy(νc) at various temperatures as a function of α∣ν−νc∣ for the ν = 2 +1/3 to 2 + 2/5 transition. α(T) is optimized to collapse the various constant-temperature data onto a single curve (the upper branch of which is for ν < νc and the lower branch is for ν > νc). From the plot of α versus T (inset of Fig. 2e) we obtain κ = 0.40 ± 0.03.

To check the validity of our scaling analysis, we perform the following error analysis: The residue in the least square fit between the scaling curves (like those shown in Fig. 2e) for each assumed value of κ is calculated. This quantity, which we call fit error’, is presented in Supplementary Information Supplementary Fig. 6 and Supplementary Fig. 7 in a semi-\(\log\) scale; we find that the fit error is indeed minimum for κ = 0.41.

Figure 3a compiles our findings. These results indicate a κ value of 0.41 ± 0.03 uniformly observed across all probed transitions between IQH and FQH states (compare with Supplementary Fig. 14 of Supplementary Information). This consistency in scaling exponents spans various transition types, including (1) transitions from one IQH state to another, (2) transitions among different FQH states, and (3) transitions between an IQH state and a neighboring FQH state. It is important to emphasize that the observed universality of κ goes beyond marking an experimental confirmation of a uniform scaling law across FQH transitions in any material. Given the distinct physics of IQH and FQH states, such constancy of the scaling exponent is remarkable and underscores the universal applicability of the scaling principle across QH transitions. This is the central result of this article.

Fig. 3: Scaling exponents for different PT.
figure 3

a Plot of κ as a function of νc corresponding to different PT evaluated from the maxima of derivative \({({\rm {d}}{R}_{xy}/{\rm {d}}\nu )}^{\max}\) near the critical point. The dotted vertical lines mark the experimentally obtained νc. The light blue symbols are for the κ values obtained for trilayer graphene, and the red symbols are for the single-layer graphene. b Plot of experimentally obtained values of critical points, νc versus those theoretically calculated νct14. The triangles are the values determined from crossing points of isotherms in Rxy, while the circles are determined from the Rxx maxima. The black dashed line fits the data points with slope = 1.00 ± 0.002. c Plot of κ versus D for the FQH transition from ν = 8/3 to ν = 13/5 states evaluated from the maxima of derivative \({({\rm {d}}{R}_{xy}/{\rm {d}}\nu )}^{\max}\) near the critical point. The error bars are determined from the least-square fits to the data.

Full size image

Locating the transition

The physics of the FQH effect of electrons at a filling factor ν can be mapped onto that of IQH of CF at a filling factor νCF, with ν = νCF/(2νCF ± 1)33. It follows that the critical points for the transition between successive FQH phases at ν =  νCF/(2νCF ± 1) and ν = (νCF + 1)/(2(νCF + 1)±1) occur at14,34:

$${\nu }_{{\rm {c}}}=\frac{({\nu }_{{\rm {CF}}}+0.5)}{2({\nu }_{{\rm {CF}}}+0.5)\pm 1}.$$
(3)

The experimentally obtained values of νc, extracted either from the crossing point of the Rxy isotherms or the maxima of Rxx, match exceptionally well with the theoretical predictions (Fig. 3b) (Supplementary Information, Supplementary Table 1).

Robustness of the critical exponents against LL mixing

A non-zero vertical displacement field D gives rise to a complex phase diagram in TLG, with the Landau levels inter-crossing multiple times, resulting in significant LL mixing as either D or B is varied35,36,37,38,39. LL-mixing can change the effective interaction between the electrons32. However, as shown in Fig. 3c, it does not significantly affect the universality of κ. This vital result suggests that as long as the anyons are weakly interacting, the critical behavior of the localization-delocalization transition remains unaltered.

Measurement of localization exponent γ

We now focus on the localized regime, far away from Ec, marked by the black rectangle in Fig. 4a. Given the presence of strong interactions, it is reasonable to assume that transport in this localized part of the energy spectrum proceeds through Efros–Shklovskii (ES) type hopping mechanism40. The localization exponent γ determines the T dependence of longitudinal conductance Gxx40,41:

$${G}_{xx}={G}_{0}{e}^{-{({T}_{0}/T)}^{1/2}}$$
(4)

with

$${k}_{{\rm {B}}}{T}_{0}\propto | \delta \nu {| }^{\gamma }.$$
(5)

The pre-factor G0 ∝ 1/T and δν = (ν−νc). Figure 4b shows plots of log(TGxx) versus T−1/2 at different values of δν; the dotted lines are linear fits to the data. The linearity of the data at low-T is consistent with transport by the ES hopping mechanism in the FQH regime (Eq. (4)). At high-T (in the region marked in Fig. 4b by a dotted ellipse), the values of Gxx become relatively large, and the plots deviate from a straight line. In passing, we note that as we move progressively closer to the center of the plateau in Rxy, where the value of Gxx ≈ 0 at low-T, the linearity of the plots persists to higher temperatures. Fitting T0 (estimated from Eqn (4)) and ∣δνCF∣ to Eq. (5), we find the estimated γ to lie in the range 2.3−2.6 (Fig. 4c) for FQH plateau-to-plateau transitions, very close to the predicted range of γ = 2.3−2.514. The fact that the exponent controlling the divergence of the localization length at criticality is almost identical for both FQH and IQH states points to an effective model of localization that is universal across the different statistics of the quasiparticles in these QH phases. Furthermore, from κ = 1/zγ ≈ 0.41 ± 0.03 and γ ≈ 2.3, we get z ≈ 1, as expected for a strongly interacting system7,9,42,43.

Fig. 4: Scaling exponent in the ES regime for ν =  3 + 2/5 to 3 + 3/7 transition.
figure 4

a Plots of the T-dependence of Gxx versus filling factor ν for two FQH states between ν = 3 and ν = 4. The black box marks the region where the ES analysis was carried out. b Fit of ES Eq. (4) (dotted lines) to the Gxx data for the transition from ν = 3 + 2/5 and ν = 3 + 3/7. Each set of data points is for a given value of δν=∣ν–νc∣ with νc = 3.416. The plots deviate from the expected ES behavior at high T (the region is marked with an ellipse). c Plots of T0 versus δνCF. The dotted line is a linear fit to the data (see Eq. (5)). The slope yields the value of γ. The error bars are determined from the least square fits to the data in (b). d Plot of scaled longitudinal conductance Gxx/s as a function of scaling parameter s = ∣δν∣γ/T for PT between ν = 17/5 and ν = 24/7. The scatter points of different colors are for different values of ∣δν∣, and the solid black line is fit to Eq. (6).

Full size image

An independent estimate of γ is obtained by casting Eq. (4) into a single-parameter scaling form44:

$${G}_{xx}\left(s\right)={\sigma }{*}s{e}^{-{({T}{*}s)}^{1/2}},$$
(6)

with the the scaling parameter s = ∣δνCF∣γ/T. Figure 4d shows the scaling plots of Gxx/s versus s1/2 for the PT in ES regime from ν = 3 + 2/5 to ν = 3 + 3/7. We find a near-perfect data collapse for all values of δνCF in the localized regime with γ ≈ 2.3, providing an independent validation of the universality of γ.

Discussion

We are now in a position to compare the universality of κ seen in the FQH PT in our high-mobility TLG with non-universality of the same measured in the high-mobility 2D semiconductors23. The large spread in the observed values of κ seen in the data in GaAs quantum wells was attributed to two main reasons23. The first is the formation of numerous emerging FQH phases between ν = 1/3 and 2/5, which limits the temperature range over which one observes the decrease of the width of Rxx with T. Note that in Fig. 1b, there are two incipient FQH phases, ν = 3 + 1/5 and 3 + 2/7, between the more robust phases ν = 3 and ν  =  3 + 1/3. The incipient phases are weak enough not to affect the scaling of the transition region in Rxy even at the lowest temperature employed here. As a result, we find κ = 0.42 ± 0.01 (Fig. 3a).

The second reason is related to the type of disorder in the sample23. Universality in κ is observed only when the effective disorder potential is short-ranged20, as in our graphite-gated high-mobility graphene devices. This is not the case in GaAs/AlGaAs systems, where long-range scattering potential from the impurities cannot be ignored23. We fabricated graphene devices without the graphite gate electrodes to probe the effect of long-range interactions on κ. The graphene channel was no longer screened from long-range Coulomb fluctuations arising from the SiO2 substrate; this was reflected in reduced mobility  ~2−5 m2/Vs. While in these devices, we do not find FQH states, the value of κ for IQH transitions varied widely between 0.45−0.64 (Supplementary Information, Supplementary Note 4), supporting the conclusions of ref. 23.

To summarize, our principal finding is that scaling properties for transitions involving Abelian FQH states and/or IQH phases are universal. Specifically, we have demonstrated the scaling of the longitudinal conductance (with a scaling exponent κ = 0.41 ± 0.02 and localization exponent γ ≈ 2.3) in the IQH and FQH states in Bernal-stacked ABA trilayer graphene. This conclusion holds for plateau-to-plateau transitions between two consecutive IQH states, two FQH states, and even between IQH and the adjoining FQH state, underlining the universal character of the scaling. This universality of κ persists even when an external displacement field hybridizes the Landau levels of Bernal-stacked TLG. In fact, we find deviations from universality in the value of κ only in devices where long-range scattering dominates. To our knowledge, ours is the first definite scaling analysis of the QPT over a series of fractional QH states.

FQH phases are underlined by strongly correlated and interacting electrons. Our results demonstrate a surprising correspondence between the FQH phase transitions and those of non-interacting electrons. The results indicate a super-universality in the localization–delocalization transitions across distinct anyonic species that represent the characteristic quasiparticles of the FQH phases. While much is known about the localization of electrons, the observed super universality motivates the study of localization in anyonic quasiparticles and the mechanism that drives their conduction in the presence of disorder and quasiparticle interactions. Our study raises the natural question of whether the universality observed in this context applies to transitions between other topological phases with fractional excitations, such as fractional Chern insulators45.

Methods

Device fabrication

Devices of dual graphite gated ABA trilayer graphene (TLG) heterostructures were fabricated using a dry transfer technique (for details, see Supplementary Information Supplementary Note 1). Raman spectroscopy and optical contrast were used to determine the number of layers and the stacking sequence. The devices were patterned using electron beam lithography followed by reactive ion etching and thermal deposition of Cr/Pd/Au contacts. Dual electrostatic gates were used to simultaneously tune the areal number density n = [(CtgVtg + CbgVbg)/e + no] and the displacement field D = [(CbgVbg−CtgVtg)/2ϵ0 + D0] across the device. Here Cbg(Ctg) is the capacitance of the back gate (top gate), and Vbg(Vtg) is the voltage of the back gate (top gate). The values of Ctg and Cbg are determined from quantum Hall measurements. no and Do are the residual number density and electric field due to unavoidable impurities in the channel.

Transport measurements

The electrical transport measurements were performed in a dilution refrigerator (with a base temperature of 20 mK) at low frequency (11.4 Hz) using standard low-frequency measurement techniques, with a bias current of 10 nA.