Deep learning resilience inference for complex networked systems

Abstract

Resilience, the ability to maintain fundamental functionality amidst failures and errors, is crucial for complex networked systems. Most analytical approaches rely on predefined equations for node activity dynamics and simplifying assumptions on network topology, limiting their applicability to real-world systems. Here, we propose ResInf, a deep learning framework integrating transformers and graph neural networks to infer resilience directly from observational data. ResInf learns representations of node activity dynamics and network topology without simplifying assumptions, enabling accurate resilience inference and low-dimensional visualization. Experimental results show that ResInf significantly outperforms analytical methods, with an F1-score improvement of up to 41.59% over Gao-Barzel-Barabási framework and 14.32% over spectral dimension reduction. It also generalizes to unseen topologies and dynamics and maintains robust performance despite observational disturbances. Our findings suggest that ResInf addresses an important gap in resilience inference for real-world systems, offering a fresh perspective on incorporating data-driven approaches to complex network modeling.

Introduction

Complex systems in diverse domains, including ecology, biochemistry, and physiology, are commonly characterized as networked systems with interconnected nodes and weighted links^1,2,3,4. Resilience^5,6,7, defined as the capacity to maintain functionality under perturbations, is a fundamental property of these systems. The foundational insights into resilience can be traced back to Robert May’s seminal work⁸, where he pioneered the investigation of stability equilibrium in these networked systems. In 1973, Holling⁹ conceptualized the notion of resilience as the degree of external perturbations a system can endure, but he provided limited insights on the empirical measurements. Later studies¹⁰ further analyzed the responses of networked systems to perturbations, evaluating the connectivity in the context of node and edge disruptions. The concept of network resilience was formally defined recently⁵, articulating that a resilient system should invariably converge to a desired, non-trivial stable equilibrium after perturbation. Prior research^11,12 indicates that the loss of resilience often has extensive implications. For instance, in ecological systems, the decline in resilience can precipitate mass species extinctions¹³. This underscores the profound consequences of resilience loss and highlights the urgent need for approaches to predict and mitigate such outcomes.

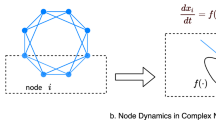
Generally, given a complex networked system G = (V, A) with N nodes, we use V to represent the node set and A to represent the weighted interaction matrix, where ${A}_{ij}\in {\mathbb{R}}$ denotes the interaction intensity between node i and j. The activity of a specific node i is represented as x_i, governed by the following non-linear differential equation:

$$\frac{d{x}_{i}}{dt}=\, {{\rm{F}}}({x}_{i})+{\sum }_{j=1}^{N}{A}_{ij}{{\rm{G}}}({x}_{i},{x}_{j}),$$

(1)

where F(x_i) on the right side signifies the self-dynamics of node i, G(x_i, x_j) characterizes the interaction dynamics between node i and j. The solution pattern of stable equilibrium for Equation (1) describes system resilience. The system is resilient if there is a non-zero unique stable equilibrium that indicates its functional state. Otherwise, it is non-resilient if there are stable dysfunctional equilibria that can trap the system or the system lacks the stable equilibrium, exhibiting chaotic behavior.

Noteworthy contributions^{5,14,15,16,17} have sought to provide analytical estimates for resilience of N-dimensional systems with complex interactions between components by reducing them to tractable one-dimensional systems based on mean-field theory, spectral graph theory, etc. Despite their groundbreaking successes, these approaches often make strong assumptions about network topology and dynamics for analytical feasibility¹⁸. We use the classic Gao-Barzel-Barabási (GBB)⁵ framework as an example to explore the constraints of these assumptions. Specifically, GBB computes a single resilience parameter ${\beta }_{{{\rm{eff}}}}\in {\mathbb{R}}$ for a networked system. The system is deemed resilient only if its resilience parameter exceeds a certain critical threshold, i.e., ${\beta }_{{{\rm{eff}}}} \, > \, {\beta }_{{{\rm{eff}}}}^{c}$ (Fig. 1d–f). However, the accurate estimation of β_eff and ${\beta }_{{{\rm{eff}}}}^{c}$ relies on the strong assumptions that node activity dynamics can be described with linear equations and the degrees of interconnected nodes are almost mutually independent. We evaluate GBB on several synthetic networked systems governed by representative mutualistic¹⁹, gene regulatory³, and neuronal dynamics²⁰ (Dynamics and datasets in Methods). In all three settings, we observe that inaccurate inferences consistently occur in networked systems with positive or negative assortativity. Taking the systems with mutualistic dynamics as examples, they are both inferred to be non-resilient due to their ${\beta }_{{{\rm{eff}}}} \, < \, {\beta }_{{{\rm{eff}}}}^{c}$ (Fig. 1d). However, the networked system with negative assortativity is, in fact, resilient (Fig. 1a, red color), because its network activity consistently converges to a single equilibrium (Fig. 1g, red curve). These findings demonstrate that classic analytic models often yield inaccurate inferences when their foundational assumptions are violated. Therefore, accurately inferring network resilience remains an unresolved challenge in practice, largely due to the divergence between the simplifying assumptions of current analytical frameworks and the complexities encountered in real-world contexts.

Fig. 1: Example cases of simplified analytical inferences.

We perform case studies on networks with mutualistic (parameter setting: B = 0.1, C = 1, K = 5, D = 5, E = 0.9, H = 0.1) (a), gene regulatory (parameter setting: f = 1, h = 2, B = 1) (b), and neuronal (parameter setting: μ = 3.5, δ = 2) (c) dynamics. Specifically, we first plot the 1-D resilience function condensed by GBB from the original high dimensional equations, where we show the stable equilibrium of x_eff (Supplementary Equation (11)) given β_eff (Supplementary Equation (12)). We analyze pairs of networks that have similar β_eff under GBB framework but different assortativity measured by degree correlation coefficient r. Network (I),(II),(V), and (VI) are all inferred as non-resilient by the classic GBB framework because ${\beta }_{{{\rm{eff}}}} \, < \, {\beta }_{{{\rm{eff}}}}^{c}$(d, f). On the contrary, Network (III) and (IV) are inferred as resilient with ${\beta }_{{{\rm{eff}}}} \, > \, {\beta }_{{{\rm{eff}}}}^{c}$(e). We further simulate the node activities using the corresponding dynamics for 100 times with varying initial conditions (Dynamics and datasets in Methods) on each network, and employ kernel density estimation (KDE) plot to visualize the distribution of its stable states. However, the ground truth simulations show Network (II), (III) and (VI) are resilient because they have a unique, non-trivial stable states (〈x〉 > 0), while Network (I), (IV) and (V) are non-resilient for having more than 1 stable states or only 1 trivial stable state (〈x〉 = 0) (g–i). Therefore, Network (II), (IV), (VI) are inaccurately inferred by the classic analytic model GBB, and they all have negative or positive assortativity.

In this study, we demonstrate how deep learning methods can effectively leverage the increasingly available observational data to extend the idea of resilience inference to real-world complex networked systems. We design a powerful deep learning framework that effectively integrates Transformer and Graph Neural Network (GNN) architectures, facilitating the learning of Resilience Inference representations (ResInf for short) across various complex networked systems. Specifically, ResInf employs stacked Transformer encoder layers²¹ to generate representations for the governing equations of node activity dynamics by modeling the complex correlations among node activities, which is subsequently merged with topological representations through GNN’s message passing mechanisms^{22,23,24,25,26}. The learned representations for multiple observations are aggregated and projected into a specialized 1-dimensional decision space, termed ‘k-space’. This space enables precise classification of resilient systems and provides insights on the systems’ closeness to critical thresholds that indicate shifts in resilience status.

We employ ResInf on real-world microbial systems in a laboratory setting where traditional analytical approaches are infeasible due to the unavailability of definitive governing equations for node activity dynamics. Our numerical results demonstrate that ResInf achieves an impressive accuracy rate, attaining an F1-score of up to 0.829 on average. Additionally, when assessed on synthetic networked systems driven by three representative equations, i.e., mutualistic, gene regulatory, and neuronal dynamics, ResInf markedly outperforms its conventional counterparts, achieving a maximum F1-score improvement of up to 41.59% and 14.32% compared to Gao-Barzel-Barabási (GBB) framework⁵ and spectral dimension reduction (SDR) approach¹⁴, respectively. If we train ResInf on data covering different patterns of resilience loss, including phase shifts and the emergence of alternative stable states, it can effectively capture these underlying patterns and leverage such generalizable knowledge to infer the resilience of systems with previously unseen dynamics. Importantly, ResInf maintains robustness under various types of observation noise, including missing or spurious links in network topologies and inaccuracies in node activity trajectories. These findings demonstrate that carefully designed deep learning models can effectively exploit observational data for complex system analysis and suggest that the proposed ResInf framework can be adapted to diverse real-world complex systems without the crutch of oversimplifying assumptions.

Results

ResInf framework

Here we formulate the resilience inference problem investigated in our work. We denote a complex networked system with N nodes as G = (V, A) with node set V and adjacency matrix ${{\bf{A}}}\in {{\mathbb{R}}}^{N\times N}$, where ${A}_{ij}\in {\mathbb{R}}$ denotes the interaction intensity between node i and j. Its node activities at time step t are denoted as ${{\bf{x}}}(t)\in {{\mathbb{R}}}^{N}$. The resilience of the networked system, i.e., the label, can be represented by a binary variable y ∈ {0, 1}. The system is resilient (y = 1) if node activities consistently converge to a non-zero and unique equilibrium regardless of initial node activity conditions. Otherwise, the system is non-resilient (y = 0) if there are stable dysfunctional equilibria that can trap the system or it lacks the stable equilibrium, only exhibiting chaotic behavior. Based on this definition, we can determine labels of system resilience through the observation of node activities without knowing underlying dynamics equations, i.e., Equation (1) of the system. Our objective is to infer the resilience y of the system in advance from a data-driven perspective. The input data comprises system topology, i.e., ${{\bf{A}}}\in {{\mathbb{R}}}^{N\times N}$, which describes interactions between components, and node activities ${{\bf{X}}}\in {{\mathbb{R}}}^{M\times N\times d}$ containing x(t) of M observed trajectories with the first d initial steps where the resilience of system remains unknown to us. Each trajectory is initiated with a unique node activity condition.

To address the problem, we present a deep learning Resilience Inference framework (ResInf, Fig. 2). Specifically, ResInf leverages stacked transformer networks²¹ as a dynamics encoder to learn dense representations for the underlying node activity dynamics from the input node activity trajectories X without any prior knowledge (Supplementary Fig. 1)^21,27. Different trajectories are encoded in parallel, thus the module produces M node activity dynamics representations for each node. Moreover, we design a topology encoder that uses graph neural network (GNN)²² to model the non-Euclidean network topology from the input adjacency matrix A with a message-passing mechanism that recursively aggregates features from neighboring nodes (Supplementary Fig. 2). It can generate discriminating topological representations for each node’s multi-hop neighborhood²⁸. We use node activity dynamics representations from the dynamics encoder module as the input of the topology encoder module, which treats them as the initial node features and incorporates them with topology information via the message passing GNN layers, thereby incorporating information of node activity dynamics to the produced topological representations. Subsequently, these learned representations are transmitted to and consolidated by a virtual global node, providing a holistic system representation describing system-level characteristics. Owing to the parallel processing of different trajectories in aforementioned procedures, we obtain M system representations, each capturing knowledge from an input node activity trajectory and integrating information from network topology. Given that network resilience is characterized by achieving a consistent stable equilibrium across different trajectories, we develop a trajectory aggregator designed to harness M system representations derived from different trajectories. It uses the self-attention network to assign weights of M system representations dynamically and fuses them to a final system representation accordingly (Supplementary Fig. 3). The fused system representation is then projected to a 1-dimensional k-space with the fully connected network, which facilitates informative visualization and accurate resilience inference. We illustrate more technical details of ResInf in Methods.

Fig. 2: The proposed ResInf framework.

ResInf leverages real-world observed or simulated network topologies and node activity trajectories to infer the resilience of networked systems without any prior assumption. It contains three modules: the dynamics encoder maps node activity trajectories to dense representations with stacked Transformer encoder layers, which models the complex correlations between node activities and produces representations for node activity dynamics; topology encoder leverages graph neural network to generate discriminating topological representations for each node’s multi-hop neighborhoods; k-space projector aggregates the representations for node activity dynamics and topologies via a virtual global node, and employs a multi-head self-attention network to fuse the representations learned from various trajectories dynamically. Subsequently, it uses a dimension reduction network to project the aggregated representation to a 1-dimensional k-space, facilitating accurate resilience inference with linear classifiers.

Resilience inference of real-world microbial systems

Microbial systems are ubiquitous in the real-world and essential for organic decomposition and nutrient cycling. Therefore, their resilience significantly contributes to the ecological balance. We employ the empirical data collected by a recent study that investigates dynamic species compositions in bacterial microcosms²⁹, where abundances of species and competition interplay between them correspond to node activities and network topology, respectively. Each data contains abundances of species from the same microbial community observed via laboratory experiments. Resilience of these systems are determined by fluctuation intensity of observed species abundances, which is consistent with the existing work²⁹ (Real-world microbial systems in Methods). Species abundances of non-resilient microbial systems with intense competition often exhibit chaotic fluctuations, as opposed to that of resilient systems marked by a stable equilibrium³⁰. We illustrate examples of the relative species abundances of resilient and non-resilient microbial systems in Fig. 3a. Real-world microbial systems often exhibit complex intrinsic activity dynamics among diverse types of bacteria^29,31, rendering them inapplicable for analytical approaches since such behavior cannot be concisely described by equations but can only be assessed through observations. Therefore, we employ our data-driven approach ResInf on microbial systems as a case study to validate its real-world performance. For each system, we input species abundances to the model along with a complete network with uniform edge weight as the default topology, following the maximum entropy principle. We randomly split the real-world microbial systems into training and test sets (85% vs 15%).

Fig. 3: Resilience inference of real-world microbial systems.

Data of each microbial system comprises abundances of species in the same microbial community observed during 11 days of laboratory experiments²⁹. The resilience of systems (i.e., labels) are determined by the fluctuation intensity of species abundances (the coefficient of variation, Real-world microbial systems in Methods). a Relative species abundances of resilient (without black slash) and non-resilient (with black slash) microbial systems. Colors are employed to distinguish between different species. Species abundances of the non-resilient microbial system display persistent fluctuation and cannot converge to a stable equilibrium. b F1-scores of different models trained on real-world microbial systems. We employ species abundances of the first three days along with a complete network with uniform edge weight as the default topology (following the maximum entropy principle) for both training the model and inferring the resilience of microbial systems. We randomly split microbial systems into training and test sets (85% vs 15%). c F1-scores of different models trained on simulated systems (Supplementary Note 2). It should be noted that conventional analytical frameworks (for example, GBB) are not applicable in this scenario since we cannot describe the system with explicit dynamics equations. Bars represent the average values, and error bars represent the standard deviation (n = 35 with different random seeds).

We compare ResInf with several representative data-driven baselines, including two deep learning architectures—the multilayer perceptron model (MLP), long short-term memory model (LSTM)³², and two graph kernel-based models—shortest path kernel model (SP)³³ and propagation kernel model (PROP)³⁴ (Supplementary Note 1.1 ~ 1.4). We utilize the F1-score (Evaluation metrics in Methods), a combined metric of precision (how many inferred resilient systems are actually resilient) and recall (how many resilient systems are correctly inferred) to quantify the performances of models. Figure 3b demonstrates that ResInf can achieve a high F1-score of 0.829 ± 0.028 in inferring the resilience of real microbial systems, which surpasses competitive baselines LSTM by 34.14%. It shows that deep learning architectures without specific designs for resilience inference are usually sub-optimal for the problem, which can also apply to graph kernel-based models SP and PROP that regard node activities as static features neglecting their temporal dependencies. Conventional analytical frameworks (for example, GBB) are even not applicable in this scenario since we cannot describe the system with explicit dynamics equations to find a theoretical bifurcation point. The results demonstrate that our data-driven deep learning framework, ResInf, effectively extends resilience inference to real-world microbial systems without prior knowledge and assumptions, holding promising potential for resilience inference across various networked systems even if their node activity dynamics are complex and difficult to describe explicitly.

In broader scenarios where real-world systems have not yet collapsed and only limited training data are available from the system under investigation, directly training ResInf becomes impractical. To avoid collecting large amounts of training data in the wild or laboratories, we propose an alternative approach that leverages simulated data to train ResInf, where node activity trajectories are generated by solving dynamics equations on synthetic topologies. We use these microbial systems as a representative test dataset to validate our approach. Specifically, we evaluate the performances of models when trained solely on simulated data from SIS dynamics (Dynamics and datasets in Methods) and subsequently apply them to infer the resilience of these real-world microbial systems (Fig. 3c, details in Supplementary Note 2). The results demonstrate that ResInf achieves a competitive F1-score of 0.807 ± 0.016. Notably, this performance shows slight differences from the F1-score of 0.829 ± 0.028 obtained when the framework is trained directly on laboratory-collected data from real microbial systems. It underscores the practical applicability of ResInf in real-world scenarios, eliminating the need and effort for extensive data collection from both laboratories and real environments.

Resilience Inference of Synthetic Networked Systems

To evaluate the performance of ResInf across various scenarios, we further conduct resilience inference experiments on synthetic networked systems governed by three representative dynamics, i.e., mutualistic, gene regulatory, and neuronal dynamics. Specifically, we use the network topologies empirically collected from ecosystems and cells for mutualistic and regulatory systems^5,35, respectively. Besides, we use the classic Erdős-Rényi³⁶ and Barabási-Albert³⁷ models to generate topologies for systems governed by neuronal dynamics, which is consistent with the setting in previous study³⁸. Moreover, it is of great importance to examine the resilience inference performance in the scenarios in which the networked systems experience specific perturbations. Therefore, we follow the settings in existing works⁵ to perform random perturbations of node removal, link removal, and global weight changes on the synthetic networked systems (Simulating critical events in Methods). Finally, the proposed ResInf and baseline models are trained on a randomly sampled subset of the synthetic networked systems, and evaluated on a test set with previously unseen networked systems. Besides the aforementioned four data-driven frameworks, including MLP, LSTM, SP, and PROP, we also introduce two conventional models—Gao-Barzel-Barabási (GBB)⁵ and spectral dimension reduction (SDR)¹⁴ frameworks (Supplementary Note 1.5 ~ 1.6). GBB offers a dimension reduction approach that effectively reduces an N-dimensional system into a one-dimensional degree-related β-space, subject to the constraint of neutral assortativity topology. SDR utilizes the dominant eigenvalue α of the system topology to achieve accurate dimension reduction grounded in a theoretical premise. These two approaches are exemplary methods for estimating resilience of networked systems from the analytical perspective.

The experiment results demonstrate ResInf consistently outperforms all baseline models in F1-score across networked systems governed by mutualistic, gene regulatory, and neuronal dynamics (Fig. 4a–c). For example, ResInf registers an F1-score of 0.977 ± 0.005 on networked systems with mutualistic dynamics, while the F1-scores of classic analytical model GBB and SDR are 0.690 ± 0.015 and 0.858 ± 0.007, respectively, despite GBB and SDR leverage explicit node activity dynamics equations. Therefore, based on just a few initial observed node activities about investigated systems compared to existing analytical frameworks, the superior performance of ResInf indicates that it effectively captures the underlying resilience loss patterns and the complex interplay between topology and node activity dynamics from observed data, shedding lights on the potential of learning-based approaches in understanding complex networked systems. ResInf also outperforms all data-driven baselines, i.e., LSTM, PROP, SP, and MLP. It is worth pointing out that LSTM and PROP have comparable performance with GBB and SDR, but only ResInf significantly outperforms GBB and SDR in all settings (p < 0.01, two-sided Student’s t-test). Besides, we find that ResInf consistently has the best performance on each subset of the networked systems classified by the aforementioned perturbation types (Supplementary Fig. 5) and in different hyper-parameter settings (Supplementary Note 4, Supplementary Figs. 12–13). Furthermore, we evaluate our framework ResInf on synthetic data with low and high assortative topologies (Supplementary Fig. 6 and Supplementary Tables 6–7). The results reveal that the performance of GBB is inferior on high-assortative networks compared to low-assortative networks. Although SDR shows some improvement, there still remains a noticeable gap in its performance on networks with mutualistic dynamics. On the contrary, our ResInf framework demonstrates consistent performance across both types of networks, with no discernible difference in its efficacy. Beyond the application to mutualistic, gene regulatory, and neuronal networks, our developed framework can also explore the resilience of other systems with different node activity dynamics and structural properties (see Supplementary Note 3 and Supplementary Fig. 7 for human interactions with epidemic spreading cases). The above results demonstrate that ResInf can make accurate resilience inference across networked systems with various settings, representing an important methodological advance that outperforms the state-of-the-art analytical model without leveraging explicit dynamics equations.

Fig. 4: Resilience inference performance on synthetic networked systems.

We evaluate resilience inference performance of ResInf along with other baseline methods on synthetic network datasets. These datasets include mixed types of perturbed networks of mutualistic (a), gene regulatory (b), and neuronal (c) dynamics, respectively (Supplementary Table 2). The parameter of each dynamics is the setting outlined in index 1 of Supplementary Table 4. The dataset of each dynamics contains 2000 samples, which are partitioned into training, validation, and test sets at a ratio of 8:1:1. For the mutualistic, gene regulatory, and neuronal dynamics, we consider 10, 5, and 11 different initial conditions, respectively. Box plots depict the median (central line) of F1-scores (n = 35 with different random seeds), the first and third quartiles (box), whiskers extending to 1.5 times the interquartile range from the first and third quartiles, respectively, and outliers are represented as individual points.

Generalizability of ResInf

The networked systems under consideration may emerge in new contexts where node activity dynamics parameters, or even the underlying equations themselves, differ from existing data, thus hindering the application of analytical approaches that rely on comprehensive knowledge of systems’ node activity dynamics. Furthermore, the lack of labels for these new systems also impedes our ability to directly retrain the models and extend their applicability to such novel contexts. In this section, we assess the out-of-sample inference performance of ResInf, demonstrating its generalizability across both dynamics parameters and dynamics equations, which underscores the model’s effectiveness in adapting to systems with varying node activity dynamics.

Networked systems with similar functions in the real-world often share identical forms of node activity dynamics, while the parameters governing these dynamics are usually different. For instance, the intrinsic mechanisms of self-growth and pairwise symbiotic effects on species abundances can be similarly described across a majority of ecosystems, however, the environmental capacities that support species vary significantly among them^7,39. An intuitive idea is to leverage data from other systems with similar functions to enhance the resilience inference of the system under investigation, which necessitates that the inference model generalizes across various dynamics parameters. To assess such generalizability of ResInf, we generate node activities within networks using the same dynamics equations but with varying parameter settings (Supplementary Table 4), which are divided into training and test parameter settings with the ratio of 2:1. We train the models using networks configured with training parameter settings and subsequently evaluate them using those with unseen test parameter settings. Results for mutualistic, regulatory, and neuronal dynamics as depicted in Fig. 5a–c indicate that our model achieves the highest out-of-sample performance, with average F1-scores of 0.921, 0.892, and 0.924, respectively, demonstrating its superior generalizability. It reveals that ResInf effectively captures the common intrinsic dynamics form through the training data with different dynamics parameter settings.

Fig. 5: Generalizability of models.

We demonstrate the generalizability of models across varying dynamics parameters and dynamics equations. a–c Generalizability of models across varying dynamics parameters of mutualistic (a), gene regulatory (b), and neuronal (c) dynamics. For each dynamics, we randomly choose six of nine parameter settings (Supplementary Table 4) for generating training data. We employ each parameter setting to simulate node activity trajectories for 1000 perturbed networks via node removal from empirical networks and combine all data of different parameter settings, formulating 6000 samples. To facilitate the training process, we randomly select 1000 samples to construct the training set. Similarly, we employ each of the other three unseen parameter settings to simulate node activity trajectories for 200 perturbed networks via node removal from empirical networks and combine all data of different parameter settings, formulating 600 samples and randomly selecting 200 samples to construct the validation/test set. d–f Generalizability of models across different dynamics equations. We employ three parameter settings of SIS and inhibitory dynamics (Supplementary Table 5) to simulate node activity trajectories for random networks with (N, p) uniformly sampled from [30,60) and [0.05,0.25), respectively. We synthesize 1600 samples under each parameter setting of each dynamics and combine all generated samples, then randomly select 1600 samples as the training set. To construct the validation/test set, we use mutualistic (d), gene regulatory (e), and neuronal (f) dynamics, respectively. We also employ three parameter settings of each dynamics (Index 2–4 of Supplementary Table 4) to simulate node activity trajectories for 160 random networks with the same (N, p) distributions as the training set. For mutualistic, gene regulatory, neuronal, SIS, and inhibitory dynamics, we consider 10, 5, 11, 11, and 11 different initial conditions, respectively. Box plots depict the median (central line) of F1-scores (n = 35 with different random seeds), the first and third quartiles (box), whiskers extending to 1.5 times the interquartile range from the first and third quartiles, respectively, and outliers are represented as individual points.

Another crucial issue concerns whether ResInf can benefit from training on data of other systems, even those with different dynamic equations, and directly infer the resilience of investigated systems, which broadens the practical applications of our framework but also necessitates generalization across different dynamics equations. Previous works^7,40 have established that the resilience loss patterns of network systems governed by diverse dynamic equations can be classified into two main categories: phase shifts and the emergence of alternative stable states. For instance, Fig. 1g shows that network systems with mutualistic dynamics may undergo a transition from a region with a unique, non-zero equilibrium to another region with the emergence of multiple stable equilibria, where the system can be trapped in an undesired dysfunctional equilibrium. From Fig. 1h, gene regulatory networks may shift to a death equilibrium where all nodes have zero activity and can never recover to their functional equilibrium. Therefore, we hypothesize that if we train our ResInf framework on a dataset of diverse network systems covering both categories of resilience loss patterns, it should be able to generalize to network systems governed by novel dynamic equations that are previously unseen in the training set. To test this hypothesis, we introduce two new forms of node activity dynamics equations: susceptible-infectious-susceptible (SIS) dynamics⁴¹ and inhibitory dynamics⁴² (Dynamics and datasets in Methods). SIS and inhibitory dynamics belong to the categories of phase shifts and the emergence of alternative stable states, respectively. We construct the training set based on network systems governed by these two dynamics equations and test ResInf on the network systems governed by mutualistic, gene regulatory, and neuronal dynamics. As shown in Fig. 5d–f, we find that ResInf can achieve good performance and consistently outperforms all baseline models, even if it is tested on networks with new forms of node activity dynamics that have not been seen in the training set. It registers F1-scores of 0.862 ± 0.025, 0.889 ± 0.023, and 0.887 ± 0.019 on networked systems with mutualistic, regulatory, and neuronal dynamics, respectively, while other methods lose generalizability and have much worse performance. It is worth pointing out that analytical models (GBB and SDR) are not applicable in this generalization scenario because the dynamic equations of testing networks are unknown to the resilience inference model. These results suggest ResInf indeed has good generalizability, i.e., a representative training set is sufficient for ResInf to perform well in novel network systems with unknown node dynamic equations. We conduct further experiments where we train ResInf on networks with either SIS or inhibitory dynamics and evaluate its generalization performance on mutualistic, regulatory, and neuronal networks. We find that ResInf shows better generalizability when the resilience loss patterns of training networks cover those of the test samples (Supplementary Fig. 8a–c). It indicates that having network systems with the same category of resilience loss patterns in the training set ensures the generalization performance of ResInf. This requirement can be easily satisfied in various scenarios, and researchers can conveniently construct adequate training sets as we illustrated above.

Beyond assessing performance across various dynamics parameters and equations, we demonstrate that ResInf maintains its superior generalizability when tested on network topology types distinct from those used during training. After training on Erdős-Rényi networks with SIS and inhibitory dynamics, ResInf consistently obtains the best F1-scores among all baselines, surpassing over 0.818 on Barabási-Albert (scale-free) networks as well as empirical networks with mutualistic, regulatory, and neuronal dynamics, respectively (Supplementary Fig. 9). The GNN-based topology encoder of ResInf is capable of learning generalizable knowledge for resilience inference without making assumptions regarding topologies or relying on specific network structures, which significantly enhances the generalizability of ResInf to previously unseen topology types.

Resilience Inference from Noisy Data

Empirical measurements of real-world networked systems are often compromised by noise. Consequently, we evaluate the robustness of our model’s performance in the presence of various types of observational noise, including noisy node activity trajectories, missing links, and spurious links. Specifically, we simulate noisy node activity trajectories by introducing Gaussian noise governed by a specified noise-to-signal ratio (NSR). Furthermore, missing and spurious links are simulated by randomly removing or adding a fraction of links to reproduce inaccurately estimated node interactions^43,44.

As depicted in Fig. 6a–c, it is evident that ResInf exhibits the best resilience inference performance when various levels of observational noise are introduced to the node activity trajectories. Taking the performance on mutualistic networks as an example, the F1-score of ResInf is 0.964 ± 0.011 in the absence of observational noise (NSR = 0), and it still remains at 0.854 ± 0.017 when NSR increases to 1, i.e., the power of the noise is as strong as the original node activity trajectories. The desirable noise-resistant feature of ResInf can be explained from the following aspects: first, the Transformer-based dynamics encoder can model temporal correlations and intrinsic dynamics of node activity from observed data and filter out uncorrelated noises adaptively^45,46,47. The added noise is stochastic in nature, which will not easily blur the average, intrinsic patterns of system dynamics. Second, the topology encoder leverages graph neural network with a message-passing mechanism, which acts as a special form of Laplacian smoothing on the network, reducing the noise transmitted from neighboring nodes^26,48. Therefore, the impact of noisy node activities can be significantly diminished, ensuring that the inference performance remains almost unaffected. It should be noted that analytical models GBB and SDR have access to precise governing dynamics equations and do not rely on observed activities. Consequently, they are unaffected by observational noise in node activity trajectories, making them not directly comparable in this context. Therefore, we assess the robustness of ResInf and analytical frameworks against the intrinsic uncertainty of the dynamics itself. Specifically, we introduce a stochastic term of Gaussian white noise with variance η into the ground truth dynamics equations to generate node activity trajectories. This uncertainty introduces a fundamental limitation in accurately describing the dynamics of node activities. From the results presented in Supplementary Fig. 10, we observe a significant decline or fluctuation in the performance of analytical frameworks, attributed to their reliance on estimating resilience solely by analyzing critical points from precise dynamics equations. Thus, these frameworks lack adaptability to real scenarios where dynamics are also influenced by intrinsic stochastic noises. In contrast, ResInf maintains remarkable performance at η = 0.4, exhibiting less susceptibility to the uncertainties of dynamic environments. These results further substantiate ResInf’s superior capability in learning node activity dynamics and resilience patterns directly from observed data, showcasing a notable advantage over traditional frameworks.

Fig. 6: The robustness of resilience inference against observational noises.

We employ the same datasets, data split ratios, the number of initial conditions considered, and dynamics parameter settings as in Fig. 4. In contrast, we introduce observational noises into their node activities or network topologies. We repeat all experiments with 35 different random seeds, corresponding to different inference model initialization and split for datasets. a–c Noisy node activity: we evaluate the models' performance when various intensity levels of Gaussian noises are added to the observed node activity trajectories. Higher noise-to-signal ratio indicates stronger noise. GBB and SDR are left out in this comparison because they are not affected by node activity trajectories. Instead, GBB and SDR rely on explicit network dynamic equations that are not available to other methods. d–f Missing link: we evaluate the models' performance on networked systems with 5 ~ 30% links randomly removed. g–i Spurious link: we randomly add 5 ~ 30% links to pairs of nodes that are not originally connected and evaluate the models' performance on the perturbed networked systems. Centers represent the average values, and shadings represent the standard deviation (n = 35 with different random seeds).

Regarding the noise in network topology, it has been found that ResInf can achieve a high F1-score of 0.933 ± 0.015 on mutualistic networks, even with 30% of the original links missing (Fig. 6d). Additionally, ResInf maintains a high F1-score of 0.945 ± 0.013 on mutualistic networks even when the rate of spurious links reaches 30% (Fig. 6g). ResInf displays similar performance curves across various levels of network topology noise in different settings (Fig. 6d–i). Conversely, the analytical frameworks GBB and SDR exhibit a notable decline in performance with increasing noise levels from missing and spurious links, highlighting their significant dependence on accurate network topologies. For example, on mutualistic networks, the F1-score of GBB significantly reduces from 0.691 ± 0.027 to 0.521 ± 0.026 as the percentage of missing links increases from 0% to 30%. The performances of MLP and LSTM remain unchanged with varying percentages of missing or spurious links, as they solely model the node activity trajectories. However, the significant performance gains of ResInf over MLP and LSTM underscore the importance of effectively representing network topologies. We further assess the models’ robustness against the missing nodes, including cases where a fraction of nodes remains undetected either persistently or at a randomly chosen time step (Supplementary Fig. 11). These results further demonstrate that ResInf is better equipped to handle the effects of noisy network topologies and to ensure its potential efficacy in real-world applications. Given the correlated activities of real connected nodes, the dynamics encoder is capable of learning the activity dynamics of each node, accounting for influences from actual neighboring nodes. As resilience is inherently a network-level property, the network aggregator in the k-space projector (Fig. 2) adaptively aggregates information across the entire network. This approach effectively mitigates the impact of missing nodes or links, thereby enhancing the framework’s robustness. In conclusion, these experimental results demonstrate that ResInf can still produce reliable inferences even in the presence of significant noise affecting both observed node activities and network topologies, highlighting a critical feature of ResInf that ensures its adaptability to real-world systems.

Visualization in 1-dimensional Decision Space

Beyond the empirical accuracy of resilience inference, the capability to visualize a system’s proximity to the critical threshold of resilience loss within a low-dimensional decision space has profound implications for various applications. Such ability would allow stakeholders to make informed operation or management decisions in complex networked systems, which has been a useful feature of analytical approaches. In our study, ResInf uses k-space projector to map the networked systems into a condensed 1-dimensional k-space (Fig. 2), which facilitates accurate resilience inference with a simple monotonic classifier (ResInf framework in Methods). Therefore, the system representation in k-space can serve as an informative visualization of the system’s resilience property. Experiments on previously mentioned synthetic networked systems show most resilient (red) and non-resilient (blue) systems are linearly separable in k-space (Fig. 7a–c). Specifically, by choosing a linear decision boundary with maximum likelihood k^c, we can classify the resilience systems with an F1-score of 0.933–0.987. The distance to the decision boundary in k-space indicates the system’s proximity to the critical point of resilience loss. Therefore, k-space representations serve as an informative visualization tool and a reliable indicator of the system’s resilience, offering a concrete way to interpret resilience inference results.

Fig. 7: Visualizing networked systems in 1-dimensional decision space.

We illustrate the probability distributions of k and β_eff and α for networked systems with mutualistic (a, d, g), gene regulatory (b, e, h), and neuronal (c, f, i) dynamics, taking one experiments of Fig. 4 for each dynamics as examples. The critical thresholds inferred by ResInf, k^c, are shown as the grey dashed lines in (a–c). The critical thresholds computed by GBB, ${\beta }_{{{\rm{eff}}}}^{c}$, are shown as grey dashed lines in (d–f). We also show the critical threshold from SDR, α^c (g–i). We find resilient and non-resilient samples (resilient sp. and non-resilient sp.) are more linearly separable in k-space than β-space and α-space, which demonstrates the stronger resilience prediction capability of our proposed approach ResInf. j–l We illustrate the receiver operating characteristic (ROC) curve of GBB, SDR, and ResInf with the same experiment settings as Fig. 4 as well as the corresponding average AUC. Transparent lines represent experiments with different random seeds (n = 50), and solid lines represent the average ROC curve.

We compare the learned k-space with the β-space and α-space (Supplementary Note 1.6) generated by the analytical models GBB and SDR, respectively. We find the distributions of resilient and non-resilient systems have a larger overlap in β-space and α-space (Fig. 7d–i). For example, 47% of resilient mutualistic systems have β values smaller than the analytically inferred critical threshold ${\beta }_{{{\rm{eff}}}}^{c}$, which will lead to inaccurate classification. As a result, the resilience inference enabled by β-space and α-space has significantly lower F1-score compared to ResInf. Additionally, we explore the ratio of true and false positives (inferred resilient systems) using the condensed 1-dimensional parameters and the decision spaces of GBB, SDR, and ResInf through the receiver operating characteristic (ROC) curve. The ROC curve indicates the trade-off between the true positive rate and the false positive rate as the discrimination threshold (ResInf framework in Methods and Supplementary Note 1.5–1.6) is varied. The area under the ROC curve (AUC) comprehensively quantifies both the sensitivity (the proportion of true positives correctly identified) and specificity (the proportion of false positives correctly avoided) of the model. An AUC of 1 indicates a perfect inference model, while an AUC of 0.5 signifies a model that performs no better than random chance (Evaluation metrics in Methods). We demonstrate ROC curves on the investigated dynamics systems (Fig. 7j–l) and find that AUCs of ResInf among these systems are all near to 1, outperforming the analytical framework. It shows that ResInf exhibits superior diagnostic accuracy. This performance underscores the effectiveness of ResInf in achieving a high true positive rate while maintaining a low false positive rate, demonstrating its superior capability of distinguishing between resilient and non-resilient networks and the reliable of employing deep learning approaches to resilience inference problems.

Discussion

In this paper, we propose a powerful deep learning framework, ResInf, to infer the resilience of complex networked systems solely based on the observational data of their topologies and node activities. It acts as a data-driven method that relieves the unrealistic assumptions of network topology and dynamics in previous state-of-the-art analytical approaches, e.g., the requirements of low assortativity topology, linear node activity dynamics, and knowing the explicit equations of node activity dynamics. The removal of these prerequisites largely broadens the application scenarios for more general complex networked systems, such as complex contagion in social networks^41,49, energy transmission in power grids^50,51, and predatory behavior in food webs⁵², where the underlying dynamics often differs from case to case and cannot be known beforehand. Our experimental results demonstrate that ResInf exhibits strong generalizability across various networks with previously unseen dynamics of different equations and parameters. Particularly, by training on network data with the identified two main resilience loss patterns⁷, ResInf consistently achieves superior performance on existing known node activity dynamics, such as mutualistic, gene regulatory, and neuronal dynamics, even when these dynamics are not present in the training set. Furthermore, ResInf demonstrates consistent generalizability across various network types, highlighting its ability to learn transferable knowledge for resilience inference. This underscores the model’s applicability to a wide range of practical scenarios, particularly when encountering novel real-world network topologies and node activity dynamics. While the existing known node activity dynamics fall into the above two resilience loss patterns, future advances in this field may identify novel resilience loss patterns beyond these two categories, which could lead to sub-optimal performance of ResInf when such previously unseen patterns are emerging. Nevertheless, we can address this challenge by incorporating these novel patterns into the training set, thereby ensuring the generalizability of ResInf. Besides, as an analogy to the analytical β-space⁵ and α-space¹⁴, our ResInf model can map networked systems to a learned k-space where the resilient property of a given system can be more granularly gauged as the distance to critical threshold k^c, providing clear interpretable information on the system’s current resilience status. As such, the system’s k value serves as an insightful indicator that offers interpretability and fine-grained resilience assessment. Therefore, ResInf represents as a paradigm shift to data-driven resilience inference in empirical complex networked systems with interpretability. Beyond this, our recent work³⁸ paves the way to revive non-resilient networks. It suggests that non-resilient networks can be recovered to resilient ones by utilizing appropriate network restructuring and single-node reigniting strategies. ResInf can effectively guide such strategy design (Supplementary Note 5, Supplementary Fig. 14). Specifically, after implementing network restructuring and reigniting, we input the restructured network and initial time steps of node activities into ResInf. The mapped k point of the recovered network in the k-space acts as an indicator to ascertain the resilience recovery, which, in turn, enables us to refine and optimize the designed recovery strategy. This perspective shifts the focus of restoration from isolated interventions to a more integrated and systemic approach by prioritizing the network’s structural integrity and the synergistic relationships among its components, which is essential for addressing complex real-world challenges.

To advance the depth and breadth of networked system resilience research, we suggest two potential directions for future investigation. First, despite the increasingly available observational data of complex networks, it remains a challenging task to sense high-quality node activity trajectories and topology in real-world networked systems, which often requires extensive laboratory environments²⁹. As a result, it underscores the growing necessity for advanced complex network simulators. A promising research direction is to leverage generative AI frameworks to build learn-to-simulate models^49,53,54, which has the potential to go beyond the simple theoretical models^36,37 to generate more accurate simulation for wide-range of complex systems. Furthermore, while our proposed ResInf offers insights into the resilience inference challenge, the development of methods to enhance system resilience directly by AI methodologies is also promising for the research field. AI can be leveraged to build an optimization model that maximizes system resilience with a given budget, e.g., adding several critical links or dropping several weakly connected nodes. This would significantly amplify the impact of network resilience research as it extends to broader downstream applications⁵⁵ where enhancing resilience is crucial. To conclude, ResInf can serve as a proof-of-concept that exemplifies the potential of data-driven methods in network resilience research, demonstrating a promising avenue for innovating complex system studies with AI methods.

Methods

ResInf framework

Dynamics encoder

As previously mentioned, the underlying dynamics of networks mainly manifest themselves in node activities. Thus, to effectively capture node activity dynamics to infer their resilience, we develop a dynamics encoder inspired by Transformer^21,56 (Supplementary Fig. 1). We input the node activity trajectories ${{\bf{X}}}\in {{\mathbb{R}}}^{M\times N\times d}$, where d, M, N denote the used length of trajectories, the number of trajectories, and the number of nodes, respectively. For node i, its activity of the p-th trajectory can be denoted as ${{{\bf{X}}}}_{i}^{p}\in {{\mathbb{R}}}^{d\times 1}$. First, we transform activities of nodes at each time step with a shared multilayer perceptron (MLP), denoted as ${{{\rm{f}}}}_{{{\rm{in}}}}:{\mathbb{R}}\to {{\mathbb{R}}}^{{d}_{e}}$, that is, ${{{\bf{e}}}}_{i}^{p}={{{\rm{f}}}}_{{{\rm{in}}}}({{{\bf{X}}}}_{i}^{p})$, where d_e denotes the embedding size at each time and ${{{\bf{e}}}}_{i}^{p}\in {{\mathbb{R}}}^{d\times {d}_{e}}$. We also add positional embeddings to the input embeddings to mark the relative positions, i.e., ${{{\bf{e}}}}_{i}^{p}\leftarrow {{{\bf{e}}}}_{i}^{p}+{{\rm{PE}}}$. At each time step t of the total d time steps, positional embeddings are formulated as ${{{\rm{PE}}}}_{(t,2n)}=\sin (t/1000{0}^{2n/{d}_{e}})$, ${{{\rm{PE}}}}_{(t,2n+1)}=\cos (t/1000{0}^{2n/{d}_{e}})$, where the second element in the tuple of the subscript (2n and 2n + 1) corresponds to the index of elements in positional embeddings. Each dynamics encoder layer comprises a self-attention sub-layer and a fully-connected feed-forward sub-layer. A residual connection is established between these two sub-layers, which is subsequently followed by the application of layer normalization⁵⁷. Taking the input e as an example, the output of the sub-layer can be formulated as LayerNorm(e + Sublayer(e)).

The self-attention sub-layer consists of multiple attention heads, which enable ResInf to concurrently integrate information from different representation subspaces while simultaneously account for diverse positional contexts. For the attention head j, taking the input ${{{\bf{e}}}}_{i}^{p}$ as an example, the result embeddings can be obtained from the query matrix Q_j and key-value pairs K_j and V_j, which can be formulated as:

$${{{\rm{head}}}}_{j}=\, {{\rm{softmax}}}\left(\frac{{{{\bf{Q}}}}_{j}{{{\bf{K}}}}_{j}^{T}}{\sqrt{{d}_{k}}}\right){{{\bf{V}}}}_{j},$$

(2)

$${{{\bf{Q}}}}_{j} \,=\, {{{\bf{e}}}}_{i}^{p}{{{\bf{W}}}}_{j}^{Q},{{{\bf{K}}}}_{j}={{{\bf{e}}}}_{i}^{p}{{{\bf{W}}}}_{j}^{K},{{{\bf{V}}}}_{j}={{{\bf{e}}}}_{i}^{p}{{{\bf{W}}}}_{j}^{V},$$

(3)

where ${{{\bf{W}}}}_{j}^{Q}\in {{\mathbb{R}}}^{{d}_{e}\times {d}_{k}}$, ${{{\bf{W}}}}_{j}^{K}\in {{\mathbb{R}}}^{{d}_{e}\times {d}_{k}}$, and ${{{\bf{W}}}}_{j}^{V}\in {{\mathbb{R}}}^{{d}_{e}\times {d}_{e}}$ are trainable parameters. Fusing the information from h attention heads, we can derive the multi-head encoded representation, which also serves as the output of the self-attention sub-layer, formulated as:

$${{\rm{Self}}}\,{\mbox{-}}\,{{\rm{attention}}}({{{\bf{e}}}}_{i}^{p})={{\rm{Concat}}}({{{\rm{head}}}}_{1},{{{\rm{head}}}}_{2},\ldots,{{{\rm{head}}}}_{h}){{{\bf{W}}}}^{O},$$

(4)

where ${{{\bf{W}}}}^{O}\in {{\mathbb{R}}}^{h\cdot {d}_{e}\times {d}_{e}}$ are trainable parameters. Therefore, the final output of the self-attention sub-layer can be formulated as:

$${\tilde{{{\bf{e}}}}}_{i}^{p}={{\rm{LayerNorm}}}({{{\bf{e}}}}_{i}^{p}+{{\rm{Self}}}\,{\mbox{-}}\,{{\rm{attention}}}({{{\bf{e}}}}_{i}^{p})),$$

(5)

where ${\tilde{{{\bf{e}}}}}_{i}^{p}\in {{\mathbb{R}}}^{d\times {d}_{e}}$ represents the final output from the self-attention sub-layer.

The fully-connected feed-forward sub-layer comprises two linear transformation layers, with a ReLU activation function applied in between them. The output of the feed-forward sub-layer can be formulated as:

$${{\rm{Feed}}}\,{\mbox{-}}\,{{\rm{forward}}}({\tilde{{{\bf{e}}}}}_{i}^{p})={{\rm{ReLU}}}({\tilde{{{\bf{e}}}}}_{i}^{p}{{{\bf{W}}}}_{1}+{{{\bf{b}}}}_{1}){{{\bf{W}}}}_{2}+{{{\bf{b}}}}_{2},$$

(6)

where ${{{\bf{W}}}}_{1}\in {{\mathbb{R}}}^{{d}_{e}\times {d}_{h}}$, ${{{\bf{b}}}}_{1}\in {{\mathbb{R}}}^{{d}_{h}}$, ${{{\bf{W}}}}_{2}\in {{\mathbb{R}}}^{{d}_{h}\times {d}_{e}}$ and ${{{\bf{b}}}}_{2}\in {{\mathbb{R}}}^{{d}_{e}}$ are trainable parameters. Therefore, the final output of the fully-connected feed-forward sub-layer can be formulated as:

$${\hat{{{\bf{e}}}}}_{i}^{p}={{\rm{LayerNorm}}}({\tilde{{{\bf{e}}}}}_{i}^{p}+{{\rm{Feed}}}\,{\mbox{-}}\,{{\rm{forward}}}({\tilde{{{\bf{e}}}}}_{i}^{p})),$$

(7)

where ${\hat{{{\bf{e}}}}}_{i}^{p}\in {{\mathbb{R}}}^{d\times {d}_{e}}$ represents the final output from the fully-connected feed-forward sub-layer.

During the encoding process, ${{{\bf{e}}}}_{i}^{p}$ serves as the input to the first layer of the dynamics encoder, yielding the output ${\hat{{{\bf{e}}}}}_{i}^{p}$. Subsequently, ${\hat{{{\bf{e}}}}}_{i}^{p}$ becomes the input for the next layer of the dynamics encoder if we use multiple layers of the dynamics encoder. The output from the final layer of the dynamics encoder, denoted as ${{{\bf{Z}}}}_{p}^{i}\in {{\mathbb{R}}}^{d\times {d}_{e}}$, plays the role of the node activity dynamics representation for node i of the p-th trajectory. It should be noted that all nodes and trajectories, i.e., (i, p) ∈ {1, 2, ⋯  , ∣V∣} × {1, 2, ⋯  , M}, are encoded via the dynamics encoder in a parallel manner. We integrate the output representations of the last time step for nodes as their final node activity dynamics representations of the p-th trajectory, which is denoted as ${{{\bf{Z}}}}_{p}\in {{\mathbb{R}}}^{N\times {d}_{e}}$.

Topology encoder

We design a graph neural network (GNN)²² with multi-hop message passing to model the impact from multi-hop neighborhoods of nodes (Supplementary Fig. 2). Given an adjacency matrix A, we design the message passing operator Ψ as ${{\mathbf{\Psi }}}={{{\bf{I}}}}_{N}-{{{\bf{D}}}}_{{{\rm{in}}}}^{-\frac{1}{2}}{{\bf{A}}}{{{\bf{D}}}}_{{{\rm{out}}}}^{-\frac{1}{2}}$, where the diagonal element in the i-th row of D_in and D_out denotes the in-degree and out-degree of node i, respectively. The l-th layer message passing can be formulated as follows:

$${{{\bf{Z}}}}_{p}^{(l)}=\tanh ({{{\bf{Z}}}}_{p}^{(l-1)}{{{\bf{W}}}}_{F}^{(l)})+\tanh ({{\bf{\Psi }}}{{{\bf{Z}}}}_{p}^{(l-1)}{{{\bf{W}}}}_{G}^{(l)}),$$

(8)

where ${{{\bf{Z}}}}_{p}^{(l)}$ represents node representations after l layers of message passing. ${{{\bf{W}}}}_{F}^{(l)}\in {{\mathbb{R}}}^{{d}_{e}\times {d}_{e}}$ and ${{{\bf{W}}}}_{G}^{(l)}\in {{\mathbb{R}}}^{{d}_{e}\times {d}_{e}}$ are trainable transformation matrices of the l-th layer, respectively. Since resilience is a system-level property, we introduce a virtual node to fuse the messages from all individual nodes called global pooling. With the virtual global node, the expanded node representation matrix of the p-th trajectory after the l-th message passing layer is denoted as ${{{\bf{Z}}}}_{p}^{*(l)}\in {{\mathbb{R}}}^{(N+1)\times {d}_{e}}$.

k-space projector

We introduce an attention module that can effectively integrate the embeddings of M trajectories (Supplementary Fig. 3). Inspired by the existing work⁵⁸, we design pooling layers that can adaptively capture crucial information for each of the M trajectories. Specifically, we calculate the average and max pooling of ${{{\bf{Z}}}}_{p}^{*(l)}$, denoted as ${{{\bf{Z}}}}_{{{\rm{avg}}}}^{(l)}\in {{\mathbb{R}}}^{M\times 1\times 1}$ and ${{{\bf{Z}}}}_{\max }^{(l)}\in {{\mathbb{R}}}^{M\times 1\times 1}$, respectively. Then the attention weight of trajectories can be calculated as:

$${{\bf{Att}}}=\sigma ({{\rm{MLP}}}({{{\bf{Z}}}}_{{{\rm{avg}}}}^{(l)})+{{\rm{MLP}}}({{{\bf{Z}}}}_{\max }^{(l)})),$$

(9)

where ${{\bf{Att}}}\in {{\mathbb{R}}}^{M\times 1\times 1}$ and $\sigma (x)=\frac{1}{1+{e}^{-x}}$ is the sigmoid activation function.

After that, we fuse representations from all M trajectories with the attention weight, formulated as

$${{\bf{Z}}}={\sum }_{p=1}^{M}{{{\rm{Att}}}}_{p} * {{{\bf{Z}}}}_{p}^{*(l)},$$

(10)

where ${{{\rm{Att}}}}_{p}\in {\mathbb{R}}$ denotes the attention weight of the p-th trajectory and ${{\bf{Z}}}\in {{\mathbb{R}}}^{(N+1)\times {d}_{e}}$ is the final representation of all nodes. We derive the network representation by employing the final representation of the virtual node, denoted as e_G. Subsequently, we propose an MLP-based resilience predictor that leverages ${{{\bf{e}}}}_{G}\in {{\mathbb{R}}}^{{d}_{e}}$ to infer the resilience of the network (Supplementary Fig. 3). In this predictor, we first map the network to a scalar k of 1-dimensional k-space and then provide the inferred network resilience $\hat{y}$ as follows:

$$k={{\rm{MLP}}}({{{\bf{e}}}}_{G}),$$

(11)

$$\hat{y}=H(\sigma (wk+b)-\gamma ),$$

(12)

where $w,b\in {\mathbb{R}}$ are the trainable weight and bias, respectively. σ( ⋅ ) denotes the sigmoid activation function, i.e., $\sigma (x)=\frac{1}{1+{e}^{-x}}$, and H( ⋅ ) represents the Heaviside step function. Without loss of generality, we set γ = 0.5 as the resilience inference threshold. Since the function f(k) = σ(wk + b) − δ is monotonic, there is only one zero point, k^c, which is defined as the critical threshold in k-space. k < k^c and k > k^c lead to the different prediction $\hat{y}$, indicating whether the network is resilient ($\hat{y}=1$) or not ($\hat{y}=0$).

The loss function used to train ResInf consists of two parts: binary cross-entropy term and l₂-regularization term, which is described as follows:

$$L=-\frac{1}{S}{\sum }_{i=1}^{S}{y}_{i}\log (\hat{{y}_{i}})+(1-{y}_{i})\log (1-\hat{{y}_{i}})+\lambda | | \Theta | {| }_{2},$$

(13)

where L is the loss function we aim to minimize. ${\hat{y}}_{i}$ denotes the resilience inference result of ResInf for the i-th sample, and y_i represents its resilience i.e., label. S denotes the number of training samples. Θ denotes all trainable parameters in ResInf and λ is a hyperparameter to control the relative weight of l₂-regularization term. We use the Adam optimizer⁵⁹ to minimize the loss function during training.

Real-world microbial systems

The dataset is comprised of species abundances of different microbial communities observed during 11 days of experiments. Each microbial community belongs to one of the species pool sizes: 3 species, 6 species, 12 species, and 24 species, and is cultivated under one of the high, medium, or low nutritional conditions. Previous research²⁹ demonstrates that high nutritional conditions and larger species pool sizes foster intense competition among species, driving the system to a non-resilient phase featured by chaotic abundance fluctuations, as opposed to a resilient phase marked by stable abundance equilibrium³⁰. To differentiate between resilient and non-resilient communities and determine their resilience labels, consistent with the existing work²⁹, we calculate the average coefficient of variation ($\overline{{{\rm{CV}}}}$) of observed species abundance of Day 7 ~ 10 in the community. It corresponds to the average value of the standard deviation for the abundance of each species over these days, scaled by the average species abundance of these days, which can be represented as follows:

$$\overline{{{\rm{CV}}}}=\frac{\langle {{\rm{Std}}}\,{{\rm{of}}}\,{x}_{i}(t)\rangle }{\langle {{\rm{Mean}}}\,{{\rm{of}}}\,{x}_{i}(t)\rangle },$$

(14)

where t runs from 7 to 10, and x_i(t) is the i-th element of x(t) at the time t. Systems with $\overline{{{\rm{CV}}}}$ in this time interval lower than a threshold 0.25 are considered converged to a stable equilibrium as resilient systems²⁹. If $\overline{{{\rm{CV}}}}$ is larger than the threshold, the investigated systems are non-resilient. A high $\overline{{{\rm{CV}}}}$ indicates that the system lacks a desired stable equilibrium and is instead trapped in persistent fluctuations.

Simulating critical events

With the synthetic and empirical networks, we simulate critical events that may result in resilience loss by employing perturbations according to the experimental setup outlined in previous study⁵. These perturbations include node removal, link removal, and global weight perturbation, which are described as follows.

Node removal. To model node failure in networked systems, we randomly select and remove n nodes (n < N) and their associated links. After the deletion, we reconstruct the derived giant component of the network and eliminate the isolated nodes.

Link removal. To model the critical events on interactions between nodes, we randomly select and remove m links, where m is less than the total number of links ∣E∣. We also eliminate the isolated nodes from the derived giant component.

Global weight perturbation. To model the impact of environmental changes on a global scale, we introduce a macroscopic perturbation that affects all link weights in the network. Specifically, we apply a random factor, denoted as r_ij, to shift the weight of the edge between node i and j such that A_ij is replaced with r_ijA_ij. The r_ij value is drawn from a uniform distribution with a mean of r < 1. As a result, the network is transformed into a perturbed state where the interaction weights are reduced to a fraction r of their original value.

Evaluation metrics

F1-score

The primary metric employed to evaluate the model’s inference ability is the F1 score. The F1-score for positive samples can be formulated as:

$${{\rm{F1}}}\,{\mbox{-}}\,{{\rm{score}}}=2\frac{{{\rm{precision}}}\cdot {{\rm{recall}}}}{{{\rm{precision}}}+{{\rm{recall}}}}=2\frac{{{\rm{TruePositive}}}}{2\cdot {{\rm{TruePositive}}}+{{\rm{FalsePositive}}}+{{\rm{FalseNegative}}}},$$

(15)

$${{\rm{TruePositive(TP)}}}={\sum }_{i=1}^{P}1 \, \left({y}_{i}=1\wedge {\hat{y}}_{i}=1\right),$$

(16)

$${{\rm{FalsePositive(FP)}}}={\sum }_{i=1}^{P}1 \, \left({y}_{i}=0\wedge {\hat{y}}_{i}=1\right),$$

(17)

$${{\rm{TrueNegative(TN)}}}={\sum }_{i=1}^{P}1 \, \left({y}_{i}=0\wedge {\hat{y}}_{i}=0\right),$$

(18)

$${{\rm{FalseNegative(FN)}}}={\sum }_{i=1}^{P}1 \, \left({y}_{i}=1\wedge {\hat{y}}_{i}=0\right),$$

(19)

$${{\rm{precision}}}=\frac{{{\rm{TP}}}}{{{\rm{TP}}}+{{\rm{FP}}}},$$

(20)

$${{\rm{recall}}}=\frac{{{\rm{TP}}}}{{{\rm{TP}}}+{{\rm{FN}}}},$$

(21)

where P denotes the number of all test samples, y_i is the resilience label of the i-th system, and ${\hat{y}}_{i}$ denotes the resilience inference result from the model. We can similarly calculate the F1-score for negative samples by interchanging the roles of “positive” and “negative” in the computation process of Equation (15). Given the potential imbalance between positive and negative samples in test datasets, we report the weighted average of F1-score for positive samples and that for negative samples, where the weights are determined by the number of instances in each class.

Receiver operating characteristic curve (ROC)

ROC curve demonstrates the performance of inference models with varying discrimination threshold γ in Equation (12), illustrating the true positive rate (TPR) with respect to the false positive rate (FPR). For example, if we lower the threshold γ in Equation (12), more samples will be regarded as resilient networks (${\hat{y}}_{i}=1$), thus increasing the number of false positive as well as true positive samples and corresponding to a different point on the curve. TPR and FPR can be formulated as follows:

$${{\rm{TPR}}}=\frac{{{\rm{TP}}}}{{{\rm{TP}}}+{{\rm{FN}}}},$$

(22)

$${{\rm{FPR}}}=\frac{{{\rm{FP}}}}{{{\rm{FP}}}+{{\rm{TN}}}},$$

(23)

where TP, FP, TN, FN are defined in Equation (16–19).

Area under the ROC curve (AUC)

Area Under the ROC Curve (AUC) quantifies the overall ability of the model to discriminate between classes across all possible thresholds γ in Equation (12), offering a comprehensive assessment of the model’s performance. Essentially, a higher AUC value for the model indicates that it is more likely to rank a randomly selected positive instance higher than a randomly chosen negative one, i.e., higher value of σ(wk + b) in Equation (12), for this positive sample. An AUC of 1.0 indicates a perfect inference model with flawless predictive capability, while an AUC of 0.5 signifies a model performing no better than random guessing.

Dynamics and datasets

Mutualistic dynamics

The mutualistic dynamics can be formulated as:

$$\frac{d{x}_{i}}{dt}=B+{x}_{i}\left(1-\frac{{x}_{i}}{K}\right)\left(\frac{{x}_{i}}{C}-1\right)+{\sum }_{j=1}^{N}{A}_{ij}\frac{{x}_{i}{x}_{j}}{D+E{x}_{i}+H{x}_{j}}.$$

(24)

where B denotes the incoming rate for species i from neighbor ecosystems. K indicates the environment carrying capacity, and C expresses the Allee effect, implying when x_i < C there is a negative effect for node activities. The third term describes symbiotic interactions with the saturated effect for the positive contribution of node j to the activity of node i. We illustrate the dynamics parameter settings for experiments in Supplementary Table 4. Mutualistic dynamics can encounter a bifurcation, where the system undergoes a transition from the resilient phase with only a single desired stable equilibrium x^H to the non-resilient phase where both desired equilibrium x^H and undesired equilibrium x^L are stable, indicating that non-resilient networks can collapse to undesired equilibrium x^L in the face of massive perturbations or low initial conditions of node activities.

We retrieve empirical networked systems from the existing works^5,60 and the Interaction Web Database (IWDB)³⁵, which contains mutualistic systems such as plant-ant, plant-pollinator, and anemone-fish. The detailed information is shown in Supplementary Table 1. Taking the mutualistic system of plant-ant as an example, the system consists of a plants and b ants, forming an bipartite network B with the size of a × b. Then we project the bipartite network to plant/ant set, resulting in two networks which contain a plants (B^I) and b ants (B^II), respectively. Link weights ${B}_{ij}^{{{\rm{I}}}}$ in the projection network of plant between node i and j can be formulated as ${B}_{ij}^{{{\rm{I}}}}={\sum }_{k=1}^{b}\frac{{B}_{ik}{B}_{jk}}{\mathop{\sum }_{s=1}^{a}{B}_{sk}}$. The formula indicates that the symbiotic interaction between plant i and j depends on two aspects: (i) the number of ants with which both plant i and j have interactions; (ii) the number of plants with which the ant k has interactions. The increase of the number in (i) will strengthen the weight ${B}_{ij}^{{{\rm{I}}}}$, while the increase of the number in (ii) will have the opposite impact. We conduct a similar procedure to the projection network of ant B^II to calculate its link weight ${B}_{ij}^{{{\rm{II}}}}$. After the network projection, there may be isolated nodes whose activities no longer rely on the primary structure of the network. Hence, we remove these isolated nodes and reconstruct the giant component of the network, which is a connected sub-network containing the maximum proportion of the original network’s nodes. To model the effect of critical events that can lead to resilience loss, we apply perturbations of different intensities, including the random removal of nodes and links, and global perturbation on link weights, to giant components of networks (Simulating critical events in Methods). The statistics of datasets comprising the derived networks are illustrated in Supplementary Table 2. We then obtain their node activity trajectories by simulating differential equation groups (24) of mutualistic dynamics using the fourth-order Runge-Kutta stepper⁶¹ with M different initial activities sampled from a logarithmic scale [10⁻², 10¹) for each node. The terminal simulation time is ${T}_{\max }=200$. The ground truths of network resilience are determined by node activities at ${T}_{\max }$. We obtain the average terminal activity ${\langle {{{\bf{x}}}}_{{{\rm{end}}}}\rangle }_{m}$ of nodes for each of M trajectories, respectively, and calculate the sum of distances between each average activity ${\langle {{{\bf{x}}}}_{{{\rm{end}}}}\rangle }_{m}$ and their mean value $\overline{\langle {{{\bf{x}}}}_{{{\rm{end}}}}\rangle }$, which is denoted as D₁, i.e., ${D}_{1}=\mathop{\sum }_{m=1}^{M}{\left\Vert {\left\langle {{{\bf{x}}}}_{{{\rm{end}}}}\right\rangle }_{m}-\overline{\left\langle {{{\bf{x}}}}_{{{\rm{end}}}}\right\rangle }\right\Vert }_{2}$. In addition, we use K-means to cluster these M average activities into two classes and calculate the sum of distances between each average activity ${\langle {{{\bf{x}}}}_{{{\rm{end}}}}\rangle }_{m}$ and its cluster center ${{{\bf{x}}}}_{m}^{{{\rm{center}}}}$, which is denoted as D₂, i.e., ${D}_{2}=\mathop{\sum }_{m=1}^{M}{\left\Vert {\left\langle {{{\bf{x}}}}_{{{\rm{end}}}}\right\rangle }_{m}-{{{\bf{x}}}}_{m}^{{{\rm{center}}}}\right\Vert }_{2}$. If ${D}_{2} < \frac{{D}_{1}}{10}$, we think the clusters generated from K-means are more reliable and regard the network as non-resilient, with two stable equilibria x^H and x^L.

Gene regulatory dynamics

The gene regulatory dynamics can be formulated as:

$$\frac{d{x}_{i}}{dt}=-B{x}_{i}^{f}+\mathop{\sum }_{i=1}^{N}{A}_{ij}\frac{{x}_{j}^{h}}{{x}_{j}^{h}+1},$$

(25)

which is also called Michaelis-Menten dynamics³. f can represent degradation (f = 1) or dimerization (f = 2), and the second term describes genetic activation, where h is the Hill coefficient and explains the degree of collaboration in gene regulation. We illustrate the dynamics parameter settings for experiments in Supplementary Table 4. x^L = 0 (also 〈x〉 = 0) is the trivial and undesired stable equilibrium. Resilient systems have another desired equilibrium x^H where the average node activity 〈x〉 > 0. Non-resilient systems cannot stay in x^H, indicating cell death with only zero node activity (〈x〉 = 0).

We collect empirical regulatory networks from yeast⁶² and E.coli⁶³, whose detailed information is shown in Supplementary Table 1. Since these networks are directed, we focus on their strongly connected components, where there is a path in both directions between each pair of nodes, and adopt the same kinds of perturbations as mutualistic networks. The statistics of datasets comprising the derived networks are illustrated in Supplementary Table 2. Node activity trajectories of these networks are obtained from differential equation groups (25) of gene regulatory dynamics using the fourth-order Runge-Kutta stepper⁶¹ with M different initial activities sampled from [3, 10) for each node, and the terminal simulation time is ${T}_{\max }=200$. The ground truths of network resilience are determined by node activities at ${T}_{\max }$. We obtain the average terminal activity of nodes for M trajectories and further calculate their mean value $\overline{\langle x\rangle }$. If $\overline{\langle x\rangle } < 1{0}^{-5}$, we can approximate $\overline{\langle x\rangle }=0$ and the network will be non-resilient.

Neuronal dynamics

The neuronal dynamics can be formulated as

$$\frac{d{x}_{i}}{dt}=-{x}_{i}+{\sum }_{j=1}^{N}{A}_{ij}\frac{1}{1+{e}^{\mu -\delta {x}_{j}}},$$

(26)

which is also called Wilson-Cowan dynamics^20,64. Since each node receives cumulative inputs from all of its neighbors, higher in-degree nodes benefit from their surroundings by having a larger aggregate activation signal. We illustrate the dynamics parameter settings for experiments in Supplementary Table 4. Non-resilient neuronal networks exhibit either a bi-stable phase with both stable desired and undesired equilibria x^H and x^L, respectively, or have only a single undesired stable equilibrium x^L. Resilient neuronal networks only have a single desired equilibrium x^H.

Following existing researches³⁸, we use Erdős-Rényi³⁶ and Barabási-Albert³⁷ models to create neuronal networks, whose detailed information is shown in Supplementary Table 1. We obtain their giant components and adopt the same kinds of aforementioned perturbations. The statistics of datasets comprising the derived networks are illustrated in Supplementary Table 2. Node activity series of these networks are simulated with differential equation groups (26) of neuronal dynamics using the fourth-order Runge-Kutta stepper⁶¹ with M different initial activities sampled from [10⁻², 10¹) for each node, and the terminal simulation time is ${T}_{\max }=200$. The ground truths of network resilience are determined by node activities at ${T}_{\max }$. First, via the same approach as in mutualistic networks, we calculate and compare D₁ and D₂ to find networks with two stable equilibria x^H and x^L, and regard them as non-resilient. For the remaining networks, we regard those whose unique stable equilibrium is closer to x^H than x^L as resilient networks. Otherwise, we consider them as non-resilient networks.

SIS dynamics

The susceptible-infected-susceptible (SIS) dynamics⁴¹ can be formulated as:

$$\frac{d{x}_{i}}{dt}=-{\delta}{x}_{i}+{\sum }_{j=1}^{N}{A}_{ij}(1-{x}_{i}){x}_{j},$$

(27)

which describes the spreading phenomena of the epidemic. The node activity x_i represents the infection probability of node i and A_ij denotes the infection rate from node j to node i. δ > 0 denotes the curing rate of node i. The parameter settings are detailed in Supplementary Table 5. Without loss of generality, we define SIS networks with equilibrium x^L = 0 (also 〈x〉 = 0) as non-resilient networks, while those with equilibrium x^H > 0 (also 〈x〉 > 0) are resilient networks. We employ equation groups (27) with the fourth-order Runge-Kutta stepper to simulate node activity trajectories for networks with M different initial activities sampled from a uniform distribution [0, 1) for each node, and the terminal simulation time is ${T}_{\max }=8.5$. The ground truths of network resilience are determined by node activities at ${T}_{\max }$. We obtain the average terminal activity of nodes for M trajectories and further calculate their mean value $\overline{\langle x\rangle }$. If $\overline{\langle x\rangle } < 1{0}^{-5}$, we can approximate $\overline{\langle x\rangle }=0$ and the network will be non-resilient.

Inhibitory dynamics

The inhibitory dynamics⁴² can be formulated as:

$$\frac{d{x}_{i}}{dt}={c}+{x}_{i}\left(1-\frac{{x}_{i}}{{f}}\right)\left(\frac{{x}_{i}}{{b}}-1\right)+{\sum }_{j=1}^{N}{A}_{ij}\frac{{x}_{i}}{1+{x}_{j}},$$

(28)

which models inhibition between genes⁶⁵ or between hosts and pathogens⁴². The self dynamics describes the logistic growth with the Allee effect, and the interaction dynamics capture the inhibition, where the population of i grows linearly with x_i, but when x_j → ∞, the rate approaches zero. Therefore, the population of j will inhibit the growth of i. The parameter settings are detailed in Supplementary Table 5. Inhibitory dynamics encounter a bifurcation, where the system transits from the resilient regime with a desired unique equilibrium x^H to the non-resilient regime with both the desired equilibrium x^H and the undesired equilibrium x^L. Consequently, the system can collapse to x^L in the face of massive perturbations or low initial conditions of node activities. We employ equations group (28) with the fourth-order Runge-Kutta stepper to simulate node trajectories for networks with M initial activities sampled from a uniform distribution [0, 1] for each node, and the terminal simulation time is ${T}_{\max }=20$. The ground truths of network resilience are determined by node activities at the terminal time ${T}_{\max }$. Similar to the process of mutualistic dynamics, we calculate D₁ and D₂ for each network and regard networks with ${D}_{2} < \frac{{D}_{1}}{10}$ as non-resilient networks.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.