Introduction

Spin is emerging as a promising alternative or complement to charge for information storage and processing1. Spin–orbit coupling (SOC) is crucial in spin-based devices, enabling manipulation of spin states through time-dependent electric fields2,3. Bernal bilayer graphene (BLG) holds potential for spintronics4 and quantum computing5, with recent studies indicating long spin relaxation times in BLG quantum dots6,7,8. However, intrinsic Kane–Mele (KM) SOC9 in graphene is weak (40–80 μeV)10,11. Various methods have been explored to enhance SOC in BLG, including interfacing with high-SOC substrates. Transition metal dichalcogenides (TMDs) have shown promise in this regard, offering significant SOC enhancements (from 1 to 10 meV) without compromising graphene’s electronic quality12,13,14. Additionally, the combination of BLG on WSe2 has recently been shown to host an unexpected superconducting phase, where the SOC seems to play a major role15,16, prompting further study of such heterostructures.

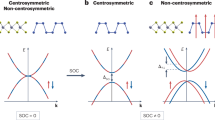
The extrinsic SOC induced in BLG by the TMDs is described by the Hamiltonian17

$${H}_{{{{\rm{SO}}}}}=\frac{{\Delta }_{{{{\rm{I}}}}}}{2}\xi {s}_{z}{{\mathbb{I}}}_{\sigma }+\frac{{\Delta }_{{{{\rm{R}}}}}}{2}(\xi {\sigma }_{x}{s}_{y}-{\sigma }_{y}{s}_{x}),$$
(1)

where ξ = ±1 represents the valley index, sx,y,z denote spin Pauli matrices, σx,y and \({{\mathbb{I}}}_{\sigma }\) are Pauli and unit matrices operating on the sublattice degree of freedom (A1, B1) within the layer in contact with the TMD (see schematic in Fig. 2e). The first term, known as the Ising SOC, acts similarly to an effective out-of-plane magnetic field with a valley-dependent sign. It lifts the four-fold spin and valley degeneracy at the K± points, forming spin-valley-locked Kramers doublets. The second term is a Rashba type of SOC18, favoring an in-plane spin polarization perpendicular to the sublattice isospin vector.

Intensive theoretical17,19,20,21,22,23 and experimental efforts12,13,14,24,25,26,27,28 in understanding and quantifying SOC proximity effects have led to a range of values for the relative strength of the two SOC terms depending on the analysis method. This is because the strength of SOC is often inferred indirectly, for example, through the extraction of relaxation times obtained from quantum interference effects such as weak antilocalization (WAL)29,30,31, or spin precession measurements32. In contrast, the fundamental frequency f = Δ(B−1) of the Shubnikov–de Haas oscillations (SdHOs) offers a direct measurement of the Fermi surface and is suitable for determining the band splitting induced by SOC33. However, the energy resolution of this technique is limited by the broadening of the Landau levels, necessitating high electron mobilities and low disorder potentials.

Here, we conduct magnetotransport experiments on a dual-gated MoS2/BLG heterostructure. First, we analyze SdHOs to quantify proximity-induced SOC. Our results confirm the presence of both Ising (ΔI = 1.55 meV) and Rashba (ΔR = 2.5 meV) SOC. Despite their comparable strength, we show that the splitting of the low-energy bands mainly arises from the Ising SOC. Additionally, we observe a non-monotonic conductivity response to an applied displacement field when BLG is charge-neutral. Our tight-binding calculations show how the displacement field D opposes the Ising SOC, closing single-particle gaps in the spin-polarized bands at a critical value of Dc and causing local maxima in the conductivity. In this critical field, the application of an external magnetic field rapidly suppresses the conductivity, challenging existing theoretical models and suggesting the involvement of many-body interactions.

Results

Proximity induced spin–orbit coupling

Determining the SOC gap in BLG via magnetotransport experiments is challenging due to disorder-induced density fluctuations δn. Shown in Fig. 1a is the schematic of our sample, comprising BLG atop three layers of MoS2, encapsulated within hexagonal boron nitride (hBN), and placed on a graphite bottom gate. The use of hBN dielectrics and a graphite layer minimizes density fluctuations34, evident from the low-density δn ~ 2 × 109 cm−2 at which conductivity saturates in our sample (Fig. 1b). High charge carrier mobilities [~5 × 105 cm2 (V s)−1 at n = 5 × 1010 cm−2, see Supplementary Note 2] indicate minimal impact of the MoS2 layer on BLG’s electronic properties compared to hBN-encapsulated Bernal BLG devices35.

Fig. 1: Magnetotransport data at zero displacement field.
figure 1

a Schematic representation of the BLG/MoS2 heterostructure, illustrating a cross-section of the layers (top right panel) and highlighting the alignment of the BLG and MoS2 layers (bottom right panel). b The conductivity is plotted as a function of carrier density on a logarithmic scale. The measurement was conducted at a temperature of approximately 30 mK. Dotted (squared) markers represent data for electron (hole) doping. The solid red line depicts a linear fit, while the black dashed line indicates the saturation of the conductivity. c Landau fan at zero displacement field (left panel) measured at a temperature T = 1.3 K. The right panel displays a vertical linecut at n = 2.7 × 1011 cm−2 (dashed line in the left panel). d Fast Fourier transform (FFT) of the Landau fan shown in (c). The FFT of Rxx(B−1) is calculated line-by-line for each density. The vertical axis has been rescaled according to nSdH = 2ef/h, where f is the frequency axis in Tesla, accounting for the valley degeneracy. Dashed lines represent densities obtained from the band structure in (e). The right panel shows a vertical linecut at n = 2.7 × 1011 cm−2 (dashed line in the left panel). e Band structure of bilayer graphene with SOC (ΔI = 1.55 meV and ΔR = 2.5 meV) close to the K+ point at zero displacement field. The bands are plotted along the relative momentum kx (or equivalently, along the line Γ−K−M of the first Brillouin zone). The horizontal axis is scaled by the lattice constant a = 2.46 Å. The color of the bands encodes the spin texture (violet for spin up and orange for spin down). f Density difference Δn obtained from the distance between the two peaks in the Fourier spectrum shown in (d). The red solid line represents a fit to the data, obtained from the band structure in (e) by determining the density of states and then the carrier densities n↓,↑ followed by calculating the difference ∣n↓−n↑∣. The fit yields the SOC parameters: ΔI = 1.55 ± 0.10 meV and ΔR = 2.5 ± 0.5 meV. The shaded area indicates the uncertainty in the fitting parameters, reflected in the uncertainty in Δn.

Full size image

We analyze SdHOs at zero displacement field (D) and low magnetic fields (B) to determine the band splitting induced by the SOC. Figure 1c shows the longitudinal resistance Rxx as a function of B and electron density n at T = 1.3 K. Pronounced minima in resistance Rxx occur at filling factors ν = ±4N (N an integer), characteristic of pristine BLG. In addition, small oscillation maxima appear in the SdH minima (highlighted by the arrow in the right panel), suggesting the presence of a broken symmetry.

To determine the oscillation frequency of the SdHOs, we employ a numerical fast Fourier transform (FFT) of Rxx(1/B) calculated line-by-line for each density, as shown in Fig. 1d. The FFT reveals two clear frequencies f1 and f2, resulting from the splitting of the Fermi surface, which is attributed to the influence of the MoS2 substrate through the spin–orbit proximity effect. The sum of the electron densities ni = 2efi/h (i = 1, 2) obtained from the SdHO matches the Hall density by accounting for the twofold valley degeneracy, as expected.

The two SOC terms in Eq. (1) yield distinct density dependencies for the spin–orbit splitting. The Ising SOC induces a constant splitting as a function of the Fermi energy (and hence density), while the Rashba term leads to a splitting that increases with the Fermi energy. Although the splitting in Fig. 1d initially appears constant with carrier density, a closer examination of Δn in Fig. 1f reveals a small but detectable slope. By aligning the density difference Δn obtained from the tight-binding model (see the “Methods” subsection “Tight-binding model” and Supplementary Notes 3–5) with the data (illustrated by the red solid line), we find ΔI = (1.55 ± 0.10) meV and ΔR = (2.5 ± 0.5) meV. The theoretically predicted densities with these parameters are overlaid against the total density in Fig. 1d as orange and violet dashed lines, demonstrating good agreement with the experimental data. We acknowledge that the numerical outcome of the fit can be subtly influenced by the choice of the tight-binding intralayer and interlayer coupling parameters of BLG, referred to as the Slonczewski–Weiss–McClure parameters. These parameters dictate the curvature of the bands, thereby affecting the conversion between energy and density, as elaborated in Supplementary Note 4.

We validate our findings at finite displacement fields, leveraging the layer-dependent SOC induced by the asymmetric structure of our sample3. This layer selectivity is demonstrated in Supplementary Note 6, where the electron wave function is polarized via the applied displacement field in one layer or the other, depending on its sign.

Next, we continue the discussion by investigating the impact of SOC on the electrical conductivity (σ) of BLG at charge neutrality (CN).

Conductivity at charge neutrality

Measurements of σ reveal a non-monotonic dependence on the displacement field (Fig. 2a), which appears in a narrow density range (n ~ 1 × 1010 cm−2) around CN. A local minimum at D = 0 is surrounded by conductivity maxima at D = ±Dc ≈ 12.5 mV/nm, as highlighted in the line cut at n = 0 presented in Fig. 2b.

Fig. 2: Displacement field dependence of the conductivity at CN.
figure 2

a Conductivity σ as a function of density and displacement field measured at T ≈ 30 mK. b Vertical line cut of σ in (a) at CN. The conductivity shows local maxima at the critical displacement Dc = ±12.5 mV/nm. c Band structure of proximitized BLG at the K point. The calculation includes an Ising SOC term with ΔI = 1.55 meV. The band structure is shown for three characteristic interlayer potential energies: U = 0 (left panel), U = 0.775 meV (central panel), and U = 2 meV (right panel). The energy axis is adjusted such that E = 0 corresponds to charge neutrality, which is marked by the horizontal dashed lines. The color code represents the layer polarization: blue indicates polarization on layer 1, while red is on layer 2, as shown in the schematics in the bottom right panel. The band structure shown in the left panel is the same as Fig. 1c, where we color-coded the bands according to the spin texture. d Conductivity at CN for D = 0 (violet) and D = Dc (orange) as a function of temperature in logarithmic scale. The crosses were measured in a dilution refrigerator, while the solid line was measured in a pumped He4 cryostat. The temperature range is divided into three regimes (A–C), according to relevant energy scales (Eth, Edis, ESO) defined in the main text. e Constant energy contours of the Fermi energy at charge neutrality for U = 0 (left panel) and U = Uc (right panel). The Fermi pockets are labeled according to their doping, electron e and holes h, and their spin (↑, ↓). Schematic: The side view of the BLG unit cell is schematically shown on a MoS2 substrate. The color bar underneath defines the polarization of the electron wave function on the low energy orbitals, which are localized on the lattice site A1 and B2 (colored blue and red, respectively).

Full size image

This dependence can be understood by taking into account the influence of SOC on the BLG band structure. From tight-binding calculations, we find that the Rashba SOC has little effect on the low-energy bands (see Supplementary Note 3 for more details). For this reason, we consider only the Ising SOC in the following discussion. The outcome of the band structure calculations is presented in Fig. 2c, shown for the K+-valley and three characteristic interlayer potential energies (U). First, we consider the case U = 0 in the left panel. We observe that the band structure comprises two pairs of bands, one split by the energy ΔI and partially layer-polarized on the bottom layer (blue), while the other pair is degenerate at two points along kx and is partially polarized on the top layer (red). Due to their partial layer polarization, the application of a displacement field shifts the two pairs of bands relative to each other based on their layer polarization. Notably, the calculations show that a band gap emerges only once the interlayer potential energy exceeds the critical value Uc = ΔI/2 ≈ 0.8 meV (right panel), i.e. once U counteracts the SOC, resulting in the closure of the gap between bands with the same spin (see Fig. 2e for the spin texture). This elucidates why, in the experiment, the conductivity starts decreasing with increasing displacement fields only when D > Dc, and associates the maxima in the conductivity with the closure of the SOC gaps. We verify this interpretation by converting Uc into a displacement field, taking into account interlayer screening (see Supplementary Note 7 for details). The conversion yields a displacement field of 11.4 mV/nm, in good agreement with the experimental value of Dc ≈ 12.5 mV/nm. Furthermore, the local conductivity minimum at D = 0 is observed only at low density and vanishes around n ~ 1 × 1010 cm−2, which corresponds to the density required to fill the spin–orbit splitting of the bands, as demonstrated in Fig. 1f.

The local minimum in conductivity at D = 0 prompts consideration of a potentially insulating phase arising from the presence of a gap, as reported for BLG fully encapsulated in TMDs14. To verify this, we examine the temperature dependence of the conductivity in Fig. 2d. Over the temperature range of 1–10 K, the conductivity increases by one order of magnitude, indicative of insulating behavior. However, the data only conforms to the Arrhenius law within a very limited temperature range (shown in Supplementary Note 8) and saturates to rather large conductivity values at low temperatures. Similarly, the conductivity at the critical field Dc also increases with temperature. Thus, although the insulating behavior is affected by the applied displacement field, it is consistently observed across all displacement fields at CN.

To further understand the temperature dependence, we compare the thermal energy Eth = kBT with the other characteristic energy scales determined by disorder (Edis) and SOC (ESO). First, we take into account the disorder potential, which induces density fluctuations of the order δn ≈ 2 × 109 cm−2. These fluctuations are converted into an energy scale Edis ≈ 0.14 meV using an effective mass approximation (m* ≈ 0.035m0, where m0 is the bare electron mass36) and taking into account the twofold valley degeneracy. At low temperatures (Eth < Edis), the conductivity is governed by disorder-induced electron–hole puddles, causing the saturation of the conductivity in the temperature range labeled A in Fig. 2d. Second, the SOC introduces gaps ESO = ΔI/2 ≈ 0.8 meV between bands of the same spin at D = 0, as illustrated in Fig. 1c (see also Supplementary Note 9). The presence of these spin-resolved gaps, even without a real band gap, could explain the insulating behavior of the conductivity. Effectively, if spin is conserved in thermal activation processes, carriers cannot be thermally excited from the highest occupied valence band into the lowest unoccupied conduction band, because these bands have opposite spin. Therefore, carriers thermally excited above the spin gap ESO should result in an increase of conductivity with increasing temperature, which is precisely happening in the temperature range labeled B in Fig. 2d. In regime C (Edis < ESO < Eth), the thermal energy surpasses the SOC gap, causing the conductivity to saturate again.

Based on the results presented above, we attribute the dependence of conductivity on displacement field, density and temperature to the presence of spin–orbit-induced gaps in the spin-polarized bands in the absence of a global band gap.

(B, D) phase diagram

In the final section of this work, we describe magnetotransport measurements at CN. Figure 3a illustrates the longitudinal conductivity σxx as a function of the out-of-plane magnetic field (B⊥) and displacement field at a temperature of T ≈ 30 mK. With the exception of the low magnetic field peaks at Dc, which we discuss below, the phase diagram depicted in Fig. 3a bears a resemblance to that of pristine BLG37,38. Drawing on previous studies37,39, we partition the parameter space into three distinct regions.

Fig. 3: Magnetotransport data at CN.
figure 3

a Conductivity as a function of B⊥ and D at T = 30 mK. This plot represents the (D, B) phase diagram of SOC proximitized BLG. Phase (I) is a gapped phase with a layer-polarized wave function. Phase (II) is another gapped phase that has been attributed to the canted antiferromagnetic phase in pristine BLG41,62. The phase boundary between phases (I) and (II) (straight dotted lines) is described in Supplementary Note 10. Phase (III) is a weakly insulating phase that arises from the presence of spin-gaps in the single-particle spectrum. b σxx plotted against D for B⊥ = 0 and two values of in-plane magnetic field: B∥ = 0 (violet) and B∥ = 1.8 T (orange). c Linecuts of panel (a) at D = 0 (violet) and D = Dc (orange). The black dashed and dotted lines highlight the 1/B dependence of the conductivity. d Differential conductance Gd = dI/dVSD as a function of the voltage bias VSD and magnetic field B⊥ at D = 0. The dotted line highlights Eg ∝ B⊥ (see discussion in Supplementary Note 11).

Full size image

Phases (I) and (II), occurring at large displacement and magnetic fields, respectively, are anticipated to mirror the behavior of the BLG system in the absence of SOC. This is attributed to the dominance of energy scales dictated by the externally applied parameters (B⊥ and D) over the SOC gap ΔI/2. Hence, we attribute phase (I) to the layer-polarized insulating state arising from the band gap induced by the displacement field, as illustrated in Fig. 2c. Phase (II) represents the insulating state of the quantum Hall ν = 0 state. In this phase, our bias spectroscopy measurements uncover the presence of a gap Eg ∝ B⊥ (Fig. 3d), which qualitatively explains the observed \({B}_{\perp }^{-1}\) suppression of the conductivity (see dotted and dashed lines in Fig. 3c). This behavior aligns with the canted antiferromagnetic phase observed in pristine BLG40. Moreover, the boundaries between Phase (I) and (II) (indicated by white dotted lines and elaborated in detail in Supplementary Note 10) exhibit common characteristics with those observed in pristine BLG: the insulator-insulator transition features enhanced conductance39,41, and the displacement field required to induce the transition is D*(B) ∝ 2e2B/h37,40,42,43.

Phase (III), emerging at B = 0 and D = 0, is expected to differ from BLG samples not in proximity with a TMD layer, due to the dominant SOC energy scale. Interestingly, a similar phase has been observed by Seiler et al.44 in BLG/WSe2 heterostructures and by Island et al.14 in WSe2/BLG/WSe2. In these cases, the insulating phase was attributed to a band gap induced either by electron correlations or SOC, respectively. Initially, the thermal activation in Phase (III) seems to support the presence of a gap. However, the temperature dependence can be explained by spin–orbit gaps in spin-polarized bands without a global band gap, as we have discussed above. In fact, while a clear gap is observed at finite magnetic fields, no gap is present at B = 0 (Fig. 3d), ruling out the existence of a global gap.

Now, we examine the sharp magnetoconductivity peaks at Dc (see an orange curve in Fig. 3c), a novel feature of spin–orbit proximitized BLG not previously reported. With current theoretical models unable to fully explain these peaks, we explore various possibilities.

At first glance, the sharp peak in the orange curve in Fig. 3c resembles the signature of WAL, expected in materials with strong SOC. This effect has been observed in numerous transport experiments in SOC-proximitized graphene13,25,29,30,45,46,47. However, with a mean-free-path exceeding 1 μm at finite density, the condition ℓϕ > ℓe (where ℓϕ and ℓe represent the phase-coherence length and mean-free-path, respectively) required to observe this effect would never be fulfilled (ℓϕ ≤ 360 nm if fitting the peak with a WAL model, as detailed in the Supplementary Note 12). Furthermore, the magnitude of the peak (~3−4e2/h) exceeds what would be expected for WAL, which typically reaches up to 0.5e2/h per conducting channel. Additionally, quantum interference effects are typically suppressed with increasing temperature due to the decrease in ℓϕ. In contrast, the magnitude of the peak in σxx remains robust against temperature changes (see Supplementary Note 12). For these reasons, we conclude that the peaks cannot arise from WAL.

Typically, distinguishing between how a magnetic field affects orbital or spin degrees of freedom involves tilting the field with respect to the plane. Orbital effects couple exclusively to B⊥, while spin couples to ∣B∣. In Fig. 3b, we compare the conductivity at B⊥ = 0 for B∥ = 0 and B∥ = 1.8 T (the maximum available in our system), where no significant effect is observed on σxx. The lack of an in-plane magnetic field dependence is consistent with the presence of Ising SOC, which is expected to align spins out-of-plane. Therefore, for an in-plane magnetic field dependence in conductivity to occur, the Zeeman energy ΔEZ = 2μB∣B∣ would need to become comparable to the spin–orbit gap ΔI/2, estimated to occur at B > 6.7 T. In our experiments, the conductivity drops by nearly a factor of 2 at B⊥ ≈ 50 mT. This magnetic field corresponds to a Zeeman energy of only 6 μeV, much smaller than the disorder. Therefore, it is unlikely that the Zeeman effect could be responsible for the observed magnetoconductivity peaks.

Since we could not find a suitable theoretical model relying solely on free-electron physics, we speculate that the non-monotonic magnetic field dependence of the conductivity at D = ±Dc (Fig. 3c) originates from many-body effects at CN. Electron interactions, which are strong near CN due to the lack of screening, were predicted to drive instability towards an excitonic insulator phase, in which carriers in valleys K+ and K− display strong particle–hole correlations48,49,50,51,52. Previous measurements, while reporting some promising results on gap opening at CN39,53, were not conclusive. This could be due to, among other reasons, a reduction in exchange interactions in the valley sector in the presence of spin degeneracy. In the present system, with spin degrees of freedom polarized by the SOC, carrier exchange responsible for the many-body physics at CN is expected to become stronger.

Taking this as a starting point and assuming a correlated excitonic order at CN similar to that occurring in quantum Hall bilayers (here represented by the K+ and K− valleys), we interpret the nonmonotonic behavior seen in Fig. 3c as a transition between a valley-coherent order and a valley polarized order. Formally this transition is analogous to the transition between excitonic layer-coherent and layer-polarized phases investigated in quantum Hall bilayers54. Here it is driven by two competing mechanisms. On the one hand, the magnetic field interacts with the orbital magnetic moments arising from the Berry curvature55. The energy related to these orbital magnetic moments in a magnetic field is \(\Delta {E}_{{{{\rm{M}}}}}(\xi )=-{{{\bf{M}}}}\cdot {{{\bf{B}}}}=\xi \,{g}_{v}^{*}{\mu }_{{{{\rm{B}}}}}B\), where \({g}_{v}^{*}\) is an effective valley g-factor, and ξ = ±1 is the valley index56,57. In nanostructures, the valley g-factor has been reported to range from  ~10 to above 100, depending on the confinement potential58, thus significantly larger than the usual spin Zeeman energy. This valley-dependent energy shift leads to the lifting of the valley degeneracy, favoring a valley-polarized state. On the other hand, valley polarization is associated with layer polarization once Landau levels form, introducing an energy cost for the polarization known as the capacitor-like Hartree energy37,38,43:

$${E}_{{{{\rm{H}}}}}(B)=\frac{1}{4\pi {\varepsilon }_{0}{\varepsilon }_{{{{\rm{BLG}}}}}}\frac{2{e}^{2}{c}_{0}}{{\ell }_{B}^{2}},$$
(2)

where εBLG is the dielectric constant of BLG and c0 is the distance between the two graphene layers. This energy counteracts the magnetization energy, thus promoting valley-unpolarized states. These mechanisms compete with each other and might contribute to the observed non-monotonic behavior in the conductivity as a function of the magnetic field.

Discussion

In this study, we demonstrated that two types of SOC are present in spin–orbit proximitized BLG. Despite the similar magnitudes of the two SOC terms, the band splitting at zero displacement field shows little dependence on the total density, indicating that the Ising SOC predominantly influences the splitting within the density range under investigation. Our results align with previous observations of Ising superconductivity in WSe2/BLG heterostructures15,16, suggesting the potential for similar phenomena to occur in MoS2/BLG systems.

Furthermore, we observed an insulating phase at D = 0, leading to a non-monotonic electrical conductivity with respect to the displacement field. Insulating phases with a similar displacement field dependence have been also observed in charge neutral suspended BLG39, albeit with an intrinsic SOC two orders of magnitude weaker than in our sample9,59. While suspended BLG exhibits a gap at B = 0 and D = 053, attributed to many-body correlations, our sample does not show this behavior (Fig. 3d), suggesting a different underlying mechanism. The absence of such correlated phases in hBN-encapsulated Bernal BLG suggests that dielectric and gate screening effects may reduce the relevance of correlation phenomena. Thus, we conclude that SOC plays a crucial role in the emergence of the observed insulating phase at D = 0. This assertion aligns with findings by Island et al.14, who reported a comparable insulating phase in BLG fully encapsulated in WSe2. While their explanation relied on SOC-driven band inversion, our observations suggest an alternative explanation, specifically single-particle SOC-induced gaps in spin-polarized bands in the absence of a global band gap (Fig. 1e). Our conclusion is supported by a detailed analysis of the SOC strength, a comparison between the band structure calculations and the displacement field dependence, as well as temperature-dependent measurements.

While the zero magnetic field data are understood in terms of single-particle physics, we could not find a suitable theoretical model to describe the data at the finite magnetic field. We speculate that the non-monotonic magnetic field dependence of σxx at D = ±Dc originates from many-body effects at CN. If this interpretation holds true, the system described here could serve as a platform to explore various intriguing effects anticipated for excitonic phases, such as vortices, merons, and the Josephson effect for charge-neutral particles.

Note from the authors. While preparing our manuscript, we became aware of a related study by Seiler et al.44, who investigated the interplay between SOC and Coulomb interaction in WSe2/BLG heterostructures, drawing conclusions on the phase diagram of SOC-proximitized BLG. It is remarkable that very similar data was obtained by two different groups, using a different TMD on bilayer graphene (MoS2 by our research group and WSe2 by Seiler et al.). While we attribute this observation to a single-particle effect (spin–orbit gaps in the spin-polarized bands), Seiler et al. offer a different interpretation based on electron-electron correlations.

Methods

Sample fabrication

We initiate the fabrication of our devices by assembling the heterostructure using a polymer-based dry transfer technique. Each layer is obtained through mechanical exfoliation of bulk crystals onto silicon/silicon dioxide wafers. The heterostructure comprises, from top to bottom, hBN, bilayer graphene (BLG), three layers of MoS2, hBN, and graphite.

The relative alignment of BLG with the MoS2 layer is known to influence the strength of the SOC20,21. While the maximum induced SOC is anticipated around 15°–20°, the SOC is most stable against small uncontrolled twist angle variations at 0°, ensuring better reproducibility. Therefore, during the fabrication process, we carefully align the edges of the MoS2 and BLG flakes, resulting in potential relative alignments of 0° or 30°. At 30°, the SOC proximity is expected to vanish, leading us to conclude that the relative angle in our sample is 0°.

Subsequently, the sample undergoes annealing in a hydro-argon atmosphere (H2/Ar:5%/95%) at 350 °C for 4 h to remove polymer residues and enhance adhesion between the layers. The metallic top gate is defined using standard electron-beam lithography, followed by electron-beam evaporation (chromium/gold) and lift-off processes. The mesa is dry-etched using a reactive ion etching process with a CHF3:O2 mixture (40:4).

In the final fabrication step, metallic edge contacts are deposited using electron-beam lithography, followed by electron-beam evaporation (chromium/gold) and lift-off processes. After resisting development, we clean the contact area using an O2 reactive ion etching process before metal deposition. This ensures the resulting contacts are ohmic and low resistive (<1 kΩ).

Dual-gated device

We employ a dual gate structure that allows for independent tuning of the charge carrier densities n and displacement field D. The density is defined as

$$n=\frac{1}{e}\left({C}_{{{{\rm{B}}}}}{V}_{{{{\rm{BG}}}}}+{C}_{{{{\rm{T}}}}}{V}_{{{{\rm{TG}}}}}\right)+{n}_{0},$$
(3)

and the displacement field is defined as

$$D=\frac{1}{2}\left({C}_{{{{\rm{B}}}}}{V}_{{{{\rm{BG}}}}}-{C}_{{{{\rm{T}}}}}{V}_{{{{\rm{TG}}}}}\right)+{D}_{0},$$
(4)

where CB = 36.7 nF/cm2 and CT = 78.2 nF/cm2 are the capacitance per area of the bottom and top gate, VBG and VTG are the voltages applied to the bottom and top gate. Additionally, n0 = −6.3E10 cm−2 and D0/ε0 = −46 mV/nm are offsets in the density and displacement field, respectively. These offsets are taken into account to compensate for the asymmetries arising from factors such as the contact potential difference between hBN and MoS217.

Measurements

The measurements were performed in a pumped Helium-4 cryostat (for temperatures above 1 K) or in a dilution refrigerator with a base temperature < 10 mK (estimated electronic temperature ≈ 30 mK).

The four-terminal resistance was measured with constant input current, by using a series resistor of 10 or 100 MΩ, depending on the resistance of the sample. The input voltage was generated at a frequency of roughly 31 Hz with a Lock-in amplifier. The current amplitude ranged from 1 to 50 nA.

The bias spectroscopy measurements were done in a two-terminal setup, where a DC voltage source was employed to generate the source–drain bias and a home-made voltage-to-current converter was used to detect the source–drain current.

Tight-binding model

To determine the band structure, we employ a four-band effective tight-binding model for BLG in the basis (A1, B1, A2, B2), where A, B are the two atoms in the unit cell of a single graphene layer, and their index represents the layer number36:

$${H}_{0}=\left(\begin{array}{cccc}-U/2&{v}_{0}{\pi }^{{{\dagger}} }&-{v}_{4}{\pi }^{{{\dagger}} }&{v}_{3}\pi \\ {v}_{0}\pi &-U/2+\Delta &{\gamma }_{1}&-{v}_{4}{\pi }^{{{\dagger}} }\\ -{v}_{4}\pi &{\gamma }_{1}&U/2+\Delta &{v}_{0}{\pi }^{{{\dagger}} }\\ {v}_{3}{\pi }^{{{\dagger}} }&-{v}_{4}\pi &{v}_{0}\pi &U/2\end{array}\right),$$
(5)

where π = ℏ(ξkx + iky), π† = ℏ(ξkx−iky), U is the inter-layer potential energy difference, Δ is an energy difference between dimer and non-dimer atoms, and \({v}_{j}=\frac{\sqrt{3}a}{2\hslash }{\gamma }_{j}\). The parameters γj are the Slonczewski–Weiss–McClure (SWM) parameters given in the “Methods” section (Table 1).

Table 1 Values of the Slonczewski–Weiss–McClure (SWM) parameters in electron-Volt (eV)
Full size table

We include the extrinsic SOC given by Eq. (1). The SOC lifts the spin degeneracy but does not mix states from different K-valleys. Therefore, the Hamiltonian becomes an 8 × 8 matrix with the basis (A1↑, A1↓, B1↑, B1↓, A2↑, A2↓, B2↑, B2↓). Since only layer 1 is in direct contact with the MoS2 layer, the SOC is taken into account only in the top-left 4 × 4 block:

$${H}_{{{{\rm{SO}}}}}=\left(\begin{array}{cc}{H}_{{{{\rm{SO}}}}}^{{{{\rm{L1}}}}}&0\\ 0&0\end{array}\right)$$
(6)

The Ising and Rashba SOC components lead to the following \({H}_{{{{\rm{SO}}}}}^{{{{\rm{L1}}}}}\) in matrix form:

$$\left(\begin{array}{cccc}\xi \frac{{\Delta }_{{{{\rm{I}}}}}}{2}&0&0&-i\frac{{\Delta }_{{{{\rm{R}}}}}(\xi -1)}{2}\\ 0&-\xi \frac{{\Delta }_{{{{\rm{I}}}}}}{2}&i\frac{{\Delta }_{{{{\rm{R}}}}}(\xi+1)}{2}&0\\ 0&-i\frac{{\Delta }_{{{{\rm{R}}}}}(\xi+1)}{2}&\xi \frac{{\Delta }_{{{{\rm{I}}}}}}{2}&0\\ i\frac{{\Delta }_{{{{\rm{R}}}}}(\xi -1)}{2}&0&0&-\xi \frac{{\Delta }_{{{{\rm{I}}}}}}{2}\end{array}\right).$$
(7)

In the ordered basis (A1↑, A1↓, B1↑, B1↓, A2↑, A2↓, B2↑, B2↓), the full Hamiltonian takes the form:

$$H ={H}_{0}+{H}_{{{{\rm{SO}}}}} \\ =\left(\begin{array}{cccccccc}\frac{{\Delta }_{{\rm {I}}}\xi }{2}-\frac{U}{2}&0&{v}_{0}{\pi }^{{{\dagger}} }&-{i}\frac{{\Delta }_{{\rm {R}}}(\xi -1)}{2}&-{v}_{4}{\pi }^{{{\dagger}} }&0&{v}_{3}\pi &0\\ 0&-\frac{{\Delta }_{\rm {{I}}}\xi }{2}-\frac{U}{2}&i\frac{{\Delta }_{{\rm {R}}}(\xi+1)}{2}&{v}_{0}{\pi }^{{{\dagger}} }&0&-{v}_{4}{\pi }^{{{\dagger}} }&0&{v}_{3}\pi \\ {v}_{0}\pi &-i\frac{{\Delta }_{{\rm {R}}}(\xi+1)}{2}&\Delta+\frac{{\Delta }_{{\rm {I}}}\xi }{2}-\frac{U}{2}&0&{\gamma }_{1}&0&-{v}_{4}{\pi }^{{{\dagger}} }&0\\ i\frac{{\Delta }_{{\rm {R}}}(\xi -1)}{2}&{v}_{0}\pi &0&\Delta -\frac{{\Delta }_{{\rm {I}}}\xi }{2}-\frac{U}{2}&0&{\gamma }_{1}&0&-{v}_{4}{\pi }^{{{\dagger}} }\\ -{v}_{4}\pi &0&{\gamma }_{1}&0&\Delta+\frac{U}{2}&0&{v}_{0}{\pi }^{{{\dagger}} }&0\\ 0&-{v}_{4}\pi &0&{\gamma }_{1}&0&\Delta+\frac{U}{2}&0&{v}_{0}{\pi }^{{{\dagger}} }\\ {v}_{3}{\pi }^{{{\dagger}} }&0&-{v}_{4}\pi &0&{v}_{0}\pi &0&\frac{U}{2}&0\\ 0&{v}_{3}{\pi }^{{{\dagger}} }&0&-{v}_{4}\pi &0&{v}_{0}\pi &0&\frac{U}{2}\\ \end{array}\right).$$
(8)

Bands and density of states

The bands are then obtained by numerically diagonalizing H = H0 + HSO. Each band is characterized by a band index m, which labels the bands from the most negative (m = 0) to the most positive (m = 7) energies.

The density of states of band m is given by

$${{{{\mathcal{D}}}}}_{{m}}(E)=\frac{1}{A}{\sum}_{\xi,{{{\bf{k}}}}}\delta (E-{E}_{{m}\xi,{{{\bf{k}}}}})$$
(9)

where ξ is the valley quantum number, and k is the wave vector. A = L2 is the area in real space. The delta function is approximated by a Gaussian function

$$\delta (E-{E}_{{m},\xi,{{{\bf{k}}}}})\approx \frac{1}{\sqrt{2\pi }\epsilon }\exp \left(-\frac{{(E-{E}_{{m},\xi,{{{\bf{k}}}}})}^{2}}{2{\epsilon }^{2}}\right),$$
(10)

with an energy broadening of ϵ < 50 μeV. The band structure Em,ξ,k is calculated on a grid in k space with finite resolution Δk ~ 1 × 105 m−1. Therefore the sum needs to be renormalized by the factor

$${\left(\frac{\Delta k}{2\pi /L}\right)}^{2}.$$
(11)

Equations (9), (10) and (11) yield the density of states of band m:

$${{{{\mathcal{D}}}}}_{m}(E)={\left(\frac{\Delta k}{2\pi }\right)}^{2}{\sum}_{\xi,{{{\bf{k}}}}}\frac{1}{\sqrt{2\pi }\epsilon }\exp \left(-\frac{{(E-{E}_{m,\xi,{{{\bf{k}}}}})}^{2}}{2{\epsilon }^{2}}\right).$$
(12)

The total density of states is obtained by summing over the band index m.

The electron density is obtained by integrating over the conduction band (m ≥ 4), while the hole density is obtained by integrating over the valence band (m < 4)

$$\begin{array}{rcl}{n}_{{\rm {e}}}({E}_{{{{\rm{F}}}}})&=&{\sum}_{m=4}^{7}\int_{-\infty }^{{E}_{{{{\rm{F}}}}}}{{{{\mathcal{D}}}}}_{m}(E){{{\rm{d}}}}E\\ {n}_{{\rm {h}}}({E}_{{{{\rm{F}}}}})&=&{\sum }_{m=0}^{3}\int_{\infty }^{{E}_{{{{\rm{F}}}}}}{{{{\mathcal{D}}}}}_{m}(E){{{\rm{d}}}}E.\end{array}$$
(13)

Out of the 8 bands, we only consider the four low energy bands (2 ≤ m ≤ 5), m = 4, 5 for the conduction band and m = 2, 3 for the valence band. The total density is obtained by summation:

$$n({E}_{{{{\rm{F}}}}})={n}_{{\rm {e}}}({E}_{{{{\rm{F}}}}})-{n}_{{\rm {h}}}({E}_{{{{\rm{F}}}}}).$$
(14)

According to our definition, hole doping corresponds to a negative density.