Introduction

Signal and image processing techniques based on integrated electric circuits suffer from speed and power consumption constraints in high-throughput data processing applications. All-optical computation is referred to as an effective alternative because of its excellent ability to implement massive parallel processing with high speed and low power consumption. As one of the most essential mathematical operations, optical analog spatial differential processing has attracted particular attention in the past few years1,2,3,4,5,6,7. It can realize real-time data compression and feature classification by extracting the edge information of the objects and, therefore, shows essential application value in highly sophisticated fields such as artificial intelligence, machine vision, autonomous driving, and biomedical imaging8,9,10,11,12,13. Unfortunately, conventional optical differential systems in the spatial and temporal domains are always composed of bulky optical components, leading to difficulties in precise alignment and high-density optical integration14,15,16,17,18.

In recent years, with the rapid development of nanotechnology, various nanophotonic materials have helped construct more compatible and compact optical differential processing systems to address these problems19,20,21,22,23. In particular, metasurfaces, as a periodic two-dimensional array of sub-wavelength artificial scatters, offer great flexibility for precise manipulation of the phase, amplitude, polarization, and frequency of incident light, thereby opening up many opportunities to this field with significant advantages24,25,26,27,28,29,30,31. Up to this point, most planar meta-optics have been limited to low-order differential operations, such as the first- or second-order14,15,16,17,18,19,20,21,22,23,24,32,33,34,35,36,37,38,39,40,41,42,43,44,45,46. Based on the nonlocality of the dielectric multilayer, a multiple-order analog spatial differentiator is proposed to realize some higher-order differential operations, such as the third- or fourth-order47. The device offers significant advantages in terms of low-complex fabrication and low sensitivity to misalignment. However, this approach limits the broadband expansion and parallel processing capabilities of optical computations. In fact, the ability to synchronously perform multiple-order differential operations on a single device over a wide band is essential for large-scale optical data processing, but unfortunately, it remains a significant challenge.

In this paper, we propose a compact platform based on a single-layer complex amplitude metasurface for multiple-order spatial differentiation across the visible region. By introducing the modulation of the Bessel vortex on the metalens, the coherent transfer function (CTF) of the device shows an exponential correlation with the order of the Bessel vortex, enabling the same order differential operation as the topological charge. As a proof-of-concept, we experimentally demonstrate the isotropic differential processing capability of the first- to fourth-order Bessel vortex modulated metalens (BVML), with the potential for unlimited orders in principle. Thanks to the wavelength insensitivity of the Pancharatnam-Berry (PB) phase employed in the metasurface design, the fabricated devices exhibit broadband response. Furthermore, to maximize the parallel processing advantages of optical computing, synchronous multiple-order radial differential operations are implemented by angle multiplexing on a single metasurface. This platform has the potential to significantly advance the field of optical analog processing, as well as contribute to the progress of artificial intelligence and biomedical imaging.

Results

Theory and principle

To achieve multiple-order two-dimensional spatial differentiation, we start by considering the BVML with rotational symmetry as schematically illustrated in Fig. 1a. Under coherent illumination, the incident light field Ein is modulated by the CTF of the metalens, and different optical differential processing results Eout are output on the image plane, which is determined by the order of the Bessel vortex. The BVML is designed to be integrated on a single-layer metasurface containing the complex amplitude of a Bessel vortex and the complex amplitude of a focusing lens, as shown in Fig. 1b. Therefore, the complex transmission coefficient of the BVML in polar coordinates (r, φ) can be described as follows:

$${M}_{l}\left(r,\varphi \right)={J}_{l}\left(\alpha r\right)\exp \left({il}\varphi \right)\cdot \exp \left(-i{k}_{0}\frac{{r}^{2}}{2f}\right)$$
(1)

where l is the topological charge of the vortex, k0 = 2π/λ is the free-space wavenumber, λ is the free-space wavelength, and f denotes the focal length of metalens. The function Jl (∙) refers to the lth-order Bessel function of the first kind. The coefficient α is defined as ξn,l/R, where R and ξn,l denote the radius of the metalens and the nth zero of the corresponding lth-order Bessel function, Jl (ξn,l) = 0. Based on the Fresnel diffraction approximation, the point spread function (PSF) of the BVML in polar coordinates (ρ, ϕ) on the back focal plane can be obtained as (see Supplementary Section 1 for details),

$${h}_{l}\left(\rho,\phi \right)=\frac{{(-i)}^{l+1}}{\alpha \lambda f}\exp \left(i{k}_{0}\left(\frac{{\rho }^{2}}{2f}+f\right)+{il}\phi \right)\delta \left(\frac{{k}_{0}}{f}\rho -\alpha \right)$$
(2)
Fig. 1: Working principle of the BVML for multiple-order radial differential operations.
figure 1

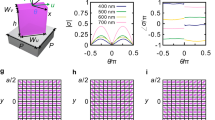
a Schematic of the proposed BVML based on a dielectric metasurface. The metasurface device modulates the incident object light field and outputs a lth-order differential image at the imaging plane according to the order of the Bessel vortex encoded in its profile. b Amplitude and phase distributions of the BVML combining a Bessel vortex and a focusing lens. c–f Simulated CTF curves for the first-, second-, third-, and fourth-order BVMLs and the corresponding fitting curves using the form \(\left|t\left({k}_{r}\right)\right|=a{\left|{k}_{r}\right|}^{l}\). The abbreviation “Sim” has the full name of “Simulation”. g–j Simulated differential processing results of the first-, second-, third-, and fourth-order BVMLs. The input object is part of the 1951 USAF test chart. The enlarged insets highlight the number of edges. Scale bars: 50 μm.

Full size image

According to the Fourier transform relation, the CTF of the BVML in the spatial frequency domain can be derived as tl(kr) = ℱ{hl(ρ,ϕ)}∝Jl(αfkr/k0), where kr = (kx2+ ky2)1/2 refers to the in-plane wavevector along the radial direction. For any non-negative integer l, the asymptotic behavior of the Bessel function with near-zero variable further ensures that the CTF fundamentally satisfies the form of tl(kr)∝(αfkr/k0)l. Therefore, based on the correspondence between the spatial differential operator (∂l/∂rl) and the transfer function (krl), the designed BVMLs show the ability to perform multiple-order radial differential operations (Eout∝∂lEin/∂rl) in the polar coordinate system by presetting the topological charge of the corresponding Bessel vortex, which enable two-dimensional optical analog signal processing.

Figure 1c–f presents the simulated CTF curves of the first- to fourth-order BVMLs, respectively. The corresponding fitted curves verify that the CTF has the form of krl around kr = 0, which is consistent with the theoretical prediction above. Then, we simulate the first- to fourth-order spatial differential processing of the optical image using the designed BVML, as shown in Fig. 1g–j. The edges of the output images are presented clearly along both the horizontal and vertical directions, thus indicating the two-dimensional processing effect. In the partially enlarged detail views of the inset of each panel, the number of edges that can be visually distinguished also represents the typical nature of the lth-order derivative processing.

Design and fabrication of BVML

The proposed BVML is a single-layer metasurface consisting of an array of rectangular-shaped amorphous silicon (α-Si) nanopillars with a height of 400 nm and a subwavelength period of 250 nm on the fused-silicon substrate, as shown in Fig. 2a. The nanopillar is optimized to be 80 nm in width and 150 nm in length, acting as a nanoscale half-wave plate (HWP) with high polarization conversion efficiency in the visible range (see Supplementary Section 2 and 3 for details). For a left-handed circularly polarized (LCP) incident light, the transmitted light with opposite chirality has a PB geometric phase factor exp(i2θ), where θ is the in-plane rotation angle of the nanopillar concerning the fast axis24,25,26,27,28,29,30,31. To implement a complex amplitude modulation on the incident light28, we arrange two groups of nanopillars alternately in a square lattice to form a super-pixel, as depicted in Fig. 2b. According to the interference principle, the transmitted field can be simplified as cos(θ2-θ1)exp(i(θ1 + θ2)), where θ1 and θ2 are the rotation angles of the two groups of nanopillars respectively (see Supplementary Section 4 for details). Thus, a continuous smooth amplitude distribution from 0 to 1 and phase distribution from 0 to 2π can be achieved independently by simply changing the orientation angle of the nanopillars, as shown in Fig. 2c. Based on the above principle, the target complex amplitude Eexp(iψ) of the designed BVML (Fig. 1b) can be encoded into the single-layer metasurface by using the following relationship,

$${\theta }_{1}=\frac{\psi {-\cos }^{-1}\left(E\right)}{2},{\theta }_{2}=\frac{\psi {+\cos }^{-1}\left(E\right)}{2}$$
(3)
Fig. 2: The BVML design and characterization.
figure 2

a Schematic of the designed metasurface. Unit cell structure is composed of rectangular shaped α-Si nanopillars on a SiO2 substrate, with the long axis L = 150 nm, the short axis W = 80 nm, the height H = 400 nm, and the period P = 250 nm. b Schematic top view of the super-pixel realizing complex amplitude modulation. c The complex amplitude value as the function of the rotation angles of the two groups of nanopillars in the super-pixel. The abbreviation “Amp.” has the full name of “Amplitude”. d The optical photographs of the fabricated metasurfaces corresponding to the first- to fourth-order BVMLs, respectively. Scale bars: 200 μm. e Top and tilted views of the SEM images of the α-Si nanopillar arrays. Scale bars: 500 nm. f–i Experimentally measured PSF of the first- to fourth-order BVMLs at the wavelength of 633 nm. Scale bars: 10 μm. j–m The experimental CTF curves for these BVMLs extracted from (f–i), respectively, and fitted by the corresponding order polynomial. The abbreviation “Exp” has the full name of “Experiment”.

Full size image

Figure 2d, e depicts the optical photographs of the fabricated first- to fourth-order BVMLs and the scanning electron microscope (SEM) images of the α-Si nanopillar array, respectively. The detailed fabrication process is described in the Methods section. All fabricated metalens have a diameter of 1.2 mm and a focal length of 1.2 mm. Figure 2f–i presents the measured PSFs of the first- to fourth-order BVMLs for LCP incident light with the wavelength of λ = 633 nm, all of which possess a donut-shaped intensity profile attributed to the orbital angular momentum (OAM) imparted by Bessel vortex. The radius of the ring gradually increases with the value of topological charges. The experimental CTF curves along the radial direction for these BVMLs are extracted from the Fourier transform of PSFs and fitted by the corresponding order polynomial, as shown in Fig. 2j–m. The consistency between the experimental and fitting curves is sufficient to meet the requirements of the devices to perform radial differential operations, as predicted by the theoretical analysis and numerical simulation.

Experimental characterization of BVML

The meticulous design of the experimental setup for multiple-order radial differential processing is schematically illustrated in Fig. 3a. The input image is placed at the object plane of the BVML, illuminated by a coherent light beam generated from a supercontinuum laser attached to an acousto-optic tunable filter (AOTF). A left-handed circular polarizer converts the incident light from linear polarization to fully circular polarization. The spatial differential image output from the BVML is collected with a 50x microscope objective and then captured by the charge-coupled-device (CCD) camera located at the rear focal plane. In order to eliminate background light that is co-polarized with the incident beam and improve the contrast, a right-handed circular polarizer is placed before the CCD.

Fig. 3: Resolution testing of the BVMLs.
figure 3

a Schematic of the experimental setup used to perform different order radial differential processing. b The standard 1951 USAF resolution test chart as the input object. c, d Imaging results of the test target 6-2 marked by the red box in (b) through the first- and second-order BVMLs. e, f Imaging results of the test target 5-4 marked by the blue box in (b) through the third- and fourth-order BVMLs. Each lower panel of (c–f): the normalized intensity distribution along the corresponding vertical dashed line.

Full size image

First, we perform the experiment with the standard 1951 United States Air Force (USAF) resolution test chart as an input object to evaluate the imaging performance of the proposed BVMLs. Figure 3b provides the image of groups 4 to 7 in the resolution test chart, while the colored boxes indicate the test targets of the experiment. Figure 3c–f shows the differential images of the first- and second-order BVMLs for the test target 6-2 (red box in Fig. 3b) and of the third- and fourth-order BVMLs for the test target 5-4 (blue box in Fig. 3b), corresponding to the spatial resolution of 6.96 μm and 11.05 μm, respectively. Here, the higher-order differential operations tend to have lower resolution, which is consistent with the increasing trend of the PSF size along with the topological charge number of the vortex. Moreover, the resolution of BVMLs is also limited by the maximum spatial frequency of the objects that the metasurface can process. In principle, this resolution can be further improved by reducing the unit structure period and increasing the effective numerical aperture (NA) of the metalens. Each lower panel of Fig. 3c–f shows the normalized intensity distribution along the corresponding vertical dashed lines. As expected, we indeed observe that l peaks show at the edge of the image when lth-order spatial differentiation is performed. The experimental measurements are in good agreement with the numerical results in terms of peak position and number.

Next, we experimentally verify the two-dimensional and broadband response of the radial differential operations performed by the proposed BVMLs. We choose a U-shaped and a circular aperture (Fig. S7) as two different amplitude objects to insert into the optical system. The corresponding outputs of the first- to fourth-order differential images under coherent illumination at the wavelength of 633 nm are presented in Fig. 4a. As expected, the step edges of the amplitude are enhanced along all directions and split into the typical l edges. The uniform edge intensity distribution in all images, especially the symmetry in every order differential image of circular aperture object, indicates that the proposed BVMLs have excellent capability of performing isotropic radial differential processing, whose order is determined by the topological charge of the Bessel vortex applied to the metalens. Furthermore, by changing the filtered output of the laser via adjusting the AOTF, we also record the first- to fourth-order differential results of circular aperture at the wavelengths of 580 nm, 532 nm, and 490 nm, respectively, as shown in Fig. 4b. The consistency of the output at different wavelengths reveals that the geometric phase metasurfaces can ultimately enable the designed BVMLs to perform multiple-order differential processing over a broad spectrum.

Fig. 4: Experimental broadband differential imaging results of amplitude objects.
figure 4

a The first- to fourth-order differential imaging results of the U-shaped and circular objects at the wavelength of 633 nm. Scale bars: 20 μm. b The first- to fourth-order differential imaging results of the circular object at the wavelengths of 580, 532, and 490 nm, respectively. Scale bars: 20 μm.

Full size image

Multichannel parallel processing using BVML

To verify the superiority of the proposed BVMLs in parallel multichannel image processing, Fig. 5a presents a schematic illustration of synchronous multi-order radial differential operations using metasurface under coherent light illumination. Here, the metasurfaces enable angle multiplexing to create multiple independent information channels that perform the zeroth- to fourth-order spatial differential operations in a single shot. In principle, there is no limit to the number of channels. Figure 5b shows the design schematic, where the complex amplitude profile of the zeroth- to fourth-order BVMLs is superimposed with different deflection phase profiles, respectively, forming a multichannel metalens. The focal-spot position is controlled by angular multiplexing, with each angle corresponding to a specific order. The analytical expression of the complex amplitude profile multiplexing all channels is given by

$$M\left(r,\varphi \right)=\mathop{\sum }\limits_{l=0}^{N}\left\{{M}_{l}\left(r,\varphi \right)\cdot \sqrt{{\omega }_{l}}\exp (i{k}_{0}{rsin}\left({\phi }_{l}\right)\cos \left(\varphi -{\varphi }_{l}\right))\right\}$$
(4)

where M(r, φ) is a complex amplitude field. Also, N denotes the total number of channels in the designed device; Ml (r, φ) denotes the complex amplitude of the lth-order BVML applied to the lth channel; ωl is the corresponding weight of each channel, which is normalized to 1/5. (ϕl, φl) are the designed polar angles and azimuth angles that determine the output position of each differential operation. The target complex amplitude distribution of the multichannel BVML can be obtained by preset (ϕl, φl) as described in Fig. 5b.

Fig. 5: The integrated multichannel BVML for parallel processing.
figure 5

a Schematic illustration of the multichannel BVMLs synchronously performing the zeroth- to fourth-order differential operations. b The design flow and complex amplitude distributions of the multichannel BVMLs. Only the central region of the complex amplitude is presented at the right side to highlight the details. Scale bars: 300 μm. c Experimentally measured PSF of the multichannel BVML at the wavelength of 633 nm. d Experimental imaging results for the unstained limewood stem cell as a phase object under the wavelength of 633 nm. e Experimental imaging results for the rough surface of transparent drop-casted ultraviolet adhesives under the wavelength of 633 nm. Scale bars of (c–e): 50 μm.

Full size image

The multichannel BVML is fabricated using the same method as above, and the corresponding optical photograph is shown in Fig. S8. The fabricated device has a diameter of 1.2 mm and a focal length of 1.5 mm for all channels. We measure the intensity distribution of the PSF of the device under LCP coherent illumination at the wavelength of 633 nm, as depicted in Fig. 5c, and the broadband response is presented in Fig. S9. They agree very well with the simulation results (Fig. S10), and each PSF shows the same uniform distribution as the single-channel BVML recorded in Figs. 2f–i, which enables each channel in the designed multichannel BVML to perform the corresponding operation independently.

Then, we select the unstained limewood stem cell as the imaging specimen to verify the synchronous multi-order differential imaging functionality of the device. This specimen only significantly affects the phase, not its amplitude, and is thus referred to as a phase object. The experimental setup is the same as in Fig. 3a. Figure 5d shows the zeroth- to fourth-order differential images captured synchronously in five channels at the wavelength of 633 nm. The zeroth-order differential channel presents a traditional bright field imaging where the overall morphology of the specimen can only be vaguely observed, while the more critical shapes and boundaries of the internal cells cannot be clearly identified because of their transparency. Moreover, the first-order differential channel realizes rough edge detection of the specimen by blocking part of the low-frequency components. In contrast, the higher-order differential channel leads to more apparent peaks at the edges of the specimen, revealing more detailed information. This ability to capture rich details will undoubtedly facilitate applications in multicellular localization and classification.

In addition, we also notice that higher-order differential operations have more significant advantages in filtering out low- and mid-frequency components and, therefore, can exhibit a more substantial sharpening effect on the edges of the sample, especially for the objects with relatively smooth changes in amplitude and phase (See the detailed results in Figs. S11 and S12). For experimental verification, Fig. 5e records the imaging results for the rough surface of the transparent drop-casted ultraviolet (UV) adhesives. It is clear that the morphological information in the zeroth-order channel is completely submerged in the low-frequency background. The imaging results in low-order differential channels are also affected by part of the mid-low frequency components stemming from rough surfaces, resulting in the unremoved background and blurred outline. With the increasing order of the differential processing, the edges of the sample are gradually sharpened in the images. The higher-order differential channel shows more significant edge enhancement and higher contrast boundaries. All of the above differential operations are parallel, without the additional power consumption and the help of the image processing algorithm, thus opening up new opportunities for advanced imaging and optical analog computing.

Discussion

In summary, we propose and demonstrate a BVML based on a single-layer complex amplitude metasurface. By presetting the topological charge of the corresponding Bessel vortex, the designed BVMLs can perform multiple-order radial differential operations in the polar coordinate system, which enables two-dimensional optical analog signal processing. Leveraging the ultra-thin and flexible design of the metasurfaces, we synchronously implement the zeroth- to fourth-order radial differential processing of the input objects on a single device by angle multiplexing different information channels, demonstrating the superiority of the proposed BVMLs in parallel processing. Therefore, we envision that the proposed compact and multifunctional BVMLs may have significant potential for application in the field of large-scale optical data processing and biomedical imaging.

Methods

Sample fabrication

The metasurface is fabricated using electron-beam lithography (EBL) on a 400 nm thick amorphous silicon (\(\alpha\)-Si) film with quartz substrate to pattern the specific arrays. Firstly, an ARP6200 electron-beam resist layer is deposited by spin-coating on the α-Si film. Then, the sample is exposed through EBL, and the patterns are revealed after the development process. Afterwards, a 30 nm thick Aluminum layer working as the hard etching mask is deposited on the sample by electron-beam evaporator, and the lift-off process is done in N-Methylpyrrolidone (NMP). Next, the patterns are transferred to α-Si film by inductively coupled plasma (ICP) etching, where C4F8 and SF6 are utilized during the etching process. The lower radio frequency (RF) power is 40 W, and the upper RF power is 500 W, the pressure being 13 mTorr. The ratio of C4F8/SF6 is tuned to 2.5 to improve the anisotropy of etching effectively. Therefore, the final sample can be obtained after removing the Al hard etching mask.