Charge stripe manipulation of superconducting pairing symmetry transition

Abstract

Charge stripes have been widely observed in many different types of unconventional superconductors, holding varying periods (${{\mathcal{P}}}$) and intensities. However, a general understanding on the interplay between charge stripes and superconducting properties is still incomplete. Here, using large-scale unbiased numerical simulations on a general inhomogeneous Hubbard model, we discover that the charge-stripe period ${{\mathcal{P}}}$, which is variable in different real material systems, could dictate the pairing symmetries—d wave for ${{\mathcal{P}}}\ge 4,s$ and d waves for ${{\mathcal{P}}}\le 3$. In the latter, tuning hole doping and charge-stripe amplitude can trigger a d-s wave transition and magnetic-correlation shift, where the d-wave state converts to a pairing-density wave state, competing with the s wave. These interesting phenomena arise from an unusual stripe-induced selection rule of pairing symmetries around on-stripe region and within inter-stripe region, giving rise to a critical point of ${{\mathcal{P}}}=3$ for the phase transition. In general, our findings offer important insights into the differences in the superconducting pairing mechanisms across many ${{\mathcal{P}}}$-dependent superconducting systems, highlighting the decisive role of charge stripe.

Introduction

Developing the universal understanding of the intertwisting mechanism between different symmetry-breaking orders is one of the most challenging goals in unconventional superconductors. Initially, the emergence of charge orders in a stripe phase was widely discovered in cuprates, e.g., La₂CuO₄^1,2, RBa₂Cu₃O₆³, Bi₂Sr₂CaCu₂O₈⁴, and other family materials, sparking significant interest in their origins⁵. Soon after that, similar charge stripes were later observed in iron-based superconductors, e.g., FeSe⁶, and Ni-based superconductors, e.g., infinite-layer nickelates^{7,8,9,10,11,12} and Ruddlesden-Popper-phase nickelates¹³. Very recently, the charge stripes were also found in the kagome-lattice superconductors CsV₃Sb₅¹⁴ and CsCr₃Sb₅¹⁵. Clearly, the widespread existence of charge stripes in variable unconventional superconductors highlights their significant role in relation to superconductivity. Interestingly, the period ${{\mathcal{P}}}$ and intensity V₀ of charge stripe are variable in different materials, which could be tunable by external factors like pressures and defects^16,17,18,19, opening potential possibilities to manipulate superconducting pairing symmetry.

Since its inception, the Hubbard model has served as an archetypal model for elucidating strongly correlated phenomena^20,21. Despite its simplicity, it can uncover rich quantum phases in condensed matter physics^{22,23,24,25,26,27,28}. For example, the Hubbard model under different conditions can effectively capture d-wave pairing symmetry^22,23, stripe order^24,25,26,29, and antiferromagnetic (AFM) order^28,30 in cuprate-like square lattices, and it can also demonstrate the interplay between these symmetry-breaking orders³¹. Interestingly, previous studies have suggested that the spontaneous formation of charge stripe in a square lattice could be sensitive to variations in model parameters and lattice boundary conditions³². Alternatively, the charge stripes can be artificially induced as external fields to explore its relationship with superconductivity. For example, in square-lattice models with ${{\mathcal{P}}}=4$ for simulating cuprates, an enhancement of d-wave pairing symmetry is observed^33,34,35 over a broad range of V₀, which can be attributed to the intensified AFM correlations between the stripes, accompanied by a π-phase shift in the system³³. Until now, however, a comprehensive understanding of the interplay between charge stripe, varying ${{\mathcal{P}}}$ and V₀ values, and superconducting pairing symmetry remains lacking, which may prevent a deeper insight into the distinct pairing symmetries observed across different systems.

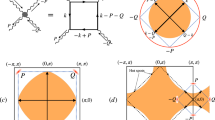
The unbiased determinant quantum Monte Carlo (DQMC) and density-matrix renormalization group (DMRG) methods are widely recognized as two highly accurate and complementary approaches to solving the Hubbard model^22,23,25. While DQMC can effectively capture the trend of physical quantities at finite temperatures, DMRG is powerful in determining them in the ground state. Here, by combining unbiased DQMC and DMRG simulations on an inhomogeneous square lattice, we discover that the existence of charge stripes with different periods ${{\mathcal{P}}}$ [defined in Fig. 1(a)] plays a very unexpected role in determining the pairing-symmetry transition. While the d-wave is always dominant for ${{\mathcal{P}}}\ge 4$, both s (note that this is an extended s-wave state afterwards) and d-waves can appear when ${{\mathcal{P}}}\le 3$. Taking ${{\mathcal{P}}}=3$ as an example, we discover that the interplay between the hole-doping concentration δ and charge-stripe amplitude V₀ can realize a remarkable d-s wave transition in a large region of the phase diagram, in which the critical V₀ (V₀, c) for the phase transition exhibits a nearly linear dependence of the on-site electron-electron repulsion strength U. The DMRG simulations further reveal that the charge-stripe-induced domain wall can generate an interesting selection rule to produce s and d-waves around the on-stripe region and inside the inter-stripe region, respectively. Therefore, the smaller the ${{\mathcal{P}}}$, the stronger the s-wave in the system. Accompanying the d-s wave transition, there is an interesting magnetic-correlation transition, weakening the AFM correlation. These results strongly indicate an inherent interplay between charge stripes, superconducting pairing, and magnetic correlation in the ${{\mathcal{P}}}$-dependent systems, in which charge stripes play a vital role in forming the d-s wave transition.

Fig. 1: Lattice structure and superconducting phase diagram.

a Geometry of the square lattice with periodic charge stripes. ${{\mathcal{P}}}$ denotes charge-stripe period, L denotes lattice size, and V₀ denotes charge-stripe amplitude. Total number of sites is N = L × L, and L = 12. Blue (red) circles label the site with (without) the inclusion of V₀, representing the on-stripe (inter-stripe) region. b Determinant Quantum Monte Carlo (DQMC)-calculated phase diagram of the inhomogeneous Hubbard model with ${{\mathcal{P}}}=3$, on-site repulsion strength U/t = 4, and temperature T = t/5, where t = 1 is the unit of energy. δ represents hole-doping concentration. Note that the d-s wave transition is observed even at zero temperature based on density matrix renormalization group (DMRG) simulations. Phase boundary of solid-line is determined by effective pairing strength ${\bar{P}}_{\alpha }$ at each (V₀, δ). Dashed-line denotes the region where d-wave state is transformed into pairing density wave (PDW) state, competing with s-wave state. Note that s-wave state is always more stable than PDW state. c Dominant pairing symmetry depends on ${{\mathcal{P}}}$, where ${{\mathcal{P}}}=3$ is a critical point.

Results

${{\mathcal{P}}}$-dependent d-s wave transition

In the following, we will mainly discuss the model system with charge stripes at ${{\mathcal{P}}}=3$ in a minimal single-${d}_{{x}^{2}-{y}^{2}}$-band Hubbard model, because this simplified model could capture the most intrinsic feature between ${{\mathcal{P}}}$ and pairing symmetry and also because a similar dominated role of single-${d}_{{x}^{2}-{y}^{2}}$-band was observed in cuprates and nickelates^36,37. As shown in Fig. 1(b), we have systematically calculated the pairing-symmetry diagram as a function of δ and V₀. Here, δ is set to the range of 0.1 ~ 0.3^38,39, and V₀ is set to the range of 0 ~ 8 based on the realistic situations. For example, the V₀ induced by variable valence Ni charge-state in the stripe of infinite-layer nickelates is estimated to be  ~6, which is further tunable under external conditions^17,18,19. When V₀ is larger than a critical value of V_0,c ~3.25, there is a clear pairing-symmetry transition from d to s waves in a large δ range of 0.1 ~ 0.23. As will be shown later, this d-s wave transition is robust against different U/t and T/t values. For comparison, we have also calculated the cases of ${{\mathcal{P}}}=2$ and ${{\mathcal{P}}}=4$. Interestingly, when ${{\mathcal{P}}}=2$, a similar d-s wave transition can be observed at an even smaller V_0,c with a much sharper transition slope (Supplementary Fig. 1). On the other hand, when ${{\mathcal{P}}}=4$, only d-wave is observed and d-s wave transition cannot exist in the same δ range (Supplementary Fig. 2). As summarized in Fig. 1(c), these calculations lead us to an interesting conclusion that ${{\mathcal{P}}}=3$ is a critical point for the pairing-symmetry transition, that is, the δ/V₀-dependent d-s wave transition can only exist when ${{\mathcal{P}}}\le 3$. Importantly, this finding is regardless of whether it is a single-band or multi-band model (Supplementary Fig. 3), being a general feature in ${{\mathcal{P}}}$-dependent superconducting systems.

To clearly understand the role of V₀ in the d-s wave transition, we have plotted the δ-dependence of effective pairing interaction ${\bar{P}}_{\alpha }$ with the typical parameters of T  = t/5 and U/t  = 4 under different V₀. As shown in Fig. 2(a), without charge stripes (V₀= 0), ${\bar{P}}_{d}$, which is strongest at δ = 0, is robust and more stable than that of ${\bar{P}}_{s}$ at different δ. Meanwhile, the s-wave pairing is suppressed (${\bar{P}}_{s} < 0$) at large δ. As shown in Fig. 2(b), when V₀= 3, ${\bar{P}}_{d}$ is rapidly decreased in a much faster way than that of ${\bar{P}}_{s}$. This indicates that s-wave pairing is more robust against the charge-stripe potential compared to d-wave pairing. Importantly, as shown in Fig. 2(c), when V₀= 4, ${\bar{P}}_{s}$ eventually becomes more stable than ${\bar{P}}_{d}$ over an extensive δ range (0 < δ ≤ 0.22), leading to a remarkable d-s wave transition. In particular, d-wave pairing is fully suppressed at 0 <  δ ≤ 0.2 under V₀= 4, eventually transformed into a d-wave PDW state to compete with s-wave state, as discussed later. As shown in Fig. 2(d), when ${V}_{0}=8,{\bar{P}}_{s}$ maintains more stable than ${\bar{P}}_{d}$ in the moderate δ (0.05 < δ ≤ 0.15). However, for sufficiently large $\delta,{\bar{P}}_{d}$ is always more stable than ${\bar{P}}_{s}$, regardless of the V₀, as also shown in the phase diagram of Fig. 1(b).

Fig. 2: Occurrence of d-s wave transition.

DQMC-calculated ${\bar{P}}_{\alpha }$ as a function of δ at T = t/5 and U/t = 4 with ${{\mathcal{P}}}=3$ on a L = 12 lattice for (a) V₀=0, (b) V₀=3, (c) V₀=4, and (d) V₀=8. Here, we divided the data into 10 bins and calculated the error of the data using the jackknife method. The horizontal dashed line represents the zero point on the y-axis. e DMRG-calculated effective zero-momentum pair-pair structure factor ${\bar{S}}_{\alpha }$ as a function of V₀ at δ=0.111 and U/t = 8 on the 6 × 6 cylinder. While a small discrepancy is observed, it will not affect our conclusion within small error bars. (f) DMRG-calculated V_0,c for d-s wave transition with different U on both 6 × 3 and 6 × 6 cylinders, exhibiting a nearly linear function of U. For comparison, DQMC result on a 12 × 12 lattice at U/t  = 4 and T  = t/5 is also marked here.

The above finite-temperature DQMC conclusion holds at a much lower temperature of T = t/12 (Supplementary Fig. 4). To further confirm the ground-state properties at zero temperature, we have systematically calculated effective zero-momentum pair-pair structure factor ${\bar{S}}_{\alpha }$ using DMRG method with different cylinders and U (Supplementary Fig. 5). For example, Fig. 2(e) shows ${\bar{S}}_{\alpha }$ as a function of V₀ at δ = 0.111 and U/t  = 8 on a 6 × 6 cylinder. ${\bar{S}}_{d}$ is dominant when V₀ is smaller than  ~ 6.2. Interestingly, when V₀ is bigger than $\sim 6.2,{\bar{S}}_{s}$ becomes more robust. Therefore, at ground state, charge inhomogeneity can also support a remarkable d-s wave transition, demonstrating that the finite-temperature trend obtained from DQMC simulations is reliable at zero temperature. In Fig. 2(f), we have plotted V_0,c as a function of U for the observed pairing-symmetry transition with two cylinders. Remarkably, V_0,c displays a nearly linear relationship with U for both 6 × 3 and 6 × 6 cylinders. As U increases, so does V_0,c, providing a guideline for understanding or manipulating the pairing-symmetry transition. For a typical U/t = 4, the DMRG-calculated V_0,c in 6 × 3 and 6 × 6 cylinders exhibit slightly different values indicating the lattice-size dependence. However, these values are overall consistent with DQMC results. Therefore, our results undisputedly demonstrate that this d-s wave transition exists in a ${{\mathcal{P}}}=3$ system and that the V_0,c depends on U.

We have further investigated the critical role of different parameters on ${\bar{P}}_{\alpha }$. Here, we choose the cases of δ = 0.3 (d-wave-dominated region) and δ = 0.18 (s-wave-dominated region). Figure 3(a)–(b) show the case of d-wave pairing at δ  = 0.3. In Fig. 3(a), we calculate the temperature-dependent ${\bar{P}}_{d}$ for different V₀. As temperature is lowered, ${\bar{P}}_{d}$ increases rapidly. Importantly, it is observed that d-wave pairing is enhanced with the increase of V₀, indicating the important role of charge fluctuation^31,33. This enhancement may be caused by the appearance of more nearly half-filled inter-stripe regions for larger V₀ at δ = 0.3 (Supplementary Fig. 6). On the other hand, Fig. 3(b) shows that the ${\bar{P}}_{d}$ is enhanced by larger U, suggesting the importance of electron-electron correlation. Importantly, the lattice size effect of ${\bar{P}}_{d}$ is weak, i.e., L = 9, 12, and 15 exhibit almost identical results.

Fig. 3: Effective pairing interactions and structure factors.

DQMC-calculated ${\bar{P}}_{\alpha }$ as a function of temperature (a) for different V₀ at δ  = 0.3, U/t  = 4, and L = 12, (b) for different U/t or L at δ  =  0.3 and V₀= 6. c–d are similar to (a–b) but for the cases of δ  = 0.18. Gray-dotted line in (c) represents the d-wave PDW at V₀ = 5. Left of (c): DMRG-calculated ${\bar{S}}_{\alpha }$ of s-wave (blue-solid) and d-wave (blue-dash), and the peak value of d-wave PDW ${\bar{S}}_{d}({{\bf{q}}})$ (gray-dash) at δ  =  0.111, U/t  =  8, V₀  =  7 on a 6 × 6 cylinder. The error of the DQMC data are calculated by using the jackknife method.

Figure 3 (c)–(d) show the case of s-wave pairing at δ = 0.18. In Fig. 3(c), we present the temperature dependence of ${\bar{P}}_{s}$, in which ${\bar{P}}_{d}$ is also plotted here for comparison. For ${V}_{0}=5 \sim 7,{\bar{P}}_{s}$ is positive and increases slowly with decreasing temperature. The larger V₀, the stronger ${\bar{P}}_{s}$. However, ${\bar{P}}_{d}$ is negative at V₀  = 5 ~ 6 and becomes positive at V₀= 7. So, below ${V}_{0}=7,{\bar{P}}_{d}$ is less stable than ${\bar{P}}_{s}$ at all the considered temperature ranges. It is curious to understand the origin of the suppression of d-wave state, which suggests that there may be an unusual phase transition. To confirm our speculation, we have systematically calculated the possible PDW state in ${{\mathcal{P}}}=3$ system. Taking V₀  = 5 as an example [Fig. 3(c)], interestingly, the peak of ${P}_{d}^{{{\rm{PDW}}}}({{\bf{q}}})$ moves away from zero momentum and the system shows a tendency to form a PDW state. Although ${P}_{d}^{{{\rm{PDW}}}}({{\bf{q}}})$ is positive, it is still less stable than ${\bar{P}}_{s}$. In addition, we further calculate the competition between ${P}_{d}^{{{\rm{PDW}}}}({{\bf{q}}})$ and ${\bar{P}}_{s}$ under different V₀ and δ (Supplementary Fig. 7), and find that s-wave state is always more stable than PDW state. This may account for the challenge to observe PDW in nickelates, whch is hidden behind the s-wave. In the phase diagram of Fig. 1(b), we have also plotted the boundary where PDW states emerge, which is close to the boundary of s-wave state. To further confirm our DQMC conclusion, we have plotted DMRG-calculated ${\bar{S}}_{\alpha }$ of the s- and d-waves, and the peak value of PDW ${\bar{S}}_{d}({{\bf{q}}})$ at δ  = 0.111, U/t  = 8, V₀  = 7 on a 6 × 6 cylinder, supporting the dominance of s-wave at zero temperature (see more cases in Supplementary Fig. 8). Figure 3(d) shows ${\bar{P}}_{s}$ as a function of temperature at different U and L. Similar to that in Fig. 3(b), it is obvious that ${\bar{P}}_{s}$ is also enhanced with increasing U and shows a very weak lattice-size effect. Furthermore, our constrained path quantum Monte Carlo (CPQMC) and DMRG simulations also suggest the possible emergence of long-range s-wave superconducting order within the investigated parameter region (Supplementary Fig. 9 and Supplementary Fig. 10).

Origin of d-s wave transition

It is interesting to understand the physics insight behind this d-s pairing-symmetry transition. In Fig. 4, based on the ground-state DMRG analysis on the condensate wave function, we realize that this phase transition is strongly related to charge-stripe-induced potential fluctuation, where the domain-walls can form around the on-stripe region (blue-circle in Fig. 4). Specifically, the DMRG-calculated dominant Cooper pair mode ζ₀(iδ_l) supports that a clear local pattern of s-wave pairing can emerge around on-stripe regions at moderate V₀ and δ, regardless of ${{\mathcal{P}}}$, where horizontal and vertical bonds have the same signs (Supplementary Fig. 11). On the contrary, inter-stripe region (red-circle in Fig. 4) is always beneficial to asymmetric d-wave, as long as ${{\mathcal{P}}}$ is sufficiently large, where horizontal and vertical bonds exhibit opposite signs (Supplementary Fig. 11). In brief, without the domain-wall, the system favors asymmetric d-wave patterns. In the presence of domain-walls, the influence of domain-walls on pairing symmetry is local, and s-wave patterns can only be prominent near on-stripe region at moderate V₀ and δ. The smaller ${{\mathcal{P}}}$, the more the s-wave components can be generated in the system. When ${{\mathcal{P}}}\ge 4$, the inter-stripe d-wave region plays a dominant role in forming global d-wave pairing in the system. However, when ${{\mathcal{P}}}\le 3$, the intensity of s-wave pattern near on-stripe region is sufficiently strong to convert the global pairing symmetry from d to s. This understanding not only can explain why the d-s wave transition is more accessible in a smaller ${{\mathcal{P}}}$ system [Supplementary Fig. 1 and Fig. 1(c)], but also suggests that the local s-wave pairing may also exist in ${{\mathcal{P}}}\ge 4$ (d-wave-dominant) systems, as long as the V₀ and δ are in a suitable region.

Fig. 4: Physical Origin of the d-s wave transition.

Sketch depicts the d-s wave transition by analyzing the condensate wave function of the dominant Cooper pair mode ζ₀(iδ_l) based on DMRG simulations. Blue (red) circles label the sites in the on-stripe (inter-stripe) region with (without) V₀. Purple (green) bonds indicate positive (negative) values of ζ₀(iδ_l). The solid line at the top illustrates the magnitude of the striped potential energy. Symmetric s-wave patterns only occur near on-stripe regions (domain-walls) at moderate V₀ and δ, i.e., horizontal and vertical bonds have the same signs. On the contrary, the inter-stripe region always benefits asymmetric d-wave, i.e., horizontal and vertical bonds have opposite signs. Due to the competition between the d- and s-wave pairing symmetries, global s-wave pattern can be stabilized with ${{\mathcal{P}}}\le 3$.

Besides the pairing-symmetry transition, it is also curious to understand the role of charge stripe on the modulation of spin susceptibility [χ_s(q)]. In Figs. 5(a) and (b), we have calculated the χ_s(q) for two different V₀ at δ  = 0.3 in the q-space (see more V₀ cases in Supplementary Fig. 12). In the d-wave region, the system behaves as the AFM correlation. One can see that the (π, π) magnetic correlation is enhanced as the V₀ increases, i.e., the system exhibits a stronger AFM fluctuation along the direction of stripes (x direction) with larger V₀. This AFM-correlation enhancement is possibly caused by more nearly half-filled inter-stripe regions (Supplementary Fig. 6), similar to the behavior of enhanced d pairing symmetry at δ = 0.3. Moreover, sub-peaks emerge at ${q}_{y}=\pi \pm \pi /{{\mathcal{P}}}=2\pi /3$ and 4π/3, reflecting the incommensurate spin correlations observed in the d-wave superconductor²⁹, and are gradually suppressed as increasing V₀ from 4 to 6.

Fig. 5: Correlation between spin susceptibility and magnetism.

DQMC-calculated spin susceptibility χ_s(q) in the first Brillouin zone at T  =  t/5, U/t  =  4 with (a) δ  = 0.3 and V₀= 4, (b) δ  =  0.3 and V₀= 6, (c) δ  = 0.18 and V₀= 4, and (d) δ  =  0.18 and V₀= 6. Here, (a–b) are for the d-wave cases, and (c–d) are for the s-wave cases.

The case is dramatically changed in the s-wave region. In Fig. 5(c) and (d), we have calculated χ_s(q) at δ = 0.18 with two different V₀, in which the s-wave pairing symmetry is dominated. Surprisingly, along with the d-s wave transition, the AFM correlation at (π, π) is weakened. In detail, χ_s(q) shows a dumbbell shape, different from the rod shape for the d-wave at δ = 0.3. The dumbbell distribution becomes more obvious as V₀ increases (see more V₀ cases in Supplementary Fig. 13). Besides, the (π, π) magnetic correlation and dominant pairing correlation exhibit a very similar temperature dependence (Supplementary Fig. 14). Given that magnetism and superconductivity simultaneously exhibit dramatical differences in these two doping cases of δ = 0.3 and 0.18, it indicates that the pairing-symmetry transition and magnetic-correlation transition are strongly interwoven.

Discussion

Both charge and spin stripes are widely observed in many superconductors. Although the spin stripe itself is interesting in a model study, it is beyond the focus for our current study. Meanwhile, although the major conclusion is described by a minimal Hubbard model, it is robust against the multi-band model (Supplementary Fig. 3) or different stripe styles (Supplementary Fig. 15). Since the charge stripe in a real material system might be tunable under some external conditions, combined with the linear relationship between V_0,c and U, our study provides an interesting idea of charge-stripe engineering of pairing symmetry. During the d-s wave phase transition, the competition between PDW and s-wave provides an important opportunity to explore the exotic intertwining phenomenon between PDW, d-wave, and s-wave.

Methods

The two-dimensional Hubbard Hamiltonian on a square lattice with nearest-neighbor hopping t and Coulomb repulsion U is written as

$$\hat{H}= -t{\sum}_{\langle {{\bf{i}}},{{\bf{j}}}\rangle \sigma }({c}_{{{\bf{i}}}\sigma }^{{\dagger} }{c}_{{{\bf{j}}}\sigma }+{c}_{{{\bf{j}}}\sigma }^{{\dagger} }{c}_{{{\bf{i}}}\sigma })+U{\sum}_{{{\bf{i}}}}{n}_{{{\bf{i}}}\uparrow }{n}_{{{\bf{i}}}\downarrow }\\ -\mu {\sum}_{{{\bf{i}}}}({n}_{{{\bf{i}}}\uparrow }+{n}_{{{\bf{i}}}\downarrow })+{V}_{0}{\sum}_{mod({i}_{y},{{\mathcal{P}}})=0}({n}_{{{\bf{i}}}\uparrow }+{n}_{{{\bf{i}}}\downarrow }).$$

(1)

Here, c_iσ (${c}_{{{\bf{i}}}\sigma }^{{\dagger} }$) annihilates (creates) electrons at site i with spin σ (σ =  ↑, ↓), and ${n}_{{{\bf{i}}}\sigma }={c}_{{{\bf{i}}}\sigma }^{{\dagger} }{c}_{{{\bf{i}}}\sigma }$ is the particle number operator for the electron. We set the nearest-neighbor hopping t = 1 as the energy unit. μ is a global chemical potential for all sites, and V₀ is an additional potential exerted on a set of on-stripe rows i  = (i_x, i_y) where i_y  =  0 modulo ${{\mathcal{P}}}$, that is, $\,{\mbox{mod}}\,({i}_{y},{{\mathcal{P}}})=0$. The larger V₀, the stronger the charge fluctuation. Accordingly, as shown in Fig. 1(a), the charge stripe with tunable oscillation strength can be introduced externally via a raised energy V₀. To further confirm our results, we have also selected a cosine-like varying modulation (Supplementary Fig. 15). Interestingly, V_0,c for the d-s wave transition becomes even smaller when we choose the cosine-like varying charge modulation.

We note that the purpose of this model is not to address the origin of the stripe formation, as this is still an open question. Instead, it allows us to estimate the characteristics of spin and pairing correlations in the presence of pre-existing charge orders. This is an appropriate approximate model when the energy scale of the stripe formation is greater than that of superconductivity^{31,33,35,38,39,40,41}.

DQMC method

Our calculations are mainly performed on the lattice shown in Fig. 1(a) using the DQMC method with periodic boundary conditions. This unbiased numerical method is powerful and reliable to investigate strongly-correlated electrons^{42,43,44,45,46}. The basic strategy of the finite-temperature DQMC method is to express the partition function $Z={{\rm{Tr}}}\exp (-\beta H)$ as a high-dimensional integral over a set of random auxiliary fields. The integration is then accomplished by Monte Carlo sampling. In our DQMC simulations, 8000 warm-up sweeps are conducted to equilibrate the system, and an additional 10,000 ~ 1,200,000 sweeps are performed for measurements, which are divided into 10 ~ 20 bins. Besides, two local updates are performed between measurements. In the process of eliminating the on-site interaction, the inverse temperature β = 1/T is discretized. And the discretization mesh Δτ  = 0.1 of β is chosen small enough so that the resulting Trotter errors are typically smaller than those associated with the statistical sampling.

We have performed a systematical analysis of the infamous sign problem⁴⁶ in our DQMC simulations. The average sign decreases quickly as the inverse temperature exceeds 3, and the sign problem gets worse for higher U and larger L. In most of our calculations, the average sign keeps as  > 0.55 (see Supplementary Fig. 16). In order to explore the lower temperature behavior of ${\bar{P}}_{\alpha }$, the average sign keeps as  > 0.4 (Supplementary Fig. 17). In short, the conclusions obtained from our DQMC calculations are reliable.

To explore the effects of the charge-density modulation on superconductivity, we define the pairing interaction as

$${P}_{\alpha }=\frac{1}{{N}_{s}}{\sum}_{{{\bf{i}}},{{\bf{j}}}}{{{\mathcal{D}}}}_{\alpha }({{\bf{i}}},{{\bf{j}}}),$$

(2)

where

$${{{\mathcal{D}}}}_{\alpha }({{\bf{i}}},{{\bf{j}}})=\int_{0}^{\beta }d\tau {\left\langle {\Delta }_{\alpha }^{{\dagger} }({{\bf{i}}},\tau ){\Delta }_{\alpha }({{\bf{j}}},0)\right\rangle }_{T}$$

(3)

gives the zero-frequency pair-pair correlation function between sites i and j, α represents the pairing symmetry, the corresponding order parameter Δ_α(i, τ)  = e^HτΔ_α(i, 0)e^−Hτ and ${\Delta }_{\alpha }^{{\dagger} }({{\bf{i}}},0)$ is written as

$${\Delta }_{\alpha }^{{\dagger} }({{\bf{i}}},0)={\sum}_{l}{f}_{\alpha }^{*}({{{\boldsymbol{\delta }}}}_{l}){{{\mathcal{C}}}}_{{{\bf{i}}}{{{\boldsymbol{\delta }}}}_{l}}^{{\dagger} }$$

(4)

with ${{{\mathcal{C}}}}_{{{\bf{i}}}{{{\boldsymbol{\delta }}}}_{l}}={c}_{{{\bf{i}}}\uparrow }{c}_{{{\bf{i}}}+{{{\boldsymbol{\delta }}}}_{l}\downarrow }-{c}_{{{\bf{i}}}\downarrow }{c}_{{{\bf{i}}}+{{{\boldsymbol{\delta }}}}_{l}\uparrow }$ denoting the operator for the Cooper pair on the sites i and i + δ_l, and f_α(δ_l) stands for the form factor of pairing function. The vectors δ_l (l  = 1, 2, 3, 4) denote the nearest-neighbor connections, and δ_l is $\pm \hat{x}$ and $\pm \hat{y}$. Considering the structure of the square lattice, the possible singlet pairing forms are given by either the extended s-wave or the d-wave, which have the following form factor^33,47,

$$s-\,{\mbox{wave}}\,:{f}_{s}({{{\boldsymbol{\delta }}}}_{l})= +1,\\ d-\,{\mbox{wave}}\,:{f}_{d}({{{\boldsymbol{\delta }}}}_{l})= \left\{\begin{array}{l}+1\,\,{\mbox{for}}\,\,{{{\boldsymbol{\delta }}}}_{l}=\pm \hat{x}\\ -1\,\,{\mbox{for}}\,\,{{{\boldsymbol{\delta }}}}_{l}=\pm \hat{y}\end{array},\right.$$

(5)

In practice, the effective pairing interaction ${\bar{P}}_{\alpha }$ is a more direct probe to identify the dominant superconducting pairing form^48,49. In order to obtain ${\bar{P}}_{\alpha }$, the uncorrelated single-particle contribution ${\tilde{{{\mathcal{D}}}}}_{\alpha }({{\bf{i}}},{{\bf{j}}})$ is also calculated, which is reached by replacing $\langle {c}_{{{\bf{i}}}\downarrow }^{{\dagger} }{c}_{{{\bf{j}}}\downarrow }{c}_{{{\bf{i}}}+{{{\boldsymbol{\delta }}}}_{l}\uparrow }^{{\dagger} }{c}_{{{\bf{j}}}+{{{\boldsymbol{\delta }}}}_{{l}^{{\prime} }}\uparrow }\rangle$ in Eq. (2) with $\langle {c}_{{{\bf{i}}}\downarrow }^{{\dagger} }{c}_{{{\bf{j}}}\downarrow }\rangle \langle {c}_{{{\bf{i}}}+{{{\boldsymbol{\delta }}}}_{l}\uparrow }^{{\dagger} }{c}_{{{\bf{j}}}+{{{\boldsymbol{\delta }}}}_{{l}^{{\prime} }}\uparrow }\rangle$. Eventually, we have the effective pairing interaction ${\bar{P}}_{\alpha }={P}_{\alpha }-{\tilde{P}}_{\alpha }$ as well as the effective zero-frequency pair-pair correlation function ${\bar{{{\mathcal{D}}}}}_{\alpha }({{\bf{i}}},{{\bf{j}}})={{{\mathcal{D}}}}_{\alpha }({{\bf{i}}},{{\bf{j}}})-{\tilde{{{\mathcal{D}}}}}_{\alpha }({{\bf{i}}},{{\bf{j}}})$. The appearance of negative effective pairing interaction may indicate that the pairing symmetry is suppressed by other competing states.

We also define the effective zero-frequency pair-pair structure factor for DQMC,

$${\bar{{{\mathcal{D}}}}}_{\alpha }({{\bf{q}}})=\frac{1}{{N}_{s}}{\sum}_{{{\bf{i}}},{{\bf{j}}}}{e}^{i{{\bf{q}}}\cdot ({{\bf{i}}}-{{\bf{j}}})}{\bar{{{\mathcal{D}}}}}_{\alpha }({{\bf{i}}},{{\bf{j}}}).$$

(6)

In particular, we use ${P}_{d}^{{{\rm{PDW}}}}({{\bf{q}}})\equiv {\bar{{{\mathcal{D}}}}}_{d}({{\bf{q}}})$ to understand the effects of the charge-density modulation on the d-wave pair-density-wave (PDW) order. In the simulations, when the peak of ${P}_{d}^{{{\rm{PDW}}}}({{\bf{q}}})$ is located at zero momentum, it indicates a lack of PDW state in the system. Otherwise, there may be a PDW state^50,51.

As magnetic excitation possibly plays an important role for the superconductivity mechanism in strong electron correlation systems, we also study the spin susceptibility in the z direction at zero frequency in the ${{\mathcal{P}}}=3$ model,

$${\chi }_{s}({{\bf{q}}})=\frac{1}{{N}_{s}}\int_{0}^{\beta }d\tau {\sum}_{{{\bf{i}}},{{\bf{j}}}}{e}^{i{{\bf{q}}}\cdot ({{\bf{i}}}-{{\bf{j}}})}{\langle {{{\rm{m}}}}_{{{\bf{i}}}}(\tau ){{{\rm{m}}}}_{{{\bf{j}}}}(0)\rangle }_{T},$$

(7)

where m_i(τ) = e^Hτm_i(0)e^−Hτ with ${m}_{{{\bf{i}}}}(0)={c}_{{{\bf{i}}}\uparrow }^{{\dagger} }{c}_{{{\bf{i}}}\uparrow }-{c}_{{{\bf{i}}}\downarrow }^{{\dagger} }{c}_{{{\bf{i}}}\downarrow }$.

DMRG method

At zero temperature, we employ the DMRG method to investigate the model Hamiltonian on a cylinder with 8, 192 SU(2) bases at most, equivalent to about 25, 000 U(1) bases, and guarantee that the truncation error is less than 10⁻⁵. We also examine the pairing-symmetry transition directly by investigating the static pair-pair structure factor

$${{{\mathcal{S}}}}_{\alpha }({{\bf{q}}})=\frac{1}{{N}_{s}}{\sum}_{{{\bf{i}}},{{\bf{j}}}}{e}^{i{{\bf{q}}}\cdot ({{\bf{i}}}-{{\bf{j}}})}\left\langle {\Delta }_{\alpha }^{{\dagger} }({{\bf{i}}},0){\Delta }_{\alpha }({{\bf{j}}},0)\right\rangle,$$

(8)

where the statistic average at a finite temperature and zero frequency in Eq. (6) is replaced with the ground-state expectation value at zero temperature here. Similarly, we also calculate the uncorrelated single-particle contribution ${\tilde{{{\mathcal{S}}}}}_{\alpha }({{\bf{q}}})$ and define the effective static pair-pair structure factor as ${\bar{{{\mathcal{S}}}}}_{\alpha }({{\bf{q}}})={{{\mathcal{S}}}}_{\alpha }({{\bf{q}}})-{\tilde{{{\mathcal{S}}}}}_{\alpha }({{\bf{q}}})$. In the calculation, we target the lowest-energy zero-magnetic-momentum state with a specified even number of electrons. Thus, the number of electrons for any species is also preserved and the spin fluctuations remain negligible. In this work, we use the effective zero-momentum pair-pair structure factors ${\bar{S}}_{s}\equiv {\bar{{{\mathcal{S}}}}}_{s}({{\bf{q}}}=(0,0))$ and ${\bar{S}}_{d}\equiv {\bar{{{\mathcal{S}}}}}_{d}({{\bf{q}}}=(0,0))$, and the emerging peak of ${\bar{{{\mathcal{S}}}}}_{d}({{\bf{q}}})$ at a finite momentum q ≠ (0, 0) to identify the s and d-wave pairing as well as the d-wave PDW, respectively.

To clearly illustrate how the pairing-symmetry transition happens at zero temperature, we further decompose Cooper pair modes from the two-particle density matrix, defined as⁵²

$$\rho ({{\bf{i}}}{{{\boldsymbol{\delta }}}}_{l},{{\bf{j}}}{{{\boldsymbol{\delta }}}}_{{l}^{{\prime} }})=\left\langle {{{\mathcal{C}}}}_{{{\bf{i}}}{{{\boldsymbol{\delta }}}}_{l}}^{{\dagger} }{{{\mathcal{C}}}}_{{{\bf{j}}}{{{\boldsymbol{\delta }}}}_{{l}^{{\prime} }}}\right\rangle,$$

(9)

where ${{{\mathcal{C}}}}_{{{\bf{i}}}{{{\boldsymbol{\delta }}}}_{l}}$ is consistent with the definition in Eq. (4). We exclude the overlapping parts for either i = j, or ${{\bf{i}}}={{\bf{j}}}+{{{\boldsymbol{\delta }}}}_{{l}^{{\prime} }}$, or j  = i + δ_l, giving rise to the local contributions from density and spin correlations. Since ρ is Hermitian, it can be diagonalized with real eigenvalues λ_n, that is,

$$\rho ({{\bf{i}}}{{{\boldsymbol{\delta }}}}_{l},{{\bf{j}}}{{{\boldsymbol{\delta }}}}_{{l}^{{\prime} }})={\sum}_{n}{\lambda }_{n}{\zeta }_{n}^{*}({{\bf{i}}}{{{\boldsymbol{\delta }}}}_{l}){\zeta }_{n}({{\bf{j}}}{{{\boldsymbol{\delta }}}}_{{l}^{{\prime} }}).$$

(10)

The eigenvector ζ_n(iδ_l) are referred to as macroscopic wave functions of Cooper pair modes. The dominant mode with the largest eigenvalue is labeled by n = 0.

CPQMC method

To further demonstrate that the system may exhibit long-range superconducting correlations for the s wave pairing, we also check the long-range part of the ground-state pair-correlation function using the CPQMC method^49,53. The CPQMC method has been successfully used to calculate the ground-state energy and other observables in various systems^49,53. We investigate the long-range superconducting correlations of dominant s-wave pairing symmetry by defining the pair-pair correlation function at zero temperature, which is written as

$${C}_{\alpha }({{\bf{r}}})=\frac{1}{N{N}_{r}}{\sum}_{{{\bf{i}}},{{\bf{j}}}}{\sum}_{| {{\bf{j}}}-{{\bf{i}}}|=r}\left\langle {\Delta }_{\alpha }^{{\dagger} }({{\bf{i}}},0){\Delta }_{\alpha }({{\bf{j}}},0)\right\rangle,$$

(11)

Here, r is the distance between site i and site j. The N_r is the total number of distance r. Similarly, we also define the uncorrelated single-particle contribution ${\tilde{C}}_{\alpha }({{\bf{r}}})$ and discuss the vertex contributions ${\bar{C}}_{\alpha }({{\bf{r}}})={C}_{\alpha }({{\bf{r}}})-{\tilde{C}}_{\alpha }({{\bf{r}}})$.