Introduction

Magnetic memories are promising for on-chip applications due to their non-volatile nature, which eliminates the need for power to maintain data storage and reduces chip-level energy consumption1,2,3. Among these, spin-transfer torque (STT) and spin-orbit torque (SOT) magnetoresistive access memories (MRAMs) stand out as potential replacements for flash or static RAM in embedded cache memories1,2,3 due to their high speed, high density, low energy consumption, and compatibility with existing complementary metal oxide semiconductor technologies. While STT-MRAMs offer a compact two-terminal design beneficial for on-chip applications, they face challenges due to the high writing current density, which can reach up to hundreds of megamperes per square centimeter4. This poses a significant obstacle in further reducing energy consumption. Conversely, SOT-MRAM devices, despite their more intricate three-terminal design accommodating both in-plane and vertical currents for writing and reading operations, respectively, exhibit a comparatively lower writing current density of several megamperes per square centimeter5,6. However, SOT switching typically necessitates the application of an external magnetic field, presenting a challenge for practical SOT-MRAM implementations7,8,9,10,11. To address these challenges, there is a need for MRAMs with a simpler two-terminal design and reduced energy consumption.

The emergence of alternative technologies, such as unidirectional spin Hall magnetoresistance (USMR) observed in ferromagnetic metal/nonmagnetic metal (FM/NM) heterostructures12,13, holds promise for addressing these challenges. USMR exhibits asymmetric behavior that is well-suited for a two-terminal design, facilitating both writing and reading of magnetization states with a lower write current density comparable to that of SOT-MRAM, as both rely on current-generated SOTs to switch the magnetization of the FM layers. This development paves the way for more compact and energy-efficient MRAM designs, enabling their widespread adoption in future on-chip applications. The output voltage in USMR-MRAM devices rely on the second-order harmonic longitudinal resistance (\({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\)) that scales with the electric current and changes sign based on the electric current direction and/or the magnetization orientation of the FM layers. The USMR effect is characterized by its magnitude, defined as the difference in \(\Delta {R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}=\left[{R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\left(+{M}_{y},+{I}_{x}\right)-{R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\left(-{M}_{y},+{I}_{x}\right)\right]\) when the magnetization switches between opposite orientations (\({{{\pm }}M}_{y}\)) with an alternating current \(I\,(={I}_{0}\sin \omega t)\) along the x-direction12. The USMR effect is intricately linked to the spin current generation efficiency of the NM layer and the population of magnons resulting from spin-dependent and electron-magnon scattering mechanisms12,13,14,15,16,17. To enhance the USMR effect, researchers have concentrated on materials with high spin current yields, such as 2D materials and topological insulators (TIs) with high spin Hall angles13,15,17,18,19, as well as controllable electron-magnon scattering20. Prominent examples of large USMR effects have been observed in Crx(Bi1−ySby)2−xTe3/(Bi1−ySby)2Te3 bilayers at 2 K13 and in the Bi2Se3/YIG bilayer at 150 K17 using the topological surface states (TSSs) of TIs and the scattering of electrons by magnons. Nevertheless, the introduction of TIs in previous studies has primarily been explored at low temperatures, posing a significant barrier to room-temperature applications. Additionally, the integration of TIs with metallic ferromagnets often results in the formation of an interfacial layer21,22,23,24, which can impede the spin current transmission from TIs to FMs due to charge transfer at the interface, disrupting the TSS of the TI25,26,27,28,29,30,31. Consequently, a primary challenge for USMR applications is the relatively small magnitude of the effect at room temperature15,17,20,32,33,34,35,36, limiting the signal-to-noise ratio and, ultimately, the reliability of USMR-based devices. Enhancing the USMR effect at room temperature remains a critical research objective for realizing its practical applications in magnetic memories.

In this work we report a large USMR at room temperature by introducing a Pt interfacial layer in FeNi/Pt/Bi2Se3 system. The interfacial Pt layer preserves the topological surface states (TSS) of Bi2Se3 and forms additional Rashba surface states29,30, thereby increasing the efficiency of spin current generation. The injection of a strong spin current not only enhances spin-dependent scattering but also generates a greater number of magnons in FeNi, augmenting electron-magnon scattering and subsequently boosting the USMR. The Pt-thickness dependent USMR, SMR and SOT efficiency in FeNi/Pt/Bi2Se3 shows the similar variation behavior and maximums when the thickness of Pt is 1.5 nm, consistently demonstrating the key role of the Pt layer with proper thickness. Based on the large USMR, we report a two-terminal MRAM device. The writing current density decreases with increasing ambient temperature, reaching a minimum of 1.44 MA/cm² at room temperature. Meanwhile, the output voltage reaches 0.22 mV when read current I0 is ~2 mA at room temperature. Furthermore, an even more remarkable performance is observed at temperatures as high as 70 °C, satisfying the demanding criteria for a commercial MRAM.

Results

Structure and band structure with/without Pt interfical layer

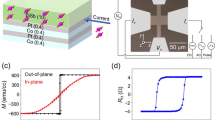
To assess the quality of Bi2Se3 thin films produced by magnetron sputtering, Raman scattering measurements were conducted on 10 nm-thick films, as shown in Fig. 1a. Prominent Raman peaks at 72, 131, and 175 cm−1 correspond to the \({A}_{1g}^{1}\), \({E}_{g}^{2}\), and \({A}_{1g}^{2}\) vibration modes of Bi2Se3, respectively. The narrow full width at half maximum of these peaks indicates good structural quality in the sputtered films, consistent with previous reports37,38. Analyzing X-ray reflectivity (XRR) spectra for FeNi(3)/Pt(tPt = 0, 0.6, 1.5, 5)/Bi2Se3(10) and FeNi(5)/Bi2Se3(10) samples using Gen’X software (details in Supplementary Notes 1) gives the depth-dependent scattering length density (SLD) profiles, as shown in Fig. 1b. Notably, significant interface diffusion is observed between Bi2Se3 and FeNi when they are in direct contact, forming an intermixing layer. However, a distinct interface emerges when the Pt layer thickness is ≥1.5 nm, evident by a plateau in the SLD profiles corresponding to the Pt layer. Additionally, the FeNi(3)/Bi2Se3(10) sample exhibits a quite thinner FeNi layer, suggesting significant interactions between FeNi and Bi2Se3 during fabrication. This sample also displays weak ferromagnetism at room temperature (detailed in Supplementary Note 2). Therefore, in Pt-thickness dependent experiments, we used a sample with a FeNi thickness of ~5 nm for comparison when \({t}_{{{\rm{Pt}}}}\) = 0 nm.

Fig. 1: Structure characterization, band structure and schematic band structure and the USMR device.
figure 1

a Raman spectra of single-layer Bi2Se3 with thickness of 10 nm, b X-ray electron scattering length density (SLD) versus depth profile of the FeNi(3)/Pt(tPt)/Bi2Se3(10) and FeNi(5)/Bi2Se3(10) samples, c The band structure projected onto the 3QL- Bi2Se3 slab along the high symmetry lines for the Bi2Se3(3QLs)/Pt(3MLs)/Ni(3MLs) (left panel) and Bi2Se3 (3QLs)/Ni(6 MLs) (right panel), d The band structure along the high symmetry lines projected onto the bottom of Pt for the Bi2Se3 (3QLs)/Pt(3MLs)/Ni(3MLs) (left panel) and of Ni for the Bi2Se3 (3QLs)/Ni(6 MLs) (right panel), e Schematic diagram for the topological surface states and Rashba surface states after Pt layer insertions, f Showing the writing process of the MRAM device with easy axis magnetization \({{\bf{M}}}\) along y direction by pulse current generated y-polarized spin accumulation \({{\boldsymbol{\sigma }}}\) and the consequently spin-orbit torque (left panel), and the reading process of the device by applying alternative current to detect the 2nd harmonic voltage \({V}_{{xx}}^{2{{\rm{\omega }}}}\).

Full size image

To investigate the influence of Pt on the surface states of the Bi2Se3, we use the fist principal calculation to reveal the band structure. To simplify the calculation, we use Ni instead of Fe19Ni81 (Py) to carry out the calculation. Six layers of Ni films or three layers of Pt and Ni films were put on top sides of Bi2Se3, forming the bilayer or trilayer heterostructures. The band structure of the Ni/Pt/Bi2Se3 slabs projected on to the 3-quintuple layer (QL) Bi2Se3 is shown in the left panel of Fig. 1c. It can be observed that a linear Dirac cone near the Γ point locates about −0.3 eV. This Dirac cone primarily originates from the top QL’s TSS, which is induced by the hybridization between the top QL and the bottom layer of the Pt. Additionally, contributions to the Dirac cone are also observed from the middle and the bottom QL. In essence, the TSS is preserved in the Ni/Pt/Bi2Se3 structure. In order to compare the effect of insertion of Pt layer, we also plotted the band structures of the pure Ni layers without the Pt covering in the right panel of the Fig. 1c. It can be observed that there is a Dirac cone located at −0.4 eV near the Γ point, which is about 0.1 eV lower than that of the Pt layer insertion case. However, with a further close observation to the projected band structure, this Dirac cone comes from the middle QL instead of the top QL, indicating the TSS is nearly destroyed due to the strong hybridizations between the top QL and the bottom layer of the Ni. The detailed band structure is shown in Supplementary Note 3. Moreover, as evident in the left panel of Fig. 1d, the insertion of Pt gives rise to a pronounced Rashba surface state (indicated by the blue square) in the Bi2Se3(3QLs)/Pt(3MLs)/Ni(3MLs) structure. This Rashba surface state cannot be observed from the Bi2Se3/Ni(111). The preserve of the magnetic moment of Ni by Pt layer insertion is also calculated and presented in Supplementary Note 3. Based on our first-principles calculations, we conclude that incorporating a Pt layer not only could preserve the TSS of Bi2Se3 but also maintains the magnetic properties of ferromagnetic layer. The simplified topological surface states and Rashba surface states is schematically shown in Fig. 1e. The coexistence of TSS and Rashba surface states suggests potentially high spin current generation efficiency and strong USMR for MRAM device design, as conceptualized in Fig. 1f. During the write operation, a pulse current is applied along the ±x-direction, generating SOTs that efficiently switch the magnetization of the FeNi layer between its two easy axes (±y-direction) without an external magnetic field. For reading, an alternating current along the x-direction enables the detection of the second harmonic voltage \(({V}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}})\) through the USMR effect.

Pt interfacial layer induced large room-temperature SOT efficiency

The spin current generation efficiency in the FeNi(3)/Pt(\({t}_{{{\rm{Pt}}}}\))/Bi2Se3(10) sample has been quantitatively characterized using the harmonic Hall voltage method37,38. In this method, the current-induced SOTs can be extracted by measuring the in-plane angular dependence of the transverse second-harmonic resistance \({R}_{{{\rm{xy}}}}^{2{{\rm{\omega }}}}\) expressed as39,40,41:

$${R}_{{{\rm{xy}}}}^{2{{\rm{\omega }}}}=-\left({R}_{{{\rm{AHE}}}}\frac{{B}_{{{\rm{DL}}}}}{{B}_{{{\rm{k}}}}+{B}_{{{\rm{ext}}}}}+{R}_{{{\rm{xy}}}}^{\nabla {{\rm{T}}}}\right)\cos \alpha+2{R}_{{{\rm{PHE}}}}\frac{{B}_{{{\rm{FL}}}}+{B}_{{{\rm{Oe}}}}}{{B}_{{{\rm{ext}}}}}(2{\cos }^{3}\alpha -\cos \alpha )$$
(1)

here, BDL, BFL, and BOe represent the current-induced effective field from the damping-like (DL) torque, field-like (FL) torque, and Oersted field, respectively. RAHE and RPHE correspond to the anomalous Hall resistance and planar Hall resistance, respectively. \(\alpha\) is the angle between the current and magnetic field in the plane of sample. \({R}_{{{\rm{xy}}}}^{\nabla {{\rm{T}}}}\) is the transverse resistance due to the Hall voltage induced by the anomalous Nernst effect (ANE) and the spin Seebeck effect (SSE)42,43. \({B}_{{{\rm{ext}}}}\) is the applied magnetic field and\(\,{B}_{{{\rm{K}}}}\) stands for the effective anisotropy field. The value of \({R}_{{{\rm{xy}}}}^{2{{\rm{\omega }}}}\) resulting from the ANE/SSE and DL-SOT scales proportionally with \(\cos \alpha\), while the \({R}_{{{\rm{xy}}}}^{2{{\rm{\omega }}}}\) arising from the FL-SOT and BOe varies in proportion to \(2{\cos }^{3}\alpha -\cos \alpha\). Owing to these distinct angular dependencies of \({R}_{{{\rm{xy}}}}^{2{{\rm{\omega }}}}\), we can distinguish between them seamlessly. Fig. 2a shows angular dependent \({R}_{{{\rm{xy}}}}^{2{{\rm{\omega }}}}\) measured at RT with different magnetic fields under ac current of 6 mA for samples with \({t}_{{{\rm{Pt}}}}\) = 1.5 nm. By fitting these experimental curves using Eq. (1), we can extract the contributions corresponding to \(\cos \alpha\) and \({2\cos }^{3}\alpha -\cos \alpha\). By examining the magnetic field dependent values corresponding to \(\cos \alpha\) in \({R}_{{{\rm{xy}}}}^{2{{\rm{\omega }}}}\), we can determine the coefficients in (\({R}_{{{\rm{AHE}}}}\frac{{B}_{{{\rm{DL}}}}}{{B}_{{{\rm{k}}}}+{B}_{{{\rm{ext}}}}}+{R}_{{{\rm{xy}}}}^{\nabla {{\rm{T}}}}\)), as shown in Fig. 2b. The slope of the linear fit gives the value of \({B}_{{DL}}\), whereas the y-intercept signifies the field-independent contribution from the ANE/SSE, represented as \({R}_{{{\rm{xy}}}}^{\nabla {{\rm{T}}}}\). By assessing the variation of \({B}_{{DL}}\) as a function of current density, we can derive the DL-torque efficiency by \({\beta }_{{{\rm{DL}}}}={B}_{{{\rm{DL}}}}/J\) through a linear fit, as shown in Fig. 2c. Ultimately, the spin Hall angle can be calculated as follows39,40:

$$\,{\xi }_{{{\rm{DL}}}}=\frac{2e{M}_{{{\rm{S}}}}{t}_{{{\rm{FM}}}}}{{{\hslash }}}\frac{{B}_{{{\rm{DL}}}}}{J}$$
(2)

where, e, \({t}_{{FM}}\), and \({{\hslash }}\) represent the elementary charge, the ferromagnetic thickness, and the reduced Planck constant, respectively. With the same procedure, the dependence of the spin Hall angle, \({\xi }_{{{\rm{DL}}}}\), on Pt thickness (\({t}_{{{\rm{Pt}}}}\)) is presented in Fig. 2d. It is evident that \({\xi }_{{{\rm{DL}}}}\) initially increases with \({t}_{{{\rm{Pt}}}}\), peaking at a value of 0.84 when \({t}_{{{\rm{Pt}}}}\) is 1.5 nm. This peak value aligns closely with previously reported values for TI/FM systems44,45. Subsequently, \({\xi }_{{{\rm{DL}}}}\) decreases and gets saturated at \({t}_{{{\rm{Pt}}}}\) = 5 nm. The enhancement SOT efficiency upon the introduction of Pt is consistent with theoretical band calculations. These calculations suggest that Pt interfacial engineering preserves the topological surface states and generates additional Rashba surface states instead of destroying them when FM layer is in direct contact with TI. This preservation and generation of these surface states contribute to the improved SOT efficiency observed in the system. It should be mentioned that the FL-SOT is quite small and the details about \({\xi }_{{{\rm{FL}}}}\) are shown in Supplementary Note 4.

Fig. 2: SOT characterization.
figure 2

a Transverse second-harmonic resistance \({R}_{{{\rm{xy}}}}^{2{{\rm{\omega }}}}\) as a function of the angle \({{\rm{\alpha }}}\) and the fitting curves using Eq. (1) for samples with \({t}_{{{\rm{Pt}}}}\) = 1.5 nm, b \({R}_{{{\rm{xy}}}}^{2{{\rm{\omega }}}}\) as a function of the inverse effective field \(1/{B}_{{{\rm{k}}}}+{B}_{{{\rm{ext}}}}\), c \({B}_{{{\rm{DL}}}}\) as a function of current density, d \({\xi }_{{{\rm{DL}}}}\) as a function of Pt thickness. The inset in (a) shows \({R}_{{{\rm{xy}}}}^{2{{\rm{\omega }}}}\) as a function of the angle \({{\rm{\alpha }}}\) at different magnetic fields for an ac current of 6 mA. Error bars represent fitting uncertainty.

Full size image

Large room-temperature USMR

Fig. 3a shows the measurement setups for harmonic longitudinal resistance measurement in a typical FeNi(3)/Pt(1.5)/Bi2Se3(10) sample. The sweeping angle of magnetization by 1 T magnetic field is defined by α, β, and γ, as shown in Fig. 3a. The angular dependent \({R}_{{{\rm{xx}}}}^{1{{\rm{\omega }}}}\) is shown in Fig. 3b. It can be seen the typical spin Hall magnetoresistance (SMR) behavior with a 180o symmetry and the relationship \({R}_{x}\) > \({R}_{z}\) > \({R}_{y}\), consistent with reports on NM/FM bilayers12,46,47. Fig. 3c further explores the angular dependence of the SMR ratio for samples with \({t}_{{{\rm{P}}}{{\rm{t}}}}\) = 0, 1.5, and 5 nm. The Pt-thickness-dependent SMR amplitude is summarized in Fig. 3d, where a non-monotonic trend is observed, peaking at a Pt thickness of 1.5 nm. This finding independently confirms the optimal Pt thickness for maximizing SOT efficiency, given that SMR scales with the square of the effective spin Hall angle.

Fig. 3: USMR characterization.
figure 3

a The schematic graph of measurement setup, b The angular dependent longitudinal first harmonic resistance \({R}_{{{\rm{xx}}}}^{1{{\rm{\omega }}}}\), c The SMR ratio for samples with the different thicknesses of Pt, d The Pt-thickness dependent SMR ratio, e The angular dependent second harmonic resistance \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\), f \({R}_{{xx}}^{2{{\rm{\omega }}}}\) as a function of magnetic field Hy at various I0 with \({t}_{{{\rm{Pt}}}}\) = 1.5 nm, g The USMR ratio \(({R}_{{{\rm{USMR}}}}/J)/{R}_{{{\rm{xx}}}}^{1{{\rm{\omega }}}}\) as a function of \({t}_{{{\rm{Pt}}}}\), h Comparison of the room-temperature USMR in different systems. Error bars represent the uncertainty of test results from multiple devices.

Full size image

The angular dependences of \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) in xy and zy rotations show a period of 360 degree, as shown in Fig. 3e. Notably, \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) undergoes a sing change and attains its maximum (or minimum) value when the magnetization aligns parallel (or antiparallel) to the spin current direction, denotes as \({{{\boldsymbol{\sigma }}}}_{y}\). This antisymmetric magnetoresistance phenomenon is termed USMR. Conversely, in the case of magnetization sweeping within the zx-plane, a flat line is observed due to the perpendicular configuration between \({{{\boldsymbol{\sigma }}}}_{y}\) and magnetization12,15. To efficiently get USMR ratio, Fig. 3f shows the \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) as a function of external field Hy under different currents. As Hy is swept from −500 to +500 Oe, a range sufficient to saturate the in-plane magnetization of FeNi, a significant variation in \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) is evident when the magnetization switches direction. Furthermore, increasing the current (I0) leads to more significant changes in \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\). Additionally, a decay in \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) with increasing Hy is observed, attributable to the gradual diminution of magnon-electron scattering as magnon excitations are suppressed at higher magnetic fields13. These observations are consistent with predictions of the USMR effect, where both spin-dependent scattering and electron-magnon scattering contribute13. However, in our system, electron-magnon scattering plays a dominant role at zero field, evidenced by the rapid decay of \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) with increasing magnetic field (detailed in Supplementary Note 5). The modulation of magnons by magnetic fields or spin currents is further corroborated by variations in magnon intensities observed using Brillouin light scattering spectroscopy48 (detailed in Supplementary Note 6). Although the ANE/SSE has contribution to the measured \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) data, it is quite small as shown in Supplementary Note 7.

To facilitate comparison with other studies, we define the USMR ratio as \(({R}_{{{\rm{USMR}}}}/J)/{R}_{{{\rm{xx}}}}^{1{{\rm{\omega }}}}\), representing the relative signal change or amplitude of the USMR across different material systems. Here, \({R}_{{{\rm{USMR}}}}=\Delta {R}_{{xx}}^{2\omega }-{R}_{{xx}}^{\nabla T}\), where \(\Delta {R}_{{xx}}^{2\omega }={R}_{{xx}}^{2\omega }\left(+B\right)-{R}_{{xx}}^{2\omega }\left(-B\right)\), \({R}_{{{\rm{x}}}{{\rm{x}}}}^{\nabla {{\rm{T}}}}\) is the longitudinal resistance due to the ANE&SSE and is obtained from the \({R}_{{{\rm{xy}}}}^{\nabla {{\rm{T}}}}\) and the ratio between the length and the width of the Hall bar12,15, J is the reading current density, and \({R}_{{{\rm{xx}}}}^{1{{\rm{\omega }}}}\) is the longitudinal resistance. The dependence of the USMR ratio on Pt thickness is illustrated in Fig. 3g with B = 0.05 T. As the \({t}_{{{\rm{Pt}}}}\) increases, \(({R}_{{{\rm{USMR}}}}/J)/{R}_{{{\rm{xx}}}}^{1{{\rm{\omega }}}}\) exhibits a non-monotonic trend. Notably, a peak emerges at \({t}_{{{\rm{Pt}}}}\) = 1.5 nm, attaining a magnitude as high as 30.6 (ppm)/(MA/cm2). This value is an order of magnitude greater than that observed in the TI/FM system at room temperature15,17.

The variation trends of SOT efficiency, SMR and USMR ratio in relation to Pt thickness can be explained by examining the structural evolution depicted in Fig. 1b. For \({t}_{{{\rm{Pt}}}}\) below 1.5 nm, the Pt layer is insufficiently thick to properly separate FeNi and Bi2Se3, leading to direct contact between these materials. This contact disruption of TSS in Bi2Se325, subsequently reducing spin current generation efficiency. However, at ~1.5 nm of Pt thickness, an optimal interface is achieved that maintains the distinct band characteristics of both the Bi2Se3 and FeNi. As a result, SOT, SMR and USMR peaks at this thickness. For \({t}_{{{\rm{Pt}}}}\) exceeding 2.0 nm, the limited spin diffusion length of Pt49,50 (detailed in Supplementary Note 8) hinders the penetration of spin current generated by the TSS at the Pt/Bi2Se3 interface. This spin current instead dissipates within the Pt interior, casing the SOT efficiency to rapidly decrease and then plateau as Pt thickness continues to increase, as illustrated in Fig. 2d. Ultimately, at \({t}_{{{\rm{Pt}}}}\) = 5 nm, the SOT efficiency stabilizes at ~0.18, which aligns with the bulk spin Hall angle reported for Pt51,52.

Comparing our optimal sample to other reports, we present the findings of the USMR across various systems in Fig. 3h. Notably, our sample exhibits a significant enhancement in the USMR ratio when compared to other systems. It’s important to mention that all USMR values reported in this article were obtained through harmonic measurements, which typically yield values that are approximately half of those derived from direct current measurements17. As shown in Fig. 3f, an even more pronounced USMR ratio can be observed in our sample at zero magnetic field. Therefore, to achieve a robust signal output suitable for USMR-MRAM applications, we measured \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) at zero magnetic field using the maximum feasible current (I0).

Performance of MRAM device

To evaluate the device’s performance, we measure the output signal \({V}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) as a function of writing pulse current (Ip). Fig. 4a depict \({V}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) as a function of the reading current I0 when the magnetization is alternately flipped by pulse current. The difference in the output signal, denoted as Δ\({V}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\), increases with the augmentation of I0, reaching up to 1.1 mV at 3.2 mA, as shown in Fig. 4b. It is noteworthy that Δ\({V}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) varies proportionally to the square of I0, while Δ\({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) is directly proportional to I0. The linear relationship between Δ\({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) and I0 yields a slope of 0.11 Ω/mA, which is about 18 times higher than that in YIG/Bi2Se3 at 150 K. The detailed comparison of USMR is shown in Supplementary Note 9. To assess the writing repeatability and signal stability, we performed a hundred iterations of the writing and reading process, alternating positive and negative pulse currents while maintaining a reading current (I0) of ~2 mA, as depicted in Fig. 4c. The consistent \({V}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) values observed throughout these iterations highlight the exceptional stability of both writing and reading in our device. It’s worth mentioning that this stability and consistency have been verified across tens of devices. Moreover, we found that \({V}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) remains nearly constant when the magnetization flips, regardless of whether it is induced by a magnetic field pulse or Ip (detailed in Supplementary Note 10.). This is because \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) solely depends on the relative orientation between \({{{\bf{M}}}}_{y}\) and the injected spin current \({{{\boldsymbol{\sigma }}}}_{y}\).

Fig. 4: Performance, repeatability and stability of the USMR device.
figure 4

a The output voltage with magnetization switched by current pulses with the variation of reading current I0, b The output change of voltage and resistance as a function of I0, c The repeatable writing and reading performance with positive and negative pulse current magnitude Ip around 6.5 mA and I0 = 2 mA. d The critical switching current (Voltage) \({I}_{C}({V}_{C})\) versus the width of the current pulse. e The output voltage of a typical MRAM device with the change of the writing pulse voltage between +50 V and –45 V for pulse width of 1 ns and the reading current \({I}_{0}=1.5\,{{\rm{mA}}}\) at room temperature. f \(\triangle {V}_{{xx}}^{2\omega }\) and critical switching current density as a function of temperature with I0 = 1 mA. The solid line in (d) is a linear fit.

Full size image

Thermal stability is a paramount in MRAM applications, particularly when utilizing a 3-nm-thick FeNi layer as the recording medium. In the context of current-induced SOT-driven magnetization switching, Joule heating generated by the pulse current poses an additional thermal challenge, beyond the usual environmental thermal fluctuations. The pulse width (tpulse) plays a pivotal role in determining the extent of Joule heating and, subsequently, influences the critical switching current density (\(\,{J}_{{{\rm{p}}}}^{{{\rm{c}}}}\))53. The relationship between \({{J}}_{{{\rm{p}}}}^{{{\rm{c}}}}\) and tpulse is expressed as \({J}_{{{\rm{p}}}}^{{{\rm{c}}}}={J}_{{{\rm{p}}}}^{{{\rm{c}}}0}\left[1-\frac{1}{\triangle }{\mathrm{ln}}\left(\frac{{t}_{{{\rm{pulse}}}}}{{\tau }_{0}}\right)\right]\), where \({{J}}_{{{\rm{p}}}}^{{{\rm{c}}}0}\) represents the zero-thermal critical switching current density, ∆ ≡ U/kBT is the thermal stability factor (with U being the energy barrier and kB being the Boltzmann constant), and τ0 ≈ 1 ns represents the inverse of the attempt frequency associated with the nanomagnet. Fig. 4d illustrates the dependence of \({{J}}_{{{\rm{p}}}}^{{{\rm{c}}}}\) on tpulse. Through linear fitting, we determined that ∆ is around 31.2. This value indicates a retention time of over 7 years for a single bit54, highlighting the robust thermal stability achieved in our design. It should be noted that the conclusion is only valid to our large device since the device thickness and volume play key roles considering the relative weak anisotropy constant of our FeNi films.

We also have demonstrated the writing capability of our MRAM device under nanosecond-width pulse voltage and its reading stability using a picosecond pulse generator at room temperature. Fig. 4e illustrates that the output voltages can consistently and predictably fluctuate between +0.12 mV and −0.12 mV when subjected to pulse voltages ranging from +50 V to −45 V with a pulse width of 1 ns, at a reading current of I0 = 1.5 mA. These findings suggest that our MRAM device exhibits writing speeds of up to GHz, marking a substantial advancement in the field.

To better understand the behavior of our MRAM device at high temperatures, we conducted measurements focusing on temperature-dependent magnetic field and pulse current writing and reading properties (detailed in Supplementary Note 11). To minimize the potential influence of Joule heating on the device’s performance at elevated temperatures, we used a reduced reading current (I0 = 1 mA). Figure 4f shows the summarized the temperature dependences of \({\Delta V}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) and the critical magnetization switching current density \({J}_{{{\rm{p}}}}^{{{\rm{c}}}}\) of our MRAM device. Specifically, as the temperature rises from 30 to 70 °C, the \({V}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) increases from 128 to 157 μV, while the critical current density decreases from 1.44 to 0.59 MA/cm2. This behavior can be attributed to the augmented number of thermally excited magnons at higher temperatures, as described by the spin-wave model for ferromagnetic materials. Consequently, this increase in magnons enhances the USMR through electron-magnon scattering. By analyzing the temperature-dependent critical switching current density and coercivity, we found that the primary reason for the reduction in critical switching current density is the more pronounced decrease in coercivity with temperature. This finding is particularly promising given the widespread issue of excessive heating in electronic devices, which often leads to significant performance degradation or even failure at elevated temperatures3,55. Furthermore, our measurements confirm that our MRAM device exhibits excellent performance and stability even at 70 °C. This robustness at high temperatures indicates that our MRAM device meets the stringent criteria for commercial applications56.

In this study, we have successfully demonstrated the existence of an exceptionally large room-temperature USMR in FeNi/Pt/Bi2Se3 heterostructures achieved through Pt interfacial engineering. This approach holds promise as a method to mitigate intermixing between FM and Bi2Se3 layers, a common challenge in memory fabrication processes, especially when utilizing Bi2Se3 as the spin current source in MRAM57. The observed room-temperature USMR surpasses that reported in other systems by an order of magnitude, owing to enhanced spin-dependent and electron-magnon scattering mechanisms. Leveraging this significant USMR, we have developed a two-terminal memory device that exhibits energy-efficient writing capabilities and a high signal-to-noise ratio during reading operations. Remarkably, these operations remain repeatable and stable even under nanosecond pulses. The simplicity and reliability of this two-terminal design, coupled with the sputtering-grown topological insulator Bi2Se3 films, render it highly compatible with current large-scale STT and/or SOT MRAM production lines. It should be mentioned that selecting appropriate materials for the insertion layer in FeNi/Bi2Se3 is crucial for optimizing spin current generation efficiency and USMR (detailed in Supplementary Note 12). Our findings pave the way for the development of advanced memory devices that combine the performance benefits of large USMR with ease of integration into existing manufacturing processes.

Methods

Sample preparation

FeNi(3)/Pt(\({t}_{{Pt}}\))/Bi2Se3(10)/Ta(2) multilayer samples were meticulously fabricated on thermally oxidized Si/SiO2 substrates, maintaining room temperature conditions throughout the process. The number in parentheses represents the thickness of the thin film, and the unit is nanometer. \({t}_{{Pt}}\) is in the range of 0–5 nm. The fabrication technique employed was direct current magnetron sputtering, ensuring a base pressure below 4.0 × 10–5 Pa. The processing gas, Argon (Ar), was maintained at ~0.5 Pa during the sputtering process. To achieve the desired film qualities, a commercial Bi2Se3 target with 99.99% purity was selected as the sputtering source. The thicknesses of the individual films were precisely controlled by adjusting the deposition time and rates. These rates were accurately calibrated using x-ray reflectometry measurements performed on thicker films. During deposition, a constant magnetic field of ~100 Oe was applied in the plane of the sample. This step was crucial to induce an in-plane uniaxial magnetic anisotropy, which is essential for the proper functioning of the magnetic layers. Subsequently, the samples were patterned into Hall bar devices specifically designed for SOT characterization. These devices featured a channel width of 20 micrometers and a length of 50 micrometers. Standard optical photolithography techniques, coupled with Argon ion milling, were used to achieve the desired device dimensions with precision. For the MRAM device performance measurements, a demonstration size of 20 micrometers by 100 micrometers was chosen. It is noteworthy that the magnetized easy axis of the FeNi layer was aligned along the shorter direction of the square, optimizing the magnetic properties for efficient memory operation.

Band structure calculations

Our first-principles calculations were carried out within the density functional theory based on the projected augmented wave pseudopotentials as implemented in the Vienna Ab-initio Simulation Package (VASP)58. The generalized gradient approximation with optPBE (Perdew–Burke–Ernzerhof) was used to including the van der Waals interaction for the Bi2Se359, and the interlayer van der Waals interaction is described using the DFT-D3 methods60. The basis set contained plane waves with a kinetic energy cutoff of 520 eV and the total energy was converged to 10−6 eV. The Brillouin zone integration is carried out with the k-pointing of 0.01 2π/Å. We constructed a slab model with 3 QL Bi2Se3 and a 16 Å vacuum. To simplify the calculation, we use Ni instead of Fe19Ni81 to carry out the calculation. Six layers of Ni films or three layers of Pt and Ni films were put on top sides of Bi2Se3, forming the bilayer or trilayer heterostructures. The atomic structure model for the Bi2Se3/Ni(111) and Bi2Se3/Pt(111)/Ni(111) interface is shown in Fig. S3a. We fixed the experimental lattice constants a = 4.189 Å for the Bi2Se3, and √3*√3 rotated (111) surface of the fcc Ni matches the Bi2Se3 with less than 4.1% mismatch. For the relaxations, we fixed the bottom Pt/Ni or the Ni, and all other geometries were optimized without any symmetry constraint until all residual forces on each atom were less than 0.01 eV/Å. Spin–orbit coupling (SOC) with a relativistic effect was included in all calculations.

Magneto-transport measurements

During the magneto-transport measurements, a specific protocol was followed to accurately capture the electrical properties of the FeNi(3)/Pt(\({t}_{{Pt}}\))/Bi2Se3(10)/Ta(2) sample. Harmonic voltage measurements were conducted by applying an alternating current (ac) with a frequency of 133 Hz through the current channel, which ran along the x-axis direction of the sample. This allowed for the precise measurement of voltage fluctuations in response to the alternating current. Both longitudinal and transverse voltage signals were collected using a high-precision data acquisition card (NI-4461), ensuring minimal loss of data integrity61. To isolate the first and second harmonic signals from the collected voltage data, a fast Fourier transform was employed. This mathematical technique enabled the separation of signals based on their frequency components, facilitating the accurate identification and analysis of the harmonic signals. The first and second longitudinal voltages, denoted as \({V}_{{{\rm{xx}}}}^{1{{\rm{\omega }}}}\) and \({V}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\) respectively, were recorded simultaneously. These voltages correspond to the electrical response of the sample at different harmonic frequencies. The corresponding resistances, \({R}_{{{\rm{xx}}}}^{1{{\rm{\omega }}}}\) and \({R}_{{{\rm{xx}}}}^{2{{\rm{\omega }}}}\), were then calculated by dividing the respective voltages by the peak value of the applied current, I0. This provided a quantitative measure of the sample’s resistance under the influence of the alternating current. To write the magnetization state of the FeNi(3)/Pt(1.5)/ Bi2Se3(10)/Ta(2) sample, a pulse current (voltage) was generated along the length direction of the sample by a Keithley 6221 current source (a PSPL 100300B picosecond pulse generator). Given the Joule heating of the writing current/voltage plays a key role in magnetization by SOT62,63,64, it follows that a narrower pulse width results in less heat generation and, consequently, more difficult complete magnetization switching. Here, to ensure the complete switching of FeNi magnetization using a 1-ns voltage pulse generated SOT, we utilize the maximum voltage available from PSPL100300B. The pulse width of the generated current could be varied, with values ranging from 10 ms to 1 ns. This flexibility allowed for the precise control of the magnetization process, enabling the investigation of magnetization dynamics at different timescales.