Sensing expectation enables simultaneous proprioception and contact detection in an intelligent soft continuum robot

Abstract

A high-level perceptual model found in the human brain is essential to guide robotic control when facing perception-intensive interactive tasks. Soft robots with inherent softness may benefit from such mechanisms when interacting with their surroundings. Here, we propose an expected-actual perception-action loop and demonstrate the model on a sensorized soft continuum robot. By sensing and matching expected and actual shape (1.4% estimation error on average), at each perception loop, our robot system rapidly (detection within 0.4 s) and robustly detects contact and distinguishes deformation sources, whether external and internal actions are applied separately or simultaneously. We also show that our soft arm can accurately perceive contact direction in both static and dynamic configurations (error below 10°), even in interactive environments without vision. The potential of our method are demonstrated in two experimental scenarios: learning to autonomously navigate by touching the walls, and teaching and repeating desired configurations of position and force through interaction with human operators.

Introduction

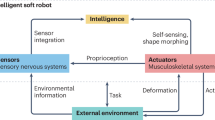
Human beings utilize their exteroceptive sensory system to dynamically interact with environments, during which they use a high-level perceptual model combining afferent sensory signals generated by external sources and efferent signals corresponding to their actions to guide sensory-guided movement control, as found in our brain mechanisms¹. Perception mechanisms are not strictly confined to the interpretation of sensory information but anticipate the consequences of self and external actions and distinguish them^2,3. While anticipation-based perceptual models have been realized in rigid robots^4,5,6, implementing these methods in soft robots will provide additional benefits by overcoming the current perception challenges related to body deformability and contribute to intelligent behavior in perception-intensive environmental interaction tasks^7,8. Although effective methods have been developed regarding soft robot low-level control and force sensing^9,10,11, high-level perception-action loops are still one of the biggest challenges in soft robotics.

There are several challenges to implementing such high-level perception-action loops in soft robots. First, the robot should be able to clearly distinguish its deformations under external contacts from those generated by their internal actuation. Perceiving external contact can be achieved through direct sensor readings and indirect models¹². Tactile sensors directly display contact information in a set area^13,14,15,16, but multiple sensors need to be setup in multiple areas and directions of interest. Indirect methods involves data-driven^17,18,19, mechanics-based model^20,21,22, intrinsic force sensing^{10,23,24,25,26}. Some of these studies aim for precise locomotion of soft continuum robots, for example, using residuals and errors for closed-loop position/force control^10,25,26. Others estimate and control contact force in given particular interactive modes^{17,18,20,21,22}. Neither of them achieves a quick reaction to rapid, unexpected interactions, and local deformation of the soft bodies in an unknown 3D environment. Second, a multi-modal perception sensory system is necessary. Proprioceptive information (strain, curvature or shape) in soft body is usually acquired through external sensing equipment (motion capture²⁷ and electromagnetic equipment²⁸) and integrated internal sensors (optic fibers^29,30,31, hall sensors³², carbon nanotubes¹², piezoresistive³³, electroluminescent material³⁴, eutectic Gallium-Indium (eGaIn)^13,35, ionic liquid^36,37, conductive hydrogel³⁸). Multiple specific sensors need to be integrated to achieve multi-modal perception including external stimuli input³⁸. A deformable soft skin with liquid metal inside can detect strain and contact simultaneously^13,35. Due to good linearity between strain and resistance, high softness, and stretchable properties, these sensors can be integrated onto the surface of soft robot^35,39.

Humans control the movements of their arms with high-level perception-action loops that do not just rely on the sensory inputs, but anticipate them. Expected sensory inputs are generated from internal models before they are conveyed through receptors and then compared with actual afferent signals^1,2,40,41. With this expected-actual signals comparison, the perception-action loop is faster, and an unexpected external stimulus is promptly detected. We propose a similar expected-actual comparison method in soft robotics (see Fig. 1B for a general framework of the method) and demonstrate the perceptual model on a two-module rod-driven soft continuum robot (RDSR) sensorized with eGaIn-based piecewise soft sensor (PSS) on its surface (Fig. 1A). We firstly anticipate the robot’s deformation by constructing the expected shape (ES) of the robot from the current controller commands, via internal piecewise constant curvature (PCC)^11,42,43 model with three segments for each module (Fig. 2A, mathematical models are presented in Supplementary Text S2), and then we estimate the actual shape (AS) of the robot based on the actual rod lengths inside the body and the sensory signals after executing the command. Stable and precise feedback of rod lengths and sensor strains exhibit good performance in posture proprioception of RDSR (1.4% estimation error, on average). By comparing between ES and AS at each perception loop, whether external stimuli and internal actuation are applied separately or simultaneously when the mismatch exceeds a set threshold, the robot can rapidly perceive external contact (detection time within 0.4 s, direction error below 10°). This is a way to distinguish deformation sources even if unexpected interactions occur. Moreover, soft sensors offer good linearity, compatibility with soft bodies, and enable multi-modal perception, including local strains induced by actuation and stimuli, and tactile information caused by direct touch.

Fig. 1: An expected-actual comparison perception-action loop in soft robots.

A Overview of the sensorized rod-driven soft continuum robot (RDSR) and the perception method. B A general framework for high-level perception-action loops. C Demonstrations of perception-intensive environmental interaction tasks: autonomous exploration and navigation of mazes by detecting contacts with the walls, and teaching and repeating tasks by interacting with human operators.

Fig. 2: Detailed scheme of expected-actual comparison method on an RDSR and the performance of soft sensors.

A Proprioception model of the sensorized RDSR. B Detailed implementation of the perception-action loop in the sensorized RDSR. C Real-time changes in sensors and the perceived AS. Cases: (1) only external contact applied, (2) only actuation applied, (3) external contact applied after actuation. The real-shape image and perceived AS under case (1) are presented in (i, ii). The results under cases (2) and (3) are shown as (iii, iv, v). All sensor data are presented in (vi). D Tip position errors between perception and camera under different loading, from 100 to 700 gf in 100 gf intervals. E Data distribution of the axial and norm distance between AS and ES under no-loading conditions. The data are on the left of the box. Each box contains the data scale, median, and mean value.

In this study, the proprioceptive model incorporating rod lengths and sensor strains is validated and generates the accurate configurations of the sensorized RDSR under several actuations and loads. We experimentally determine the threshold to identify the difference between ES and AS. Then, the robot system presents the rapidity and robustness of contact detection by interacting with different positions and materials during dynamic motion. We also showed that the perception system is able to perceive the contact direction in both static and dynamic configurations, even in interactive environments without vision. Finally, we demonstrate the potential of our system and method in two intensive interaction tasks (Fig. 1C): one for autonomous exploration and navigation of mazes by detecting contacts with the walls, and another for teaching and repeating tasks by interacting with human operators.

Results

Perception performance

We fabricated and assembled a two-module RDSR with PSS (detailed process seen in “The integration and fabrication process of RDSR with PSS” section and supplementary materials (Figs. S1–S3)). Flexible rods provide precisely known lengths inside the soft body compared with cable and fluid actuation. The PSS, consisting of three pieces (1st, 2nd, 3rd piece), is integrated as close as possible to the corresponding rods.

Each module is virtually split into three segments by a virtual constrained plane (VCP). Starting from base disk (BD) to the end disk (ED), the first VCP locates between the 1st and 2nd piece of all PSS, and the second VCP locates between the 2nd and 3rd piece (Fig. 2A). The detailed implementation of expected-actual comparison method on the sensorized RDSR is presented (Fig. 2B). The Expected Shape (ES) is calculated from the actuation commands L_ij, generated by the controller (j-th flexible rod of i-th module (i = 1, 2, j = 1, 2, 3)). After executing the command, real-time sensing of Actual Shape (AS) is estimated based on the equivalent length L_ikj for j-th flexible rod of k-th segment of i-th module (k = 1, 2, 3, …, n). The kinematics of each segment is obtained based on the mapping relationships from actuation space (length L_ikj) to configuration space (arc length Lc_ik, the angle of bending plane ϕ_ik, and the bending angle β_ik).

The equivalent length L_ikj for each segment is calculated from the real rod length L_ij inside the soft body and the sensor strain S_ikj of each piece of PSS (the “Equivalent length and actual shape (AS)” section, Fig. S4).

$${L}_{{ikj}}=\frac{{L}_{{ij}}\left(1+{S}_{{ikj}}\right)}{{\sum }_{k=1}^{3}(1+{S}_{{ikj}})}$$

(1)

By calculating the difference, defined as contact index ε (ε = p_ES – p_AS), between the tip positions of AS and ES, we obtain the following information: the presence of external contact, the deformation source (internal actuation or external contact), and the extent or direction of contact. We set an index threshold ε₀ to judge whether external stimuli exist. If the norm or absolute axial value (||ε ||, | ε_x| , |ε_y| , |ε_z|) of ε is larger than the index threshold ε₀, we identify the deformation caused by external stimuli, detect the presence of the contact and re-plan the next step of actuation before entering the controller. Otherwise, there is no contact and the deformation is generated by internal actuation. The controller continues to execute the planned actuation. Besides, the presence of external contact can be detected by directly analyzing whether the sensor’s value is within the calibration range (Fig. S4).

The perception function and sensor performance are verified through a one-module RDSR with PSS. All sensors are calibrated before starting testing. Results show that the sensor has good linearity with a goodness of fit close to 1 (Fig. S4). Then, the perceived AS and sensor response in real-time were demonstrated under three cases (Fig. 2C, Movie 1): applying (1) only external stimuli without actuation, (2) only actuation without stimuli, and (3) stimuli after actuation. For the first case (Fig. 2Ci), the robot was in the initial configuration, and we arbitrarily applied external stimuli to the tip. For the second one (Fig. 2Ciii), we manually set the target length of three flexible rods to 0.15 m, 0.15 m, and 0.16 m, respectively. Afterward, arbitrary stimuli were also applied to the actuated configuration, which is the third case (Fig. 2Civ). The sensor data varies with different cases. Each embedded sensor can respond to local deformation caused by internal actuation and external stimuli individually or simultaneously (Fig. 2Cvi). The perceived AS (Fig. 2Cii, v) reflects the robot shape in real-time based on the sensed deformation and current actuation length. Figure 2Cii presents the perceived shape with case (1). The cyan and magenta shape in Fig. 2Cv are estimated under cases (2) and (3), respectively.

Another test focuses on the accuracy of proprioceptive tip position and determination of contact threshold ε₀. Considering the symmetric characteristic of a one-module RDSR, we did not take all configurations over the workspace, and randomly generated 500 configurations based on the following parameters: arc length Lc that ranges from 0.155 to 0.165 m, the angle ϕ of bending plane that ranges from 0 to 2π/3, and the bending angle β that ranges from 0 to π/3 (Fig. S5). We actuated these configurations with different tip load conditions: no load, 100–700 gf (gram-force) in 100 gf intervals. Among the tested loads, the maximum is 700 gf, which is more than 4 times of the robot’s own weight (160 g). For each configuration and each load condition, the perceived 3D tip position is obtained from AS and ES, which are estimated from the proposed perception method. The real tip position is obtained from an RGB-D camera (RealSense D435, 0.001 mm resolution in image, 1 mm resolution in depth). The perception error is calculated from the tip positions of the perceived shape (AS and ES) and RGB-D camera (Fig. 2D). The error on average of AS ranges from 2.4 mm to 3.2 mm with respect to different tip loads. The error percentage of AS, with and without load, is 1.4% and 2% relative to the whole length (0.16 m), respectively. The accuracy of the perceived AS remains almost unchanged regardless of the increase in tip load. However, as the load increases from 100 gf to 700 gf, the perceived error of ES increases from 2.4 to 18.7 mm, and the percentage changes from 1.4% to 11.7%. Therefore, the perceived AS achieves better accuracy than ES due to the fact that PSS captures the local deformation caused by tip loads in real-time. External loads or contacts will magnify the difference between AS and ES, and even then, AS achieves accurate perceptual precision.

Considering that the difference between AS and ES increases with increasing the external contacts, contact index ε can be used to identify whether the external load exists. To more precisely interpret the contact information, the boundary of the contact index ε should be determined. The principle for obtaining the boundary value is to evaluate the axial and norm distances of the contact index ε under no-tip loading conditions. The experimental results without tip loads in the perception accuracy test were used to determine the threshold of the contact index ε. The calculated axial and norm distance between the tip position of ES and AS are presented on the left side of the boxplot (Fig. 2E). The distribution, scale, median, and mean values of the data are displayed in the box. Different configurations have different distances. The axial distance ranges from −2 to 5 mm and the norm distance ranges from 0 to 5 mm. As the distribution boxplot shown, although the absolute distance is mostly lower than 3.5 mm, in order to ensure that the external contact can be detected, the upper limit of the absolute distance of 5 mm is determined as the index threshold ε₀. The robot is considered to be in contact with external stimuli when the norm or absolute axial value (||ε ||, |ε_x| , |ε_y| , |ε_z|) of the contact index ε is greater than the threshold ε₀ = 5 mm.

Proprioception and simultaneous contact detection

Two kinds of contact experiments, different body positions, and different material contacts, were carried out to demonstrate simultaneous proprioception and contact detection as well as its rapidity and robustness.

For the first one, three different cases, namely tip contact (Fig. 3A, Movie 2), body contact except for the sensor part (Fig. S6), and direct sensor contact (Fig. 3, Movie 2), were tested. The robot is controlled by three sets of sequential actuations (Fig. S7), respectively. Then, we set obstacles to block the continuous motion of the RDSR. Figure 3 presents the results of tip contact. When the robot bends to the opposite side of the obstacle in the first 10 s, the deformation is only generated by the self-actuation as the perceived AS and ES nearly coincide, and the contact index ε, including axial and norm distances, remains below 5 mm. When the robot bends towards the obstacle, an external contact is detected for a duration of approximately 12.5 s–15 s, as the norm and absolute axial value of ε is larger than 5 mm. We can observe a clear difference between AS and ES. The local deformation is caused by self-actuation and external stimuli. Besides, the proprioceptive shape and tip path are achieved, whether external stimuli are applied or not. The same results were obtained in the second case (Fig. S6), including the proprioceptive tip path, the norm, and the axial value of ε. The robot’s contact with obstacles is detected from 4 s to 6 s. An obvious difference in tip path can be observed during this period. Another method to detect direct stimuli on the sensor is shown in Fig. 3. The sensor S₂₁ is in direct contact with the obstacle during movement. Hence, the changes in sensor resistance are not only produced by the surface tension of the soft body but also by the normal contact pressure. To distinguish the calculation error caused by direct contact on the sensor, we evaluated the resistance change of the sensors embedded on the robot and showed that if not been directly contacted, the sensors’ resistance changes will not exceed 10% during regular actuation (Fig. S4). While the effect on the sensors is negligible (<1%) when applied normal force is smaller than 10 gf (Fig. S8B, see Supplementary Text S3 for more details) because resistance change smaller than 1% only brings 2 mm in ||ε || and 1.5 mm in perception error (Fig. S9B, C), the applied normal force (>16 gf) can be directly recognized once resistance exceeds 10% of its initial value (Fig. S8B). Therefore, unexpected errors will only exist when the normal force applied directly on the sensors is within the range of 10–16 gf (shown as red area in Fig. S8Biii), which is very small and rarely seen during daily usage. Thus, the external contact is detected once the change of sensor data is larger than 0.15 Ω (the initial value of S₂₁ is 1.5 Ω) (Fig. 3).

Fig. 3: Proprioception and simultaneous contact detection during motion.

Given the different sets of continuous control commands, the robot is blocked by obstacles and actively perceives (A) tip contact detection and (B) sensor contact detection. C The experiment on contact with material of varying softness, including Ecoflex10 (Smooth-On, Inc. 55 kPa), Ecoflex30 (69 kPa), Dragonskin10 (151 kPa), Dragonskin30 (593 kPa), and printed PLA (Rigid).

For the other one, we found that the robot can detect the tip contact with obstacles of different stiffness (Young’s Modulus from 55 kPa to rigid) (Fig. 3, Movie 3). When given the same actuation, although the final deviation of the robot tip decreases when the stiffness of the touched obstacles increases, the norm value ||ε || of the contact index ε increases from 7.4 mm when touching 55 kPa obstacle to 9.7 mm when touching rigid one. As a result, when setting a threshold norm value ||ε₀ || = 5 mm, the detection of contact with obstacles of different stiffness can be achieved within 0.4 s and the corresponding force is under 44 gf, the higher stiffness, the faster contact detection (See Supplementary Text S4 and Fig. S10 for more details of contact detection on material with different stiffness.).

Contact force and shape detection under a dark environment

We demonstrate the capabilities of the sensing expectation approach in perceiving contact direction and the corresponding force in static (Fig. 4A, Movie 4) configurations. External contacts from different directions, ranging from 0 to 315° in intervals of 45°, are applied to the tip in the initial configuration (Fig. 4Ai). We found that the perceived shape after each contact is almost the same as the real one (Fig. 4Aii). Calculating from contact index ε, the sensed direction in x- and y-axes is compared with the real contact reflected from a multi-axis force sensor (ATI nano 25). The results show that our approach senses the contact direction in an accurate way, with an average error of about 10° (Fig. 4Aiii, iv). Besides, our hand drags the tip in the same configuration to make it spin in a continuous circle (Fig. S11A, Movie 4). The proposed method can quickly sense and calculate the contact index (ε_x and ε_y), whose changing trend is the same as the real force (f_x and f_y). On this basis, the relationship between contact index and force is fitted (Fig. S11B). The goodness of these linear fits approaches 1. Contact forces (f_x and f_y) can be estimated from the contact index (ε_x and ε_y). In the dynamic configuration test experiment (Fig. 4B, Movie 4), the robot initially performs a circle movement under predefined bending commands (Fig. 4Bi). We then apply continuous contact to make the tip move in a smaller circle with the same bending sequence (Fig. 4Bii). The sensed contact index (ε_x and ε_y) shows the direction and force of the external contact. The deviation between the two paths with and without contact is consistent with the distribution of the estimated forces. The greater the contact force, the greater the deviation (Fig. 4Biii). The average angle error of the perceived direction is kept below 10° compared to the real one (Fig. 4Biv). The same results are obtained in another dynamic perception test where we applied backward and forward contact during bending (Fig. S11C). The above-mentioned perception of contact direction and force can be achieved not only at the tip but also any position along the soft body by simply estimating the contact index at the corresponding point. We demonstrate this functionality at middle position along the body in both static and dynamic configurations (Fig. S12).

Fig. 4: Perception of contact direction, force, and shape.

The capabilities in perceiving contact direction and force in static (A) and dynamic (B) configurations. C Detection and perception experiments under ink. (i) Experimental setup. (ii) The image of a real shape under the ink. (iii) Detected shapes with and without the proposed EP method. (iv) Contact index ε_x and ε_y along x- and y-axes. (v) Perceived contact force profiles and vectors.

Furthermore, these capabilities are presented to perceive surrounding shapes and interaction forces under ink (Fig. 4C). Our robot reaches into the ink and detects the environmental structures around the task area. Four different shapes of obstacles (convex, wave, flat, and rough) are setup in this demonstration (Fig. 4Cii). With the input of predefined commands, the robot explores the dark environments and perceives and obtains the tip path from ES and AS respectively. The former one reflects the outer boundaries of these obstacles and is ideally considered a non-contact situation, while the latter one shows their true contours and is a real-time perception of the actual state of the robot (Fig. 4Ciii). As mentioned previously, we compare AS and ES, calculate the contact index ε (ε_x, ε_y, and ε_z), and identify the different interaction information including direction and magnitude (Fig. 4Civ). Therefore, the force vector at each contact point is estimated based on these indexes and the fitting results. We found that the force profile is consistent with the obstacle contour (Fig. 4Cv).

Automatic exploration and navigation of mazes

Detection of interactions with the environment improves the intelligent behavior of soft robots in exploration and manipulation. Our proposed high-level perception-action loops, on the one hand, obtain the accurate proprioception-based closed-loop motion control (Supplementary Text S6, Movie 5), and on the other hand, tunes the actuation strategy based on simultaneous contact detection. Its first experimental scenario is the autonomous exploration of a maze by detecting contact with the maze walls. Without loss of generality, three different kinds of mazes are tested, including a simpler labyrinth with a single continuous path (Fig. S17, Movie 6), a circular maze with multiple intersections (Fig. 5, Movie 7), and a standard maze (Fig. S21, Movie 8). The end-effector of the soft robot is inserted into the channel of mazes. Initially, we set a general motion direction and a forward step. The robot will automatically explore and navigate in the maze by touching the walls, updating target points, searching for the right path, and finding the exit.

Fig. 5: Soft robots automatically explore and navigate a circular maze.

A Photograph of the experimental setup for maze exploration. The maze is designed with multiple intersections and barrier walls. The end-effector of the soft robot is inserted into the channel to touch the wall and find a pathway. B Top view of the successful right path and its relative position in the maze. Each right waypoint is determined from the exploration process. The robot will record and repeat them after finishing the process. C Tip coordinates and the corresponding norm, x, and y-axis value of ε when the robot moves along the right path. D The norm, x, and y-axis value of ε throughout the automatic exploration process. E Partial enlarged view of the norm, x and y-axis value of ε from 130 to 200 s. F Display of the whole exploration process including updated target point, perceived ES and AS position, and their relative location in the maze. G Partial enlarged view of the exploration process from 130 to 200 s.

Before exploring a maze with multiple intersections and obstacles, a simpler labyrinth with a single continuous path is tested (Fig. S17, Movie 6). A control algorithm is proposed to automatically explore this maze (Fig. S18). Each target position is adjusted according to the contact index ε and the current perceived AS position. Based on the predefined general update rule that sets the motion direction and the forward step, the controller generates the next target position. Afterward, the robot can reach that through the proprioception-based closed-loop motion control. If ||ε ||, |ε_x| , and |ε_y| exceed the contact threshold, the controller will readjust the target potion and repeat the motion control. The whole exploration process, including the targets, and the perceived tip of ES and AS, is presented in Fig. S17D. The corresponding contact index provides feedback on the interaction information between the tip and the wall (Fig. S17C).

After successfully exploring the right path and exit of a simpler labyrinth, the same idea is adapted to finish a much more complex one, a circular maze, but with more challenges to address. It requires the soft robot to find each right exit, identify the wall along radial and tangential directions, adjust general motion rules, record correct path points, and repeat them. Our robot addresses these challenges and makes its way out of a more complex maze (Fig. 5, Movie 7). The control algorithm is modified from the one applied in the simpler labyrinth. Two control blocks are added to find each right exit and change the general motion rules based on the identified wall (Fig. S19). Figure 5B presents the final right-searched path and its relative location in the maze. The coordinates denoted in x_m-o_m-y_m plane and the corresponding ||ε ||, ε_x, and ε_y are recorded (Fig. 5c). Our robot automatically explores and successfully navigates the maze within the threshold ε₀ of the contact index. The updated targets and the perceived tip position from ES and AS are recorded. Their relative position in the maze is displayed in Fig. 5F. Calculating the difference between the ES and AS tip, the corresponding ||ε ||, ε_x, and ε_y interprets the interaction information between the robot and the environment (Fig. 5D). The key points of the exploration include proprioceptive position, collision detection on the radial and tangential wall, and direction of the decision movement (counterclockwise or clockwise). Figure 5G displays the detailed exploration process. The related ||ε ||, ε_x, and ε_y are presented in Fig. 5E. Detailed process descriptions are presented in the “Motion control based on proprioception and contact” section. The robot follows the exploration principle until it gets out of the maze. All actuation lengths, throughout the whole exploration process (Fig. S20A), are generated from the optimization-based method (Fig. S14, Supplementary Text S5). All of them serve two purposes. One is used to approach the updated target points. Another is used to touch the wall. The former is recorded and repeated (Fig. S20B) to achieve movement along the right path in the maze (Fig. 5A–C). Furthermore, the automatic exploration and navigation in a standard maze were also carried out (Movie 8). The robot detects the walls on the left and on the direction of movement, updates the target position by itself, and automatically moves along the maze channel. The exploring process and experimental results (Fig. S21, Supplementary Text S7) are similar to the circular maze. Detailed descriptions are included in Supplementary Text S7.

Teaching and repeating tasks

Different control strategies are applied to realize the second experimental scenario, which is teaching and repeating tasks. A human operator can manually teach the robot to perform the required task, and the robot repeats the recorded actions and completes the taught behavior. Initially, the principle for teaching and repeating the desired configuration is explained and demonstrated in detail (the “Motion control based on proprioception and contact” section). And the interaction force between the human operator and robot is also tested and compared.

Furthermore, our soft robot is mounted on top of a manikin lying horizontally to test the teaching and repeating function in a massage task (Fig. 6Ai). Ten desired positions ranging from p₁ to p₁₀ are marked in green on the manikin surface (Fig. 6Aii). Two additional sensors R_e and R_s are attached near the tip, to manually control the pushing force between the manikin and the robot, which is monitored by a uniaxial force sensor placed along the z-axis (Fig. 6Aiii). The control algorithm for this task (Fig. S24), which adds pushing force monitor and control, is modified from that for the uniaxial demonstration test (Fig. S22). The process of teaching the robot to move to the desired configuration of position and force is manual (Movie 11). Firstly, the human operator takes the end-effector and moves it to the desired position in the x-y plane. Then, the R_e sensor is pressed to adjust the configuration and increases the pushing force to the desired level. Afterward, we release the R_e sensor and press the R_s sensor to decrease that force (Fig. 6Bii). Finally, we move the robot to the next marker and adjust the force using the same process as above. The real-time change in force sensor is used to manually monitor the pushing force (Fig. 6Bi). The human operator can view this force, and adjust through the R_e and R_s sensors. The detailed process of force tuning at desired positions p₂ and p₇ is shown around moments t₁ and t₂ during the teaching period (Fig. 6Bii). Our controller memorizes all satisfactory actuation, tip positions, and forces based on the control algorithm (Fig. S24). All data are rearranged together in equal time intervals (Fig. S25). Then, we apply the sequential actuation to repeat the recorded position and force (Movie 12). The repeated configurations are almost the same as the taught ones at desired positions p₂ and p₇ around t₁ and t₂ (Fig. 6Biii, iv). Tip positions are obtained from the perceived AS. The recorded and repeated 3D trajectories are almost consistent and reach all target markers (Fig. 6C). The axial and norm position errors are calculated, by comparing repeated and recorded ones, with a maximum of less than 6 mm (Fig. S25B). In particular, the maximum position error for all the target markers is less than 0.0045 m (Fig. 6D). Similarly, the taught forces at each marker are repeated very well, with maximum force errors less than 0.6 N (Fig. 6E). The profile of the repeated force is nearly identical to that of the recorded force during teaching (Fig. S25C). Notably, the maximum active pushing force is about 8 N, which is difficult to achieve in soft robots.

Fig. 6: Teaching and repeating test on a manikin.

The human operator teaches the robot to move to the desired configuration of position and force. Then, the robot repeats them. A Experimental setup for manikins and soft robots. (i) Overview of the setup. The manikin is lying horizontally, and the soft robot is mounted on top of it. (ii) Top view of the manikin with desired positions. The desired points are marked in green. The robot moves sequentially from p₁ to p₁₀. (iii) A detailed setup image of the sensors controlling and measuring the desired force. A uniaxial force sensor is mounted vertically to measure the pushing force between the manikin and the robot. Two soft sensors R_e and R_s are attached near the tip to control the magnitude of the force. B Teaching the robot to move to the marked position in the manikin and apply the desired pushing force to it. (i) the real-time sensor data including force, R_e, and R_s sensors during the teaching period. (ii-iii) the sensor data and robot configurations at moment of t₁ and t₂. C The tip trajectories in the x-y plane during teaching and repeating. D Tip position errors at all target markers after repeating. E The repeated and taught force at each marker.

Discussion

In this study, we propose a high-level perception-action method involving ES and AS and demonstrate how this method can be used to advance the intelligent behavior of soft robots. Our robot perceives its shape in the 3D environment with precise, coherent, and stable references from soft-bodied actuation rods and real-time deformation sensing from soft sensors. AS is estimated from the equivalent length L_ikj for each segment, which is calculated from the current rod length L_ij inside the soft body and the ratio of each piece relative to each PSS (the “Equivalent length and actual shape (AS)” section). This hybrid mapping that combines rod length and sensor strain is advantageous compared to direct mapping from sensor strain to length. We can avoid mapping errors caused by the fabrication and calibration of the PSS. Global environmental perturbations like temperature, oxidation of liquid metal, and hysteresis bring deviations in sensor resistance, but the equivalent length L_ikj will not produce large errors. Our method and robot system can robustly distinguish between internal and external interactions, and rapidly achieve posture proprioception and contact detection. On this basis, our soft robot successfully realizes autonomous exploration and navigation in mazes by touching walls, and it is taught to repeat the desired configuration of positions and forces with the guidance of a human operator. Although we can face variable changes in internal actuation, external loads, and surrounding environments, adapting to these scenarios due to internal defects and external damage remains a great challenge for our expected-perception methods and systems. There is still a need to develop soft skin sensors with higher performance to perceive the presence and position of these defects and damages.

Our perception method, inspired by human brain mechanisms, shows how to dynamically distinguish between local deformation generated by internal actuation and those generated by external stimuli in a rapid and robust way. It is a general method that can be applied to realize the intelligent behavior of any soft robot. The main process is to calculate the expected perception (EP), built from a copy of motor command and internal models, and interpret the sensory feedback from sensors. Visentin et al.⁴⁴ preliminarily identified external contact through a mismatch between expected and measured positions but with only static force sensing and only comparison by the position of one point. Currently, the PCC-based forward model acts as the internal model to predict the deformation. Some other models such as the mechanics-based model^45,46,47,48 or learning-based model^12,49,50 can also act as internal models to describe soft robots. The choice of different models requires a trade-off between model accuracy and computational efficiency. We provide a perception framework in soft robotics that is different from the conventional frameworks that focus on how to achieve the predefined target, such as PD-like controllers for shape regulation and tracking⁵¹, learning-based⁹, or model-based controller¹⁰ for force/position tracking. These works use the residual or errors between target and real measurement, target and model calculation, or model calculation and real measurement to optimize and update the actuation strategy to reach the predefined goals. In our research, we do not analyze quantitatively the computational cost in comparison with other methods. We just present the capabilities of the EP-based approach for soft robot proprioception and simultaneous contact detection. Based on the error comparison between the expected state and the actual state, we can distinguish the body deformation in soft robots caused by internal actuation from those generated by external contact. It should be noted that the EP-based controller applied in rigid robots is less computationally demanding and more energy efficient when compared to a standard predictive controller^4,5, which will favor the mechanics-based model control in soft robots.

The contact index ε is experimentally obtained from the difference between ES and AS of the one-module RDSR and varies due to different configurations. The precision of the match and comparison is dependent on the threshold ε₀. If the threshold is too large, we will not detect external stimuli, even if the robot has a large extent of contact with the environment. Contrarily, the stimuli will be falsely detected due to signal noise or model accuracy. The upper limit of the absolute distance range is determined as the threshold ε₀ to ensure that external contact is detected. This threshold is not affected by the number of modules, since the kinematics are identical for each module, and are calculated from the actuation length and sensor data. Apart from comparing the contact index ε, external stimuli can also be detected when the sensor resistance exceeds 10% of its initial value. But, in this case, the position feedback from the perceived AS is not accurate (Fig. 3B). Currently, we cannot resolve the inaccurate position feedback due to direct contact with sensors. We can easily and fast recognize direct contact when it happens. After that, we stop the robot and replan a new configuration to avoid direct contact. To completely resolve this problem, the first method is to use machine learning to decouple the effect of the strains caused by normal force and stretching. The second approach is to propose another model to identify and exclude some sensors that are in direct contact with external stimuli and estimate the robot shape based on the remaining sensors.

A similar capability, namely simultaneous localization and mapping (SLAM) without vision and lidar sensors, is achieved through the proposed RDSR and perception method. Autonomous navigation of mazes demonstrates the ability of the soft robot to explore the environment. We do not need specific sensors at the tip for intelligent control compared with traditional approaches (tactile sensors at the tip for contact detection and bending sensors for shape sensing). Meantime, the perceived AS feeds back the current position regardless of whether external contact occurs. By benefiting from these, our robot actively and automatically interacts with external environments, detects contact, and constructs the surface contours of terrain and objects. It has great potential for applications including, but not limited to maze exploration, such as shape detection through lateral scanning^52,53, and organ geometry estimation based on joint-level force sensing¹⁰. One more thing to note is that, as shown in Fig. S19 and Movie 7, the robot touches the wall from step 6, to avoid an infinite loop in the first circular channel. A properly adjusted step size can also avoid the same.

Methods

The integration and fabrication process of RDSR with PSS

The RDSR and PSS are fabricated separately by using silicone molding technology (Fig. S3). For RDSR⁵⁴, the flexible rods (NiTi alloy) and 3D-printed disks are first assembled. The silicone tube, as an outer sheath, hosts the NiTi rod and helps to decrease the viscous friction between the rod and the soft body. Three rods are evenly located in the circumferential direction, fixed to the end disk by the lock ring, and freely slide through the base disk and silicone tube. A 3D-printed core plug keeps the equal distance constraint between the base and end disk. These molds are sprayed with a release agent for easier demolding. Then, the assembled parts are put into the 3D-printed shell mold, with threads for string fiber, and silicone rubber (Silicone 0030, Ecoflex, Smooth-on Inc.) is poured into the mold. Once completely cured, the silicone-based body is removed from the shell mold, and Kevlar string is twined along the threads. For PSS, silicone rubber is poured into the bottom mold with a protruding structure to form a bottom layer with microchannels. Meanwhile, silicone rubber is poured into the top mold and cured under 50 °C for 5–6 min. Then, the completely cured bottom layer is put above the top layer to form a PSS substrate with sealed microchannels. After the two layers have cured together, cut off the excess top layer. The conductive eGaIn is injected into each channel, and copper wires are inserted at both ends. Sil-Poxy is used to seal the channel and prevent eGaIn from oxidation. Finally, the soft body of RDSR is shortened from L₀ to L′₀ by vertically pressing the base disk. The unstretched PSS is then glued to the shortened body surface by Sil-Poxy. Each PSS is close enough to the corresponding actuation rod for each module. When the soft body and PSS are glued together, we release the pressing force and restore the original length of the RDSR. The initial state of the PSS is stretched and can capture bidirectional strain changes. The detailed comparisons and studies of multi-modal sensory soft robot systems are listed in the Table S1^55,56,57. 

Equivalent length and actual shape (AS)

The rod length L_ij inside the soft body for each module is definitely known to us according to the feedback of the servo motor, but the equivalent length L_ikj for k-th segment of i-th module is hard to determine directly. Each branch has one PSS mounting near the actuation rod of the corresponding module. The sensed strain of PSS in real-time reflects the deformation generated by the actuation and external stimuli. Without prior knowledge of the internal or external factors, such as actuation or tip load, we can estimate the robot configuration or tip position after obtaining the equivalent length L_ikj. Considering that the PSS is attached closely to the actuation rod, the ratio of the sensor length les_ikj to the total length of each skin is the same as the ratio of the equivalent length L_ikj to the rod length L_ij. The ratio w_ikj is estimated firstly as follows:

$$\begin{array}{c}{{{w}}}_{{ikj}}=\frac{{{{les}}}_{{ikj}}}{{{{les}}}_{{ij}}}=\frac{{{{les}}}_{{ikj}}}{{\sum }_{k=1}^{3}{{{les}}}_{{ikj}}}=\frac{{{les}0}_{{ikj}}(1+{S}_{{ikj}})}{{\sum }_{k=1}^{3}{{les}0}_{{ikj}}(1+{S}_{{ikj}})}\\=\frac{{{les}0}_{{ikj}}(1+{S}_{{ikj}})}{{{les}0}_{{ikj}}{\sum }_{k=1}^{3}(1+{S}_{{ikj}})}=\frac{(1+{S}_{{ikj}})}{{\sum }_{k=1}^{3}(1+{S}_{{ikj}})}\end{array}$$

(2)

Then, the equivalent length L_ikj is estimated by the following.

$${L}_{{ikj}}={w}_{{ikj}}{L}_{{ij}},$$

(3)

where les_ikj and ε_ikj are the real-time length and strain of the j-th sensor on the k-th segment of the i-th module. les0_ikj is the initial length of each piece. Since the fabricated channel length and the initial straight state of each sensor are the same, the length les0_ikj of all sensors is the same. Therefore, the ratio w_ikj is only related to the sensor strain ε_ikj.

There is no coupling effect between modules for a one-module RDSR. The above formula (3) can be directly used to obtain the equivalent variable length L_ikj. The strong coupling effect should be considered for a two-, or multiple-module RDSR. Taking a two-module RDSR as an example to explain how to obtain equivalent variable length L_ikj. The total length of flexible rods connected with 1st module is L₁₁, L₁₂, L₁₃. The total length of flexible rods connected with 2nd module is L₂₁, L₂₂, L₂₃. Firstly, the coupled length L_21-1, L_22-1, L_23-1 in the 1st module of the 2nd module flexible rod is estimated. Then, we obtain the rod length embedded in the 2nd module by subtracting the coupled length L_21-1, L_22-1, L_23-1 in the 1st module from the total length L₂₁, L₂₂, L₂₃ of the 2nd module. Finally, combined with sensor data on the 2nd module, we can obtain the equivalent variable length L_2kj from Eq. (3). Thus, the Actual Shape (AS) for a two-module RDSR is calculated. The coupled kinematics for multiple modules is presented in Supplementary Text S2.

Contact detection and force estimation

For each perception and control loop, ES will be predicted based on the future rod length L_ij, and AS is estimated from the equivalent length L_ikj. Both perceived shapes are calculated from the same kinematics model (Supplementary Text S2). Then, the contact index ε is calculated as ε = p_ES – p_AS (ε_x, ε_y, ε_z), which is the difference between the tip positions of AS and ES. If ||ε||, | ε_x| , |ε_y| , or |ε_z| > ε₀ (defined as 5 mm in the “Perception Performance” section), we identify the presence of external contact and also estimate the direction and degree of this contact. The contact direction in the x-y plane are sensed as: ${\theta }_{sensed}={\tan }^{-1}{\varepsilon }_{{y}}/{\varepsilon }_{{x}}$. The magnitude of ε_x, ε_y, ε_z represents the degree of contact. Besides, we calibrate the relationship between the difference (ε_x, ε_y) in tip position and the contact force (f_x, f_y), respectively (Fig. S11B). Then, the force can be estimated by ${f}_{x}=8.39{\varepsilon }_{x}-0.004$, and ${f}_{y}=10.25{\varepsilon }_{y}-0.005$.

Motion control based on proprioception and contact

Regarding the exploration and navigation of the circular maze. The control and motion process, in other words, is like our left hand touches the left side after each step to see if there is a wall or an exit. If we find an exit, we go in. If we find it to be a wall, we continuously move forward. If we contact the wall while in a moving direction, we turn and change the direction of movement. For example, after reaching a target point, the robot tries to move a little distance along the radial direction. If external contact is detected (||ε||, |ε_x| , or |ε_y| > 5 mm), the next target is updated clockwise, as the previous one, and the robot moves to the next (Fig. 5Gi, ii). If not, the next target is updated based on the current perceived position (Fig. 5Giii, iv). If the robot makes contact with the wall while moving forward to the next target for three consecutive loops, an obstacle in the tangential direction is detected (Fig. 5Gv, vi, vii). The robot goes back to the starting point of these three loops and plans the next target counterclockwise (Fig. 5Gviii). On this basis, the presence of multi-directional walls is identified in real-time. We use the difference or contact index to adjust the target and find the exit (Fig. S19A–C, F).

Regarding the teaching and repeating tasks. The motion control principle is to monitor and control the absolute contact index ε to be less than 5 mm (Fig. S22). A uniaxial demonstration test is conducted to display the process (Fig. S23A, Movie 9). During the test, a human hand pulls and pushes the robot tip along the y-axis (Fig. S23Ai). Local deformations are generated when external forces are applied, and the norm and axial value of the contact index ε increase. When the index is larger than 5 mm, the controller actuates the robot to decrease them to less than 5 mm (Fig. S23Aiii). Each teaching point, including proprioceptive position, and actuation, will be recorded. Afterward, the robot repeats the taught behavior by applying the recorded actuations (Fig. S23Aii). At the same time, the tip position is obtained from the perceived AS of each repeated configuration. Then, the repeated position error |dp_y| is calculated between the repeated and recorded points (represented by the blue bar in Fig. S23Aiii), with a maximum error of less than 0.007 m. Additionally, a uniaxial force sensor (DYMH-103, DAYSENSOR Ltd., Anhui, China) is setup along the y-axis (Fig. S23Biii), to measure the applied force between the robot and the human hand while teaching. To compare the interaction force, the human hand slightly and slowly pulls the tip along the y-axis, with and without teaching (Fig. S23Bi, ii, Movie 10). The robot moves with the movement of the human hand, and the force is maintained around 0.6 N with teaching. Inversely, the force increases with the displacement by up to 3 N (Fig. S23Biv). The teaching and repeating in our soft robot can be realized with a small repeating error and a low interaction force.