Introduction

Seabed detection plays a crucial role in safeguarding marine ecosystems. Effective management and protection of seabed ecosystems are facilitated by meticulously identifying and documenting the distribution and abundance of vital ecosystems, such as seabed organisms, coral reefs, and seagrass beds. High-definition visual information enables the capture of both color and texture nuances of the seabed, thereby facilitating the identification of biota distribution. Furthermore, clearer and more detailed images can serve as valuable supplements to traditional large-scale ocean observations. In current oceanographic research, image data is extensively utilized across various fields for environmental monitoring, such as the pigmentation reaction score (PRS), which is crucial in assessing coral reef health1. Additionally, the video data were essential to add value and create relationships between the morphology of the seabed, the composition of the sediments, and the geochemistry of the gases2. Moreover, high-quality images are essential for constructing accurate topographic maps, aiding ecological assessments3.

Despite many efforts to enhance underwater image clarity4,5, obtaining sharper raw images remains the optimal solution. However, the clarity of visual information depends on the visibility of the water column and the distance to the target. Refraction and scattering caused by water degrade image quality, and this effect intensifies with distance6. Therefore, positioning the robot closer to the seabed directly improves the quality of the captured images. However, the robot’s activities may disturb seabed sediment, causing them to suspend and consequently impairing the field of view. Additionally, the rugged topography of the seabed poses challenges to the robot’s mobility, hindering objective achievement.

Currently, the most common types of robots used for near-seabed detection are wheeled or tracked vehicles that can be remotely controlled7,8 or operated autonomously9. However, these benthic machines are confined to the seabed plane, limiting both their workspace and field of view. Wheeled and tracked robots are advantageous in long-term monitoring tasks because of their stability and passive positioning capabilities. Nonetheless, they face significant challenges when navigating rocky terrain; they usually require relatively continuous ground movements10,11. Furthermore, their movement can resuspend sediment on the seafloor, compromising the quality of the recorded videos. The footprints left by these robots may disrupt or harm benthic organisms, which can have lasting effects12.

Underwater-legged robots generally enhance their mobility across various types of terrain by adjusting their buoyancy. For example, previous studies on SLVER213 and its precursors14,15,16 have emphasized the significance of buoyancy in facilitating underwater jumping. This enables robots to employ a specific jumping gait to overcome obstacles of approximately 20 cm in height14,15. However, legged robots are often restricted to relatively flat areas because of the complex seafloor topography encompassing vertical cliffs, slopes, rock formations, and coral reefs. Additionally, direct physical contact with legged robots may not be suitable in delicate environments, such as coral reefs and areas with sea anemones.

Floating robots offer a suitable solution for enhancing continuous near-seabed observations. These robots can navigate benthic environments and overcome the challenges posed by complex seabed topography, particularly in fragile ecosystems; therefore, a method that avoids direct contact with the seabed during the observation process is preferable. Numerous studies have focused on employing floating robots for seabed observation. For instance, unsteady hydrodynamics have been used to replicate the pectoral fins of marine organisms17 or fishtails18, both of which can be categorized as body-caudal fin (BCF) or median paired fin (MPF) swimming19. BCF involves undulating motions of the caudal fin and body, generating waves that propagate from the head to the tail and accelerate the water column, subsequently generating thrust20. The MPF creates traveling waves that push water backward, resulting in thrust through the conservation of momentum17. In both cases, mimicking the behavior of aquatic organisms accelerated the water to produce thrust. However, relying solely on imitating shapes and biomimetic locomotion methods results in the loss of the benefits of engineered materials and mechanisms that can be exploited to surpass animal performance21,22, and it is difficult to accomplish the corresponding tasks when the fluid velocity changes23,24. Typically, many research efforts have utilized propellers to improve the performance of bionic robots25.

Propeller-driven underwater robots dominate ocean observations, primarily encompassing underactuated vehicles equipped with rudder-propeller devices26 and fully actuated vehicles featuring multiple propellers27,28. Rudder-propeller-driven vehicles primarily generate wake currents parallel to the hull, yet they can achieve steering, lifting, and sinking by adjusting the rudder angle. However, they usually maintain a distance of 5–50 m29,30,31 from the seabed to avoid downward suction and pitching moments induced by the wall effect when operating near the seabed32 due to the small area occupied by the rudder makes it challenging to resist the forces and moments on the entire body, potentially causing the robot to make contact with the seabed and fail its mission, while have study asserts that rudder-propeller-driven underactuated robots can operate at a distance of 3 m from a relatively flat seabed, however, the elevation exceeds 5 m for 50% of the tracking duration and peaks at 12 m throughout the tracking process33, these types of robots typically necessitate the use of vertical thrusters to achieve proximity to the seabed34,35,36. Fully actuated robots with multiple propellers rely directly on water reaction forces for directional control, which necessitates pushing the water in reverse to adjust the distance from the seabed. However, as excessive wake strength can resuspend seabed sediments37, which impedes the observation field of view, these types of robots need to maintain a certain distance from the seabed (2–5 m)38,39.

Although numerous methods exist to mitigate bottom disturbances, their applicability to near-seabed exploration remains limited. For instance, an alternative method is buoyancy adjustment40,41,42. Although it does not require an additional power output, it has drawbacks such as sluggish response times and substantial energy consumption for a single buoyancy adjustment. The robot encounters delays and heightened energy consumption when navigating terrains with frequent changes in seabed height. In contrast, underwater robots employing positive buoyancy43,44 do not generate a wake perpendicular to the seabed while controlling the distance from the seabed; however, this method requires extra energy consumption to resist positive buoyancy to maintain depth. At the same time, when ascending using positive buoyancy, greater positive buoyancy needs to be provided when increasing the rate of ascent, resulting in higher energy consumption to maintain depth.

In the context of near-seabed exploration, the influence of the wall effect with a time-varying nature due to the complex topography of the seabed and unsettled seabed sediments presents challenges for robotic seabed exploration. To overcome these challenges, the following two aspects of this study address these problems.

  1. (1)

    In terms of body design, we introduced a maneuverable underwater vehicle for near-seabed observation (NS-MUV), as shown in Fig. 1a, b. The body was intentionally flattened (Fig. 2b) with the propeller mid-axis positioned at an angle to the mid-axis of the body (Fig. 2c). The design configuration of the robot facilitates low-disturbance movement away from the seabed based on the principle that when the wake current is aligned parallel to the seabed, an angle exists between the forward direction of the body (x axis) and the seabed plane. The wake, parallel to the seabed, propels the robot along both the x- and z axes. Owing to a significant discrepancy in damping between the x-axis and z-axis, the robot prefers movement along the less damped x axis, moving away from the seabed. This design contrasts with that of an all-drive robot, which relies directly on reaction forces for approaching or distancing from the seabed. This significantly magnifies the impact of the wake on seabed sediments, given that this approach necessitates the wake to be perpendicular to the seabed. The rudder-propeller-driven underdriven navigator can regulate its distance from the seabed by increasing the forward distance45,46. When the wake currents are parallel to the seabed, the NS-MUV can reduce the forward distance by more than seven times. Its capability to maneuver within a near-seabed environment within a range of 20–30 cm was validated through real-world experimentation.

    Fig. 1: Field experiment.
    figure 1

    a Movement over sandy-gravel terrain, the diameter of the propeller fairing is labeled. b Upper coral reef movement. c Images of sandy-gravel terrain. d–f Images of coral reefs.

    Full size image
    Fig. 2: Main electronics and mechanical components.
    figure 2

    a The relationship between the rotational speed of the thruster and the resultant force and torque can be described as follows in the airframe coordinate system. The thrust, denoted as T, corresponds to the force generated along the x axis. Additionally, the moments generated on the x, y, and z axes of the airframe coordinate system are represented by K, M, and N, respectively. b The overall structure of the robot. c Side view of the thruster arrangement, with arrangement parameters such as the distance B and the angle of the central axis of the thruster \(\delta\). d Main electronics components.

    Full size image
  2. (2)

    We employed model identification and angular acceleration feedback to promptly detect external disturbances and mitigate the detrimental effects of wall and current disturbances on the stability of robot motion. We propose an angular acceleration observation method to address the limitations of the inertial measurement unit (IMU) that solely provides angular velocity information. By indirectly observing the angular acceleration using an accelerometer, we circumvent the noise amplification issues inherent in the angular velocity differentiation (AVD) process, thereby obtaining more reliable angular acceleration data. By leveraging these data, we can discern the dynamic model of the robot and integrate it with the real-time angular acceleration feedback to promptly detect external disturbances. By utilizing real-time observations of external disturbances, we can plan the attitude and velocity of the robot, effectively averting the risks of unstable motion and hitting the seabed owing to wall effects and current disturbance.

The NS-MUV propeller moves the robot forward and enables it to steer along the axis. Control of the distance between the robot and the seabed is achieved by adjusting the angle between the plane of the body and the seabed plane such that no wake perpendicular to the seabed plane is generated during distance control. Although this distance control method introduces some control delay in resisting environmental disturbances, the passive stability of the robot along the z-axis adeptly compensates for this drawback.

Here, we show that the wake distribution exhibited by the robot significantly reduces the disturbance to the seabed compared to fully actuated vehicles and validates the robustness of the controller in controlling the distance between the robot and the bottom, as well as the ability of the robot to observe the seabed in a real environment. Several tests show that the NS-MUV can resist the disturbance torque generated by the impact of a load equivalent to up to 25% of its mass (even if the load is stationary, the disturbance torque generated by it accounts for more than 60% of the maximum torque that the robot can output), proving that it has considerable robustness in controlling the angle between the plane of the body and the plane of the bottom, thus enhancing its applicability in real environments. The vertical displacement of the robot is only 0.02–0.03 m within 0.5 s after the occurrence of different impact loads, which proves that although the distance control method proposed in this study, there is a delay in resisting external disturbance, can be offset by the passive stability of the robot. We conduct multiple tests in various marine environments, including sandy areas, coral reefs, and sheer rock, to successfully verify the robot’s low sediment disturbance and adaptability to rugged underwater terrain.

Results

Robotic systems overview

The NS-MUV mass is 16.3 kg. the robot’s overall length is 0.62 m, a maximum width of 0.93 m at the fuselage, and the highest point of the robot structure is 0.245 m (detailed information in Supplementary Note 7). It comprises three subsystems: the control system, propeller drive, and disk fuselage. During active maneuvering, the NS-MUV can achieve a maximum velocity of 2 m s−1 (3 bl (body length) s−1) and steer at a maximum angular velocity of 180o s−1.

Figure 2b illustrates the overall structure of the NS-MUV, which employs four propellers. Approximately 90% of the thrust from all the propellers was utilized for moving forward and steering, thereby enhancing the ability of the NS-MUV to move forward and steer.

The primary aim of the robot introduced in this paper is to minimize sediment disturbance during its ascent. In this study, we present a design concept for the low-disturbance ascent of a levitating robot. When the force generated by the propeller is also parallel to the seabed, it typically does not induce a tendency for the robot to move away from the seabed. However, by tilting the propeller at an angle with the robot, this parallel force can be decomposed into the two planes of the robot. As depicted in Fig. 3i, the force from the bottom propeller, parallel to the seabed, is resolved to the x-direction and z-direction of the robot. The x-direction force propels the robot away from the seabed, while the z-direction force draws it closer. By adjusting the damping in these two directions, we can maneuver the robot away from the seabed while maintaining the wake parallel to the seabed (detailed information in Supplementary Note 5).

Fig. 3: Bottom disturbance.
figure 3

a A maneuverable underwater vehicle for near-seabed observation (NS-MUV) moving away from the planar platform. b Traditional structure moving away from the planar platform. c Vehicle (4.5 kg, yellow) using propellers to directly disturb the small balls at the bottom. d Bottom disturbance by vehicle (3.9 kg, white). e Bottom disturbance by NS-MUV. f Acceleration curves during the ascent of robots with different structures. g Depth curves during the ascent of robots with different structures. h Schematic of the wake as NS-MUV moves closer to the seabed. i Schematic of the wake as NS-MUV moves away from the seabed. j NS-MUV moving away from the seabed in a real environment. k Traditional structure moving away from the seabed in a real environment. Source data are provided as a Source Data file.

Full size image

The axial distance between the propellers on the same side determines the pitch control moment of the arm, and increasing this distance facilitates better control of the NS-MUV pitch angle. Considering design consistency, the distance is controlled not to exceed the height of the NS-MUV cabin. The propeller arrangement of the NS-MUV enables the robot to rotate along the x, y, and z axes, as well as to advance along the x axis. This layout offers us the flexibility to adjust the robot’s forward vector dynamically, facilitating the execution of diverse and intricate trajectories. Consequently, it enhances the robot’s capability to adapt effectively to the intricate seabed environment.

Increasing the tilt angle of the thrusters during the design phase will enhance the speed of the low-disturbance ascent; however, this change entails a trade-off, as a larger tilt angle will reduce both the robot’s forward efficiency and the maximum pitch control torque. An analysis of this trade-off is presented in Supplementary Note 5.

Vehicle disturbance to the bottom

Figure 3a, b show a planar platform, while Fig. 3c–e depict a trapezoidal platform. Multiple plastic spheres are scattered across the surfaces of both platforms. These spheres are used to observe disturbance at the bottom, as they exhibit oscillations when slightly disturbed (detailed information in Supplementary Note 8).

Experiments were conducted on the platform using two fully actuated vehicles, with masses of 3.9 kg (white) and 4.5 kg (yellow), respectively, along with NS-MUV, presented in this paper. As illustrated in Fig. 3e, NS-MUV achieves a motion speed of approximately 0.8 m s−1 while tracking the terrain (speed calculated using the ratio of motion distance to total motion time). Owing to the NS-MUV configuration and motion, the ball at the bottom remained unaffected by the propeller wake while tracking the specified terrain. However, a slight wobble of the bottom ball was observed during the test (Fig. 3e), occurring after the NS-MUV passed through the area, and the overall wobble amplitude remained consistent (Supplementary Video 2). If it affects the ball because of the NS-MUV propeller wake, it does not exhibit this type of consistent wobble (Fig. 3c). We reasonably infer that owing to the viscosity of the fluid, NS-MUV induces movement in a portion of the surrounding fluid during its locomotion, resulting in a slight wobbling of the bottom plastic ball. This impact, stemming from the inherent properties of the fluid, is unavoidable for all vehicles; however, adjusting the speed of the vehicle according to the specific environment can minimize the impact.

Figure 3d, e depict a vehicle weighing 3.9 kg and the NS-MUV traversing the same area. It is evident that despite the 3.9 kg vehicle propeller exerting a maximum thrust equivalent to only 9.3% of the mass of the NS-MUV (when measured in kilograms). When the propeller wakes directly influences the bottom ball, the swing of the ball is significantly larger than that induced by the fluid propelled by the NS-MUV during the motion. This observation suggests that the impact of the fluid viscosity was considerably smaller than that of the propeller wake. This confirms that the NS-MUV can effectively minimize the disturbance to the bottom by mitigating the impact of the propeller wake on the seabed.

The impact of the underwater vehicle on the seabed primarily manifests when the vehicle moves away from the seabed. During this motion, the vehicle accelerates the water flow and ascends with the assistance of the reaction force, resulting in a direct impact of the accelerated water flow on the seabed (refer to Fig. 3c). Notably, the NS-MUV presents a markedly distinct wake distribution compared with fully actuated vehicles; the NS-MUV can be far from the seabed, even when the wake is parallel to the seabed (Fig. 3i).

The analysis reveals that variations in bottom disturbance are primarily attributed to differing wake distributions during the robot’s ascent. To effectively emphasize the advantages of the structure presented in this paper and to mitigate the impact of shape and mass discrepancies on the comparison results, the thruster layout of the existing NS-MUV structure was modified to resemble those of other underwater vehicles designed specifically for seabed exploration47. For clarity, the structure depicted in Fig. 3a will be referred to as the NS-MUV, while the structure shown in Fig. 3b will be designated as the traditional structure. Detailed modifications are elaborated upon in Supplementary Fig. 8.

We conducted experiments with robots equipped with two distinct thruster structures, allowing them to ascend on the planar platform. Figure 3a, b illustrate that the NS-MUV exerts significantly less disturbance on the bottom plastic balls during ascent compared to the traditional structure. Figure 3f, g reveal that there is no substantial difference in the initial rate of depth change between the two robot types. However, the NS-MUV demonstrates greater speed and acceleration in the subsequent ascent phase, while causing less disturbance to the bottom than the traditional structure. To assess the environmental impact of the two designs, we performed experiments in a natural sandy environment. In Fig. 3j, resuspension of seabed sediments is not observed due to the ascent of NS-MUV. In contrast, the traditional structure stirs up considerable sand, resulting in turbid water (Fig. 3k). Field experiments have confirmed that the NS-MUV is capable of minimizing seabed sediment disturbance when the robot is moved away from the seabed.

We conducted a meticulous analysis to clarify the mechanisms that allow the NS-MUV to exhibit minimal disturbance to the seabed. As shown in Fig. 3i, the NS-MUV movement away from the seabed is achieved by altering the angle between the body and seabed planes. This is achieved by exploiting the force imbalance at this time and ensuring that the wake generated during the angle change does not impact the seabed; instead, it tilts upward. When the wake is parallel to the seabed, the NS-MUV experiences torque M and forces Fxoy and Fyoz. Under the influence of force Fxoy, the NS-MUV undergoes only a slight displacement because of its high damping in the XOY plane; additionally, as the body plane already exhibits a certain angle with the seabed plane, the NS-MUV can offset the displacement caused by force Fyoz when moving away from the seabed along the direction of force Fxoy. Consequently, the overall outcome was that the NS-MUV moved away from the seabed. As depicted in Fig. 3h, the NS-MUV avoids generating a wake directed towards the seabed when close to the seabed.

Terrain tracking

Owing to the intricate nature of the seabed terrain, which encompasses vertical cliffs, rock piles, and coral reefs, vehicles must move agilely through the rugged underwater landscape during near-seabed exploration. We substantiated the capability of the NS-MUV to traverse challenging terrains through a series of tests conducted in test pools and real-world environments. The results, as depicted in Fig. 4a, b, demonstrate the capability of the NS-MUV to move through vertical walls. Additionally, a real environment test further verifies the successful traversal of the coral reef terrain.

Fig. 4: Terrain tracking.
figure 4

a Snapshot of the experiment of traversing a vertical wall. b Real-world environmental obstacle-crossing. c Testing pool bottom scanning. d, e First-person perspective of bottom scanning. f Traces of benthic robot movement.

Full size image

We conducted an initial test of the capability of the NS-MUV to observe the bottom closely using manual direction control. To accomplish this, the NS-MUV was diving at the bottom of the pool, and a comb-scanning method was employed to observe the bottom. In this experiment, only a body-mounted camera was used for video recording. The figure below illustrates the bottom scanning process. Throughout the entire process, NS-MUV maintained a distance of 0.2–0.3 m from the bottom. Although the pool bottom used in the experiment did not simulate a real seabed, video images captured during the test revealed the presence of silt and traces of benthic vehicles at the bottom (Fig. 4d–f). Throughout the observation process, it was observed that the NS-MUV movement did not disrupt the silt or impact the field of view. Furthermore, a comparison of the topographic images captured during two consecutive passes at the same position (Fig. 4d, e) indicated no change in the characteristics of the bottom.

Anti-disturbance algorithms

In this study, the NS-MUV regulated the separation between itself and the seabed by adjusting the angle between the body and seabed planes. The stability of the angle control ensured that the NS-MUV maintained a safe distance from the seabed.

We observed the disturbance torque through model identification and angular acceleration feedback, a method distinct from commonly employed approaches, such as active disturbance rejection control (ADRC)48 or proportional integral derivative (PID)49 control, which are known for their slower response to external disturbances50. The incorporation of angular acceleration feedback enhances control robustness51. Notably, our method of observing angular acceleration differs from relying on an external motion capture system51. We obtained this observation using our sensors, improving their usability in real-world environments.

The current IMU only obtains angular velocity information and does not provide feedback on angular acceleration information. To obtain feedback on the angular acceleration, we performed the following: Fig. 5a illustrates the configuration of the sensor array in the NS-MUV system. We measured angular acceleration from three perspectives: two AVDs and an observed form of acceleration. Unlike angular velocity, acceleration data require no differential processing, which serves as the reference for subsequent filtering, with the primary purpose being to mitigate the amplification effect of noise caused by differential processing. For instance, when the return frequency of the sensor is 200 Hz, direct differential processing can amplify the sensor noise by up to 200 times its original magnitude.

Fig. 5: Observation of external disturbances.
figure 5

a Sensor arrangement and corresponding angular acceleration acquisition method. \(\lambda\) represents the distances from the center of the body for inertial measurement unit (IMU) (2) and IMU (3). p, q, and r represent the angular velocities of the sensor along its own x, y, and z axes, respectively. Moreover, ay and az represent the accelerations of the sensor along its axis. b Comparison of the estimated angular acceleration by the offline learning model and the actual observed angular acceleration used for external disturbance observation is studied.\(\dot{\omega }\) represents the actual observed angular acceleration, \(\hat{\dot{\omega }}\) represents the angular acceleration predicted by the offline model, \(\hat{\phi }\),\(\hat{\theta }\) and \(\hat{\psi }\) represent the error increments utilized for resisting disturbances in the attitude controller during roll, pitch, and yaw control.

Full size image

In Fig. 6g, we present the results of the angular acceleration measurement using the AVD and acceleration measuring angular acceleration (AMA) methodologies. A statistically significant disparity was observed in the original data distribution between the angular acceleration measurements obtained using the two methods. When the NS-MUV was subjected to an impact load, the AVD exhibited 2.6 times more outliers than the AMA at the same sampling frequency. For AVD, the upper and lower edges of the observed data range from −35.75 rad s−2 to 30.25 rad s−2. On the other hand, for AMA, the upper and lower edges of the observed data range from −4.8 rad s−2 to 10.8 rad s−2. The data analysis revealed that AVD has a 4.2 times higher degree of dispersion than AMA. During the stabilization phase, neither approach resulted in outliers; however, AVD exhibited a data dispersion 6.3 times greater than that of AMA. From practical results, it has been observed that differentiating the angular velocity to obtain the angular acceleration can magnify the sensor noise and result in the instability of observations. Measurements of angular velocity and acceleration obtained from the IMU are prone to interference from vibrations, leading to alterations in its noise characteristics52, and differential processing amplifies the noise, resulting in amplified distortion in the filtered data53. Therefore, this study favored the utilization of acceleration as a metric for measuring angular acceleration owing to its non-reliance on differential processing during measurement.

Fig. 6: Resistance to instantaneous strong disturbances.
figure 6

a Sensor information of the NS-MUV includes the pitch angle and depth control curves during disturbance resistance, as well as the pulse width modulation (PWM) values of the propellers. b Snapshots of the NS-MUV during the experiment of resisting two impacts generated by a 4 kg load. c Control effect of the disturbance resistance algorithm proposed in this paper under constant disturbance conditions. d Angular acceleration data at a 4 kg load, where \(\dot{q}\)(fitted) represents the angular acceleration data obtained using least-squares weighted filtering. e Enlarged view of box I in c. f Enlarged view of box II in c. g Stability analysis was conducted on angular acceleration observations (Mann–Whitney U test: median, mean, and 25th to 75th percentiles); I1 and I2 denote the angular acceleration obtained by the angular velocity differentiation (AVD) and acceleration measuring angular acceleration (AMA) in d, respectively (number of data: 100). S1 and S2 represent the angular acceleration obtained by AVD and AMA in e, respectively (number of data: 300). h Control effect of the PID algorithm under constant disturbance conditions. Source data are provided as a Source Data file.

Full size image

Gathering data from an NS-MUV operating in a static water environment is imperative to observe disturbances. This allowed us to establish relationships between the angular acceleration and various parameters, such as the actuator output, angular velocity, and attitude angle. We developed a kinetic model for the NS-MUV behavior in a static water environment by employing offline learning on the collected data. Because the hydrostatic environment is free from external environmental disturbances, it can be considered a reference for estimating disturbances when an NS-MUV is exposed to external disturbances.

Resistant to strong disturbances

To address the issue of maintaining the distance between the NS-MUV and the bottom in the presence of external disturbances, we decompose the distance control into two components based on the NS-MUV movement: attitude planning and speed planning based on distance error. Regarding the resistance to external disturbances, we decoupled a portion of the error increment from the attitude controller to be used as a feed-forward for disturbance rejection. Specifically, the output of the attitude controller is decomposed into two parts: one represents the output for tracking the desired attitude, and the other represents the output for disturbance resistance. Subsequently, we conducted an experimental verification to assess the effectiveness of the proposed approach for handling both constant and transient strong disturbances.

We assessed the capacity of the NS-MUV to withstand constant disturbance by introducing a 2.25 kg heavy block at its front end. Testing was conducted in a pool with a water depth of 0.5 m. When the NS-MUV is submerged, the distance between the bottom of the NS-MUV and the pool bottom is approximately 0.3 m. We compared the proposed algorithm with the ability of the PID algorithm to resist external disturbances. The experimental results reveal that, while the NS-MUV exhibits passive stability in the direction perpendicular to the bottom, its ability to counteract external disturbances that influence its attitude effectively is crucial. The slower response of the PID algorithm to external disturbances caused the NS-MUV to collide with the bottom within ~1.2 s of initiating the movement (Fig. 6h). In contrast, the algorithm proposed in this study demonstrates a great capacity to identify and resist external disturbances; consequently, the NS-MUV continuously maintains a stable distance from the bottom (Fig. 6c).

Subsequent experiments involved testing the NS-MUV in a pool to assess its ability to maintain the distance between the vehicle and the bottom amid strong transient disturbances caused by falling weights. As the weights lack sufficient space to fall when they are too close to the bottom, it is necessary to appropriately distance the NS-MUV from the bottom. In order to apply these disturbances, tests were conducted in shallow water near the operator. Consequently, we replaced the control of the bottom distance with that of the NS-MUV depth during the experiment. As our objective was to validate the ability of the controller to resist external disturbances, the alteration in the control targets did not affect our logic for resisting external disturbances or the subsequent analysis of the performance of the control method.

A heavy block was affixed to the front end of the NS-MUV by using a rope. As the NS-MUV commenced its movement, the block descended, generating an impact load when the falling distance exceeded the rope length (Supplementary Video 1). This impact load comprises two components: an instantaneous torque owing to the force point at the front end of the NS-MUV and a perpendicular impact force to the bottom. Figure 6 illustrates the control effect of the NS-MUV when subjected to the impact of a 4 kg heavy block (~25% of the NS-MUV mass). During the test, the NS-MUV experienced two impacts: the first when the heavy block contacted the body, and the second when the block fell beyond the rope length. The interval between impacts was 0.65 s, after which the NS-MUV encountered continuous loading induced by the heavy block. The results indicate a minimal depth variation following the impacts, and the NS-MUV experienced a depth fluctuation of only 0.1 m under continuous loading. The NS-MUV successfully maintained its depth through continuous planning.

We analyzed the variation in NS-MUV depth under different impacts. Figure 7a shows the depth distribution of the NS-MUV 0.5 s after various impacts. Despite the different impacts experienced by the NS-MUV, the passive stability of the NS-MUV in the XOY plane ensures that, as long as the NS-MUV actively stabilizes its attitude under the influence of external disturbances, the transient impacts do not significantly affect NS-MUV depth. The test results illustrated that the boundaries of the depth distribution were consistently maintained between 0.02 m and 0.03 m.

Fig. 7: Anti-disturbance performance.
figure 7

a Depth distribution in 0.5 s after impact (number of data: 10, Mann–Whitney U test: mean and 25th to 75th percentiles). b Output torque as a percentage of maximum output torque for disturbances generated by 3 kg and 4 kg loads. The upper figure represents the torque distribution after the impact. The lower graphs I and II represent the torque distribution after the first and second impacts occur, respectively. fq represents pitch control force. c Angular velocity profiles in 0.5 s after different impacts generated by 3 kg and 4 kg loads. d Stability analysis of angular velocity after stabilization of 3 kg (number of data: 33,000) and 4 kg (number of data: 26,400) loads (Mann–Whitney U test: the median, mean, and 25th to 75th percentiles). Source data are provided as a Source Data file.

Full size image

After applying impact torque, the NS-MUV underwent angular acceleration, and the angular velocity continued to increase if the torque was not resisted. Based on the depicted angular velocity curves in Fig. 7c, it is evident that the controller effectively countered the increase in angular velocity during different impacts within the time interval of 0.04 s to 0.06 s. Among the impacts, the 4 kg (II) impact lasted the longest, with a resistance time of 0.06 s. On the other hand, the 4 kg (I) impact, which involved a heavy block directly impacting the body of NS-MUV without cushioning by rope, resulted in a less smooth response compared to the 3 kg and 4 kg (II) impacts, partly attributed to sensor noise, resulted in a slightly jittery angular velocity during the resistance process. Nonetheless, the angular velocity ceases to increase after 0.057 s following the occurrence of the impact.

Figure 7b plots the NS-MUV output torque, expressed as a percentage of the maximum output torque. From the torque distribution, the torque output required by the NS-MUV to resist its disturbance, even if the weight of the applied disturbance is stationary, accounts for 60–65% of the maximum torque that can be output. The fluctuation in torque is mainly due to the wobbling of the block during movement. At the moment of impact, the output torque of 4 kg (II) reached 100% momentarily, indicating that the instantaneous impact force exceeded the maximum torque capability of the thruster, which is probably the reason why it took the longest time to resist the increase in angular velocity at 4 kg (II).

Figure 7d shows the angular velocity statistics of the NS-MUV when the load was relatively stable. The data show that the 3 kg load data are mainly distributed in the range of −0.048–0.077 rad s−1, and the 4 kg load data are mainly distributed from −0.049 rad s−1 to 0.056 rad s−1. The angular velocity is relatively stable, and there is no sudden change due to the influence of the load.

The disturbance resistance algorithm presented in this paper is based on a proportional derivative (PD) controller that utilizes the estimated value of external disturbances as a feed-forward component to enhance the controller’s ability to counteract disturbances.

We conducted additional comparative tests using the adaptive algorithm54 and the PID controller, respectively (Supplementary Video 3). The adaptive algorithm utilizes both an adaptive term and tanh-sigmoid-surface control laws to enhance the controller’s anti-disturbance capabilities. The experimental results indicate that its response speed is significantly superior to that of the PID controller; specifically, with the adaptive controller, the time required for the pitch angle to stop decreasing after the disturbance was applied decreased from 1.23 s with the PID controller to 0.55 s. Additionally, the depth control error was also reduced. However, during the subsequent weight block stabilization stage, the adaptive algorithm exhibited substantial fluctuations in the pitch angle, ranging from −0.416 rad to 1.021 rad. In contrast, the algorithm presented in this paper showed much smaller fluctuations in pitch angle during the weight block stabilization stage, ranging from −0.025 rad to 0.198 rad, with the fluctuation amplitude of the adaptive algorithm being 7.16 times larger than that of our algorithm. Detailed data and an in-depth analysis of the experimental results are provided in Supplementary Note 6.

It is evident that, although the PD controller chosen for the disturbance resistance algorithm in this paper exhibits a slower control response compared to the tanh-sigmoid-surface control laws of the adaptive algorithm, it offers significant advantages in control stability by swiftly detecting and effectively compensating for external disturbances. The disturbance resistance algorithm described in this paper effectively stabilizes the pitch angle soon after exposure to transient strong disturbances, significantly reducing fluctuations in pitch angle and depth.

The experimental findings affirm the substantial robustness of the NS-MUV in controlling the distance between the body and the bottom. The proposed disturbance resistance algorithm markedly enhances the control robustness, preventing the external disturbance torque from affecting the forward direction of the NS-MUV and causing it to hit the bottom.

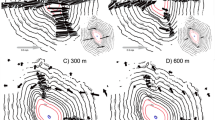
Field experiment

We assessed the NS-MUV capability of the NS-MUV to observe near-seabed in various terrains, including sandy-gravel terrain areas and rugged locations such as coral reef plates. Snapshots of these real environment tests are presented in Fig. 1, showing the ability of the NS-MUV to capture detailed information about the seabed, including sand grain texture and distinct color characteristics of coral reefs, through proximity observation. The NS-MUV demonstrated minimal disturbance to the bottom during observations in the sand-gravel substrate. Across multiple trials, NS-MUV maintained a proximity of no more than 20 cm from the seabed most of the time. Remarkably, despite this proximity, no disruption of sandy gravel by the NS-MUV was observed, thereby avoiding adverse impacts on the seabed environment during observation (Supplementary Video 1).

We assessed the robot’s capability to move through the various terrains in the real world (Supplementary Video 4). The robot is equipped with one degree of freedom for forward motion and another for steering, complemented by two additional degrees of freedom for rotation (pitch and roll). Our field experiments demonstrated that increasing these rotational degrees of freedom significantly enhances the robot’s ability to traverse rugged undersea terrains. The experiments were conducted with the driver utilizing camera feedback from the user interface to adjust the robot’s pose (Fig. 8a–d).

Fig. 8: Field terrain tracking.
figure 8

a Ascending along a sloping terrain. b Using roll motion to closely approach a sloped terrain. c Executing continuous pitch maneuvers to traverse undulating terrain. d Performing roll maneuvers to evade obstacles ahead. e Field scanning motion.

Full size image

The pitch degrees of freedom enable the robot to regulate its depth and facilitate rapid diving and ascent to a designated depth. During seabed observation missions, encountering elevated terrain is inevitable. By leveraging these pitch degrees of freedom, the robot can ascend steep terrain (Fig. 8a). Additionally, the ability to pitch is crucial for navigating continuous undulating terrain. As illustrated in Fig. 8c, the robot rapidly approaches the terrain and avoids obstacles within the undulating landscape through continuous pitching motions.

The robot’s roll degree of freedom enables it to navigate along inclined seabed walls by keeping its plane as parallel as possible to the terrain through roll motion (Fig. 8b). Additionally, this feature alters the collision relationship between the robot and the obstacle, enabling it to bypass the obstacle ahead without changing its forward direction. As illustrated in Fig. 8d, the robot avoids obstacles in its path through continuous rolling motions without altering its forward direction.

We executed the scanning task in a real undersea environment by pre-programming the speed (constant forward force) and direction, with the driver providing the desired altitude through camera feedback. As depicted in Fig. 8e, the primary challenge faced by the robot during task execution is the presence of undulating terrain. It is evident that the robot effectively utilizes its pitching degree of freedom to navigate and mitigate the impact of the undulating terrain on the task execution process. We analyzed the data from the scanning motion, identifying a maximum angular velocity of 0.91 rad s−1 when the robot encountered the undulating terrain shown in Fig. 9d. Furthermore, according to the pitching moment data in Fig. 9c, the peak pitching moment used by the robot during the scanning process was only 21.3% of the maximum pitching moment it can deliver. This indicates that the robot retains considerable pitch control force, which is sufficient for handling more complex terrains.

Fig. 9: Field scanning motion data.
figure 9

a PWM values of the propellers. b Yaw curves. c Pitch angle and pitch control force data. d Angular velocity data. Source data are provided as a Source Data file.

Full size image

Discussion

With the ongoing advancement of ocean observation, the significance of image information in seabed exploration has grown considerably. The richness of image data offers significant value for a variety of applications, including the detection of hydrothermal vents on the seabed55, the detection of minerals on the seabed56, environmental protection57, high-precision measurements of coral reef structure3, and the detection of plant health1.

The use of image information has significantly enhanced our understanding of the undersea world, and with the continuous advancement of technology, it is expected to play an even more central role in underwater observation in the future. However, we cannot overlook the impact of water refraction and scattering on image contrast and color accuracy, particularly for seabed state analysis based on image data. For example, in the coral reef pigmentation response, the attenuation of red light by the water column makes it challenging to detect PRS lesions, which typically appear bright pink1. Furthermore, water turbidity hampers the creation of high-precision topographic images through imagery3. The resolution decreases as smaller targets occupy fewer pixel dots due to the large distance from the target58. Additionally, the autonomous classification of biota based on underwater imagery results in diminished accuracy as the altitude of the imaging robot increases59. The primary factor influencing the extent of light refraction and scattering in water is distance. As the distance increases, the effects become more pronounced6. Therefore, a practical approach to mitigating these challenges is to minimize the robot’s distance from the seabed.

Among existing ocean observation robots, wheeled and legged types encounter significant challenges in rough terrains, where obstacles and sloped surfaces can hinder their functionality. In contrast, floating robots can navigate above challenging seabed terrain, but their operations near the seabed, especially during ascent, could disturb sediment. This disturbance often results in sediment resuspension, which obscures visibility.

This study introduced a maneuverable underwater robot configuration tailored for near-seabed observations, effectively addressing the aforementioned limitations. Our robot was meticulously designed to navigate a specified terrain swimming style, enabling the NS-MUV to closely examine the seabed and significantly minimize the impact of the propeller wake on sedimentation. As illustrated in Fig. 3, our robot could avoid propeller wake impacts on the seabed compared to a typical underwater machine. Leveraging the passive stability of the NS-MUV enhances its ability to withstand environmental disturbances without active power input, ensuring disturbance resistance without generating a wake perpendicular to the seafloor. Additionally, the passive stability compensates for inherent delays in the altitude control method outlined in this study, resulting in overall robustness in distance control. Active control of the distance between the NS-MUV and seabed is achieved by adjusting the angle between the fuselage and seabed planes. This control strategy not only allows for distance control but also avoids the impact of the wake on the seabed, ensuring optimal observation conditions. We successfully addressed the challenge posed by environmental disturbances in controlling the distance between the NS-MUV and the seabed, which enhances its practical applicability in real-world environments.

NS-MUV, such as rudder-propeller-driven underdriven robots, need to control their distance from the seabed by increasing their forward distance; when the wake currents are parallel to the seabed, NS-MUV can reduce the forward distance by more than seven times45,46. Naturally, applying rudder-propeller-driven underactuated vehicles can augment the rudder surface area to reduce forward distance, as observed in underwater gliders with substantial hydrofoils to enhance the lift-to-drag ratio60. However, it is imperative to note that an extensive rudder area decreases maneuvering precision, potentially leading to contact with the seabed owing to control instability.

In our real-world experiment, we did not observe a disturbance of the NS-MUV to the seabed sediments during its movement, as depicted in Fig. 1a, showing the capability of NS-MUV to approach the sand closely. The sea conditions at the test site were recorded, with wave heights of approximately 0.2–0.3 m and the distance between the robot and the water surface about 1.0–2.0 m. From the test results, the robot maneuvered in the near-seabed, unaffected by the surrounding flow field and contact with the seabed.

During our attempts to move away from the seabed, illustrated in Fig. 3j, the seabed sediment was unaffected by the wake generated by the NS-MUV. Our robot demonstrated a markedly distinct wake distribution compared to conventional underwater robots, as illustrated in Fig. 3b–d, k. This characteristic enables the NS-MUV to close to or move away from the seabed without perturbing the seabed sediments, thereby facilitating closer seafloor observation. Owing to the intrinsic limitations of the floating robot, specifically its inadequate fixed-point observation capability, an avenue for improvement can be pursued through additional research, which involves enhancing the NS-MUV with seabed habitat capability and leveraging the research foundation established in this study. The objective is to facilitate a seamless transition from a benthic state without disturbing seabed sediments, and this approach is anticipated to address the deficiencies in fixed-point observation capabilities.

During the actual environmental test, the NS-MUV demonstrated its capability to conduct close observations on diverse terrains with varying substrates. Even when faced with easily disturbed sandy gravel terrain, the NS-MUV completed observations without causing disruption, showcasing its minimal disturbance to the seabed environment. This study introduced an approach for near-seabed observations using a floating robot. The proficiency of the NS-MUV in traversing rugged terrains proves advantageous for detecting seabed environments. We have effectively addressed the challenges encountered by NS-MUV in close-proximity seabed observations, mitigating disturbances to seabed sediments and avoiding contact with the bottom influenced by the flow field.

This paper presents a robot specifically designed for near-seabed observation and introduces a floating robot that minimizes disturbance to seafloor sediments while maintaining the robot’s agility. The NS-MUV and its design concepts offer biologists enhanced seafloor exploration capabilities, including low-disturbance designs that facilitate the development of observation robots positioned closer to the seabed to improve image quality for various image-based seafloor observation missions, aiding biologists in distinguishing textures and colors. Simultaneously, a study shows that incorporating seabed texture information can improve terrain-matching navigation61, with image-based texture information yielding more detailed features than traditional sonar. Since global navigation satellite system (GNSS) signals are unavailable underwater the inertial navigation approach is prone to accumulate errors underwater62. Underwater localization base stations, such as short baseline (SBL) or ultrashort baseline (USBL) can provide specific positional information for robots; however, these devices are costly. One solution, simultaneous localization and map building (SLAM), improves the robot’s localization capabilities in GNSS-denied environments and is widely adopted. ORB-SLAM, which has been tested with mobile robots in various scenarios, has achieved promising results63. Nonetheless, integrating image data in SLAM to enhance accuracy remains challenging due to the effects of illumination and turbidity on underwater images64. The NS-MUV capabilities enhance image clarity, aiding in seabed positioning and advancing the autonomy of seabed observations. Moreover, optical information delivers significantly richer details than sonar, and a study has shown that LiDAR can enhance the classification of underwater ores65. NS-MUV’s ability to observe the seafloor at close range can help minimize light refraction and scattering underwater, which could facilitate the practical application of such research. This advancement potentially increases the efficiency and sustainability of marine resource exploration and management.

Methods

Mathematical modeling of robots

The following equation can represent the general model of underwater robots.

$${{\bf{M}}}\dot{{{\bf{v}}}}+{{\bf{C}}}({{\bf{v}}}){{\bf{v}}}+{{\bf{D}}}({{\bf{v}}}){{\bf{v}}}+{{\bf{g}}}({{\boldsymbol{\eta }}})={{\boldsymbol{\tau }}}+{{{\boldsymbol{\tau }}}}_{{{\bf{d}}}{{\bf{i}}}{{\bf{s}}}}$$
(1)

where \({{\bf{M}}}\) denotes the inertia matrix; \({{\bf{C}}}({{\bf{v}}})\) represents the Coriolis matrix; \({{\bf{D}}}({{\bf{v}}})\) is the damping matrix; \({{\bf{g}}}({{\boldsymbol{\eta }}})\) represents the restoring force matrix; \({{\boldsymbol{\tau }}}\) represents the control force; \({{{\boldsymbol{\tau }}}}_{{{\bf{d}}}{{\bf{i}}}{{\bf{s}}}}\) represents the force of the external environment acting on the robot;\({{\bf{v}}}={[u,p,q,r]}^{T}\) represents the parameters associated with the velocity and angular velocity of the robot; and \({{\boldsymbol{\eta }}}={[\phi,\theta,\psi ]}^{T}\) represents the attitude angle of the robot. The following equation represents the conversion relationship between the output force of the thruster and the control force of the robot:

$$\left[\begin{array}{c}X\\ K\\ M\\ N\end{array}\right]=\left[\begin{array}{cccc}\cos \delta & \cos \delta & \cos \delta & \cos \delta \\ -R\,\sin \delta & R\,\sin \delta & R\,\sin \delta & -R\,\sin \delta \\ \frac{h}{2}\,\sin \delta & -\frac{h}{2}\,\sin \delta & \frac{h}{2}\,\sin \delta & -\frac{h}{2}\,\sin \delta \\ R\,\cos \delta & R\,\cos \delta & -R\,\cos \delta & -R\,\cos \delta \end{array}\right]\left[\begin{array}{c}{F}_{1}\\ {F}_{2}\\ {F}_{3}\\ {F}_{4}\end{array}\right]$$
(2)

where \(\delta\) is the angle of the central axis of the ipsilateral thruster, R is the distance between the left and right propellers, and h is the distance from the central axis of the ipsilateral thruster. X represents the output force along the x-axis of the body coordinate system, and K, M, and N represent the torques of the body coordinate systems x, y, and z, respectively. \({F}_{1},{F}_{2},{F}_{3},{F}_{4}\) represent the thruster output force.

Calculate angular acceleration

During the observation of angular acceleration, the data obtained from the three IMUs of the robot are collected and labeled as follows: IMU (1) is denoted as \({{{\boldsymbol{\varsigma }}}}_{{{\bf{1}}}}={[p,q,r]}^{T}\), IMU (2) as \({{{\boldsymbol{\varsigma }}}}_{{{\bf{2}}}}={[{a}_{z},q,{a}_{y}]}^{T}\), and IMU (3) as \({{{\boldsymbol{\varsigma }}}}_{{{\bf{3}}}}={[p,{a}_{z},r]}^{T}\). In the observation of angular acceleration, the sampling rate for all three IMUs is 200 Hz. IMU (1) collects angular acceleration data denoted as \({\dot{{{\boldsymbol{\omega }}}}}_{{{\bf{1}}}}={[\dot{p},\dot{q},\dot{r}]}^{T}\), IMU (2) collects angular acceleration data denoted as \({\dot{{{\boldsymbol{\omega }}}}}_{{{\bf{2}}}}={[{a}_{z}/\lambda,\dot{q},{a}_{y}/\lambda ]}^{T}\), and IMU (3) collects angular acceleration data denoted as \({\dot{{{\boldsymbol{\omega }}}}}_{{{\bf{3}}}}={[\dot{p},{a}_{z}/\lambda,\dot{r}]}^{T}\). The angular acceleration after filtering is denoted by \(\dot{{{\boldsymbol{\omega }}}}={{{\bf{p}}}}_{{{\bf{1}}}}{\dot{{{\boldsymbol{\omega }}}}}_{1}+{{{\bf{p}}}}_{{{\bf{2}}}}{\dot{{{\boldsymbol{\omega }}}}}_{2}+{{{\bf{p}}}}_{{{\bf{3}}}}{\dot{{{\boldsymbol{\omega }}}}}_{3}\), where \({{{\bf{p}}}}_{\ast }\) represents the filtering parameter. The value of \({{{\bf{p}}}}_{\ast }\) is determined using a least-squares-based filtering method.

Static water environment data collection

We collected data for an underwater robot in a static water environment to investigate the relationship between the angular acceleration and thruster output, angular velocity, and attitude angle. The data collection process involved the robot rotating along its x, y, and z axes and moving along the x-axis within the water pool. During these movements, various parameters were collected, including the angular acceleration measured by sensors, PWM values of the thrusters, angular velocity, and attitude angle. This data collection aimed to establish an underwater model for the robot under still-water conditions. Under such conditions, the general model of an underwater robot can be simplified to the following equation, owing to the absence of external environmental forces:

$${{\bf{M}}}\dot{{{\bf{v}}}}+{{\bf{C}}}({{\bf{v}}}){{\bf{v}}}+{{\bf{D}}}({{\bf{v}}}){{\bf{v}}}+{{\bf{g}}}({{\boldsymbol{\eta }}})={{\boldsymbol{\tau }}}$$
(3)

In this formulation, as none of the parameters of the robot have been pre-modeled for \({{\bf{M}}}\), \({{\bf{C}}}({{\bf{v}}})\),\({{\bf{D}}}({{\bf{v}}})\),\({{\bf{g}}}({{\boldsymbol{\eta }}})\), they are all unknown. Despite their unknown nature, we can derive the following characterization relationship:

$$\dot{{{\bf{v}}}}={{{\bf{M}}}}^{-1}{{\bf{f}}}({T}_{1},{T}_{2},{T}_{3},{T}_{4})-{{{\bf{M}}}}^{-1}{{\bf{C}}}({{\bf{v}}}){{\bf{v}}}-{{{\bf{M}}}}^{-1}{{\bf{D}}}({{\bf{v}}}){{\bf{v}}}-{{{\bf{M}}}}^{-1}{{\bf{g}}}({{\boldsymbol{\eta }}})$$
(4)

where \({{\boldsymbol{\tau }}}={{\bf{f}}}({T}_{1},{T}_{2},{T}_{3},{T}_{4})\) represents the mapping between the PWM output of the thruster and the control force \({{\boldsymbol{\tau }}}\) exerted on the body. The offline learning stage of the robot model can be defined based on the following characterization equation:

$$\dot{{{\bf{v}}}}={{\bf{H}}}({T}_{1},{T}_{2},{T}_{3},{T}_{4},{{\bf{v}}},{{\boldsymbol{\eta }}})$$
(5)

According to the aforementioned requirement, during the offline learning phase, it is necessary to gather information on the parameter \(\dot{{{\bf{v}}}},{{\bf{v}}},{{\boldsymbol{\eta }}}\) and PWM value \({T}_{\ast }\) of the thruster. The robot operated at a control frequency of 50 Hz, which coincided with a sampling frequency of 50 Hz for data collection. Because the IMU had a return frequency of 200 Hz, at least four IMU readings were recorded within each sampling cycle. The average of this dataset is computed and used as the IMU output for a particular control cycle. After gathering the data, we establish a suitable fit for the kinetic model depicted in Eq. 5. The specific methods are as follows, we collect data on the three rotational degrees of freedom concerning PWM input values, attitude angles, angular velocities, and angular accelerations in a static water environment. A classical underwater dynamics model is then used to determine the relationship between each dynamic parameter and the robot’s state66 (identification results are provided in Supplementary Note 1). Subsequently, the robot’s dynamic parameters obtained through least-squares fitting serve as the foundation for observing external disturbances.

Planning algorithm for altitude maintenance

The altitude maintenance of a robot can be partitioned into two components: attitude and velocity planning. Attitude planning is utilized to determine the motion direction of the robot, whereas velocity planning addresses the issue of ensuring that the altitude changes as anticipated following the determination of the motion direction. The velocity vector of the robot in the body coordinate system is denoted by \({{\bf{n}}}={[{n}_{x},0,0]}^{T}\), and the corresponding velocity of the robot in the world coordinate system is denoted by \({{{\bf{V}}}}_{{{\bf{c}}}}={[{v}_{x},{v}_{y},{v}_{z}]}^{T}\). The transformation relationship between the coordinate systems is given by \({{{\bf{V}}}}_{{{\bf{c}}}}={{\bf{J}}}{{\bf{n}}}\), where \({{\bf{J}}}\) represents a transformation matrix.

$${{\bf{J}}}=\left[\begin{array}{ccc}c\psi c\theta & -s\psi c\phi+c\psi s\theta s\phi & s\psi s\varphi+c\psi c\phi s\theta \\ s\psi c\theta & c\psi c\phi+s\phi s\theta s\psi & -c\psi s\phi+s\theta s\psi c\phi \\ -s\theta & c\theta s\phi & c\theta c\phi \end{array}\right]$$
(6)

where s and c stand for sin and cos, respectively. From the attitude perspective, we can determine the robot speed \({v}_{z}=-{n}_{x}s\theta\) on the z axis of the world coordinate system. Evidently, the speed, which determines the tendency of increasing or decreasing altitude, only depends on the attitude angle \(\theta\). Therefore, it is sufficient to focus on planning for the attitude angle \(\theta\) to control the altitude. We map the altitude error derror onto \(\theta\). Considering that \(sin(\theta )\approx arctan(\theta )\) when \(\theta\) is small and \(sin(\theta )=arctan(\theta )\) when \(\theta=0\) and that the range of the arctangent function is \((-\pi /2,\pi /2)\), which precisely corresponds to situations where the altitude error is excessively large, the robot can reach the specified altitude through either vertical ascent or descent. We design the attitude planning function as\({\theta }_{dir}=\arctan (k{d}_{error})\), where k is a positive real number. Varying the value of k can determine the level of aggressiveness in tracking the specified altitude.

The speed control of the robot can also be determined based on altitude error. A desired base speed exists when the robot is in motion. However, when a robot encounters external disturbances, it may be unable to adjust its altitude by running at the desired speed. In such cases, the robot must plan its speed based on the altitude error. The planning amount was then added incrementally to the base speed as compensation. The planning amount is determined by

$$\Delta v={k}_{p}{d}_{error}(t)+\sum _{j=1}^{t}{k}_{i}{d}_{error}(j)$$
(7)

where \({d}_{error}(t)\) represents the accumulated altitude error at the given moment t, \({k}_{i}\) represents the gain coefficient, \({k}_{p}\) represents the integration coefficient. Detailed proof of Eq. (7) is provided in the Supplementary Note 4.

Anti-disturbance algorithms

We separate the components of the attitude controller to be utilized for disturbance resistance, and the specific logic of the algorithm is as follows:

Algorithm 1:

Anti-disturbance algorithm

Input: Desired altitude \(D\); Actual altitude \(d\); Actual observed angular acceleration \(\dot{\omega }\); Predicted angular acceleration \(\dot{\hat{\omega }}\)

Output: Velocity correction \(\varDelta v\); Attitude error increment \(\hat{\phi },\hat{\theta },\hat{\psi }\)

1: Start moving

2: Start observing \(\dot{\omega },\hat{\dot{\omega }}\)

3: while: (abs(\(\dot{\omega }-\hat{\dot{\omega }}\)) > \({\dot{\omega }}_{\min }\) or abs(\(D-d\)) > \(\beta\)) do

4: if abs(\(\dot{\omega }-\hat{\dot{\omega }}\)) > \({\dot{\omega }}_{\min }\) and abs(\(D-d\)) >\(\beta\) then

5: Start planning \(\Delta v\) and \(\hat{\phi },\hat{\theta },\hat{\psi }\)

6:else if abs(\(\dot{\omega }-\hat{\dot{\omega }}\)) > \({\dot{\omega }}_{\min }\) and abs(\(D-d\)) \(\le\) \(\beta\) then

7:Start planning \(\hat{\phi },\hat{\theta },\hat{\psi }\)

8:end if

9: end while

\({\dot{\omega }}_{\min }\) and \(\beta\) denote the thresholds for angular acceleration error and depth error, respectively, serving as decision conditions for the anti-disturbance algorithm. We decoupled the partial output force of the attitude controller for use as the disturbance resistance. The logic of decoupling is as follows: First, the attitude controller utilizes PD control, where the control force is characterized as follows: \({{{\boldsymbol{\tau }}}}_{Attiude}=-{{\bf{K}}}({{\bf{s}}}+\hat{{{\boldsymbol{\eta }}}})-{{{\bf{K}}}}_{{{\bf{D}}}}\dot{{{\bf{s}}}}\), where\(\hat{{{\boldsymbol{\eta }}}}={[\hat{\phi },\hat{\theta },\hat{\psi }]}^{T}\), where\({{\bf{K}}}\) represents the matrix associated with the gain coefficients, \({{{\bf{K}}}}_{{{\bf{D}}}}\) represents the matrix associated with the differential coefficients. \({{\bf{K}}}=diag({K}_{1},{K}_{2},{K}_{3})\),\({{{\bf{K}}}}_{{{\bf{D}}}}=diag({K}_{D1},{K}_{D2},{K}_{D3})\), \({{\bf{s}}}={[\tilde{\phi },\tilde{\theta },\tilde{\varphi }]}^{T}\) represents attitude error, \({{{\boldsymbol{\tau }}}}_{{{\bf{c}}}}=-{{\bf{K}}}{{\bf{s}}}-{{{\bf{K}}}}_{{{\bf{D}}}}\dot{{{\bf{s}}}}\). The specific planning algorithm for \(\hat{{{\boldsymbol{\eta }}}}\) can be arranged as follows. In model \(\dot{{{\bf{v}}}}={{\bf{H}}}({T}_{1},{T}_{2},{T}_{3},{T}_{4},{{\bf{v}}},{{\boldsymbol{\eta }}})\), the angular acceleration error can be calculated using the observed actual angular acceleration data \(\dot{{{\boldsymbol{\omega }}}}\) and the predicted angular acceleration \(\hat{\dot{{{\boldsymbol{\omega }}}}}\) obtained from the model. Because the angular acceleration is correlated with the instantaneous torque, the angular acceleration error can signify the error that exists prior to the external disturbance \({{{\boldsymbol{\tau }}}}_{d}\) and attitude control force \({{{\boldsymbol{\tau }}}}_{c}\). We plan to conduct \(\hat{{{\boldsymbol{\eta }}}}\) using the following equation:

$$\hat{{{\boldsymbol{\eta }}}}(k+1)=\left\{\begin{array}{cc}\hat{{{\boldsymbol{\eta }}}}(k)+{\int }_{0}^{{t}_{\max }}\rho ({{{\boldsymbol{\tau }}}}_{d}-{{{\boldsymbol{\tau }}}}_{c})dt \quad t > {t}_{\max } \hfill \\ \hat{{{\boldsymbol{\eta }}}}(k)+{\int }_{0}^{t}\rho ({{{\boldsymbol{\tau }}}}_{d}-{{{\boldsymbol{\tau }}}}_{c})dt \quad {\int }_{0}^{t}\rho ({{{\boldsymbol{\tau }}}}_{d}-{{{\boldsymbol{\tau }}}}_{c})dt > {\hat{{{\boldsymbol{\eta }}}}}_{{{\bf{m}}}{{\bf{a}}}{{\bf{x}}}} \end{array}\right.$$
(8)

where\(\rho\) is a positive real number, and \({\hat{{{\boldsymbol{\eta }}}}}_{{{\bf{m}}}{{\bf{a}}}{{\bf{x}}}}={[{\eta }_{1},{\eta }_{2},{\eta }_{3}]}^{T}\) refers to the maximum allowable increment for individual planning, which serves as a mechanism to expedite loop termination and effectively address impact loads. \({t}_{\max }\) denotes the temporal interval of individual planning.

Statistics and reproducibility

We utilize boxplots and interval plots to analyze control stability and assess differences in data distribution across algorithms. In boxplots, the thick horizontal line represents the median; the box extends to the upper and lower quartile; the upper/lower whiskers extend to the maximal/minimal observation that falls between the upper/lower quartile and 1.5 times the interquartile range; circles represent outliers, that is observations that fall beyond the whiskers. Notches on the box represent a 95% confidence interval on the median. In interval plots, the upper/lower whiskers extends to the maximal/minimal observation that falls between the upper/lower quartile and 1.5 times the interquartile range, circles represent mean.

All the algorithm’s control parameters are detailed in Supplementary Table 3.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.