Introduction

Oceanus Procellarum, the largest mare on the Moon’s near side, is characterized by extensive basaltic plains and significant volcanic activity1. Uncovering its subsurface structures is pivotal for understanding lunar volcanism. Gravity data, which have played a crucial role in studying magma plumbing systems on rocky planets and satellites2,3,4,5,6, provide the ideal tool for such an investigation of Oceanus Procellarum. Forward modeling and inversion of gravity anomaly data enable the creation of density models of various magmatic structures that exhibit a density contrast with the surrounding rocks, such as shallow intrusions7,8,9, magmatic-related deposits10, and plutons11,12. Data from NASA’s Gravity Recovery and Interior Laboratory (GRAIL) mission have generated a high-resolution global map of the Moon’s gravity field. By modeling the gravity field to a spherical harmonic degree and order of 1200, a spatial resolution of 4.5 km by 4.5 km at the Moon’s equator was achieved13,14. Combined with topographic data from the Lunar Orbiter Laser Altimeter (LOLA), these data aid the detection of small-scale features such as dykes7, ancient igneous intrusions3, buried impact craters15, and empty lava tubes16,17.

The volcanic legacy of the Oceanus Procellarum is exemplified by the Marius Hills volcanic complex (MHVC), a 35,000 km2 plateau, which exhibits the densest concentration of extrusive volcanic features on the Moon in the form of volcanic domes/shields and cones18,19. This region has consistently emerged as a prominent site for lunar exploration, primarily due to its distinctive geological characteristics and the valuable insights it offers into lunar volcanism20,21,22,23. Utilizing gravity data from the Lunar Prospector spacecraft24 and the GRAIL mission25,26, two quasi-circular, positive gravity anomalies within the MHVC (north and south) were identified and modeled as two massive sill/dyke groups that are responsible for the volcanic activity in this region. Investigation into the surface distribution of volcanic vents confirms the presence of the zones of magma accumulation27. However, magmatic structures beneath the MHVC and surrounding areas and processes by which magma is transported to the shallow crustal depths remain enigmatic to date28,29.

GRAIL gravity data revealed a pattern of narrow linear anomalies that border the Procellarum KREEP Terrane (PKT)5. The source of anomalies is interpreted to be solidified lava within rifts and the feeder dykes beneath them, which likely served as the magma plumbing system for much of the nearside mare volcanism. The MHVC is positioned roughly 200 km east of the PKT’s western border structures. Previous research has primarily examined these volcanic systems independently5,24,25,26,27,30, overlooking the critical magmatic structures between them and their collective impact on volcanism in the Oceanus Procellarum. This oversight underscores a significant gap in our understanding of the magmatic architecture beneath the MHVC and the PKT’s western border, highlighting the importance of considering these systems as interconnected entities to comprehend the extensive volcanic activity fully in the Oceanus Procellarum region.

In this work, to better understand the magmatic architecture beneath the Oceanus Procellarum, we apply a three-dimensional (3D) inversion technique to the GRAIL gravity data to construct detailed 3D density models. The magmatic structures, characterized by higher density than the host rocks, can be recovered through the inversion of the Bouguer gravity anomaly, which plays a key role in understanding the magmatic sources and processes2,7,9,31. This study encompasses the southern and northern MHVC, the western border structures of the PKT, and their neighboring areas, enabling a comprehensive understanding of their interconnections, and facilitating their integration into the wider PKT region. The detailed modeling of these magmatic structures provides valuable information regarding the formation of volcanic landforms, magma transport, and energy exchange across various lunar systems.

Results

Bouguer gravity data and topography

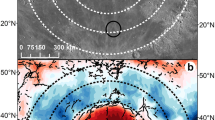
Figure 1a shows the topography of the lunar nearside derived from the MoonTopo2600p model based on data collected by the Lunar Reconnaissance Orbiter mission32. GRAIL gravity data extracted from the GRGM1200B model13 were used for this study. The Bouguer gravity anomaly (Fig. 1b) used for imaging the subsurface structures was derived from SHTools33 with a reference radius of 1738 km. To remove the gravitational contribution of the surface topography, a crust density of 2800 kg/m3 was used for Bouguer correction34. To eliminate long-wavelength variations in the crustal structure and short-wavelength noise, we filtered the Bouguer gravity data to include data between degree and order 7 and degree and order 660, yielding a half-wavelength surface resolution of ~8 km. A cosine taper was implemented between degrees 550 and 660 to reduce high-frequency ringing35.

Fig. 1: Topographic and gravity features of the lunar nearside.
figure 1

a Topography and b GRAIL gravity anomaly map shown with an azimuthal equal-area projection. The topography is derived from the MoonTopo2600p model32,97 and the GRAIL gravity data were extracted from the GRGM1200B model13. Both the topography and gravity models are referenced to a lunar sphere radius of 1738 km. A crust density of 2800 kg/m3 was used for the Bouguer correction. Bouguer gravity data were filtered to include data between degree and order 7 and degree and order 660 to eliminate long-wavelength variations in the crustal structure and short-wavelength noise. The solid black polygons indicate the locations of two study areas labeled as A and B. Procellarum KREEP Terrane (PKT) boundary (black dotted line) is according to Jolliff et. al.98 corresponding to the areas that incorporate most pixels that have >3.5 ppm Th.

Full size image

Study area A (Fig. 1) covers the MHVC and partial western border structures of the PKT5. The Bouguer gravity anomaly (Figs. 1b and 2b) reveals two quasi-circular mass anomalies, marked as Marius-NH (northern half) and Marius-SH (southern half) based on their locations relative to the Marius crater26. The two anomalies exhibit maximum amplitudes of 165 and 169 mGal, respectively. Marius Hills plateau, corresponding to the northern anomaly, contains most domes and cones situated in a localized highland. In contrast, the southern anomaly covers fewer volcanic domes without elevated topography. A narrow linear positive gravity anomaly, ranging from ~40 to ~70 mGal, connects these two quasi-circular anomalies, forming a “bridge” that has been identified in an earlier study24. Furthermore, a significant high-gravity anomaly belt, spanning ~800 km with a NNW–SSE orientation and peaking at 183 mGal, is identified. This belt has been interpreted to be part of the magmatic border structures of the PKT region5. The linear gravity anomaly extends NNW and diverges into three thinner branches at the northwestern border of the PKT (Figs. 1b and 3b). Study area B (Figs. 1 and 3a, b) includes the western and middle branches of the northwestern border, each marked by distinct linear gravity anomalies with a general NNW–SSE orientation, spanning over 500 km and displaying values from ~30 to 138 mGal. The western edges of the belt gravity anomalies (Figs. 2b and 3b) are generally coincident with steep topographic gradients leading up to the adjacent highlands (Figs. 2a and 3a), while their eastern sides show less topographical correlation. Prominent wrinkle ridges (Supplementary Fig. 1) run parallel to the belt gravity anomaly in study area A and the belt gravity anomalies of the middle and eastern branches in study area B, exhibiting a NNW–SSE orientation. Also, a distinct set of wrinkle ridges (Supplementary Fig. 1) traversing the Marius Hills region predominantly adheres to this NNW–SSE trend36.

Fig. 2: Gravity anomaly features of study area A.
figure 2

a Topography and b GRAIL Bouguer gravity anomaly map shown with an equidistant cylindrical projection. c Iso-surface map of the high-density anomalies from the 3D inversion. d Iso-surface map of the high-density anomalies at the northern MHVC (Marius Hills volcanic complex). e Iso-surface map of the high-density anomalies at the southern MHVC. The location of study area A is indicated by solid black polygons in Fig. 1. The red surfaces in (c)–(e) indicate the density contrast iso-surface of 160 kg/m3, which outlines high-density anomalies and is interpreted as magmatic bodies. The yellow surfaces depict a density contrast iso-surface of 350 kg/m3 to delineate the even denser magmatic bodies. Marius-NH (northern half) and Marius-SH (southern half).

Full size image
Fig. 3: Gravity anomaly features of study area B.
figure 3

a Topography and b GRAIL Bouguer gravity anomaly map shown with an equidistant cylindrical projection. c Iso-surface map of the high-density anomalies from the 3D inversion. d Iso-surface map of the high-density anomalies beneath the Briggs B and Lichtenberg craters. e Iso-surface map of the high-density anomalies beneath the Seleucus crater. The location of study area B is indicated by solid black polygons in Fig. 1. The red surfaces in (c)–(e) indicate the density contrast iso-surface of 160 kg/m3, which outlines high-density anomalies and is interpreted as magmatic bodies. The yellow surfaces depict a density contrast iso-surface of 350 kg/m3 to delineate the even denser magmatic bodies. The symbols “I, II, III, IV, V” in (c) represent distinct magma chamber compartments. These compartments are inferred to have gradually interconnected at higher levels during the filling process.

Full size image

3D inversion density models from Bouguer gravity data

The 3D inversion technique applied here is based on the probabilistic method37 to generate 3D density models by inverting gravity data. The method was assessed and proven successful in identifying the density structures of both the upper and lower crust of the Earth9,38,39,40,41,42,43,44. A significant advantage of this inversion approach is its capacity to integrate a priori information regarding physical properties, spatial extent, depth, and orientation of the source bodies via the covariance matrix to construct an accurate and reliable solution. To address the non-uniqueness inherent in the inversion process, we performed a sensitivity analysis on several critical parameters that could affect the inversion results, including the covariance matrix parameter, the depth weighting function, and the depth extent of the inversion domain (see “Methods” section for more details).

Figures 2c–e and 3c–e display the 3D density models for the two study areas, which represent optimal models obtained from inversions using the best-fitting parameters (see “Methods” section for more details). The 3D density models recovered from the Bouguer gravity data with a half-wavelength surface resolution of ~8 km facilitate the investigation of complex subsurface magmatic structures in detail. Given the geological evidence for potential intrusive activity24,25,27, the 3D continuous density inversions are volumed-rendered using discrete cutoffs to delineate the extent of possible intrusive bodies. The red surfaces indicate the density contrast iso-surface of 160 kg/m3, which outlines high-density bodies that we interpret as magmatic bodies. The yellow surfaces depict a higher density contrast iso-surface of 350 kg/m3 to delineate even denser magmatic bodies. The top depth corresponds to either the shallowest limit of the magmatic bodies or the deepest extent of impact brecciation, where the density contrast fades. The bottom depth denotes the base of the magmatic bodies or where the density contrast with surrounding rocks significantly diminishes. Figures 4 and 5 show horizontal and vertical cross-sections through the inverted density models for the two study areas. The blue dashed lines indicate the 160 kg/m3 density contrast contour lines. The assumed density contrast iso-surface of 160 kg/m3 for the magmatic body does not consider potential density changes amongst the magmatic rocks, and could over- or underestimate the size and depth of the magmatic bodies and thus presents a limitation and potential source of error in interpretation. When using the iso-surfaces of 150 and 170 kg/m3 as the interpreted magmatic bodies, the total volume increases by 5% and decreases by 6%, respectively, compared to the 160 kg/m3 iso-surfaces.

Fig. 4: Horizontal and vertical sections of the inverted 3D density model for study area A.
figure 4

a–c Horizontal slices at depths of 3.5, 5.5, and 10 km. d–i Vertical depth slices. The locations of the vertical depth slices are indicated by black dotted lines in (a)–(c). The blue dashed lines in (a)–(i) correlate with the 160 kg/m3 density contrast contour line, which is taken to be the magmatic body surfaces. The vertical axis is exaggerated by a factor of 10 relative to the horizontal axis. PKT Procellarum KREEP Terrane, Marius-NH (northern half), Marius-SH (southern half).

Full size image
Fig. 5: Horizontal and vertical sections of the inverted 3D density model for study area B.
figure 5

a–c Horizontal slices at depths of 3.5, 5.5, and 10 km. d–g Vertical depth slices. The locations of the vertical depth slices are indicated by black dotted lines in (a)–(c). The blue dashed lines in (a)–(i) correlate with the 160 kg/m3 density contrast contour line, which is taken to be the magmatic body surface. The vertical axis is exaggerated by a factor of 10 relative to the horizontal axis. The symbols “I, II, III, IV, V” in (a)–(c) represent distinct magma chamber compartments.

Full size image

Figures 2c, 3c, 4, and 5 exhibit distinct belt structures oriented NNW–SSE with density contrasts ranging from 160 to ~700 kg/m3. These belt structures correspond to the belt gravity anomalies depicted in Figs. 2b and 3b and match the PKT border magmatic intrusions as identified in a previous study5. We observe that the density contrast of the intrusions from the inversion gradually decreases from the center to the edges. This is mainly due to the smoothing nature of the inversion method used44; the actual density contrast variation within the intrusions may not be as pronounced. The density model for area A (Figs. 2c and 4) shows that the border intrusion spans from near the surface down to depths of 10–13 km with a length of ~800 km, a thickness of 8–11 km, and a width of 130–270 km. In study area B, the western branch intrusion is ~600 km in length, ~140 km in width, and ~8–10 km in thickness, and the middle branch intrusion is about 550 km long, 80 km wide, with a thickness ranging from 5 to 9 km. The western PKT border intrusions become thinner and narrower, and the depth of the top surface increases toward the north.

The inversion density model indicates that the Marius-NH intrusion (Figs. 2d and 4f, h) and Marius-SH intrusion (Figs. 2e and 4e, h), reported in the literature24,25, extend down to depths of 11 and 12 km, with thicknesses of 10.2 and 9.7 km, respectively. The Marius-NH body spans ~100 km in diameter, while the Marius-SH body spans ~130 km. The density contrasts of these two intrusions lie between 160 and 720 kg/m3, with the maximum value in the upper center of the intrusions. Both intrusions have a bowl-like shape. Moreover, a significant magmatic body (located at 55.7° W, 12.9° N; see Figs. 2c, d and 4a, b, f) characterized by a quasi-circular configuration is located adjacent to the west of the Marius-NH intrusion. This body has a diameter of ~90 km, a thickness of ~6 km, and is positioned beneath the more subdued western inclines of the elevated Marius Hills plateau. A magmatic body (located at 55.3° W, 6.3° N; see Figs. 2c, e and 4a, b, e) of similar dimensions, with a diameter of ~80 km and a thickness of ~5 km, is identified. The intrusion is located directly beneath the Reiner crater at a shallow depth (3.5 km; Fig. 4a) and tilts slightly southwestward at a deeper depth (5.5 km; Fig. 4b). Both of these two magmatic bodies were neither discovered nor mentioned in previous studies15,24,25,26.

It is noteworthy that the inversion density model for study area A (Figs. 2c and 4) reveals a complex network of connectivity among the various volcanic systems under investigation. The Marius-NH and Marius-SH intrusions are interconnected with a narrow corridor of dense rocks extending ~80 km in length, 50 km in width, and 5 km in thickness (Figs. 2c and 4a, b, h). The narrow corridor is sill-like in structure and nearly horizontal. Furthermore, another two sill-like narrow corridors connect the two intrusions with the western border structures. The southern magmatic conduit, which traverses the intrusion beneath the Reiner crater, is ~130 km long, 50 km wide, and 5 km thick (Figs. 2c and 4a, b, e). The northern magmatic conduit, crossing the quasi-circular intrusion adjacent to the west side of the Marius-NH intrusion, measures ~110 km in length, 55 km in width, and 6 km in thickness (Figs. 2c and 4a, b, f).

A lower density of 2560 kg/m3 and a higher density of 3000 kg/m3 were also used for Bouguer corrections to derive the Bouguer anomalies, which were then inverted to construct density models, as detailed in Supplementary Fig. 2. The impact of conducting the Bouguer correction using different density values on the resultant Bouguer gravity anomaly is especially pronounced in regions with significant terrain variations, such as the Reiner crater (Supplementary Fig. 3a) and Marius-NH (Supplementary Fig. 4a). The higher density of 3000 kg/m3 yields the best-fit Bouguer correction for the craters (Supplementary Fig. 3a), which is similar to the mean density estimated for the mare45 (~3090 kg/m3) and the bulk density estimated for the Marius Hills surface basalts (3150 kg/m3) based on observations from the Lunar Prospector Gamma Ray Spectrometer46,47. However, it also significantly enhances the western belt gravity anomalies (Supplementary Fig. 3a) due to the relatively low topography in that area. Ultimately, we opted for a density of 2800 kg/m3 as a more representative choice for the entire region. The comparison of inversion models (Supplementary Fig. 2) shows that as the Bouguer correction density is increased, there is a slight increase in the volume of the western PKT border intrusion in study area A and the western branch in study area B. Conversely, the volumes of the middle branch intrusion in study area B, the Marius-NH intrusion, and the sill-like narrow corridors identified above decrease slightly. However, these effects are limited, and the main structural characteristics of the high-density bodies in this region exhibit highly consistent geometries.

To minimize the potential influence of crustal thinning on the inversion models, which is characterized by relatively long-wavelength positive gravity signals, we filtered signals with wavelengths <11 degrees (Supplementary Fig. 5a,c), and a subsequent 3D inversion was performed. The inversion results (Supplementary Fig. 5b, d) indicate a modest reduction in the lateral spread of the PKT border structures and a 2–3 km shallowing of their bases. These two inversion models may more accurately reflect the border structures by removing the effect of crustal thinning. Nevertheless, we observed reduction in both the volume and maximum density contrast of the intrusions beneath Marius-SH and Marius-NH as well as the sill-like narrow corridors (Supplementary Figs. 3e, 4e, and 5b), where mantle uplift is deemed improbable24,25,48,49. Moreover, the middle branch structures of the northwestern border become discontinuous (Supplementary Fig. 5d). Thus, it seems that filtering out gravity signals lower than degree and order 11 has simultaneously affected the long-wavelength signals associated with shallow sources.

Beyond study areas A and B, we also examined the Flamsteed region (labeled as C in Supplementary Fig. 1) and the Aristarchus plateau region (labeled as D in Supplementary Fig. 1) within the Oceanus Procellarum. These features were also analyzed, though the interpretation of magmatic structures remains uncertain. However, neither the southern Aristarchus plateau nor the Flamsteed region appears to connect with the western PKT border intrusions. As a consequence, our discussion is focused on the inversion models (Figs. 2–5) in study areas A and B, which are derived from the Bouguer gravity data spanning from degree and order 7 to degree and order 660, following Bouguer correction with a crust density of 2800 kg/m3.

Discussion

Our research utilizing 3D density models, derived from the inversion of GRAIL Bouguer gravity data, has unveiled a complex magmatic architecture beneath the Procellarum Oceanus region. This intricate architecture reveals significant connectivity between the northern and southern magmatic intrusions beneath the MHVC and the PKT border magmatic structures. Our findings indicate an extensive network of magmatic connectivity beneath Oceanus Procellarum, which was previously unidentified and warrants further investigation and explanation.

The magmatic evolution of the Marius Hills region was suggested to have extended over a prolonged period, characterized by early edifice-forming and later mare-forming episodes19,50,51,52. Recent research has mapped these mare flows on the plateau, with age estimates ranging from ~3.3 to 1.0 Gyrs (billion years ago)50,53,54,55. The Marius-SH and Marius-NH were suggested to be impact craters that have been buried by mare basalt and/or impact ejecta due to the circularity of the positive Bouguer gravity anomaly15. Other researchers24,25 indicated that extra high-density material is necessary in order to explain the large amplitude of the two positive gravity anomalies. The two main zones of high-density material were interpreted as the magma chambers that fed the overlying volcanism24. Some researchers suggested from forward modeling that a total thickness of ~10 km, with a density contrast of 350 kg/m3, is needed for a sill model25. However, the lack of significant topographic uplift at the Marius-SH area makes the existence of such large magma chambers unlikely. Consequently, an alternative dyke swarm model is favored, which could extend from the crust-mantle boundary to the floors of mare-filled impacts25. The 3D inversion density model (Fig. 2d, e) reveals that the magmatic intrusions beneath Marius-NH and Marius-SH extend from the surface/near surface to depths of 11 and 11.8 km, with thicknesses of 10.2 and 9.7 km, respectively, and a density contrast range of 160–720 kg/m3 (an average density contrast of 321 kg/m3). This is in good agreement with previously suggested dyke/sill models24,25. In contrast, the 3D inversion model reveals more detailed characteristics of the intrusions and surrounding areas. The northern intrusion is situated beneath the highest topography, and many of the domes and cones within the Marius Hills plateau are positioned immediately above this intrusive body (Fig. 2d). It was suggested that volcanic features in the Marius Hills region could be intruded sills beneath craters and concluded that impact craters may create crustal weaknesses favorable for sill and dike intrusions26. Our inversion models are consistent with these findings. Moreover, the observed interconnection of these anomalies, as discussed below, further supports their interpretation as intrusive bodies. Besides the two bowl-like features in Marius Hills, intrusions with various volumes have been discovered beneath many craters, as detailed in the following. The intrusion adjacent to the west of the Marius-NH intrusion (Figs. 2d and 4a, b, f) displays a quasi-circular shape in the horizontal plane. The corresponding Bouguer gravity anomaly (Fig. 2b) also displays a quasi-circular shape with a maximum value of 71 mGal, which is characteristic of mare-filled impact craters15,26. Hence, similar to the Marius-NH and Marius-SH anomalies, this anomaly might also represent a buried and filled impact crater. The placement of this intrusion coincides with the position of the groups of volcanic vents 5 and 7 as previously identified in the literature27. Given the spatial relationship between the volcanic vents and the intrusions, the three intrusions beneath the MHVC could have played a role in facilitating the volcanic eruptions occurring above them.

The intrusion model5 obtained through forward modeling of the average Bouguer gravity profile suggests that the middle branch in the northwest has a density contrast of 550 kg/m3, a width of 82 km (with a variability of −36 to +19 km), and a thickness of 6 km (with a range of −1 to +3 km). Our density model from 3D inversion (Figs. 3c and 5b, e) displays comparable parameters for the middle branch: it has a thickness of 5–9 km, a density contrast ranging from ~160 to ~620 kg/m3, and spans ~80 km in width. Furthermore, the 3D inversion model shows that the middle branch may have formed from three initially discrete magma chamber compartments (indicated by I, II, III in Figs. 3c and 5a, b), which gradually interconnected at higher levels throughout the filling process, a formation style reminiscent of the Great Dyke56, where development also involved a sequence of initially isolated chambers. The eastern branch seems to have undergone a similar formation process; however, our inversion model only covers two of its chambers (indicated by IV, IV in Figs. 3c and 5a, b). The same linear gravity anomalies have been assumed and modeled to arise from variations in the thickness of the maria and the underlying feldspathic crust5. Given the potential magma chamber compartments revealed by the 3D inversion model, as well as intrusions identified beneath the Marius Hills that could have contributed to facilitating surface volcanism, the interpretation of linear anomalies as large intrusions appears to be geologically reasonable.

Dyke-related eruptions are the primary effusive style responsible for the extensive mare volcanism observed across the lunar maria57. Dyke propagation and emplacement lead to numerous distinct volcanic landforms29. For instance, when dykes reach the surface and erupt, they produce high-flux, high-volume effusive eruptions, resulting in extensive lava flows and sinuous rilles26. The dyke models beneath the Marius-NH and Marius-SH are suggested to extend to the crust-mantle boundary25. Our inversion model reveals a pair of sill-like intrusions with 10.2 and 9.7 km thicknesses, respectively. However, these intrusions do not extend to the crust-mantle boundary estimated at depths of ~17–25 km for the study area (Supplementary Fig. 8)34. The following factors could account for this discrepancy. Seismic data from the Apollo missions revealed a marked increase in velocity within the upper 20–25 km of the crust, correlating with porosity decrease due to increasing overburden pressure. For instance, it has been reported that lunar interior models M1 and M3 estimate subsurface densities of 2680 kg/m3 at 10 km and 3050 kg/m3 at 20 km for M1, and 2760 kg/m3 at 10 km and 2890 kg/m3 at 20 km for M3, respectively58. Our inversion model indicates that the density contrast of the intrusions varies between 160 and 720 kg/m3, with the denser regions (larger than 350 kg/m3) predominantly at depths between 2 and 9 km (Figs. 4 and 5). Given the inferred denser lunar crust at depth, it is plausible that the gravity anomaly from the deeper parts of the intrusions was much weaker due to the lower density contrast. Moreover, the amplitude of the gravity anomaly decays rapidly with depth59. As a result, the gravity anomaly caused by the intrusion models at depth was not detected and consequently failed to be recovered in the 3D density model. Similarly, this phenomenon may also explain why the PKT border magmatic intrusions did not penetrate to greater depths in the model.

The western border intrusions, the northwestern middle branch intrusions, and the Marius-SH intrusion exhibit a strong correlation with the overlying wrinkle ridges (Supplementary Fig. 1). Lunar wrinkle ridges are thought to result from tectonic compression, causing upper crustal shortening after major mare emplacement during the Nectarian-Late Imbrian period60,61,62,63,64 (~4.0–3.2 Gyrs). Evidence of ponded flows on mare ridges indicates that structural relief can form concurrently with and after the emplacement of mare basalts60,61. The estimated average formation time of the wrinkle ridges in Oceanus Procellarum is \({3.35}_{-0.11}^{+0.067}\) Gyrs, ~370 Myrs (million years ago) after the earliest observable basalt eruptions in this region65. The wrinkle ridges parallel to the border structures are thought to be associated with compression in the upper lithosphere caused by the loading of basalts from volcanic infilling of the rifts5. Our 3D density model suggests that in addition to the volcanic infilling, magmatic border intrusions could also play a significant role in controlling the formation and structure of wrinkle ridges. These intrusions may contribute by creating structural supports beneath the surface and/or by providing heat and material that facilitated volcanic activity. The extent of the Marius-SH intrusion aligns with the overlying quasi-circular wrinkle ridges (Fig. 2e and Supplementary Fig. 1), which primarily trend NNW–SSE with a relatively small number of volcanic vents situated on their broad arches27. This observation has been interpreted to indicate that pre-existing faults in a compressional tectonic setting (induced by mass-loading) contributed to the formation of wrinkle ridges and subsequent structural adjustments which potentially triggered volcanic eruptions in mare basins30. Our 3D density model supports this interpretation, indicating that the Marius-SH intrusion has likely played a critical role in the local structural evolution of wrinkle ridges. The faults linked to these ridges may have enabled structural adjustments, potentially initiating volcanic eruptions in the Marius-SH region. In contrast to the Marius-SH, the Marius-NH region exhibits fewer wrinkle ridges. However, it cannot be ruled out that the wrinkle ridges in this area may have been obscured by subsequent extensive volcanic activity.

Remarkably, the architecture illuminated by the 3D inversion models suggests a sophisticated and interlinked magmatic network beneath the Oceanus Procellarum (Figs. 2c and 4). We interpret the three narrow near-horizontal sheeted magmatic structures as sill-like magmatic conduits. However, the origin of the magmatic conduits, their role in the regional magmatic transport, and their impact on the volcanic evolution in the Procellarum Oceanus region demand further inquiry. The phenomenon of magma traversing substantial horizontal distances within the Earth’s crustal layers has been documented in a range of volcanic environments, including large igneous provinces66,67,68, hot spot volcanoes69,70, mid-oceanic ridges71, and island arc volcanoes72,73,74. It has been demonstrated that a network of sills and inclined sheets, known as a sill complex, enables magma to ascend vertically up to 12 km and spread laterally to distances of ~4100 km75,76, indicating that volcanoes that are fed by these sill complexes can be situated a considerable distance laterally from their primary melt source. In contrast, it has been argued that the accelerated ascent of magma through dykes from deep lunar mantle sources generally favors vertical dykes over lateral sills77. However, in shallow crustal regions where the structures were altered by impacts, lateral formations can develop77. GRAIL gravity data analysis of about 1200 complex craters reveals that the lunar megaregolith, which constitutes the uppermost and most fragmented layers of the lunar crust, is at least 8 km thick35. Lateral magmatic sill-like conduits identified within Oceanus Procellarum, spanning from the surface to a depth of 6–8 km correspond to this depth. Therefore, we infer that the megaregolith’s fragmented nature and significant thickness could have facilitated lateral magma transport in the shallow crustal layers.

Previous studies have suggested that systemwide pressure gradients can propagate quickly through the magmatic web, facilitating lateral magma transport in different volcanic systems, such as beneath Hawaiian70 and Kamchatka volcanoes78. The prolonged and extensive volcanic activity in the Marius Hills region, which produced domes, cones, and mare flows, might have caused pressure gradients between the plumbing system beneath the PKT border and the Marius Hills region. These pressure gradients could have facilitated rapid magma propagation through the fractures that prevail in lunar megaregolith from the PKT border to the Marius-SH and Marius-NH areas, as depicted in Fig. 6a. Furthermore, the pressure gradient caused by extensive eruptions at the northern Marius Hills might also have driven magma transportation from Marius-SH toward the Marius-NH area (Fig. 6b). This is consistent with the lack of topographic anomalies in the Marius-SH area and the smaller number of eruptive centers observed there. The magmatic conduit connecting Marius-SH and Marius-NH shows a NNW–SSE trend that aligns with the regional trend in the Marius Hills region, which is considered to be related to pre-existing weak zones/fractures79,80. It is likely that the movement of magma between the Marius-SH and Marius-NH areas could proceed through the reactivation of these pre-existing fractures.

Fig. 6: Cartoon summarizing observations.
figure 6

a The horizontal pressure gradient81 along the rift, coupled with the pressure gradient caused by eruptions and intrusions at Marius-SH, drive the magma to propagate from the rift to Marius-SH. The fractures created by the Reiner impact event and the megaregolith’s fragmented nature facilitate this magmatic activity. b Extensive eruptions and intrusions at Marius-NH cause pressure gradients to propagate rapidly through the regional weak zones/fractures79,80 to Marius-SH. Magma beneath Marius-SH is laterally transported along the fractures from Marius-SH to Marius-NH. To illustrate the magma transport process more clearly, the vertical axis is exaggerated by a factor of ~10 relative to the horizontal axis. PKT Procellarum KREEP Terrane, Marius-NH (northern half), Marius-SH (southern half).

Full size image

Lateral dyke intrusions traveling along the axis of magmatic rifts play an important role in accreting the uppermost part of the elastic–brittle oceanic lithosphere81. These intrusions are suggested to be driven by a horizontal pressure gradient along the rift, which is influenced by an increase in the thickness of the elastic–brittle layer81 and/or a slope descending toward the ends of the rift segment35. The PKT border structures are interpreted as lava-filled rifts and underlying feeder dykes5. The formation of the rifts is considered to be a response to thermal stresses that arose from the differential cooling of the province compared to its surroundings. It is anticipated that horizontal pressure gradients might have developed during the formation of the rifts along the border of the PKT region, which exerted a local structure control on driving the lateral migration of magma along the slope of the rift zone. This process may have been further enhanced by pressure gradients caused by the volcanic eruptions at the Marius-SH and Marius-NH. The fractures resulting from the Reiner event and the inferred cratering events at the Marius-SH, Marius-NH, and the western Marius-NH, combined with the extensive pre-existing fractures in the lunar megaregolith, could have created channels that enabled the flow of magma toward the Marius-SH and Marius-NH. This hypothesis aligns with the view that the lunar crust, extensively fractured and reworked by cratering, enables the exchange of substances and energy among different lunar systems26.

Building on this framework, it is suggested that the magma plumbing system located beneath the western border of the PKT might not have achieved a state of complete cooling and solidification prior to these events, particularly before the formation of the Reiner crater, which dates back to the Eratosthenian epoch (~3.2 to ~1.1 Gyrs)82. Consequently, the magma plumbing system beneath the PKT border is likely long-lasting and possibly involved reactivation of the system through injection of multiple batches of magma. This is consistent with the surface ages of the nearby maria, which range from 4.0 to 1.2 Gyrs83. It has been suggested that the feeder dykes under the PKT border could have served as the magma plumbing system for much of the nearside mare volcanism5. The identified magmatic conduits likely played a crucial role in this process by providing pathways for transporting magma from the plumbing system under the PKT border, fueling mare volcanism in surrounding areas, including the southern and northern Marius Hills. Higher-than-average heat flux6 in the PKT region could also have played a role in these magmatic activities. According to geodynamic models, the elevated heat flux, driven by shallow enrichment in heat-producing elements, may have induced mantle upwelling, which in turn fueled the long-lived volcanism observed in the PKT region84,85.

The revelation of the connectivity between the PKT border structures and the Marius Hills intrusions from our inversion models might account for the compositional distinction between the domes and surrounding and embaying mare in the Marius region. According to the Moon Mineralogy Mapper (M3) spectral analysis, the domes of the MHVC originated from more Fe/Mg-rich magmas, whereas the mare flows, which are considered younger than the domes19,51 were generated from more Ca-rich magmas51. Previous research suggests that these compositional differences could be indicative of the lengthy and intricate volcanic history of the region19,51,52. The connectivity revealed by the inversion model suggests that it is possible that the younger mare flows might originate from deep feeder dykes located beneath the western border of the PKT before the magma plumbing system completely cooled and solidified. Moreover, the mare basalt on the floor of the Marius crater has an olivine‐rich signature19. The floor-filling process is believed to represent the most recent volcanic activity within the MHVC, triggered by the reactivation of fractures from the crater’s impact event19. Lunar Orbiter images indicate that the rim of Marius crater remains intact, implying that the floor of the crater was likely filled from the bottom through numerous fractures and faults caused by the impact19. Supporting this idea, our 3D density model (Figs. 2d and 4g) shows a smaller intrusion directly beneath the crater, which may have contributed to the floor-filling process. The intrusion might be connected to the sill-like conduit linking the Marius-NH and Marius-SH intrusions, however, due to the limited resolution of the Bouguer gravity data and the inversion model, the interconnection is not clear. Further detailed rheological and compositional analysis of the domes/cones and mare flows, along with surface age determination, will enhance our understanding of the origin of mare basalts in the MHVC. The 3D density model presented in this study suggests a possible origin through integrating MHVC into the broader context of the PKT.

Additionally, intrusions of various volumes have been discovered beneath many craters, including but not limited to the inferred filled and buried crater adjacent to the Marius-NH (Fig. 2d), Reiner crater (Fig. 2e), Marius crater (Fig. 2d), Briggs B crater (Fig. 3d), Lichtenberg crater (Fig. 3d), and Seleucus crater (Fig. 3e). A potential filled and buried impact crater (located at 55.7° W, 3.6° N; see Fig. 4b, c, i) situated to the southwest of the Reiner crater has been detected. The corresponding Bouguer gravity anomaly (Fig. 2b) exhibits a quasi-circular shape with a maximum value of 107 mGal. The intrusion beneath it directly connects to the PKT border structure (Fig. 4i). The estimated age of the Lichtenberg crater is ~1.68 Gyrs1. It has been suggested that younger mare basalts, characterized by high concentrations of iron oxide (FeO) and titanium dioxide (TiO2), have accumulated over the southern and eastern ejecta rays following the impact event1,86. These basalts are thought to represent one of the youngest basaltic units on the Moon86,87. Prior to the impact, an older basalt layer was already present, covering a felsic pre-mare crust, which is now exposed to Lichtenberg’s rays1. The magmatic body beneath the Lichtenberg crater is directly connected to the middle branch intrusion, suggesting that the magma chambers (labeled as II in Figs. 3c, d and 5a, b) forming the middle branch intrusion may have contributed to the emplacement of younger mare basalts observed to the south and east of the crater.

Previous research suggests that internal excess pressure-generated fractures, impact-induced surface unloading, impact-induced fractures, and basin fractures played a significant role in facilitating magma ascent, intrusion, and eruption in mare-filled craters29,88,89,90,91,92,93. The discovery of intrusions with various volumes beneath many craters supports these interpretations and suggests that magma accumulation beneath craters is likely a common process. Notably, the source of the magma may not always be directly from the deep lunar mantle. Instead, magma could have laterally migrated through fractures within the lunar crust to accumulate beneath impact craters. These findings, along with the observed connections between PKT border structures and northern and southern Marius Hills intrusions, underscore the important role of lateral magma transport in the Moon’s volcanic evolution. Understanding these transport mechanisms is crucial for advancing knowledge of lunar volcanic processes and should be a key focus of future research. The study also emphasizes the importance of considering regional geological context when analyzing magmatic activity on the Moon, offering important insights into the magma plumbing system and subsurface behavior. Further improvements in lunar gravity data could lead to more accurate identification of smaller intrusions and the connections between different volcanic systems, which would significantly impact our understanding of lunar volcanic history and aid in the future exploration of lunar resources.

Methods

The 3D inversion technique used in this research leverages a probabilistic method to generate 3D density models from gravity data37, which has been shown to be effective in identifying crustal structures on Earth9,38,39,94. The objective function employed for the inversion of gravity data is as follows:

$${{\mathbf{\Phi}}}={\left({{\mathbf{Gm}}}-{{{\mathbf{d}}}}_{{{\rm{obs}}}}\right)}^{T}{{{\mathbf{C}}}}_{{{\rm{D}}}}^{-1}\left({{\mathbf{Gm}}}-{{{\mathbf{d}}}}_{{{\rm{obs}}}}\right)+{\left({{\mathbf{m}}}-{{{\mathbf{m}}}}_{{{\rm{apr}}}}\right)}^{T}{{{\mathbf{C}}}}_{{{\rm{M}}}}^{-1}\left({{\mathbf{m}}}-{{{\mathbf{m}}}}_{{{\rm{apr}}}}\right) .$$
(1)

Here, m represents the model parameter vector, values of the densities of the cells, d is the gravity data vector, and G is the forward modeling matrix where Gm = d. The first term of Eq. (1) signifies the data misfit function, weighted by the data error covariance matrix, CD. The second term corresponds to the stabilizing function, which accounts for the deviation of model parameters m from a reference model mapr, weighted by the model covariance matrix CM.

The a priori information, including physical properties, spatial extent, depth, and orientation of the source bodies, can be incorporated via CM to constrain the inversion and achieve an accurate and reliable solution.

To minimize the objective function, the solution is derived below37

$$\widetilde{{{\mathbf{m}}}}={{{\mathbf{m}}}}_{{{\rm{apr}}}}+{{{\mathbf{C}}}}_{{{\rm{M}}}}{{{\mathbf{G}}}}^{T}{\left({{\mathbf{G}}}{{{\mathbf{C}}}}_{{{\rm{M}}}}{{{\mathbf{G}}}}^{T}+{{{\mathbf{C}}}}_{{{\rm{D}}}}\right)}^{-1}\left({{{\mathbf{d}}}}_{{{\rm{obs}}}}-{{{\mathbf{Gm}}}}_{{{\rm{apr}}}}\right) .$$
(2)

To counteract the natural decay of the forward modeling matrix with increasing depth, a depth weight function with the following form was used:

$$w(z)=1/(z_{{\rm{max}}}-z)^{\beta },$$
(3)

where zmax is the maximum depth of the inversion domain and z is the depth of each cell. \(\beta\) is the exponent of the depth weight function and \(\beta=1\) was used for this study.

The solution with the depth weighting function is:

$$\widetilde{{{\mathbf{m}}}}={{{\mathbf{m}}}}_{{{\rm{apr}}}}+{{{{\mathbf{W}}}}^{-1}{{\mathbf{C}}}}_{{{\rm{M}}}}{{{\mathbf{W}}}}^{-1}{{{\mathbf{G}}}}^{T}{\left({{\mathbf{G}}}{{{\mathbf{W}}}}^{-1}{{{\mathbf{C}}}}_{{{\rm{M}}}}{{{\mathbf{W}}}}^{-1}{{{\mathbf{G}}}}^{T}+{{{\mathbf{C}}}}_{{{\rm{D}}}}\right)}^{-1}\left({{{\mathbf{d}}}}_{{{\rm{obs}}}}-{{{\mathbf{Gm}}}}_{{{\rm{apr}}}}\right) .$$
(4)

The parameters of the model covariance matrix CM for areas A and B are listed in Table 1. We utilized a nested covariance model, as detailed in the second and third rows of Table 1, since the Bouguer gravity anomaly (Figs. 2b and 3b) within this region displays characteristics that span multiple scales. Specifically, the border structures of the PKT present larger linear formations trending NNW, while anomalies like the Marius-SH and Marius-NH appear to be relatively smaller quasi-circular in nature. Data error covariance matrix CD is a diagonal matrix where each diagonal element is set at 2 mGal, representing an approximate estimate of the noise level in the Bouguer gravity data. A zero-reference model (\({{{\bf{m}}}}_{{{\rm{apr}}}}={{\boldsymbol{0}}}\)) was used for the inversions.

Table 1 The parameters of the model covariance matrix CM for the areas A and B
Full size table

Before conducting the inversion, the Bouguer gravity data were transformed from spherical to Cartesian coordinates. The inversion domain was divided into numerous prism cells with dimensions of 1.5 km × 1.5 km × 0.25 km in the x, y, and depth directions, respectively. The depth extent of the inversion domain was set at 20 km. To mitigate edge effects during the inversion, the spatial dimensions of the inversion domain were expanded by 30 km in all lateral directions beyond the data coverage. This parameterization results in a model with 534 × 526 × 80 cells in study area A, 433 × 467 × 80 cells in study area B. The top of the inversion domain was constrained by the topographic data. Therefore, the cells above the terrain were removed and not inverted. By constraining the top of the terrain, it is possible to mitigate the effects caused by inaccurate terrain-corrected densities and fully take into account the rapid changes in depth within the craters, thereby improving the accuracy of the inversion model. We observed positive topographic elevations in specific localized sections, mainly the rims of large craters located in the lower left corners of areas A (Fig. 2a) and B (Fig. 3a). During the inversion process, the topographic elevations of these regions were set to zero, as their very limited area did not impact our inversion results.

Supplementary Fig. 9a, b shows the difference maps between the observed gravity anomalies (Figs. 2a and 3a) and the predicted gravity anomalies calculated from the 3D inversion models (Figs. 4 and 5). The difference maps show how well the inverted models resemble the observed gravity. The standard deviations of the differences for study areas A (Supplementary Fig. 9a) and B (Supplementary Fig. 9b) are 1.3 and 1.2 mGal, respectively, with a mean of 0.0 mGal. In Supplementary Fig. 9a, we observe short-wavelength fluctuations appearing as narrow strips, with widths of 6–10 km and lengths spanning 20–100 km, exhibiting a distinct S-N orientation. The short-wavelength jitters presented in Supplementary Fig. 9b lack a clear directional pattern. The short-wavelength jitters are mainly related to the orbit‐parallel striping in the GRAIL data at high degree17. These fluctuations are not anticipated to disrupt the primary magmatic structures in this study, as the latter possess scales significantly larger than those of the strips.

The inversion method introduced above was proposed in the Cartesian coordinate system and can be directly extended to the spherical coordinate system. However, the inversion process can be much more efficient in the Cartesian coordinate system, where the inversion space can be divided into a series of adjacent prisms of the same size, and the FFT technique can highly speed up the inversion process94. To investigate the effect of the lunar curvature for this study, we inverted the Bouguer gravity in study areas A and B in the spherical coordinate system separately (Supplementary Fig. 10a, b). The resulting density models show a high degree of similarity to the models obtained in the Cartesian coordinate system (Figs. 2c and 3c) in terms of the density contrasts and the spatial extent of the inverted anomalies. However, due to the utilization of finer cells (1.5 km × 1.5 km × 0.25 km), the model in the Cartesian coordinate system reveals more detailed structures than in the spherical coordinate system (0.15° × 0.15° × 0.25 km), in which the cell size was limited by computational performance. Therefore, this study presents and discusses the inversion results using the Cartesian coordinate system.

Several factors can influence inversion results when using the probabilistic method described above, including the parameters of the model covariance matrix (CM), the depth weighting function, and the depth extent of the inversion domain. To assess the impact of these factors, we conducted a sensitivity analysis and compared the inversion results obtained with varying parameter settings (refer to the Supplementary for details; Supplementary Figs. 11, 12, and 13). These factors primarily have a modest impact on the thicknesses of the high-density bodies. The connectivity between the western PKT border intrusion and the northern and southern intrusions remains distinctly apparent. After comparing the inversion density models with previous studies on the northern and southern intrusions of the Marius Hills24,25 and the middle branch intrusion5 in study area B, through forward modeling, we selected the optimal models for study areas A and B shown in Figs. 2 and 3, as they demonstrate better agreement with these earlier studies. These models are derived using a β value of 1, an inversion domain depth extent of 20 km, and the model covariance parameters are listed in Table 1.