Introduction

High-quality (Q)-factor optical resonators with ultranarrow spectral linewidth (\({\varGamma }_{\omega }={\omega }_{0}\)/Q, where \({\omega }_{0}\) is the resonance frequency) play a crucial role in modern photonics and quantum optics1,2, facilitating extreme temporal coherence3, with lifetime on the time scale of ~Q/\({\omega }_{0}\). Numerous essential applications, including optical frequency combs4,5, monochromatic lasers6,7, low-photon-number nonlinear optics8, unidirectional nano-emitters9, and cavity quantum electrodynamics studies10, critically depend on high-Q resonators. This has led to extensive efforts in designing ultrahigh-Q resonators across different spectral regimes. However, experimentally realizing very large Q-factors at shorter wavelengths, e.g., visible wavelengths, remains an outstanding challenge due to material and fabrication constraints. The primary difficulty lies in fabrication imperfections that cause unwanted scattering loss and deviations from the intended design1,11,12,13, which are much more severe in visible-wavelength devices because their small feature sizes are on a similar scale as fabrication defects.

At visible wavelengths, million-scale (106) Q-factors have been accessed in individual photonic resonators such as evanescently-coupled micro-ring and micro-disk cavities1,14, and free-space-coupled microtoroids15. Due to tight spatial confinement of light, one can minimize the defect-sensitive area in these resonators. In contrast, free-space lattice-resonant implementations such as metasurfaces and photonic crystal slabs have larger functional areas (which enable large space-bandwidth product), and thus are highly defect-sensitive and face additional challenges, including long-range non-uniformity, substrate-induced out-of-plane asymmetry, and modal dispersion. Experimentally reported Q-factors in these free-space resonators typically fall within a scale of only 103 (see Table 1)16,17,18,19,20,21 in the visible regime.

Table 1 Experimentally reported Q-factors in free-space optics at visible wavelengths
Full size table

Despite these challenges, there is an outstanding and ever-growing demand for ultrahigh-Q free-space optics due to their distinct advantages of large space-bandwidth product, easy free-space access, and parallel signal/data operations22,23. These unmet needs have spurred research into topological metasurfaces that are meticulously engineered to be more resilient to fabrication defects24,25,26, for instance, by merging multiple bound states in the continuum (BICs) in momentum space24. However, in these approaches, the substrate needs to be removed to minimize out-of-plane asymmetry and the lack of lossless high-index materials at visible wavelengths may also limit design feasibility. Moreover, despite the improvements, the experimental Q-factors still fall short by orders of magnitude compared to those in integrated-optics resonators.

Here we design and experimentally demonstrate a million-scale ultrahigh-Q guided mode resonance (GMR) at near-visible wavelengths in a resist-based etch-free metasurface (Fig. 1). Etching is the major process that introduces roughness and defects. An ‘etch-free’ design procedure aims to minimize fabrication imperfections, rather than engineering the device’s robustness to imperfections. The advantage of this novel concept was recently validated by Huang et al. in a near-infrared ultrahigh-Q metasurface27 and by Ko et al. in a mid-infrared ultrahigh-Q microresonator28, among others29,30. Expanding on these findings, we adapt the etch-free metasurface strategies27,29,30 under the material constraints of visible regime, and advance visible-wavelength free space meta-optics into a new era of million-Q performance. We achieve this by using a perturbed multilayer-waveguide configuration as shown in Fig. 1a with material refractive indices not exceeding 2.0 (SiN). We emphasize that low-loss high-index materials are rare at visible wavelengths, and hence our moderate-index design facilitates generalization across different platforms.

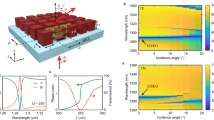
Fig. 1: Ultrahigh-Q guided mode resonances (GMRs) in an etch-free metasurface at visible wavelengths.
figure 1

a Schematic showing the unit cell of the etch-free metasurface. From top to bottom, the geometry includes a 58 nm-thick patterned PMMA layer, a 100-nm-thick SiN layer, and a 1470 nm-thick SiO2 layer on a Si substrate. The patterning is defined by the period P and defect hole size L. b Design principle, from guided modes to ultrahigh-Q GMRs: Top-left, Schematic of an air/58-nm-PMMA/100-nm-SiN/SiO2 multilayer slab waveguide; Top-right, Wave vector analysis when a periodic perturbation is patterned at the PMMA layer. The Bloch momentum kBloch \(=2\pi /P\) introduced by periodic patterning couples guided modes into free space. kGM and \(\beta\) are the in-plane and out-of-plane components of the guided mode wave vector, respectively. kGMR is the GMR wave vector; Bottom, Dispersion of the TE1 guided mode in the studied system, which guides the design of GMR. The dashed black lines show an example of designing a \(\Gamma\)-point resonance at 779 nm. The insets are the corresponding 779 nm GMR mode profiles when P = 500 nm and L = 50 nm. c Q-factor of GMR as a function of L when P is fixed as 500 nm. The red curve is predicted by an eigenmode solver in COMSOL Multiphysics®. The dashed black curve comes from the Fano fitting of the simulated reflectance spectra from Lumerical RCWA. The experimental results using the same fitting method are highlighted as three stars, up to one million Q. The inset is an SEM image of the fabricated metasurface under top view. False colors are added to highlight the patterned PMMA. Scale bar, 500 nm. d–f Simulated and experimentally measured momentum-space-resolved reflectance spectra of our meta-resonators. With a fixed P of 500 nm, devices with different L are studied: (d) L = 90 nm, (e) L = 70 nm, (f) L = 50 nm. A spectrometer with a 1200-lines/mm grating is used to differentiate the wavelength in spectra. The arrows in (f) guide the eyes towards the GMR feature of interest that is vague due to the ultranarrow linewidth beyond the wavelength resolution. A difference operation is performed, subtracting the background (at unpatterned-PMMA areas) signals from the device signals, to eliminate the multilayer interference influence. The spectra are normalized to their respective maxima (see Methods).

Full size image

To characterize a million-Q resonance under free-space visible wavelength excitations, we develop a new laser-scanning momentum-space-resolved spectroscopy technique. It combines a tunable-wavelength laser and a momentum-space imaging system to visualize the modal dispersion24,31,32,33,34 in the full energy-momentum space with ultrahigh resolution in wavelength (~0.42 pm) and angle (~0.028 ̊).

Our platform can be readily used in various applications including optical sensing, filtering, quantum light sources, and few-photon nonlinear optics. As an example, we integrate monolayer WSe2 into our ultrahigh-Q meta-optical resonator and demonstrate highly unidirectional and narrow-linewidth exciton emission. The ultrahigh-Q cavity effectively boosts the density of states at the \(\Gamma\) point, and a pump-power-dependent emission concentration towards the \(\Gamma\) point under continuous-wave (CW) laser pumping is observed at room temperature.

Results

Design of ultrahigh-Q GMR meta-resonator

The proposed metasurface configuration and the design flow from a nonradiative guided mode to a radiative ultrahigh-Q GMR are illustrated in Fig. 1a, b, respectively. To begin, we consider the four-layer slab waveguide in Fig. 1b, which comprises, from top to bottom, of a semi-infinite air superstrate, a 58-nm-thick layer of polymethyl methacrylate (PMMA), a 100 nm-thick layer of SiN, and a semi-infinite SiO2 substrate. This stack supports both transverse electric (TE) and transverse magnetic (TM) guided modes with different cut-off wavelengths. For simplicity, we target the wavelengths where only the fundamental TE modes exist (see Supplementary Note 1), for which the electric field is \({{\rm{E}}}(x,z)=\hat{{{\rm{y}}}}{E}_{y}\left(z\right){{{\rm{e}}}}^{i{k}_{{{\rm{GM}}}}x}\). kGM is the propagation constant (i.e., in-plane component of the guided mode wave vector), which can be found by solving the transcendental dispersion equation (detailed derivation in Supplementary Note 1),

$$\tan {\beta }_{3}{h}_{{SiN}}=\frac{{\beta }_{3}\left({\kappa }_{1}{\kappa }_{4}-{\beta }_{2}^{2}\right)\tan \left({\beta }_{2}{h}_{{PMMA}}\right)+{\beta }_{3}{\beta }_{2}\left({\kappa }_{1}+{\kappa }_{4}\right)}{\left({\beta }_{3}^{2}{\kappa }_{1}+{\beta }_{2}^{2}{\kappa }_{4}\right)\tan \left({\beta }_{2}{h}_{{PMMA}}\right)+{\beta }_{2}\left({\beta }_{3}^{2}-{\kappa }_{1}{\kappa }_{4}\right)}$$
(1)

In this equation, \({\beta }_{2}={\left[{n}_{{{\rm{PMMA}}}}^{2}{k}_{0}^{2}-{k}_{{{\rm{GM}}}}^{2}\right]}^{1/2}\) and \({\beta }_{3}={\left[{n}_{{{\rm{SiN}}}}^{2}{k}_{0}^{2}-{k}_{{{\rm{GM}}}}^{2}\right]}^{1/2}\) are the out-of-plane wave vector components in the PMMA and SiN layers, respectively, where \({k}_{0}=2{{\rm{\pi }}}/\lambda\); \({\kappa }_{1}={\left[{k}_{{{\rm{GM}}}}^{2}-{n}_{{{\rm{ai}}}r}^{2}{k}_{0}^{2}\right]}^{1/2}\), and\(\,{\kappa }_{4}={\left[{k}_{{{\rm{GM}}}}^{2}-{n}_{{{\rm{Si}}}{{{\rm{O}}}}_{2}}^{2}{k}_{0}^{2}\right]}^{1/2}\) are the decay constants in air and SiO2, respectively. The symbols n and h represent the refractive indices and thicknesses of different media. The plot in Fig. 1b shows the dispersion of the effective index neff = kGM / k0 of the TE1 mode obtained by solving Eq. (1). In Supplementary Fig. S1, we also examine a simplified three-layer model that ignores the very thin resist layer27, showing a significant deviation of neff compared with the complete four-layer model. This suggests that the very thin PMMA plays a crucial role here, and the optical near field is expected to be effectively trapped in both the SiN and PMMA layers.

By creating a square periodic array of perturbations in the PMMA layer as shown in Fig. 1a, we introduce a structure-induced Bloch momentum kBloch \(=2\pi /P\) to compensate for kGM and thereby open a radiative leaky channel for the infinite-Q guided mode to couple into free space. A wave vector analysis sketch is presented in the top-right panel of Fig. 1b. This leads to a GMR with wave vector kGMR, whose resonance wavelength is determined by the period of perturbation P and the guided mode dispersion, as shown in the bottom panel of Fig. 1b. For instance, to design a \(\Gamma\)-point (normal-incidence) GMR at a given wavelength λ, we need a kGMR with zero in-plane component, \({n}_{{{\rm{eff}}}}\bullet \frac{2\pi }{\lambda }-\frac{2\pi }{P}=0\). The dashed lines in the dispersion plot give an example of determining the value of P for a resonance at 779 nm. Moreover, with a fixed P, we can use the guided mode dispersion curve to predict the GMR dispersion (Supplementary Fig. S2). The inset shows the simulated mode profiles of a 779 nm resonance at the \(\Gamma\) point when P = 500 nm and the defect hole size L = 50 nm. From the side view, the resonant near field is clearly trapped at the interface of SiN and PMMA, as predicted by the four-layer model. This feature can guide the design strategy to maximize the field overlap with the integrated functional materials, which will be further discussed in the last section.

Similar to a quasi-BIC leaky mode26,35, the extent of periodic perturbations (hole size) applied on a photonic bound state (nonradiative guided mode) determines the Q-factor and radiative amplitude of the leaky mode (GMR)27. In our metasurface, a smaller L induces a larger Q-factor as shown in Fig. 1c, accompanied by a decreased reflectivity amplitude as shown in Supplementary Fig. S3 (the amplitude decrease is negligible for the hole sizes chosen in our experimental demonstration). The predicted Q-factors in Fig. 1c are obtained through eigenmode simulations (red solid line) and Fano fitting of simulated reflection data (black dashed line). The close agreement between these methods validates the fitting approach, which is then applied to all experimental spectra (see Methods).

Three metasurfaces with fixed P = 500 nm and varying L (90, 70, 50 nm) are fabricated and characterized. Note that, to ease the fabrication without affecting the design (Supplementary Fig. S4), the samples are fabricated on 1470 nm-SiO2-on-Si wafers as illustrated in Fig. 1a. The Q-factors of these three devices (stars in Fig. 1c) all show excellent agreement with the theoretical expectation, yielding a record-high Q of a million scale. Such good quantitative agreement is thanks to the reduced amount of fabrication imperfection enabled by the etch-free design, where only the PMMA layer is patterned by electron-beam lithography and a development process, eliminating the need for etching.

Visualization of GMR dispersions

Random device defects, environmental noise, light path misalignment, or even dust on optical components can cause ‘ghost’ narrow-linewidth spectral features in visible-wavelength free-space measurements. When the linewidth of the studied resonance mode is comparable to these high-frequency background signals, experimental spectral analysis becomes less convincing. To properly characterize an ultrahigh-Q meta-resonator, we need momentum-space-resolved spectroscopy that enables the visualization of the complete modal dispersions, thereby distinguishing the real resonances from various noise sources24,32,34. Here, we start with a conventional energy-momentum reflectance spectroscopy that uses a white light source and a grating (see the optical setup in our previous publications36,37). As shown in Fig. 1d–f, the measured dispersion of all three devices matches well with the simulated GMR response in Fig. 1d, confirming the GMR nature of the measured high-Q modes and again proving the near-ideal performance of our etch-free metasurfaces. Figure 1d also reveals the co-existence of different resonance modes with s- or p-polarization. A full eigenmode analysis can be found in Supplementary Note 2. In the main text, we focus on the s-polarized ultrahigh-Q GMR with a clean linear dispersion, as highlighted by the arrows in Fig. 1f.

We find that, as the Q-factor increases with decreasing L (from Fig. 1d–f), the ultrahigh-Q GMR dispersion curve becomes faint. This suggests that the linewidth of the studied resonance mode is much smaller than the wavelength resolution (~0.05 nm) of the 1200-lines/mm grating in the setup. Since interference-induced high-Q resonances typically manifest as an asymmetric Fano shape with one peak and one dip, insufficient wavelength resolution can average out the peak and dip, causing incorrect or missing spectral information.

To tackle this intriguing dilemma arising from a record-high Q in visible-wavelength free-space optics—a unique and new task that could become common as our strategy can be easily generalized—we introduce a laser-scanning momentum-space-resolved spectroscopy technique, as shown in Fig. 2a. Analogous to integrated photonic resonator measurements, a tunable laser is employed to scan the wavelength with extremely high resolution. Distinctively, the wavelength-scanning laser is integrated into a 4-f momentum-space imaging system, and a two-dimensional charge-coupled device (2D CCD) continuously captures the iso-frequency contours of the photonic band structures at different wavelengths determined by the tunable laser.

Fig. 2: Laser-scanning momentum-space-resolved spectroscopy with ultrahigh resolutions in wavelength and angle of signal.
figure 2

a Schematic of the optical setup and how laser-scanning defines wavelength in momentum-space-resolved spectroscopy. L1-4, lens. BS, beamsplitter. OBJ, objective. CCD, charged-coupled device camera. More details in optical setup and measurements can be found in Methods. b–d Comparison of the measured momentum-space-resolved reflectance spectra under different wavelength and angle resolutions. Spectra of the device with P = 500 nm and L = 90 nm are presented as an example. A spectrometer with a 1200-lines/mm grating provides a wavelength resolution of ~0.05 nm/pixel in (b), while a resolution of ~2.1 pm/pixel is achieved in (c, d) via a tunable laser. The angle resolution is ~0.076 ̊ /pixel in (b) with a 10X objective, and ~0.044 ̊ /pixel in (c, d) with a 2X objective. Insets on top highlight the numbers of pixels summed along X axis on CCD when evaluating the momentum-dependent spectral response along Y axis. The more pixels summed, the more severe the dispersion-induced mode broadening is. e Reflectance spectra extracted at arbitrary k values in the momentum space from (d).

Full size image

With full access to the multi-dimensional information in the wavelength/energy-momentum (E-k) space, we can visualize any E-k cross-section, such as a cut along \({\hat{{{\bf{k}}}}}_{{{\rm{y}}}}\) in Fig. 2b–d. In most cases, we enable a small number of pixels on the 2D CCD, only collecting the desired E-k information, to save scanning time. See Methods and Supplementary Note 3 for technique details. As an aside, we target the 779-nm GMR designs for our experimental demonstrations because the only accessible tunable laser in our lab covers 765 to 781 nm. Devices working at shorter wavelengths have also been fabricated and studied (Supplementary Fig. S5). Ultrahigh-resolution quantitative characterization can readily be performed using the same method as long as a tunable laser is available at the relevant wavelength.

Figure 2b–d compare the results of conventional energy-momentum reflectance spectroscopy with our laser-scanning-integrated approach. Measured spectra from the metasurface with P = 500 nm and L = 90 nm are presented as an example. Dramatic improvements can be found in Fig. 2c, d (laser-scanning) compared to Fig. 2b (conventional), successfully detecting the ultrahigh-Q spectral feature in visible-wavelength free-space measurements.

Besides improving the resolution in wavelength and momentum (angle), we also examine the influence of the number of pixels summed along the direction perpendicular to the visualized E-k cross-section (e.g., ∆kx in X axis for a E-k cross-section cut along the Y axis). In common spectroscopy approaches using gratings, a slit must be applied as shown in the top inset of Fig. 2b. The slit width needs to balance the grating efficiency and resolution, and the optimal width in our setup turns out to be at least 20 pixels wide. This causes extra dispersion-induced mode broadening37. Excitingly, our technique allows to sum an arbitrary number of pixels, as illustrated in the top insets of Fig. 2c, d. With more pixels summed (Fig. 2c), the signal-to-background ratio is higher, while the single pixel case (Fig. 2d) can provide the narrowest GMR feature, closer to the intrinsic GMR property. In the following, we display the E-k spectra with a few pixels summed and extract Q-factors from single-pixel data.

Direct measurement of a million Q

With sufficient resolutions in E-k space and a clear GMR dispersion picture, we can extract high-wavelength-resolution 1D spectra at arbitrary k values and confidently identify the high-Q peaks originating from the GMR meta-resonator, as shown in Fig. 2e.

Based on this, we fit a Fano lineshape to the extracted 1D spectra at the \(\Gamma\) point (k = 0, highlighted by the arrow in the right panel of Fig. 3a) and determine the Q-factors of three fabricated metasurfaces to be \(1.10\pm 0.09\) million (L = 50 nm, Fig. 3a), \(313\pm 8\) thousand (L = 70 nm, Fig. 3b), and \(144\pm 5\) thousand (L = 90 nm, Fig. 3c), respectively. As concluded in Table 1, our report of a million Q in the experiment is orders of magnitude higher than state-of-the-art demonstrations in visible-wavelength free space meta-optics16,17,18,19,20,21.

Fig. 3: Experimental demonstration of million-Q GMR at near-visible wavelengths.
figure 3

a Left, Reflectance spectra of the device with P = 500 nm and L = 50 nm at \(\Gamma\) point (normal incidence). The Fano fitting (pink curve) reveals a Q factor of 1.10 million. The \(\Gamma\)-point data are extracted from extra-fine laser-scanning momentum-space-resolved reflectance spectroscopy with a wavelength resolution of ~0.42 pm/pixel and an angle resolution of ~0.028 ̊ /pixel; Right, the momentum-space-resolved spectra where the \(\Gamma\)-point data is extracted from. Note that a 0.28 ̊ range (10 pixels) of data are summed to broaden the ultranarrow mode linewidth for the convenience of visualization here, but only single-pixel data are used for Fano fittings. The same momentum-space-resolved spectra are plotted twice, one with the pink dashed lines highlighting the dispersion of GMR. The arrow points to the \(\Gamma\)-point resonance. b, c The same as (a) but for the devices with (b) L = 70 nm and (c) L = 90 nm. The fitted Q factors are 313 and 144 thousand respectively.

Full size image

Looking beyond the million-Q achievements, further advancements will require a faster 2D camera and a more stable tunable laser. Here, to obtain enough data points for accurately fitting a million-Q resonance, we reduce the laser scanning speed while the 2D CCD capture frequency is already at its maximum, achieving a wavelength resolution as fine as ~0.42 pm. However, as shown in the right panel of Fig. 3a, an unwanted stripe-like background emerges in this extra-fine momentum-space-resolved spectrum, resulting from laser instability over the longer scanning time.

A unidirectional and narrow-linewidth exciton emitter

In this last section, we demonstrate the practical advantages of our ultrahigh-Q meta-optical platform by integrating monolayer WSe2 into the metasurface and showcasing a highly unidirectional and narrow-linewidth exciton emitter at room temperature beyond the intrinsic material limitation. Monolayer transition metal dichalcogenides (TMDs) such as WSe2 are promising next-generation nano-emitters but suffer from poor emission directionality38 and broad spectral linewidth at room temperature39. As shown in the left part of Fig. 4a (white-to-purple colormap), the room temperature photoluminescence (PL) of a monolayer WSe2 (under a 532 nm CW laser pumping) in our unpatterned multilayer structure has a full-width-at-half-maximum (FWHM) spectral linewidth (\({\varGamma }_{\lambda }\)) of ~25.12 nm and shows very poor directivity with a FWHM linewidth in far-field emission angle (\({\varGamma }_{\theta }\)) of ~120.95 ̊ (see simulated 3D emission directionality in Supplementary Fig. S6). Our ultrahigh-Q platform can substantially narrow both of these important figures of merit by more than 96% (Fig. 4b).

Fig. 4: Highly unidirectional and narrow-linewidth exciton emission from monolayer WSe2 when coupled with the ultrahigh-Q meta-resonator at room temperature.
figure 4

a Left, Energy-momentum photoluminescence (PL) spectra of monolayer WSe2 in the unpatterned structure. Pumped by a 532 nm 0.555 kW/cm2 CW laser. The broad full-width-at-half-maximum (FWHM) linewidths in far-field emission angle (\({\varGamma }_{\theta }\)) and spectral wavelength (\({\varGamma }_{\lambda }\)) are highlighted; Right, Energy-momentum reflectance spectra of the WSe2-metasurface hybrid system, where P = 480 nm and L = 70 nm. b Narrowing the WSe2 PL in both spectral and angular dimensions. Top, Schematics of monolayer WSe2 in the unpatterned structure and patterned meta-resonator on a fused silica substrate (no Si wafer), respectively. The same device is measured before and after PMMA patterning. Bottom, Comparison of WSe2 PL linewidths before and after patterning, in both spectral (Left) and angular (Right) dimensions. c–e Extracted emission properties of the WSe2-metasurface hybrid from the energy-momentum PL spectra (Supplementary Fig. S7) as a function of pump power density (logarithmic scale): (c) spectral linewidth, FWHM \({\varGamma }_{\lambda }\), (d) angular linewidth, FWHM \({\varGamma }_{\theta }\), and (e) integrated PL counts (logarithmic scale) at sin \(\theta\) = 0.012 (orange dots) and sin \(\theta\) = 0 (black dots), respectively. The error bars in (c, d) are determined by spectra fittings (see Methods). The integrated PL in (e) were measured by first increasing the laser power and then decreasing it by 3 times. The error bar shows the standard deviation.

Full size image

As shown in the right part of Fig. 4a (grayscale), we select a metasurface period P of 480 nm to match the \(\Gamma\) point of GMR with the WSe2 PL in wavelength. A defect hole size L of 70 nm is used, yielding a Q-factor of ~297 thousand, which is still higher than any reported Q in literatures16,17,18,19,20,21. As illustrated in Fig. 4b, monolayer WSe2 is placed between SiN and PMMA layers for better field overlap (see the mode profile inset in Fig. 1b). This is easily achieved by first transferring the functional material, i.e., exfoliated WSe2, onto SiN and then performing the spin coating and lithography in PMMA.

The WSe2 PL linewidths in the unpatterned structure and patterned ultrahigh-Q meta-resonator are compared in Fig. 4b, in both spectral (left panel) and angular (right panel) dimensions, showing laser-like monochromaticity and unidirectionality when coupled with the metasurface at room temperature, albeit without any operating power density threshold. The applied CW pumping power density is as low as 0.555 kW/cm2. The spectral and angular plots in Fig. 4b are extracted from the energy-momentum PL spectra of the WSe2-metasurface hybrid in Supplementary Fig. S7, which reveal the highly concentrated emission at the \(\Gamma\) point of GMR. Such achievement enables the practical applications of 2D TMD materials in displays and optical communications. We emphasize that, compared to the 2D material integration with nanostructured cavities, our approach of sandwiching TMDs between two thin layers can be well extended to large-scale integration with chemical vapor deposition (CVD)-grown layered materials.

Additionally, as we increase the 532 nm pump power density, we observe obvious PL narrowing in both spectral (\({\varGamma }_{\lambda }\)) and angular (\({\varGamma }_{\theta }\)) dimensions. A power-dependent analysis is performed, and the extracted crucial parameters are presented in Fig. 4c–e. It should be emphasized that the heating effect is carefully excluded in our CW laser pumping tests. Referring to a literature40 that studied 532 nm laser-induced heating on WSe2 (the same laser wavelength and material) with rigorous experiments and simulations, we set our CW laser power density to a safe range where no detectable temperature increase was found40.

As shown in Fig. 4c, d, the FWHM \({\varGamma }_{\lambda }\) is narrowed from 1.334 nm to 0.957 nm (by ~28%), and FWHM \({\varGamma }_{\theta }\) is narrowed from 0.805 ̊ to 0.545 ̊ (by ~32%) under 14.33 kW/cm2 CW pumping. To better understand this narrowing phenomenon, in Fig. 4e, we examine the integrated PL counts at \(\Gamma\) point (k = 0) and at k = 0.012, slightly deviated from the \(\Gamma\) point, as a function of pump power density. We choose a very small deviation from the \(\Gamma\) point because the emission is already well concentrated even before we increase the pump power and PL signals at larger k values are near zero. As shown in Fig. 4e, a nonlinear increase of PL counts at k = 0 is found, while there is a saturation trend in term of PL counts at k = 0.012, suggesting amplified spontaneous emission (ASE) in our system because of the extremely high density of state at the \(\Gamma\) point thanks to the record-high Q-factors.

We have also conducted PL studies at higher power densities by using a 532 nm 100-picosecond pulsed laser and a consistent power-dependent narrowing tendency is found (Supplementary Fig. S8), further supporting the ASE assumption. The narrowed FWHM \({\varGamma }_{\lambda }\) and \({\varGamma }_{\theta }\) eventually saturate at 0.587 nm and 0.269 ̊ under pulsed pumping. More discussions can be found in Supplementary Note 4.

Lastly, we notice strong in-plane scattering at the boundaries of the finite-size WSe2 flake (see Supplementary Note 4 and Figs. S7, S10), possibly because of the significant refractive index difference between WSe2 (n > 4.4) and our multilayer waveguide structure (n < 2.0). Consequently, we hypothesize that both the strong temporal confinement of our ultrahigh-Q GMR and the considerable spatial confinement due to the high-index WSe2 monolayer disk (acting like an in-plane resonator) contribute to the observed extreme emission concentration at RT and under CW pumping. Further studies are inspired but beyond the scope of this work.

Discussion

In conclusion, we have experimentally demonstrated a record-high million-scale ultrahigh-Q GMR at near-visible wavelengths under free-space excitation using an etch-free metasurface. Advancing free space meta-optics into a new era of million-Q performance, we have also developed a laser-scanning momentum-space-resolved spectroscopy technique to accurately characterize arbitrary dispersive ultrahigh-Q modes in the challenging free-space optical measurements. With material refractive indices not exceeding 2.0 in the demonstrated million-Q device and the simple resist-based fabrication procedure, our strategy can be easily generalized across various platforms at visible wavelengths, inspiring more complicated meta-resonator designs (chiral41, topological24,25,26,27, nonreciprocal42, reconfigurable43, etc.) and functional material integration.

Furthermore, we have integrated monolayer WSe2 into our ultrahigh-Q meta-optical resonator and demonstrated a highly unidirectional and narrow-linewidth exciton emitter operating at RT and under CW pumping. Extreme PL concentration with FWHM linewidths as narrow as 0.269° in far-field emission angle and 0.587 nm in wavelength has been achieved, offering a laser-like light source without any power density threshold requirement. Pump-power-dependent linewidth narrowing and nonlinear increase in PL counts are observed, suggesting ASE in our system and highlighting the potential of our ultrahigh-Q meta-optics platform for studying cavity-modulated quantum emitters and low-photon-number nonlinear optics. Additionally, our result holds great promise for applications like optical sensing, filtering, and metrology.

Methods

Metasurface fabrication

All metasurfaces without WSe2 emitter integration (Figs. 1–3 and Supplementary Fig. S5) are fabricated on a 1470 nm-thick SiO2 on silicon substrate (UniversityWafer, Inc.). The device for WSe2 integration and PL measurements (Fig. 4) is fabricated on a JGS1 fused silica substrate (UniversityWafer, Inc.). A 100 nm-thick layer of Si3N4 is grown on top of the substrates through low-pressure chemical vapor deposition (LPCVD) by UniversityWafer, Inc. The wafer is then diced into 8×8 mm2 chips (DAD321, Disco America).

The chips are thoroughly cleaned by sonication in acetone, followed by isopropyl alcohol (IPA), each for 5 min. After that, the SiN surface is treated by oxygen plasma at 150 W for 5 min to dry the surface and remove any solvent residue (AutoGlow, Glow Research). Subsequently, a 58 nm-thick layer of positive-tone resist PMMA is spin-coated and annealed under 180 °C for 3 min. After cooling the chip to room temperature, a layer of conductive polymer (DisCharge H2O) is spin-coated on top. The metasurface pattern is defined using a JEOLJBX-6300FS 100 kV electron-beam lithography system, followed by development in a cold water/IPA mixture for 2 min. The fabrication is etch-less, ensuring minimized sidewall roughness of the patterns.

Preparation of monolayer WSe2

WSe2 flakes are directly transferred onto the SiN surface using the standard tape exfoliation method. Monolayers are identified by checking the imaging contrast under optical microscope and confirmed using atomic force microscopy (AFM).

Optical setup and measurement

Optical characterizations are performed using a custom-built optical setup (Fig. 2a). Light is introduced into the setup via a single-mode fiber. The tunable laser (Newport TLB-6712), continuous-wave pump (Laserglow Technologies 532 nm DPSS Laser), and pulsed pump (NKT SuperK FIU-15 Laser, 78 MHz repetition rate, with a SuperK SELECT tunable multi-channel filter) are all coupled in this manner. The light is first focused on a 75 μm iris using L1 (focal length, f = 60 mm) and L2 (f = 75 mm) to ensure a uniform Gaussian beam. An objective lens is used to both focus the light onto the sample and collect the reflection/PL signals. To obtain the momentum-space-resolved spectrum, a telescope consisting of lenses L3 (f = 180 mm) and L4 (f = 150 mm) is employed. Here, L3 and L4 are confocal, L3 is in focus with the back focal plane of the objective lens, and L4 is in focus with the spectrometer CCD (Princeton Instruments Isoplane 160 with PIXIS 400).

In the laser-scanning momentum-space-resolved reflectance measurements (Fig. 2c, d and Fig. 3), a 2X Mitutoyo Plan Apo Infinity Corrected Long WD Objective (numerical aperture, NA 0.055) is used. To improve the signal-to-noise ratio, a crossed-polarization measurement method24,27 (Supplementary Note 3) is employed by inserting two linear polarizers into the excitation and collection light paths, respectively, as shown in Fig. 2a. The second polarizer also determines the polarization of the GMR modes. Note that there is no mirror between Polarizer1 and BS in the actual setup, and a plate beamsplitter is used instead of a cube beamsplitter to avoid extra interference caused by reflections at the optical interfaces. For signal collection, we use the 2D CCD in the commercial spectrometer with the grating disabled. The wavelength scanning of the tunable laser and the data capture by the CCD are synchronized and controlled by a Python script.

In the PL measurements (Fig. 4), a 10X Olympus PLN Objective (NA 0.25) is used. With a 650 nm short-pass filter in the excitation pathway and a 550 nm long-pass filter in the collection pathway, we filter the pump laser and ensure a clean PL signal. A single linear polarizer is inserted into the collection light path to ensure a clean s-polarized GMR signal. For signal collection, we use the commercial spectrometer with the 1200-lines/mm grating enabled.

Spectroscopy data processing

In the reflectance measurements (Figs. 1, 2, 3), both the device and background (the unpatterned-PMMA areas next to the device) spectra are collected — \({R}_{{{\rm{device}}}}\) and \({R}_{{{\rm{BG}}}}\). First, a difference operation is performed, \({R}_{0}={R}_{{{\rm{device}}}}-{R}_{{{\rm{BG}}}}\), to eliminate the multilayer interference influence. Then, low-frequency noise signals are filtered, as our ultrahigh-Q GMR signal is super high-frequency. The noise involves light source fluctuation, photodetector background, and the interference introduced by optical components like beamsplitters and lenses (the interference is severe when a tunable laser with good coherence is applied). The noise filtering is achieved via a customized two-dimensional bandpass filter in MATLAB, which transforms the data to the Fourier space by fast Fourier transform and selects the frequency components within an anisotropic elliptical donut-shaped region. The cutoff frequency is carefully chosen such that only the relatively low-frequency noise is filtered without affecting the high-Q signal. A linearly gradual cutoff is implemented to mitigate the ‘ring’ artifact due to abrupt frequency cutoff. The code is available on: https://github.com/charey6/2D-frequency-filter.git. Finally, the spectra are normalized to their respective maxima.

In the PL measurements (Fig. 4), after subtracting the setup background signals, the measured spectra are directly normalized to their respective maxima.

Spectra fittings

Spectra fittings are performed using a commercial software MagicPlot. For the spectra fittings in Fig. 3, the Fano fitting equation44 below is manually written into the software:

$${R}_{{{\rm{Fano}}}}(\lambda )=a\left[\frac{{\left(b+2\left(\lambda -{\lambda }_{0}\right)/\varGamma \right)}^{2}}{1+{\left(2\left(\lambda -{\lambda }_{0}\right)/\varGamma \right)}^{2}}c+\left(1-c\right)\right]$$

where \({R}_{{{\rm{Fano}}}}\) is the spectrum to be fitted. \(a\), \(b\), \(c\) are constant real numbers. \(\varGamma\) and \({\lambda }_{0}\) are the resonance FWHM linewidth and center wavelength. The Q-factor is then determined by Q = \({\lambda }_{0}/\varGamma\).

For the linewidth fittings in Fig. 4c, d, the Gaussian equation below is used:

$${PL}(X)=A\cdot {{{\rm{e}}}}^{-{{\mathrm{ln}}}(2)\frac{{\left(X-{X}_{0}\right)}^{2}}{{(\varGamma/2)}^{2}}}$$

where \({PL}(X)\) is the spectrum to be fitted. \(X\) can be the wavelength or momentum (angle). \(A\) is a constant real number. \(\varGamma\) is the FWHM linewidth in wavelength or momentum (angle), and \({X}_{0}\) is the center wavelength or zero angle (normal incidence).

The fitting errors are evaluated through the residual standard deviations automatically generated by the software in the fitting process. In specific, the software uses iterative Levenberg-Marquardt nonlinear least squares curve fitting algorithm to find the minimum residual sum of squares. Then, the corresponding residual standard deviation is used to describe the root mean square of the error (over all the data points) for the fitted parameters.

Numerical simulations

The commercial software Ansys Lumerical is used to simulate the momentum-space-resolved reflectance spectra of the metasurfaces (Fig. 1d) using rigorous coupled-wave analysis method (RCWA). As confirmed by ellipsometry (J.A. Woollam M-2000), we consider a 58 nm-thick PMMA with a refractive index of 1.46, a 100 nm-thick SiN with a refractive index of 1.99, and a 1470 nm-thick SiO2 with a refractive index of 1.44. Based on SEM measurements (Thermo Fisher Scientific Apreo 1), a slightly deviated device period P of 504 nm is applied. The SEM images can be found in Supplementary Fig. S11. Additionally, through AFM (Bruker Dimension Icon), we find that the defect hole depth is only ~40 nm, not completely penetrating the PMMA layer. This factor is also considered in the simulations.

Eigenmode analyses are conducted using a commercial finite element method solver, the wave optics module in COMSOL Multiphysics® 5.2 and 6.0. For each valid complex eigenfrequency f = Ω + i·Γ/2 found, where Ω and Γ are respectively the resonance frequency and damping rate, the Q-factor is determined by Q = Ω/Γ.