Introduction

Ferroelectric domain walls (FDWs) have been regarded as functional interfaces that separate ferroelectric domains with different polarization orientations in ferroelectric materials1,2,3. Controlling FDW dynamics enables the engineering of electrical output in ferroelectric devices4,5,6,7. An FDW can be electrically neutral8,9 or charged10,11,12, depending on the relative orientation of the ferroelectric order parameters across a domain wall13. An FDW can be perpendicular or parallel to the surface of a multilayer thin film, and these structures are denoted as out-of-plane (OOP)14,15 or in-plane (IP) FDWs1,16. The charged FDWs were demonstrated to exhibit high spatial mobility under electric fields1,3,17, indicating that they can be dynamically created, moved and erased on demand. However, it remains challenging to precisely control the FDW type and movement and reveal the in-depth mechanism of ferroelectric polarization switching, which are essential for property modulation and functional design in ferroelectric devices9,18.

Two-dimensional (2D) α-In2Se3, a unique van der Waals (vdW) ferroelectric semiconductor, shows exciting promise for nonvolatile memory and neuromorphic computing devices19,20,21,22,23,24. Ferroelectric semiconductor junction (FSMJ) devices made of metal/α-In2Se3/metal heterostructures exhibit exotic hysteresis in the electrical transport, which has been phenomenally postulated to involve the ferroelectric polarization control over the Schottky barrier at the metal/ferroelectric interfaces7,20,25,26. However, the lack of information on the FDW structure and FDW motion characteristics in α-In2Se3 has hampered the in-depth understanding of the FSMJ device mechanism, since the dynamics of polarization switching under electric fields has only been indirectly confirmed through piezoresponse force microscopy and electrical transport measurements, without real-space visualization of atomic-level structures (e.g., FDWs and metal/ferroelectric interfaces). Furthermore, In2Se3 has, at least, two stacking configurations (2H stacking and 3R stacking) and three phases (α phase, β phase, and β’ phase)27,28,29, displaying the diverse polymorphism. It remains unclear how the stacking configurations and phase structures affect the FDW microstructure and FDW motion, thereby determining the corresponding device’s resistive switching characteristics. Therefore, it is essential to select the In2Se3 polymorphism to study FDW dynamics in In2Se3 FSMJ devices.

In this work, we demonstrate the distinct ferroelectric polarization switching mechanisms in 2H and 3R α-In2Se3 FSMJ devices by direct visualization of stacking-dependent FDW. Specifically, α-In2Se3 display stacking-dependent FDW structures characterized in the atomic-level scanning transmission electron microscopy (STEM). And the first-principles density functional theory (DFT) calculations reveal that this peculiar stacking-selected FDW is associated with the different interlayer interactions and charge redistributions. In α-In2Se3 FSMJ devices, a combination of macroscopic electrical transport and the microscopic FDW motion confirm that the stacking configuration affects the FDW dynamics, leading to distinct ferroelectric polarization switching mechanisms and I–V hysteresis window (HW). Under a high electric field, the in situ electrical STEM results combined with DFT calculations indicate a strong layer-stacking dependency of the atomic displacement dynamics during the ferro-paraelectric phase transition in In2Se3. Our work provides an atomically resolved real-space visualization of polarization switching and introduces a pioneering strategy for selecting FDW types and dynamics by interlayer stacking engineering, laying the foundation for designing versatile ferroelectric devices.

Results and discussion

Stacking-selected ferroelectric domain walls

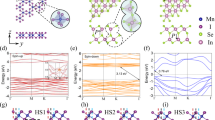
The unit cell of monolayer α-In2Se3 comprises five atoms arranged in an atomic sequence of Se-In-Se-In-Se, which are bonded by covalent bonds (Fig. 1a). The ferroelectricity in the monolayer originates from the displacement of the central Se layer from the symmetric positions23,30. As shown in Fig. 1a, when the central Se atoms in monolayer In2Se3 are shifted downwards and vertically aligned with the upper In layer, the electric dipole points upwards and the polarization direction is defined as Pup. When the central Se atoms are shifted upward, the polarization direction is defined as Pdown.

Fig. 1: Atomically resolved characterization of the ferroelectric domain configuration in 2H and 3R α-In2Se3.
figure 1

a Side views of two oppositely polarized α-In2Se3 monolayers. b, c HAADF STEM images of 2H and 3R α-In2Se3 along the [100] orientation, respectively. d, e HAADF STEM images of the IP FDW in 2H α-In2Se3 (d) and OOP FDW in 3R α-In2Se3 (e). The bottom panels of (d) and (e) show the magnified STEM images of the regions marked with boxes in (d) and (e), respectively. f, g Schematic illustrations of IP FDW in 2H α-In2Se3 (f) and OOP FDW in 3R α-In2Se3 (g). h, i OOP off-center displacements of central Se atoms in 2H (h) and 3R (i) α-In2Se3 for the structures displayed in (d) and (e), respectively. The central line within each box represents the median value, while the mean value is indicated by a small square inside the box. The top and bottom edges of the box correspond to the 75th and 25th percentiles, respectively, defining the interquartile range (IQR). The whiskers extend to 1.5 times the IQR from the quartiles. The atomic rows are parallel to the FDWs in 2H and 3R In2Se3, respectively, with sequence of the atomic row spanning from area 1 to area 3. A positive value of OOP off-centre displacement indicates that the displacement is along the positive direction of c-axis, as indicated in the insets in (h).

Full size image

In our exfoliated samples, two stacking orders were found, a hexagonal structure (2H, P63/mmc space group) and a rhombohedral structure (3R, R3m space group), both of which are the common stacking variants of the same α-In2Se3 monolayers, as illustrated in Fig. 1b, c. In 2H α-In2Se3, monolayers are stacked in an ABAB pattern, where the B layer is an in-plane rotation of the A layer by 60°. In 3R stacking, monolayers are arranged in an ABCABC manner, where three ABC layers are oriented parallel to each other without twisting. The cross-sectional high-angle annular dark field (HAADF) STEM images in Fig. 1b, c and the low-frequency Raman spectroscopy in Supplementary Fig. 1 confirmed the 2H and 3R lattice stacking of the exfoliated α-In2Se3 samples.

Differently from previous reports21,31,32, FDW microstructures in α-In2Se3 were revealed (Figs. 1d, e and S3), and IP and OOP FDWs were observed to be dependent on the 2H and 3R stacking configurations, respectively. The dependence of FDWs on stacking configurations is robust, as verified by STEM images acquired from several 2H and 3R In2Se3 samples (Supplementary Fig. 3). Figure 1d displays a STEM image of an atomically flat in-plane domain wall in 2H α-In2Se3. In the blue region of Fig. 1d, the polarization direction is Pdown, while in the red region, the polarization direction is Pup, indicating the presence of an IP ‘head-to-head’ FDW (Fig. 1f). An IP domain wall with a ‘tail-to-tail’ configuration was also observed in 2H α-In2Se3 (Supplementary Fig. 3b). Figure 1e shows a STEM image of an out-of-plane domain wall in 3R α-In2Se3 with two domains in a 180° orientation relation. The polarizations of the left (blue) and right (red) sides of the FDW are oriented antiparallelly in a side-by-side manner (Fig. 1g), namely, Pup (Pdown) for the left (right). We statistically measured the off-center displacements of central Se atoms in both 2H and 3R α-In2Se3 based on Fig. 1d, e to evaluate the magnitude of spontaneous polarization (Fig. 1h, i). The off-center displacement is calculated by the distance between the central Se atoms and the symmetric position along the c direction, which is ~0.4 Å in both 2H and 3R In2Se3, thus determining the magnitude of the OOP electric dipoles (~ 0.11 eÅ/unit cell from our theoretical calculations).

Furthermore, the atomic configurations of IP and OOP FDWs in 2D ferroelectric α-In2Se3 were systematically studied, revealing a stacking-selected atomic structure in the domain wall region. As shown in Fig. 1h, FDWs of 2H In2Se3 displays a uniform nonpolarity state with the central Se atomic layer in the center of two neighboring In layers, indicating a sharp flip of the polarization vector from Pdown to Pup (transition state in Fig. 1d), which is quite unusual in conventional bulk ferroelectrics3,16,33,34. In 3R In2Se3 with OOP FDW, there are three transition states during the transition from the Pup state to the Pdown state (Fig. 1i). The central Se atoms moved to a subpolarization position before reaching the center of the quintuple layer (7th and 9th atom rows in Fig. 1i), reflecting a gradual change in the electric dipoles (transition state in Fig. 1e). Furthermore, considering that α-In2Se3 exhibits both OOP and IP electric polarizations (dipole-locking effect)30,31,35, the IP displacements of Se atoms have also been statistically analyzed in the supporting information (Supplementary Fig. 4).

Ferroelectric polarization switching in ferroelectric semiconductor-metal junction devices

To investigate the impact of the stacking configuration and different FDWs on electrical transport, ferroelectric semiconductor-metal junction (FSMJ) devices based on different stacking α-In2Se3 were constructed (Supplementary Fig. 5). Firstly, Au was adopted as both top and bottom electrodes in FSMJ devices. As depicted in Fig. 2a, b, both 2H and 3R α-In2Se3 FSMJ exhibit non-volatile behavior with a counterclockwise hysteresis in I–V curves, indicating the switching between low resistance state (LRS) and high resistance state (HRS).

Fig. 2: Electrical characterization of α-In2Se3 FSMJ devices.
figure 2

a, b Representative I-E curves for 2H and 3R α-In2Se3 FSMJ devices with Au electrodes. c, d Representative I-E curves for α-In2Se3 FSMJ devices with Ag electrodes. The Inset shows the schematic diagram of the corresponding device. e Band diagrams illustrating the FSMJ in different resistance states as observed in the I-E curves. f Band diagrams of 2H and 3R α-In2Se3 FSMJ devices at the bottom α-In2Se3/metal interface.

Full size image

To understand the underlying mechanism of the counterclockwise and non-volatile characteristics in electrical transport, the band diagram of the FSMJ is shown in Fig. 2e. Since α-In2Se3 is a ferroelectric semiconductor, the current is predominantly determined by the Schottky-barrier height (SBH) at the semiconductor-metal interface. During polarization reversal, the bound charges produced by polarization will induce the accumulation of free charges at the interfaces and therefore determine the SBH. It is assumed that the polarization of α-In2Se3 in the FSMJ devices initially points upward. The negative polarization charges at the bottom metal/In2Se3 interface will reduce the electron concentration of n-type In2Se3 and raise the SBH for electron transport. When a small positive voltage is applied to the top electrode, electrons must overcome the high SBH between the bottom electrode and In2Se3 (Pup), placing the device in an HRS state (state I, Fig. 2e). As the applied voltage exceeds the coercive voltage, the polarization at the bottom interface switches to Pdown, reducing the SHB and shifting the device to the LRS state (state II, Fig. 2e). When a negative voltage is applied, electron injection occurs from the top electrode to In2Se3. In our FSMJ device, the upper metal/In2Se3 interface displays high defect density caused by thermal evaporation, which has been demonstrated by STEM image of the upper Au/ In2Se3 interface (Supplementary Fig. 6). Three typical types of defect layers with their specific atomic structures are provided in Supplementary Fig. 7. These defects result in the formation of polarized interfacial dipoles that favor the growth of fixed polarized domains hardly controlled by voltage bias36. The corresponding SBH at the upper metal/In2Se3 interface is low and the device remains in the LRS (state III, Fig. 2e). Upon further increasing the negative voltage, the polarization at the bottom interface reverts to Pup, increasing the SBH at the bottom interface and returning the device to the HRS (state IV, Fig. 2e). Notably, the ferroelectric polarization switching occurs primarily around the bottom metal/α-In2Se3 interface. This is because the lower metal/In2Se3 interface (STEM image in Supplementary Fig. 6), formed through a dry transfer process, shows vdW interactions, facilitating the reversal ferroelectric polarization switching. This suggests that electrical transport features associated with bottom In2Se3/metal interface are more closely related to ferroelectric polarizations.

We define the currents in the LRS and HRS as ILRS and IHRS, respectively, and quantify the HW by the ILRS/IHRS ratio. Although similar transition between two distinct resistance states were observed in both 2H and 3R FSMJ devices, the hysteresis window in 2H α-In2Se3 FSMJ is significant smaller than that in 3R α-In2Se3 FSMJ under both positive and negative biases (Fig. 2a, b). To investigate the origin of the HW difference (especially the relation to intrinsic ferroelectric effect of α-In2Se3) and eliminate the contact effect, Ag electrodes were further adopted in FSMJ devices. As shown in Fig. 2c, d, replacing the Au electrode with Ag increases the HW in 2H α-In2Se3 FSMJ under negative biases (Fig. 2a, c). As α-In2Se3 is an n-type ferroelectric semiconductor, the low-work-function Ag can reduce the Schottky barrier at upper metal/α-In2Se3 interfaces and reduce (increase) the LRS resistance (current) at state III. Therefore, the HW difference between Ag and Au FSMJ devices under negative biases indicates different contact effects at upper Ag/α-In2Se3 and Au/α-In2Se3 interfaces. Under positive biases, the smaller ILRS/IHRS ratio in 2H α-In2Se3 FSMJ compared to 3R α-In2Se3 FSMJ, independent of electrode type, suggests that the HW pattern under positive voltage is related to the stacking-dependent ferroelectric polarization switching instead of the contact effects. Consequently, the hysteresis data under positive bias in α-In2Se3 FSMJ devices are used to discuss the ferroelectric polarization behaviors of different stacking configurations in the following context.

As shown in Fig. 2a, c, the lower current densities and higher resistivities in state I (HRS state) is responsible for the stronger hysteresis in 3R In2Se3 FSMJ devices. This suggests that 3R In2Se3 FSMJ exhibits a higher SBH at the electron-injecting interface (bottom α-In2Se3/metal interface) under a positive bias (Fig. 2g), due to increased hole concentration caused by more negative bound charges (higher degree of polarization). Since polarization switching involves the formation, movement, and erasure of FDWs, OOP FDWs in 3R α-In2Se3 facilitate polarization switching and lead to a high intensity of polarization, whereas IP FDWs in 2H α-In2Se3 impose difficulties for polarization switching and result in the incomplete polarization switching around the bottom In2Se3/metal interface. Two dominant factors influence the polarization switching capacity of IP and OOP FDWs. First, it has been reported that mobile charges are required to compensate for the change in bound polarization charges at the ferroelectric/electrode interface during FDW motion37. In 2H α-In2Se3, the layer-by-layer switching mode of IP FDWs necessitates the complete polarization reversal of the bottom In2Se3 layer. In contrast, OOP FDWs in 3R α-In2Se3 enable nucleation of reverse domains in smaller regions. Given that the effective electric field is not uniform across the entire In2Se3-metal interface, it is challenging to provide sufficient carriers in all regions simultaneously. Therefore, OOP FDWs are more favorable for polarization switching, leading to more complete switching in 3R α-In2Se3 than in 2H α-In2Se3 at the bottom interfaces. Second, IP FDWs are more difficult to move than OOP-FDWs because IP-FDWs span micrometer-scale areas, whereas OOP-FDWs align with the material’s thickness, typically at the tens of nanometer scale1. In our work, we observed that OOP motion of IP FDWs in 2H α-In2Se3 encounters impediments at defects sites, leading to incomplete reversion (Fig. S8a). In contrast, for the 3R α-In2Se3, the OOP FDWs’ polarization reversal is only locally affected by defects, leaving overall FDW motion intact (Supplementary Fig. 8b). As a result, the SBH in 3R FSMJ devices is higher in state I, leading to a larger ILRS/IHRS ratio due to suppressed HRS current.

Moreover, FSMJ devices with different α-In2Se3 thicknesses have been constructed. To enhance ferroelectric polarization and device stability of FSMJ devices, In2Se3 with a thickness range of 40–80 nm are utilized (Supplementary Figs. 9 and 10). In all devices, the ILRS/IHRS ratios under positive bias are larger in 3R In2Se3 FSMJ than that in 2H In2Se3 FSMJ (Supplementary Fig. 11). Notably, for both 2H and 3R In2Se3 FSMJ devices, the maximum ILRS/IHRS ratios increase with device thickness. This is due to the weakening of the depolarization field and a decrease in the coercive field as thickness increases, as reported in prior studies38 and consistent with the behavior of conventional ferroelectric materials39. Under a certain electric field (e.g., 30 mV/nm), the ILRS/IHRS ratio of 2H In2Se3 FSMJ devices is less influenced by thickness compared to 3R devices. It is because the IP FDW motion in 2H In2Se3 presents significant challenges for polarization switching, leading to incomplete reversal despite the weak depolarization field in a 71-nm-thick device. In contrast, the ILRS/IHRS ratio in 3R In2Se3 FSMJ devices is significantly affected by the thickness due to the ease of polarization switching and the dominant effect of depolarization field. In 3R In2Se3, applying a higher electric field effectively counters the depolarization field, resulting in a larger hysteresis window.

Mechanism of stacking-dependent ferroelectric domain walls

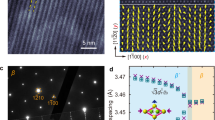
We conducted DFT calculations to uncover the mechanism underlying the selection of IP and OOP FDWs based on stacking sequences. The fully relaxed in-plane lattice constant of α-In2Se3 was found to be 4.07 Å in our work, which is comparable to that reported in literatures (4.05 Å)28,29. Other structural details are presented in Table S1, consistent with the structure parameters extracted from our experimental results. The fully relaxed atomic structures of the experimentally observed IP (in 2H, denoted 2H-IP) and OOP (in 3R, denoted 3R-OOP) FDWs, plotted alongside associated STEM images, are depicted in Fig. 3a, b (highlighted with yellow shadows, hereinafter). For comparison, we also considered two other OOP FDWs in 2H α-In2Se3 (Fig. 3c, d, 2H-OOP-A and -B) and another IP FDW in 3R α-In2Se3 (Fig. 3e, 3R-IP) to broaden the discussion.

Fig. 3: Mechanism of stacking-dependent FDW in α-In2Se3.
figure 3

a IP FDW atomic model after relaxation in 2H α-In2Se3 based on the atomic structures observed in the STEM image. b OOP FDW atomic model after relaxation in 3R α-In2Se3 based on the atomic structures observed in the STEM image. c, d Two simulated atomic models of OOP FDWs in 2H α-In2Se3 after relaxation. e The simulated IP FDW atomic model in 3R α-In2Se3 after relaxation. f Top and side views of differential charge density at IP FDW interfaces in 2H-stacked α-In2Se3 (area in vdW gap I in (a)). g Top and side views of the differential charge density at IP FDW interfaces in 3R-stacked α-In2Se3 (area in vdW gap II in (e)).

Full size image

For the 2H α-In2Se3 stacking, the formation energy of the experimentally observed 2H-IP FDW was calculated at 0.26 eV/In2Se3, representing a moderate value among the three 2H FDWs considered. The most stable FDW lies in 2H-OOP-A, which has a formation energy of 0.15 eV/In2Se3. However, its boundary structures exhibit non-uniformly distributions, alternating between two different structures (Fig. 3c). Thus, the growth of this nonuniform structure is, most likely, limited by kinetics, posing obstacles to its experimental observation. Although the FDW structures are uniformly arranged in the other OOP FDW in 2H α-In2Se3, denoted as 2H-OOP-B, the interlayer stacking order of the 2H-OOP-B FDW deviates from that of pristine 2H α-In2Se3 and the FDW possesses the highest formation energy, calculated at 0.31 eV/In2Se3. The experimentally observed 2H-IP FDW preserves the original stacking configuration in 2H α-In2Se3, features a uniformly arranged boundary structure, and a reasonably lower formation energy. Figure 3f plots the interlayer differential charge density of the 2H-IP FDW, highlighting significant charge transfer from each Se atom within the FDW region to the three nearest-neighboring Se atoms in the adjacent quintuple layers (indicated with blue springs). Such an interfacial charge transfer, contrasting with the charge sharing noted in 2H-OOP-B (as detailed in Supplementary Fig. 12b, c), effectively reduces the Pauli repulsive energy encountered at the vdW gaps in metal selenides40,41. This reduction in repulsion yields a formation energy of the 2H-IP FDW that is 0.05 eV/In2Se3 lower than that of the 2H-OOP-B FDW. Considering both structural uniformity and formation energy, the above analysis explains the preferential formation of IP FDWs in the 2H stacked In2Se3 few-layers.

For the 3R stacking configuration, it demonstrates an enhanced stability of 4 meV/In2Se3 over the 2H stacking in pristine α-In2Se3 layers. The 3R α-In2Se3 facilitates the formation of a uniform OOP FDW, denoted 3R-OOP, which was experimentally observed, as shown in Fig. 3b. An IP FDW, denoted 3R-IP, is presented in Fig. 3e for comparison. The formation energy of the 3R-OOP FDW is quantified at 0.22 eV/In2Se3, rendering it 0.06 eV/In2Se3 more energetically favorable than that of the 3R-IP FDW (0.28 eV/In2Se3). This result aligns remarkably well with the exclusively observed OOP FDWs in STEM images of 3R α-In2Se3. The 3R-OOP FDW preserves the 3R stacking order for, at least, the outermost Se layers of each quintuple layer (Supplementary Fig. 12e, f). In contrast, the 3R-IP FDW is against to uphold this energetically preferred interfacial 3R stacking. As illustrated in Fig. 3e, the formation of an IP FDW from the inherent stacking of 3R-In2Se3 positions each interfacial Se atom within the vdW gap II at a bridge site between two Se atoms in the adjacent In2Se3 layer. Their interfacial Se–Se interactions are elucidated via red springs for clarity. Meanwhile, the original 3R stacking is indicated by blue springs in the vdW gap I. Figure 3g plots the differential charge density at the vdW gap II of the 3R-IP FDW, clearly showing a Se atom interacting with only two nearest neighboring Se atoms across the gap (upper panel). This reduction in the number of interacting neighbors weakens the interfacial Se–Se interactions in comparison to those observed in the 2H-IP FDW (Fig. 3f), leading to a higher formation energy and diminished stability of the 3R-IP FDW. Nevertheless, for the top In2Se3 quintuple layer shown in Fig. 3e, a collective lateral shift by 1/3 of a unit-cell could significantly reduce the formation energy at the vdW gap II. However, this shift introduces a stacking fault in the upper In2Se3 domain, thereby further compromising the stability of the entire In2Se3 domain adjacent to the IP FDW. In summary, through the calculation of formation energies and examination of interfacial electronic interactions, we have delineated the formation mechanism of the stacking-locked IP and OOP FDWs in α-In2Se3, which essentially relies on structural uniformity and stacking-dependent interlayer interactions. Additionally, the formation energies of different model sizes are taken into consideration (Supplementary Fig. 13), which shows consistent conclusion.

Atomic mechanism for ferroelectric degradation under an electric field

During the operation of a ferroelectric device, a high electric field may induce a phase transition or even the breakdown of ferroelectric materials42,43,44. It is important to investigate the atomic mechanism for ferroelectric degradation in ferroelectric devices by applying an excessively large electric field. The ferroelectric α phase to paraelectric β phase transition in In2Se3 was observed via selected area electron diffraction in previous works45,46,47, but atomic details of characterizing this phase transition process are lacking, and the relationship between the atomic-level transition dynamics and the α-In2Se3 stacking order has yet to be established. We therefore conducted in situ electrical STEM experiments (Supplementary Fig. 14) on 2H and 3R α-In2Se3 to investigate the atomic displacement with increasing electric field and discuss the impact of stacking configurations on the kinetic pathways of phase transition processes. Both 2H and 3R In2Se3 undergo an α to β phase transition under a high electrical field. The in situ STEM images indicate that the transition pathway is dependent on the stacking order, revealing that 2H and 3R In2Se3 follow the interlayer (Fig. 4a, b and c) and intralayer (Fig. 4d, e and f) phase transition pathways, respectively.

Fig. 4: In situ electric field-driven α-In2Se3 to β-In2Se3 phase transitions.
figure 4

a, d HAADF-STEM images of the α/β In2Se3 interfaces in the process of α to β phase transformation in 2H (a) and 3R (d) stacking, respectively. b, e Schematics of interlayer phase transition in 2H In2Se3 (b) and intralayer phase transition in 3R In2Se3 (e). c, f Atomic models of α/β In2Se3 interfaces in 2H and 3R In2Se3 based on the STEM images in (a) and (d), respectively. g, i Atomic models of two pathways (Path-O and Path-I) in the phase transition process of 2H and 3R, respectively. h Energy difference between MS1-O-2H/MS1-I-2H and 2H α-In2Se3 under various external fields. j Energy difference between MS1-O-3R/MS1-I-3R and 3R α-In2Se3 under varying external fields.

Full size image

First, we present the atomic details of the phase transition process within 2H- and 3R-stacked In2Se3. An atomically resolved cross-sectional STEM image, as shown in Fig. 4a, unequivocally displays an interface between 2H stacked α-In2Se3 and β-In2Se3. The left of the image depicts a cross-sectional side-view of α-In2Se3, where the lower terminating Se atom of a Se-In-Se tri-atomic layer is positioned above an In atom of the In-Se bi-atomic layer of the same In2Se3 quintuple layer, resulting in a kinked Se-In-Se-In-Se configuration within the α-In2Se3 quintuple layer. The right segment of the image illustrates the straightening of this kicked configuration. The In-Se bi-atomic layer of the lowermost α-In2Se3 layer covalently bonds with the Se-In-Se tri-atomic layer of the second uppermost α-In2Se3 layer, forming a β-In2Se3 layer where the Se-In-Se-In-Se atoms are almost aligned. The real-time in situ imaging of the atomic phase transition dynamics under a mild electric field (ranging from 0 to 0.28 V/nm) unveils a decrease in the interlayer distance from 3.1 to 2.3 Å (Supplementary Fig. 15). Upon an increased electric field exceeding 0.5 V/nm, the In atoms in the In-Se bi-atomic layer (labelled as In2 in Fig. 4c) descend across the bottom Se layer and eventually settle in the vdW gap, forming covalent bonds with Se atoms from the adjacent α-In2Se3 quintuple layer. Figure 4g delineates atomic configurations associated with this process as metastable states 1 (MS1-O), 2 (MS2-O) and final β-phase (β-phase-2H), thus identifying this transition pathway as interlayer OOP atomic migration (Path-O).

Figure 4d depicts a STEM image of the 3R stacking α-In2Se3/β-In2Se3 interface, highlighting that the phase transition is initiated by the intralayer sliding of In and Se atoms. This process begins with a collectively lateral displacement of the Se-In-Se tri-atomic layer within an α-In2Se3 quintuple layer to the right, until the lateral position of the In atom in the Se-In-Se tri-atomic layer aligns with the midpoint of the two neighboring In atoms in the In-Se bi-atomic layer (under an electric field of 0.3 V/nm, for STEM images and atomic structures, see Supplementary Fig. 16). Upon application of a higher electric field (~0.6 V/nm), the central Se atom within the In2Se3 quintuple layer descends to the center of quintuple layer (Fig. 4f), thus forming a β-In2Se3 quintuple layer. Consequently, this transition pathway is designated as intralayer in-plane atomic migration (Path-I in Fig. 4i), which is consistent with the theoretical prediction in previous reports48,49.

These findings elucidate that the transition pathways from the α- to β-phase transition are intrinsically correlated with the stacking orders. To uncover the mechanism underpinning this correlation, we performed DFT calculations to assess the energetics involved in the transition processes for 2H and 3R In2Se3. Figure 4h, j plot the energies of the first meta-stable state (EMS1, with structures delineated in MS1 of Fig. 4g, i), relative to the pristine α-phase In2Se3, across the transition processes for both the Path-O and Path-I pathways in both 2H and 3R stacked In2Se3 under various electric fields.

In the 2H stacking configuration, the EMS1 for Path-O (denoted EMS1_O, represented by red dots in Fig. 4h) is 0.08 eV/In2Se3, which is 0.02 eV/In2Se3 lower than that of Path-I (denoted EMS1_I, represented by black dots in Fig. 4h) in the absence of an external electric field. The application of an external electric field further reduces EMS1_O, reaching −0.05 eV/In2Se3 under 0.3 V/Å, while the electric field exerts negligible effect on EMS1_I. This difference in energy response to the electric field is primarily ascribed to the large polarization strength arising from intralayer atomic splitting and interlayer atomic recombination in the MS1 configuration for Path-O. Therefore, Path-O is thermodynamically more favorable for the α- to β-phase transition in 2H In2Se3, particularly under the influence of applied electric fields.

Supplementary Fig. 17a, b indicate that the transition barrier from the pristine 2H In2Se3 to MS1 for Path-O (0.43 eV/ In2Se3) is significantly higher than that for Path-I (0.13 eV/In2Se3) without an electric bias. The imposition of an electric field of 0.3 V/Å increases the transition barrier of Path-O to 0.67 eV/In2Se3. Nevertheless, this barrier energy remains surmountable through thermal excitation at room temperature or under a high electric current density, as predicted by the Arrhenius equation50. By combining these theoretical and experimental results, we conclude that the preferred Path-O transition pathway (characterized by intralayer-splitting/interlayer-reconstruction) in the 2H stacking is primarily determined by thermodynamic considerations.

For the 3 R stacking, EMS1-I = 0.11 eV/In2Se3 (black dots in Fig. 4j) is substantially lower than that of Path-O (EMS1-O = 0.59 eV/In2Se3, red dots in Fig. 4j). Both energies are almost unaffected by the external electric field applied normal to the layers, rendering Path-I the preferred pathway because of its lower energy cost. Moreover, the structural transition barrier from pristine 3R In2Se3 to MS1 for Path-I is approximately 0.13 eV/In2Se3 (Supplementary Fig. 17c), which is much lower than that for Path-O in the 2H stacking and could be effortlessly overcome at room temperature. Thus, the 3R stacking exhibits a preference for Path-I (intralayer sliding transition) from both thermodynamic and kinetic points of view.

Moreover, it is observed that FSMJ devices undergo irreversible transition to low-resistance state under high sweep voltage (Supplementary Fig. 18a, b). To establish the links between micro in situ experiment and macro FSMJ devices, STEM characterization was conducted on FSMJ devices after they transitioned to an irreversible low-resistance state. In both 2H and 3R FSMJ samples, large regions of β-phase In2Se3 were observed (2H-β in Supplementary Fig. 19b and 3R-β in Supplementary Fig. 19d), indicating that the α to β phase transition in In2Se3 occurs when the device switches to an irreversible low-resistance state. From another aspect, during the in situ STEM experiments, the I-E characteristics have also been recorded (Supplementary Fig. 20) and the device resistance shifted from a high-resistance state to a low-resistance state when the electric field reached a threshold (0.5 V/nm in 2H, 0.6 V/nm in 3R) during the α to β phase transition. Independent of the applied voltage, the device remained in the low-resistance state and was unable to revert to the high-resistance state. This resistance change in in situ experiments aligns with the significant current increase observed in FSMJ devices at specific voltages, verifying that the irreversibility of the transport characteristics after applying a threshold bias to the device is associated to an irreversible structural phase transition.

Overall, the stacking order of the 2D ferroelectric semiconductor In2Se3 determines the FDW type, the ferroelectric switching behavior and the phase transition pathways. We propose that the selection of stacking order can further result in versatile ferroelectric properties, which establishes a foundation for future ferroelectric device engineering based on controlled layer stacking.

In summary, we demonstrate that the stacking order of vdW α-In2Se3 primarily determines the polarization switching manner and results in a varied HW in FSMJ devices. The proposed mechanism was verified by STEM characterization and DFT calculations, which revealed that the type and motion of ferroelectric domain walls—either IP or OOP—are dependent on the specific stacking configurations of α-In2Se3. The atomic arrangement of 2H stacking promotes the occurrence of IP FDWs and OOP FDW motion, whereas 3R stacking tend to favor the emergence of OOP FDWs and IP FDW motion. Moreover, we demonstrated that the stacking configuration also affects the atomic mechanism for ferroelectric degradation under an electric field. This result reveals that 3R In2Se3 undergoes an α to β phase transition through intralayer atomic gliding, while 2H In2Se3 experiences a more complex phase transition involving intralayer bond dissociation and interlayer bond reconstruction. These groundbreaking insights enhance our understanding of FDW dynamics in 2D ferroelectric materials, and establish an unique platform for the engineering of ferroelectric materials and ferroelectric devices through layer stacking modulation.

Methods

Material characterization

Multilayer α-In2Se3 nanoflakes were mechanically exfoliated from 2H-stacked bulk single crystals purchased from Shanghai Onway Technology Co., Ltd and 3R-stacked crystals from 2D semiconductor Inc. The 3R and 2H α-In2Se3 films were characterized by Raman spectroscopy (WITec, alpha300 R; 532 nm laser; spectral resolution 1–2 cm−1; laser power 3.002 mW) and transmission electron microscopy (TEM) (FEI Titan3 Themis G3 60–300 operated at an accelerating voltage of 300 kV). The laser beam of the Raman system was focused onto the samples with a diameter of about 1–2 μm, and the power density is calculated to be 9.5 × 104 W/cm².

HAADF-STEM measurements and in situ electrical experiments

The specimens for the STEM study were fabricated by a focus ion beam (FIB) in a Helios G4 UC DualBeam scanning electron microscope (Thermo Fisher Scientific). Few-layer α-In2Se3 flakes were mechanically exfoliated from the bulk crystals and then transferred to TEM grids by FIB. More details of the FIB process are provided in the supporting information. Atomic-scale HAADF-STEM images of 3R and 2H In2Se3 were obtained by a FEI Titan3 Themis G3 60–300. A TEM electrical holder (Gatan) and specialized four-electrode chips are utilized in the in situ electrical TEM experiments. The voltage used in the in situ TEM experiments was generated by a Keithley 4200A-SCS.

Device fabrication and characterization

Multilayer α-In2Se3 nanoflakes were mechanically exfoliated from bulk crystals and then transferred by polydimethylsiloxane onto the bottom electrode lines. The bottom Ti/Au electrode lines with a thickness of 5/20 nm were sequentially patterned by sputtering (DENTON DISCOVERY-635). After transferring multilayer α-In2Se3, 40 nm thick Au was patterned and deposited by thermal evaporation as the top electrode followed by a standard lift-off process. As FSMJ devices are operated through thermionic emission across a Schottky barrier, utilizing In2Se3 with a thickness range of 40–80 nm can enhance ferroelectric polarization and device stability, facilitating a more comprehensive investigation of the FDW manifestation within the device. All electrical measurements for the α-In2Se3 FSMJ devices were performed in a cryogenic probe station (Lakeshore) under vacuum and in a dark environment and measured with a Keithley 4200 A semiconductor parameter analyzer.

DFT calculations

DFT calculations were performed using the generalized gradient approximation in the Perdew-Burke-Ernzerhof (PBE) form51 for the exchange-correlation potential, the projector augmented wave method52, and a plane-wave basis set as implemented in the Vienna ab-initio simulation package53. Grimme’s D3 form vdW correction was considered with the PBE exchange functional (PBE-D3)51,54 for all structural relaxations. The structures were fully relaxed until the residual force per atom was less than 0.05 eV/Å. An energy cut-off of 500 eV was used for the plane wave basis set in all structures. The structures of the OOP FDW were considered in a \(7\sqrt{3}\) × 1 × 1 supercell, and a k-mesh of 1 × 22 × 2 was used to sample the first Brillouin zone. The structure of IP FDW is a slab model made of five layers of In2Se3, and a k-mesh of 12 × 22 × 1 was used to sample the first Brillouin zone in a \(\sqrt{3}\) × 1 × 1 supercell. A vacuum layer larger than 15 Å was used in the slab model to avoid interactions between the slabs of adjacent supercells. The formation energy E for FDW is defined as \({E}_{\text{formation energy}}\,=\,({E}_{\text{total}}-n\,\cdot {E}_{\text{bulk}})/{n}_{\text{In}2\text{Se}3}\). \({E}_{\text{total}}\) is the total energy with FDW, \(n\) is the number of In2Se3 unit cells,\(\,{E}_{\text{bulk}}\) is the total energy per In2Se3 unit cell of pristine bulk In2Se3, and \({n}_{\text{In}2\text{Se}3}\) is the number of In2Se3 unit cells on the domain wall. The phase transition barrier was estimated by using the nudged elastic band method55.