Abstract
Episodic memory involves the processing of spatial and temporal aspects of personal experiences. The lateral entorhinal cortex (LEC) plays an essential role in subserving memory. However, the mechanisms by which LEC integrates spatial and temporal information remain elusive. Here, we recorded LEC neurons while male rats performed one-dimensional tasks. Many LEC cells displayed spatial firing fields and demonstrated selectivity for traveling directions. Furthermore, some LEC neurons changed the firing rates of their spatial rate maps during a session (rate remapping). Importantly, this temporal modulation was consistent across sessions, even when the spatial environment was altered. Notably, the strength of temporal modulation was greater in LEC compared to other brain regions, such as the medial entorhinal cortex, CA1, and CA3. Thus, we demonstrate spatial rate mapping in LEC neurons, which may serve as a coding mechanism for temporal context, and allow for flexible multiplexing of spatial and temporal information.
Similar content being viewed by others
Introduction
Our memory of everyday experiences involves proper representation of spatial and temporal context. The hippocampal memory system plays an essential role in episodic memory. Indeed, diverse mechanisms for representing space and time have been revealed in the hippocampus and its neighboring regions1,2,3,4. However, the exact neural mechanisms responsible for representing space and time upstream of the hippocampus remain unknown.
The lateral entorhinal cortex (LEC) and medial entorhinal cortex (MEC) constitute the major cortical inputs to the hippocampus, and they exhibit important anatomical and functional specializations5,6. MEC contains functional cell types such as grid cells, boundary/border cells, head direction cells, non-grid spatial cells, and speed cells7,8,9,10,11. The presence of these cells strongly supports the hypothesized role of the MEC in constructing a universal, allocentric map through the computation of path integration12,13,14. In contrast, LEC neurons display comparatively little allocentric spatial information15,16. LEC neurons receive rich multisensory information about the external world and can respond to olfactory, visual, and auditory stimuli17,18,19. LEC cells encode spatial information related to the objects or items in the environment20,21,22,23, and they appear to primarily represent this information in an egocentric coordinate frame22,23. Additionally, LEC is involved in encoding temporal information across time scales spanning seconds to hours24. This finding is corroborated by the evidence of a positive correlation between blood-oxygen-level-dependent activity in LEC and the precise temporal position judgment of movie-frames within a movie by human subjects25. Thus, LEC encodes forms of both spatial and temporal information, but how LEC neurons integrate these types of information remains largely unexplored.
In the hippocampus, such integration of spatial and nonspatial factors has been studied in the context of the remapping phenomenon. Remapping is the change of representation by spatial coding cells, which could signal alterations in spatial context26,27 or nonspatial factors28. Global remapping entails alterations in the recruitment of cells and the firing locations of place fields, establishing an orthogonal relationship between different representations27. In contrast, rate remapping is a type of remapping in which the recruited population of cells and their firing locations remain constant but the firing rates of the cells within their place fields are altered29. Rate remapping has been suggested to constitute a multiplexed code that supports episodic memory, in which a spatial framework for binding information about the various aspects of an event is represented by place cell firing locations30,31, and the specific information about the content of the event itself is represented by the firing rates of the neurons within their place fields29. For instance, Sun et al. have shown that lap identity information can be decoded from the firing rate patterns of hippocampal place cells32. Although rate remapping has been observed in the hippocampus and MEC29,33,34, its relevance to understanding the role of LEC in episodic memory is unclear. LEC is known to represent temporal information24,25, and recent work has demonstrated that under certain conditions, LEC cells can show a previously unknown degree of spatial tuning35,36,37. These findings allow a test of whether LEC performs rate remapping of a spatial signal similar to that shown previously in the hippocampus and MEC, which would allow the LEC to interact with these two regions using a consistent representational scheme.
In this work, we characterized the neural activity of LEC while rats ran on 1-D linear and circular tracks. We found that many LEC neurons showed robust spatial selectivity in these tasks, showing sensitivity to both the direction of travel and manipulation of the spatial environment. In addition, the spatial rate maps demonstrated temporal modulation across laps within a session, suggesting the representation of temporal information through spatial rate remapping. The results reveal a flexible, spatially and temporally multiplexed code in LEC.
Results
Behavioral setup
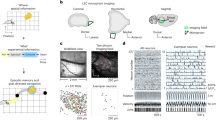
We used three types of one-dimensional tasks: the double rotation task, the circular track task, and the linear track task. In the double rotation task38, rats moved clockwise on a circular track for irregularly placed food reward; local cues on the track and global cues on a curtain in the periphery of the room were put into conflict during Mismatch sessions (i.e., local and global cues were rotated by equal increments in opposite directions, generating mismatch angles of 45°, 90°, 135°, and 180°) (Fig. 1a). In the circular track and linear track tasks (Fig. 1b, c), food wells were fixed at the ends of the journeys, and the rats were required to traverse the same locations in two different directions. For the circular track task, a dark session in which lights were turned off was placed between two standard (Light) sessions. These task structures enabled us to investigate the representation of spatial and temporal information in LEC. A subset of the data was reported in prior studies24,39 to address questions that were different from the present report.
a Schematics of the double rotation task. Three standard (STD) sessions were interleaved with two mismatch (MIS) sessions. In the MIS sessions, local cues on the track were rotated counterclockwise and the global cues along the curtain at the periphery of the room (the black outer ring) were rotated clockwise. The subjects foraged for food scattered at arbitrary locations on the track (~2 rewards/lap) while moving clockwise. b The circular track task. Two sessions recorded in the light condition were separated by a session in the dark. c Linear track. For both the circular track and linear track, the animals shuttled back and forth to retrieve food pellets in the food wells placed at the ends of the journeys. d Spatial firing patterns of three example LEC neurons in the double rotation task. For each cell, the spatial rate map of the session is shown at the top (the number on top indicates the spatial information score) and the lap-wise spatial rate map is shown at the bottom (the number on top shows the peak firing rate of the map). e The session-wise spatial rate maps and lap-wise spatial rate maps of two LEC cells in the circular track task. The rate maps of the two movement directions are separately shown for each cell. f Histograms of the distribution of spatial information scores for all LEC neurons in the three behavioral tasks. Source data are provided as a Source Data file.
LEC neurons showed spatial selectivity in one-dimensional tasks
We recorded a total of 368 LEC neurons from 8 male Long-Evans rats (Fig. S1) in the three tasks (119 neurons from 3 rats in the double rotation, 239 neurons from 5 rats in the circular track, and 231 neurons from 5 rats in the linear track task; some neurons were recorded over multiple tasks). We excluded cells that fired <20 spikes within a session (defined as minimally active cells) or whose firing rate was >10 Hz (putative interneurons15). To characterize the spatial firing patterns of these neurons in one-dimensional tasks, we first linearized the position in the circular track task and double rotation task. There were frequent off-track head scanning events in the double rotation task. We detected and removed position frames during these scanning events (Fig. S2a), as these events were typically spatially inhomogeneous and behaviorally distinct from the dominant forward movement behavior in these tasks40. Unlike previous studies of LEC in empty, 2-D arenas that showed minimal amounts of allocentric spatial representation15,16, some LEC cells in all three tasks showed clear spatial firing fields in allocentric rate maps (Figs. 1d–f and S2b–d)35,37. For some neurons, the spatial selectivity and reliability were similar to those of hippocampal neurons. Overall, the median spatial information score in the double rotation task was 0.27 (Interquartile range (IQR) = 0.14–0.60); in the circular track task was 0.141 (IQR = 0.077–0.336); and in the linear track task was 0.140 (IQR = 0.073–0.341). We classified cells as significant spatially tuned cells with spatial information score and shuffling controls (see Methods) (double rotation task: 24/97; circular track task: 38/231 for at least one movement direction; linear track task: 34/217 for at least one movement direction) (Fig. S2). The spatial representations of LEC neurons were sensitive to changes in the environmental context, such as rotation of landmarks and extinction of lights (Fig. S3).
The spatial firing of LEC neurons was sensitive to movement direction
Hippocampal and MEC neurons show direction selectivity when rats perform shuttling tasks on one-dimensional tracks41,42,43,44,45,46. We found that the spatial firing of LEC neurons also distinguished traveling directions in the circular track and the linear track tasks (Figs. 2a and S4). For some neurons, the overall firing was greater for one direction than the other; for other neurons, the cell preferred different directions at different locations on the track. A permutation method was adapted from ref. 47 to identify the cells with significant direction selectivity (see Methods). Approximately 40% of LEC neurons (circular track task: 97/213, linear track task: 90/211) had a significant preference for travel direction in at least one location. The distribution of directionally selective locations is significantly different from a uniform distribution, as the locations with directional selectivity were biased toward the ends of the track (Fig. 2b, Rayleigh test, p < 0.001 for both standard and dark circular track data; Fig. 2c, Monte Carlo test, p < 0.001 for linear track data).
a Left, four example LEC neurons showing directionally selective firing on the circular track. Shaded red and blue colors denote the mean ± SEM for counterclockwise and clockwise movement, respectively. The black line denotes the difference between the firing rates for the two directions. Colored lines and dotted lines are thresholds for detecting pointwise and family-wise significant regions, respectively. Bold color lines at the top denote regions of significant direction selectivity. Right, four neurons with direction selectivity in linear track paradigm. Same conventions as for the circular track (left). b Distribution of locations with peak direction selectivity index (see Methods) for each cell on the circular track. c Same as Fig. 3b for the linear track. d Four example LEC neurons with strong distance coding in the circular track task. All four cells fired comparably depending on the distance from the start of the journey. e Same as panel (d) for four cells in the linear track task. f Left: sorted spatial rate maps for the two directions in the circular track task. Right: population correlation matrix between the two directions. A high correlation in the main diagonal (bottom left to top right) indicates consistent firing at the same location for the two directions, whereas a strong signal in the minor diagonal (top left to bottom right) indicates consistent firing at the same journey distance from the track ends. g Left, the observed mean correlation of bins along the minor diagonal of the correlation matrix (i.e., from top left to lower right showing the correlation between the same distances from the start position in both directions) is shown as the red line and the null distribution is simulated with a permutation analysis. Right, the observed correlation difference (the red line) and the null distribution comparing the distance coding from the starting position (the first 4 bins) and the end position (the last 4 bins). h, i Same as panels (f) and (g) for the linear track task. Source data are provided as a Source Data file.
In some cases in which a cell preferred different directions at different locations on the track, the locations were symmetrically organized (Fig. 2d, e; Fig. 2f, h). In other words, the cells appeared to be sensitive to the distance traveled along the track in each direction. Figure 2f, h shows the rate maps of all cells on the circular and linear tracks, respectively, in each direction, ordered by the peak firing rate in the first direction. The lack of a strong diagonal in the ordered rate maps of the opposite direction demonstrates the prevalence of directional firing. To the right of the ordered rate maps are correlation matrices of the ordered rate maps for each direction. For the circular track (Fig. 2f), the correlation matrix shows an X-shaped pattern, indicating that some cells fired at the same locations in both directions (the main diagonal), whereas other cells showed distance coding (the minor diagonal). The average correlation along the minor diagonal was significantly larger than a null distribution (Fig. 2g, left, p < 0.001). Similar results were observed on the linear track (Fig. 2h; Fig. 2i, left, p < 0.001), although there was a strong asymmetry between the strength of the correlations on the upper left and the lower right quadrants of the correlation matrix. This asymmetry indicates that the distance coding was significantly stronger at the start of the journey than at the end, a result not observed in the circular track task (circular track: Fig. 2g right, p = 0.29; linear track: Fig. 2i right, p = 0.007). However, a significant difference in the differential distance tuning for the start vs. the end of the journey was not observed between the linear track and the circular track (p = 0.24, permutation test, not shown). The lack of a statistical difference between linear and circular track data made the apparent difference in the correlation matrices ambiguous.
Representation of trial progression by LEC neurons
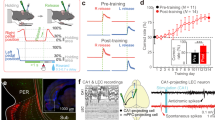
Because the entorhinal cortex has been implicated in the processing of temporal information24,25,48,49,50,51, we explored whether LEC cells encode information about the temporal progression of trials. When lap-wise spatial rate maps were created for LEC, the spatial firing rates for different laps showed clear modulation across the session (Figs. 3 and S5). Singular value decomposition (SVD) is a popular technique used to decompose the spatiotemporal or spectro-temporal receptive fields of visual or auditory neurons52,53,54. This procedure can extract the single component that could account for most of the variance/shape in the lap-wise rate maps, with the remaining components being orthogonal to it. Therefore, this method has the advantage of the ease of interpretation of the resulting decomposition. We used SVD to decompose the lap-wise spatial rate maps into spatial and temporal firing profiles, which we termed spatial modulation fields and temporal modulation fields, respectively (Fig. 4a and S6; see Methods). Figure 4b, c demonstrates the reproducibility across sessions of temporal modulation fields for 12 neurons with highly reproducible temporal firing profiles in the double rotation and circular track tasks (see Fig. S5 for examples of other cells with less reproducible firing). We quantified this reproducibility by calculating correlation coefficients of temporal modulation fields across sessions for each neuron. The mean correlation coefficients of all neurons were significantly greater than those from null distributions obtained by permuting cell labels in the second session (the double rotation task: Fig. 4d, STD 1 vs. STD 2, p = 0.022, STD 1 vs. STD 3, p = 0.018; the circular track task: Fig. 4e, direction 1, p = 0.011, direction 2, p < 0.001). We operationally classified cells with significant temporal information scores and between session correlations as temporally tuned neurons (see Methods). For the double rotation task, 10/87 cells passed the criteria; for the circular track task, 38/135 cells passed the criteria for at least one movement direction. Some LEC cells showed consistent temporal modulation in the absence of strong spatial selectivity (Fig. S5) (double rotation task: 6/10; circular track task: 17/21 and 17/20 for the two directions), which suggests that a temporal signal could be present independent of spatial selectivity24. Altogether, our results demonstrate that LEC might represent temporal information about trial identity through spatial rate remapping.
a Three example cells. Each row shows the lap-wise spatial rate maps for an LEC neuron in three STD sessions in the double rotation task. Cell 1 decreases its firing over the laps of the session, whereas cells 2 and 3 increase their firing from near silence on lap 1 to robust firing at specific locations in later laps. b Same as panel (a) for three cells in the circular track task. Source data are provided as a Source Data file.
a Schematics for decomposition of the lap-wise spatial rate maps into spatial and temporal modulation fields. b The temporal modulation fields of six example cells across sessions in the double rotation task. Each cell shows similar temporal modulation in all sessions. c Same as panel (b) for six neurons in the circular track task. d The observed correlation (red line) and null distribution of correlations between the temporal modulation fields in two sessions in the double rotation task. Left: STD1 vs. STD2; right: STD1 vs. STD3. e Same as panel (d) for data in the circular track task. Left: Light 1 (STD1) vs. Light 2 (STD2) in direction 1; Light 1 (STD1) vs. Light 2 (STD2) in direction 2. f Same as panel (d) for correlations between temporal modulation fields in STD sessions and manipulated sessions in the double rotation task (left) and the circular track task (right). Source data are provided as a Source Data file.
We next investigated if the temporal signal about trial progression was robust to alterations of the spatial environment. We compared the temporal modulation fields of STD and MIS sessions in the double rotation task and the temporal modulation fields of STD and dark sessions in the circular track task. For some cells, the temporal modulation fields in STD sessions and MIS sessions were similar (cells that had a correlation coefficient greater than 0.3: double rotation task, 40/85; circular track task, 44/140 and 46/137 for the two directions; Fig. 4b, c). The mean correlations between STD sessions and manipulated sessions were significantly larger than the null distribution created by permuting the cell identities in the second session (Fig. 4f; p < 0.001 for both the double rotation task and the circular track task). The temporal modulation fields were also significantly correlated between the two movement directions within a session for the circular track task and the linear track task (Fig. S7). Weak theta modulation55 and no theta phase precession were observed in LEC cells, which is a finer-scale temporal representation (Fig. S8).
Comparison of spatial and temporal representation across the hippocampal entorhinal circuit
The encoding of temporal information has been reported in the hippocampus and related regions1,3,56,57, and rate remapping has also been found in both CA131,58 and CA329. Here, we extended our analyses to recordings from CA1, CA3, and MEC while the subjects performed the double rotation task. We computed the spatial and temporal modulation fields of neurons in the four brain regions (Fig. 5a, b). There were significant differences across brain regions in the spatial information scores (from the spatial modulation fields) and the temporal information scores (from the temporal modulation fields) in the first STD session (Fig. 5c, d; Kruskal–Wallis test; spatial information: χ2 = 342.86, p < 0.001; temporal information: χ2 = 15.7, p = 0.0013). The four brain regions, ranked in the order of spatial selectivity, were CA1, CA3, MEC, and LEC (median spatial information score, LEC: 0.36, MEC: 0.57, CA3: 1.49, CA1: 1.75; post-hoc Wilcoxon rank-sum tests, p < 0.001 for all tests, corrected for family-wise error rate with the Holm–Bonferroni method). (Note that the difference between CA1 and CA3 would be affected by the recording location along the transverse axis of these regions, which was not controlled for in these experiments59,60,61). In contrast, LEC showed stronger temporal information coding than the other three brain regions (median temporal information score, LEC: 0.14, MEC: 0.099, CA3: 0.092, CA1: 0.10; post-hoc Wilcoxon rank-sum tests, LEC vs. MEC: Z = 2.65, p = 0.008, LEC vs. CA1: Z = 2.42, p = 0.015, LEC vs. CA3: Z = 3.25, p = 0.001; with Holm–Bonferroni corrections), and CA1 was stronger than CA3 (Wilcoxon rank-sum test, Z = −2.71, p = 0.007), consistent with earlier reports24,62,63. We also compared the correlation coefficients between temporal modulation fields of standard sessions across these regions. There were significant differences between these regions (Fig. 5e; Kruskal–Wallis test, χ2 = 15.53, p = 0.0014; median correlation coefficient, LEC: 0.13, MEC: 0.02, CA3: 0.08, CA1: 0.02; post-hoc Wilcoxon rank-sum tests, LEC vs. MEC: p = 0.004, LEC vs. CA1: p = 0.0071, CA1 vs. CA3: p = 0.0037, corrected for family-wise error rate with the Holm–Bonferroni method; Fig. S9).
a Sorted spatial modulation fields for LEC, MEC, CA3, and CA1. b Sorted temporal modulation fields for the four brain regions. c The distributions of spatial information scores across regions. Gray dots, data for each neuron; black dots, the median value. Two-sided Wilcoxon rank-sum test with Holm–Bonferroni correction, LEC vs. MEC: p < 10−3; LEC vs. CA1: p < 10−10; LEC vs. CA3: p < 10−10; MEC vs. CA1: p < 10−10; MEC vs. CA3: p < 10−10; CA1 vs. CA3: p < 10−10. d The distributions of temporal information scores across regions. LEC vs. MEC: p = 0.008; LEC vs. CA1: p = 0.015; LEC vs. CA3: p = 0.001; CA1 vs. CA3: p = 0.007. e The distributions of Pearson’s correlation coefficients between standard sessions across regions. Two-sided Wilcoxon rank-sum test with Holm–Bonferroni correction, LEC vs. MEC: p = 0.004; LEC vs. CA1: p = 0.0071; CA1 vs. CA3: p = 0.0037. *p < 0.05; **p < 0.01. Source data are provided as a Source Data file.
Discussion
In this study, we found that LEC could represent temporal information about trial progression through spatial rate remapping in one-dimensional navigation tasks. To support this conclusion, we first needed to establish the spatial firing properties of LEC cells. We found that a portion of LEC cells were selective for spatial location on linear or circular tracks, similar to results shown previously using imaging techniques in head-fixed mice running linear trajectories in virtual reality35,37. Although the spatial selectivity of LEC was generally weaker than that of MEC and other hippocampal regions6,15,39, a proportion of cells showed spatial precision and reliability similar to neurons in the hippocampal regions and the MEC. Moreover, in 1-dimensional shuttling tasks in the present experiments, many LEC neurons exhibited directional and distance selectivity in their spatial firing. Within a session, the firing rate of the spatial firing fields often showed temporal modulation. This coding of trial progression in LEC was robust to manipulations of the spatial environment, such as cue rotations and the absence of visual inputs. Finally, this temporal coding through spatial rate remapping was stronger in LEC compared to MEC, CA1, and CA3.
Previous studies have examined the nature of spatial representation in LEC15,16,20,21,22,39. In 2D empty arenas, the allocentric spatial tuning was weak15,16, but in the presence of objects, a subset of LEC neurons showed greater selectivity both around the objects and away from the objects20. A small number of LEC cells fired in locations that were previously occupied by objects20,21, thereby demonstrating memory traces of the object’s previous locations21. In the current study, the presence of a reliable spatial code may perhaps be attributed to the surface cues on the track in the double rotation paradigm, as well as the reward near the end of the journey in the circular and linear track shuttling tasks providing stable, local anchoring points for the LEC spatial signal. The persistence of spatial firing in the dark (Fig. S2g) suggests that the spatial code in LEC could be supported by either olfactory input or other cognitive variables, or perhaps from path integration signals provided by the MEC inputs to LEC. In addition, we found that the spatial coding ability was correlated between 1D and 2D tasks (Fig. S2e, f), which supports the idea that there was intrinsic heterogeneity in coding spatial information among LEC cells. Consistent with a previous study analyzing the same data, we have confirmed that the spatial representation in LEC rotated with local cues39. This finding suggests that LEC may be involved in biasing the responses of CA3 neurons to local cues60,64 and in segmenting the firing of CA1 neurons based on local surface boundaries65. Two recent studies35,37 demonstrated the presence of spatial selectivity on linear tracks in virtual reality setups, consistent with our results. Our results provided additional information using standard real-world, bidirectional shuttling tasks, making it possible to compare the results with the numerous studies on the hippocampus and related structures with similar behavioral tracks. We observed cells with high spatial tuning in almost all tasks in our study, which involves different combinations of cues, such as boundaries (circular track task and linear track task) and tactile cues (double rotation task). In addition, the presence of directionality and visual cues was not required for the existence of spatial selectivity, as the double rotation task was unidirectional and the dark session of the circular track task had no visual cues, yet both conditions showed cells with spatial tuning. Thus, we could not attribute the spatial tuning to any one of these factors.
An unresolved question from these data is whether the spatial coding on the 1-D tracks is allocentric or egocentric. Ref. 22 demonstrated that in 2-D open fields, LEC cells represent the animal’s location in an egocentric frame of reference, that is, as an egocentric bearing and distance to a specific point in the environment (such as the center or nearest boundary, an object, or a goal location). In contrast, MEC cells represented location in the classic allocentric frame of reference associated with spatial representations of place cells in the hippocampus. Because of the behavioral constraints imposed by the rat’s trajectories on linear and circular tracks, we do not have adequate sampling to determine whether the spatial firing of LEC in the present paper indicates an egocentric or allocentric representation. We speculate that consistent with the results in open fields, the spatial firing is egocentric (e.g., the cell fires at a particular bearing relative to the goal location or relative to a salient external landmark). The geometric constraints on the rat’s behavior limit the sampling of specific egocentric bearings at specific allocentric locations, perhaps allowing more reliable firing of LEC neurons at specific locations compared to the more unconstrained trajectories and combinations of egocentric bearings and allocentric locations available in open fields. Resolving this question will require further experiments with proper controls to tease apart allocentric from egocentric coding in such 1-D tasks.
The directional movement on one-dimensional tracks generates a strong context signal that influences the spatial representation within the hippocampal-entorhinal circuit41,42,43,44,45,46,66,67. Our results provide the evidence of LEC neurons displaying a directional preference during shuttling tasks on a one-dimensional apparatus, which was not possible to study in unidirectional virtual reality experiments. This finding contributes to the existing evidence that LEC neurons might carry context-related information19,68,69. Given the rich bidirectional connections of LEC with the hippocampus and MEC70,71, it is conceivable that the directional maps created by hippocampal or MEC neurons could contribute to the observed direction selectivity in LEC. Nevertheless, certain features may be unique to LEC cells: (1) the directional preference of some LEC neurons spanned a large proportion of the track; (2) the directional preferences showed a concentration around the goal, possibly indicating leave- or approach-related egocentric preferences22,23; (3) the selectivity for movement direction might partly result from the distance coding exhibited by some of the LEC cells. These features might aid in maintaining and stabilizing the differential representation of contexts in the hippocampal navigation circuits, and contribute to the manifestation of distance coding properties in the downstream hippocampus under specific conditions72. In conclusion, our results suggest that spatial representations for travel directions are present across LEC, MEC, and hippocampal regions.
The distance tuning near the end of the track (Fig. 2f, h) could be interpreted as leave or approach signals related to the rewards. Similar reward/goal-related distance firing has been demonstrated in LEC using virtual reality setups35,37, although the spatial tuning resolution in Issa et al. was less obvious and they were interpreted as pre- and post-reward cells37. As distance tuning could be confounded with a change of speed profile or other behavioral confounds37, further investigation is needed to fully address the properties of apparent distance representation in LEC.
When the animal was performing shuttling tasks on one-dimensional tracks, the movement sequence became stereotyped; thus, there existed a tight coupling between sensory-motor signals and particular positions on the track. For example, the speed profiles for approaching or leaving the terminals of the track, and their corresponding optic flow patterns, would mostly be consistent across laps. This coupling might not only provide spatial anchoring of the activity of LEC cells but also endow LEC cells with directional and distance-related activity profiles. Furthermore, some cells had multiple regions of direction selectivity, even for the same travel direction. These properties could not be easily predicted from the egocentric coding properties from open field tasks22,23. Thus, both direction and distance selective firing of LEC cells were consistent with the idea that LEC may function as a ‘local view’ processor73.
The hippocampus is essential for processing nonspatial information integral to episodic memory31,74. A proposed coding scheme involves the combination of spatial and nonspatial coding via rate modulation of the spatial firing profile, i.e., rate remapping27,29,31. LEC has been shown to be involved in rate remapping of CA3 cells68. Our study provides the evidence that LEC cells could signal temporal information about trial progression using the same feature-in-place type of rate-remapping mechanism. Note that the spatial representation may reflect the coding of elapsed time since the start of the lap trajectory, as reported in a previous study by ref. 24. On such tasks in which well-trained rats run stereotyped trajectories on linear tracks, it can be difficult to dissociate spatial firing from temporal firing. However, our findings of the multiplexing of information through rate remapping remain unchanged, even if the within-trial dynamics reflected elapsed time from the lap start rather than spatial location. In this case, the rate remapping would reflect temporal representations of different scales (i.e., time within a trial vs. time within a session) multiplexed in the firing rates of LEC neurons. Ref. 24 demonstrated higher-than-expected decoding of trial identity in tasks that have repetitive event structure, although the decoding performance for trials is significantly lower than the tasks with low behavioral demand (e.g., foraging in square boxes with the wall color changed across sessions). Consistent with this study, the across-region differences in temporal coding in our study (Fig. 5) were smaller than those reported in Tsao et al. for 2-D foraging tasks. The exact way LEC represents spatial and temporal information is still unclear. The spatial rate remapping for representing temporal information reported in our study constitutes an efficient way to multiplex spatial and temporal information. Temporal information could also be represented through a higher-order mechanism; for example, decoding of temporal information remains high with non-ramping cells24. It is thus likely that parallel mechanisms exist for coding time.
Note that the differences in temporal coding between LEC and other brain regions were smaller than those reported by ref. 24. One possibility is that the double rotation task involved more stereotypical behaviors than the open field foraging task in two-dimensional boxes used in that study. The structured behavior could diminish temporal information about trials or sessions24, thus obscuring the distinctions among brain areas. In tasks involving the repeated traversal of one-dimensional tracks, we demonstrated LEC carried more minute-scale temporal information than MEC, CA1, and CA3, which supports the view that LEC plays an essential role in coding time information24,25. Our results were different from stochastic drifts62,63,75,76. Two recent studies77,78 have demonstrated that the intervening experience was critical in determining the amount of drift in CA1 neurons, whereas our results support the idea that the activity of LEC neurons was reset to a predetermined pattern once the sessions started, even after a session with the spatial context manipulated. Thus, the reset of a network pattern to a fixed initial state can help suppress arbitrary drift across sessions in other cortical areas79. Consistent with this proposal, inactivating LEC led to decreased representational consistency in the medial prefrontal cortex for stimuli80.
Our results are in line with previous reports that CA1 neurons could use rate remapping to represent temporal information32,58,63,81,82. For example, in the study by ref. 32, the authors demonstrated that some CA1 neurons could represent the identity of laps through rate remapping. In addition, the representation was robust to manipulations of the environment, such as the change of the shape of the track. This is similar to our results in that the time code about lap number in LEC was largely independent of the change in spatial contexts. Thus, LEC and CA1 may function together to represent and track lap-specific experiences, which may facilitate the selection of specific lap experiences for consolidation and retrieval83. Together, our results suggest that, as one of the major inputs to the hippocampus, LEC may contribute to the representation of time in the hippocampus24,25.
In conclusion, our data have demonstrated reliable spatial processing in LEC neurons, and LEC neurons represent temporal information about trial progression through spatial rate remapping. The temporal modulation of place fields, together with time cells, ramping cells, representational drift, etc., provide a hierarchical framework to code temporal information. The integration of space and time processing in LEC and other areas suggests a shared organizational feature across the MTL memory system2,3,57,84.
Methods
Subjects and surgical procedures
The circular and linear track paradigm
Five male, 5–6 months old, adult Long-Evans rats obtained from Envigo performed the circular track and linear track tasks. The animals were housed individually on a 12:12 h reversed light-dark cycle with ad libitum access to water. Experiments were carried out in the dark phase of the cycle. Animal care, surgical procedures, and euthanasia complied with NIH guidelines and were approved by the Institutional Animal Care and Use Committee at Johns Hopkins University. Detailed surgical procedures were reported elsewhere22. Briefly, for surgical implantation of recording electrodes, rats were anesthetized with an initial dose of 60 mg/kg ketamine and 8 mg/kg xylazine followed by isoflurane inhalation to effect. A hyperdrive targeting LEC in the right hemisphere was implanted (7.55–7.6 mm posterior to bregma, 3.0 mm lateral to the midline) with the tetrode bundles angled at 25° mediolaterally. Rats were food-restricted until their body weight reached 80–90% of their free-feeding weights. The tetrodes were lowered slowly toward LEC over the course of 1–2 weeks.
Double rotation paradigm
Neurons from 60 rats in the double rotation task (3 LEC rats, 6 MEC rats, 32 CA1 rats, and 29 CA3 rats; in some rats two areas were recorded simultaneously) were analyzed using previously published data sets. Details of the surgical procedures conducted on these rats can be found in previous papers16,39,60,64,85.
Electrophysiology and recording
Tetrodes were made from 12 μm or 17 μm nichrome or platinum-iridium wire (California Fine Wire, Grover Beach, CA, USA or Kanthal, Palm Coast, FL). The electrode tips were electroplated with gold to 200–500 kΩ with 0.2 µA current or 120 kΩ with 0.075 µA plating current. Platinum iridium wires were not plated and had an impedance of ~700 kΩ. During recordings, the electrophysiological signal was either processed by a 64-channel wireless transmitter system (Triangle Biosystems International, Durham, NC) or a unity-gain preamplifier headstage (Neuralynx, Bozeman, MT). The data were then collected with Cheetah Data Acquisition System (Neuralynx, Bozeman, MT). For single-unit recordings, the signal was band-pass filtered (600 Hz to 6 kHz) and thresholded (~70 µV) to produce the waveforms of the spikes. We used red and green LEDs or arrays of infrared LEDs on the head of the subjects to track the positions of the animals, and a color or infrared CCD camera with a 30 Hz sampling rate was used to capture the color or infrared signals, respectively. The behavioral trajectories of the rats were smoothed with a 5-frame boxcar filter (150 ms) and speed filtered (3 cm/s).
Histological processing procedures
The rats were perfused transcardially with 4% formalin. The brains were extracted and submerged in a 30% sucrose formalin solution. Brain tissue was then cryosectioned at 40 µm thickness and mounted onto glass slides. Standard Nissl staining was performed to identify the tetrode tracks. Free-D software86 was used to register tetrode tracks to the tetrode bundle configuration of the drive. Recording locations of each session were determined based on the amount of tetrode turning each day and histological reconstructions of electrode tracks15.
The demarcations of LEC followed conventions in previous studies (Fig. S1)87,88,89. Briefly, LEC was distinguished by the large and darkly stained neurons that formed discontinuous islands in layer II, and the presence of a cell-sparse lamina dissecans between layer III and layer V.
To investigate the spatial and temporal coding properties of different subregions of LEC, LEC cells were divided into groups based on either the layers the cells were located or which part of the hippocampus they project to in the dorsoventral axis. Cells located in layers 2 and 3 were considered superficial-layer LEC cells, whereas cells that were in layers 5 and 6 were grouped as deep-layer LEC cells90. LEC cells were divided into dorsolateral, intermediate, and ventromedial bands, which project to the dorsal, intermediate, and ventral hippocampus, respectively. The demarcation approximated that described in refs. 87,89. The dorsolateral band lies close to the rhinal fissure; layer I is not very thick; layer II is narrow and contains densely packed, darkly stained large neurons. For the intermediate band, layer I is narrow; layer II contains big, round cells; layer III is wide, and contains clusters of cells. For the ventromedial band, layer II is also narrower and layer III is made up of densely packed, medium-sized pyramidal neurons.
For details on the identification of MEC, please refer to a previous study39.
Behavioral tasks
The circular track and linear track task
Animals were trained to run back and forth between food wells for food pellets (BioServ) on a circular track (diameter 97 cm, width 10 cm). The food wells were separated by a 15 cm tall black barrier with 0.4 cm sidewalls; thus, the animals needed to run almost 360° in each direction to obtain the next food reward. The linear track task was similar to the circular track task, except the apparatus was a 5-foot long, 8-cm wide linear track. Each session consisted of 7 to 25 laps. Part of the data has been reported in a previous paper (supplementary Fig. 9 of ref. 24).
The double rotation task
The data collected in the double rotation task have been reported for other purposes39,40,60,64,85. Briefly, the animals were trained to run on a circular track with local texture cues in the clockwise direction (outer diameter: 76 cm, inner diameter: 56 cm). The subjects foraged for food scattered at arbitrary locations on the track (~2 rewards/lap) while moving clockwise for about 15 laps. The apparatus was surrounded by a black curtain with salient cues. The experiment lasted for four days and was conducted during the dark portion of the light/dark cycle. There were two types of sessions: standard sessions (STD) and mismatch sessions (MIS). In STD sessions, the relationships between local and global cues remained fixed; in MIS sessions, local and global cues were rotated by an equal amount in opposite directions, thus generating mismatch angles of 45°, 90°, 135°, and 180° (only 135° and 180° were used here for analysis of spatial coding properties, as we concentrated on the two most extreme manipulations). Each session consisted of about 15 laps. Rats either ran five sessions (STD, MIS, STD, MIS, STD) or six sessions (STD, STD, MIS, STD, MIS, STD). In the case of the six-session configuration, the data in the first STD were considered as the baseline, and not analyzed in the current paper.
To compare the spatial coding properties in one-dimensional and two-dimensional spatial tasks, we also included data from five rats performing foraging on a circular platform (122 cm diameter) or a square box (135 × 135 × 30 cm3)90. The spatial bin size was set to 6 cm. The standard deviation of the 2D spatial Gaussian smoothing kernel was one bin.
Unit isolation
Single units were isolated manually with custom-written spike-sorting software (Winclust, developed by J. Knierim). The peak amplitude and energy of the waveforms were used to isolate cells. The quality of each unit was rated with a score ranging from 1 (very good) to 5 (poor). The cluster isolation quality was assigned completely independent of any behavioral correlates of the cells. Units rated as 4 or 5 were excluded from the analysis.
Data analysis
All analyses were performed with Matlab. All statistical tests were two-sided.
Linearization of the trajectories and detection of head scanning events
In the linear track paradigm, the long edge of the apparatus was aligned with the vertical dimension in the camera’s field of view. Therefore, we linearized the position of animals’ trajectories with only the vertical data. In the circular track paradigm and double rotation paradigm, we transformed the data to a polar coordinate with the center of the track as the origin.
In the double rotation paradigm, head scanning events were detected following a previous study40. Briefly, head scanning events were defined as lateral head movements off the track with a minimum duration of 0.4 s and a minimum radial extent of 2.5 cm. These behavioral epochs and spikes associated with them were removed from the analyses. See ref. 40 for a detailed description of these procedures.
Spatial firing rate maps
The spatial bin was set to 6 cm, and a Gaussian kernel (sigma: 1 bin) was used to smooth the final rate map. The spatial information score was calculated following a previous study91.
where pi was normalized occupancy in the ith spatial bin, λi was the spatial response (firing rate) in the ith bin, and λ was the average response.
For the circular track task and the linear track task, we concatenated the spatial rate maps for two directions to avoid double counting cells, as the spatial rate maps for the two movement directions may not be independent of each other.
We operationally defined a cell as a significant spatial tuning cell if the cell met the following criteria: (1) its spatial information score was >the 95th percentile of a null distribution of scores generated from 1000 random shuffles of the spike times relative to position samples of that neuron; (2) the spatial information score was greater than 0.5 bits/spike. Note that different methods and thresholds could result in different proportions; thus, the percentage of functional cells reported should be interpreted with caution.
The standard spatial information score may not correlate well with the accuracy of spatial decoding. We adopted a normalization procedure established in a previous study92. We created a series of shuffled control lap-wise spatial rate maps. In a single instance, each lap was circularly shifted by different amounts. The final normalized spatial information score was calculated as the z-score relative to the shuffled distribution (500 times).
Temporal rate map
We have calculated the temporal rate map as the average firing rate for each lap. Temporal information score was calculated in the same way as the spatial information score from the temporal rate map.”
To define a cell with significant temporal tuning of the lap numbers, the following criteria were used: (1) The correlation coefficient between the temporal modulation fields from two different sessions was greater than 0.3. (2) For the double rotation task, where we had more sessions, we also performed an additional shuffling control: for each cell, we randomly rearranged the lap order in each specific session and created a null distribution of the temporal information score. We compare the temporal information score of the original temporal rate map (with the average rate for each lap calculated from all sessions) with the null distribution. A significance level of 0.05 was applied.
Spatial and temporal modulation fields
To estimate the spatial and temporal firing properties of neurons, we applied SVD to the lap-wise spatial rate map matrix formed by stacking spatial rate maps from each lap. Any lap that had less than 70% coverage of the track was removed as in some laps the animals turned back before they reached the target. The remaining unvisited spatial bins were set to 0 before performing the decomposition. The resulting Euclidean norm (vector length) of both the spatial and temporal modulation fields was 1. The temporal and spatial modulation fields were smoothed with a Gaussian kernel (standard deviation: 1 bin). The information score was calculated from the spatial and temporal modulation fields in the same way as the section above. Note that flipping the signs of both spatial and temporal components would not affect the decomposition, but for ease of interpretation, in our procedure, we made sure the sign of the spatial component was positive, which would result in a regularized temporal component.
To quantify the performance of rank-1 approximation of the original data matrix, we calculated the amount of variance explained by the first singular value component:
where σ is the singular value and σ1 is the first and largest singular value. This measure quantifies the proportion of the total variance that is explained by our rank-1 model.
The non-negative matrix factorization (NMF) technique was also applied to decompose the lap-wise spatial rate maps into spatial and temporal modulation fields. This method was used to confirm that the results we obtained were not due to limitations of the SVD method. The NMF procedure was performed with the Matlab function nnmf. A rank-1 approximation of the lap-wise spatial rate map matrix was obtained. The resulting spatial and temporal components were not further smoothed.
We also performed an analysis for normalizing the temporal information score with a procedure similar to the one used in normalizing the spatial information score (see the section above). For each cell, we created an aggregate lap-wise spatial rate map matrix by concatenating each lap-wise spatial rate map from each specific session. Then, the SVD decomposition was applied to get the temporal modulation field and the resulting temporal information score. The observed temporal information score was normalized to a null distribution formed by randomly rearranging the lap order in each specific session.
Correlation matrix
The population correlation matrix was constructed following previous studies60 for both spatial and temporal rate maps (or modulation fields). For each cell, we first normalized the rate maps by the peak of the two spatial rate maps to be compared. The normalized firing from all cells for a bin was used to create a population vector. Population vectors for every bin were correlated to those in the second session using Pearson product-moment correlation. The resulting matrix was termed the population correlation matrix. In this study, the correlation matrix method was only used as a visualization tool.
Permutation test for consistency of temporal and spatial modulation across sessions
To characterize the similarity of spatial or temporal firing patterns between two sessions, for each cell, we calculated Pearson correlation coefficients between a pair of firing maps or modulation fields and obtained the mean correlation of the population. Then, the cell identities in the second session were randomly permuted, and the average correlation was recomputed for these random pairs. This operation was repeated 1000 times to build a null distribution of correlation values. The observed average correlation coefficient was then compared to a null distribution with a significance level of 0.05.
Direction selectivity analysis
To determine if cells show significant direction selectivity on regions in the one-dimensional track, we adopted the nonparametric permutation method of Fujisawa and colleagues47 to set the threshold for significant differences between firing in the two movement directions. The lap-wise spatial rate map was obtained separately for two movement directions. We obtained averaged rate maps across these laps to get the session-wise mean firing and their differences at each spatial bin. Then the labels of the movement direction were permuted, and the differences in firing rate for the resampled groups were calculated. These operations were repeated 500 times. For each spatial location, both the pointwise and the global acceptance bands were obtained. The pointwise acceptance bands were defined as the 97.5 percentile and 2.5 percentile of the resampled null distribution. To maintain a familywise error rate of 5% for detecting the presence of directional firing at a location, we calculated a global acceptance band as follows. We increased the pointwise acceptance bands defined from the original 500 resampling statistics in steps of 0.1 percentile. We repeated the permutation operation 500 times for each step until the number of cases that crossed the upper and lower acceptance bands at any spatial bin was fewer than 25 times (5% of the total number of simulations). The resulting percentiles defined the global acceptance band. If the difference in firing between the two directions crossed outside the global acceptance bands, then the cell was considered to be directionally selective at this location. We then used the pointwise acceptance bands to define the size of the direction-selective region. For each global crossing, we measured the extent of the difference in firing between the directions that remained outside the bands of the pointwise acceptance bands.
The direction selectivity index was defined as:
where \(Rat{e}_{Dir1}\) and \(Rat{e}_{Dir2}\) represent the firing rates at a particular position for two movement directions. The possible range of DI is 0 (no direction selectivity) to 1 (cell only fires for one direction, i.e., strongest possible direction selectivity).
Test for distribution of direction-selective regions
For the circular track data, we converted the peak of the direction-selective region to polar coordinates, and the Rayleigh test was used to test for the non-uniformity of the resulting circular data. For the linear track data, we performed a Monte Carlo test. We divided the track into two regions: the center region and the end region. The end region was the portion of the track close to either track end (a quarter of the whole track). The center region occupied half of the track in the center. We calculated the proportion of the data that belongs to the end regions and compared the proportion both from real data and randomly generated numbers (1000 times, null distribution). The data was considered to have a significant preference to concentrate close to the end if the observed proportion was significantly larger than the 95th percentile of the null distribution.
Test for distance coding properties of LEC neurons in shuttling tasks
We averaged the values along the minor diagonal of the population correlation matrix created with the spatial rate maps for the two movement directions. This mean correlation was compared to the null distribution created by permuting the cell identity in the opposite direction 1000 times.
To test whether there was an equal amount of distance tuning in the starting and ending position of the journey, the starting position was defined as the first 4 spatial bins and the ending position was the last 4 spatial bins. We calculated the observed difference of correlation between the two regions and compared that value with a simulated null distribution obtained by 1000 permutations of the direction labels. The significance level was 0.05.
Theta phase precession analyses
The local field potential was filtered between 1 and 475 Hz, and was acquired at 1000 Hz. The local field potential was bandpass-filtered with a Kaiser filter between 6 Hz and 11 Hz. The theta phase locking index was defined as the mean vector length of theta phases when the spikes occurred. The theta phase was estimated with the Hilbert transform from the band-passed signal. Phase precession analysis was performed following previous studies93,94. For each spike, the theta phase and the position of the animal when the spike occurred were obtained and plotted.
Statistics & reproducibility
The primary statistical methods included Wilcoxon rank-sum test, Wilcoxon signed-rank test, permutation test, Kruskal–Wallis test with Holm–Bonferroni correction, applied as appropriate. No statistical method was used to predetermine the sample size. The sample size followed commonly accepted in the field. No data were excluded from the analyses. The experiments involving the different brain regions were not randomized, as the authors reanalyzed data from previously collected data.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
Source Data are provided with this paper. The data generated in this study have been deposited in the Zenodo database under the accession code: https://doi.org/10.5281/zenodo.14029802.
Code availability
Codes can be accessed from the following site: https://doi.org/10.5281/zenodo.14029802.
References
Eichenbaum, H. Time cells in the hippocampus: a new dimension for mapping memories. Nat. Rev. Neurosci. 15, 732–744 (2014).
Buzsáki, G. & Llinás, R. Space and time in the brain. Science 358, 482–485 (2017).
Issa, J. B., Tocker, G., Hasselmo, M. E., Heys, J. G. & Dombeck, D. A. Navigating through time: a spatial navigation perspective on how the brain may encode time. Annu. Rev. Neurosci. 43, 73–93 (2020).
Tsao, A., Yousefzadeh, S. A., Meck, W. H., Moser, M.-B. & Moser, E. I. The neural bases for timing of durations. Nat. Rev. Neurosci. 1–20 https://doi.org/10.1038/s41583-022-00623-3 (2022).
Canto, C. B., Wouterlood, F. G. & Witter, M. P. What does the anatomical organization of the entorhinal cortex tell us? Neural Plast. 2008, 381243 (2008).
Knierim, J. J., Neunuebel, J. P. & Deshmukh, S. S. Functional correlates of the lateral and medial entorhinal cortex: objects, path integration and local-global reference frames. Philos. Trans. R. Soc. Lond. B Biol. Sci. 369, 20130369 (2014).
Hafting, T., Fyhn, M., Molden, S., Moser, M.-B. & Moser, E. I. Microstructure of a spatial map in the entorhinal cortex. Nature 436, 801–806 (2005).
Sargolini, F. et al. Conjunctive representation of position, direction, and velocity in entorhinal cortex. Science 312, 758–762 (2006).
Savelli, F., Yoganarasimha, D. & Knierim, J. J. Influence of boundary removal on the spatial representations of the medial entorhinal cortex. Hippocampus 18, 1270–1282 (2008).
Solstad, T., Boccara, C. N., Kropff, E., Moser, M.-B. & Moser, E. I. Representation of geometric borders in the entorhinal cortex. Science 322, 1865–1868 (2008).
Kropff, E., Carmichael, J. E., Moser, M.-B. & Moser, E. I. Speed cells in the medial entorhinal cortex. Nature 523, 419–424 (2015).
McNaughton, B. L., Battaglia, F. P., Jensen, O., Moser, E. I. & Moser, M.-B. Path integration and the neural basis of the ‘cognitive map’. Nat. Rev. Neurosci. 7, 663–678 (2006).
Moser, E. I., Moser, M.-B. & McNaughton, B. L. Spatial representation in the hippocampal formation: a history. Nat. Neurosci. 20, 1448–1464 (2017).
Savelli, F. & Knierim, J. J. Origin and role of path integration in the cognitive representations of the hippocampus: computational insights into open questions. J. Exp. Biol. 222, jeb188912 (2019).
Hargreaves, E. L., Rao, G., Lee, I. & Knierim, J. J. Major dissociation between medial and lateral entorhinal input to dorsal hippocampus. Science 308, 1792–1794 (2005).
Yoganarasimha, D., Rao, G. & Knierim, J. J. Lateral entorhinal neurons are not spatially selective in cue-rich environments. Hippocampus 21, 1363–1374 (2011).
Young, B. J., Otto, T., Fox, G. D. & Eichenbaum, H. Memory representation within the parahippocampal region. J. Neurosci. 17, 5183–5195 (1997).
Leitner, F. C. et al. Spatially segregated feedforward and feedback neurons support differential odor processing in the lateral entorhinal cortex. Nat. Neurosci. 19, 935–944 (2016).
Pilkiw, M. et al. Phasic and tonic neuron ensemble codes for stimulus-environment conjunctions in the lateral entorhinal cortex. eLife Sci. 6, e28611 (2017).
Deshmukh, S. S. & Knierim, J. J. Representation of non-spatial and spatial information in the lateral entorhinal cortex. Front Behav. Neurosci. 5, 69 (2011).
Tsao, A., Moser, M.-B. & Moser, E. I. Traces of experience in the lateral entorhinal cortex. Curr. Biol. 23, 399–405 (2013).
Wang, C. et al. Egocentric coding of external items in the lateral entorhinal cortex. Science 362, 945–949 (2018).
Wang, C., Chen, X. & Knierim, J. J. Egocentric and allocentric representations of space in the rodent brain. Curr. Opin. Neurobiol. 60, 12–20 (2020).
Tsao, A. et al. Integrating time from experience in the lateral entorhinal cortex. Nature 561, 57–62 (2018).
Montchal, M. E., Reagh, Z. M. & Yassa, M. A. Precise temporal memories are supported by the lateral entorhinal cortex in humans. Nat. Neurosci. 1 https://doi.org/10.1038/s41593-018-0303-1 (2019).
Muller, R. U. & Kubie, J. L. The effects of changes in the environment on the spatial firing of hippocampal complex-spike cells. J. Neurosci. 7, 1951–1968 (1987).
Colgin, L. L., Moser, E. I. & Moser, M.-B. Understanding memory through hippocampal remapping. Trends Neurosci. 31, 469–477 (2008).
Wood, E. R., Dudchenko, P. A., Robitsek, R. J. & Eichenbaum, H. Hippocampal neurons encode information about different types of memory episodes occurring in the same location. Neuron 27, 623–633 (2000).
Leutgeb, S. et al. Independent codes for spatial and episodic memory in hippocampal neuronal ensembles. Science 309, 619–623 (2005).
O’Keefe, J. & Nadel, L. The Hippocampus as a Cognitive Map (Oxford: Clarendon Press, 1978).
O’Keefe, J. & Krupic, J. Do hippocampal pyramidal cells respond to nonspatial stimuli? Physiol. Rev. 101, 1427–1456 (2021).
Sun, C., Yang, W., Martin, J. & Tonegawa, S. Hippocampal neurons represent events as transferable units of experience. Nat. Neurosci. 23, 651–663 (2020).
Diehl, G. W., Hon, O. J., Leutgeb, S. & Leutgeb, J. K. Grid and nongrid cells in medial entorhinal cortex represent spatial location and environmental features with complementary coding schemes. Neuron 94, 83–92.e6 (2017).
Ismakov, R., Barak, O., Jeffery, K. & Derdikman, D. Grid cells encode local positional information. Curr. Biol. https://doi.org/10.1016/j.cub.2017.06.034 (2017).
Bowler, J. C. & Losonczy, A. Direct cortical inputs to hippocampal area CA1 transmit complementary signals for goal-directed navigation. Neuron 111, 4071–4085.e6 (2023).
Huang, X. et al. Distinct spatial maps and multiple object codes in the lateral entorhinal cortex. Neuron 111, 3068–3083.e7 (2023).
Issa, J. B., Radvansky, B. A., Xuan, F. & Dombeck, D. A. Lateral entorhinal cortex subpopulations represent experiential epochs surrounding reward. Nat. Neurosci. 27, 536–546 (2024).
Knierim, J. J. Dynamic interactions between local surface cues, distal landmarks, and intrinsic circuitry in hippocampal place cells. J. Neurosci. 22, 6254–6264 (2002).
Neunuebel, J. P., Yoganarasimha, D., Rao, G. & Knierim, J. J. Conflicts between local and global spatial frameworks dissociate neural representations of the lateral and medial entorhinal cortex. J. Neurosci. 33, 9246–9258 (2013).
Monaco, J. D., Rao, G., Roth, E. D. & Knierim, J. J. Attentive scanning behavior drives one-trial potentiation of hippocampal place fields. Nat. Neurosci. 17, 725–731 (2014).
McNaughton, B. L., Barnes, C. A. & O’Keefe, J. The contributions of position, direction, and velocity to single unit activity in the hippocampus of freely-moving rats. Exp. Brain Res. 52, 41–49 (1983).
Battaglia, F. P., Sutherland, G. R. & McNaughton, B. L. Local sensory cues and place cell directionality: additional evidence of prospective coding in the hippocampus. J. Neurosci. 24, 4541–4550 (2004).
Brun, V. H. et al. Progressive increase in grid scale from dorsal to ventral medial entorhinal cortex. Hippocampus 18, 1200–1212 (2008).
Hafting, T., Fyhn, M., Bonnevie, T., Moser, M.-B. & Moser, E. I. Hippocampus-independent phase precession in entorhinal grid cells. Nature 453, 1248–1252 (2008).
Navratilova, Z., Hoang, L. T., Schwindel, C. D., Tatsuno, M. & McNaughton, B. L. Experience-dependent firing rate remapping generates directional selectivity in hippocampal place cells. Front. Neural Circuits 6, 6 (2012).
Yoon, K., Lewallen, S., Kinkhabwala, A. A., Tank, D. W. & Fiete, I. R. Grid cell responses in 1D environments assessed as slices through a 2D lattice. Neuron 89, 1086–1099 (2016).
Fujisawa, S., Amarasingham, A., Harrison, M. T. & Buzsáki, G. Behavior-dependent short-term assembly dynamics in the medial prefrontal cortex. Nat. Neurosci. 11, 823–833 (2008).
Kraus, B. J. et al. During running in place, grid cells integrate elapsed time and distance run. Neuron 88, 578–589 (2015).
Heys, J. G. & Dombeck, D. A. Evidence for a subcircuit in medial entorhinal cortex representing elapsed time during immobility. Nat. Neurosci. 21, 1574 (2018).
Bright, I. M. et al. A temporal record of the past with a spectrum of time constants in the monkey entorhinal cortex. Proc. Natl Acad. Sci. USA 117, 20274–20283 (2020).
Aghajan, Z. M., Kreiman, G. & Fried, I. Minute-scale periodicity of neuronal firing in the human entorhinal cortex. Cell Rep. 42, 113271 (2023).
De Valois, R. L., Cottaris, N. P., Mahon, L. E., Elfar, S. D. & Wilson, J. A. Spatial and temporal receptive fields of geniculate and cortical cells and directional selectivity. Vis. Res. 40, 3685–3702 (2000).
Theunissen, F. E., Sen, K. & Doupe, A. J. Spectral-temporal receptive fields of nonlinear auditory neurons obtained using natural sounds. J. Neurosci. 20, 2315–2331 (2000).
David, S. V., Vinje, W. E. & Gallant, J. L. Natural stimulus statistics alter the receptive field structure of V1 neurons. J. Neurosci. 24, 6991–7006 (2004).
Deshmukh, S. S., Yoganarasimha, D., Voicu, H. & Knierim, J. J. Theta modulation in the medial and the lateral entorhinal cortices. J. Neurophysiol. 104, 994–1006 (2010).
Pastalkova, E., Itskov, V., Amarasingham, A. & Buzsáki, G. Internally generated cell assembly sequences in the rat hippocampus. Science 321, 1322–1327 (2008).
Ekstrom, A. D. & Ranganath, C. Space, time, and episodic memory: The hippocampus is all over the cognitive map. Hippocampus https://doi.org/10.1002/hipo.22750 (2017).
Manns, J. R., Howard, M. W. & Eichenbaum, H. Gradual changes in hippocampal activity support remembering the order of events. Neuron 56, 530–540 (2007).
Henriksen, E. J. et al. Spatial representation along the proximodistal axis of CA1. Neuron 68, 127–137 (2010).
Lee, H., Wang, C., Deshmukh, S. S. & Knierim, J. J. Neural population evidence of functional heterogeneity along the CA3 transverse axis: pattern completion versus pattern separation. Neuron 87, 1093–1105 (2015).
Deshmukh, S. S. Distal CA1 maintains a more coherent spatial representation than proximal CA1 when local and global cues conflict. J. Neurosci. 41, 9767–9781 (2021).
Mankin, E. A. et al. Neuronal code for extended time in the hippocampus. Proc. Natl Acad. Sci. USA 109, 19462–19467 (2012).
Mankin, E. A., Diehl, G. W., Sparks, F. T., Leutgeb, S. & Leutgeb, J. K. Hippocampal CA2 activity patterns change over time to a larger extent than between spatial contexts. Neuron 85, 190–201 (2015).
Lee, I., Yoganarasimha, D., Rao, G. & Knierim, J. J. Comparison of population coherence of place cells in hippocampal subfields CA1 and CA3. Nature 430, 456–459 (2004).
Wang, C.-H., Monaco, J. D. & Knierim, J. J. Hippocampal place cells encode local surface-texture boundaries. Curr. Biol. 30, 1397–1409.e7 (2020).
Jung, M. W. & McNaughton, B. L. Spatial selectivity of unit activity in the hippocampal granular layer. Hippocampus 3, 165–182 (1993).
Gothard, K. M., Skaggs, W. E., Moore, K. M. & McNaughton, B. L. Binding of hippocampal CA1 neural activity to multiple reference frames in a landmark-based navigation task. J. Neurosci. 16, 823–835 (1996).
Lu, L. et al. Impaired hippocampal rate coding after lesions of the lateral entorhinal cortex. Nat. Neurosci. 16, 1085–1093 (2013).
Keene, C. S. et al. Complementary functional organization of neuronal activity patterns in the perirhinal, lateral entorhinal, and medial entorhinal cortices. J. Neurosci. 36, 3660–3675 (2016).
Dolorfo, C. L. & Amaral, D. G. Entorhinal cortex of the rat: organization of intrinsic connections. J. Comp. Neurol. 398, 49–82 (1998).
Kerr, K. M., Agster, K. L., Furtak, S. C. & Burwell, R. D. Functional neuroanatomy of the parahippocampal region: the lateral and medial entorhinal areas. Hippocampus 17, 697–708 (2007).
Ravassard, P. et al. Multisensory control of hippocampal spatiotemporal selectivity. Science https://doi.org/10.1126/science.1232655 (2013).
Redish, A. D. Beyond the Cognitive Map: From Place Cells to Episodic Memory (A Bradford Book, Cambridge, Mass, 1999).
Eichenbaum, H. Hippocampus: cognitive processes and neural representations that underlie declarative memory. Neuron 44, 109–120 (2004).
Ziv, Y. et al. Long-term dynamics of CA1 hippocampal place codes. Nat. Neurosci. 16, 264–266 (2013).
Rubin, A., Geva, N., Sheintuch, L. & Ziv, Y. Hippocampal ensemble dynamics timestamp events in long-term memory. eLife 4, e12247 (2015).
Geva, N., Deitch, D., Rubin, A. & Ziv, Y. Time and experience differentially affect distinct aspects of hippocampal representational drift. Neuron 111, 2357–2366 (2023).
Khatib, D. et al. Active experience, not time, determines within-day representational drift in dorsal CA1. Neuron 111, 2348–2356.e5 (2023).
Rule, M. E., O’Leary, T. & Harvey, C. D. Causes and consequences of representational drift. Curr. Opin. Neurobiol. 58, 141–147 (2019).
Pilkiw, M., Jarovi, J. & Takehara-Nishiuchi, K. Lateral entorhinal cortex suppresses drift in cortical memory representations. J. Neurosci. 42, 1104–1118 (2022).
MacDonald, C. J., Lepage, K. Q., Eden, U. T. & Eichenbaum, H. Hippocampal “time cells” bridge the gap in memory for discontiguous events. Neuron 71, 737–749 (2011).
Liu, Y. et al. Consistent population activity on the scale of minutes in the mouse hippocampus. Hippocampus 32, 359–372 (2022).
Yang, W. et al. Selection of experience for memory by hippocampal sharp wave ripples. Science 383, 1478–1483 (2024).
Eichenbaum, H. On the integration of space, time, and memory. Neuron 95, 1007–1018 (2017).
Neunuebel, J. P. & Knierim, J. J. CA3 retrieves coherent representations from degraded input: direct evidence for CA3 pattern completion and dentate gyrus pattern separation. Neuron 81, 416–427 (2014).
Andrey, P. & Maurin, Y. Free-D: an integrated environment for three-dimensional reconstruction from serial sections. J. Neurosci. Methods 145, 233–244 (2005).
Insausti, R., Herrero, M. T. & Witter, M. P. Entorhinal cortex of the rat: cytoarchitectonic subdivisions and the origin and distribution of cortical efferents. Hippocampus 7, 146–183 (1997).
Burwell, R. D. & Amaral, D. G. Cortical afferents of the perirhinal, postrhinal, and entorhinal cortices of the rat. J. Comp. Neurol. 398, 179–205 (1998).
Dolorfo, C. L. & Amaral, D. G. Entorhinal cortex of the rat: topographic organization of the cells of origin of the perforant path projection to the dentate gyrus. J. Comp. Neurol. 398, 25–48 (1998).
Wang, C. et al. Superficial-layer versus deep-layer lateral entorhinal cortex: Coding of allocentric space, egocentric space, speed, boundaries, and corners. Hippocampus 33, 448–464 (2023).
Markus, E. J., Barnes, C. A., McNaughton, B. L., Gladden, V. L. & Skaggs, W. E. Spatial information content and reliability of hippocampal CA1 neurons: effects of visual input. Hippocampus 4, 410–421 (1994).
Souza, B. C., Pavão, R., Belchior, H. & Tort, A. B. L. On information metrics for spatial coding. Neuroscience 375, 62–73 (2018).
O’Keefe, J. & Recce, M. L. Phase relationship between hippocampal place units and the EEG theta rhythm. Hippocampus 3, 317–330 (1993).
Skaggs, W. E., McNaughton, B. L., Wilson, M. A. & Barnes, C. A. Theta phase precession in hippocampal neuronal populations and the compression of temporal sequences. Hippocampus 6, 149–172 (1996).
Acknowledgements
The Strategic Priority Research Program of the Chinese Academy of Sciences (XDB1010102) to C.W., STI2030-Major Projects (2022ZD0205000) to C.W., NIH Grant R01 (MH094146) to J.J.K., NIH Grant (R01 NS039456) to J.J.K., Shenzhen Key Laboratory of Precision Diagnosis and Treatment of Depression (ZDSYS20220606100606014) to C.W., Guangdong Basic and Applied Basic Research Foundation (2021A1515010809) to C.W., National Natural Science Foundation of China (32171043) to C.W., CAS Key Laboratory of Brain Connectome and Manipulation (2019DP173024) to C.W., Guangdong Provincial Key Laboratory of Brain Connectome and Behavior (2023B1212060055) to C.W.
Author information
Authors and Affiliations
Contributions
J.J.K. and C.W. conceived the study. J.J.K. and C.W. supervised the experiments. C.W., H.L., and G.R. performed recording experiments. C.W. performed data analyses. C.W. and J.J.K. wrote the first draft of the manuscript. All authors commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wang, C., Lee, H., Rao, G. et al. Multiplexing of temporal and spatial information in the lateral entorhinal cortex. Nat Commun 15, 10533 (2024). https://doi.org/10.1038/s41467-024-54932-5
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-024-54932-5