Introduction

Twisting two monolayer graphene sheets by an angle of θ ≈ 1. 1° creates magic-angle twisted bilayer graphene (MATBG), in which several new phases of matter have been realized1,2,3,4,5,6,7,8. A much broader range of novel physics can be unveiled in closely related structures having three or more sheets of graphene. Early experiments investigated the strongly correlated and topological physics arising in twisted monolayer-bilayer and double-bilayer graphene, noting intriguing similarities between the two systems that were, nevertheless, qualitatively distinct from MATBG9,10,11,12,13,14,15,16,17,18,19,20. Whereas the investigation of MATBG has expanded to alternating-twist structures up to five layers21,22,23,24,25, the study of structures that include Bernal-stacked components has until now been limited to just those two, despite many others in the twisted M + N family carrying predictions of closely related flat bands (tM + N, where M and N are positive integers representing the number of Bernal-stacked graphene layers twisted atop one another)26.

From a symmetry perspective, tM + N structures differ fundamentally from the family of alternating-twist magic-angle graphene stacks by the breaking of C2z symmetry (in-plane rotation by 180°). This allows a gap to be opened between the lowest valence and conduction bands at charge neutrality by an electric displacement field, D. The collective Berry curvature of many graphene layers contributes to a non-zero valley Chern number of the moiré bands, yielding topological electronic states when interactions generate a spontaneous valley polarization. Experimentally, an intriguing result is that the correlated electronic states appearing in t1 + 2 are rich with emergent topology9,10,11,12, and are furthermore remarkably similar to many of the states seen in t2 + 214,15,16,17,18,19,20. The intertwined correlated and topological states are most similar when the direction of D is oriented from the monolayer to the bilayer of t1 + 2, which localizes the conduction band mostly to the bilayer side.

In this work, we extend the study of tM + N graphene structures to include configurations as thick as six total layers, focusing on t1 + 3, t2 + 3, t1 + 4, and t2 + 4. Despite the inclusion of these additional layers of graphene in the moiré structure, we find striking commonalities in both the non-interacting and correlated physics across this entire family. Continuum model calculations indicate that these unexpected similarities likely arise because low-energy states in the conduction band are localized to just three graphene sheets, irrespective of the total number of layers in the structure: the two layers at the twisted interface and one more immediately adjacent. Ultimately, the result is that adding graphene sheets above and below does not significantly affect the band structure, simply protecting the trio of active layers and strengthening the roles of topology and correlations in shaping the electronic system.

Results

Isolated moiré–localized flat bands

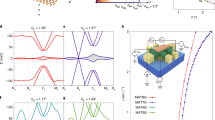
We first compare the band structures of various representative tM + N structures (t1 + 2, t1 + 3, t2 + 3, t2 + 4, Fig. 1a–d) as predicted by the Bistritzer–MacDonald continuum model3 (see Methods). Upon incorporating an interlayer potential arising from an external D pointing from the thinner to the thicker graphene constituent, the moiré conduction band in each of these structures (purple in Fig. 1a–d) becomes relatively flat and isolated by gaps to both the moiré valence band and higher moiré conduction band. Other gaps between neighboring bands can also open for each particular tM + N construction, with the details depending sensitively on θ and both the magnitude and sign of D owing to broken mirror symmetry (see Methods).

Fig. 1: Non-interacting features of tM + N graphene.
figure 1

a Band structure calculations for t1 + 2 at its nominally optimal twist angle (θ = 1.13°) and interlayer potential (δ = 50 meV); defined as when the moiré conduction band (purple curve) has the narrowest dispersion while being simultaneously gapped (grey shaded regions) from both neighboring bands. Energy is measured with respect to the bottom of the moiré conduction band. The calculated valley Chern number, Cv, is shown for the moiré conduction band (see Methods for details). Similar calculations for b t1 + 3 (θ = 1. 3°, δ = 50 meV); c t2 + 3 (θ = 1.45°, δ = 90 meV); and d t2 + 4 (θ = 1.15°, δ = 50 meV). e Resistivity at zero magnetic field as a function of ν and D in a t1 + 2 device at θ = 1.13°. Gray color denotes experimental artifacts where negative resistance is observed, attributed to the effects of highly resistive states. Similar measurements for f t1 + 3 with θ = 1.29°; g t2 + 3 with θ = 1.50°; and h t2 + 4 with θ = 1.15°. Positive D is defined as pointing from the thin component to the thick component for all systems. Measurements taken at T = 1.7 K, except for e, where T = 0.3 K. i–l Layer–resolved LDOS calculated for the moiré conduction band, corresponding to the layer combinations and parameters in panels (a–d). The LDOS is normalized to the maximum value in each panel. Red and orange shadings delineate the M and N layers above and below the twisted interface. The interlayer potential used in the calculations corresponds to positive D in the experiment.

Full size image

Band structure predictions for each of these structures are corroborated by maps of the longitudinal resistivity, ρxx. The data are collected as a function of top- and back-gate voltages, shown in Fig. 1e–h after converting the gate voltages to moiré band filling, ν, and displacement field, D (see Methods). In qualitative agreement with the band structure calculations, all exhibit insulating states at the charge neutrality point (ν = 0) and at full-filling of the lowest moiré valence and conduction bands (ν = ±4) over certain ranges of D, marked by large values of ρxx that exceed h/e2 and diverge as the temperature is lowered (h is Planck’s constant and e is the charge of the electron).

It is not immediately obvious that isolated flat bands would form in many of these tM + N structures. Bernal graphene films with three or more layers feature multiple low-energy bands27,28, all of which must hybridize with the bands from the other twisted constituent to yield an isolated moiré band. To help explain how different tM + N constructions form similar moiré flat bands, Fig. 1i–l shows calculations of the layer-resolved local density of states (LDOS) at full-filling of the lowest moiré conduction band (i.e., integrated over the purple bands in Fig. 1a–d).

Considering first the t1 + 2 structure (Fig. 1i), the moiré potential localizes the LDOS on a triangular lattice of ABB-stacked sites, with most weight appearing on the graphene sheet one below the moiré interface. The layer-resolved LDOS configuration of t1 + 2 recurs in the thicker tM + N structures, with the additional layers of graphene away from the twisted interface carrying a comparatively small density of states. In this sense, the t1 + 2 structure can be considered as the basic building block of all of the thicker tM + N constructions. Given that their low-energy bands are all similarly localized nearby the moiré interface, it is natural to expect that the physics of all of these tM + N structures may exhibit common features.

Common features of the correlated phases

The transport measurements in Fig. 1e–h exhibit insulating states at certain integer values of ν beyond those predicted by the single-particle band structure. As previously observed in a variety of other moiré systems, these correlated insulators arise as a consequence of spontaneous symmetry breaking within the moiré flat bands due to Coulomb interactions1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25. The most prominent correlated insulators for the devices in Fig. 1 appear for D > 0, where the asymmetry with D is due to the lack of mirror-symmetry (see Methods). The differences between the D > 0 and D < 0 correlated insulators has been explored in detail for the case of t1 + 29,12. Here, we turn our attention to analyzing the properties of the correlated phases common across the family of tM + N structures, i.e., for D > 0, comparing to what is known about the symmetry-broken states in t1 + 2 and t2 + 2.

Figure 2 shows high-resolution zoom-ins of both longitudinal and Hall resistances, ρxx and Rxy, for t1 + 2, t2 + 2, t1 + 3, and t2 + 3, along with simple schematics of the material structure. As was seen for the non-interacting features in Fig. 1e–h, the qualitative arrangement of correlated states are similar across all of these tM + N constructions. The most robust insulating state arises at ν = 2 in all, spanning the largest range of D and exhibiting the largest value of ρxx at low temperature. Rxy reverses sign across the ν = 2 state, consistent with an interaction-induced band gap with hole-like carriers at ν ≲ 2 and electron-like carriers at ν ≳ 2. Previous measurements of the evolution of the ν = 2 states in t1 + 2 and t2 + 2 with in-plane magnetic field indicate that they are likely spin polarized9,14,15,16; analogous measurements in our t1 + 3 and t2 + 3 samples are also consistent with spin-polarized insulators (see Supplementary Fig. 2). All samples exhibited a region of ν and D surrounding the insulator at ν = 2 characterized by a slight increase in ρxx and an abrupt sign reversal in Rxy. These features have previously been explained for t1 + 2 and t2 + 2 as arising due to the formation of a spin-polarized half-metal state with a reduced isospin degeneracy of two.

Fig. 2: Symmetry-broken states in various tM + N systems.
figure 2

a Map of the longitudinal resistivity around the correlated states in the t1 + 2 device at θ = 1.13°. The map is symmetrized at B = ±0.5 T. b Similar map of the Hall resistance, anti-symmetrized at B = ±0.5 T. Analogous ρxx maps for the c t2 + 2 device with θ = 1.30°; e t1 + 3 device with θ = 1.29°; and g t2 + 3 device with θ = 1.50°. d, f, h Analogous Rxy maps for the same set of devices. Schematics in the top panels indicate the layer combination for each measurement. The measurements are performed at nominal sample temperatures of a, b T = 300 mK, c–f T = 20 mK, g, h T = 100 mK.

Full size image

Resistive states additionally appear at ν = 1 and 3 in each of the ρxx maps in Fig. 2. These feature additional sign reversals (or large enhancements) in Rxy, indicating the formation of additional symmetry-broken states with no remaining isospin degeneracies. Previous studies of t1 + 2 and t2 + 2 suggest that the ground-state ordering of these odd ν phases is less consistent, as spin-valley polarized (SVP) states compete closely with intervalley coherent (IVC) states9,10,11,12,14,15,16,17,18. These two can be challenging to distinguish in an experiment, as we discuss in more detail in the Methods.

It is interesting to note that the t2 + 4 device from Fig. 1d, h, l, as well as the additional t1 + 4, t2 + 4 and t2 + 5 devices we have studied, did not show correlated insulating states or pronounced regions of enhanced resistivity with an Rxy sign reversal at a small magnetic field (Supplementary Figs. 3 and 10). This may be due to: (i) the smaller band gaps to higher moiré bands in these thicker structures, (ii) bands that are more dispersive in reality than those predicted by calculations, (iii) devices made away from the optimal flat-band twist angle for each layer number construction, or some combination of all of these. Indications of a symmetry-broken Fermi surface at ν = 2 in t2 + 4 did appear over a small range of magnetic field around B ≈ 4 T (see Supplementary Fig. 4). However, this correlated phase is quickly suppressed by competing quantum Hall states originating from ν = 0. Nevertheless, the new Fermi surface formed at ν = 2 in a modest magnetic field indicates that this sample is also close to a strongly correlated regime.

Abundance of correlated states in t2 + 3

Among all the tM + N samples we have studied, t2 + 3 devices had the largest extent of symmetry-broken phases as a function of ν and D (Fig. 3, see also Supplementary Fig. 5). In addition to exhibiting symmetry-broken correlated insulators for both signs of D in the lowest moiré conduction band, the samples showed evidence for symmetry broken phases distinct from the usual states seen in the other tM + N systems (see Fig. 1g, Supplementary Figs. 6, and 11).

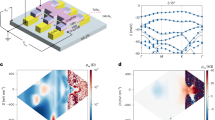
Fig. 3: Correlated states in t2 + 3 graphene.
figure 3

a Summary phase diagram determined from magnetotransport measurements in the θ = 1.50° device (see Methods for the determination of different features). Black vertical features indicate insulating states (Ins). The ν = 1 and 3 states are in shaded dark grey to indicate that it is a weakly–developed resistive state corresponding to an incipient insulator. Shaded regions indicate where the metallic states are either normal–metals (NM), half-metals (HM), or quarter–metals (QM). White regions within the bounding box indicate situations in which the degeneracy cannot be uniquely determined. Solid red lines denote likely van Hove singularities (vHS) with Rxy = 0. Dashed black lines denote abrupt jumps in Rxy. b Map of ρxx acquired at T = 20 mK and symmetrized at B = ± 0.9 T, corresponding to the black dashed box in (a). Spacing of the quantum oscillations (Δν) indicates the degeneracy of the metallic phases. Corresponding schematics indicate the degeneracy for representative regions of normal–metal (Δν = 4, top), half–metal (Δν = 2, bottom right), and quarter–metal (Δν = 1, bottom left) phases. c Fourier transform analysis (FFT) of the SdH measurements taken along the dashed black line at D = 0.41 V/nm in (b). The FFT amplitude is normalized to the maximum value of the measurement, and the frequency of oscillations is normalized to the density (see Methods for details). d Measurements of ρxx for three t2 + 3 devices with different θ acquired around ν = 0. All measurements are performed at T = 2 K. e Temperature dependence of ρxx as a function of D, acquired in the θ = 1.41° device at ν = 0. Line cuts at select values of D are shown for each state in the inset, normalized by their respective values at T = 2 K. The gray shaded region indicates a region of the data influenced by artifacts from the electrical contacts.

Full size image

Figure 3a summarizes our experimental observations for a t2 + 3 device with a 1.50° twist angle, incorporating observations from Figs. 2g, h, and 3b, c, and Supplementary Fig. 7. States labeled in black or dark gray are insulating or highly resistive (the unexpected gapped state at ν = 0.25 will be discussed in future work). Solid red curves denote sign changes in Rxy that likely correspond to van Hove singularities, whereas dashed black curves denote abrupt jumps in Rxy without a sign change, possibly indicating the formation of a new interaction-induced Fermi surface. Shaded regions in Fig. 3a correspond to metallic states with different isospin degeneracies. Experimentally, the degeneracy can be identified either from the spacing, Δν, between Shubnikov de Haas (SdH) oscillations in ν − D maps taken at finite magnetic field (Figs. 2g and 3b) or from the Fourier transform of SdH oscillations collected by sweeping the magnetic field at fixed gate voltage (Fig. 3c and Supplementary Fig. 7). The degeneracy extracted from Δν is four outside the correlated region (e.g., Δν = 4 in the top of the map shown Fig. 3b), consistent with the fourfold spin and valley degeneracy of graphene. The degeneracy is reduced to two inside the region surrounding the correlated insulator at ν = 2 (light red in Fig. 3a), consistent with our inference of a spin-polarized ground state.

The degeneracy is harder to discern in the regions surrounding ν = 1 and 3 (see Methods and Supplementary Fig. 8), although there is a region of ν closely surrounding ν = 1, colored in purple, where Δν is unambiguously one. There is also a small pocket of a symmetry-broken phase over a narrow range of D ≈ 0.4 V/nm between ν = 0 and ν ≈ 0.21. Figure 3c shows the normalized Fourier transform of the SdH oscillations measured at a fixed D cutting through this small pocket, as denoted by the horizontal black dashed line in Fig. 2b (see Methods for further description of the analysis). We see that all isospin degeneracies are lifted in this pocket, corresponding to a quarter-metal phase for ν < 0.21. This is, to our knowledge, the first observation of a quarter-metal state in the tM + N family that is not directly associated with the ν = 1 insulator, pointing to the unusually strong interactions in this system. Interestingly, it does not exhibit the anomalous Hall effect (AHE), suggesting that it may either carry a very small Berry curvature or instead be in an IVC ordered state (Supplementary Fig. 9).

We further see an unexpected insulating state at ν = 0 near D = 0 across several t2 + 3 devices with different twist angles (Fig. 3d and Supplementary Fig. 5). Our single-particle band structure calculations do not predict such a gap for any reasonable model parameters (see Methods), suggesting that it may arise spontaneously. This hypothesis is supported by measurements of the temperature dependence at ν = 0 for the device with θ = 1.41° (Fig. 3e). The sample resistance at ∣D∣ > 0.3 steadily increases as the temperature is lowered (grey and black curves in the inset), consistent with a band insulator. Near D = 0, on the other hand, insulating behavior abruptly onsets below T ≤ 10 K (purple curve in the inset). Thermal activation measurements of this state yield a maximum gap size of \({\Delta }_{\max }^{\nu=0}=1.54\pm 0.05\,{{{\rm{meV}}}}\) (see Supplementary Fig. 13). Although not definitive, the abrupt emergence of the gapped state with temperature at D ≈ 0 and its relatively small size suggests that it may arise owing to interactions, similarly to the correlated insulators at charge neutrality in bilayer graphene29,30,31,32 and rhombohedral few-layer graphene33,34,35,36. Overall, it remains an open question as to why t2 + 3 exhibits the most robust and prevalent symmetry-broken phases over a wide range of ν and D, as our band structure modeling does not predict that the bandwidth should be small compared to other tM + N structures.

Topological states in tM + N graphene

Finally, we turn our attention to the topological properties of the tM + N moiré bands. The AHE has been seen previously in both t1 + 2 and t2 + 29,10,12,18. In the former, anomalous Hall resistances close to the quantized values h/2e2 and h/e2 have been observed, consistent with a SVP state formed from bands with a θ-dependent valley Chern number of either Cv = 1 or 29,10. The AHE is typically not observed in t2 + 2 at ν = 1 and 3, despite strong indications of a valley Chern number of 2, potentially indicating IVC order14,15,16,17. Nevertheless, in select cases it has been observed for ν > 3, pointing to the emergence of a SVP state18.

In our t1 + 3 sample, the correlated state at ν = 1 is too weakly developed to determine its isospin ordering (even with an applied magnetic field, as shown in Supplementary Fig. 11). However, the state at ν = 3 exhibits a clear AHE characterized by hysteresis in Rxy upon sweeping B back and forth, as shown in Fig. 4a at optimal doping and displacement field. Figure 4b shows the doping dependence of the AHE, characterized by the difference between forward and backward sweeps in a magnetic field, \(\Delta {R}_{xy}=({R}_{xy}^{\uparrow }-{R}_{xy}^{\downarrow })/2\). The AHE state is most pronounced close to ν = 3 and is quickly suppressed upon doping. The corresponding Landau fan diagram shows that the gapped state drifts to smaller ν upon applying B (Fig. 4c), with a slope indicating a Chern number of C = −2 as determined by the Středa formula (\(\frac{dn}{dB}=C\frac{e}{h}\)). These observations are all consistent with an incipient quantum anomalous Hall effect (QAHE) owing to a SVP state at ν = 3. Band structure modeling predicts a valley Chern number of Cv = 2, consistent with our observation. The QAHE is not well developed, likely due to a combination of a small energy gap and substantial magnetic disorder in the sample37. These topological properties are reminiscent of those seen in t1 + 2 devices with similar twist angles10.

Fig. 4: Anomalous Hall effects in t1 + 3 and t2 + 3 devices.
figure 4

a Rxy measurement in the t1 + 3 device (θ = 1.29°) acquired as B is swept back and forth at ν = 3.02 and D = 0.523 V/nm. b Doping dependence of the AHE effect at the same displacement field characterized by the difference in the forward and backward sweeps, \(\Delta {R}_{xy}=({R}_{xy}^{\uparrow }-{R}_{xy}^{\downarrow })/2\). c Landau fan diagram of Rxy versus B around ν ≈ 3. The correlated Chern insulator emerging from ν = 3 exhibits a slope consistent with C = −2. d Rxy measurement in the t2 + 3 device (θ = 1.50°) acquired at ν = 0.75 and D = 0.532 V/nm. e Doping dependence of the AHE in the same device. f Landau fan diagram of ρxx versus B around ν ≈ 1. The correlated state at ν = 1 projects vertically, consistent with C = 0. All data acquired at T = 20 mK.

Full size image

The topological properties of t2 + 3 are more unusual. We again find a valley Chern number of Cv = 2 in our band structure calculations and see clear signatures of an AHE, in this case below ν = 1 (shown in Fig. 4d for ν = 0.75). The magnitude of the AHE is small, but persists over a wide range of doping and vanishes very near ν = 1 (Fig. 4e). However, the corresponding Landau fan diagram exhibits an insulating state emerging from ν = 1 with zero slope up to high magnetic field (Fig. 4f), indicating that the ν = 1 symmetry-broken state is topologically trivial. Although the C = 0 state may arise due to IVC ordering, the application of a modest B should favor a first-order phase transition to a SVP state. Notably, however, the absence of such a transition to a C = 2 Chern insulator state is inconsistent with this scenario. An alternative possibility is that, upon opening a gap at ν = 1, interactions renormalize the Chern number of the filled band to C = 0. In this scenario, the AHE can arise due to Berry curvature hot spots in the reconstructed bands formed by spontaneous symmetry breaking, while the total Berry curvature of the symmetry-broken band integrates to zero. Further theoretical and experimental work is needed to better resolve the nature of this state.

Discussion

Taken collectively, our measurements establish a family of moiré graphene structures composed of Bernal-stacked graphene thin-film constituents with a small interfacial twist. By extending prior studies of twisted monolayer-bilayer and twisted double-bilayer graphene to thicker tM + N variants, we discover a number of striking commonalities in both the single-particle and correlated states across this entire family.

The localization of low-energy states to the layers at and just below the moiré interface, which underlies this phenomenon, may also generalize to moiré systems built from other vdW materials. For instance, a promising future direction would be to extend studies of twisted homobilayer transition metal dichalcogenides to similar multilayer constructions. This could, for example, help to establish new control knobs over the recently discovered fractional quantum anomalous Hall states in twisted bilayer MoTe238,39,40,41. Accurately modeling these structures will require the development of new theoretical analyses beyond those considered here, including the effects of electrostatic screening of D and crystal fields at the twisted interface42. In parallel, further experimental studies into the largely unexplored physics of twisted monolayer-trilayer and bilayer-trilayer graphenes are very likely to reveal exciting new topological states. Our results thus establish a way to greatly expand the palette of topological flat bands available for study.

Methods

Device fabrication

To fabricate tM + N structures, we first optically identified an exfoliated graphene flake with a step, such that one portion of the flake is M layers thick whereas another portion is N layers. We next isolated regions of the M- and N-layer components using polymer-free anodic oxidation nanolithography43,44,45. We used standard dry transfer techniques with a polycarbonate (PC)/polydimethyl siloxane (PDMS) stamp46 to stack isolated flakes with an interlayer twist by rotating the stage by an angle θ after the M-layer flake was picked up. These structures were encapsulated with hexagonal boron nitride flakes and graphite gates, and then transferred onto a Si/SiO2 wafer. We used standard electron beam lithography and CHF3/O2 plasma etching to define vdW stacks into a Hall bar geometry and standard metal deposition techniques (Cr/Au)46 to make electrical contact to the graphene multilayers. Optical images of all completed devices measured in this work are shown in Supplementary Fig. 1, and a summary of our observations across all devices is provided in Supplementary Table 1.

We note that, in principle, there could be regions of the exfoliated graphene flakes with metastable stacking orders other than Bernal. However, these non-Bernal domains are known to relax to the ground-state Bernal stacking configuration during stacking unless great care is taken to isolate only non-Bernal domains and minimize strains during transfer47. Since we do not take any such precautions, it is overwhelmingly likely that all non-Bernal domains relax to the Bernal configuration in our final samples. Another possible ambiguity in our sample construction is AB vs. BA stacking configurations between the twisted components. For example, t2 + 2 can host symmetry-broken states when twisted slightly away from 0° (tAB + AB) or away from 60° (tAB + BA)48. While we fabricated all of our devices by twisting slightly away from 0°, it is known that AB–BA stacking faults naturally exist in bilayer graphene flakes49, and these cannot be observed optically. It is therefore possible that tM + N devices with M ≥ 2 and N ≥ 2 have unintentional domains of AB–BA at the twisted interface. These could, in principle, have different band structures and valley Chern numbers. Further work is needed to carefully distinguish these potential scenarios.

Transport measurements

Transport measurements were carried out in various cryogen-free systems using a lock-in amplifier with frequencies between 13.33 and 17.77  Hz and a.c. bias between 1 and 10 nA. All data presented in the main text were acquired in Bluefors dilution refrigerators with nominal base temperatures between 10 and 30 mK unless otherwise noted. Data reported at and above 1.5 K (e.g., Fig. 3d, e) were acquired in a Cryomagnetics variable temperature insert.

The top and bottom gate voltages were used to independently control the carrier density, n, and perpendicular displacement field, D according to the following relations: n = (VtCt + VbCb)/e and D = (VtCt − VbCb)/2ϵ0, where Ct and Cb are the capacitance per unit area of the top and bottom dielectrics, respectively, Vt and Vt are the top and bottom gate voltages, respectively, and ϵ0 is the vacuum permittivity. When specified, we perform field symmetrization (antisymmetrization) of ρxx and Rxy following ρxx = [ρxx(B) + ρxx(−B)]/2 and Rxy = [Rxy(B)−Rxy(−B)]/2.

We estimate the twist angle, θ, between M- and N-layer flakes by fitting the sequences of quantum oscillations emerging from ν = 0 and ν = ±4 in Landau fan diagram measurements of ρxx and Rxy as a function of n and magnetic field, B. From the Landau fan fit, we determine the superlattice density, ns, and extract the twist angle using the relation \({n}_{s}=4\frac{2{\theta }^{2}}{\sqrt{3}{a}^{2}}\), where a = 0.246 nm is the graphene lattice constant.

Extraction of Fermi surface degeneracy from quantum oscillations

The frequency of quantum oscillations, fν, is extracted from low-field Landau fan measurements taken at constant D (Supplementary Fig. 7) The frequency of oscillations, fB, is first extracted from the Fourier transform (FFT) of each field sweep with respect to 1/B. The frequency is then normalized by the total carrier density, fν = fB/(Φ0n). For the case of a singly connected Fermi surface at the Fermi level, the inverse quantity \({f}_{\nu }^{-1}\) represents the degeneracy of charge carriers47. Supplementary Fig. 7b, c shows the analysis outside of the correlated region of the t2 + 3 device, where there is a sharp peak in the FFT signal at \({f}_{\nu }^{-1}=4\), consistent with the fourfold degeneracy of graphene. Various line cuts are shown in the remainder of Supplementary Fig. 7, and indicate quarter metal (\({f}_{\nu }^{-1}=1\)) and half metal (\({f}_{\nu }^{-1}=2\)) states formed over certain ranges of n and D.

Multiband transport in t2 + 3 graphene

Regions of parameter space in the t2 + 3 device shown in Fig. 3a colored in white correspond to situations in which we are unable to unambiguously determine the degeneracy of the Fermi surface. Especially around ν = 3, this ambiguity likely arises due to multiple Fermi surface pockets coexisting within the moiré Brillouin zone. Supplementary Fig. 8 shows evidence for this in the form of curved trajectories of quantum Hall states seen in Landau fan diagrams. Such curved trajectories violate the Středa formula, which always predicts linear trajectories of topological gapped states, and generally arise due to the need to fill charge carriers simultaneously into two separate bands that each have their own sequence of Landau levels50.

Determination of isospin polarization at integer band fillings

We employ a combination of out-of-plane and in-plane magnetic field measurements of ρxx and Rxy in order to infer the isospin polarization of the correlated states seen at ν = 1, 2, and 3. In-plane magnetic field couples primarily to the spin degree of freedom in graphene owing to its very weak spin-orbit coupling strength (although there can be orbital contributions in multilayer graphene samples51). Previous measurements of the correlated insulator at ν = 2 in t1 + 2 and t2 + 2 showed that the energy gap, as extracted from thermal activation measurements, grows with in-plane field9,14,15,16. This behavior is consistent with spin-polarization, as the in-plane field adds a Zeeman contribution to the energy gap. We have performed similar measurements in our t1 + 3 (θ = 1.29°) and t2 + 3 (θ = 1.50°) devices. Supplementary Fig. 2a, b shows measurements of ρxx as a function of ν in the moiré conduction band at various values of the in-plane magnetic field, B∣∣. In both devices, ρxx is highly sensitive to B∣∣ very near ν = 2, exhibiting enhanced resistance for larger in-plane fields. These observations are consistent with spin-polarized correlated insulators at ν = 2 in t1 + 3 and t2 + 3. For the t1 + 3 device, we further performed temperature-dependent measurements at several values of B∣∣. In the Arrhenius plot shown in Supplementary Fig. 2c, we can extract the gap size of the ν = 2 insulator in the thermally activated regime following \({\rho }_{xx}^{\nu=2}\propto {e}^{{\Delta }^{\nu=2}/2{k}_{B}T}\), where Δν=2 is the gap size and kB is the Boltzmann constant. The results are shown in Supplementary Fig. 2d. The measured gap size grows monotonically as a function of B∣∣. By fitting with a line, assuming Δν=2(B) = gμBB + Δν=2(0), we find g ≈ 2, consistent with a spin-polarized insulating state.

At ν = 1 and 3, calculations typically find the most competitive ground states to be either IVC states or SVP states51. When Cv is non-zero, these states are distinguished by the Chern number of the symmetry-broken state, which is 0 for the IVC and non-zero for the SVP. A well-developed IVC state with non-zero Cv would be a trivial insulator at integer band filling, whereas an SVP would exhibit the QAHE. Although these are in principle straightforward to distinguish, there can be various complicating factors in experiments. One example is twist-angle inhomogeneity in the sample, which can greatly obscure the QAHE. Another is that the correlated state may not be fully gapped at zero magnetic field, preventing a straightforward determination of the topology of the state. There are also exotic forms of IVC ordering that break time-reversal symmetry, leading to a metallic AHE12. Although band structure calculation of Cv can provide guidance, the complexity of the calculation for thick tM + N structures may result in incorrect predictions. Furthermore, interactions can potentially renormalize the Chern number of the symmetry-broken states at partial band filling. In general, we are not able to unambiguously determine the ground state ordering at ν = 1 and 3 in our devices, except for the select cases shown in Fig. 4 in the main text.

Symmetries of tM + N structures

All tM + N structures studied here break C2z symmetry, thus enabling a gap to be opened at the CNP by D. Structures with M = N have mirror symmetry about the twisted 2D plane, and thus exhibit (approximately) identical transport for D > 0 and D < 0. In contrast, all structures with M ≠ N break this mirror symmetry, and thus have different transport properties depending on the sign of D. This was explored in detail for the case of t1 + 2 in refs. 9,12, and is also evident for the new, thicker structures studied here (Fig. 1). In cases where correlated states are seen for both signs of D, their properties are distinct owing to substantial differences in the layer-polarization of the LDOS and corresponding differences in the non-interacting bands.

Band structure calculations

We utilize a generalized Bistritzer–MacDonald Hamiltonian for the single-particle band structure calculations. The effective Hamiltonian can be written as

$$H=\left(\begin{array}{cc}{H}_{M}&{H}_{{{{\rm{int}}}}}^{{{\dagger}} }\\ {H}_{{{{\rm{int}}}}}&{H}_{N}\end{array}\right),$$
(1)

where HM and HN are Hamiltonians for the M- and N-layer graphene, respectively, and Hint captures the interlayer coupling of the twisted moiré interface. The multilayer graphene Hamiltonians are given by

$${H}_{M}=\left(\begin{array}{ccccc}{H}_{1}-{\Delta }_{1}&\Gamma &\tilde{\Gamma }&0&\\ {\Gamma }^{{{\dagger}} }&{H}_{1}-{\Delta }_{2}&{\Gamma }^{{{\dagger}} }&{\tilde{\Gamma }}^{{\prime} }&\\ \tilde{\Gamma }&\Gamma &{H}_{1}-{\Delta }_{3}&\Gamma &\\ 0&{\tilde{\Gamma }}^{{\prime} }&{\Gamma }^{{{\dagger}} }&{H}_{1}-{\Delta }_{4}&\\ &&&&\ddots \end{array}\right),$$

with

$${H}_{1}=\left(\begin{array}{cc}0&\frac{\sqrt{3}}{2}{\gamma }_{0}({k}_{x}-i{k}_{y})\\ \frac{\sqrt{3}}{2}{\gamma }_{0}({k}_{x}+i{k}_{y})&0\end{array}\right),$$
$$\Gamma=\left(\begin{array}{cc}-\frac{\sqrt{3}}{2}{\gamma }_{4}({k}_{x}-i{k}_{y})&-\frac{\sqrt{3}}{2}{\gamma }_{3}({k}_{x}+i{k}_{y})\\ {\gamma }_{1}&-\frac{\sqrt{3}}{2}{\gamma }_{4}({k}_{x}-i{k}_{y})\end{array}\right),$$
$$\tilde{\Gamma }=\left(\begin{array}{cc}\frac{1}{2}{\gamma }_{2}&0\\ 0&\frac{1}{2}{\gamma }_{5}\end{array}\right),\,{\tilde{\Gamma }}^{{\prime} }=\left(\begin{array}{cc}\frac{1}{2}{\gamma }_{5}&0\\ 0&\frac{1}{2}{\gamma }_{2}\end{array}\right),$$
$${{{\rm{and}}}}\,{\Delta }_{i}=\left(\begin{array}{cc}{\delta }_{i}&0\\ 0&{\delta }_{i}\end{array}\right)$$
(2)

The Hamiltonian is appropriately truncated according to how many layers there are. We use hopping parameters (γ0, γ1, γ2, γ3, γ4, γ5) =(2610, 361, −20, −283, −140, 20)meV. The parameter δi captures the effect of a potential difference across the layers. For simplicity, we assume that the potential drops uniformly across the structure with a total magnitude given by \(\delta={\sum }_{i=1}^{M+N}| {\delta }_{i}|\). For example, the potentials for the t1 + 2 system would be δ1 = δ/2, δ2 = 0, and δ3 = −δ/2. By this definition, δ > 0 corresponds to an experimentally applied D > 0 that points from the top to the bottom, or thin to thick layer as shown in Fig. 1. In the continuum approximation, the M- and N-layer systems are coupled when the Bloch wave vectors differ by \({\overrightarrow{q}}_{j}\), where \({\overrightarrow{q}}_{0}=(0,0),\,{\overrightarrow{q}}_{1}=1/{L}_{M}(-\frac{2\pi }{\sqrt{3}},-2\pi )\), \({\overrightarrow{q}}_{2}=1/{L}_{M}(\frac{2\pi }{\sqrt{3}},-2\pi )\), and LM = a/θ is the moiré wavelength. The interlayer Hamiltonian is then given by

$${H}_{{{{\rm{int}}}}}=\mathop{\sum }_{j=0}^{2}{t}_{M}\left(\begin{array}{cc}\alpha &\exp \left(-i\frac{2\pi j}{3}\right)\\ \exp \left(i\frac{2\pi j}{3}\right)&\alpha \end{array}\right),$$
(3)

where tM = 110 meV and α = 0.5.

Example band structures calculated for the t1 + 3 system are shown in Supplementary Fig. 15a–c. Across many tM + N constructions, we generally find overlap between the moiré conduction and valence bands with δ = 0. Further, the moiré valence band tends to be more dispersive than the moiré conduction band, consistent with our experimental observations that correlated states primarily occur on the electron-doped side. We performed a series of calculations for a range of θ and Δ for all tM + N layer combinations up to t3 + 6, resulting in over 5000 individual band structures. To inform our experimental search, we quantify how isolated and flat the moiré conduction band is for each set of parameters by defining

$$\phi=\xi \frac{| {\Delta }_{+4}| | {\Delta }_{0}| }{\delta E},$$
(4)

where Δ+4 (Δ0) is the energy difference between the top (bottom) of the moiré conduction band and the remote conduction band (moiré valence band), and δE is the bandwidth of the moiré conduction band (Supplementary Fig. 15c). We define ξ = +1 when Δ+4 and Δ0 are both positive, and ξ = −1 otherwise.

With this definition, ϕ becomes more positive as the moiré conduction band becomes more flat and isolated. When ϕ is negative, the moiré conduction band overlaps with the moiré valence band and/or the remote conduction band. Supplementary Fig. 15d–g shows δE, Δ+4, Δ0, and ϕ as function of θ and δ for the t1 + 3 system, in which we find the optimal angle condition (defined as when ϕ achieves its largest positive value, shown in purple) to be at θ ≈ 1.30° and δ ≈ +75 meV. Detailed results for each layer combination are shown in Supplementary Figs. 16–29. We summarize the results for all layer combinations in Supplementary Fig. 14, where each data point is color-coded according to the maximum value of ϕ that is obtained for each system. Systems up to t2 + 3 have appreciably flat and isolated moiré conduction bands, but for t1 + 4, t2 + 4, and thicker, ϕ is very small or negative. For each layer combination in which we find that a flat and isolated moiré conduction band is predicted (i.e., ϕmax > 0), we further calculate the valley Chern number of the moiré conduction band at the optimal parameter condition (i.e., for the values of θ and δ where \(\phi={\phi }_{\max }\)). We find that all systems have non-zero Cv, reaching as large as Cv = 3 for thicker layer combinations.

We note that we use the continuum model predictions of the nominally optimal twist angle only as a rough guide for our experiments. Theoretically, it is not clear whether band flatness, band isolation, or some specific combination of the two is the most important parameter to optimize for achieving strongly correlated states. Even upon choosing a metric for the nominally optimal twist angle in theory, the particular value differs for each tM + N construction and depends on detailed parameters in the continuum model which are not necessarily well known. Experimentally, determining the optimal twist angle for even a single tM + N construction requires studying dozens of devices, which is also beyond the scope of this work. We thus leave a careful determination of the evolution of the optimal twist angle on the layer number construction to future efforts.

Finally, we consider the effect of changing the Hamiltonian parameters to potentially explain the unexpected insulating state at ν = 0 and D ≈ 0 in t2 + 3 system (Fig. 3d–e). Within reasonable values of the tight binding parameters (γi), we find that there is always band overlap for twist angles between 1.33° and θ = 1.72°. The only parameter that has a significant effect at ν = 0 and D = 0 is the strength of the moiré coupling, tM. In Supplementary Fig. 30, we show band structure calculations varying tM around the nominal value of 110 meV. Increasing tM has the effect of flattening the bands further, but does not create a gap at charge neutrality. Reducing tM can create a small gap at charge neutrality, but in this case the moiré bands are much more dispersive and overlap with the remote bands. Both scenarios are inconsistent with the observations in our experiment. Taken together with the temperature dependence measurements shown in Fig. 3e, we conclude that the insulating state at ν = 0 and D ≈ 0 is most likely to be a correlated state.

Berry curvature and Chern number calculation

We use the method from ref. 52 to calculate Berry curvature. The moiré Brillouin zone (MBZ) is discretized into a 50 × 50 grid. For each k in the MBZ, we calculate the U(1) link:

$${U}_{\mu }({{{\bf{k}}}})=\frac{\langle u({{{\bf{k}}}}+\delta {k}_{\mu }{\hat{k}}_{\mu })| u({{{\bf{k}}}})\rangle }{{N}_{\mu }({{{\bf{k}}}})},$$
(5)

where \({N}_{\mu }({{{\bf{k}}}})=| \langle u({{{\bf{k}}}}+\delta {k}_{\mu }{\hat{k}}_{\mu })| u({{{\bf{k}}}})\rangle |\) and μ = 1, 2. The Berry curvature is then given by:

$$\Omega ({{{\bf{k}}}})=-\frac{{{{\rm{i}}}}\ln W({{{\bf{k}}}})}{\delta {k}_{1}\delta {k}_{2}},$$
(6)

where W(k) is \({U}_{1}({{{\bf{k}}}}){U}_{2}({{{\bf{k}}}}+\delta {k}_{1}{\hat{k}}_{1}){U}_{1}^{-1}({{{\bf{k}}}}+\delta {k}_{2}{\hat{k}}_{2}){U}_{2}^{-1}({{{\bf{k}}}})\). We ensure that \(-\pi < -{{{\rm{i}}}}\ln W({{{\bf{k}}}})\le \pi\). The valley Chern number is calculated as:

$${C}_{v}=\frac{1}{2\pi }{\int}_{\!\!\!{{{\rm{MBZ}}}}}{d}^{2}{{{\bf{k}}}}\Omega ({{{\bf{k}}}})$$
(7)

where MBZ denotes an integration over the moiré Brillouin zone.