Introduction

Hydrogen as a carbon-free energy carrier can contribute to meeting the world’s growing energy needs in a reliable, affordable, and sustainable manner1,2. Hydrogen-powered fuel cells provide clean energy, offering a highly efficient and reliable system without the intermittency of other renewable energy3. Global hydrogen demand is expected to grow significantly. One of the key challenges in establishing a commercially viable hydrogen supply chain is to cost-effectively store and transport hydrogen over large distances in a reliable and safe manner due to its very low volumetric energy density at ambient conditions, which bridges the gap between hydrogen production and fuel cells. Physical hydrogen storage systems typically demand harsh conditions such as a high-pressure tank (up to 700 bar) for gas or cryogenic temperature (20.2 K) for liquid, still suffering from a low volumetric storage density and substantial energy loss by boil-off, respectively4,5. In this respect, solid-state hydrogen storage can be a viable option for offering a high storage density as well as ultimately ensuring operational safety and low cost.

In particular, metal hydrides received a large amount of research attention for efficient solid-state hydrogen storage since the lightweight metal intrinsically allows a high gravimetric and volumetric storage density. Also, metal hydrides have modest equilibrium pressure over hydrogen, thereby granting relatively low pressure below 100 bar for hydrogen storage6, which not only leads to a reduction in cost but also allows efficient storage and stability. Among a variety of metal hydrides, MgH2 is considered a promising candidate due to its availability and high hydrogen storage capacity, amounting to 7.6 wt%7,8, which makes it suitable for mobile applications9. Despite the aforementioned merits of Mg as a solid-state hydrogen storage system, the sluggish kinetics of hydrogen ab/desorption caused by the dissociation of hydrogen molecules on the surface and the slow diffusion of hydrogen atoms into the bulk phase of Mg results in prolonged re/discharging10. It also requires a high desorption temperature because of thermodynamically stable MgH2−indicative of a strong Mg-H binding11,12. Furthermore, Mg is highly reactive and vulnerable to oxidation and other undesirable reactions even with a trace amount of foreign species13.

Many research efforts have been devoted to offset the disadvantages of bulk Mg, such as tuning surface oxidation14, severe plastic deformation15,16, catalyst addition, and incorporation of different species17,18. Among other strategies, many studies demonstrated the promise of nanoscaled Mg in enhancing hydrogen storage properties19. The high surface-to-volume ratio and small crystalline size increase the exposed surface of Mg for hydrogen sorption. The size of crystallite in the nanoscale can reduce the diffusion distance of hydrogen or provide a faster diffusion pathway by adding defects9,14,20. Furthermore, it is possible to improve the hydrogen storage performance of Mg via transition metal doping, which lowers the activation energy barriers of the hydrogen adsorption and dissociation process, serving as a catalyst21,22. Although transition metal doping is mainly employed in terms of kinetic enhancement, it also collaterally changes the thermodynamic properties by forming an alloy with Mg9,13, wherein the strong Mg-H bonding state is weakened to enable hydrogen ab/desorption at a lower temperature.

Meanwhile, nanoporous metals have been formulated, taking advantage of both nanosized and porous structures. In addition to organic framework-based porous materials, such nanoporous metal structures can be effectively utilized in various fields due to their tunable pore structure, large specific surface area, and high electrical conductivity. These structural characteristics have the advantages of increased reactive sites between reactants as well as improved electron mobility and thermal conductivity along metal ligaments. In addition, it potentially allows faster kinetics for molecular or atomic transport, attributed to a facilitated diffusion pathway through the pores. In this regard, the nanoporous Mg structure enables the expedited transport of hydrogen through pores, simultaneously improving the hydrogen sorption kinetics by effectively reducing the diffusion length due to its large surface area and nanosized ligaments. Also, the potential structural collapse caused by a volume change upon hydrogen ab/desorption−corresponding to 33% for Mg−can be alleviated through the porous structure20,23.

There are several methods to generate porous metal structures such as template synthesis, surfactant-mediated synthesis, and dealloying24,25. The most well-known and reported to be effective is dealloying, in which case porous metals can be obtained by preferentially removing less noble metals from metal alloys via chemical or electrochemical etching26. However, it requires a laborious step of preparing a homogeneous metal alloy precursor as a starting material for the sake of a uniform structure27, and more critically this dealloying method relies on the use of a corrosive acid or base as an etching solution28,29,30,31. Based on such approaches, different kinds of porous metals have been prepared, mostly the synthesis of transition metals such as Au, Pd, Pt, Ag, Cu, and Zn28,29,30,31. However, in the case of various alkali and alkaline earth metals which are largely exploited for energy applications, few studies on the synthesis of porous structures were reported. Such highly reactive metals are vulnerable to oxygen and moisture, easily losing their unique characteristics by reacting with those impurities−even with a minimal amount. Accordingly, under a corrosive environment in the conventional method, reactive metals would readily react with oxygen and inevitably produce a substantial amount of dead mass, which is undesirable for targeted applications.

In this report, we synthesized porous Mg nanostructures through a solution-based method without a corrosive etching for advanced solid-state hydrogen storage. As opposed to conventional dealloying using metal alloys under harsh environments, metal compounds are employed as a starting material whereby a porous structure is evolved in the solution of an organic reducing agent due to the difference of reduction potentials. By selectively dissolving anions from the initial compound via a reduction-induced decomposition (RID), nanoporous metal structures can be obtained through percolation dissolution32,33. The bicontinuous nanoporous Mg structure with a small ligament size contributes to facilitating hydrogen transport. Essentially, we report the synthesis of porous nanostructure for reactive metals such as Mg under mild conditions without corrosive reagents. Furthermore, given that porous metal structures evolve spontaneously upon an adequate selection of the reducing solution and the target porous metal in consideration of their reduction potentials, this approach can be readily adapted to prepare various kinds of reactive porous metals for advanced energy applications.

Results

Nanoporous Mg structure via a facile solution-based reduction-induced decomposition

In this study, nanoporous Mg structures–pristine porous Mg (pMg) and transition metal doped porous Mg (porous Mg/Ni and Mg/Co bimetallic system, referred to as pMgNi and pMgCo, respectively)–were synthesized via a facile solution-based one-pot RID method, in which an organic solvent is employed as a reducing agent (please see “Method” section and also Supplementary Note 1 for details), whereas a conventional dealloying approach to preparing porous metals utilizes a strong acid as an etching solvent. The precursor material for RID was prepared by completely melting the corresponding metal compound powder (MgCl2) at a temperature above its melting point to form a single mass. Subsequently, the insoluble precursor was immersed in a highly reductive lithium naphthalenide solution at room temperature, evolving into a porous structure. Figure 1a illustrates the process of such reduction reaction, followed by the formation of a porous structure and its hydrogen sorption. While the cations are reduced to a zero-valent metal structure, the counter anion \({X}^{m-}\) (for example, \({{Cl}}^{-}\) in the case of MgCl2) must be successfully eluted into the solution phase, and accordingly, a solvent with high anion solubility is selected32. The metal nucleation occurs at the interface between the metal precursor and the reductive solution, and the full-scale metal phase formation occurs. Through the low interfacial energy between the metal phase and the metal compound, the newly formed metal phase is connected to the metal compound without being separated into the solution to form the bicontinuous metal ligament structure34,35.

Fig. 1: Nanoporous Mg structure via the environmentally benign reduction-induced decomposition (RID) reaction for solid-state hydrogen storage.
figure 1

a Schematic illustration of RID reaction (a black porous chunk represents MgCl2 turning into Mg). XRD patterns of as-synthesized (b) pMg, (c) pMgNi, and (d) pMgCo; the inset is the camera picture of each porous metal powder and the scale bar is 5 mm. Source data are provided as a Source Data file.

Full size image

In the previous study, the continuum percolation theory provides a volumetric threshold \({p}_{v}\) for the continuous formation of porous structures without structural collapse32,36. The appropriate range of the molar volume change between metal compound and pure metal (\(\Delta {V}^{m}\)) is proposed as \({p}_{v} < \,\Delta {V}^{m} < 1-\,{p}_{v}\) (volumetric threshold, \({p}_{v}\,\)~ 14–16%), in which all kinds of 3-dimensional structures are feasible37. Accordingly, the upper and lower limit for volume change between the metal compound and the pure metal generated during dissolution is obtained, which corresponds to 14–16% and 84–86%32. Specifically, the theoretical molar volume change between MgCl2 and Mg is calculated to be 65.93%, and this value falls within the aforementioned range; therefore, the relevant percolation dissolution of Mg compound into pure Mg is expected with open pores and continuous metal phase. Furthermore, a bimetallic porous structure composed of Mg and transition metal (Ni, Co) was also synthesized via the same protocol, along with the addition of a small amount (5 mol.%) of a transition metal compound in the initial step of melting to form a single mass. In this study, NiI2 and CoCl2 were selected, based on their similar melting points with MgCl2 and higher reduction potentials than lithium naphthalenide.

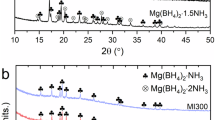
Both pristine and bimetallic pMg systems exhibit a distinct Mg crystalline structure in the X-ray diffraction (XRD) patterns, without any peak corresponding to the precursor MgCl2 or impurities (Fig. 1b-d). This indicates that the precursor MgCl2 is successfully converted into the well-defined Mg crystalline structure through the reduction. Even though some residual impurities including Cl are identified in the XPS survey scan (Supplementary Fig. 1 and Supplementary Note 2), a high hydrogen capacity of porous Mg supports that it mostly consists of metallic Mg, which will be discussed in the later section. Interestingly, pMg exhibits a notably high peak intensity for the Mg (002) close-packed plane compared to that of typical polycrystalline Mg. This suggests that Mg crystals were textured with a specific preference on the close-packed plane with the lowest surface energy in our system, attributed to the sufficiently slow diffusion-based reduction reaction38.

The nanoporous Mg structures with irregular pore sizes were observed in transmission electron microscope (TEM) images (Supplementary Fig. 2). The pores are sized in a range of a few tens of nm, yet it is rather difficult to distinguish a single pore clearly because the thin porous Mg layers are stacked on top of each other. Nonetheless, the metal structure with pores is readily identified by the HRTEM images, and the crystalline structure is also confirmed. Scanning electron microscope (SEM) images (Supplementary Fig. 3) show that the metal ligaments with a thickness of ~200 nm are continuously connected, and the open pores between such ligaments in the nanoporous structure are also presented. The porous characteristics of pMg, pMgNi, and pMgCo were confirmed with Brunauer–Emmett–Teller (BET) N2 isotherms, and the corresponding pore size distributions were obtained using Barrett, Joyner, and Halenda (BJH) analysis (Fig. 2 and Supplementary Fig. 4). In particular, the N2 adsorption-desorption isotherms of pMg demonstrate IUPAC type IV BET curve, indicating the mesoporous structure39. In BJH analysis, the pore size distribution of porous Mg composites also supports the presence of mesopores (Supplementary Fig. 5). The porous characteristics for all synthesized structures are summarized in Table 1. The BET surface area is measured as 3.10–15.89 m2 g−1 with the average pore width of 23.13–52.68 and 18.98–41.90 nm for adsorption and desorption, respectively. The surface area and average pore size values of nanoporous Mg are in a similar range with the previous reports (Supplementary Fig. 4e)40,41. These results demonstrate that the nanoporous Mg has been successfully prepared, despite its high reactivity and intricate control of microstructure. Furthermore, it suggests that other highly reactive alkali and alkaline earth metals can potentially be manipulated into an analogous nanoporous structure through a facile solution-based method.

Fig. 2: Characterization of porous metal structure.
figure 2

BET analysis of (a) as-synthesized pMg and (b) hydrogen-cycled pMg. Source data are provided as a Source Data file.

Full size image
Table 1 BET surface area and pore size values for each sample before and after hydrogen sorption cycling
Full size table

Hydrogen storage performance of porous Mg structures

To investigate the effect of nanoporous structures on the hydrogen storage performance of Mg, the kinetic and thermodynamic properties of hydrogen ab/desorption were evaluated. For the initial survey of a hydrogen sorption behavior for each nanoporous sample, hydrogen absorption and desorption were conducted under 15 bar H2 at 200 °C and under 10−4 bar at 300 °C, respectively (Fig. 3). All porous Mg samples exhibit the hydrogen storage capacity of more than 6 wt.% calculated from the total weight value, and the phase transformation from Mg to MgH2 upon hydrogen absorption is confirmed in the subsequent XRD measurement (Supplementary Fig. 6). Compared to spherical Mg nanoparticle having an average size of 269 nm similar to porous Mg, pMg exhibits much faster hydrogen absorption kinetics at the same condition such as 15 H2 bar at 200 °C (Supplementary Fig. 7). Even the measurement temperature and hydrogen pressure increase up to 30 H2 bar and 300 °C, spherical Mg nanoparticles only uptake ~1 wt. % for 24 h. This comparison demonstrates the advantage of porous structure in the aspect of enhanced hydrogen sorption kinetics. It is noteworthy that the hydrogen uptake capacity is well-maintained in the bimetallic system−reaching 6.41 wt.% for pMgNi−despite the dead mass as a result of the addition of transition metal. Furthermore, pMgNi presents greatly accelerated hydrogen sorption rates, ascribed to the catalytic Ni dopant which promotes the dissociation of H2 by lowering the related energy barrier42,43. Interestingly, both hydrogen ab/desorption kinetics and capacity are gradually enhanced as the cycle proceeds for all three samples–more pronounced for pristine Mg–which is saturated at the 4th cycle. In the case of the bimetallic system in which a transition metal component is introduced (pMgNi and pMgCo), the kinetic saturation occurs faster compared to pure Mg. In the previous studies, it was reported that the initial activation process is required for metal hydride-based solid-state hydrogen storage44,45,46,47, in which both hydrogen capacity and sorption kinetics are sluggish at early stages and improved through the activation processes. It was deduced that the passivation layer such as oxides formed on the external surface gets fractured during the activation, and consequently, the internal active metal/metal hydrides are exposed to successfully absorb or release hydrogen45. Typically such activation is executed only with the first cycle, and both hydrogen absorption and desorption show a slightly improved capacity and kinetics, which are similarly maintained in subsequent cycles. However, in our study, the activation process continues in the further cycles, not completed until the 4th cycle. In the meantime, the hydrogen ab/desorption capacity gradually increases as the cycle proceeds, and its kinetics is simultaneously enhanced. Notably, our porous samples demand more hydrogen sorption cycles for activation compared to other metal hydrides reported, while the capacity and kinetic improvements are much more evident. It is speculated that they undergo different structural changes or activation mechanisms from the aforementioned metal hydrides.

Fig. 3: Hydrogen absorption and desorption kinetics for porous Mg structures.
figure 3

a pMg, (b) pMgNi, and (c) pMgCo. Source data are provided as a Source Data file.

Full size image

To evaluate the cycle stability of synthesized porous Mg composite, we measured the hydrogen capacity of pMgNi based on 2 h of hydrogen absorption and 1 h of desorption, repeated over 50 cycles. The kinetics of pMgNi gradually improved from the initial absorption capacity of 2 wt.% to the stabilized capacity of approximately 6 wt.% for absorption and 6.5 wt.% for desorption in subsequent cycles (Supplementary Fig. 8). The measured hydrogen capacity slightly decreases by 0.8 wt.% at the 40th cycle and 1.1 wt.% at the 50th cycle. Although a small decrease in capacity was observed, likely due to the potential oxidation from continuous exposure to small amounts of oxygen during high-temperature vacuum processes, the pMgNi demonstrates excellent cycle stability with rapid hydrogen sorption rates.

Structural changes of porous Mg upon hydrogen cycling

To unravel the correlation between the unique activation process and the gradual improvement of kinetics, we monitored the change in the chemical state of the pMg surface upon hydrogen cycling by in-situ X-ray photoelectron spectroscopy (XPS). The pMg sample was placed under 2 bar of H2 at 200 °C for about 15 h for absorption, and ultra-high vacuum (10−11 bar) at 300 °C for about 15 h for desorption. All samples were transferred through the pre-vacuum chamber interconnected to the analysis chamber to minimize air exposure. The deconvoluted XPS spectra of Mg 1 s are shown in Fig. 4a, where the peaks observed at 1304.4 eV and 1303.2 eV are attributed to pristine pMg (green) and hydrogen absorbed pMg state (pMgHx, blue), respectively (please read Supplementary Note 3 for the deconvolution detail and Supplementary Fig. 9 for the full spectra). As hydrogen absorption and desorption are repeated, the Mg 1 s peak is accordingly shifted, indicating that it is caused by each hydrogen sorption reaction. However, the pattern of such peak shift is somewhat different because zero-valent metallic Mg should be observed at the lower binding energy region than hydrogenated Mg, representing the hydrogen desorbed and absorbed state, respectively. Based on the deconvolution of Mg 1 s for as-synthesized pMg (Supplementary Fig. 1c and also see Supplementary Note 2), we speculate that the surface of pMg consists of metallic Mg and MgO, which leads to such representative peak at the higher binding energy region, while it successfully absorbs hydrogen to evolve MgH2. This trend is consistent with the O 1 s spectra obtained during the same in-situ measurement (Supplementary Fig. 10 and also see Supplementary Note 4), and also the bulk Mg result measured for the reference (Supplementary Fig. 11).

Fig. 4: Surface state analysis of pMg with hydrogen sorption cycles.
figure 4

a Deconvoluted Mg 1 s in-situ XPS spectra for sequential hydrogen ab/desorption cycles. The blue and green shading describe the deconvoluted peak of pMgHx and pMg, respectively. (See Supplementary Fig. 9 for the full spectra). b The binding energy and (c) relative intensity changes in the deconvoluted Mg 1 s spectra as a function of the hydrogen ab/desorption step. Each shaded region in (b) and (c) emphasizes the gradual trends in binding energy and relative intensity of pMg and pMgHx. Source data are provided as a Source Data file.

Full size image

With the hydrogen sorption cycles, the alternate changes in the peak intensity are observed, where pMgHx (blue) stems from the chemical interaction between hydrogen and Mg. For the quantitative analysis, the XPS result is summarized in Fig. 4b, c. The peak corresponding to pMgHx is gradually shifted toward the higher binding energies as indicated in the gray area (Fig. 4b), which suggests that the surface structure is changed to one that energetically favors hydrogen absorption. It is noted that the increase in binding energy is referenced to the hydrogen absorbed state during the first cycle (Fig. 4b). Thus, the increased binding energies observed during the subsequent absorbed states do not originate from the stress that develops in the hydrogen absorbed states compared to the desorbed states. Further, it shows the exponential increment pattern as the hydrogen cycling proceeds (Fig. 4c). Eventually, it leads to the improved hydrogen storage capacity and kinetics, which will be discussed later along with the change of crystalline structure.

In addition, the change of Mg crystalline structure upon hydrogen cycling was also observed by XRD (Fig. 5a). The atypically intense peak of the (002) plane is reduced and the overall pattern is consistent with the reference state. Such change can be attributed to the gradual recovery from the initial Mg structure with textured surfaces to its polycrystalline state, and it may induce an improvement in hydrogen storage performance. For the doped nanoporous Mg samples, the intensity reduction of the Mg (002) plane is also observed in pMgNi, notwithstanding the marginal change (Supplementary Fig. 12a). Essentially, its initial intensity in pMgNi is not as high as that in pMg, and presumably this is related to fewer activation cycles required for the pMgNi compared to the pMg. Also, the aforementioned catalytic role of Ni in hydrogen sorption may influence such phenomenon, along with the evolution of Mg2Ni and slight changes in chemical states of Ni for pMgNi (Supplementary Fig. 13). In the case of pMgCo, some impurity peaks corresponding to the CoO phase are detected due to the oxidation as opposed to the XRD results of pMgNi and pMg, and also the intensity change of Mg (002) facet is not prominent before and after hydrogen cycling (Supplementary Fig. 12). Interestingly, this observation is consistent with the relatively rapid completion of the activation process for pMgCo. This suggests that the close-packed Mg (002) facet with low surface energy is preferentially exposed through a sluggish diffusion-based reaction, and it is translated into the gradual improvement of hydrogen storage performance as this (002) plane decreases during the activation process of hydrogen sorption cycling. It is speculated that there should be a crystalline facet-dependent energy barrier for hydrogen sorption, which will be discussed in the following section.

Fig. 5: Investigation of crystalline structure and kinetics changes with hydrogen sorption cycle.
figure 5

XRD patterns of (a) as-synthesized and hydrogen-cycled pMg. Crystalline facet-dependent energy barriers relevant to hydrogen sorption: (b) H2 adsorption and dissociation barrier on Mg surfaces and (c) penetration barrier for the adsorbed H atoms into subsurface octahedral sites. (d) The absorbed hydrogen content on three distinct Mg surfaces of (002), (100) and (101). The absorption time is normalized by the total simulation time for direct comparison among the surfaces. (e–g) The absorbed hydrogen content as a function of position and time for (e) (002), (f) (100) and (g) (101) Mg surfaces. 0 and 100 in the relative positions indicate the ligament core and adsorption surfaces, respectively. Surface adsorption is modeled to occur uniformly in the region that extends from the relative position of 97 to 100. The color bar depicts the H concentration ranges (x) in MgHx. Source data are provided as a Source Data file.

Full size image

The clear structural change upon hydrogen cycling was further examined with TEM (Supplementary Fig. 2). For as-synthesized samples, several overlapping pores are readily distinguishable, while more particle-like structures are observed after cycling. Also, the crystalline size of pMg increases from 47.48 nm to 70.61 nm after hydrogen cycling, obtained from XRD results, presumably due to the exposure to high temperature and repeated volume change during hydrogen absorption and desorption (Supplementary Table 1). Nevertheless, the porous structures are well-preserved or even more developed during the cycling based on the BET measurements, with the pMg surface area increased from 3.10 m2 g−1 to 8.45 m2 g−1 upon cycling and the average pore width reduced from 52.68 nm and 41.90 nm to 35.20 nm and 26.46 nm for adsorption and desorption, respectively (Table 1). For pMgNi and pMgCo, both the surface areas and the average pore widths increase upon cycling. SEM images of pMgNi and pMgCo also confirm structural changes upon hydrogen cycles through hydrogenated states (Supplementary Fig. 3b–c and 14). Compared to hydrogen-cycled pMg composites, the repeated volume expansion of Mg ligament leads to distinct porous structures which is consistent with BET measurements.

Kinetics analyzes of Mg geometry-dependent hydrogen sorption

To unravel how the crystallographic facets impact the overall hydrogenation kinetics, we construct an atomically informed continuum-scale kinetics model for Mg ab/desorption. The 1D continuum-scale kinetics model is inspired by Kitagawa and Tanabe’s work48. The model assumes that hydrogen absorption proceeds by the following three serial steps: Step 1) H2 adsorption and dissociation onto the Mg surface, Step 2) surface penetration of adsorbed H atom and Step 3) H diffusion inside the Mg bulk (Supplementary Fig. 15). The activation energies for steps 1) and 2) are obtained from atomistic simulations, as shown in Fig. 5b, c. The dissociation reaction exhibits similar kinetic barriers for all the facets considered, namely 0.80 eV for (002) surfaces, 0.84 eV for (100) surfaces, and 0.91 eV for (101) surfaces. The surface penetration barriers are overall lower than the dissociation barriers, yet show larger surface dependence, with 0.57 eV for (002) surfaces, 0.38 eV for (100) surfaces, and 0.67 eV for (101) surfaces. The H diffusion inside sub-surface Mg is assumed independent of the crystallographic directions, and the H diffusion barrier of 0.25 eV/atom is assumed for diffusion inside the Mg bulk, obtained from a previous report49. The model employs position-dependent H diffusivity, with the H penetration barrier incorporated in the form of modified diffusivity at the surface (please refer to Supplementary Note 5 for the details of the continuum model). The computed absorption curves show that the hydrogenation kinetics exhibits a strong Mg surface facet-dependence and decreases in the order of (100), (002), and (101) Mg surfaces (Fig. 5d). The computed hydrogen absorption maps show that H diffusion significantly affects all three surfaces, as the sloping H concentration with respect to relative position is apparent from the computed maps (Fig. 5e-g). In the map, 0 and 100 in the relative positions indicate the ligament core and adsorption surfaces, respectively. Hydrogen adsorption, as indicated by the color changes at the surface layer extending from the relative position of 97 to 100, saturates in the decreasing order of (002), (100), and (101), identical to the trend in the computed adsorption energy barriers in Fig. 5b. Yet, (002) exhibits slower hydrogen absorption than (100) surface. Since both (002) and (100) surfaces are modeled with the identical bulk H diffusion barrier, the change in absorption kinetics among the two surfaces originates from the different surface penetration barriers for H. The effect of surface penetration is identified by the discontinuity in H concentration near the surface. For instance, (002) surface exhibits rapid surface saturation within the normalized time of 0.1, as represented by the yellow color at the surface layers in Fig. 5e. On the other hand, H penetration to the bulk interior proceeds at a reduced rate that we observe discontinuity in H concentration (represented by color in Fig. 5e) from the relative positions of 95 (subsurface) and 100 (surface). The discontinuity in H concentration persists until the normalized time of ~0.5. While the surface penetration-limited kinetics is notable for (002) and (101) surfaces, (100) surface exhibits little discontinuity in H concentration from the subsurface and surface. It is noted that the dominant kinetics alters under lowered charging pressure. The high charging pressure provides sufficient reactant concentration such that the dissociation kinetics does not limit the overall kinetics, as observed in Supplementary Fig. 16.

The constructed kinetics models rationalize the experimentally observed difference during hydrogen sorption cycling. The results are also consistent with the results of XRD analysis before and after hydrogen cycling. The relatively large proportion of (002) surfaces and a small proportion of (100) surfaces retards the hydrogen absorption reaction. After the activation process, pMg reduces (002) surfaces, increasing the relative amount of (100) surfaces. It can also be explained by the XRD result in Fig. 5a that the (002) peak, which is abnormally intense before cycling, decreases after cycling. With the increased relative proportion of (100) surfaces, it is expected that the overall absorption kinetics improves with increased sites for facile surface penetration, especially for pMg with a large amount of surface area.

The change in the Mg-Mg bond lengths upon a small amount (0.17 wt.%) of subsurface H atom insertion is computed for (002), (100), and (101) Mg surfaces (Supplementary Table 2). The H-added slab models pMg states in the hydrogen-absorbed phases. The average Mg-Mg bond lengths for pristine Mg are 3.196, 3.182, and 3.194 Å for (002), (100), and (101) surfaces, respectively. Upon 0.17 wt.% subsurface H atom insertion, the average Mg-Mg bond length decreases for the (101) surface by 0.23% while it remains approximately identical for the (100) surface or increases by 0.44% for the (002) surface. The histogram analyzes (Supplementary Fig. 17) also show that the Mg-Mg bond length with the maximum probability shifts towards a reduced value of 3.18 Å for the (101) surface while that for the other two surfaces remains identical at 3.21 Å. Also, the computed bond lengths present that subsurface H insertion results in stretched Mg-Mg bonds with the maximum bond lengths of 3.39 Å for (002) and 3.41 Å for (100) surfaces while that for (101) remains at 3.31 Å. It is also noted that the average Mg-H bond lengths for (002), (100), and (101) are 2.316, 2.358, and 2.283 Å, respectively, with the shortest Mg-H bond lengths observed for (101) surfaces. This anisotropic response qualitatively matches well with the observed in-situ XPS data in Fig. 4. The increasing Mg 1 s binding energy in the H absorbed states in Fig. 4b matches with the transformation from (002)-textured Mg surfaces to polycrystalline surfaces with more pronounced (101) surfaces, given that only (101) surface reduces the Mg-Mg bond lengths upon slight H addition. Notably, the Mg-Mg binding energies for the desorbed states remain almost identical throughout the cycles, possibly due to the similar Mg-Mg bond lengths among pristine (002) and (101) surfaces. It remains challenging to rationalize the increased binding energies of pMgHx in the absorbed states, since the Bravais lattice for MgHx differs from that of pristine Mg, making it difficult to assess the effect of surface texture on the Mg-H binding energy. Yet, the decreasing order of Mg-H bond lengths from (100) to (002) and (101) suggests that the Mg-H interaction is stronger in the (101) facet. It is noted that the anisotropic Mg-Mg bond response differs in principle from the stress-induced Mg-Mg bond length changes. As mentioned above, the shift in Mg-Mg binding energy among the H absorbed upon cycling precludes the effect of MgHx nucleation-induced stress on pristine Mg.

Similar crystallographic facet dependence is observed for H desorption kinetics from MgH2. The kinetic model for H desorption incorporates an additional hydrogen flux (jdec) from MgH2 decomposition that contributes to the mobile hydrogen concentration (please see Supplementary Note 5 for details). The decomposition flux was not considered in absorption since MgH2 decomposition is considered slow and insignificant during hydrogenation. Similar to absorption, the kinetics model assumes that desorption proceeds by four serial processes, namely, Step 1) MgH2 decomposition, Step 2) surface H recombination and desorption (H desorption from this point on), Step 3) diffusion of subsurface H atom to surface H vacancy (H penetration) and Step 4) bulk H diffusion inside MgH2 crystal towards the surface (H diffusion). We consider three low-index MgH2 facets of (001), (110), and (101) for the kinetic analyzes. In our calculations, (200) planes covered with H atoms spontaneously formed H2 molecules by surface recombination and were excluded from the analyzes. The surface H desorption (step 2 in the desorption process) for three low-index facets of (001), (110) and (101) for the tetragonal MgH2 shows a strong facet-dependence, with the computed activation energies of 1.77 eV, 1.17 eV and 1.41 eV for (001), (110) and (101) surfaces, respectively (Supplementary Fig. 18a). The H penetration barriers to the surfaces (step 3) vary from 0.77 eV for (001) surface to 0.63 eV for (101) surface and 0.29 eV for (101) surface (Supplementary Fig. 18b). The penetration barriers to the surfaces are slightly higher than the bulk diffusion barrier in MgH2 (step 4), which is computed to be 0.58 eV on average. The constructed kinetic models with the computed sets of activation energies reveal anisotropy in H desorption kinetics in MgH2 (Supplementary Fig. 19). As expected from the computed desorption energies, (001) facet exhibits the slowest desorption kinetics. The other two surfaces, (101) and (110), exhibit similar desorption kinetics, indicating that the effect of desorption activation energy saturates at some point. All three surfaces exhibit the significant effect of H diffusion on the initial kinetics (normalized time < 0.5), as evidenced by the sloping colourmap over the relative position. The latter part of the simulation process (normalized time > 0.5) exhibits a distinct anisotropic behavior. While (110) and (101) surfaces exhibit close to complete dehydrogenation, (001) surface exhibits surface H desorption limiting the overall dehydrogenation kinetics. In this regime, we observe that the dehydrogenation rate continuously decreases over time (Supplementary Fig. 19a), potentially resulting in kinetically limited desorption capacity.

It is also anticipated that porous Mg undergoes distinct stress states compared to Mg particles and thus the effect of stress on the dehydrogenation kinetics is analyzed. Assuming that the hydrogenated phase forms a stable interface with the unreacted Mg, the geometries during hydrogenation for both particle and porous Mg are described in Supplementary Fig. 20. Following the derivations by Zhao et al50., we show that porous geometries with insertion from surfaces are reported to undergo constraint-induced compression at the surface while particle geometries form core-shell geometries and undergo tension at the surface (Supplementary Fig. 21 and Supplementary Note 6). To reflect the effect of this stress difference on the desorption kinetics, we first performed activation energy calculations for surface H desorption (step 2) and H diffusion (step 4) in strained MgH2 systems. H desorption from the (001) surface exhibits the lowered activation barrier as compressive stress gets applied to MgH2 (Supplementary Fig. 22a). When 3% biaxial compressive strain is applied, the H desorption barrier decreases from 1.78 eV to 1.55 eV while it increases to 1.97 eV under 3% biaxial tension. A similar decrease in H desorption barrier is also observed for the (110) surface (Supplementary Fig. 22b). The H diffusion barriers (step 4), on the other hand, exhibit the opposite trends with respect to compression (Supplementary Fig. 23). Among the three symmetrically distinct H diffusion paths considered for H vacancy diffusion inside MgH2 (labeled Paths 1, 2 and 3)51, one of the paths (Path 3) exhibits a notable increase in the diffusion barrier with compressive strain. The surface penetration barrier exhibits a similar trend, in which the computed barrier for (001) MgH2 (0.77 eV) increases to 0.98 eV upon 3% compression and decreases to 0.58 eV upon 3% tension (Supplementary Fig. 24). When incorporated into the kinetics model, we observe that desorption from the (001) facet gets critically affected by the stress states. While compressive strain significantly enhances the desorption kinetics compared to the unstrained case, tensile strain significantly retards the desorption kinetics such that any desorption is barely observed during the same amount of time (Supplementary Fig. 25). This indicates that the desorption process on (001) surface gets strongly affected by the surface recombination (step 2) process. While other facets are expected to behave differently, as supported by the computed desorption activation energies, the (001) surface serves as an example where porous geometry may exhibit enhanced kinetics compared to spherical geometry by the effect of distinct stress states during cycling.

The effect of Ni catalyst on the desorption kinetics of MgH2 was also investigated through the kinetics analysis. The computed H diffusion barriers with the presence of Ni next to the migrating H show that Ni consistently lowers the diffusion barriers for all migration paths considered compared to undoped MgH2, also consistently observed for the strained (both tensile and compressive strain) cases (Supplementary Fig. 26). In the vicinity of Ni, the average H diffusion barriers reduce to 0.28 eV and 0.26 eV from 0.61 eV and 0.58 eV with and without 3% compression, respectively. With the presence of surface Ni, the surface H desorption activation energy under 3% compression decreases from 1.55 eV to 0.98 eV compared to undoped MgH2 (Supplementary Fig. 27). Similar trends are observed for Ni-doped MgH2 under no strain and 3% tension. The dramatically reduced activation energies for all stress conditions translate to significantly enhanced dehydrogenation kinetics in the kinetics model for (001) surface under 3% compression (Supplementary Fig. 28), qualitatively reproducing the experimentally observed kinetic enhancement in pMgNi. The constructed models show that Ni doping enhances steps 2 and 4 in our desorption model (surface H desorption and H diffusion), while the model currently assumes that Ni does not affect the hydride decomposition (step 1) and surface penetration barrier (step 3). The modeled desorption kinetics in Ni-added (001) surface matches closely with the hydride decomposition rate, indicating that the kinetics in Ni-doped MgH2 is limited by hydride decomposition (step 1), as the other steps become sufficiently fast with Ni incorporation (Supplementary Fig. 29).

Kinetic and thermodynamic properties of nanoporous Mg structures for hydrogen sorption

The kinetic and thermodynamic parameters relevant to the hydrogen storage performance of nanoporous Mg samples were experimentally acquired to examine the effect of unique porous structures. To investigate the kinetic properties, the activation energy for hydrogen ab/desorption is calculated by plotting the reaction rates at three different temperatures as a function of hydrogen amount ab/desorbed in Arrhenius equation–hydrogen absorption under 15 bar H2 at 200, 225, 250 °C and hydrogen desorption under 10−4 bar at 275, 300, 315 °C (Supplementary Fig. 30-31). The overall activation energy values for all samples are summarized in Table 2. As reported in numerous literatures, the activation energy values change with hydrogen concentration in hydrides as hydrogen ab/desorption proceeds, implying that the kinetic characteristics cannot be represented with one single value52,53. Despite such varied values, the activation energy decreases for all three samples compared to the bulk Mg (160–200 kJ/mol and 200-240 kJ/mol for absorption and desorption, respectively) in both absorption and desorption processes54. The activation energy of transition metal-doped samples−pMgNi and pMgCo−is lower than that of pMg for both absorption and desorption, consistent with their well-known effective catalytic effect and concomitantly improved kinetic properties. Specifically, Ni- and Co-based phases in bimetallic pMg composites were investigated by XRD and bright field-scanning transmission electron microscopy (BF-STEM) (Supplementary Figs. 12 and 32). The bimetallic phases such as Mg2Ni and Mg2Co in Mg are known to serve as fast hydrogen pathways, providing various grain boundaries and thermodynamically unstable hydride phases (i.e. Mg2NiH4)55,56. To figure out the evolution of specific phases, the bimetallic pMg composites in as-synthesized, hydrogenated, and hydrogen-cycled states are analyzed, in which crystalline Mg with Mg2Ni and Mg2Co is identified in hydrogen-cycled samples by XRD patterns and BF-STEM. These newly formed phases are uniformly distributed as particle-like status smaller than 5 nm (Supplementary Fig. 32). Furthermore, BF-STEM images reveal hydrogenated phases such as Mg2NiH4 which are challenging to observed in XRD patterns (Supplementary Fig. 32a). Thus, it can be deduced that Ni and Co are integrated with Mg to form bimetallic phases during repeated hydrogen cycling and to provide such notable catalytic effect.

Table 2 Summary of kinetic and thermodynamic parameters of pMg, pMgNi, and pMgCo
Full size table

Furthermore, we investigated the rate-determining steps of hydrogen absorption and desorption by employing various kinetic models such as diffusion models (1D, 2D, and 3D), Johnson-Mehl-Avrami (JMA) model, and geometrical contraction models (R2 and R3) for pMg and pMgNi. The fitting curves based on these models were expressed as \(f\left(\alpha \right)={kt}\), where \(\alpha\) is the reacted fraction, \(k\) is the reaction constant, and \(t\) is the reaction time. For pMg, the 3D diffusion model is found to be well-suited for absorption, identifying hydrogen diffusion as the rate-controlling step, while the JMA model with n = 3 fits well for desorption, indicating nucleation and growth control (Supplementary Figs. 33–34 and Supplementary Table 3). Also, pMgNi exhibits a similar behavior for absorption, with the 3D diffusion model dominating. On the other hand, for desorption, JMA models with both n = 2 and n = 3 are combined as the inclusion of Ni alters Mg nucleation and growth behavior at different temperatures (Supplementary Figs. 35–36 and Supplementary Table 4). In comparison with the previously reported other Mg nanostructures such as nanosheets and nanoparticles (Supplementary Table 5), our samples exhibit relatively enhanced hydrogen sorption kinetics, dictated by more exposed reactive sites and faster pathways for hydrogen sorption due to the unique nanoporous structure46,57.

Furthermore, the enthalpy and entropy values are obtained to evaluate the thermodynamic characteristics of the porous structures for hydrogen sorption. The pressure-composition-temperature (PCT) curve at each temperature shows a distinct plateau region which indicates the transformation of Mg to MgH2 (Fig. 6), and the equilibrium pressure values are fitted into the van’t Hoff plot (Supplementary Fig. 37). The PCT measurement was also conducted with bulk Mg under the same condition, but at higher temperatures due to its larger size (Supplementary Fig. 38–39). All three nanoporous structures exhibit reduced enthalpy values for hydrogen absorption compared to the bulk Mg, while slightly higher or similar enthalpy values are obtained for desorption (Table 2). Possibly the unique porous structure in this study could induce such thermodynamic change during cycling. Initially, nanoporous Mg has a rather open-pore structure connected to each other. However, such open pores are gradually filled after hydrogen absorption, and some of them could change to closed pores, turning into a closed-cell-like structure. In a closed-end pore, the hydrogen sorption behavior may be different as a result of different shapes, curvature, and radius of the meniscus58. Meanwhile, it was reported that the evolution of dislocation configuration and density could be expedited under compressive stress for porous metal structures59. The porous Mg structures undergo plastic deformation during hydrogen absorption, leading to the rapid increase of dislocation density. Such a high density of dislocation could result in the shift of Gibbs free energy relative to the equilibrium as hydrogen sorption proceeds60,61. However, other various factors could be involved, which collectively cause a larger desorption enthalpy, and it requires further detailed study to elucidate such enthalpy difference and the corresponding structure-property relationship. Nevertheless, it should be noted that the porous Mg structures show a comparable hydrogen storage performance to a few nm sizes of Mg nanoparticles, despite that the size of the Mg ligament in our study is estimated at up to 200 nm (Supplementary Table 5). It implies that the nanoporous Mg structures have the advantage of significantly enhanced hydrogen storage performance over conventional nanoparticles. It is expected that they should be able to exhibit drastically improved hydrogen ab/desorption properties with a reduced ligament size—when it comes to the similar size to typically studied Mg nanoparticles—presenting a great potential of porous structured metal hydrides for hydrogen storage.

Fig. 6: Thermodynamic parameters for hydrogen ab/desorption of porous Mg structures.
figure 6

The PCT isotherms of pMg, pMgNi, and pMgCo for hydrogen (a) absorption and (b) desorption. Source data are provided as a Source Data file.

Full size image

Discussion

In conclusion, we successfully synthesized a highly reactive Mg nanoporous system through a facile organic solution-based approach without a harsh etching for advanced solid-state hydrogen storage. At the early stage of synthesis, metallic Mg is nucleated from the surface of the metal compound in a reducing solution, wherein the interfacial energy balances their structure. It leads to the formation of an equilibrated crystalline phase in which a specific facet is more exposed. During the hydrogen sorption cycle, the crystalline phase returns to the equilibrium state as in the reference, which is found to be a factor in the gradually improved hydrogen storage performance–with respect to both hydrogen sorption rate and capacity–for the nanoporous Mg system. The atomically-informed continuum models show that the penetration barriers for the crystalline facets and the stress state in porous Mg play significant roles in the overall kinetics, and the obtained results are consistent with the progressively enhanced hydrogen storage performance and the structural change confirmed by analysis of surface chemistry and crystalline structure. Furthermore, we envision that the nanoporous structure of various reactive metals can be readily produced on a large scale through this approach, which provides new opportunities for advanced energy applications.

Methods

Synthesis of porous Mg via RID

All reaction was performed under Ar atmosphere. The MgCl2 precursor was prepared by melting MgCl2 powder in an alumina crucible. The MgCl2 powder (0.952 g, 0.01 mol) was melted by raising the temperature to 750 °C for 1 h and maintaining it for 10 minutes under Ar gas flow. Subsequently, it was cooled down to room temperature, and then the whole furnace tube was placed in a glove box to maintain the inert environment. To prepare lithium naphthalenide solution, a fresh-cut lithium sheet (0.207 g, 0.03 mol) was put into an anhydrous THF solution in which naphthalene was dissolved beforehand (naphthalene 3.85 g, 0.03 mol in 0.06 L THF). The solution was stirred at room temperature in an Ar glove box until the lithium was completely dissolved (approximately 3 h). The reduction of MgCl2 precursor to Mg porous structure was performed by immersing the precursor into the solution for 4 days with stirring. Upon the completion of reduction, the sample was washed with anhydrous THF three times, followed by drying under vacuum. Porous Mg doped with transition metal components was also prepared through the same protocol except that the mixture of NiI2 or CoCl2 (5 mol %) and MgCl2 (95 mol %) was used in the precursor synthesis process. The MgCl2/NiI2 mixture was melted at 800 °C instead of 750 °C.

The atomistic computations of migration barriers

Neural network interatomic potentials available via Matlantis software were used for the calculation of activation energies. The interatomic potentials were trained on ab initio databases with Perdew-Burke-Erzenhof pseudopotentials with D3 van der Waals corrections. All activation energies, including surface H adsorption/desorption, surface H penetration, and bulk vacancy diffusion, were computed using climbing-image nudged elastic band (CINEB) methods. In the NEB calculations, at least 5 intermediate states are employed between two endpoints. The structural parameters during the NEB run were fixed while all ionic positions were allowed to fully relax. The obtained activation energies were employed in the 1D continuum model, explained in Supplementary Note 5 in detail.

Calculation of kinetic parameters

The activation energy was calculated from the hydrogen ab/desorption kinetic curves obtained at different temperatures. After initial activation cycles (4 cycles), the hydrogen absorption at 200, 225, and 250 °C and desorption at 285, 300, and 315 °C were conducted. Using the Arrhenius equation with three kinetic curves obtained at three different temperatures, the activation energy values for hydrogen ab/desorption were calculated. The hydrogen sorption rate, which indicates the change in the amount of absorbed or desorbed hydrogen over time, was calculated from the kinetics measurement results obtained at each temperature. This data was smoothed via the Lowess method and the curves were divided into 1000 points for the same designated range of hydrogen weight percent. The log(rate) versus 1/T curve was obtained, a straight line connecting three points corresponding to three different temperatures was obtained. The activation energy value can be calculated through the curve’s slope by the Arrhenius equation at each hydrogen weight percent.

Calculation of thermodynamic parameters

To evaluate the thermodynamic parameters of porous Mg for hydrogen ab/desorption, the enthalpy and entropy change were calculated. The pressure-composition-temperature (PCT) curves were obtained at three different temperatures– at 250, 300, and 315 °C for absorption and 285, 300, and 315 °C for desorption–and the equilibrium pressure values at each temperature were acquired when the reaction rate was less than 0.00005 wt.% min−1 and the reservoir pressure was increased by 1 bar. By fitting the plateau pressure values as a function of temperature to the van’t Hoff plot, the enthalpy and entropy change can be calculated.