Alleviating batch effects in cell type deconvolution with SCCAF-D

Feng, Shuo; Huang, Liangfeng; Pournara, Anna Vathrakokoili; Huang, Ziliang; Yang, Xinlu; Zhang, Yongjian; Brazma, Alvis; Shi, Ming; Papatheodorou, Irene; Miao, Zhichao

doi:10.1038/s41467-024-55213-x

Download PDF

Article
Open access
Published: 30 December 2024

Alleviating batch effects in cell type deconvolution with SCCAF-D

Nature Communications volume 15, Article number: 10867 (2024) Cite this article

5004 Accesses
5 Citations
1 Altmetric
Metrics details

Subjects

Abstract

Cell type deconvolution methods can impute cell proportions from bulk transcriptomics data, revealing changes in disease progression or organ development. But benchmarking studies often use simulated bulk data from the same source as the reference, which limits its application scenarios. This study examines batch effects in deconvolution and introduces SCCAF-D, a computational workflow that ensures a Pearson Correlation Coefficient above 0.75 across simulated and real bulk data for various tissue types. Applied to non-alcoholic fatty liver disease, SCCAF-D unveils meaningful insights into changes in cell proportions during disease progression.

Benchmarking integration of single-cell differential expression

Article Open access 21 March 2023

Interpretable and context-free deconvolution of multi-scale whole transcriptomic data with UniCell deconvolve

Article Open access 11 March 2023

scMD facilitates cell type deconvolution using single-cell DNA methylation references

Article Open access 02 January 2024

Introduction

Understanding the cell-type composition change during disease progression is critical in studying disease mechanisms¹. To date, some large-scale databases, including the Gene Expression Omnibus (GEO)², ArrayExpress³, Genotype-Tissue Expression (GTEx)⁴, The Cancer Genome Atlas (TCGA)⁵, Therapeutically Applicable Research To Generate Effective Treatments (TARGET) (https://ocg.cancer.gov/programmes/target), International Cancer Genome Consortium (ICGC)⁶, and etc, have amassed extensive repositories of bulk RNA sequencing (RNA-seq) data resources crucial for both biological and clinical investigations. Of note, bulk RNA-seq fails to discern gene expression differences among individual cells, thereby masking cellular heterogeneity. For instance, a significant risk factor for the progression from non-alcoholic fatty liver disease (NAFLD) to hepatocellular carcinoma (HCC) is the degree of liver fibrosis⁷. The existing databases encompass vast quantities of bulk RNA-seq data pertaining to liver fibrosis staging, yet they lack key information on cellular proportion changes during disease progression. Deconvolving bulk RNA-seq samples using reference data provides an alternative, which may make full reuse of the existing bulk RNA-seq data by generating the cell composition of these samples^{8,9,10,11,12,13,14,15,16,17}, indicating the biological variation during disease progression.

Tens of computational deconvolution methods have been proposed, while reference-based methods are more accurate when reliable reference data is available^11,18. Before applying deconvolution algorithms, it is necessary to benchmark their capabilities and limitations with “gold standard” datasets of known cell proportions. For the establishment of “gold standard” benchmark data, one approach is to determine the cell proportion in bulk data using alternative experiments, e.g., flow cytometry and immunohistochemistry, when identical samples are available. Another approach takes single-cell RNA sequencing¹⁹ (scRNA-seq) data as ground truth and simulates bulk RNA-seq data, as ‘pseudobulk’^18,20, by aggregating the expression values in scRNA-seq, where the cell composition is known. Based on this ‘pseudobulk’ simulation, some previous benchmark studies¹⁸ used a ‘self-reference’ setting, in which both the simulated ‘pseudobulk’ and the reference data originate from the same dataset. However, this “self-reference” setting may not accurately represent a realistic scenario where batch effects exist. In realistic applications of deconvolution, the bulk data and the reference data normally come from different experimental batches, studies or sources, termed as a ‘cross-reference’ setting. Considering batch effects can arise when adding replicates from different sources, such as laboratories, donors, or sequencing platforms, using reference data in cell type deconvolution from a different source may lead to unexpected variations. Therefore, we term this situation as batch effects in deconvolution, which should be benchmarked with a ‘cross-reference’ setting. To date, benchmarking of cell type deconvolution has exclusively been conducted under the ‘self-reference’ setting, leaving the performance of deconvolution in the ‘cross-reference’ setting unclear.

This work demonstrates that batch effects in the ‘cross-reference’ setting affect the deconvolution accuracy to a large extent, while the existing deconvolution approaches show limited capabilities in dealing with such batch effects. Therefore, we present ‘SCCAF-D’ (Single-Cell Clustering Assessment Framework optimised reference for Deconvolution), a framework that achieves stable accuracies about 0.75 Pearson Correlation Coefficient (PCC) in a ‘cross-reference’ setting via optimally prepared reference data. In particular, we delineate the capabilities and robustness of SCCAF-D through the benchmarking of both simulated datasets across five different tissues and eight real bulk datasets from both healthy and diseased samples. Applying SCCAF-D to bulk NAFLD data, we discover the continuous cell proportion changes of cholangiocytes, hepatic stellate cells (HSCs), and hepatocytes during disease progression.

Results

Batch effects hinder cell type deconvolution

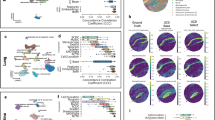
We have observed inconsistencies in cell proportion statistics across 15 datasets due to donor, study, and sequencing technology effects (Fig. 1 and Supplementary Figs. 1, 2). According to the human pancreas single-cell datasets from Baron et al.²¹, distinct cell types are clearly discriminated in the Uniform Manifold Approximation and Projection (UMAP) through our analysis (Fig. 1a). Donor effects manifest in both variations in the gene expression profile (Fig. 1b) and the cell proportion (Fig. 1c and Supplementary Data 1). For instance, acinar cells were exclusively observed in donors 1 and 3 but not in donors 2 and 4. Notably, such batch effects in the transcriptional profiles and in the cell proportions also exist between different single-cell studies (Fig. 1d–f). And the cell proportions also differ among samples in bulk RNA-seq (Fig. 1g) or scRNA-seq (Fig. 1h), resulting in unforeseen biases in deconvolution.

**Fig. 1: Batch effects exist in cell type deconvolution.**

To understand the deconvolution capability in a ‘cross-reference’ setting, we first identified candidate algorithms from a ‘self-reference’ benchmarking of 25 deconvolution algorithms on 44 datasets (Supplementary Data 2). Here, we define ‘self-reference’ as the situation when the simulated pseudobulk data for testing comes from the same dataset as the reference data, while ‘self-reference’ is assumed to be a simpler case than ‘cross-reference’. Six top-ranking algorithms (DWLS²², FARDEEP¹⁴, MuSiC²³, NNLS²⁴, RLR (see Methods), and EpiDISH¹²) (Supplementary Fig. 3 and Supplementary Data 3) according to the ‘self-reference’ results, were used for ‘cross-reference’ studies. Several ‘cross-reference’ studies were designed as below. In a ‘cross-donor’ setting, single-cell data (Barga et al.²⁵) from one donor is used to simulate ‘pseudobulk’, while data from another donor is used as reference. The deconvolution approach using the DWLS algorithm yields varying accuracies depending on simulated bulk and reference data utilised (Fig. 1i, j). Subsequently, in a ‘cross-study’ setting, data from one study is used to simulate ‘pseudobulk’, while another study of the same experiment is used as reference. When the dataset from Marquina-Sanchez et al.²⁶ was treated as pseudobulk and the dataset from Muraro et al.²⁷ was used as the reference, the predicted proportions of the seven cell types (including alpha, beta, and duct cells) showed a PCC of 0.59 with the ground truth (Fig. 1k). Conversely, when the Muraro et al.²⁷ dataset was used as pseudobulk and the Marquina-Sanchez et al.²⁶ dataset served as the reference, the predicted cell type proportions exhibited a higher PCC of 0.85 with the ground truth (Fig. 1l). It shows similar results as in the ‘cross-donor’ setting, while certain cell types are either overestimated or under-estimated, indicating the batch effects. Importantly, all algorithms are affected by such batch effects to a certain extent (Supplementary Fig. 4), suggesting the necessity of alleviating batch effects in deconvolution.

SCCAF-D: Alleviating batch effects in deconvolution using optimised references

The deconvolution accuracy highly depends on the reference data, whose quality is not detectable a priori. To achieve stable deconvolution accuracy, we introduce SCCAF-D, a computational framework designed to alleviate batch effects through optimised single-cell references, coupled with the DWLS algorithm to infer cell-type composition from bulk-profiled samples. It first integrates multiple datasets and selects the ‘self-consistent’ part of the data as reference. Given that a single dataset can be biased on certain batch effects, SCCAF-D integrates multiple datasets to optimise the cell type annotation for the reference data. Specifically, SCCAF-D integrates datasets by using Harmony²⁸ and then re-annotates the cell type according to the Leiden clustering and cell type labels obtained from the original publications, resulting in a more coherent cell type annotation across datasets.

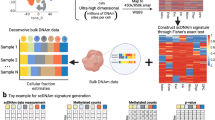
Although multiple datasets suffer from batch effects, they share the same biology, which should be ‘self-consistent’. Therefore, if a machine learning model can effectively extract the biology from part of the dataset, it should successfully recover the cell type labels in the rest of the data. SCCAF-D selects a ‘self-consistent’ part of the data as an optimised reference based on a ‘self-projection’ approach²⁹. It first trains a machine learning (Logistic Regression) model based on part of the data together with the cell type labels, and predicts the cell types labels on the rest of the data, known as ‘self-projection’²⁹ (Fig. 2, see Methods). A cell whose original cell type label is the same as the machine learning assigned label is ‘self-consistent’, meaning that its expression profile is discriminative in machine learning. We hypothesise that each cell type has a set of differentially expressed genes that allow it to distinguish from other cell types. If the labels are self-consistent, the differentially expressed genes can be encoded both by the machine learning model and its original gene expression profile. These self-consistent cells, who are discriminative to each other, can better represent their biology and be a good reference for deconvolution.

SCCAF-D achieves a high accuracy on simulated bulk datasets

The performance of SCCAF-D was tested on simulated ‘pseudobulk’ data of a ‘cross-reference’ setting, where the ‘pseudobulk’ data and the reference data come from two single-cell datasets of known cell proportions, see Methods. SCCAF-D was compared with other five top-ranking deconvolution algorithms (FARDEEP, MuSiC, RLR, EpiDISH, and NNLS) on 20 scRNA-seq datasets of five tissue types (4 datasets each), including pancreas (n = 34 specimens), lung (n = 61 specimens), peripheral blood mononuclear cells (PBMCs) (n = 90 specimens), brain (n = 43 specimens) and spleen (n = 21 specimens). For each tissue, one dataset was used to simulate the pseudobulk, while each of the other three datasets is used as the reference in the ‘cross-reference’ setting. In comparison, SCCAF-D integrates these three datasets as an optimised reference. We then quantitatively evaluate the deconvolution performance by computing PCC, Root-mean-square error (RMSE) (Supplementary Data 4), and Jensen-Shannon Divergence (JSD) values (Supplementary Fig. 5a–c, and Supplementary Fig. 6a, b) between the estimated cell-type composition and ground truth.

When deconvolving the pancreas pseudobulk of Baron et al.²¹ using the DWLS algorithm (Fig. 3a and Supplementary Fig. 7a), reference Marquina et al.²⁶ yielded PCCs of 0.37, while reference Segerstolpe et al.³⁰ resulted in PCC of 0.60. Similarly, when using reference Muraro et al.²⁷ to deconvolve the pseudobulk of Baron et al.²¹, PCCs were 0.15, 0.15 and 0.40 for EpiDISH, RLR and MuSiC, respectively. Although DWLS demonstrates top-ranking accuracies in many cases, PCC can decrease to 0.37 in certain cases (e.g., when Baron et al.²¹ dataset is used for pseudobulk, Marquina-Sanchez et al.²⁶ dataset as reference), while other algorithms also exhibit low PCCs in some cases (EpiDISH: 0.15; FARDEEP: −0.63; MuSiC: 0.40; NNLS: 0.11; RLR: 0.15) indicating potential failures.

**Fig. 3: Deconvolving simulated ‘pseudobulk’ samples from five tissues.**

As for lung (Fig. 3b and Supplementary Fig. 7b) and PBMC datasets (Fig. 3c and Supplementary Fig. 7c), SCCAF-D also demonstrates PCCs above 0.82 and 0.89, respectively, suggesting a reliable performance. Specifically, DWLS performs better than others when using one dataset as reference, yet its accuracy depends on the choice of reference data. In lung datasets, the lowest PCCs for DWLS, FARDEEP, MuSiC, NNLS, RLR, EpiDISH are 0.66, 0.42, 0.62, 0.11, 0.42, 0.42, respectively. The same PCCs are as low as 0.60, 0.09, 0.04, 0.16, 0.16, 0.16 in PBMC datasets.

We also performed simulations on the human brain (Fig. 3d and Supplementary Fig. 8a) and spleen (Fig. 3e and Supplementary Fig. 8b) datasets to evaluate the performance of SCCAF-D, which achieved PCCs above 0.93 and 0.80, respectively. Of note, when using DWLS with a single reference, the PCCs vary from −0.24 to 0.99 and RMSEs change from 0.02 to 0.22. By contrast, using the SCCAF-D optimised reference, the PCCs improved to the range of 0.93 to 0.99. Furthermore, using any spleen dataset as a reference, DWLS consistently shows a positive correlation between predicted and true cell proportions, outperforming the other five algorithms. Similarly, the accuracy of DWLS on the spleen is influenced by the choice of the reference (PCCs from 0.41 to 0.99), while the accuracy for the SCCAF-D optimised reference increased to a range of 0.80 to 0.99.

The deconvolution accuracy of the DWLS algorithm depends on the choice of the reference dataset, with PCCs ranging from 0.37 to 0.99, 0.66 to 0.98, 0.60 to 0.98, −0.24 to 1, and 0.41 to 0.99 for pancreas, lung, PBMC, brain, and spleen pseudobulk datasets, respectively. In comparison, SCCAF-D improves PCCs to ranges of 0.86 to 0.99, 0.82 to 0.98, 0.89 to 0.98, 0.93 to 0.99, and 0.80 to 0.99, respectively, guaranteeing reliable deconvolution performance (>0.80 PCC).

Deconvolving real bulk datasets using SCCAF-D

Further benchmarks of these six algorithms were performed on real bulk PBMC datasets of RNA-seq or microarray (Finotello et al.³¹, Newman et al.³² and Monaco et al.³³, see Methods), whose cell proportions were known a priori according to the flow cytometry count data. The single-cell reference datasets were sourced from Arunachalam et al.³⁴ (n = 12 specimens), Lee et al.³⁵ (n = 15 specimens), Schulte et al.³⁶ (n = 49 specimens) and Wilk et al.³⁷. (n = 14 specimens). To evaluate both the accuracy and robustness of SCCAF-D in predicting cell type proportion changes in disease states, SCCAF-D was applied to type 2 diabetes (T2D) data from Fadista et al.³⁸ (n = 89 specimens) and idiopathic pulmonary fibrosis (IPF) data from McDonough et al.³⁹ (n = 84 specimens), Sivakumar et al.⁴⁰ (n = 72 specimens), and Furusawa et al.⁴¹ (n = 206 specimens).

In cross-reference benchmarking with a single reference dataset, DWLS shows higher accuracies than others (Fig. 4a, b). When deconvolving the Finotello et al.³¹ dataset, DWLS demonstrated the highest PCC of 0.86 and lowest Root-mean-square error (RMSE) of 0.06 with Wilk et al.³⁷ dataset as reference, being higher than the second PCC of 0.64 (RMSE of 0.10) from MuSiC. Similarly, when using reference datasets from Arunachalam et al.³⁴, Lee et al.³⁵, and Schulte et al.³⁶, DWLS consistently outperformed other methods, exhibiting PCCs of 0.82, 0.64, and 0.78 (RMSE: 0.09, 0.12 and 0.08), respectively. For Monaco et al.³³ (microarray) dataset, when utilising the reference dataset from Schulte et al.³⁶, the DWLS achieves the highest PCC of 0.67 and lowest RMSE of 0.10, while NNLS ranked second with a PCC of 0.51 and a RMSE of 0.26 using Arunachalam et al.³⁴ as reference. When deconvolving the RNA-seq dataset from Monaco et al.³³, DWLS maintained its superior performance over other algorithms (EpiDISH: 0.47, RLR: 0.47, FARDEEP: 0.45, MuSiC: 0.35, NNLS: 0.44), achieving the highest PCC of 0.87 and the lowest RMSE of 0.07 using Arunachalam et al.³⁴ as reference. Using Lee et al.³⁵ dataset as reference, DWLS achieved the highest PCC of 0.94 and lowest RMSE of 0.07 when deconvolving the Newman et al.³² dataset, while MuSiC obtained a PCC of 0.92 and an RMSE of 0.10. In spite of the top performance of DWLS in both simulated and real bulk data, its accuracies highly depend on the choice of the reference, showing a wide range of accuracies. In the datasets of Finotello et al.³¹, Monaco et al.³³ (RNA-seq and microarray), and Newman et al.³², its PCCs ranged from 0.64 to 0.86, 0.47 to 0.67, 0.14 to 0.87 and −0.16 to 0.94, respectively (Supplementary Fig. 9). Consequently, without a clear understanding of which reference data to utilise, the deconvolution performance is not promising.

**Fig. 4: The benchmarking analysis of deconvolution in different real bulk datasets.**

Fortunately, SCCAF-D shows top-ranking performance. This approach consistently achieves top-ranking accuracies across microarray dataset from Monaco et al.³³, while also demonstrating exceptional performance on the other RNA-seq datasets. In comparison with DWLS with a single reference dataset (of lowest PCC −0.16 and highest RMSE of 0.32) (Fig. 4a, b), SCCAF-D achieves a lowest PCC of 0.75 and a highest RMSE of 0.10, suggesting a reliable accuracy (Supplementary Data 4). The other five algorithms (EpiDISH, FARDEEP, MuSiC, NNLS, and RLR) show improved deconvolution accuracy across four real bulk datasets by using optimised references, though none outperforms SCCAF-D. Following deconvolution with optimised references, the algorithms of EpiDISH, FARDEEP, MuSiC, NNLS, and RLR show higher PCCs on the Finotello et al.³¹ dataset compared to the lowest values (0.58, 0.24, 0.24, 0.19, 0.58, for these five algorithms, respectively.). Furthermore, SCCAF-D achieves stably high accuracies on other three datasets (microarray and RNA-seq in Monaco et al.³³, and Newman et al.³²). But the combinations between optimised reference and other five deconvolution algorithms do not always give improved accuracies as SCCAF-D, which is the combination between optimised reference and DWLS. Additionally, for each cell type across different bulk samples, relative cell proportion predicted from SCCAF-D exhibits a reliable positive correlation with the experiment determined proportion (Fig. 4c, Supplementary Figs. 10–12 and Supplementary Data 5), except for some minor cell populations (e.g., cDC), indicating the potential application in cross sample comparison.

Using the optimised reference derived from Baron et al.²¹, Marquina et al.²⁶, Muraro et al.²⁷ and Segerstolpe et al.³⁰, 89 human pancreatic islet samples reported by Fadista et al.³⁸ were deconvolved by SCCAF-D (Supplementary Fig. 13a). We identified a reduced proportion of β cells in diabetes samples, with a negative correlation observed between these proportions and haemoglobin A1C (HbA1c) levels (Supplementary Fig. 13b, c and Supplementary Data 5). This distribution aligns with existing knowledge^42,43, suggesting the potential of SCCAF-D in inferring cell type composition under disease conditions.

In addition, SCCAF-D is able to recover the cell type proportion changes in IPF disease, which often leads to respiratory failure and death, with pathological features including alveolar epithelial cell injury, and excessive fibroblast proliferation^44,45. SCCAF-D was applied to three human bulk RNA-seq datasets from both IPF (n = 198 specimens) and healthy lung tissues (n = 164 specimens), using two optimised references. One generated from the Adams⁴⁴ (n = 107 specimens), Reyfman⁴⁶ (n = 17 specimens), and Tsukui⁴⁷ (n = 15 specimens) datasets (Fig. 5a), while another generated from the Habermann⁴⁸ (n = 29 specimens), Valenzi⁴⁹ (n = 11 specimens), and Morse⁵⁰ (n = 17 specimens) datasets (Fig. 5b and Supplementary Data 5). In the IPF group, the proportions of alveolar epithelial type I (AT1) and type II (AT2) cells decrease compared to the control group, while the proportions of fibroblasts and basal cells increase, in consistency with known pathological features.

**Fig. 5: SCCAF-D deconvolution of real bulk datasets in IPF.**

SCCAF-D captures changes in cell proportions during NAFLD progression

Given that SCCAF-D achieves stable accuracies (PCCs above 0.75) on both simulated and real bulk data, it may reveal actual cell proportion changes during disease progression. Taking the Non-alcoholic fatty liver disease (NAFLD) as a test case, single-cell liver datasets, including MacParland et al. ⁵¹, Guilliams et al.⁵², Wang et al.⁵³ and Tabula Sapiens-Liver et al.⁵⁴, were used as references to deconvolve the bulk samples at liver fibrosis stages from 0 to 4, where 0 means no fibrosis and 4 means severe fibrosis. NAFLD bulk RNA-seq data with clinical information from Powell et al.⁵⁵ (87 specimens) and Govaere et al.⁵⁶ (206 specimens) were collected and the major 14 cell types were considered in SCCAF-D deconvolution (Fig. 6).

**Fig. 6: The application in NAFLD bulk dataset.**

SCCAF-D first integrated the four reference datasets and optimised the cell type labels according to leiden clusters, Fig. 6a. Based on this integrated data with optimised labels, SCCAF-D trains a logistic regression model, in which the cell type related marker genes are encoded, as shown in Fig. 6b. Subsequently, SCCAF-D selects the ‘self-consistent’ cells, whose original cell type label is the same as assigned by the logistic regression model. These cells show clear separation between each other on the UMAP plot (Fig. 6c), indicating that they are representing more discriminative features for each cell type.

Proportions of main liver cell types, including hepatocytes, cholangiocytes, endothelial cells, HSC, plasma cells and T cells, change significantly across the fibrosis stages (Fig. 6d and Supplementary Data 6). The relative cell proportion of cholangiocytes increases gradually during fibrosis progression, while HSCs show significant increase in stage 4 compared with stage 0. In contrast, the relative cell proportion of hepatocytes decreases over fibrosis stages (Fig. 6e). Given the limited sample size in one dataset (87 specimens in Powell et al.⁵⁵), data from Govaere et al.⁵⁶ with 206 NAFLD specimens were utilised for validation. SCCAF-D with the same optimised reference was applied to Govaere et al.⁵⁶, revealing similar patterns of cell type proportion changes across fibrosis stages (Supplementary Fig. 14).

Discussion

Batch effects between bulk and reference data have not yet been considered in cell type deconvolution. Due to the limited availability of reference datasets, previous studies and benchmarks always depend on a single reference dataset and a ‘self-reference’ setting which is over optimistic. In a more realistic ‘cross-reference’ setting, where the bulk (or simulated bulk) data from different sources than the reference, many deconvolution algorithms show low accuracies in certain datasets, despite demonstrating top-ranking accuracy in ‘self-reference’ tests (Figs. 3 and 4).

As the single-cell datasets accumulate over the past decade, more than one reference dataset are available for each tissue type. However, it is difficult to know which dataset to use as reference to achieve a good deconvolution result. But using a single reference dataset may result in a failure in certain cases that can lead to false conclusions when applying to real datasets⁵⁷. Our benchmark results on both simulated and real bulk data highlight that the success of deconvolution depends on the choice of the reference data. Furthermore, the PCC evaluation metric demonstrates a partial bias of high values when multiple cell types are predicted around zero, which may hinder the deconvolution of heterogeneous datasets. For instance, with Lee et al.³⁵ as the reference dataset, the PCC for CD8⁺ T cells in Newman et al.³² dataset reaches 0.66, yet the predicted cell proportion approaches zero (Fig. 4c). The bias is evidently present due to the prevalence of zero values, a phenomenon also observed by Jin et al.⁵⁸.

To mitigate the effects from the reference data, SCCAF-D takes the advantage of multiple available reference datasets to obtain an optimised reference, which can achieve reliably high accuracies in combination with DWLS. It first optimises the cell type annotation through data integration, and then selects the discriminative (or self-consistent) cells as reference using a self-projection approach. In both simulated bulk and real bulk tests, it illustrated PCCs above 0.75 on all the datasets, guaranteeing a general success of deconvolution, which cannot be achieved by other single reference approaches. Furthermore, we applied SCCAF-D to real bulk data from T2D and IPF, inferring the cell-type composition of disease-relevant tissues. Given the established knowledge that beta cells are gradually lost during T2D progression^42,43, estimates of cell type abundances from various computational deconvolution methods in some studies^23,59 further corroborate the cell type proportion changes revealed by SCCAF-D. For real bulk applications in IPF, Adams et al.⁴⁴ used scRNA-seq to reveal an increased proportion of basal cells and substantial decline in alveolar epithelial cells (AT1 and AT2) in IPF lungs compared to non-diseased tissue, which supports our findings. Similarly, Mayr et al.⁴⁵ deconvoluted Visium and scRNA-seq data, observing an increase in fibroblast and basal cell frequencies and a decrease in AT1 and AT2 cell frequencies in IPF compared to control patient lung tissue. These validation cases demonstrate that the correct inference of cell type proportion changes by SCCAF-D exerts potentials in identifying cellular targets for treatment. Application on two distinct real NAFLD datasets, SCCAF-D consistently demonstrated gradual changes in cell proportion of cholangiocytes, HSCs and hepatocytes during disease progression. In consistency with our results, several NAFLD studies^60,61 have provided additional clues to our discovery of an increased cell proportion of cholangiocytes and HSCs in the late fibrotic stages.

However, obtaining ‘gold standard’ datasets of known cell proportions for evaluating deconvolution methods remains a key challenge. While most bulk samples with cell type proportions are from flow cytometry, the accuracy of cell counting can be compromised for rare cell types due to challenges in sample isolation, enrichment, and potential retention in the flow cytometer⁶². We cannot rule out the possibility that this can be one explanation for the observed negative correlation between the estimated and flow cytometry defined proportions of cDCs in Finotello et al.³¹. As single-cell technology demonstrates good capability in quantifying rare cell types, analysing the same sample with bulk RNA-seq together with scRNA-seq may generate alternative benchmark data for understanding the cell proportions. On the other hand, since the deconvolution accuracy depends on the choice of the reference data, deconvolving disease samples with healthy reference data from atlases need to consider the possible existence of disease-specific cell types.

With the stable accuracy of SCCAF-D, it may exert additional potential in deconvolving large-scale databases of different tissue types. To achieve this, further efforts could be made in providing a best reference dataset for each tissue type. With the accumulation of human large-scale single-cell atlas, such as the Human Cell Atlas⁶³, HuBMAP⁶⁴, and Human Tumor Atlas Network (HTAN)⁶⁵, the issue of selecting optimal reference datasets for tissue-specific deconvolution using SCCAF-D is poised to be further addressed.

Methods

Data collection

All bulk RNA-seq and scRNA-seq utilised in this study were collected from published publications, Gene Expression Omnibus (GEO)² (https://www.ncbi.nlm.nih.gov/geo/), ArrayExpress³ (https://www.ebi.ac.uk/arrayexpress/), UCSC Cell Browser⁶⁶ (https://cells.ucsc.edu/), COVID-19 cell atlas (https://www.covid19cellatlas.org/), Neuroblastoma Cell Atlas⁶⁷ (https://www.neuroblastomacellatlas.org/) and CELLxGENE⁶⁸ (https://cellxgene.cziscience.com/). Detailed description of all the dataset can be found in Supplementary Data 2 and 7. The bulk datasets were processed as counts or Transcripts Per Million (TPM), as indicated in the table. ID conversion of bulk data, including the conversion of ‘Probe ID’, ‘entrez’ or ‘ensembl’ to ‘gene symbols’, was performed using the AnnoProbe⁶⁹(v.0.1.7) or AnnotationDbi⁷⁰ (v.1.60.2) R packages.

Single-cell data processing

We downloaded the raw count matrix and cell type annotations for each dataset from the corresponding websites (Supplementary Data 2 and 7). All single-cell datasets were analysed by SCANPY⁷¹ (v. 1.9.1) and Seurat⁷² (v. 4.4.0) packages. Cells with fewer than 200 detected genes and genes expressed in fewer than 3 cells were excluded. For datasets from Hrvatin et al.⁷³, Liao et al.⁷⁴, Aizarani et al.⁷⁵, and Segerstolpe et al.³⁰, we removed cells annotated as ‘not applicable’ or ‘unclassified’. ERCC genes were removed from the data for Muraro et al.²⁷. For data from Moncada et al.⁷⁶, the cell type labels were reannotated as follows: ‘Cancer clone A’ and ‘Cancer clone B’ were combined into ‘Cancer’; ‘Ductal - APOL1 high/hypoxic,’ ‘Ductal - CRISP3 high/centroacinar like,’ ‘Ductal - MHC Class II,’ and ‘Ductal - terminal ductal like’ were consolidated into ‘Ductal’; ‘Macrophages A’ and ‘Macrophages B’ were merged into ‘Macrophages’; and ‘mDCs A’ and ‘mDCs B’ were combined into ‘mDCs.’ For data from Vieira et al.²⁵, the cell labels ‘Type 1’ and ‘Type 2’ were consolidated into ‘Alveolar’ (Supplementary Fig. 3).

For human lung^48,49,77,78 and PBMC datasets (Arunachalam et al.³⁴, Lee et al.³⁵, Wilk et al.³⁷ and Schulte-Schrepping et al.³⁶), cells with total counts below 200 or exceeding 6000 were removed. Additionally, cells with a percentage of mitochondrial contents exceeding 15% of the total counts were discarded. Minor cell types of fewer than 40 cells from per dataset were removed. Doublets were predicted by ‘Scrublet’ (v. 0.2.3) and cells with doublet scores higher than 0.25 were excluded. For human pancreas datasets, cells with more than 20% mitochondrial content were excluded, while for human brain datasets, the threshold was set at 10%. For spleen datasets and IPF datasets from Adams et al.⁴⁴, Reyfman et al.⁴⁶, and Tsukui et al.⁴⁷, cells with more than 6000 detected genes were excluded, as were those with mitochondrial content exceeding 20%. Additionally, cells with doublet scores above 0.3, as predicted by Scrublet (v.0.2.3), were removed. For spleen datasets and IPF datasets from Habermann et al.⁴⁸, Valenzi et al.⁴⁹, and Morse et al.⁵⁰, cells with fewer than 400 or more than 8,000 detected genes were excluded, along with those exhibiting mitochondrial content greater than 12%.

For MacParland et al.⁵¹, Guilliams et al.⁵², and Tabula Sapiens-Liver⁵⁴ datasets from human liver tissue, we applied the same thresholds for total counts, genes and doublet scores. Considering the liver tissue is metabolically more active the threshold for percentage of mitochondrial contents is set to 50%. We removed cells expressing more than 100,000 genes in the Wang et al.⁵³ dataset.

After quality control, we performed standard SCANPY single-cell data analysis workflow, including normalisation, highly variable gene selection (2000 genes), principal component analysis (PCA, 50 components) and UMAP visualisation. Datasets from different studies were integrated by Harmony²⁸ with the batch key set as the ‘sampleID’. FindNeighbors and FindClusters functions were used on the Harmony derived latent space. For cell type annotation, we retained the original annotations from each study and manually curated them to achieve a consistent level of granularity (Supplementary Fig. 15).

SCCAF-D workflow for generating optimised references

SCCAF-D first integrates multiple datasets to optimise cell type annotation for reference data. Considering batch effects from different studies normally do not overlap each other, integrating multiple datasets may mitigate batch effects. While it is still difficult to recognise which dataset is a better reference when only two datasets are available, we propose to use at least three datasets for integration, copying the common number of biological replicates in experiments⁷⁹. Specifically, SCCAF-D makes cell type annotations more consistent across datasets by integrating datasets using Harmony²⁸ and then re-annotating cell types based on Leiden clustering and cell type labels obtained from the original publication.

Single-cell data information can be divided into biological and batch parts. Different data sources will be affected by batch, resulting in differences between different data, but the biological part of single-cell data from different sources should be the same, which is called ‘self-consistent’. Based on this assumption, we use SCCAF-D to select the optimised reference.

When preparing an optimised reference from single-cell data, we follow the Single-Cell Clustering Assessment Framework (SCCAF)²⁹ workflow, which is a method for the automated identification of putative cell types from scRNA-seq according to the self-projection. We first divide the data into two parts: a training set and a test set. Our splitting strategy is based on the number of cell types. If the number of cells for a particular cell type exceeds 500, we randomly select 500 cells from this type as the training set. However, if the number of cells for a cell type is less than 500, we split it in half, randomly selecting one half of the cells as the training set and the other half as the test set. Next, we use a logistic regression model for training, as it has already demonstrated advantages in well-established algorithms (such as SCCAF²⁹, CellHint⁸⁰ and CellTypist⁸¹) in identifying cell types. This model learns to predict cell types based on the data in the training set and assigns a prediction score to each cell within each cell type, generating a score matrix with cells as rows and cell types as columns. We assume that the training set contains sufficient information for cells to distinguish themselves from cells of other cell types, and this is known as self-projection.

Once the model is trained, we apply it to the test set and compare the predicted cell types of the test set with the true cell types in the original data, this process called ‘self-consistent’. We select those cells whose predictions match the true cell types and sort them based on their prediction scores. Finally, we select the top 100 cells with the highest prediction scores from each cell type to generate the final single-cell reference dataset.

User defined reference and deconvolution in SCCAF-D

The SCCAF-D computational framework allows users to customise the preparation of optimised reference data and select from 25 deconvolution methods, including DWLS²², FARDEEP¹⁴, MuSiC²³, NNLS²⁴, RLR⁸², EpiDISH¹², OLS⁸³, EPIC⁸⁴, ElasticNet⁸⁵, Lasso⁸⁵, ProportionsInAdmixture⁸⁶, Ridge, CIBERSORT⁸, SCDC⁵⁹, BisqueRNA⁸⁷, CDSeq⁸⁸, CPM⁸⁹, DCQ⁹⁰, DSA¹⁷, DeconRNASeq⁹¹, TIMER⁹², Deconf⁹³, Dtangle¹¹, ssFrobenius¹⁶, and ssKL⁹⁴ (Supplementary Data 3). All these deconvolution algorithms have been implemented as a package, Critical Assessment of Transcriptomic Deconvolution (CATD)²⁰. For optimised reference preparation, users have the flexibility to choose their preferred methods for building reference from single-cell datasets, including data processing, integration, clustering, and cell type annotation, or they can choose the default SCCAF-D settings. By default, we use the standard procedure in SCCAF-D to prepare optimised references and perform cell type deconvolution on the input data using DWLS.

To achieve an unbiased comparison, we incorporated 25 available deconvolution algorithms methods (Supplementary Data 3) into SCCAF-D, allowing users to estimate cell-type proportions from their own bulk RNA-seq data. When conducting deconvolution with SCCAF-D, users can customise their approach based on data type, deconvolution methods, and parameter settings: (a) reference data in Seurat format can be user-provided or generated by SCCAF-D as optimised references; (b) the bulk matrix can be derived from counts or normalised data; (c) four data input transformations are available (none, log, sqrt, vst); (d) 18 normalisation methods are supported (column, row, mean, column z-score, global z-score, column min-max, global min-max, LogNormalize, none, Quantile Normalisation (QN), Trimmed Mean of M-values (TMM), Upper Quartile (UQ), median ratios, TPM, SCTransform, scran, scater, Linnorm); (e) all other parameters follow the default settings of specific deconvolution algorithms. Besides, we advise users to keep consistent normalisation methods for both reference and bulk data to ensure reliable results.

Benchmarking workflow

In the ‘self-reference’ setting, we benchmarked all 25 deconvolution methods using data from 44 datasets and selected six methods with better performance: DWLS²², EpiDISH¹², FARDEEP¹⁴, MuSiC²³, NNLS²⁴, and RLR⁸² for comparative analysis (Supplementary Fig. 3). To simulate pseudobulk, we generated a total of 1000 synthetic simulated bulk profiles as samples of simulated bulk data. For each simulated sample, we randomly selected 10,000 cells with replacement to ensure that the number of each cell type is greater than one and that the sum of all cell type proportions is 1. The selection was based on successful deconvolution across all datasets, with PCCs above 0.3. According to the type of reference provided, these methods can be classified into bulk and single-cell methods. EpiDISH, FARDEEP, NNLS and RLR are common bulk deconvolution methods, while DWLS and MuSiC take single-cell expression profiles as input to get the specific features in order to deconvolve. We allocated 50% of the single-cell data to generate pseudobulk samples, utilising the remaining 50% as a reference dataset to deconvolute the simulated bulk data.

Under the ‘cross-reference’ setting, we evaluated each single-cell reference dataset and selected the best combination of method and reference. The same bulk data (simulated or real bulk data) was used to assess the performance of each reference and algorithm. Twenty scRNA-seq datasets, with four datasets from each tissue type (pancreas, lung, PBMC, brain, and spleen), were used for the deconvolution of simulated ‘pseudobulk’ data. For each tissue type, one dataset was used to simulate pseudobulk (following the methods described in the ‘self-reference’ benchmarking), while the remaining three datasets were processed using the SCCAF-D standard workflow to generate optimised references.

For the deconvolution of real bulk datasets, four PBMC datasets from Arunachalam et al.³⁴, Lee et al.³⁵, Wilk et al.³⁷, and Schulte et al.³⁶ were used to generate the optimised reference. Deconvolution with flow cytometry data as ground truth was performed utilising four bulk datasets with known cell type proportions, which were derived from the studies of Finotello et al.³¹, Newman et al.³² and Monaco et al.³³. Considering that the flow cytometry count data included some finer-granularity cell types not present in our reference data, we summarised the proportions of these finer cell types with their corresponding broader cell types. In the analysis of cell type proportions determined by flow cytometry as reported in Finotello et al.³¹, we have added the proportions of regulatory T cells (Tregs) into the counts for CD4 positive T cells. For the flow cytometry count data from Monaco et al.³³, we have attributed the proportions of the following CD4 positive T cell subsets to the overall CD4 positive T cell count: ‘T CD4 Naive’, ‘Tregs’, ‘Tfh’, ‘Th1’, ‘Th1/Th17’, ‘Th17, and ‘Th2’. Similarly, the proportions of the following CD8 positive T cell subsets have been added to the total CD8 positive T cell count: ‘T CD8 Naive’, ‘T CD8 CM’, ‘T CD8 EM’, and ‘T CD8 TE’.

Deconvolution analysis of bulk-profiled disease samples

We obtained one T2D bulk dataset associated with HbA1c levels from Fadista et al.³⁸, three IPF datasets from McDonough et al.³⁹, Sivakumar et al.⁴⁰, and Furusawa et al.⁴¹, and two NAFLD datasets linked to liver fibrosis stages (0–4) from Powell et al.⁵⁵ and Govaere et al.⁵⁶. The corresponding reference data were obtained for T2D from Baron et al.²¹, Marquina-Sanchez et al.²⁶, Segerstolpe et al.³⁰ and Muraro et al.²⁷; for IPF, datasets from Adams et al.⁴⁴, Reyfman et al.⁴⁶, and Tsukui et al.⁴⁷ were used to generate the first set of optimised reference, while those from Habermann et al.⁴⁸, Valenzi et al.⁴⁹ and Morse et al.⁵⁰ were used for the second; and for NAFLD, references were drawn from MacParland et al.⁵¹, Guilliams et al.⁵², Wang et al.⁵³ and Tabula Sapiens-Liver et al.⁵⁴. First, optimised references for T2D, IPF, and NAFLD were generated from single-cell data using the standard SCCAF-D workflow. No transformations were applied to the bulk data. Both the optimised references and bulk data were then subjected to TMM normalisation. Finally, deconvolution was performed using the optimised reference in combination with the DWLS algorithm following the default settings.

Graphics visualisation

Heatmaps of PCCs between estimated cell type proportions and ground truth were generated using the ComplexHeatmap⁹⁵ (v.2.15.4) package. All bar plots, scatter plots, violin plots, and box plots were visualised with the ggpubr⁹⁶ (v.0.6.0) and ggplot2⁹⁷ (v.3.4.2) packages. Sankey plots comparing original labels to manually curated cell type labels were visualised using Matplotlib⁹⁸ (v.3.8.1).

Metrics for deconvolution performance evaluation

Pearson correlation coefficient (PCC, or Pearson’s R) and Root mean square error (RMSE) were used to estimate the performance of cell type deconvolution. These two metrics were implemented as in CATD programme and calculated using the ‘dplyr’ (v. 1.1.3) R package. Details of these two metrics as well as the Jensen-Shannon divergence are introduced as below.

$${PCC}=\frac{\sum_{i=1}^{N}(x_i - \overline{x})(y_i - \overline{y})}{\sqrt{\sum_{i=1}^{N}(x_i - \overline{x})^2}\sqrt{\sum_{i=1}^{N}(y_i - \overline{y})^2}}$$

(1)

For the calculation of Pearson correlation coefficient between the true cell type proportions X and the deconvolution derived cell type proportions Y (equation 1), N is the number of observations, while X and Y are vectors. Therefore, ${x}_{i}$ means the proportion of each cell type for sample in X, while ${y}_{i}$ corresponds to that in a sample from Y. $\bar{x}$ and $\bar{y}$ are mean values for X and Y, respectively.

$$RMSE=\sqrt{\frac{\sum_{i=1}^N (x_i - y_i)^2}{N}}$$

(2)

For the calculation of RMSE, ${x}_{i}$, ${y}_{i}$ and N are the same as in PCC.

The Jensen-Shannon divergence (JSD) is a symmetric and smoothed variant of the Kullback-Leibler (KL) divergence, used to measure the similarity between two probability distributions. JSD is implemented using the philentropy (v.0.8.0) R package. The KL divergence is defined as follows:

$${KL}(P \parallel Q)=\sum_{t \in T} P(t) \log \left( \frac{P(t)}{Q(t)} \right)$$

(3)

In the calculation, ${P}$ and ${Q}$ are the predicted and true cell type probability distributions over cell type space T, whereas log is base 2.

For the calculation of JSD, it is defined as:

$${JSD}(P \parallel Q)=\frac{1}{2} {KL}(P \parallel M)+\frac{1}{2} {KL}(Q \parallel M)$$

(4)

in which,

$$M=\frac{1}{2}\left(P+Q\right)$$

(5)

Statistics and reproducibility

No statistical methods were used to pre-determine sample sizes. No data were excluded from the analyses. No randomisation was used in our study. The Investigators were not blinded to allocation during experiments and outcome assessment.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.

Data availability

The publicly available single-cell datasets used in this study can be accessed using the following accession codes or URLs: GSE84133, GSE142465, GSE85241, E-MTAB-5061 for human pancreas; syn21041850, GSE135893, GSE128169, and PRJEB31843 for human lung; GSE155673, GSE149689, GSE150728, and EGAS00001004571 for PBMCs; GSE115469, GSE192742, GSE189539, and Tabula Sapiens-Liver (https://cellxgene.cziscience.com/e/6d41668c-168c-4500-b06a-4674ccf3e19d.cxg/) for Liver; GSE186538, GSE157827, GSE160189, and GSE179590 for brain; E-MTAB-11536, PRJEB31843, GSE159929 for spleen; GSE136831, GSE122960, GSE132771, GSE135893, GSE128169, and GSE128033 for IPF. The bulk data used in this article is publicly available and can be downloaded via Gene Expression Omnibus (GEO) with accession number GSE107572, GSE127813, GSE107019, GSE225740, GSE50244, GSE124685, GSE134692, GSE150910, and GSE135251. Source data are provided with this paper.

Code availability

An open source implementation of SCCAF-D is available at GitHub github.com/rnacentre/SCCAF-D/, and Zenodo (https://doi.org/10.5281/zenodo.14211888)⁹⁹ while codes for reproducing the paper is available at: github.com/rnacentre/SCCAF-D_reproducibility/. Example data for code execution is available at: https://doi.org/10.6084/m9.figshare.27232896.

References

Kuhn, A., Thu, D., Waldvogel, H. J., Faull, R. L. M. & Luthi-Carter, R. Population-specific expression analysis (PSEA) reveals molecular changes in diseased brain. Nat. Methods 8, 945–947 (2011).
Article CAS PubMed Google Scholar
Edgar, R., Domrachev, M. & Lash, A. E. Gene expression omnibus: NCBI gene expression and hybridization array data repository. Nucleic Acids Res. 30, 207–210 (2002).
Article CAS PubMed PubMed Central Google Scholar
Parkinson, H. et al. Array express-a public database of microarray experiments and gene expression profiles. Nucleic Acids Res. 35, D747–D750 (2007).
Article CAS PubMed MATH Google Scholar
GTEx Consortium et al. Genetic effects on gene expression across human tissues. Nature 550, 204–213 (2017).
Article PubMed Central Google Scholar
International Cancer Genome Consortium et al. International network of cancer genome projects. Nature 464, 993–998 (2010).
Zhang, J. et al. International cancer genome consortium data portal-a one-stop shop for cancer genomics data. Database 2011, bar026 (2011).
Article PubMed PubMed Central Google Scholar
Taylor, R. S. et al. Association between fibrosis stage and outcomes of patients with nonalcoholic fatty liver disease: a systematic review and meta-analysis. Gastroenterology 158, 1611–1625.e12 (2020).
Article CAS PubMed MATH Google Scholar
Newman, A. M. et al. Robust enumeration of cell subsets from tissue expression profiles. Nat. Methods 12, 453–457 (2015).
Article CAS PubMed PubMed Central MATH Google Scholar
Du, R., Carey, V. & Weiss, S. T. deconvSeq: deconvolution of cell mixture distribution in sequencing data. Bioinformatics 35, 5095–5102 (2019).
Article CAS PubMed MATH Google Scholar
Frishberg, A. et al. Cell composition analysis of bulk genomics using single-cell data. Nat. Methods 16, 327–332 (2019).
Article CAS PubMed PubMed Central MATH Google Scholar
Hunt, G. J., Freytag, S., Bahlo, M. & Gagnon-Bartsch, J. A. dtangle: accurate and robust cell type deconvolution. Bioinformatics 35, 2093–2099 (2018).
Article MATH Google Scholar
Teschendorff, A. E., Breeze, C. E., Zheng, S. C. & Beck, S. A comparison of reference-based algorithms for correcting cell-type heterogeneity in Epigenome-Wide Association Studies. BMC Bioinform. 18, 105 (2017).
Article Google Scholar
Aliee, H. & Theis, F. J. AutoGeneS: Automatic gene selection using multi-objective optimization for RNA-seq deconvolution. Cell Syst. 12, 706–715.e4 (2021).
Article CAS PubMed Google Scholar
Hao, Y., Yan, M., Heath, B. R., Lei, Y. L. & Xie, Y. Fast and robust deconvolution of tumor infiltrating lymphocyte from expression profiles using least trimmed squares. PLoS Comput. Biol. 15, e1006976 (2019).
Article CAS PubMed PubMed Central ADS Google Scholar
Li, Z. & Wu, H. TOAST: improving reference-free cell composition estimation by cross-cell type differential analysis. Genome Biol. 20, 190 (2019).
Article PubMed PubMed Central MATH Google Scholar
Gaujoux, R. & Seoighe, C. CellMix: a comprehensive toolbox for gene expression deconvolution. Bioinformatics 29, 2211–2212 (2013).
Article CAS PubMed MATH Google Scholar
Zhong, Y., Wan, Y.-W., Pang, K., Chow, L. M. L. & Liu, Z. Digital sorting of complex tissues for cell type-specific gene expression profiles. BMC Bioinform. 14, 89 (2013).
Article Google Scholar
Avila Cobos, F., Alquicira-Hernandez, J., Powell, J. E., Mestdagh, P. & De Preter, K. Benchmarking of cell type deconvolution pipelines for transcriptomics data. Nat. Commun. 11, 5650 (2020).
Article CAS PubMed PubMed Central ADS Google Scholar
Tang, F. et al. mRNA-Seq whole-transcriptome analysis of a single cell. Nat. Methods 6, 377–382 (2009).
Article CAS PubMed MATH Google Scholar
Pournara, A. V. et al. CATD: a reproducible pipeline for selecting cell-type deconvolution methods across tissues. Bioinform. Adv. 4, vbae048 (2024).
Baron, M. et al. A single-cell transcriptomic map of the human and mouse pancreas reveals inter- and intra-cell population structure. Cell Syst. 3, 346–360.e4 (2016).
Article CAS PubMed PubMed Central MATH Google Scholar
Tsoucas, D. et al. Accurate estimation of cell-type composition from gene expression data. Nat. Commun. 10, 2975 (2019).
Article PubMed PubMed Central ADS MATH Google Scholar
Wang, X., Park, J., Susztak, K., Zhang, N. R. & Li, M. Bulk tissue cell type deconvolution with multi-subject single-cell expression reference. Nat. Commun. 10, 380 (2019).
Article CAS PubMed PubMed Central ADS MATH Google Scholar
NNLS: The Lawson-Hanson Algorithm for Non-Negative Least Squares (NNLS). Comprehensive R Archive Network (CRAN) https://CRAN.R-project.org/package=nnls (2024).
Vieira Braga, F. A. et al. A cellular census of human lungs identifies novel cell states in health and in asthma. Nat. Med. 25, 1153–1163 (2019).
Article CAS PubMed MATH Google Scholar
Marquina-Sanchez, B. et al. Single-cell RNA-seq with spike-in cells enables accurate quantification of cell-specific drug effects in pancreatic islets. Genome Biol. 21, 106 (2020).
Article CAS PubMed PubMed Central Google Scholar
Muraro, M. J. et al. A single-cell transcriptome atlas of the human pancreas. Cell Syst. 3, 385–394.e3 (2016).
Article CAS PubMed PubMed Central MATH Google Scholar
Korsunsky, I. et al. Fast, sensitive and accurate integration of single-cell data with Harmony. Nat. Methods 16, 1289–1296 (2019).
Article CAS PubMed PubMed Central MATH Google Scholar
Miao, Z. et al. Putative cell type discovery from single-cell gene expression data. Nat. Methods 17, 621–628 (2020).
Article CAS PubMed MATH Google Scholar
Segerstolpe, Å. et al. Single-cell transcriptome profiling of human pancreatic islets in health and type 2 diabetes. Cell Metab. 24, 593–607 (2016).
Article CAS PubMed PubMed Central Google Scholar
Finotello, F. et al. Molecular and pharmacological modulators of the tumor immune contexture revealed by deconvolution of RNA-seq data. Genome Med. 11, 34 (2019).
Article PubMed PubMed Central MATH Google Scholar
Newman, A. M. et al. Determining cell type abundance and expression from bulk tissues with digital cytometry. Nat. Biotechnol. 37, 773–782 (2019).
Article CAS PubMed PubMed Central MATH Google Scholar
Monaco, G. et al. RNA-Seq signatures normalized by mRNA abundance allow absolute deconvolution of human immune cell types. Cell Rep. 26, 1627–1640.e7 (2019).
Article CAS PubMed PubMed Central MATH Google Scholar
Arunachalam, P. S. et al. Systems biological assessment of immunity to mild versus severe COVID-19 infection in humans. Science 369, 1210–1220 (2020).
Article CAS PubMed PubMed Central ADS MATH Google Scholar
Lee, J. S. et al. Immunophenotyping of COVID-19 and influenza highlights the role of type I interferons in development of severe COVID-19. Sci. Immunol. 5, eabd1554 (2020).
Schulte-Schrepping, J. et al. Severe COVID-19 Is marked by a dysregulated myeloid cell compartment. Cell 182, 1419–1440.e23 (2020).
Article CAS PubMed PubMed Central MATH Google Scholar
Wilk, A. J. et al. A single-cell atlas of the peripheral immune response in patients with severe COVID-19. Nat. Med. 26, 1070–1076 (2020).
Article CAS PubMed PubMed Central MATH Google Scholar
Fadista, J. et al. Global genomic and transcriptomic analysis of human pancreatic islets reveals novel genes influencing glucose metabolism. Proc. Natl. Acad. Sci. USA. 111, 13924–13929 (2014).
Article CAS PubMed PubMed Central ADS Google Scholar
McDonough, J. E. et al. Transcriptional regulatory model of fibrosis progression in the human lung. JCI Insight 4, e131597 (2019).
Sivakumar, P. et al. RNA sequencing of transplant-stage idiopathic pulmonary fibrosis lung reveals unique pathway regulation. ERJ Open Res. 5, 00117–2019 (2019).
Furusawa, H. et al. Chronic hypersensitivity pneumonitis, an interstitial lung disease with distinct molecular signatures. Am. J. Respir. Crit. Care Med. 202, 1430–1444 (2020).
Article CAS PubMed PubMed Central MATH Google Scholar
Sayyed Kassem, L., Rajpal, A., Barreiro, M. V. & Ismail-Beigi, F. Beta-cell function in type 2 diabetes (T2DM): Can it be preserved or enhanced? J. Diabetes 15, 817–837 (2023).
Article CAS PubMed PubMed Central Google Scholar
Hara, M., Fowler, J. L., Bell, G. I. & Philipson, L. H. Resting beta-cells - A functional reserve? Diabetes Metab 42, 157–161 (2016).
Article CAS PubMed Google Scholar
Adams, T. S. et al. Single-cell RNA-seq reveals ectopic and aberrant lung-resident cell populations in idiopathic pulmonary fibrosis. Sci. Adv. 6, eaba1983 (2020).
Article CAS PubMed PubMed Central ADS Google Scholar
Mayr, C. H. et al. Spatial transcriptomic characterization of pathologic niches in IPF. Sci. Adv. 10, eadl5473 (2024).
Article CAS PubMed PubMed Central MATH Google Scholar
Reyfman, P. A. et al. Single-Cell Transcriptomic Analysis of Human Lung Provides Insights into the Pathobiology of Pulmonary Fibrosis. Am. J. Respir. Crit. Care Med. 199, 1517–1536 (2019).
Article CAS PubMed PubMed Central MATH Google Scholar
Tsukui, T. et al. Collagen-producing lung cell atlas identifies multiple subsets with distinct localization and relevance to fibrosis. Nat. Commun. 11, 1920 (2020).
Article CAS PubMed PubMed Central ADS MATH Google Scholar
Habermann, A. C. et al. Single-cell RNA sequencing reveals profibrotic roles of distinct epithelial and mesenchymal lineages in pulmonary fibrosis. Sci. Adv. 6, eaba1972 (2020).
Article CAS PubMed PubMed Central ADS Google Scholar
Valenzi, E. et al. Single-cell analysis reveals fibroblast heterogeneity and myofibroblasts in systemic sclerosis-associated interstitial lung disease. Ann. Rheum. Dis. 78, 1379–1387 (2019).
Article CAS PubMed MATH Google Scholar
Morse, C. et al. Proliferating SPP1/MERTK-expressing macrophages in idiopathic pulmonary fibrosis. Eur. Respir. J. 54, 1802441 (2019).
MacParland, S. A. et al. Single cell RNA sequencing of human liver reveals distinct intrahepatic macrophage populations. Nat. Commun. 9, 4383 (2018).
Article PubMed PubMed Central ADS MATH Google Scholar
Guilliams, M. et al. Spatial proteogenomics reveals distinct and evolutionarily conserved hepatic macrophage niches. Cell 185, 379–396.e38 (2022).
Article CAS PubMed PubMed Central Google Scholar
Wang, Z. et al. Single-cell analysis reveals a pathogenic cellular module associated with early allograft dysfunction after liver transplantation. bioRxiv https://doi.org/10.1101/2022.02.09.479667 (2022).
Article PubMed PubMed Central Google Scholar
Tabula Sapiens Consortium*. et al. The Tabula Sapiens: A multiple-organ, single-cell transcriptomic atlas of humans. Science 376, eabl4896 (2022).
Article Google Scholar
Powell, N. R. et al. Clinically important alterations in pharmacogene expression in histologically severe nonalcoholic fatty liver disease. Nat. Commun. 14, 1474 (2023).
Article CAS PubMed PubMed Central ADS Google Scholar
Govaere, O. et al. Transcriptomic profiling across the nonalcoholic fatty liver disease spectrum reveals gene signatures for steatohepatitis and fibrosis. Sci. Transl. Med. 12, eaba4448 (2020).
Garmire, L. X. et al. Challenges and perspectives in computational deconvolution of genomics data. Nat. Methods 21, 391–400 (2024).
Article CAS PubMed MATH Google Scholar
Jin, H. & Liu, Z. A benchmark for RNA-seq deconvolution analysis under dynamic testing environments. Genome Biol. 22, 102 (2021).
Article CAS PubMed PubMed Central MATH Google Scholar
Dong, M. et al. SCDC: bulk gene expression deconvolution by multiple single-cell RNA sequencing references. Brief. Bioinform. 22, 416–427 (2021).
Article CAS PubMed MATH Google Scholar
Richardson, M. M. et al. Progressive fibrosis in nonalcoholic steatohepatitis: association with altered regeneration and a ductular reaction. Gastroenterology 133, 80–90 (2007).
Article PubMed MATH Google Scholar
Kisseleva, T. & Brenner, D. Molecular and cellular mechanisms of liver fibrosis and its regression. Nat. Rev. Gastroenterol. Hepatol. 18, 151–166 (2021).
Article PubMed MATH Google Scholar
Nguyen, H., Nguyen, H., Tran, D., Draghici, S. & Nguyen, T. Fourteen years of cellular deconvolution: methodology, applications, technical evaluation and outstanding challenges. Nucleic Acids Res. 52, 4761–4783 (2024).
Article PubMed PubMed Central MATH Google Scholar
Regev, A. et al. The human cell atlas. Elife 6, e27041 (2017).
HuBMAP Consortium. The human body at cellular resolution: the NIH Human Biomolecular Atlas Program. Nature 574, 187–192 (2019).
Article CAS ADS Google Scholar
Rozenblatt-Rosen, O. et al. The human tumor atlas network: charting tumor transitions across space and time at single-cell resolution. Cell 181, 236–249 (2020).
Article CAS PubMed PubMed Central MATH Google Scholar
Speir, M. L. et al. UCSC Cell Browser: visualize your single-cell data. Bioinformatics 37, 4578–4580 (2021).
Article CAS PubMed PubMed Central MATH Google Scholar
Kildisiute, G. et al. Tumor to normal single-cell mRNA comparisons reveal a pan-neuroblastoma cancer cell. Sci. Adv. 7, eabd3311 (2021).
Megill, C. et al. Cellxgene: A performant, scalable exploration platform for high dimensional sparse matrices. bioRxiv https://doi.org/10.1101/2021.04.05.438318 (2021).
Annotate the Gene Symbols for Probes in Expression Array [R package AnnoProbe version 07]. (2022).
AnnotationDbi. Bioconductor http://bioconductor.org/packages/AnnotationDbi/ (2024).
Wolf, F. A., Angerer, P. & Theis, F. J. SCANPY: large-scale single-cell gene expression data analysis. Genome Biol 19, 15 (2018).
Article PubMed PubMed Central MATH Google Scholar
Butler, A., Hoffman, P., Smibert, P., Papalexi, E. & Satija, R. Integrating single-cell transcriptomic data across different conditions, technologies, and species. Nat. Biotechnol. 36, 411–420 (2018).
Article CAS PubMed PubMed Central Google Scholar
Hrvatin, S. et al. Single-cell analysis of experience-dependent transcriptomic states in the mouse visual cortex. Nat. Neurosci. 21, 120–129 (2018).
Article CAS PubMed MATH Google Scholar
Liao, M. et al. Single-cell landscape of bronchoalveolar immune cells in patients with COVID-19. Nat. Med. 26, 842–844 (2020).
Article CAS PubMed MATH Google Scholar
Aizarani, N. et al. A human liver cell atlas reveals heterogeneity and epithelial progenitors. Nature 572, 199–204 (2019).
Article CAS PubMed PubMed Central Google Scholar
Moncada, R. et al. Integrating microarray-based spatial transcriptomics and single-cell RNA-seq reveals tissue architecture in pancreatic ductal adenocarcinomas. Nat. Biotechnol. 38, 333–342 (2020).
Article CAS PubMed MATH Google Scholar
Travaglini, K. J. et al. A molecular cell atlas of the human lung from single-cell RNA sequencing. Nature 587, 619–625 (2020).
Article CAS PubMed PubMed Central ADS MATH Google Scholar
Madissoon, E. et al. scRNA-seq assessment of the human lung, spleen, and esophagus tissue stability after cold preservation. Genome Biol 21, 1 (2019).
Article CAS PubMed PubMed Central Google Scholar
Blainey, P., Krzywinski, M. & Altman, N. Points of significance: replication. Nat. Methods 11, 879–880 (2014).
Article CAS PubMed Google Scholar
Xu, C. et al. Automatic cell-type harmonization and integration across Human Cell Atlas datasets. Cell 186, 5876–5891.e20 (2023).
Article CAS PubMed MATH Google Scholar
Domínguez Conde, C. et al. Cross-tissue immune cell analysis reveals tissue-specific features in humans. Science 376, eabl5197 (2022).
Article PubMed PubMed Central Google Scholar
Support Functions and Datasets for Venables and Ripley’s MASS [R package MASS version 7.3–61]. (2024).
Chambers, J., Hastie, T. & Pregibon, D. Statistical Models in S. Compstat. 317–321 (1990).
Racle, J., de Jonge, K., Baumgaertner, P., Speiser, D. E. & Gfeller, D. Simultaneous enumeration of cancer and immune cell types from bulk tumor gene expression data. Elife 6, e26476 (2017).
Friedman, J., Hastie, T. & Tibshirani, R. Regularization paths for generalized linear models via coordinate descent. J. Stat. Softw. 33, 1–22 (2010).
Article PubMed PubMed Central MATH Google Scholar
Applied Research Applied Research Press. WGCNA: An R Package for Weighted Correlation Network Analysis. (2015).
Jew, B. et al. Accurate estimation of cell composition in bulk expression through robust integration of single-cell information. Nat. Commun. 11, 1971 (2020).
Article CAS PubMed PubMed Central ADS MATH Google Scholar
Kang, K. et al. CDSeq: A novel complete deconvolution method for dissecting heterogeneous samples using gene expression data. PLoS Comput. Biol. 15, e1007510 (2019).
Article PubMed PubMed Central Google Scholar
Song, L., Sun, X., Qi, T. & Yang, J. Mixed model-based deconvolution of cell-state abundances (MeDuSA) along a one-dimensional trajectory. Nat. Comput. Sci. 3, 630–643 (2023).
Article CAS PubMed PubMed Central MATH Google Scholar
Altboum, Z. et al. Digital cell quantification identifies global immune cell dynamics during influenza infection. Mol. Syst. Biol. 10, 720 (2014).
Article PubMed PubMed Central MATH Google Scholar
Gong, T. & Szustakowski, J. D. DeconRNASeq: a statistical framework for deconvolution of heterogeneous tissue samples based on mRNA-Seq data. Bioinformatics 29, 1083–1085 (2013).
Article CAS PubMed MATH Google Scholar
Li, T. et al. TIMER: A Web Server for comprehensive analysis of tumor-infiltrating immune cells. Cancer Res. 77, e108–e110 (2017).
Article CAS PubMed PubMed Central ADS MATH Google Scholar
Repsilber, D. et al. Biomarker discovery in heterogeneous tissue samples -taking the in-silico deconfounding approach. https://doi.org/10.1186/1471-2105-11-27 (2010).
Gaujoux, R. & Seoighe, C. Semi-supervised Nonnegative Matrix Factorization for gene expression deconvolution: a case study. Infect. Genet. Evol. 12, 913–921 (2012).
Article CAS PubMed MATH Google Scholar
Gu, Z. Complex heatmap visualization. Imeta 1, e43 (2022).
Article PubMed PubMed Central MATH Google Scholar
Kassambara, A. ‘ggplot2’ Based Publication Ready Plots [R package ggpubr version 0.6.0]. (2023).
Create Elegant Data Visualisations Using the Grammar of Graphics [R package ggplot2 version 3.5.1]. (2024).
Hunter, J. D. Matplotlib: A 2D graphics environment. https://ieeexplore.ieee.org/document/4160265 (2007).
Feng, S. & Miao, Z. Alleviating batch effects in cell type deconvolution with SCCAF-D. Zenodo. https://doi.org/10.5281/ZENODO.14211888. (2024).

Download references

Acknowledgements

Shuo Feng would like to thank Prof. Haiyan Liu for supervision and Dr. Yin Huang for discussion. This work is funded by the National Key R&D Programmes of China (2023YFF1204700, 2023YFF1204701), the Natural Science Foundation of China (32270707), the R&D Programmes of Guangzhou Laboratory, Grant No. GZNL2024A01002, GZNL2023A01006, SRPG22-003, SRPG22-006, SRPG22-007, HWYQ23-003, YW-YFYJ0102, the Postdoctoral Research Project Funding of Guangzhou (BSHF23-087).

Author information

These authors contributed equally: Shuo Feng, Liangfeng Huang.

Authors and Affiliations

GMU-GIBH Joint School of Life Sciences, The Guangdong-Hong Kong-Macao Joint Laboratory for Cell Fate Regulation and Diseases, Guangzhou Laboratory, Guangzhou Medical University, Guangzhou, China
Shuo Feng, Liangfeng Huang, Ziliang Huang & Zhichao Miao
Division of Life Sciences and Medicine, University of Science and Technology of China, Hefei, 230027, China
Shuo Feng
Translational Research Institute of Brain and Brain-Like Intelligence and Department of Anesthesiology, Shanghai Fourth People’s Hospital Affiliated to Tongji University School of Medicine, Shanghai, China
Liangfeng Huang & Zhichao Miao
European Molecular Biology Laboratory, European Bioinformatics Institute, EMBL-EBI, Wellcome Genome Campus, Cambridge, CB10 1SD, UK
Anna Vathrakokoili Pournara, Alvis Brazma & Zhichao Miao
Department of Obstetrics and Gynaecology, Harbin Red Cross Central Hospital, Harbin, 150001, China
Xinlu Yang
Harbin Medical University the Sixth Affiliated Hospital, Harbin, 150023, China
Yongjian Zhang
School of Life Science and Technology, Harbin Institute of Technology, Harbin, 150001, China
Ming Shi
Earlham Institute, Norwich Research Park, Norwich, NR4 7UZ, UK
Irene Papatheodorou
Medical School, University of East Anglia, Norwich Research Park, Norwich, NR4 7UA, UK
Irene Papatheodorou

Authors

Shuo Feng
View author publications
Search author on:PubMed Google Scholar
Liangfeng Huang
View author publications
Search author on:PubMed Google Scholar
Anna Vathrakokoili Pournara
View author publications
Search author on:PubMed Google Scholar
Ziliang Huang
View author publications
Search author on:PubMed Google Scholar
Xinlu Yang
View author publications
Search author on:PubMed Google Scholar
Yongjian Zhang
View author publications
Search author on:PubMed Google Scholar
Alvis Brazma
View author publications
Search author on:PubMed Google Scholar
Ming Shi
View author publications
Search author on:PubMed Google Scholar
Irene Papatheodorou
View author publications
Search author on:PubMed Google Scholar
Zhichao Miao
View author publications
Search author on:PubMed Google Scholar

Contributions

S.F. designed the algorithm, conducted the analyses and wrote the manuscript. Z.M. conceived the project, designed the algorithm, did the analyses and wrote the manuscript. A.V.P. contributed the analyses. L.H. interpreted the results and wrote the manuscript. Z.H. designed the algorithm. X.Y., Y.Z. and M.S. contributed to the collection of scRNA-seq data. A.B., M.S., I.P. and Z.M. Supervised the project. All authors reviewed, edited, and approved the final paper.

Corresponding authors

Correspondence to Ming Shi, Irene Papatheodorou or Zhichao Miao.

Ethics declarations

Competing interests

The authors declare no competing interests.

Peer review

Peer review information

Nature Communications thanks Mingon Kang, Yang Xiao and the other, anonymous, reviewer(s) for their contribution to the peer review of this work. A peer review file is available.

Additional information

Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Supplementary information

Supplementary Information

Description of Additional Supplementary Files

Supplementary Dataset 1-7

Reporting Summary

Transparent Peer Review file

Source data

Source Data

Rights and permissions

Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.

Reprints and permissions

About this article

Cite this article

Feng, S., Huang, L., Pournara, A.V. et al. Alleviating batch effects in cell type deconvolution with SCCAF-D. Nat Commun 15, 10867 (2024). https://doi.org/10.1038/s41467-024-55213-x

Download citation

Received: 07 May 2024
Accepted: 02 December 2024
Published: 30 December 2024
DOI: https://doi.org/10.1038/s41467-024-55213-x

This article is cited by

MOADE: a multimodal autoencoder for dissociating bulk multi-omics data
- Jiao Sun
- Ayesha A. Malik
- Qian Li
Genome Biology (2025)