A Bayesian active learning platform for scalable combination drug screens

Abstract

Large-scale combination drug screens are generally considered intractable due to the immense number of possible combinations. Existing approaches use ad hoc fixed experimental designs then train machine learning models to impute unobserved combinations. Here we propose BATCHIE, an orthogonal approach that conducts experiments dynamically in batches. BATCHIE uses information theory and probabilistic modeling to design each batch to be maximally informative based on the results of previous experiments. On retrospective experiments from previous large-scale screens, BATCHIE designs rapidly discover highly effective and synergistic combinations. In a prospective combination screen of a library of 206 drugs on a collection of pediatric cancer cell lines, the BATCHIE model accurately predicts unseen combinations and detects synergies after exploring only 4% of the 1.4M possible experiments. Further, the model identifies a panel of top combinations for Ewing sarcomas, which follow-up validation experiments confirm to be effective, including the rational and translatable top hit of PARP plus topoisomerase I inhibition. These results demonstrate that adaptive experiments can enable large-scale unbiased combination drug screens with a relatively small number of experiments. BATCHIE is open source and publicly available (https://github.com/tansey-lab/batchie).

Introduction

Single-agent treatment interventions in cancers, viruses, and bacterial infections impose evolutionary selective pressures that can lead to therapeutic resistance and poor outcomes for patients. Combination therapies have the ability to constrain multiple potential avenues of evolutionary escape and thus reduce the likelihood of treatment resistance. Consequently, rational combination therapies have long formed the basis for rapidly evolving pathogens like HIV¹ and are increasingly seen as the future of antibiotics² and cancer therapies^3,4.

Screening for effective drug combinations presents the singular challenge of scale. The number of possible experiments in a combination screen grows at a rate of n × m^d × t^d for n conditions, m drugs, t doses, and d-way combinations. For instance, a single-agent screen of 100 drugs and 50 cell lines at 5 doses would only comprise 25K experiments whereas a pairwise drug screen on the same libraries would require 6.2M experiments. Given the rapid growth of the experimental design space, even the most efficient high-throughput screening team would struggle to conduct an exhaustive pairwise combination screen of a modest-sized drug library over a modest number of doses and cell lines. Conducting such a screen is currently a substantial undertaking requiring large funding, detailed planning, advanced equipment, and several years of experiments. Thus, even the largest published combination screens have been restricted to libraries of less than 120 drugs^5,6,7.

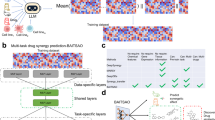
The intractability of combination drug screens has led to the development of machine learning methods for predicting drug combinations^8,9,10,11,12. The goal of such modeling is to use the predictive model to simulate experiments in silico and filter the list of combinations down to a set of top hits to be validated in vitro. However, predictive models are fundamentally limited by the data on which they are trained. Small libraries, which allow for exhaustive enumeration of the combination landscape, are limited to discoveries involving those drugs in the library. If the library is too small, it simply may not contain any useful candidate combinations and thus machine learning models will extract no meaningful signals (Fig. 1a). Larger libraries may contain useful combinations, but if a screen is performed on a random or fixed-design subset, then it is unlikely to generate observations of the most surprising and informative combinations. Models fit to pre-designed observations are likely to then have poor accuracy and may be unable to confidently pinpoint the maximally useful combinations (Fig. 1b). Thus, while a number of sophisticated models have been proposed, their success as discovery tools for rational combinations has been limited.

Fig. 1: Benefits of adaptive experimental design.

a, b Traditional approaches to combination studies entail exhaustive enumeration of a small library or random subsampling of a large library. In either case, the resulting models generally are not powerful enough to find clinically relevant discoveries. c Adaptive experimental design allows exploration of a large library. By focusing on the most informative experiments, one can create a powerful model that is capable of finding clinically relevant discoveries. Created in BioRender. Tansey, W. (2024) BioRender.com/k20w361.

We sought to overcome both the wet lab scalability and predictive modeling challenges of combination screens by rethinking the experimental design approach. Rather than performing a fixed-design experiment and fitting a model post-hoc, we instead drew on the long history of Bayesian optimal sequential experimental design¹³. In the sequential setup, experiments are conducted in small batches where each batch is designed adaptively based on the results of the previous batches. When designs are driven by a machine learning model that aims to acquire the most informative training data in each batch, the sequential experimental design task is known as active learning¹⁴. Active learning has experienced a recent burst in interest in the drug discovery literature^15,16,17,18 where the objective is to design de novo molecules aimed at better docking on a target. We are aware of only one recent method, RECOVER¹⁹, that has attempted to integrate adaptive experimentation and combination screening. RECOVER uses a multi-armed bandit algorithm to search for top synergistic hits for a single cell line at each iteration. Unfortunately, the RECOVER bandit approach provides no clear way to scale to large sample libraries, provides no theoretical guarantees that designs are optimal, and can only target single cell line synergy which is generally rare⁶ and does not typically characterize successful combination therapies in the clinic^20,21,22,23. Thus, while using active learning to identify useful molecules has seen robust investigation, its application to discover rational combinations from large libraries of existing drugs has not been thoroughly explored.

We note that a natural alternative to active learning is Bayesian optimization^24,25, which also adaptively collects information while taking into account an internal model’s uncertainty of possible experiments. Unlike active learning, whose goal is to model the entire experimental space (perhaps subject to some resolution), Bayesian optimization seeks to find a single optimizer of some objective function, and it assumes the ability to observe evaluations of this function. For the types of objectives considered in this work, such as the therapeutic index, individual evaluations require experiments on drug combinations that span several cell lines, which is potentially wasteful. The active learning approach considered here, meanwhile, has the ability to leverage all observed experiments, regardless of how many cell lines an individual combination is observed on, and it has the added benefit that the end product is a model that makes predictions across the entire space, allowing us to identify many promising candidates instead of just one.

In this work, we introduce Bayesian Active Treatment Combination Hunting via Iterative Experimentation (BATCHIE) as a framework for orchestrating large-scale combination drug screens through sequential experimental design. BATCHIE uses a Bayesian active learning^26,27 strategy to design sequential experiments. These sequential designs are theoretically near-optimal (see Supplementary Information for theory and proofs) and guarantee that BATCHIE designs are efficient. Pragmatically, BATCHIE enables sequential experimental designs that will best improve any user-provided probabilistic (Bayesian) model. Thus, while we implemented an initial model for our experiments, BATCHIE can alternatively be paired with any existing and future Bayesian machine learning method for combination drug response. The end result of a BATCHIE screen is a maximally informative dataset and an optimal predictive model that enables the discovery of more effective combinations than in a fixed design (Fig. 1c). We validate the empirical performance of BATCHIE using retrospective simulations and through a prospective study. We first use data from large-scale, pan-cancer combination screens^5,6,7 to retrospectively simulate adaptive screens. BATCHIE consistently outperforms fixed designs in these simulations and better prioritizes effective combinations as top hits. We then implement BATCHIE in a drug screening facility and use it to conduct a combination drug screen across a 206 drug library over 16 cancer cell lines, focusing on pediatric sarcomas. The BATCHIE screen generates a model with near-optimal predictive accuracy on random unseen combinations. Further, we use the model to prioritize ten combinations to validate experimentally for a panel of Ewing sarcoma lines; all ten combinations achieve a high therapeutic index score. The top identified hit corresponds to a PARP inhibitor (talazoparib) plus a topoisomerase I inhibitor (topotecan), a biologically rational combination and the subject of two of the five NCI-supported Phase II combination therapy clinical trials for Ewing sarcoma currently underway. BATCHIE is readily available as open source, along with accompanying tutorials.

Results

Adaptive experimental design for combination drug screens

BATCHIE uses an active learning algorithm to choose the most informative data to collect in each sequential batch of experiments (Fig. 2). In the initial batch, BATCHIE uses a design of experiments approach²⁸ to cover the drug and cell line space efficiently (Fig. 2a). The initial batch is then run (Fig. 2b) and used to train a Bayesian predictive model that estimates a distribution over drug combination responses for each cell line (Fig. 2c). For subsequent batches, BATCHIE uses the model’s posterior distribution to simulate plausible outcomes of candidate combination experiments along with how they would change the model (Fig. 2d). BATCHIE then measures how much each experiment is expected to reduce the posterior uncertainty over the drug responses (Fig. 2e) and uses a submodular approach to design a maximally informative batch (Fig. 2f). After designing an optimal batch, the batch is run, the model is updated with the new results, and the next optimal batch is constructed. When the exploratory budget runs out or the model converges to a concentrated posterior, the active learning loop ends. The optimally trained model is then used to predict effective combinations that are prioritized for experimental validation (Fig. 2g).

Fig. 2: BATCHIE overview.

a The BATCHIE workflow begins by specifying a cell line library, a drug library, and an initial ‘seed batch’ of plates to cover every cell line and drug with at least one experiment. b Selected plates are assembled, run, measured, and post-processed to obtain viability scores. Quality control (QC) checks filter out problematic wells. c A Bayesian tensor factorization model is fit to the current data. Posterior samples are drawn via MCMC. d The joint distributions of candidate experiments are estimated using the current set of posterior samples. e The active learning criterion is applied to the joint distribution estimates to score the utility of individual experiments. f The scores of individual experiments are aggregated to define the most informative batch of experiments to run next, possibly subject to design constraints. g After terminating the active learning loop, the most recently fitted Bayesian model is used to predict top hits for individual combinations. These top hits can then be validated in vitro and, potentially, in vivo. Created in BioRender. Tansey, W. (2024) BioRender.com/t08h139.

To design experiments, BATCHIE uses a modification of the Diameter-based Active Learning criterion^26,27, called Probabilistic Diameter-based Active Learning (PDBAL), that is suitable for probabilistic and noisy outcomes like those encountered in drug screening (see “Methods”). The key idea behind PDBAL is to select experiments which will minimize the expected distance between any two posterior samples after observing the outcomes of the selected experiments. PDBAL comes with theoretical guarantees ensuring that combination screen designs will be near-optimal regardless of the drug library, sample library, or combination search space (see Supplementary Information for PDBAL theory). In addition to theoretical guarantees, we benchmarked PDBAL across a wide array of different predictive modeling scenarios and objectives (Supplementary Fig. 13). PDBAL consistently performs as well or better than conventional methods like expected information gain or posterior variance maximization.¹⁴ Given the strong empirical performance of PDBAL and its theoretical guarantees, we used it as the foundation for the overall BATCHIE algorithm.

BATCHIE is compatible with any Bayesian model capable of modeling combination drug screen data. There have been many models developed for modeling this type of data^11,29,30,31. Integrating any of these models into BATCHIE would be possible by reformulating them as fully Bayesian models capable of quantifying posterior uncertainty. In our implementation, we use a hierarchical Bayesian tensor factorization model (Fig. 2c). The model contains embeddings for each cell line and each drug-dose, as well as embeddings that capture the effects of drug interactions. The BATCHIE model assumes that the response of a combination of drugs on a cell line can be decomposed into the individual effects of the drugs and an interaction term. Specifically, the model posits an embedding ${u}^{(k)}\in {{\mathbb{R}}}^{d}$ for each cell line k and embeddings ${v}_{1}^{(i)},{v}_{2}^{(i)}\in {{\mathbb{R}}}^{d}$ for each drug-dose i, which capture the individual and interaction effects of the drug-dose, respectively. When drug-doses i and j are applied to cell line k, the logit-transformed viability is assumed to be normally distributed with mean μ_ijk satisfying

$${\mu }_{ijk}={\sum}_{t=1}^{d}({v}_{1,t}^{(i)}+{v}_{1,t}^{(j)}+{v}_{2,t}^{(i)}{v}_{2,t}^{(j)}){u}_{t}^{(k)}+{v}_{0}^{(i)}+{v}_{0}^{(j)}+{u}_{0}^{(k)}+\alpha,$$

(1)

where ${v}_{0}^{(i)}\in {\mathbb{R}}$ is a drug-dose specific offset, ${u}_{0}^{(k)}\in {\mathbb{R}}$ is a cell line specific offset, and $\alpha \in {\mathbb{R}}$ is a global offset. The variance of the normal distribution is assumed to be a global parameter. Hierarchical priors are placed on top of the embeddings, offsets, and variance to automatically adapt to the complexity of the data³². The priors are chosen to be conditionally conjugate with the likelihoods, allowing the entire model to sampled efficiently using blocked Gibbs sampling (see “Methods” for modeling details).

To make BATCHIE practical to implement in a high-throughput screening facility, we consider pools of experiments in the form of microwell plates (Supplementary Fig. 3a). Each plate is formed by combining a single cell line with a row plate and a column plate. Here, a row plate is an n × m plate in which every well of a particular row contains the same drug at the same dose. Similarly, a column plate is of the same size, but constructed so that each column contains the same drug at the same dose. When a row plate and a column plate are overlaid, the resulting combination plate contains all possible combinations of their constituent drug-doses. Row and column plates are constructed with high and low control wells so that all associated drug-doses are measured singly and viabilities can be computed. In this way, the number of plates that need to be stamped scales linearly with the drug library size, as opposed to quadratically as the number of possible combinations (see Methods).

Validation of BATCHIE on existing combination datasets

The core goal of BATCHIE is to reduce the number of experiments needed to make useful discoveries. To benchmark the effectiveness of BATCHIE in pursuit of this goal, we conducted retrospective simulations that compared the performance of a BATCHIE-trained model after a small number (≤ 15) of rounds against (a) a model that was trained on the entire dataset and (b) a model that was trained on a random subset of the dataset matching the size and constraints of BATCHIE’s.

We benchmarked BATCHIE using three large, publicly-available, pan-cancer combination drug screen datasets: the NCI ALMANAC study⁵ (ALMANAC), the Genomics of Drug Sensitivity in Cancer combination screen⁶ (GDSC²), and Merck’s unbiased combination drug screen⁷ (MERCK). The three datasets differed in cell line library size (60 for ALMANAC, 126 for GDSC², 39 for MERCK) and drug library size (104 for ALMANAC, 66 for GDSC², 38 for MERCK). The ALMANAC screen covered the NCI-60 panel of cell lines³³, spanning leukemia, lung, colon, central nervous system, melanoma, ovarian, renal, prostate, and breast cancers. The GDSC² screen covered breast, colon and pancreatic cancer cell lines. The MERCK screen covered a panel of lung, ovarian, melanoma, colon, breast, and prostate cancer cell lines. All three screens used fixed experimental designs but differed in the subset of the combination space to explore. Consequently, the overall sparsity pattern varies substantially between datasets (Fig. 3(b, c)).

Fig. 3: Retrospective study design and results.

a Retrospective studies are conducted by processing an existing dataset into candidate row/column plates of the kind considered in this work and simulating the choices made by both the Random and BATCHIE data collection procedures. After data collection, the models are trained on the data collected by each of the procedures and evaluated for accuracy. Created in BioRender. Tansey, W. (2024) BioRender.com/i97p897. b Statistics for the datasets used in our retrospective studies. Created in BioRender. Tansey, W. (2024) BioRender.com/e57c809. c Heatmaps showing the fraction of possible experiments observed for each drug combination. d BATCHIE outperforms Random when both are evaluated after 15 rounds of data collection; p-values derived from a two-sided Mann-Whitney U-Test with no adjustments made for multiple comparisons. e The number of additional experiments needed for Random to achieve comparable performance to BATCHIE grows with the number of BATCHIE rounds across all datasets. Lines represent mean values; error bars denote standard deviations. f The number of additional batches needed for Random to achieve comparable performance to BATCHIE grows with the size of the cell line library; ρ_spear is Spearman’s rho for nonparametric rank correlation with a two-sided test for the p-value with no adjustments made for multiple comparisons. For boxplots in (d, f), center lines denote means, box limits denote standard deviations, and whiskers denote extremal values. d–f n = 25 replicates for all plots. Source data are provided as a Source Data file.

To simulate the behavior of BATCHIE in a realistic adaptive data collection screen, the existing datasets were divided into simulated plates (Fig. 3a). Plates were designed to replicate the statistics of the plates used in our prospective study (“Methods”). The data collection processes (BATCHIE and Random) were given batch constraints that approximately 10% of cell lines be selected at every round and three combination plates be selected per chosen cell line. We stopped the Random and BATCHIE screens after 15 batches, the same as in our prospective study. We randomly held out 10% of all experiments as a test set to evaluate predictive performance of the resulting models. Model performance was compared relative to a model trained on the full set of experiments conducted, not including the test set. We repeated the simulations 25 times per dataset, with different randomly-organized row and column plates for stamping.

At the end of 15 batches, the Random and BATCHIE models observed 1.7–20.4% of the full training dataset (1.66–1.7% for ALMANAC, 10.3–11.1% for GDSC², and 19.3–20.4% for MERCK). Total observed percentages varied due to the difference in the original screen designs. Across the three datasets, BATCHIE produced models with holdout R² accuracy within 5–7% of the models that were fit using all available training data and significantly outperformed the models trained on data collected by the Random strategy with the same number of rounds (Fig. 3d).

We also tracked the number of experiments that the Random strategy would need to perform in order to achieve comparable performance to BATCHIE. We observed that the number of experiments saved grew as a function of the number of BATCHIE rounds, with the number of experiments saved by round 15 numbering in the 10s of thousands for the ALMANAC and MERCK datasets to over 100K for the GDSC² dataset (Fig. 3e). When we looked at the excess number of experiments needed to achieve a certain normalized accuracy, BATCHIE shows an exponential speedup as the model accuracy threshold increases (Supplementary Fig. 1c). When measured by the number of batches needed for Random to achieve BATCHIE-level performance, we again saw a similar exponential trend, but the scale is more consistent across datasets (Supplementary Fig. 1b). Similar trends were seen when measuring the number of excess batches required for the Random model to reach the equivalent performance of the BATCHIE model at each round (Supplementary Fig. 1d).

To test how well BATCHIE scales with the size of the experimental landscape, we simulated smaller experimental spaces by restricting each dataset to a random subsample of 20%, 40%, 60%, or 80% of cell lines. For all datasets, we observed a strong positive correlation (ρ_spear = 0.38, 0.64, 0.48, $\max (p)=1.6\times 1{0}^{-5}$) between the size of the experimental landscape and the improvement offered by BATCHIE over Random (Fig. 3f). These results indicate that BATCHIE screens become increasingly more efficient as the overall landscape becomes larger.

While these results confirm that BATCHIE produces accurate models with few experiments, average predictive accuracy alone does not ensure that the model will be able to identify highly effective combinations. This is because desirable properties for treatments, such as high therapeutic index (TI)²², often correspond to extremal points, which are not average by definition. To evaluate the ability of BATCHIE to discover effective combinations, we used the BATCHIE-trained model to estimate the TI of all drug combinations using all pairs of cell lines as targets and controls. We chose the top 20 predictions and calculated their average observed TI. For all of the datasets, the BATCHIE-trained model selections had significantly higher TI ($\max (p)=0.001$) than those selected by the Random-trained model (Supplementary Fig. 1e). We also observed that BATCHIE was better at identifying high TI combos in terms of area under the curve (AUC) of the receiver operating characteristic (ROC) curve (Supplementary Fig. 1f).

BATCHIE can be implemented with any active learning selection criterion. We investigated the effect of interchanging the default PDBAL strategy with the expected information gain (EIG) and posterior predictive variance maximization (Variance) strategies. We found that BATCHIE with PDBAL performed as well or better than the other active learning strategies across all three benchmark datasets (Supplementary Fig. 15a–c). We also investigated the effect of interchanging the default PDBAL mean-squared distance (MSD) with a TI-aware distance (TID) and found that there was no significant difference in performance (Supplementary Fig. 15d–f). Given the comparable performance between the two distance metrics, we chose the simpler MSD as it does not rely on a specific choice of downstream objective and lends itself naturally to the interpretation of constructing a maximally informative dataset.

To evaluate the robustness of BATCHIE to different goals than therapeutic index, we implemented BATCHIE in the setting where the goal is solely to model synergy or antagonism (Supplementary Fig. 2a). We adapted our retrospective setup so that all single drug data was made available to the models before data collection and predictions were only over Bliss scores. We also implemented a synergy-only Bayesian hierarchical model, making this benchmark an example of the flexibility of BATCHIE to adapt to new designs and alternative models (Methods). Synergy detection is a challenging task as synergies are rare⁶. In the three benchmark datasets, only 0.12–1.19% of combinations are synergistic and 0.09–0.82% are antagonistic (Supplementary Fig. 2b). We again observed significant gains ($\max (p)=1{0}^{-7}$) in predictive accuracy on held-out data when comparing BATCHIE to the Random design baseline (Supplementary Fig. 2c). We also confirmed that the BATCHIE-trained model is better at detecting top synergy hits and top antagonism hits (Supplementary Fig. 2d,e). Across all three datasets, the BATCHIE model saves approximately 25K experiments compared to the Random strategy by round 15 with similar upward trends in each dataset (Supplementary Fig. 2f).

A prospective pediatric sarcoma study with BATCHIE

Current treatments for many pediatric sarcomas have unacceptably high failure rates, particularly for metastatic and recurrent presentations³⁴. Ewing sarcoma³⁵ (EWS), Rhabdomyosarcoma (RMS), and osteosarcoma³⁶ (OST) are amongst the most common pediatric sarcomas in need of improved treatments. We conducted a large-scale combination drug screen on pediatric cell lines, with a focus on pediatric sarcomas. The study covered 16 cell lines: 5 Ewing sarcoma lines (A673, MSKEWS-38338, MSKEWS-66647, SKNEP, TC-71), 5 osteosarcoma lines (MG-63, MSKOST-11890, SAOS-2, SJSA-1 U2OS), 1 rhabdomyosarcoma line (MSKRMS-12808), 3 other cancer cell lines (Kelly, MDA-MB-231, Wit49), and 2 non-cancer lines (RPE, BJ)(Fig. 4a). The non-cancer lines were included in the study to allow us to evaluate meaningful notions of TI, as high activity in a target cell line alone does not necessarily translate to clinical utility²². Mathematically, we defined therapeutic index to be the minimum viability of the control cell lines (i.e., RPE and BJ) minus the median viability of the target cell lines (e.g., all EWS lines). Thus, a high TI indicates a drug has high activity in the target lines and not in the control lines.

The drug library consisted of 206 drugs, both FDA-approved and investigational. In order to ensure adequate coverage of complementary mechanisms, the drug library was chosen to span a variety of targets (Fig. 4b). We ensured that the library included inhibitors of the most theoretically promising targets for Ewing sarcoma and osteosarcoma such as PARP, CDK4/6, and CD99^37,38 as well as commonly-used chemotherapy drugs. Each drug was tested at two concentrations: 0.1 μM (the low dose) and 1 μM (the high dose). All drugs on a single row or column plate were plated at the same concentration, allowing each drug combination to occur at 4 dose combinations (low-low, low-high, high-low, and high-high). Each active learning batch consisted of choosing 3 cell lines and 3 combination plates for each chosen cell line, resulting in 9 plates in total per batch. To control for potential artifacts from the plate design, including plate edge and dosing effects, one could use state-of-the-art compound transfer techniques³⁹. Our approach, starting in Phase II, was to use independent duplicates to filter out potential failed wells. All BATCHIE-collected plates had Z’-factors greater than 0.5, indicating reliable results across all experiments.

Fig. 4: Prospective study design and random validation results.

a Prospective study cell line library broken down by type. b Prospective study drug library broken down by mechanism of action. c Overview of prospective study: after 15 rounds of BATCHIE data collection, approximately 4% of possible combinations were observed. Created in BioRender. Tansey, W. (2024) BioRender.com/a40a996. d Observation breakdown by cell line and drug mechanism of action; p-values were computed using Pearson’s chi-square test where the null hypothesis is that experiments were sampled uniformly at random. Colors in the left panel match the corresponding type colors from (a). e Scatter plot of mean BATCHIE predictions v.s. observed viabilities on random validation data. Orange line indicates regression of predictions onto observations, and black line denotes the identity line. f Pearson correlation between predictions and observed viabilities, broken down by cell line, observation status, concentration and cancer type. Maximum p-value satisfies p < 10⁻¹⁵, with no corrections made for multiple comparisons. g ROC curve for synergy identification on random validation data. Synergy is defined here as having an observed Bliss score larger than 0.25. p-value was computed using a one-sided permutation test over 100K permutations. e, f ρ is Pearson’s ρ correlation coefficient, with p-values calculated under a two-sided alternative. Source data are provided as a Source Data file.

The screen was divided into two phases (Supplementary Fig. 3b). In phase I, we started with a focus on OST, using 4 OST lines and a single line each of EWS and RMS. We also included three non-sarcoma cancer cell lines and used a single control line (RPE). After 10 rounds of BATCHIE, we observed the model was converging, as measured by a diminishing improvement of cross-validation accuracy (Supplementary Fig. 3d). We, therefore, paused the screen and assessed the model’s predictions on the three sarcoma types. We observed over three times as many combinations predicted to have high therapeutic index in the EWS line compared to either the OST lines or the RMS line (Supplementary Fig. 3f). As a preliminary test, we selected three drugs (Clofarabine, Eltanexor, and Talazoparib) each of which was predicted to have high TI on the EWS lines at the low concentration when paired with another of the three at the low concentration. We experimentally validated that the three hits had TI in the 90th percentile of all observed combinations through round 10 (Supplementary Fig. 3g).

Since the phase I results suggested that our drug library may contain effective combinations particularly for EWS, in phase II we focused the screen on EWS. We added four EWS lines and removed the other non-sarcoma cancer cell lines. We also added an additional control line (BJ) to increase the robustness of our control set in TI estimates; a fifth OST line (MG-63) was also added. After the single initial seed batch for the newly added cell lines, the BATCHIE model quickly learned that the EWS lines were highly related. Two of the four EWS lines introduced in phase II had significant positive correlation with the phase I EWS line and none of the other phase II lines (Supplementary Fig. 3h). Phase II proceeded for five rounds of BATCHIE until we again observed the model’s cross-validation accuracy converging (Supplementary Fig. 3e). We then ended the adaptive portion of the screen and moved to the validation phase.

In total, we ran BATCHIE for 15 rounds of data collection, generating approximately 54K unique cell line, drug-dose pair combinations. As the full design space was approximately 1.4M possible experiments, BATCHIE explored approximately 4% of the total landscape (Fig. 4c). This dataset exhibited significant variability (p < 10⁻¹⁵) in the sampling frequencies with respect to both cell lines and drug classes (Fig. 4d), indicating that certain cell lines and drugs were more informative than others to the model. The correlations among predictions made by the final model reveal that it clearly learned to separate the EWS cell lines from the OST and control lines (Supplementary Fig. 4f). The OST lines were less homogeneous in the model predictions, as expected due to OST being a disease marked by chromothripsis which leads to potentially hundreds of random chromosomal translocations and thus high genomic heterogeneity compared to relatively stable EWS cancers⁴⁰.

At the drug level, the predictions of the model correlated strongly amongst drugs of similar mechanisms. Hierarchical clustering of predictions (Supplementary Fig. 4d) grouped targeted therapies (top left) distinctly from more broad-spectrum cytotoxic agents (bottom right). Among the targeted therapies, the predictions clearly distinguished androgen receptor inhibitors and MEK inhibitors. Within the broad-spectrum cytotoxic agents, the predictions identify two clades. The first of these contained taxanes and vinca alkaloids, drugs whose mechanisms of action (MoAs) all target mitosis. The majority of the drugs in the other clade, containing anthracycline topoisomerase inhibitors, nucleoside metabolic inhibitors, selective inhibitors of nuclear transport, and anthelmintics, were predominantly focused on targeting DNA replication. Across both groups, we observed that the finer-grained drug class structure was largely respected by the hierarchical clustering. In an orthogonal analysis, we projected high dose predictions to 2d using t-SNE and again observed drug clustering by MoA with the dominant spatial axis corresponding to drug potency (Supplementary Fig. 4e).

Validation of BATCHIE predictions on random unseen combinations

To evaluate the accuracy of the BATCHIE-trained model, we constructed a test set of randomly selected combination plates from the remaining unexplored experimental space. We randomly selected from among the experimental plates that had no overlap in any cell line, drug-dose pair combinations with the BATCHIE-collected data. One plate was selected for every cell line that was under investigation in phase II. One of the test plates (cell line MG-63) did not pass the quality control checks and was excluded from performance measurement.

The BATCHIE model predictions were highly accurate on the unseen validation data (Fig. 4e, Pearson’s ρ = 0.91, p < 10⁻¹⁵). The accuracy of the model was robust to stratification by cell line, previous observation status, drug concentration, and cancer type (Fig. 4f). Indeed, for 10 of the 11 cell lines, Pearson’s ρ was above 0.82 and was above 0.91 for 9 of the 11. The previous observation status of the drug on the cell line also appeared not to make a large difference, as the correlation remained above 0.91 regardless of whether one, both, or neither of the drugs had previously been observed on the chosen cell lines. We observed that there was dip in performance to ρ = 0.84 when restricting to the low-low doses. This decrease in performance however is confounded since, by chance, half of the low-low validation set was on the SJSA-1 cell line, the cell line on which BATCHIE performed worst. SJSA-1 is an OST line that shares little predictive similarity to the other OST lines (Supplementary Fig. 4f), which may explain its relative difficulty in the test set.

Similar to previous combination cell line screens^6,7, we found very few synergistic combinations in the random validation set. Of the 3465 observed combinations, only 13 (0.004%) resulted in a Bliss score larger than 0.25. Nevertheless, the BATCHIE model accurately identified these combinations (Fig. 4g), achieving an AUC of the ROC curve of 0.846 (p = 10⁻⁵).

BATCHIE discovers rational drug combinations for Ewing sarcoma

To validate BATCHIE’s ability to discover effective combinations, we used the BATCHIE model to identify combinations with an high expected therapeutic index. We ranked the drug combinations by looking at their predicted viabilities at low concentrations and taking the difference between the minimum predicted viability on the two non-cancer lines and the median viability on the OST and EWS lines. We found that no combinations were predicted to be robust across all OST lines such that the TI would be high. However, we did identify several drug combinations that were predicted to have high TI across a range of EWS lines. We selected 10 of the top-ranked candidates and collected a fine-grained dose-response matrix spanning 0.006 nM–400 nM via four-fold dilution (“Methods”), which included the low concentration combination (Fig. 5a). We also selected 13 negative control combinations that exhibited a large predicted differential effect for at least two cell lines but were not predicted to have a high TI over the five EWS lines.

Fig. 5: Prospective study validation of top hits.

a Pipeline for top hit selection and validation in the prospective study. The model fit on BATCHIE-collected data is used to simulate outcomes for drug combinations at the low (0.1 μM) concentration. Those simulated values are collected into confidence-rated predictions of TI values. The top hits are then selected for further in vitro experimentation, collecting observations over the full dose-response matrix. Created in BioRender. Tansey, W. (2024) BioRender.com/l79r044. b Observation status of selected top hits in BATCHIE-collected data. c Mean predictions and observed viabilities for selected top hits at 0.1 μM concentration. Pearson’s correlation ρ = 0.92 with p < 10⁻¹⁵ with a two-sided alternative. d Histogram of observed single model EWS TI values for combinations at 0.1 μM concentration in BATCHIE-collected data (gray, n = 659) and top predicted hits (orange, n = 100). Percentiles are drawn with respect to BATCHIE-collected data. e Observed AUCs with respect to the TI dose-response surface for selected top hits and not top hits. d, e p-values computed using a two-sided Mann-Whitney U-Test. Source data are provided as a Source Data file.

The top hit selections for EWS had not been observed in the training data at the low concentration for any cell line, and the general observation pattern was sparse (Fig. 5b). Nevertheless, at the low concentration there was a strong correlation (Pearson’s ρ = 0.92, p < 10⁻¹⁵) between the predicted viabilities and the observed viabilities (Fig. 5c). This accuracy at the viability level translated to the observed TIs being large, with the median TI score in the top hit predictions being higher than the 98th percentile of observed TI scores in the 54K training observations (Fig. 5d).

Although the top hits were chosen solely on the basis of their predicted TI at a specific concentration, we found that they generally exhibited high TI across a wide range of dose pairs. After computing the TI for each entry of the dose-response matrix, we calculated the area under the TI surface (2d curve) and observed that the top hits exhibited significantly higher AUC values than the reference combinations (p = 0.002, Fig. 5e).

The selected combinations exhibit biologically plausible rationales in Ewing sarcomas. Ewing sarcomas frequently exhibit EWS-FLI1 genomic fusions, which tend to interact with the DNA repair protein PARP-1⁴¹. Talazoparib is a PARP inhibitor, and combining PARP inhibitors with treatments that induce DNA damage has previously been shown to lead to cytotoxicity in preclinical Ewing sarcoma studies⁴². These observations have led to clinical trials combining PARP inhibitors with irinotecan (a topoisomerase 1 inhibitor) and temozolomide (an alkylating agent) for Ewing sarcoma and related cancers^43,44,45. Topotecan is a topoisomerase 1 inhibitor, mitomycin is an alkylating agent that cross-links complementary DNA strands, and epirubicin is an anthracycline that blocks the action of topoisomerase 2. Thus, these selected combinations with talazoparib may facilitate the utility of PARP inhibition by accelerating DNA damage.

Of the remaining drugs, cytarabine and GSK1324726A may act by reducing the overall abundance of the EWS-FLI1. This has been directly shown for cytarabine in vitro⁴⁶. On the other hand, GSK1324726A is a BET bromadine inhibitor, and it has been shown that BET bromadine proteins are required for EWS-FLI1 transcription^47,48. Clofarabine and cladribine are deamination-resistant analogs of deoxyadenosine, and as such interfere with DNA synthesis through incorporation into DNA^49,50. Both drugs have been shown to inhibit Ewing sarcoma growth in vitro by binding to C99, which is overexpressed in Ewing sarcoma⁵¹. EWS-FLI1 also suppresses SPRY1, a downstream feedback inhibitor of certain Ras-activating receptors⁵². Tipifarnib is a farnesyltransferase inhibitor that interferes with the Ras signaling pathway⁵³. Combining tipifarnib with drugs that induce DNA damage can be seen as targeting two separate downstream effects of EWS-FLI1.

To evaluate whether the results from our screen on established cell lines would potentially translate to the clinic, we tested six of the combination hits in an ex vivo study on two EWS patient-derived samples. Each hit was evaluated across a fine-grained grid spanning 0.02 nM–1 μM (Supplementary Fig. 5a). After linearly interpolating (in log-space) to align with the concentration grid applied to the previous EWS lines, we computed the TI scores for the individual ex vivo models. We found a robust TI response on both models, particularly for the top cell line hit topotecan and talazoparib (Supplementary Fig. 5b). The TI AUC scores were broadly comparable with the median EWS cell line TI AUC scores (Supplementary Fig. 5d). Similar to the results on EWS cell lines, we found that the ex vivo single model TI scores at the low dose were significantly higher than those found in the training set (Supplementary Fig. 5c, p < 10⁻¹⁴). Moreover, the median ex vivo TI score fell in the 96th percentile of TI scores in the training set.

Finally, we hypothesized that higher-order combinations could be discovered through analysis of the pairwise screens. To test this, we ran a triplet screen on the drugs talazoparib, topotecan, and mitomycin over a fine-grained grid spanning 0.1 nM–400 nM (see “Methods”, Supplementary Fig. 6a). Each pairwise combination of the three drugs appeared in our EWS top hits screen, suggesting that the triplet combination of the three would enable additional efficacy. At the single agent level, talazoparib was observed to have low activity with an IC50 nearly 40x higher than topotecan and 4x higher than mitomycin (Supplementary Fig. 6b). Pairwise combinations with talazoparib yielded higher TI for both mitomycin and talazoparib. However, isotonic interpolation analysis revealed that for many choices of cumulative concentration, the addition of mitomycin did not lead to substantial improvements over the combination of talazoparib and topotecan (Supplementary Fig. 6c). Instead, the optimal concentration strategy allocates more towards talazoparib as the total concentration increases but actually reduces the other two drugs (Supplementary Fig. 6d-g). This further supports preclinical evidence that PARP inhibitors sensitize EWS cells to DNA damage^54,55, with less of the two DNA-damaging drugs needed as talazoparib dosing increases. Overall, the inability of the triplet combination to meaningfully improve on the pairwise score indicates that simple pairwise additivity is insufficient to detect effective higher-order combinations.

BATCHIE discovers useful interactions between osteosarcomas and Aurora A kinase inhibitors

We next investigated the ability of BATCHIE to identify high TI combinations for OST lines. The BATCHIE model did not predict any drug pairs would have high TI values over a broad section of OST lines. This is in line with the observation that OSTs are more genomically diverse than EWS as OSTs often undergo chromothripsis leading to each tumor having a unique set of rearrangements^56,57. Instead of broadly active pairs, we used the BATCHIE model to identify six drugs that were predicted to have high TI values in some pairwise combination for at least one OST line: eltanexor, talazoparib, cladribine, cytarabine, alisertib, and trametinib.

We evaluated all $(\begin{array}{c}6\\ 2\end{array})$ combinations at all four possible high/low dose combinations across all five OST lines and our two control lines. The SJSA-1 cell line failed our quality control checks and was removed from our results. We observed a high concordance (Pearson’s ρ = 0.81, p < 10⁻¹⁵) between the predicted viabilities and the observed viabilities (Fig. 6a) on the remaining four lines and six drugs. We grouped each observation by degree of sensitivity or resistance and noted a clear separation between predicted sensitivity level and therapeutic index (Fig. 6b).

Fig. 6: Validation of top osteosarcoma hits.

a Scatter plot of predicted viability against observed viability on OST hit validation data, colored by cell line. ρ is Pearson’s ρ correlation; p-value computed under two-sided alternative. b Observed single cell line TI scores broken down by prediction status, where highly sensitive/sensitive/resistant/highly resistant correspond to TI scores in the range (0.2,1.0]/(0.1,0.2]/[0.2,−0.1)/[−1.0,−0.2), respectively (n = 61, 33, 32, 24); p-values were computed using a two-sided Mann-Whitney U-Test with no adjustments made for multiple comparisons. Box plot center lines denote means, box limits denote standard deviations, and whiskers denote extremal values. c, d Z-scores of RNA expression and CRISPR knockout scores from DepMap grouped by gene and colored by cell line. e Observed single cell line TI scores; entries correspond to largest mean observed TI score over 4 pairwise concentration combinations. Predicted effect designations are identical to those in (b). f Interpolated TI values for the drug triplet alisertib, talazoparib, trametinib on SJSA-1 and U2OS when the total concentration is held fixed at 1 μM; optimal concentration is denoted by a star. g Per-drug concentrations that optimize single cell line TI score as a function of total concentration. TZP = talazoparib, TRM = trametinib, ALS = alisertib. Source data are provided as a Source Data file.

For all pairwise combinations of alisertib, trametinib, and talazoparib, we observed high TI values on U2OS, and both alisertib/trametinib and alisertib/talazoparib achieved substantial TI on both MG-63 and SAOS-2. Alisertib is an Aurora A kinase (AURKA) inhibitor. Using data from DepMap^58,59, we investigated the mechanistic rationale behind alisertib as a component of an effective combination. We found that the MG-63, SAOS-2, SJSA-1, and U2OS lines all have high RNA expression levels of AURKA (Fig. 6c) and high sensitivity to CRISPR knockout (Fig. 6d). Related work has found AURKA inhibition generally and alisertib in particular, has been shown to increase the BRCAness of cells in vitro⁶⁰, where BRCAness is defined by defects in the homologous repair pathway that mimick the loss of BRCA1/2⁶¹. BRCAness has been shown to be correlated with increased sensitivity of OST lines to PARP inhibitors in vitro^62,63, making the combination of alisertib and talazoparib particularly rational.

Trametinib is from the class of MEK inhibitors, which have been shown to increase sensitivity to PARP inhibitors in RAS mutant cancer lines⁶⁴ and ovarian and pancreatic cancer models⁶⁵. This increased sensitivity to PARP inhibition is possibly due to the downregulation of BRCA2 expression and disruption of the homologous repair pathway⁶⁵, similar to the effects of AURKA inhibition. While the MEK-PARP approach has been investigated in these other cancers, we are not aware of the combination of MEK-AURKA being investigated in OST. Again using DepMap data, we observed that all lines in our panel are sensitive to MAP2K1/2 knockout (Fig. 6d) and overexpress MAP2K1 and/or MAP2K2 (Fig. 6d).

Motivated by the pairwise results, we hypothesized that a triplet combining alisertib and talazoparib with one of cladribine, topotecan, and trametinib would be rational. We included cladribine and topotecan as their mechanisms of DNA damage had been shown to lead to increased TI in EWS models in combination with talazoparib, and trametinib was included due to its efficacy in the pairwise combination screen. We evaluated each triplet over a fine-grained grid spanning 0.02 nM–1 μM. Isotonic interpolation analysis revealed that in all triplets, on all cell lines, and on most total concentrations, the concentration mixtures that achieved optimal TI scores were dominated by alisertib (Supplementary Figs. 7,  8a). Indeed, only for the highest total concentrations on MSKOST-11890 did we observe diminishing returns for alisertib (Supplementary Fig. 8a). However, we did observe that non-negligible proportions of talazoparib and trametinib made up the optimal mixtures on SJSA-1 and U2OS (Fig. 6f, g). We also found that the inclusion of higher concentrations of alisertib led to a more robust TI score as evidenced by the increased TI AUC scores for all combinations considered in conjunction with alisertib (Supplementary Fig. 8b, Spearman’s ρ = 0.3, p = 0.0036). Overall, the results provide evidence for high doses of alisertib combined with low-to-moderate doses of trametinib and talazoparib for a subset of OST patients.

Translation of alisertib-based therapy is challenging as it is currently discontinued due to failing its phase III trial. To evaluate the translatability of the mechanistic combination, we replicated the above triplet screen with LY329566, an investigational AURKA inhibitor, in place of alisertib. The results of this screen were similar to those with alisertib, with LY329566 generally dominating the optimal concentrations (Supplementary Figs. 9,  10a) and leading to more robust TI scores (Supplementary Fig. 10b). Also similar to the alisertib results, we found that on U2OS, non-negligible mixtures of LY329566, talazoparib, and trametinib led to improved TI scores (Supplementary Figs. 9,  10a).

Discussion

We introduced BATCHIE, an active learning platform that enables large-scale combination drug screens. We derived theory guaranteeing that the batches designed by BATCHIE will always be relatively informative. Retrospective simulations on data from previous large-scale combination screens confirmed strong empirical performance of BATCHIE. A prospective study on pediatric cancer cell lines showed BATCHIE screens can enable the rapid discovery of efficacious and synergistic drug combinations within libraries of hundreds of drugs.

One natural question is whether large-scale adaptive combination screens are even necessary. Ideally, biological knowledge of the disease of interest and the mechanisms of action of the individual drugs would suffice to enable scientists to rationally design combination agents. Unfortunately, most diseases are heterogeneous across patients and most drugs have complicated mechanisms of action that include off-target effects. For instance, we have found that drugs in GDSC² are twice as likely to correlate best with a drug outside their mechanistic class, compared to a drug within their class (Supplementary Fig. 14a, b). Further, analysis of an expert-designed non-small cell lung cancer (NSCLC) combination panel^66,67 showed that in 9 out of 10 pairwise drug classes in the NCI ALMANAC, less than half of NSCLC lines were optimally targeted by the expert-chosen combinations (Supplementary Fig. 14c). The expert panel also performs suboptimally in other cancer cell lines: in 26 of 27 pairwise drug combination classes in GDSC², less than half of the cell lines were optimally targeted by the expert panel drugs (Supplementary Fig. 14d). These results suggest that picking the best drugs within a given class is challenging. Overall, we see these results as motivating the need to conduct combination screens to obtain empirical evidence that can be buttressed with expert interpretation and clinical experience.

The probabilistic modeling required in BATCHIE is modular. Our algorithm is able to take any Bayesian model and design optimal batches with respect to that model. We evaluated two different hierarchical models, one focused on viability and another on synergy prediction. BATCHIE showed performance gains with both models, but each could be improved with more sophisticated modeling, possibly taking advantage of genomic and chemoinformatic features. Any modeling improvements that lead to predictive performance gains would be complementary to the efficiency gains from BATCHIE-designed screens. Thus, as new predictive models continue to be developed, they can be readily integrated into BATCHIE for improved screening efficiency.

Both our retrospective and prospective experiments were conducted on cancer cell lines. Immortalized 2d cell lines have a number of well-understood limitations, and better 3d models such as spheroids and organoids are rapidly being developed to replace them in drug screening⁶⁸. BATCHIE screens transfer seamlessly to the 3d setting and are arguably more useful here since 3d models tend to have longer doubling times and require more expensive equipment and media, exacerbating the need for efficient screens.

We have focused our implementation on pairwise drug viability screens as they are the most common in the combination literature. However, BATCHIE can be readily adapted to screen the drug interactome for any measurable outcome where experiments are batched. New technologies are emerging that enable a wide range of phenotypic measurements, such as proteome-wide drug effects⁶⁹, but are currently limited to single-agent screens. Multiplexed CRISPR perturbation screens⁷⁰ enable combinatorial screens but require specifying a small library of genes. BATCHIE could be used to design optimal libraries in order to efficiently discover synthetic lethal combinations.

Drug combinations represent an increasingly important therapeutic strategy in cancer and other diseases. We expect that approaches such as BATCHIE will be critical to overcoming the combinatorial explosion in the experimental design space as preclinical screens grow to larger libraries and higher-order combinations like triplets and quadruplets. In doing so, these methods will play an integral role in enabling the discovery new combination therapies.

Methods

Ethical statement

This study complies with all relevant ethical regulations. MSKCC patients provided informed and signed consent and enrolled onto a tumor profiling research study (Genomic profiling in cancer patients; NCT01775072) approved by the MSKCC Institutional Review Board under protocols #12-245, #06-107, and #17-387 to enable tumor cell line generation. PDX tumor models were generated in compliance with MSKCC Institutional Animal Care and Use Committee protocol #16-08-011, which requires that mice are euthanized before tumors reach 2000 mm³ in volume or 2 cm in the largest linear dimension.

Bayesian tensor factorization model for predicting combination drug response

We use a hierarchical generative model that simultaneously models both single and combination drug observations. We treat each drug at each dose individually as a single drug-dose. Observations are modeled as

$${y}_{ik}^{(n)} \sim {{{\mathcal{N}}}}\left({\mu }_{ik},1/\tau \right)$$

(2)

$${y}_{ijk}^{(n)} \sim {{{\mathcal{N}}}}\left({\mu }_{ik}+{\mu }_{jk}+{\Delta }_{ijk},1/\tau \right)$$

(3)

$$\tau \sim \,{\mbox{Gamma}}\,(1.1,1.1)$$

(4)

$${\mu }_{ik}={\sum}_{t=1}^{d}{v}_{1,t}^{(i)}{u}_{t}^{(k)}+{v}_{0}^{(i)}+{u}_{0}^{(k)}+\alpha$$

(5)

$${\Delta }_{ijk}={\sum}_{t=1}^{d}{v}_{2,t}^{(i)}{v}_{2,t}^{(j)}{u}_{t}^{(k)}-{u}_{0}^{(k)}-\alpha$$

(6)

where ${y}_{ik}^{(n)}$ is the n-th logit-transformed viability measurement of applying drug-dose i to cell line k. Similarly, ${y}_{ijk}^{(n)}$ is the logit-transformed viability measurement of applying the combination of drug-doses i and j to cell line k. We also have that τ is the global precision of the observations, μ_ik is the mean response of applying i to k, Δ_ijk is the combination effect of i and j applied to k, and α is the global mean of all the observations. ${{{{\boldsymbol{u}}}}}^{(k)}\in {{\mathbb{R}}}^{d}$ is the embedding of cell line k with the following generative process:

$${u}_{t}^{(k)} \sim {{{\mathcal{N}}}}\left(0,1/{\tau }_{t}\right)$$

(7)

$${\tau }_{t} \sim {\prod}_{s=1}^{t}{\gamma }_{s}$$

(8)

$${\gamma }_{s} \sim \,{\mbox{Gamma}}\,({a}_{s},1),$$

(9)

where ${{{\boldsymbol{\tau }}}}\in {{\mathbb{R}}}^{d}$ is the vector of precisions for each cell line embedding coordinate, and it follows a Gamma process prior with elements γ_s. The hyper-parameters of the Gamma process are chosen as a₁ = 2 and a_s = 3 for s ≥ 2.

The vector ${{{{\boldsymbol{v}}}}}_{\ell }^{(i)}\in {{\mathbb{R}}}^{d}$ is the order ℓ (for ℓ ∈ {1, 2}) embedding of drug-dose i with the following Horseshoe prior, also known as a local shrinkage model⁷¹:

$${v}_{\ell,t}^{(i)} \sim {{{\mathcal{N}}}}\left(0,{\lambda }_{\ell,t}^{(i)}\right)$$

(10)

$${\lambda }_{\ell,t}^{(i)} \sim {{\mbox{Cauchy}}}^{+}(0,1.1)$$

(11)

where ${\lambda }_{\ell,t}^{(i)}$ encourages sparsity and Cauchy⁺ is the Cauchy distribution truncated to the positive real numbers.

Also included in the model are offsets ${v}_{0}^{(i)}\in {\mathbb{R}}$ (for drug-dose i) and ${u}_{0}^{(k)}\in {\mathbb{R}}$ (for cell line k). These follow the generative process:

$${v}_{0}^{(i)} \sim {{{\mathcal{N}}}}\left(0,{\lambda }_{0}^{(i)}\right)$$

(12)

$${\lambda }_{0}^{(i)} \sim {{\mbox{Cauchy}}}^{+}(0,1.1)$$

(13)

$${u}_{0}^{(k)} \sim {{{\mathcal{N}}}}\left(0,1/{\tau }_{0}\right)$$

(14)

$${\tau }_{0} \sim \,{\mbox{Gamma}}\,(1.1,1.1),$$

(15)

where ${\lambda }_{0}^{(i)}$ encourages sparsity and τ₀ are precisions.

To fit this model, we utilize Gibbs sampling to sample from the posterior distribution, since all of the relevant priors are conditionally conjugate. For the prospective study, the Gibbs samplers were run for 20K steps. Our implementations were done in Python, making use of the numpy⁷² and scipy⁷³ packages.

Bayesian model for predicting combination drug synergy

For the pure synergy modeling setting, we use the following model.

$${s}_{ijk}^{(n)} \sim {{{\mathcal{N}}}}\left({\mu }_{ijk},1/\tau \right)$$

(16)

$${\mu }_{ijk}={\sum}_{t=1}^{d}{v}_{t}^{(i)}{v}_{t}^{(j)}{u}_{t}^{(k)}$$

(17)

$$\tau \sim \,{\mbox{Gamma}}\,(1.1,1.1)$$

(18)

Here, ${s}_{ijk}^{(n)}$ is the n-th synergy score between drug-doses i and j on cell line k. It is calculated as ${s}_{ijk}^{(n)}={\bar{v}}_{ik}{\bar{v}}_{jk}-{v}_{ijk}^{(n)}$, where ${v}_{ijk}^{(n)}$ is the n-th observed viability of applying i and j to k, and ${\bar{v}}_{ik}$ is the average observed viability of applying i to k. When ${\bar{v}}_{ik}$ is not available because drug-dose i was not tested directly on k, then it is imputed by linear interpolation (in log-concentration space) of neighboring concentrations of the same drug.

μ_ijk is the mean synergy value of applying i and j to k and τ is global observational precision, and ${{{{\boldsymbol{u}}}}}^{(k)}\in {{\mathbb{R}}}^{d}$ is the embedding of cell line k that follows the same prior as its counterpart in the previous model:

$${u}_{t}^{(k)} \sim {{{\mathcal{N}}}}\left(0,1/{\tau }_{t}\right)$$

(19)

$${\tau }_{t} \sim {\prod}_{s=1}^{t}{\gamma }_{s}$$

(20)

$${\gamma }_{s} \sim \,{\mbox{Gamma}}\,({a}_{s},1),$$

(21)

where ${{{\boldsymbol{\tau }}}}\in {{\mathbb{R}}}^{d}$ is the vector of precisions for each cell line embedding coordinate, and it follows a Gamma process prior with elements γ_s. The hyper-parameters of the Gamma process are chosen as a₁ = 2 and a_s = 3 for s ≥ 2.

The drug-dose embeddings ${{{{\boldsymbol{v}}}}}^{(i)}\in {{\mathbb{R}}}^{d}$ also follow the same prior as the counterparts in the previous model:

$${v}_{\ell,t}^{(i)} \sim {{{\mathcal{N}}}}\left(0,{\lambda }_{\ell,t}^{(i)}\right)$$

(22)

$${\lambda }_{\ell,t}^{(i)} \sim {{\mbox{Cauchy}}}^{+}(0,1),$$

(23)

where ${{{{\boldsymbol{\lambda }}}}}_{\ell }^{(i)}\in {{\mathbb{R}}}^{d}$ is a vector of scales for the embedding of drug-dose i.

This model is also fit via Gibbs sampling.

Active learning algorithm

Our active learning procedure is a generalization of an optimal active learning procedure called Diameter-based Active Learning (DBAL)^26,27. Our approach applies to general probabilistic models that consist of an experimental space ${{{\mathcal{X}}}}$, an outcome space ${{{\mathcal{Y}}}}$, and a set of parameters Θ. We assume that the likelihoods factorize so that for a sequence $({x}_{1},{y}_{1}),\ldots,({x}_{n},{y}_{n})\in {{{\mathcal{X}}}}\times {{{\mathcal{Y}}}}$ and parameter θ ∈ Θ, we have

$${p}_{\theta }({y}_{1},\ldots,{y}_{n}| {x}_{1},\ldots,{x}_{n})={\prod}_{i=1}^{n}{p}_{\theta }({y}_{i}| {x}_{i}).$$

(24)

A plate of experiments is a sequence P = (x₁, …, x_b) of experiments ${x}_{i}\in {{{\mathcal{X}}}}$. For a corresponding set of outcomes (y₁, …, y_b), we use the shorthand y_P to denote the sequence and ${p}_{\theta }({y}_{P}| P)={\prod }_{i=1}^{b}{p}_{\theta }({y}_{i}| {x}_{i})$ to denote the likelihood of the outcome sequence for a given plate.

In the combination drug setting, the parameters θ include all of the parameters from the tensor factorization model, i.e., the μ_ijk’s, the ${v}_{\ell,t}^{(i)}$’s, etc. The experiment space consists of triples (i, j, k) and pairs (i, k) where i and j are drug-doses and k is a cell line. Outcomes in this setting are logit-transformed viabilities, and so the outcome space corresponds to the reals, i.e., ${{{\mathcal{Y}}}}={\mathbb{R}}$.

Given a prior distribution π over Θ and a set of observations $({x}_{1},{y}_{1}),\ldots,({x}_{n},{y}_{n})\in {{{\mathcal{X}}}}\times {{{\mathcal{Y}}}}$, the posterior distribution over Θ is given by

$${\pi }_{n}(\theta )=\frac{\pi (\theta ){\prod }_{i=1}^{n}{p}_{\theta }({y}_{i}| {x}_{i})}{{\int}_{\Theta }\pi (d{\theta }^{{\prime} }){\prod }_{i=1}^{n}{p}_{{\theta }^{{\prime} }}({y}_{i}| {x}_{i})}.$$

(25)

Let d( ⋅ , ⋅ ) be a bounded, non-negative, symmetric distance over Θ. The goal of DBAL-style active learning procedures is to run batches of experiments that will rapidly lead to a posterior π_n with small average diameter:

$$\,{\mbox{avg-diam}}\,({\pi }_{n})={{\mathbb{E}}}_{\theta,{\theta }^{{\prime} } \sim {\pi }_{n}}\left[d(\theta,{\theta }^{{\prime} })\right].$$

(26)

Given a plate P and a current posterior distribution π_n, our active learning strategy assigns an ideal score to each plate:

$${s}_{n}(P)={{\mathbb{E}}}_{\theta,{\theta }^{{\prime} },{\theta }^{\star } \sim {\pi }_{n}}\left[d(\theta,{\theta }^{{\prime} }){L}_{{\theta }^{\star }}(\theta,{\theta }^{{\prime} };P){e}^{2{H}_{{\theta }^{\star }}(P)}\right],$$

(27)

where

$${L}_{{\theta }^{\star }}(\theta,{\theta }^{{\prime} };P)={{\mathbb{E}}}_{{y}_{P} \sim {p}_{{\theta }^{\star }}(\cdot | P)}\left[d(\theta,{\theta }^{{\prime} }){p}_{\theta }({y}_{P}| P)\right]$$

(28)

and H_θ(P) is the Shannon entropy of the plate P under θ, i.e.,

$${H}_{\theta }(P)=\mathop{\sum}_{{x}_{i}\in P}{{\mathbb{E}}}_{{y}_{i} \sim {p}_{\theta }(\cdot | {x}_{i})}\left[\log \frac{1}{{p}_{\theta }({y}_{i}| {x}_{i})}\right].$$

(29)

In the case of the normal likelihood (among others), one can explicitly compute the functions ${L}_{{\theta }^{\star }}(\theta,{\theta }^{{\prime} };P)$ and H_θ(P).

Since computing s_n(P) requires integrating over the posterior, we cannot hope to do so directly. Instead, we compute a Monte Carlo approximation of s_n(P) by sampling θ₁, …θ_m ∼ π_n and computing

$${\widehat{s}}_{n}(P)=\frac{1}{\left(\begin{array}{c}m\\ 3\end{array}\right)}{\sum}_{i < j < k}d({\theta }_{i},{\theta }_{j}){L}_{{\theta }_{i}}({\theta }_{j},{\theta }_{k};P){e}^{2{H}_{{\theta }_{i}}(P)}.$$

(30)

This sum can be further approximated by sub-sampling triples (i, j, k) and computing the Monte Carlo average only over the selected triples.

Armed with the estimator ${\widehat{s}}_{n}(P)$, our active learning procedure is to enumerate a set of candidate plates P₁, …, P_T and select the plate ${P}_{{i}^{\star }}$ with the lowest score ${\widehat{s}}_{n}({P}_{{i}^{\star }})$. In the supplement, we show that this strategy leads to provably near-optimal guarantees. Specifically, we prove that the convergence rate of BATCHIE is upper-bounded by a function of a problem-specific parameter, called the splitting index, that determines the complexity of the learning problem in the sense that any active learning strategy, regardless of computational power, must have a convergence rate that is lower-bounded by this same splitting index.

To select a batch of plates, we select sequentially. We first select ${P}_{{i}_{1}^{\star }}$ as the plate minimizing ${\widehat{s}}_{n}({P}_{{i}_{1}^{\star }})$. Having selected plates ${P}_{{i}_{1}^{\star }},\ldots,{P}_{{i}_{b}^{\star }}$, we select plate ${P}_{{i}_{b+1}^{\star }}$ as the plate minimizing ${\widehat{s}}_{n}([{P}_{{i}_{1}^{\star }},\ldots,{P}_{{i}_{b+1}^{\star }}])$, where $[{P}_{{i}_{1}^{\star }},\ldots,{P}_{{i}_{b+1}^{\star }}]$ is the plate formed by concatenating the constituent plates ${P}_{{i}_{1}^{\star }},\ldots,{P}_{{i}_{b+1}^{\star }}$. Observe that this is equivalent to selecting ${P}_{{i}_{b+1}^{\star }}$ conditioned on having already selected ${P}_{{i}_{1}^{\star }},\ldots,{P}_{{i}_{b}^{\star }}$. This iterative strategy of optimization has been shown to enjoy strong theoretical guarantees^74,75.

Empirical evaluation of PDBAL

PDBAL was evaluated on several probabilistic regression settings in which the model was parameterized by a coefficient vector $\theta \in {{\mathbb{R}}}^{d}$. The regression models include linear regression with homoscedastic Gaussian noise, logistic regression, Poisson regression with the exponential link function, and Beta regression under the mean parameterization⁷⁶:

$${P}_{\theta }(y;x)=\,{\mbox{Beta}}\,(y| \phi \mu,\phi (1-\mu )),$$

(31)

where $\mu=\frac{1}{1+{e}^{-\langle {{{\boldsymbol{x}}}},{{{\boldsymbol{\theta }}}}\rangle }}$, ${{{\boldsymbol{x}}}}\in {{\mathbb{R}}}^{d}$ is the feature vector, and ϕ > 0 is a fixed constant. For all experiments, we used a normal prior distribution on ${{{\boldsymbol{\theta }}}}\in {{\mathbb{R}}}^{d}$ with identity covariance. For the linear regression setting, the posterior was computed in closed form. The other models were implemented in PyStan⁷⁷, and posterior samples were generated by the No-U-Turn Sampler (NUTS)⁷⁸.

We considered five objectives, specified by a given distance:

• First coordinate: $d({{{\boldsymbol{\theta }}}},{{{{\boldsymbol{\theta }}}}}^{{\prime} })={\mathbb{1}}[\,{\mbox{sign}}({\theta }_{1}) \, \ne \, {\mbox{sign}}\,({\theta }_{1})]$.

• Max coordinate: $d({{{\boldsymbol{\theta }}}},{{{{\boldsymbol{\theta }}}}}^{{\prime} })={\mathbb{1}}[\arg {\max }_{i}| {\theta }_{i}| \, \ne \, \arg {\max }_{i}| {\theta }_{i}| ]$.

• Euclidean: $d({{{\boldsymbol{\theta }}}},{{{{\boldsymbol{\theta }}}}}^{{\prime} })=\parallel {{{\boldsymbol{\theta }}}}-{{{{\boldsymbol{\theta }}}}}^{{\prime} }{\parallel }_{2}$.

• Kendall’s tau: $d({{{\boldsymbol{\theta }}}},{{{{\boldsymbol{\theta }}}}}^{{\prime} })=\frac{1}{2}(1-\tau (| {{{\boldsymbol{\theta }}}}|,| {\theta }^{{\prime} }| ))$, where $\tau (| \theta |,| {\theta }^{{\prime} }| )$ is Kendall’s tau correlation of the pairs $(| {\theta }_{1}|,| {\theta }_{1}^{{\prime} }| ),\ldots,(| {\theta }_{d}|,| {\theta }_{d}^{{\prime} }| )$.

• Influence: $d({{{\boldsymbol{\theta }}}},{{{{\boldsymbol{\theta }}}}}^{{\prime} })={{\mbox{Pr}}}_{{{{\boldsymbol{x}}}}}\left(\, {{\mbox{sign}}}\,(\langle {{{{\boldsymbol{x}}}}}_{1:d/2},{{{{\boldsymbol{\theta }}}}}_{1:d/2}\rangle ) \, \ne \, \, {{\mbox{sign}}}\,(\langle {{{{\boldsymbol{x}}}}}_{1:d/2},{{{{\boldsymbol{\theta }}}}}_{1:d/2}^{{\prime} }\rangle )\right)$, where x_1:d/2 denotes restriction of the vector x to its first d/2 coordinates.

We compared against 3 baselines: Random, Var, and EIG. Random chooses uniformly at random from the pool of available queries. Var chooses queries based on maximizing the posterior predictive variance:

$${{\mbox{var}}}_{y \sim {\pi }_{n}({{{\boldsymbol{x}}}})}(y)={{\mathbb{E}}}_{{y}_{ \sim }{\pi }_{n}({{{\boldsymbol{x}}}})}[{y}^{2}]-{{\mathbb{E}}}_{{y}_{ \sim }{\pi }_{n}({{{\boldsymbol{x}}}})}{[y]}^{2}.$$

(32)

EIG uses the BALD formulation⁷⁹ to maximize expected mutual information between the outcome and the parameter θ:

$${{{\mathcal{I}}}}(y;{{{\boldsymbol{\theta }}}}| {{{\boldsymbol{x}}}},{\pi }_{n})={H}_{{\pi }_{n}}({{{\boldsymbol{x}}}})-{{\mathbb{E}}}_{{{{\boldsymbol{\theta }}}} \sim {\pi }_{n}}[{H}_{\theta }({{{\boldsymbol{x}}}})],$$

(33)

where ${H}_{{\pi }_{n}}({{{\boldsymbol{x}}}})$ is entropy of the posterior predictive distribution at x. For linear regression, this was computed in closed form, while for the other settings, it was approximated numerically.

In all experiments, the ground truth θ^⋆ was drawn uniformly from vectors of length 2. Data points were drawn from a mixture distribution: with probability 1 − p, they were drawn uniformly from vectors of length 1, and with probability p, each coordinate was set to 0 with probability 1/d and the remaining coordinates drawn so the resulting vector has length 1. For some objectives, this sparse distribution is particularly informative. In all simulations, d = 10 and p = 1/10.

Retrospective simulations

Data retrieval and preparation

We downloaded the ALMANAC⁵, GDSC²⁶, and MERCK⁷ datasets from their respective sources (see Data Availability). For the MERCK dataset, viabilities were provided. For the ALMANAC dataset, PercentGrowth values were provided. We converted these to viability scores using the formula

$$\begin{array}{r}\,{\mbox{viability}}=\frac{{\mbox{PercentGrowth}}\,+100}{200}.\end{array}$$

(34)

For the GDSC² dataset, well intensity values were provided, along with high control and low control intensities. These were converted to viability scores using the same formula as in the prospective study. For all studies, replicates were averaged to produce a single viability measurement for all recorded cell line, drug-dose 1, drug-dose 2 triplets. Drug-doses that were not present in combination experiments were dropped.

Plate and random holdout construction

From the viability measurements, we constructed synthetic plates to closely match the plates used in the prospective sarcoma study. Drug-doses were randomly divided into groups of 20, and initial plates we constructed by considering each cell line c and each pair of groups $g,{g}^{{\prime} }$ and collecting all measurements satisfying that the cell line is in c, one of the drug-doses is in g, and the other drug-dose is in ${g}^{{\prime} }$. Due to the biased sampling of drug combinations in the three experimental designs, this resulted in plates of unequal sizes. We corrected for this by greedily merging the two smallest plates within a cell line until a minimum size threshold was met. We then performed a single pass through the plates for each cell line and merged the largest plate with the smallest plate. To align the plate sizes, we selected a threshold and dropped all plates smaller than the threshold and dropped observations from plates larger than the threshold until they had the same number of observations. The threshold was chosen to minimize the total number of observations removed. In each simulation, a random holdout set was created by subsampling 10% of the observations from every plate.

Experimental design

For a given dataset and plate construction, we first created an initial covering plate by randomly selecting observations to greedily cover the cell lines and drug-doses. Given the same dataset, set of plates, and initial covering plate, we ran both the Random and BATCHIE methods. At each round of data collection, the methods picked K cell lines and 3 plates per cell line. K was selected to be 1/10th the number of cell lines in the dataset, rounded down (K = 6 for ALMANAC, K = 12 for GDSC², and K = 3 for MERCK).

Posterior inference

At each round, before selecting plates, 200 MCMC samples were drawn from the current posterior using 5 parallel chains, each with a burn-in period of 2000 steps and a thinning factor of 40. These samples were then used to evaluate accuracy on the holdout set and, for BATCHIE, used to select the next set of plates to observe. For each dataset, we ran the plate construction and simulation using 25 different random seeds.

Cell line restrictions

For the cell line restriction simulations, cell lines were subsampled uniformly at random. The number of cell lines chosen per round was adjusted accordingly (1/10th of the number of selected cell lines). The number of plates per cell line in each round remained 3.

Metrics

For each dataset construction, we trained a model using the full training set, i.e., everything except for the holdout validation set, by drawing 200 MCMC samples from the posterior using 5 parallel chains, each with a burn-in period of 2000 steps and a thinning factor of 40. Given a holdout set of experiment/viability pairs $({x}_{1},{y}_{1}),\ldots,({x}_{m},{y}_{m})\in {{{\mathcal{X}}}}\times [0,1]$, a fully trained predictor ${f}_{{{{\rm{full}}}}}:{{{\mathcal{X}}}}\to [0,1]$, and a candidate predictor $f:{{{\mathcal{X}}}}\to [0,1]$, the normalized accuracy is given by the ratio of R² scores:

$$\, {{\mbox{Normalized}}} \, {{\mbox{accuracy}}} (\;f; \,{f}_{{{{\rm{full}}}}})=\frac{{R}_{n}^{2}(\;f)}{{R}_{n}^{2}(\;{f}_{{{{\rm{full}}}}})},$$

(35)

where

$${R}_{n}^{2}(f)=1-\frac{{\sum }_{i=1}^{n}{({y}_{i}-f({x}_{i}))}^{2}}{{\sum }_{i=1}^{n}{({y}_{i}-\bar{y})}^{2}}$$

(36)

and $\bar{y}=\frac{1}{n}\mathop{\sum }_{i=1}^{n}{y}_{i}$ is the empirical mean of observed viabilities.

Efficiency gains/batches saved and experiments saved were computed by calculating the holdout R² of the BATCHIE-trained model (at round 15, unless otherwise specified) and then searching for the earliest round at which a Random-trained model had comparable performance. BATCHIE and Random models were only compared within the same random seed, and therefore only on the same dataset and plate set construction.

As none of the retrospective datasets have control/non-cancer lines, we calculated TI values by taking all pairwise differences across cell lines. To calculate the Average TI @ Top 20, we computed all TI values from the models’ mean viability predictions, selected the top 20 predicted TI hits, and averaged the corresponding ground truth TI values. To calculate the Top hit AUC, we computed the AUC of the ROC curve, where the ground truth labels correspond to whether or not the TI value occurs in the top 99th percentile of TIs and the predicted values are the predicted TIs formed from the models’ mean viability predictions.

Baseline comparisons

In addition to the Random baseline, which chooses plates uniformly at random subject to the experimental design constraints, we also compared against strategies that maximize the expected information gain (EIG) and posterior predictive variance (Variance). We used the same formulations of these strategies as in the regression comparison setting to calculate the scores of individual wells and averaged across wells to score the corresponding plate.

PDBAL distances

The default distance we use for PDBAL with normal likelihoods is the mean-squared distance over predicted mean viabilities (MSD). Given two sequences of mean viability predictions over the same set of wells (y₁, …, y_n) and $({y}_{1}^{{\prime} },\ldots,{y}_{n}^{{\prime} })$, the MSD is calculated as

$$\frac{1}{n}\mathop{\sum }_{i=1}^{n}{({y}_{i}-{y}_{i}^{{\prime} })}^{2}.$$

(37)

For the retrospective datasets, the prediction set is the set of all cell line, drug-dose 1, drug-dose 2 triplets covered in the dataset. For the prospective study, the prediction set is the set of all possible triplets spanned by the cell lines and drug-doses in the dataset.

For the TI-aware distance (TID), we transform mean viability predictions to TI predictions by computing all pairwise differences across cell lines. For two sets of TI predictions, (t₁, …, t_n) and $({t}_{1}^{{\prime} },\ldots,{t}_{n}^{{\prime} })$, we select the top K indices from each to get (i₁, …, i_K) and $({i}_{1}^{{\prime} },\ldots,{i}_{K}^{{\prime} })$. The TID is then given by

$${{{{\rm{max}}}} \left( \frac{1}{K} \mathop{\sum}_{k=1}^{K} {{t}_{ik}} - {{t}_{{i}_{k}^{\prime}}},\, \frac{1}{K} {\sum}_{k=1}^{K} {{t}_{{i}_{k}^{\prime}}^{\prime} } - {{t}_{ik}^{\prime} }\right)}$$

(38)

In our simulations, we chose K = 20.

Pediatric sarcoma combination screen

Study design

The prospective sarcoma study consisted of 15 rounds of data collection. At each round, different subsets of cell lines were available based on doubling time and the extent to which they had been used in previous rounds (Supplementary Fig. 3c). Adaptive batches were constrained to 3 combination plates each for 3 available cell lines. In the first round and the eleventh round, unseen cell lines were introduced and the plates were selected to greedily cover unseen drug-doses and drug-dose combinations over the new cell lines. In the remaining rounds, plates were selected using the BATCHIE active learning procedure outlined above with the constraint that 3 separate cell lines be chosen, leading to 9 selected plates in total.

In rounds 1–10, each plate was run singly. During the phase I validation, we identified that BATCHIE was sensitive to undetectable random well failures producing corrupted data. To address this, in rounds 11–15, plates were run in duplicate and quality control checks flagged wells whose duplicates differed by more than 0.5 in viability.

Combination plates

Supplementary Fig. 3a shows the general schematic for our combination plate setup. Plates consisted of 384 wells with 16 rows and 24 columns. For row plates, 15 of the rows consist of a single drug applied to each of the corresponding column wells at a particular concentration, except two columns that corresponded to high control and low control. The remaining row of the row plate was filled with Dimethylsulfoxide (DMSO), also with two control columns. For column plates, 21 of the columns consist of a single drug applied to each of the corresponding row wells at a particular concentration. The remaining three columns are the high and low control columns (aligned to spatially match the corresponding high/low columns in the row plate) and a column filled only with DMSO.

When a row and column plate are combined, the resulting combination plate contains 15 × 21 = 315 wells that correspond to all combinations of the constituent drug-doses, 15 + 21 = 36 wells that correspond to all single drug-doses, 15 high-control wells, and 15 low-control wells.

Our drug library consisted of 206 drugs, with four of the drugs duplicated to allow for the resulting 210 drugs to be evenly divided over 14 row plates and 10 column plates. Each row and column plate was constructed at 2 different doses: 0.1 μM and 1 μM, leading to a total of 28 row plate choices and 20 column plate choices.

Finally, a full plate consists of a cell line, a row plate, and a column plate. Viabilities for a non-control well w are calculated as

$$\,{{\mbox{viability}}} \, ( {{\mbox{well}}}\,w)=\frac{ {{\mbox{count}}} \, ({{\mbox{well}}} \, w)- {{\mbox{average}}} \, {{\mbox{low}}} {\mbox{-}} {{\mbox{control}}} \, {{\mbox{count}}}} {{{\mbox{average}}} \, {{\mbox{high}}} {\mbox{-}} {{\mbox{control}}} \, {{\mbox{count}}} {-} {{\mbox{average}}} \, {{\mbox{low}}}{\mbox{-}}{{\mbox{control}}} \,{{\mbox{count}}}}$$

(39)

where count (well w) is the reading at well w and average high/low-control counts are the averages of the readings at the corresponding high/low-control wells.

Therapeutic index

We define the in vitro therapeutic index (TI) to be a differential score that compares two groups of viabilities: one for the target set of cell lines and one for the control set. A high TI corresponds to low viability for most target cells and high viability for all control cells. To calculate TI, we take the difference between the minimum viability on the control lines and the median viability on the target lines:

$$\, {{\mbox{TI}}} \,(i,\, j)={{\mbox{minimum}}} \, {{\mbox{V}}}\, (i,j;C)\, {{\mbox{for}}} \, C \in \, {{\mbox{Controls}}} - {{\mbox{median}}} {{\mbox{V}}} \, (i,j;T) \, {{\mbox{for}}}\, T \in \, {{\mbox{Target}}}\,.$$

(40)

where V(i, j; N) is the viability of drug-dose pair (i, j) on cell line N.

Model visualizations

To determine if BATCHIE discerned the relative mechanistic similarities and differences of the drugs tested in an unsupervised manner, we labeled each drug assessed with simplified mechanisms of action (MoAs) and used low-rank approximation and dimensionality reduction to visualize resulting clusters. We used MoAs from the Genomics of Drug Sensitivity in Cancer (GDSC) database⁸⁰ to annotate the 98 drugs assessed in both our study and the GDSC. For the remaining 112 drugs in our library that were not in the GDSC, we manually added MoAs that conformed to the GDSC categories. Mechanisms were adjudicated according to drugs’ International Nonproprietary Name (INN) suffixes, documented mechanisms in the literature, and U.S. Food and Drug Administration (FDA) package inserts for approved molecules. All drugs were categorized as belonging to one of nineteen MoA categories.

Predicted viabilities of the drugs administered as monotherapies were logit-transformed and normalized to a zero-one range. Non-negative matrix factorization (NMF) was performed using the Python package scikit-learn’s NMF module at a random initialization⁸¹. The decomposed feature matrix represented latent embeddings of the drugs, where each dosage and drug combination was treated as a unique entry, and the coefficient matrix represented latent embeddings of the cell lines tested. By assessing the mean squared error of the resulting low-rank approximation, we determined 15 to be the optimal number of latent components using the elbow method as implemented in the kneed Python package⁸². For plotting purposes, we reduced the dimensionality of the feature matrix using t-distributed stochastic neighbor embedding (t-SNE) as implemented in the scikit-learn t-SNE module⁸¹. Results from this analysis are shown for high dose (1.0 μM) drugs in Supplementary Fig. 4e.

To determine if BATCHIE also discerned more fine-grained drug MoAs, we selected 8 more refined molecular mechanisms or pharmaceutical classes that were recurrent among the drugs evaluated. We then identified 2-3 drugs belonging to each such group. We calculated the Pearson correlation coefficients between the BATCHIE-predicted combination therapy viabilities for each drug at both doses assessed. We plotted the resulting hierarchically clustered heatmap using the Python package Seaborn’s clustermap function⁸³. These results are show in Supplementary Fig. 4d.

Ex vivo analysis

For six of the drug combinations from the top EWS hits, we collected dose-response data on 2 additional patient-derived cell lines. The drugs were tested on a regular grid spanning 0.02nM - 1000nM, and the plates were run in duplicates.

As the concentrations tested in this stage did not align with the concentrations tested in the top hit validation, we performed linear interpolation of the mean observed viabilities (in ${\log }_{10}$ concentration space), in order to compute TI scores with respect to the control data observed in the top hit validation analysis.

Triplet analysis

For our triplet studies, we collected dose-response data along a regular grid (0.1 nM–400 nM for the Ewing study and 0.02 nM–1 μM for the osteosarcoma study). Plates were run in duplicate.

For each cell line and triplet of drugs under consideration, we fit a multi-dimensional isotonic regression to the observed viabilities, restricting the regressed variables to monotonically decrease as a function of dose. Mathematically, we solved

$$\, {{\mbox{minimize}}} {\sum}_{{d}_{1}\in {D}_{{{{\rm{tzp}}}}}} {\sum}_{{d}_{2}\in {D}_{{{{\rm{top}}}}}} {\sum}_{{d}_{3}\in {D}_{{{{\rm{mit}}}}}} {({\hat{v}}_{{d}_{1},{d}_{2},{d}_{3}}-{v}_{{d}_{1},{d}_{2},{d}_{3}})}^{2}\\ \, {{\mbox{s.t.}}} \, {\hat{v}}_{{d}_{1},{d}_{2},{d}_{3}}\ge {\hat{v}}_{{d}_{1}^{{\prime} },{d}_{2}^{{\prime} },{d}_{3}^{{\prime} }}\, {{\mbox{for}}} \, {{\mbox{all}}}\,{d}_{1}^{{\prime} } \, \ge \, {d}_{1},{d}_{2}^{{\prime} }\ge {d}_{2},{d}_{3}\ge {d}_{3}^{{\prime} },$$

(41)

where D_x is the set of concentrations used on drug x, and ${v}_{{d}_{1},{d}_{2},{d}_{3}}$ is the mean observed viability applying drug 1 at concentration d₁, drug 2 at concentration d₂, and drug 3 at concentration d₃. For any candidate set of concentrations, we linearly (in log-concentration space) interpolated its viability from the smoothed values ${\hat{v}}_{{d}_{1},{d}_{2},{d}_{3}}$.

Gene expression and CRISPR knockout analysis

Both the RNA expression data and CRISPR knockout data were obtained from the DepMap data portal⁸⁴. The RNA expression data is represented as a matrix $X\in {{\mathbb{R}}}^{N\times G}$, where N is the number of DepMap cell lines, G is the number of protein coding genes in the DepMap library, and ${X}_{cg}={\log }_{2}(1+{{\mbox{TPM}}}_{c,g})$, where TPM_c,g is the transcripts per million (TPM) for gene g in cell line c. Z-scores for the gene expression data were computed by standardizing over cell lines, i.e.,

$${Z}_{g}=\frac{{\bar{X}}_{g}}{\sqrt{\frac{1}{N}{\sum }_{c=1}^{N}{({X}_{c,g}-{\bar{X}}_{g})}^{2}}},$$

(42)

where $\bar{{X}_{g}}=\frac{1}{N}{\sum }_{c=1}^{N}{X}_{c,g}$.

The CRISPR knockout data is represented as a matrix ${{{\boldsymbol{Y}}}}\in {{\mathbb{R}}}^{N\times G}$, where Y_c,g is a harmonized score representing the effect of knocking out gene g in cell line c.

Rational combination analysis

All drug mechanism data was obtained from the Genomics of Drug Sensitivity in Cancer (GDSC) portal⁸⁰. Drugs that do not have GDSC mechanism of action (MoA) annotations were not included in the analysis.

Mechanism of action analysis

Using the GDSC² dataset, a single dose-response curve for each drug was formed by considering each observed dose and taking the 5th percentile of mean viabilities over observed cell lines. For each drug, we computed its IC₅₀ concentration over its corresponding dose-response curve, discarding drugs for which no concentrations had corresponding values below 0.5.

For each drug i, we considered all cell lines j and drugs k at concentrations c that co-occured with i on j in the dataset to form the tensor ${{{\boldsymbol{V}}}}\in {{\mathbb{R}}}^{{n}_{{{{\rm{drug}}}}}\times {n}_{{{{\rm{cell}}}}}\times {n}_{{{{\rm{drug}}}}}\times {n}_{{{{\rm{conc}}}}}}$ where V_ijkc is the log-concentration interpolated mean viability of combining drug i at its IC₅₀ concentration with drug k at concentration c on cell line j, wherever it is validly computable from the data. For two drugs i, ${i}^{{\prime} }$, their distance is computed as

$$d(i,{i}^{{\prime} })=\frac{1}{n}{\sum}_{j,k,c}| {V}_{ijkc}-{V}_{{i}^{{\prime} }jkc}|,$$

(43)

where the sum is taken over only those values for which both V_ijkc and ${V}_{{i}^{{\prime} }jkc}$ are valid, and n is the total number of such valid values.

CROCS analysis

Combinations of drugs in which both members belonged to the ‘clinically relevant oncology combination screen’ (CROCS) for non-small cell lung cancer (NSCLC)⁶⁶ were classified as CROCS combinations. All other combinations of drugs were identified as non-CROCS combinations. For both the ALMANAC dataset and GDSC² dataset, wherever feasible, we computed an 8 × 8 evenly-spaced (in ${\log }_{10}$-concentration space) dose-response matrix by linearly interpolating mean observed viabilities. For every pair of drugs i and j and every pair of cell lines c and t, we calculated the TI of i and j where c is control and t as

$$TI(i,j;c;t)=\mathop{\max }_{{d}_{i},{d}_{j}}{V}_{c,i,{d}_{i},j,{d}_{j}}-{V}_{t,i,{d}_{i},j,{d}_{j}}$$

where ${V}_{c,i,{d}_{i},j,{d}_{j}}$ is the interpolated viability of cell line c under drug i at dose d_i and drug j and dose d_j and the maximum ranges over the dose grids for drugs i and j, respectively. For ALMANAC, we only considered those TI values for which the target cell line was NSCLC and the control cell line was not NSCLC, while for GDSC² we considered all possible TI values.

Data visualizations

All plots were made in Python using the matplotlib⁸⁵ and seaborn⁸³ packages.

Statistical analyses

All Mann-Whitney U-tests, Spearman’s rho calculations, Pearson’s rho calculations, Pearson’s chi-square calculations were computed using Scipy’s⁷³stats package, using the default settings. All p-values from Mann-Whitney U-tests, Spearman’s rho tests, and Pearson’s rho tests were computed using two-sided alternatives. The permutation test in Fig. 4g was custom coded. Unless otherwise noted, all tests were performed independently of each other.

Wetlab protocols

Cell lines

Established cell lines (SJSA-1, U2OS, SAOS-2, MG-63, A673, SKNEP, MDA-MB-231, RPE and BJ) were obtained from the American Type Culture Collection (ATCC). TC-71 was obtained from the Children’s Oncology Group cell line repository. Wit49 was provided courtesy of Dr. Herman Yeger (Toronto, Canada). Kelly was obtained from the DSMZ-German Collection of Microorganisms and Cell Cultures GmbH. MSKEWS-83311, MSKEWS-83033, MSKEWS-38338, MSKEWS-66647, MSKOST-11890, and MSKRMS-12808 were generated from patient-derived xenograft (PDX) tumor tissue established from patient tumors treated at Memorial Sloan Kettering Cancer Center (MSKCC). Tumor tissue was dissociated utilizing the Human Tumor Dissociation Kit (Miltenyi Biotec) according to manufacturer’s recommendations or using an in-house combination of Collagenase Type II (Gibco), Dispase II (Millipore Sigma), Deoxyribonuclease I (Millipore Sigma) in DMEM (Gibco) containing 10% fetal bovine serum (Corning), followed by mechanical dissociation with Macs dissociator (Miltenyi). MSKCC patients provided informed and signed consent and enrolled onto a tumor profiling research study (Genomic profiling in cancer patients; NCT01775072) approved by the MSKCC Institutional Review Board under protocol IRB#12-245, #06-107, and #17-387 to enable tumor cell line generation. PDX tumor models were generated under MSKCC Institutional Animal Care and Use Committee protocol #16-08-011. All PDX-derived samples utilized NGS mice (NOD.Cg-Prkdcscid Il2rgtm1Wjl/SzJ, Jackson Labs Strain #005557), aged between 5 and 8 weeks. Mouse sex was not recorded. Additional cell line information and culture conditions are detailed in Supplementary Data 1. Media was supplemented with 1% Anti-Anti (Gibco) at the time of drug screening. Authentication of established cell lines by short tandem repeat (STR) was performed. Validation and authentication of PDX-derived cell lines were accomplished by next-generation targeted sequencing using MSK-IMPACT⁸⁶ and matched with source patient tumor. Optimal seeding densities for drug screens were empirically determined for each cell line.

Sex information of the cell lines is shown in Supplementary Data 1. Sex information for publicly available cell lines was taken from Cellosaurus. Sex information for PDX-derived cell lines was self-reported. Sex was not considered in the study design. Samples were grouped together based on cancer subtype, with insufficient sample sizes to distinguish differences between female- and male-derived samples due to the unique functional profile of each cell line and ex vivo sample.

Drugs

The studies were comprised of 206 drugs obtained from multiple sources including Selleckchem, MedChemExpress, Sigma-Aldrich, Tocris, LKT laboratories Inc., Xcess Biosciences, and the National Cancer Institute (NCI) Division of Cancer Treatment and Diagnosis. A list of all screened chemicals and sources are provided in Supplementary Data 2.

BATCHIE plates

All assay plates contained baseline viability (high control) and complete cell killing controls (low control) consisting of 1% DMSO (v/v) and 1 μM “killer mix”, a proprietary mixture of cytotoxic drugs at 1% DMSO (v/v), respectively. Phase I and phase II drugs were prepared in 100% DMSO (v/v) and added onto 384-well microplates to generate the “200X source plates” with drugs at a concentration of either 200 μM or 20 μM. To facilitate combination testing, drugs were arrayed in a “row” or “column” format with “row plates” consisting of 15 drugs arrayed in rows per plate and “column plates” consisting of 21 drugs arrayed in columns per plate with the same drug concentration for each drug in both plate configurations. Drugs were combined using the Apricot Designs Personal Pipettor (SPT Labtech) which mixes a row plate with a column plate and water into a new 384-well plate to generate a “10X intermediate plate” of 10 μM or 1 μM in 10% DMSO (v/v). Subsequently, the 10X intermediate plates are stamped into “assay plates” to be combined with cells generating the final 1X concentration of 1 μM or 0.1 μM in 1% DMSO (v/v) (Supplementary Figs. 11,  12a).

For validation studies, 2-drug combinations were evaluated for random unseen combinations in five osteosarcoma, five Ewing sarcoma, and two non-cancer cell lines; high predicted therapeutic index (TI) in five Ewing sarcoma and two non-cancer cell lines; and Ewing sarcoma ex vivo in two Ewing sarcomas (Supplementary Fig. 11). 7-doses (Plate 1) and 9-doses (Plate 2) 4-fold serial dilutions were prepared into 96-well plates to generate 20X source plates at 8 μM or 20 μM in 10% DMSO (v/v) as the highest concentrations. The plates were further consolidated and combined into 384-well 10X intermediate plates at 4 μM or 10 μM in 10% DMSO (v/v). The 10X intermediate plates were then transferred into assay plates along with cells to produce a 1X concentration of 0.4 μM or 1 μM in 1% DMSO (v/v) (Supplementary Fig. 12b).

Higher order validation plates for Ewing sarcoma and osteosarcoma studies (Supplementary Fig. 11) were performed by first generating 7-doses (Drug 1), 5-doses (Drug 2) and 5-doses (Drug 3) 4-fold serial dilutions, obtaining 30X source plates at 12 μM or 30 μM in 10% DMSO (v/v) as the highest concentrations. The three 30X source plates were combined to create the 10X intermediate plates with maximum concentrations of 4 μM or 10 μM in 10% DMSO (v/v) and stamped to combine with cells to yield 1X assay plates of 0.4 μM or 1 μM in 1% DMSO (v/v) (Supplementary Fig. 12c). Five Ewing sarcoma and two non-cancer cell lines were used for the Ewing sarcoma validation studies and five osteosarcoma lines for the osteosarcoma studies.

For osteosarcoma studies validating agents with high predicted therapeutic indices (TI), drugs were plated in 384-well 20X source microplates using the row and column format described above for phase I and phase II (Supplementary Fig. 11) at 20 μM or 2 μM in 10% DMSO (v/v). The sources plates were combined into 10X intermediate plates yielding 10 μM or 1 μM in 10% DMSO (v/v). Assay plates were stamped from the 10X intermediate plate and combined with cells for a final drug concentration of 1 μM (high concentration) or 0.1 μM (low concentration) in 1% DMSO (v/v). All possible two drug combinations were obtained—high/high, high/low, low/high and low/low. Five osteosarcoma and two non-cancer cell lines were used.

Cytotoxicity assay

Cells were plated at their optimized seeding densities and in their corresponding media (Supplementary Data 1) into 384-well clear-bottom black assay plates (BATCHIE plates) using the MultiDrop® 384 dispenser (Thermo Fisher Scientific). After incubating cells in drug for 72 h at 37 ^∘C and 5% CO2 in a Heracell™ 240i incubator (Thermo Fisher Scientific), Alamar Blue (Sigma-Aldrich) is added using the MultiDrop™ Combi 384 dispenser (Thermo Fisher Scientific) and incubated for another 24 h. Fluorescence signal readout was acquired using a Cytation™ 5 multimode reader (Agilent Biotek) using the monochromator with an excitation of 555/20 nm and emission of 596/20 nm. A summary of the screening protocol is available in Supplementary Data 3.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.