Introduction

Doping of semiconductors by the introduction of impurities imparts novel electrical1,2 and optical3,4 properties that discretely depend on the dopant level. In lightly doped semiconductors, impurities are isolated down to as small as a single atom, and optically addressable electronic and spin states are produced5,6,7. In heavily doped semiconductors, the increased charge carrier concentration leads to metal-like behavior8,9. Localized surface plasmon resonances have been observed10,11, but unlike metals, the resonant frequency is tunable over an order of magnitude or more by varying the charge carrier concentration12,13.

Among semiconductor materials, diamond holds a special place, as it is endowed with exceptional transmissibility from ultraviolet to microwave frequencies, thermal conductivity, breakdown field, and charge carrier mobility at room temperature14. Doping to relatively high concentrations can be achieved with a charge acceptor, boron, which has a small atomic radius and is thus highly soluble in the relatively dense diamond lattice15. At very high concentrations (>1020 cm−3), metallic properties have been observed in boron-doped diamond (BDD), including the emergence of superconductivity16. The band dispersion has been measured by angle-resolved photoemission spectroscopy and the metallicity has been linked to holes in the intrinsic diamond bands17. However, other effects of hole doping beyond electronic conductivity remain unexplored. In particular, the opening of intervalence band (IVB) transitions, as reported for other hole-doped semiconductors18,19, and theorized to be responsible for changes in phonon frequencies20, should leave a direct imprint on the electronic excitation spectrum.

In this work, we employ scanning transmission electron microscope-valence electron loss spectroscopy (STEM-VEELS) and near-field infrared (IR) spectroscopy to probe low-energy excitations in BDD. We develop a first-principles model to calculate the measured inelastic loss and optical absorption from the dielectric function. Our results reveal that the origin of the material response, which is absent in undoped diamond, is IVB transitions created by hole doping, and the response is plasmonic in character.

Results

Electronic band structure of BDD

Figure 1a presents the band structure of intrinsic diamond near the center of the first Brillouin zone. With a band gap of ~5.5 eV, there are effectively no free charge carriers in intrinsic diamond at room temperature and any electrical conductivity that has been measured is the result of electrochemically-mediated surface transfer doping21. Doping diamond with single boron impurities results in an acceptor level ~0.37 eV above the top of the valence band (Fig. 1b)22. Electrons at the top of the valence band are able to fill the relatively low-energy acceptor states, creating holes in the valence band. With increasing boron concentration, more and more electrons depopulate the valence band, leaving behind more and more holes deeper and deeper within the valence band. In p-type semiconductors like BDD, the formation of holes in the valence band opens up intervalence (IVB) transitions between degenerate subbands, specifically the light-hole (LH) and heavy-hole (HH) bands.

Fig. 1: IVB transitions in diamond enabled by boron-doping.
figure 1

Calculated band structures of intrinsic diamond (a) and BDD (b), showing the valence band (green), the conduction band (light blue), and the acceptor energy state (Ea) introduced by boron doping of diamond at ca. 0.37 eV (dark blue). Electrons in the top of the valence band move to the boron acceptor state, resulting in empty states that open up IVB transitions (inset, b). c Schematic of STEM-VEELS (left) and near-field IR spectroscopy (right) showing two different experimental approaches to probing the contribution of IVB transitions to the dielectric function of BDD using either an electron beam or a tip-enhanced mid-infrared (MIR) laser.

Full size image

For this study, BDD samples were synthesized by the high-pressure, high-temperature (HPHT) method and as observed by transmission electron microscopy (TEM), were found to consist of highly crystalline particles ~1 µm in diameter, shaped like “broken glass” because of the grinding process after synthesis (Supplementary Figs. 1 and 2). As a reference, nearly identical undoped HPHT diamond particles were also synthesized by the same procedure (Supplementary Figs. 1 and 2). The boron concentration in the BDD was below the detection limit of core-loss EELS (Supplementary Note 1 and Supplementary Figs. 2 and 3).

Phononic properties of BDD

We initially characterized the BDD by micro Raman spectroscopy which shows the well-known zone center phonon (ZCP) of diamond at ca. 1332 cm−1 (Fig. 2a). In comparison to undoped diamond, boron doping is found to produce an asymmetry in the Raman lineshape of the ZCP, commonly attributed to the Fano resonance effect, i.e., an interference between the Raman-active phonon and a continuum of electronic states. The observation of a Fano resonance in BDD provides a first hint of the modification of the electronic structure by the free hole population. Indeed, the nature of the Fano-type lineshape in BDD is sensitive to the boron concentration, and was fit based on a previously reported model to determine a hole density of \(\sim 5\times {10}^{19}\) cm−3 in our sample (Supplementary Note 2)23. We note that with a laser spot size of 10 µm, the boron concentration obtained by micro Raman spectroscopy represents an average over several particles. In order to probe variations in the boron concentration not only particle to particle, but potentially within a particle, tip-enhanced Raman spectroscopy (TERS) was carried out, which overcomes the diffraction limit of micro Raman spectroscopy. By extending our analysis of the Fano-induced asymmetry in the ZCP peak, we found that the boron concentration varied between particles and even within particles from \(3\times {10}^{19}\) cm−3 to \(1.8\times {10}^{20}\) cm−3 (Supplementary Note 3 and Supplementary Fig. 4). The fundamental origin of the electronic transitions in BDD that result in the Fano effect has not yet been explained by theory or probed by experiments, but in boron-doped silicon has been correlated to IVB transitions whose energy overlaps with that of the ZCP24. In addition to the asymmetric Raman lineshape, the ZCP peak is also slightly red shifted, which has been attributed to the interaction of the phonon with IVB transitions20. This negligible change of the ZCP is also seen by comparing first-principles simulations of the full phonon density (phonon density of states (PDOS)) of BDD and undoped diamond (Fig. 2b).

Fig. 2: Effects of boron doping on the vibrational properties of diamond.
figure 2

a Micro Raman spectra obtained from BDD and undoped diamond (left) showing the ZCP at ca. 1332 cm−1. The spectrum for BDD has an asymmetric Fano lineshape (right) caused by the interference of the ZCP with electronic states created by hole doping which can be modeled as an electronic continuum (EC) that, along with phononic contributions, gives rise to this characteristic lineshape (Supplementary Note 2). b First-principles calculation of the phonon density-of-states (PDoS) of BDD for an equivalent boron concentration of ~2300 ppm, and intrinsic diamond.

Full size image

Experimental measurements of the dielectric response of BDD

To further probe the electronic structure of BDD, we performed STEM-VEELS and near-field IR spectroscopy (Fig. 1c). In VEELS, fast electrons in the electron beam are inelastically scattered by a material. Recent advancements in electron microscopy, including monochromated electron beams, high-resolution electron energy-loss spectrometers, and a narrow zero-loss peak (ZLP) tail, have made it possible to analyze energy losses down to 10 meV25. In comparison, near-field IR spectroscopy measures the optical response of materials. Here, we employ two variations of near-field IR spectroscopy: (1) photo-induced force microscopy (PiFM) and (2) scattering scanning near-field optical microscopy (s-SNOM), which are both techniques broadly based on atomic force microscopy (AFM) and focusing a laser onto the tip to create a local field that confines light-matter interaction at the nanoscale. While PiFM utilizes the resultant localized mechanical deflection of the tip to measure optical absorbance26,27, s-SNOM measures the optical amplitude and phase shift of the scattered field, which can then be demodulated at higher harmonics to extract the near-field optical interaction28,29,30. In addition, these techniques allow for a sample’s optical response to be mapped on a length scale far exceeding the diffraction limit of light. Together, STEM-VEELS and near-field IR spectroscopy provide nanometer-scale spatial resolution in the low-energy range necessary to probe IVB transitions (<0.5 eV), while complementing each other in that the combination of the two yields a complete view of longitudinal and transverse excitations, respectively.

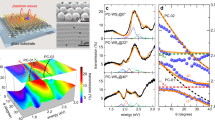
Representative VEELS measurements for BDD and undoped diamond are shown in Fig. 3a. The spectrum for BDD consists of an elastic ZLP and a clearly observable shoulder, corresponding to an inelastic contribution between ~0.1 and 0.3 eV. The inelastic signal was isolated by fitting the ZLP to a vacuum spectrum and fitting a Voigt profile (Supplementary Note 4 and Supplementary Fig. 5). Similar spectra were detected and analyzed across different regions of a given particle, as well as from many different BDD particles (Supplementary Fig. 6). In comparison, no inelastic signal is present in the representative spectrum for undoped diamond (see Fig. 3a) or any of the additional spectra that were collected across a given particle surface and different particles (Supplementary Fig. 7).

Fig. 3: VEELS characterization of BDD.
figure 3

a Analysis of representative VEEL spectra measured from a 1 × 1 nm region of BDD (top) and undoped diamond (bottom) by fitting the ZLP to a vacuum spectrum and thereby isolating an inelastic signal at roughly 0.15 eV that only appears for BDD. The total fit, i.e., the sum of the vacuum and the inelastic contributions, agrees well with the raw spectrum. All spectra are normalized to the maximum intensity of the ZLP. b Annular dark field (ADF)-STEM image of a section of a BDD particle (top left) and undoped diamond particle (top right), and false color maps showing the spatial variation of the normalized inelastic VEEL signal across BDD (bottom left) and undoped diamond (bottom right) at an energy slice of 0.15 eV. All scale bars equal 10 nm.

Full size image

While only the BDD produced an observable inelastic VEELS signal, we applied the same fitting procedure to all spectral analyses of undoped diamond as well (Supplementary Figs. 5 and 7). The lack of any signal other than the ZLP peak is consistent with the large band gap of undoped diamond, which suppresses any electronic contribution. Since our VEELS measurements were carried out at the optical limit, i.e., with the momentum transfer or scattering vector, \({{{{\boldsymbol{q}}}}}_{\perp }=0\), phonon modes are not probed for a nonpolar material like diamond31,32. As optical phonons can be excited in both doped and undoped diamond, as shown by Raman spectroscopy, we conclude that the VEELS inelastic signal is not phononic in nature. In addition, this signal at <0.5 eV is clearly distinct from the volume plasmon peak found at ~34 eV, which is present in both the BDD and the undoped samples (Supplementary Fig. 2) and originates from collective electronic excitations of electrons from the valence to the conduction band.

To study the spatial dependence of the inelastic signal measured by VEELS, we collected and analyzed spectra over a particle area. The signal was affected by the thickness of the particle and was higher near the edge where the particle is thinner. Using the log-ratio method, we estimate that the thickness varies from ~2–3 nm near the edge, to ~15–20 nm at the thickest part of the particle that was characterized (Supplementary Note 4)33. Nonetheless, we were able to obtain signal ~tens of nm away from the edge and normalize the measurements by referencing with the ZLP, which provided a measure of the overall signal attenuation. Figure 3b shows a STEM image and corresponding map of the inelastic signal for a 134 × 39 nm section of a representative BDD particle, where the color intensity corresponds to the integrated normalized intensity of the inelastic loss peak at an energy of 0.15 eV, the nominal energy value obtained from VEELS. For reference, a STEM image and map are also shown for a 120 × 46 nm section of a representative undoped diamond particle. The inelastic signal intensity is observed to vary across the BDD particle, exhibiting a striated pattern, but does not appear to be localized to a specific part of the particle such as the edge, or depend on the loss energy. Maps of other BDD particles showed similar random intensity distributions (Supplementary Fig. 8) and did not show any correlation with particle thickness (Supplementary Fig. 9). As expected based on VEELS spectra, the maps of undoped diamond samples did not show any appreciable intensity (Fig. 3b and Supplementary Fig. 10). These results indicate that the primary signal does not arise from defects intrinsic to the material such as at the surface, which should also be present in undoped diamond, but that boron doping is responsible. The spatial variations in the boron concentration, which was indicated by TERS analysis, could be related to the distribution of the boron atoms in the diamond lattice, which is known to prefer certain crystal directions34,35, or structural heterogeneities that have been recently found to impact the properties of other impurity dopants in diamond at the atomic scale36.

Representative PiFM spectra are shown in Fig. 4a for BDD and undoped diamond. A peak is observed for BDD centered at ca. 0.13 eV, close to the energy values measured by VEELS. Additional spectra were collected from different regions and different particles for both BDD and undoped diamond (Supplementary Fig. 11). Once again, spectral features were only found in BDD samples. In comparison to VEELS, there is no interference with the peak of interest and the broad nature is clear. Using a laser frequency close to the nominal peak observed in PiFM of 1048 cm−1, s-SNOM imaging was conducted (see Supplementary Note 5 and the Methods section for details). Figure 4b–g shows representative AFM topography, optical amplitude, and optical phase images obtained from isolated crystals of BDD and undoped diamond. Similar quantitative changes are observed in the amplitude for both BDD and undoped diamond (see Fig. 4d, e and Supplementary Fig. 12), but importantly, a distinct and uniform contrast in the phase is observed across BDD that is completely absent in undoped diamond (see Fig. 4f, g, and Supplementary Fig. 12).

Fig. 4: Near-field infrared spectroscopic characterization of BDD.
figure 4

a Representative photo-induced force microscopy (PiFM) spectra collected from BDD and undoped diamond. b–g Representative s-SNOM images collected from BDD and undoped diamond: atomic force microscopy (AFM) topography images (b) and (c), respectively, amplitude, \(s(\omega )\), (d) and (e), respectively, and phase, \(\varphi \left(\omega \right),\) (f) and (g), respectively. Laser energy was 1048 cm−1 (~0.13 eV), corresponding to the resonance observed in (a). The amplitude and phase signals correspond to the second harmonic of the tip oscillation frequency and were normalized with reference to the Si substrate. All lateral scale bars correspond to 1 µm.

Full size image

Modeling the complex dielectric function of BDD

VEELS and near-field IR spectroscopic techniques like PiFM and s-SNOM probe the frequency-dependent dielectric response of a material to an external electric field. Specifically, VEELS measures the energy dissipation, i.e., loss channels, and is represented by the negative imaginary part of the inverse dielectric function, and PiFM and s-SNOM measure quantities related to absorption, which is proportional to the imaginary part of the square root of the dielectric function37. In doped semiconductors, the charge carriers introduced into the valence or conduction band can enable electronic transitions beyond the ones present in the undoped case and lead to additional contributions to the complex dielectric function. Specifically, for a p-type semiconductor such as BDD, electrons in the hole-doped band may be excited within the band, so-called intravalence band transitions. At the same time, holes also allow the excitation of an electron from the filled LH band into the hole of the HH band, so-called IVB transitions (see Fig. 1b). To understand the physical origin of the electronic transitions, we model these various modes of excitations.

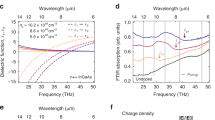
First, a modified version of a one-frequency Drude–Lorentz model known as the Thomas–Fermi model, which has been previously reported for hole excitations in doped semiconductors, was applied18,38. At a hole density of \(\sim 5\times {10}^{19}\) cm−3 corresponding to our BDD sample, we calculate a loss peak at 0.7 eV, which is at much higher energy than our experimentally-measured VEELS inelastic signal peak at ~0.15 eV, and indicates that the origin is not Drude-like, i.e., not due to intravalence band excitations (Supplementary Fig. 13 and Supplementary Note 6). Next, we consider IVB transitions opened up by the depopulation of electrons and formation of holes in the valence band, as illustrated in Fig. 1b. To find the complex inverse dielectric function, we performed first-principles calculations (Supplementary Note 7). At the moderate concentrations of boron studied here, we assumed that the band structure of BDD is equivalent to intrinsic diamond, with an effective Fermi level related to the boron-induced free hole density, as depicted in Fig. 5a, which has been previously shown to successfully reproduce the vibrational band structure of BDD as a function of boron concentration20. The Fermi energy was obtained by matching the numerically integrated occupancies of all electronic valence band states to the hole density. The resulting non-linear relation of the Fermi energy shift in BDD, \(\Delta {{{{\rm{\varepsilon }}}}}_{F}\), with the hole density is shown in Fig. 5b. We then calculated the contribution of all possible IVB transitions to the complex macroscopic dielectric function. The total dielectric function was determined by adding the static dielectric constant of intrinsic diamond, which accounts for additional contributions of high-energy electronic transitions from the valence-to-conduction bands. A static approximation for these interband contributions is justified as our analysis focuses on low excitation energies (<0.5 eV) that are much smaller than the band gap of intrinsic diamond (ca. 5.5 eV). Finally, the VEELS loss function and the IR absorption coefficient are obtained, as detailed in the Methods section. We chose to model the absorption coefficient as both the signal measured by PiFM and the phase contrast detected by s-SNOM have been found to be linked to optical absorption30,39.

Fig. 5: First-principles model of dielectric function for BDD based on IVB transitions.
figure 5

Illustration of the Fermi level shift which is modeled as an effective Fermi level that starts at the top of the valence band for intrinsic diamond, and is lowered as a result of boron doping which introduces carriers in the form of holes (a), and calculated results for the Fermi energy shift as a function of hole density, nH which follows a \(\Delta {\varepsilon }_{F}\propto {n}_{H}^{2/3}\) trend, as expected from a parabolic energy dispersion in three dimensions (b). c Simulated valence electron energy-loss (VEEL) spectra (left) and simulated infrared absorption coefficients (right) as a function of hole density. The dashed lines indicate the shift in the peak energies. d Intervalence plasmon frequency calculated from the loss function as a function of hole density, and e full-width at half-maximum (FWHM) of the loss-function peak (c, left) as a function of hole density.

Full size image

The resulting simulated spectra for VEELS loss and IR absorption are shown in Fig. 5c. The spectral position of the maximum loss for both loss mechanisms is found to strongly depend on the hole density. The simulated VEELS peaks shift from 0.05 eV at \(\sim 1.8\times {10}^{19}\) cm−3 to 0.3 eV at \(\sim 1.8\times {10}^{20}\) cm−3. In comparing with experimental results, we note that the measured VEELS peak energies vary slightly from particle to particle and across particles in the range of 0.1–0.2 eV (Supplementary Figs. 6 and 8), which according to the simulation results shown in Fig. 5c would correspond to a range of hole densities from ~3.5 to 8 × 1019 cm−3, which agrees well with the variation in the boron concentrations obtained by TERS analysis. To quantify the experimental variation in VEELS, spectra were analyzed from every 1 × 1 nm spot of the representative particle analyzed in Fig. 3, and a distribution of peak energies was compiled and found to exhibit the most frequent occurrence at ~0.12–0.13 eV, corresponding to a hole density of \(3.5\times {10}^{19}\) cm−3, which agrees well with the average boron concentration obtained by micro Raman analysis (Supplementary Fig. 14). The simulated IR loss peaks display a similar dependence on hole density, shifting from 0.1 eV at \(\sim 1.8\times {10}^{19}\) cm−3 to 0.3 eV at \(\sim 1.8\times {10}^{20}\) cm−3. In comparing with experiment results, the measured PiFM peak energy and the resonant condition of s-SNOM at ~0.13 eV would, based on simulations, correspond to a hole density of \(\sim 5\times {10}^{19}\) cm−3, which agrees well with the average boron concentration obtained by micro Raman analysis.

By analyzing the modeled dielectric function, we observe that the peak present in the loss spectrum corresponds to a zero-crossing (i.e., negative band crossing) of the real part of the dielectric function, indicating a clear transition to metallic properties (Supplementary Fig. 15). This result is qualitatively consistent with s-SNOM measurements where a difference was observed in the phase for BDD without a change in amplitude from undoped diamond. Furthermore, the blue shift in the frequency of this resonance (Fig. 5d) and the resulting loss peak, as well as the increase in the intensity of the loss peak with increasing hole density, are consistent with plasmonic behavior. Overall, these insights lead us to define the collective electronic transitions in the valence subbands of BDD as intervalence plasmons. Note that this type of plasmon is entirely different from both the Drude-like plasmons found in metals linked to intra-band transitions, and from the volume plasmon also found in undoped semiconductors at higher energies, which arise from valence-to-conduction band transitions. By analyzing the full-width-half-maximum (FWHM) of the loss-function peak, we find that the damping constant which is proportional to the inverse lifetime of a plasmon, is well below the eigenfrequency, indicating that the observed intervalence plasmon is a well-defined quasi-particle (Fig. 5e). The damping increases with hole concentration, as the available phase space for the individual electron-hole pair decay channel increases, stemming from the monotonically increasing density of IVB transition states in diamond. However, the plasmon frequency likewise increases with hole concentration, such that the intervalence plasmon is not subject to overdamping. To further underscore the well-defined quasi-particle nature, we compare the position and FWHM of the simulated loss-function peak with a direct calculation of the plasmon frequency and lifetime from the real and imaginary part of the dielectric function (Supplementary Fig. 15) and find excellent agreement.

Discussion

Through a combination of experimental measurements and ab initio modeling, we report plasmonic behavior at IR frequencies in BDD that can be attributed to hole doping, not directly as free charge carriers, but more indirectly by enabling subband transitions for valence band electrons. This mechanism is distinct from the intravalence band excitations of free charge carriers of a particular type (e.g., holes for p-type semiconductors) that have typically been modeled by the Drude model to explain the optical response of doped semiconductors40. The question of whether the same models used to describe the plasmonic response from metals are applicable has recently been raised41, and our results provide key physical insight into how doped semiconductors are different. We note that BDD may be unique because of its wide band gap, large acceptor level energy, and low dielectric polarizability as compared to other, similar doped semiconductors. As a result, the IVB response may be unfettered compared to, for example, either a narrow-band gap semiconductor, or one where the dopant level is closer to the valence band. The broader implication of our study is a much richer and more complex picture for the effect of doping on electronic transitions in semiconductors, which could enable the engineering of semiconductor-based plasmonic materials with different types of band-to-band excitations.

Unlocking plasmonic properties in diamond also adds another interesting element to this remarkable material. Diamond has recently attracted attention because of the ability to host emissive point defects with quantum properties, which combined with its small spin-orbit coupling and zero nuclear spin42, permits the electron spin to be initialized, manipulated, and optically read-out at room temperature43,44. However, the emitters have been limited by long fluorescent lifetimes, low photon rates, and poor quantum efficiency, which are important for quantum applications. In general, co-doping impurities that are electronically active and color centers, respectively, could use plasmonic excitation to enhance the photoluminescence and speed up the emission rates45. In addition, the charge state of the point defects could be altered as a result of the shift in the Fermi level and pinning induced by the electronic dopant, such as in the case of the recently reported neutralization of SiV− to SiV0, to produce new emitters with disruptive improvements in properties46. The discovery of these and other point defects is rapidly expanding the toolkit for engineering quantum emitters47. Electronic doping provides another lever to optimize the optical and spin properties. Future studies will need to focus on controlling the nanoscale concentration of dopants such as boron to tune the various effects.

Methods

Synthesis of diamond powders

Diamond powders were synthesized by metal-catalyzed (Fe and Ni) HPHT methods using graphite as the carbon precursor. Boron carbide (B4C) was mixed with the graphite as the boron source to obtain BDD. Both the as-synthesized undoped and boron-doped powders were washed thoroughly and treated with hydrochloric acid to eliminate metal contaminants and remove amorphous carbon.

TEM imaging

TEM was performed using a FEI Tecnai G2 F20 microscope at an accelerating voltage of 200 kV. Samples were prepared by drop-casting a suspension of diamond particles in 200 proof ethanol onto lacey carbon grids (Ted Pella, Inc.) and air-drying before transferring into the microscope.

Micro Raman characterization

Micro Raman spectra were acquired at room temperature using a Nanophoton Raman 11 confocal Raman/PL microscope. Samples were prepared by drop-casting a suspension of diamond particles in 200 proof ethanol onto 1 × 1 cm pieces of MgO (100) (MTI Corporation). The spectrometer was calibrated using a Ne lamp spectrum as well as the Si T2g phonon mode at ~520.2 cm−1. An excitation wavelength of 532 nm was used, and the laser power was limited to 0.5 mW to avoid sample heating. Spectra were collected in the range of 250–2200 cm−1 with a spectral resolution of 1.6 cm−1 and a peak position accuracy of 0.1 cm−1 using a 600 groove/mm grating. A 50× (NA = 0.8) objective lens was used to focus the laser down to a spot size of ~10 µm.

Tip-enhanced Raman spectroscopy

Spatially resolved Raman spectroscopy measurements were performed using a Horiba XploRA PLUS Raman Microscope head-based TERS system allowing for co-localized and simultaneous TERS and AFM measurements with a lateral resolution of ~50 nm. In our measurements, the spatial resolution was limited by the photon collection volume needed to maximize signal-to-noise to 200 nm. Samples were prepared by drop-casting a suspension of BDD particles in 200 proof ethanol onto Si(100) with a 50 nm Au coating. Spectra were collected in near-field mode using an Au-coated conductive cantilever (Opus 160AC-GG) with an excitation wavelength of 532 nm and a spectral resolution of 1.4 cm−1 using a 1200 groove/mm grating. Prior to all measurements, the spectrometer was calibrated using the Si T2g phonon mode at 520.2 cm−1.

STEM-VEELS

STEM-VEELS measurements were performed using a Thermo Scientific Themis Z microscope equipped with a dual-EELS spectrometer for simultaneous measurement of low-loss and core-loss EELS, and a monochromated field emission gun with a spectral resolution of 100 meV. All measurements were conducted at an accelerating voltage of 300 kV in order to obtain a high spatial resolution of 1 nm2. Samples were prepared the same as described above for TEM measurements. Raw spectra were first corrected using the built-in tools of the Gatan Digital Micrograph software to account for any drift in energy experienced during the scan by aligning the ZLP maximum at 0 eV. All spectra were normalized to the ZLP maximum to account for varying thickness across a given particle and from particle to particle.

Photo-induced force microscopy (PiFM)

PiFM measurements of BDD and undoped diamond were performed using a Molecular Vista One microscope. Samples were prepared by drop-casting suspensions of BDD and undoped diamond in ethanol onto glass slides with an IR-reflective coating to minimize interference from the substrate. The samples were subsequently baked in vacuum at 100 °C for 1 h to eliminate any solvent residue. AFM cantilevers with conductive Pt-Ir coated tips (Molecular Vista, Inc.) were used to obtain spectra down to ~102 nm spatial resolution and 1 cm−1 spectral resolution at a laser power of 2 mW. The spectrometer and all accompanying optics were calibrated using a standard polyethersulfone sample before each measurement.

Infrared scattering scanning near-field optical microscopy (IR s-SNOM)

s-SNOM measurements of BDD and undoped diamond were performed using a Neaspec IR-NeaSCOPE with a broadband MIR laser tunable from 700 to 2200 cm−1 and a pseudoheterodyne detector to simultaneously acquire the near-field amplitude and phase. Samples were prepared by drop-casting suspensions of BDD and undoped diamond particles in ethanol onto clean pieces of Si(100), which also served as a reference for normalizing optical signals. In order to achieve a good optical contrast, a Pt-Ir5 coated silicon AFM probe (NanoWorld Arrow™ NCPt), featuring a tip radius of 25 nm, was used for all measurements48. Scans were performed on 5 × 5 µm2 area, with a pixel area of 100 × 100 pxl2 using an integration time of 33 ms. The signal was demodulated at the second harmonic to obtain a purely optical response. Experimental drifts were monitored and corrected in the Gwyddion software49, using the mechanically and spectrally stable Si wafer as a reference.

First-principles calculation of energy-loss function and absorption coefficient

The energy-loss function and absorption coefficient were obtained by evaluating all quantities in the outlined three-step procedure from first principles using density functional theory (DFT) as implemented in the PWscf code of the QuantumESPRESSO suite50. Norm-conserving pseudopotentials generated with the van Barth-Car approach were used to describe the electron-nuclei interaction. The electron-electron interaction was approximated on the level of the local density approximation in the parametrization of Perdew and Zunger. The electron wave functions were expanded in a plane wave basis using an energy cutoff of 90 Ry. We use the established lattice constant of a = 3.523 \({{\text{\AA}}}\) for the diamond geometry.

The main challenge in calculating the Fermi energy shift and the contribution of valence band transitions to the macroscopic dielectric function is the evaluation of the integrals over the first BZ. As the effective Fermi level is close to the top of the valence band, a high resolution in k-space is needed, making it necessary to sample the BZ with a dense, uniform grid of points in order to achieve convergence. As the calculation of all energies and position operator matrix elements on such a dense k-point mesh is computationally demanding, we first obtained DFT band energies and wave functions on a coarse 8 × 8 × 8 k-point mesh. Subsequently, we used an interpolation scheme on the basis of maximally localized Wannier functions, as implemented in the Wannier90 code. The electronic band structure and the matrix elements of the velocity operator were then interpolated using the EPW code to a fine 200 × 200 × 200 k-point mesh. Finally, the position operator matrix elements were obtained via

$$\left\langle {{{\bf{k}}}}n | {\hat{r}}_{i} | {{{\bf{k}}}}m\right\rangle=-\frac{i{{\hslash }}}{{m}_{e}}\frac{\left\langle {{{\bf{k}}}}n | {\hat{p}}_{i} | {{{\bf{k}}}}m\right\rangle }{{\varepsilon }_{{{{\bf{k}}}}n}-{\varepsilon }_{{{{\bf{k}}}}m}}+\frac{\left\langle {{{\bf{k}}}}n \left| \left[{\widehat{H}}_{{non}-{local}},{\hat{r}}_{i}\right] \right| {{{\bf{k}}}}m\right\rangle }{{\varepsilon }_{{{{\bf{k}}}}n}-{\varepsilon }_{{{{\bf{k}}}}m}}{{{\rm{for}}}}\, {\varepsilon }_{{{{\bf{k}}}}n}\ne {\varepsilon }_{{{{\bf{k}}}}m},$$

where \({m}_{e}\) denotes the electron mass and the \({\hat{H}}_{{non}-{local}}\) the non-local part of the pseudopotential.

Ab initio calculations of phonon density of states

First-principles calculations of the PDOS were performed with the same settings and approximations as the ground state calculations previously described for the macroscopic dielectric function. For the undoped PDOS, an 8 × 8 × 8 k-point mesh was used for integration of the electronic BZ. The phonon frequencies were obtained from density functional perturbation theory as implemented in the PHonon code of the QuantumESPRESSO suite. A threshold of 10−14 was assumed for the squared perturbed self-consistent potential in the self-consistency cycle. The phonon frequencies and dynamical matrices were first computed on a uniform 8 × 8 × 8 q-point mesh in the first phonon BZ, and subsequently, Fourier interpolated to a denser 16 × 16 × 16 q-point mesh for the calculation of the PDOS, using the “crystal” acoustic sum rule to preserve exact translation invariance. The number of frequency points between the highest and lowest frequency was 1000 and the broadening was 4 cm−1. To calculate the PDOS of BDD, we constructed a 6 × 6 × 6 supercell of the diamond lattice, with 432 atoms in total, and replaced 1 carbon atom replaced by a boron atom, which corresponds to a boron concentration of ~2300 ppm. Any lower concentration would require a larger supercell which proved to be computationally prohibitively expensive. The atomic positions and lattice constant were both relaxed at convergence thresholds for the total energy of 10−7 Ry and for the total force components of 10−8 Ry/Bohr. As the system is formally metallic, a Fermi–Dirac smearing using a smearing of 0.002 Ry was applied. The value of the optimized lattice constant was found to be 21.141 \({{\text{\AA}}}\), corresponding to an average unit cell lattice constant of 3.523 \({{\text{\AA}}}\). Due to the size of the supercell, both the electronic and phonon BZ were sampled at only one point without interpolating the phonons.