Introduction

Machine learning (ML), owing to its ability to analyze vast datasets and identify complex correlations, has revolutionized the material science landscape1,2,3,4. Currently, a widely-used ML approach, known as forward design, involves utilizing ML algorithms to establish structure-property relationships and predicts properties of unknown materials through element substitution within existing materials5,6,7,8,9. However, it is extremely challenging to identify novel and useful candidates in chemical spaces that are overwhelming in size, e.g., the chemical space of inorganic compounds, which contains approximately 10 N possible configurations for compounds with N atoms in the unit cell10. Furthermore, a fundamental drawback of the forward design is that it cannot generate materials beyond structural prototypes of existing materials. In recent years, generative models, particularly those based on deep learning architectures, have emerged as powerful tools to overcome the drawbacks of forward design for discovering materials (Figure S1)11,12. These models leverage large datasets of material properties and structures to learn complex patterns and correlations. By capturing the intricate interplay between various material attributes, generative models can generate new materials that meet specific criteria. This strategy is named inverse design11. This transformative capability not only accelerates the discovery process but also expands the scope of materials exploration beyond what was previously conceivable13.

Two popular generative models, the variational autoencoder (VAE) and the generative adversarial network (GAN) have been successfully applied to inversely design stable V-O14, Bi-Se15, Mg−Mn−O16 material systems, zeolites with desired methane heat of adsorption17, stable cubic semiconductors18,19 and MOFs for carbon dioxide separation20. However, these generative models are often limited to the generation of structures with a given symmetry or composition. Most recently, the crystal diffusion variational autoencoder (CDVAE) based on graph neural networks (GNN) has been developed to generate diverse crystal structures with acceptable quality21, i.e., structures that have reasonable compositions (overall charge neutrality), proper bond lengths, and thermodynamic stability. Nevertheless, generative models inherently learn patterns from large and diverse training datasets to achieve the generation of high-quality structures. Consequently, they tend to generate material structures that closely resemble the training dataset, where material structures with superior properties are usually rare. This suggests we need additional algorithms to guide the generative model to escape away from the restriction of the training data and simultaneously maintain the generation quality. Meanwhile, the immensity of the material property space presents significant challenges for global and efficient exploration. On the other hand, the current inverse design methods used for designing materials with targeted properties lack universality, necessitating the training of different generative models for different properties14,15,16,17,18,19,20. This methodology fails to leverage a plethora of accurate property prediction models already available, which use various material descriptors, both compositional and structural6,7,9,22,23,24,25. As a result, the capability of inverse design is restricted to a narrow set of properties, primarily formation energy.

In this work, we address the aforementioned challenges by developing a general inverse design framework, Material Generation with Efficient global Chemical space Search (MAGECS), which integrates bird swarm algorithm (BSA)26,27, crystal diffusion variational autoencoder (CDVAE) and supervised graph neural network (GNN). The introduction of BSA can efficiently steer the generator towards generating structures with target property via optimizing latent space vectors, which serve as the input for generative models to construct structures, in the property space. This transforms the generation of structures from the traditional random generation to purposeful and efficient exploration of property space based on targeted properties. Using MAGECS, we realize the first generative model-based inverse design of novel alloy electrocatalysts for CO2 reduction reaction (CO2RR)—a pivotal step in mitigating greenhouse gas emissions and promoting the carbon cycle28,29,30,31. To effectively evaluate the CO2RR activity of alloys, we utilize the optimal adsorption energy of CO (ΔECO), which is usually the key intermediate in electrocatalytic CO2RR8,32. Out of the 250,000 alloy surfaces we generated, the proportion of structures with high CO2RR activity is 2.5 times higher than structures randomly generated by CDVAE. Next, among these highly active alloy surfaces, we further consider the competitive hydrogen evolution reaction (HER) and thermodynamic stability, and screen the top 110 potential surfaces for further verification with first-principles calculations. To the end, we successfully synthesized five innovative alloy catalysts, CuAl, AlPd, Sn2Pd5, Sn9Pd7, and CuAlSe2, and two of which exhibit high CO2RR activity (−600.6 mA cm−2 and −296.2 mA cm−2 current density under −1.1 V vs. RHE) and selectivity (around 90% CO2RR Faraday efficiency).

Results

Inverse design framework of MAGECS

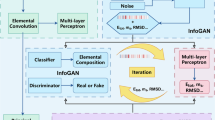
Our inverse design framework MAGECS comprises two primary domains of operation: the generation of new surfaces in structure space and the global optimization of generated surfaces in property space (Fig. 1). First, we employ the CDVAE pretrained generative model to create new surfaces with both high quality and diversity. The CDVAE model is trained on a database containing various catalyst surfaces created by Tran et al. (GASpy) (Table S1) and generates new structures (i.e., surfaces in this work) from latent vectors (steps I–II in Fig. 1). Specifically, these latent vectors are fed into three fully connected neural networks which respectively output the atomic number, lattice constant, and composition/stoichiometry (Figure S2). A surface can be built using these outputs and randomly generated atom coordinates. Then, the surface stoichiometry and coordinates were adjusted to be reasonable by the Langevin dynamics in CDVAE.

Fig. 1: Schematic diagram of inverse design materials with desired properties using our framework (surfaces for CO2RR in this work).
figure 1

It contains three main parts: surface structures generation from latent vectors via generative model (step I–II), CO adsorption energy prediction via supervised GNN model (step III–IV) and optimization of CO2RR properties via BSA (step V).

Full size image

Second, to realize the optimization of generated surfaces in property space, we need to rapidly assess the CO2 activity of these generated surfaces. Here the adsorption energy of the key intermediate CO (ΔECO) is selected as the learning target. To this end, we enumerate all possible adsorption sites on the surface and add CO on these sites (step III in Fig. 1). We trained a supervised graph neural network (DimeNet + +), recognized for its invariance to crystal structures and high accuracy in predicting material properties33,34, to predict the ΔECO of all sites. To ensure the applicability of predicting the ΔECO of generated surfaces, the DimeNet + + model was trained using exactly the same surface structures used to train the generation model. Next, the minimal predicted adsorption energies of all sites are used as fitness for evaluating latent vectors (step IV in Fig. 1). It is noteworthy that our framework is compatible with any form of property prediction model, regardless of the type of material descriptors they utilize, whether based on composition or structure. This enables our framework to optimize any material properties without altering the generative model.

Third, to steer the generator toward generating active surfaces for CO2RR (i.e., to globally optimize the latent vectors in the property space), we integrate the BSA algorithm which was inspired by the swarm intelligence observed in bird swarms. As depicted in Figure S2, birds in nature exhibit three main social behaviors: foraging, vigilance, and flight. By modeling these interactions, BSA not only exhibits superior optimization efficiency but also has a high capability of escaping from local optimum. In this work, BSA first generates a batch of birds (i.e., latent vectors in Figure S3), which can be used to generate an equal number of surface structures. The activity of these surfaces is evaluated by DimeNet + + and then fed back to BSA to generate new latent vectors (step V in Fig. 1). This process will be iterated until a number of predetermined generations are reached.

To sum up, the BSA and supervised models are employed to guide (arrows in Fig. 2a) the optimization of the CDVAE-generated structures in the property space, enabling rapid discovery of new structures beyond the training database (blue points in Fig. 2a) with good properties (peaks in Fig. 2a). Figure 2b visualizes the T-SNE plot of generated and training surface structures using latent space vectors (features) obtained by the encoder in CDVAE, revealing that our framework indeed explores a much larger chemical space with potentially high CO2RR activity than that covered by the training database. Notably, this training database, deriving from active learning methods and automated DFT calculations, already covers a vast chemical space. This further proves the superiority of our inverse design framework in globally and efficiently exploring the chemical space.

Fig. 2: Advantages of MAGECS.
figure 2

a Structures generated by CDVAE (colored dots) are optimized by BSA and supervised models (arrows), facilitating the global and efficient exploration of the property space. The contour lines represent the topography of the property space, where the peaks correspond to materials with desirable properties (e.g., high performance), and the valleys indicate regions of lower property values. The density of the contour lines reflects the gradient of the property landscape, with closer lines indicating steeper changes in properties. b T-SNE visualization of the structures in dataset (blue points) and MAGECS generated structures (orange points) using our framework. The darker the color of the point, the better the CO2RR activity. c Comparison of the distribution of |ΔECO + 0.67 | , the average value of |ΔECO + 0.67| (X-axis of columns) and the proportion of structures satisfying |ΔECO + 0.67 | ≤ 0.15 eV (Y-axis of columns) among MAGECS, CDVAE generated structures and training set structures. From top to bottom, the four figures illustrate the comparison where MAGECS generated 100, 1000, 10,000, and 50,000 structures, respectively.

Full size image

Results of inverse design framework and evaluation of generated surfaces

To realize the global optimization of generated surfaces for CO2RR in the property space, the optimization target is first required to be set. The optimal ΔECO value for CO2RR is −0.67 eV, which was used in a pioneering study on active learning for CO2RR alloys8. This value was identified by microkinetic modeling, which ΔECO exhibits a volcano plot relationship with the experimental CO2 reduction rate and selectivity, with the peak of the volcano corresponding to ΔECO at −0.67 eV32. Considering the mean absolute error (MAE) of the DimeNet + + model (0.143 eV on testing data), we set the criterion with |ΔECO + 0.67 | ≤ 0.15 eV to be favorable and used it as the optimization target for BSA.

MAGECS was then executed three times, each comprising 500 BSA steps (100 structures each step). In all three runs, the BSA can lead the generative model to go beyond the training data (Figure S4), demonstrating the effectiveness of MAGECS. Note that there is no further improvement in the number of generated surfaces meeting |ΔECO + 0.67 | ≤ 0.15 eV after 200-300 BSA steps. In order to validate this finding and generate more promising surface structures with high CO2RR activity, one additional run with 1000 BSA steps was conducted. Hence, a total of 250,000 alloy surfaces were generated.

To reveal the advantage of MAGECS, we employed the conventional CDVAE model to produce 50000 new surfaces and compare the distribution of predicted |ΔECO + 0.67| across surfaces generated by MAGECS, CDVAE, and those within the training set. As shown in Fig. 2c, the CDVAE successfully reproduced the distribution of |ΔECO + 0.67| of training surfaces, with both the average |ΔECO + 0.67| and proportion of surfaces satisfying |ΔECO + 0.67 | ≤ 0.15 eV (highly active surfaces) closely aligning. In contrast, among the 100, 1000, 10,000 and 50,000 structures iteratively generated by MAGECS, the proportion of highly active surfaces was rapidly improved, ultimately being 2.5 times higher than those generated by CDVAE and from training data. The above merits showcase the efficacy of our BSA to steer the generative model to mass-generate structures with properties beyond training data.

Building upon this, we conducted a thorough analysis of BSA optimization process using the average performance of four runs (Figure S4-S6 detail the results of each run) and the mean value of every ten BSA steps considering the deviation during optimization. The proportion of surfaces with |ΔECO + 0.67 | ≤ 0.15 eV out of 100 generated surfaces in each step increases rapidly as BSA runs, eventually maintaining around 38% after 200 steps, which yields a considerable number of desired surfaces (Fig. 3a). Meanwhile, 78.9% of the generated surfaces exceed the training and validation sets, proving the powerful capability of MAGECS to create new materials with enhanced properties. To further demonstrate the efficiency of MAGECS, we compared the BSA-guided property optimization with three other optimization approaches, each generating 50,000 surfaces: (I) Jointly trained property predictor combined with gradient descent (JTPP-GD), (II) particle swarm optimization (PSO), (III) genetic algorithm (GA). In JTPP-GD, a ΔECO predictor network was jointly trained with the encoder and decoder. This network directly predicted the optimal ΔECO based on latent vector encoded from surface structure, without information about adsorbed CO molecules and adsorption sites. The ΔECO of generated surfaces were then optimized using gradient descent. As shown in Fig. 3a, property optimization based on the BSA algorithm demonstrates the best efficiency compared to the JTPP-GD, PSO, and GA approaches. Notably, the jointly trained latent space vectors—ΔECO predictor constantly failed to optimize, with the proportion of surfaces generated in each generation with |ΔECO + 0.67 | ≤ 0.15 eV remaining around 20% due to its inaccuracy (MAE = 0.402 eV on testing data).

Fig. 3: Results of inverse design alloy surfaces for CO2RR.
figure 3

a Average proportion of surfaces with |ΔECO + 0.67 | ≤ 0.15 eV measured at every ten steps of the optimization process using bird swarm algorithm (BSA) (orange), Jointly trained property predictor combined with gradient descent (JTPP-GD) (grey), particle swarm optimization (PSO) (green) and genetic algorithm (GA) (blue). b Mean surface similarity ratio in every ten steps during BSA optimization of four runs. Inset shows the number of steps rediscovering formerly reported surfaces with high CO2RR performance. c Preferences of elements across 250,000 generated surfaces, with increasing orange intensity indicating the greater quantity of element. d Predicted activity distribution for generated bimetallic alloy surfaces. The more orange the color, the lower the average of the lowest ten |ΔECO + 0.67| of surfaces. e Top composition of 250,000 generated surfaces with |ΔECO + 0.67 | ≤ 0.15 eV. The more orange the color, the more frequently this composition appears. The number on the bar represents the rank, the subfigure shows the crystal system distribution of the bulk structure of these surfaces.

Full size image

Moreover, as shown in Fig. 3b, a distinctive feature of the BSA optimization process is the approximately 55% similarity between the surfaces generated in successive BSA steps. This continuous generation of novel and superior surfaces, even after identifying those with the lowest |ΔECO + 0.67 | , demonstrates MAGECS’s capability to transcend local minima and undertake a global exploration of the chemical space. More importantly, among the generated surfaces, we found a number of them have been experimentally verified to exhibit high CO2RR performance in previous studies (Fig. 3b)3,35,36,37,38,39,40,41,42. As shown in Figure S7, these rediscovered surfaces indeed have low |ΔECO + 0.67 | , demonstrating the reliability of MAGECS in generating highly active surface structures for CO2RR.

While these generated structures exhibit commendable CO2RR activity, it is imperative to ensure their validity and diversity. We first applied the structure validity and diversity evaluation methods from the CDVAE work, showing that our CDVAE model trained on the GASpy database achieved comparable or superior COV-R (diversity) and COV-P (quality) compared to that trained on the Materials Project database (Table S1). However, the structure validity metric used by CDVAE only ensures that the distance between any two atoms is greater than 1 Å, which does not consider the thermodynamic stability of the structure. Thus, we employed formation energy (Ef) as the structure evaluation metric and utilized a high-precision graph neural network model (MEGNet) to predict Ef, bypassing the need for time-consuming DFT calculations. As shown in Figure S8a, the Ef of generated surfaces predicted by MEGNet have a mean value and distribution closely matching those of the training and validation surfaces. This indicates the capability of generating high-quality structures of the generation model in our inverse design framework. Furthermore, we validated our structure evaluation metric by adding random noise to atom coordinates within structures. As the noise level increases, the structural validity should deteriorate. This noise-distinguished method proved that MEGNet-predicted formation energy is an effective structure evaluation metric as it increases with noise, leveling off beyond 0.5, as seen in training and validation sets (details discussed in Supplementary Method S1).

After validating the rationality of 250,000 generated surfaces, an in-depth analyze of the elemental, compositional, and structural distributions across these surfaces helps identify key factors in CO2RR. We first visualized the frequency of occurrence for each element across the 250,000 alloy surfaces (Fig. 3c), where Cu and Al are emerged as the most prevalent elements. To further elucidate combinations of elements favorable for CO2RR, we computed the average of the smallest ten |ΔECO + 0.67| values for binary alloys (Fig. 3d). Overall, binary alloys comprising Cu and Al in combination with other elements exhibit the most favorable CO2RR activity, alongside numerous high-activity binary alloy surfaces yet to be explored, such as AlPt, AlPd, and SnPd. Beyond binary alloys, 250,000 surfaces include pure metals, ternary and quaternary alloys, with 1,549 out of a total of 4573 compositions satisfying |ΔECO + 0.67 | ≤ 0.15 eV. Figure 3e showcases the foremost ten compositions, with AlCu, CuAu, AlPd, and AlPt topping the list, meanwhile highlighting promising yet unexplored compositions like CuAlSe (23rd) and SnPd (41st). These statistical analyses on elements and compositions offer significant guidance for designing CO2RR alloys and align with experimental evidence. Specifically, it is well-known that Cu is the most used element for CO2RR and various Cu-based alloys like CuAl, CuAu, CuPd, CuGa have demonstrated the exceptional ability in reducing CO2 to diverse product3,36,43,44,45,46,47. CuAl alloy, in particular, has been experimentally demonstrated to have state-of-the-art Faraday efficiency in producing ethylene as well3.

Furthermore, we conducted a statistical analysis of the bulk symmetry of the generated surfaces. Since the surface structures were directly generated via the CDVAE model, we determined their bulk symmetry and surface orientation by a workflow that involved removing the vacuum layer, predicting the space group via XRD pattern48, and matching the cleaved surface from reconstructed bulk structures (see Supplementary Method 2 and Figure S14 for details). Following the identification of bulk symmetry, we found that close-packed arrangement with face-centered cubic (fcc) or hexagonal close-packed (hcp) phase constitutes the majority of the surfaces meeting the |ΔECO + 0.67 | ≤ 0.15 eV, accounting for 26.7% or 23.3%, respectively. Meanwhile, due to the presence of main group elements, some non-close-packed structures were also generated, including orthorhombic, tetragonal phases, etc. These results also support the reliability of our framework in generating stable structures.

Identification of suitable surfaces for CO2RR via DFT calculations

Above our framework has successfully generated a large number of rational and potential surfaces with high CO2RR performance. Specifically, 89,875 surfaces satisfy |ΔECO + 0.67 | ≤ 0.15 eV (the first selection criterion). Next, considering the limitation of computational resources, we try to select the best few surfaces among these surfaces for DFT verification. During CO2RR, HER needs to be suppressed because it competes for active sites on surfaces with CO2RR. According to the work by Greeley et al49., ΔGH exhibits a volcano plot relationship with the experimental current density for HER, with ΔGH = 0.03 eV (ΔEH = −0.27 eV) being most favorable for HER. Thus, the |ΔEH + 0.27| should be as high as possible. On the other hand, ΔEH should not be too negative, otherwise the *H intermediate will occupy too many active sites and cause catalyst poisoning. Thus, the second selection criterion is set as ΔEH + 0.27 ≥ 0.6 eV. In addition, the thermodynamic stability is also very important, which can be roughly evaluated by close to zero or negative formation energy Ef. Considering the computational error 0.1 eV/atom from DFT50 and the MAE of 0.016 eV/atom in our trained ML model, we set Ef < −0.1 eV/atom as the third criterion to make the generated surface as reasonable as possible.

The above three selection criteria for stable surfaces with high stability, activity and selectivity for CO2RR were achieved by accurate GNNs. The adsorption energies in the first two criteria were predicted by two DimeNet + + models. As depicted in Fig. 4a, b, the DimeNet + + models accurately predict CO and *H adsorption energies on the independent test set with MAEs of 0.143 eV and 0.131 eV, and R2 of 0.860 and 0.805, respectively. Considering the complexity of the training data (13,000 various structures), our models’ accuracy is satisfactory and outperforms both the random forest model and GNN model in the literature8,51 that used the same data set. The hyperparameters and training details of our DimeNet + + models are shown in Table S2 and Figure S15-16, respectively. As for the third selection criterion, the pre-trained MEGNet model for the formation energy achieves an MAE of 0.017 eV/atom on the independent test data after being trained with data from the OQMD dataset44. With the help of three GNNs, 110 best surfaces were selected based on the three selection criteria and are shown as dots in the rectangle area in Fig. 4c. Similar to the initial 250,000 surfaces, the most commonly used elements of 110 surfaces are still Cu and Al (Figure S17), and the most frequent element combinations are AlCu, AlCuSe and AlPd (Figure S18). Notably, after considering selectivity, the unexplored AlCuSe and the non-copper-based alloys SnPd, AlAu, and SbPt have emerged among the top 15 leading compositions.

Fig. 4: DFT validation and screening of generated alloy surfaces for experimental validation.
figure 4

DimeNet + + predicted a CO and b H adsorption energies vs DFT calculated adsorption energies on independent testing data. c |ΔECO + 0.67| vs |ΔEH + 0.27| of 250,000 surfaces, the color represents the value of MEGNet predicted formation energy. 110 surfaces selected for DFT validation are in the rectangle area. d DimeNet + + predicted ΔECO vs DFT calculated ΔECO on 110 surfaces selected for DFT validation. The subfigure shows the range of ML-predicted and DFT-calculated ΔECO + 0.67 for the most stable adsorption sites of 110 surfaces, the orange and grey rectangle border ranges from −0.2 to 0.2 eV (orange solid line) and −0.15 to 0.15 eV (grey dash line), respectively. e DFT calculated |ΔECO + 0.67| vs |ΔEH + 0.27| of 110 surfaces. Pure metals, CuAl, AlPd, SnPd, CuAlSe and other surfaces are marked with orange, red, blue, purple, green and grey points, respectively. Five surfaces selected for experimental validation are in the rectangle area and marked with triangles. f Top 3 metal elements among 110 surfaces and top 2 alloys of Cu, Al, and Pd-based surfaces. Structure, crystal system of bulk and miller index of the five example surfaces.

Full size image

Next, we carried out DFT verification on the selected 110 surfaces. First, all possible adsorption sites were enumerated on each surface, then DFT calculations were performed to determine the adsorption energies after adding *CO and *H species. The most negative adsorption energies across different sites on each surface were taken as the final adsorption energies. As shown in Fig. 4d, our DFT-calculated ΔECO (a total of 1385 calculations on all sites) show good agreement with those predicted by the DimeNet + + model, with an MAE of 0.094 eV and R2 of 0.813, even though differences may exist in calculation parameters between our calculations and previous literature8. More importantly, the subfigure of Fig. 4d shows that 97% of the 110 generated surfaces have a DFT-calculated |ΔECO + 0.67 | ≤ 0.2 eV for the most stable adsorption sites (with a maximum value of 0.210 eV), which is five times higher than that of the training data (19.6%), highlighting the effectiveness of MAGECS to inverse design alloy surfaces with potentially high CO₂RR activity (small |ΔECO + 0.67 | ). As a result, the distribution of |ΔECO + 0.67| of generated surfaces is much closer to 0 eV than that of surfaces in the database (Figure S19).

Identification of suitable surfaces for CO2RR via experiments

However, due to the challenges in accurately modeling materials under catalytic conditions, a gap persists between DFT-calculated CO2RR performance and experimental values. Thus, we select promising alloys for experimental validation. Considering synthesizability, our selection was narrowed to alloys composed of three or fewer elements. The compositions frequently observed across the screened 110 surfaces are promising for superior CO2RR activity and selectivity. Thus, we first identified the most prevalent metal elements among 110 surfaces: Cu, Al, and Pd. Subsequently, we focused on surfaces primarily composed of Cu, Al, and Pd, selecting the top two compositions for each (Fig. 4e). As a result, CuAl, AlPd, Sn2Pd5, Sn9Pd7, and CuAlSe2 were chosen, with their exampled surface structures and bulk crystal systems illustrated in Fig. 4f.

However, experimentally synthesized surfaces typically exhibit a mix of crystal orientations (Miller indices), with the dominant ones corresponding to the strongest XRD peaks. Due to this complexity, studies on surface catalytic reactions often focus on modeling these dominant orientations, as they most accurately represent the catalyst behavior52,53,54. Therefore, to experimentally validate the CO2RR performance of predicted CuAl, AlPd, Sn2Pd5, Sn9Pd7, and CuAlSe2 surfaces, we aimed to synthesize these structures with bulk XRD pattern and surface orientation on XRD peak that match the generated surface structures. Successfully, the synthesized surfaces that match the generated structures (Figure S20) were situated close to the edge of the screening rectangle (Figure S21), which were theoretically predicted to exhibit high CO2RR activity and selectivity.

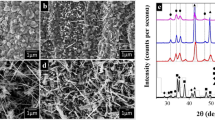
The Scanning electron microscopy (SEM) images (Figure S22) and transmission electron microscopy (TEM) images (Fig. 5a) show that CuAl alloys exist as amorphous nanoblocks. The high-resolution TEM (HRTEM) image of the CuAl (inset in Fig. 5a) displays clear lattice fringes with a lattice distance of 0.2 nm corresponding to the (-311) plane of the prepared catalyst, which aligns with the Miller index of the generated CuAl surface. The energy dispersive spectroscopy (EDS) elemental mapping analysis indicates a homogeneous distribution of the two elements in the alloys without significant phase separation (Fig. 5a). The powder X-ray diffraction (XRD) pattern (Fig. 5b) confirmed the successful synthesis of the alloy. The surface elemental composition of CuAl alloys was investigated through X-ray photoelectron spectroscopy (XPS) measurements, revealing the presence of Cu, Al, and O elements on the surface (Figure S23a). High-resolution Cu LMM and Cu 2p spectra indicate the presence of metallic Cu and copper oxide (Figure S23b and c). Figure S23d illustrates the presence of metallic and oxidized aluminum states on the surface of the alloy. The presence of the atmosphere leads to partial oxidation of the surface of the synthesized nano-alloys. We evaluated the performance of CuAl in electrochemical CO2RR using the timed-current method in a flow-type cell equipped with a three-electrode system in a 1 M KOH solution. Gaseous and liquid products were analyzed using online gas chromatography and nuclear magnetic resonance (NMR) spectroscopy. The presented data demonstrate the high performance of CuAl catalysts in CO2RR reactions (Figs. 5c and 5g). At -0.7 V vs. RHE, the catalyst exhibited the highest CO2RR performance, achieving an overall Faraday efficiency (FE) of 87.73% (Fig. 5c and S24). This significantly outperformed the pure Cu, whose FE of C₁ + C₂ and C₂ products was 84.83% and 40.96%, respectively, at -0.9 V vs. RHE (Figure S25-26). Furthermore, the catalyst retained a relatively high overall FE after 24 hours of continuous electrolysis at -0.7 V vs. RHE (Fig. 5h), presenting outstanding electrochemical stability. Notably, while the CuAl catalyst has been synthesized in previous studies3, the elemental ratio reported (Cu:Al = 2:1) differs from the 1:1 ratio in our catalyst.

Fig. 5: Experimental validation of generated alloy surfaces.
figure 5

a TEM images and EDS elemental mapping images of Cu, Al for CuAl alloys (inset: HRTEM image). b XRD patterns of CuAl alloys and simulated XRD of the bulk structure of generated CuAl surface (subfigure visualizes the generated CuAl surface). c The FEs towards CO2RR products under a range of applied potentials in 1 M KOH (pH = 13.93) of CuAl alloys. (d) TEM images and EDS elemental mapping images of Pd, Sn for Pd5Sn2 alloys (inset: HRTEM image). e XRD patterns of Pd5Sn2 alloys and simulated XRD of the bulk structure of generated Pd5Sn2 surface (subfigure visualizes the generated Pd5Sn2 surface). f FEs towards CO2RR products under a range of applied potentials in 1 M KOH of Pd5Sn2 alloys. g LSV curves of CuAl alloys and Pd5Sn2 alloys (scan rate = 5 mV·s−1, catalyst mass loading = 1 mg·cm-3). h Electrochemical stability test of the CuAl catalyst at −0.7 V vs. RHE and Pd5Sn2 catalyst at −0.8 V vs. RHE at room temperature (FE is the total of the CO2RR to carbon products, gas flow = 20 sccm).

Full size image

In contrast, the Pd5Sn2 materials synthesized through wet chemistry comprise agglomerated nanoparticles (Figure S27). TEM images also indicate that the alloy particles exhibit a uniform size of around 10 nm (Fig. 5d). HRTEM images showed the lattice spacings of 0.22 nm (inset in Fig. 5d), corresponding to the (111) planes of Pd and the Miller index of the generated Pd5Sn2 surface. Additionally, EDS elemental mapping analysis demonstrates the uniform distribution of Pd and Sn across the chosen area (Fig. 5d). The XRD pattern illustrates that Pd5Sn2 displays a pattern similar to that of Pd (JCPDS No. 46-1034), lacking peaks attributed to Sn-based compounds. However, a shift to lower angles, in comparison to the pattern of Pd, suggests the uninformed doping of Sn into Pd (Fig. 5e). The survey XPS spectrum in (Figure S28) validates the presence of Pd and Sn elements on the nanoparticle surface. The assessment of Pd5Sn2 in CO2RR was conducted under identical conditions. The catalyst achieved a faradaic efficiency exceeding 80% for the conversion of CO2 to carbon products within the voltage range of -0.6 to -1.0 V vs RHE. Moreover, the faradaic efficiency (FE) for CO production remained steady at approximately 80% across the potential window, consistently generating CO with an average FE as high as 91.86% at −0.8 V vs RHE (Fig. 5f and S29). By comparison, the pure Pd and Sn only achieve FE of 50.09% at -0.6 V vs. RHE and 76.63% at -0.9 V vs. RHE, respectively, considerably lower than that of Pd5Sn2 (Figure S30-33). Furthermore, Pd5Sn2 maintained good stability in terms of FE of ~90% for CO2RR to carbon products at -0.8 V vs. RHE, remaining stable for 24 hours. In addition, Pd7Sn9, PdAl, and CuAlSe2 were synthesized and all exhibited good CO2RR properties. The FEs for CO2RR to carbon products at specific voltages were all above 70% (Figure S34-44).

Discussion

In summary, we have developed a general property-to-structure inverse design framework, MAGECS, which enables comprehensive exploration of vast chemical spaces and consistent generation of high-quality material structures with target properties. This merit has been realized by innovatively integrating the bird swarm algorithm with state-of-the-art GNNs to effectively navigate the generative model toward materials with superior properties. The efficiency of MAGECS has been robustly demonstrated in the application of designing alloy surfaces for electrocatalytic CO2RR. A total of 250,000 rational and promising alloy surfaces were generated and 110 surfaces were subjected to first-principles calculations, due to their high predictive activity, selectivity, and stability. Significantly, the ratio of surfaces exhibiting high activity for CO2RR surpasses the training data benchmarks by a remarkable 2.5 times. On this basis, we synthesized and characterized five predicted alloys—CuAl, AlPd, Sn2Pd5, Sn9Pd7, and CuAlSe2. Among these, two alloys demonstrated approximately 90% Faraday efficiency in CO2RR (high selectivity) and -600.6 mA/cm2 and -296.2 mA/cm2 current density current density under -1.1 V vs. RHE (high activity), with CuAl notably achieving 76% efficiency for C2 products.

While our developed MAGECS demonstrates considerable capability in the inverse design of CO2RR electrocatalysts, there is still potential for further enhancements. Specifically, the accuracy of supervised GNN models presents room for improvement, as it currently limits the efficiency of our framework. Moreover, numerous functional materials, such as photocatalysts, require the simultaneous satisfaction of multiple target properties including band gap, band edge, and stability. This necessitates the development of efficient multi-objective optimization strategies integrated with inverse design. Finally, considering the gap between thermodynamic stability and experimental synthesizability, integrating a universal model to predict synthesizability into our framework will undoubtedly catapult MAGECS to a greater height.

Methods

Crystal diffusion variational autoencoder

CDVAE consists of two GNNs (GemNet and DimeNet + + are used in this work) and three fully connected neural networks (NNs). While training, the DimeNet + + was trained to encode the original material structures into latent vectors and the GemNet was trained to denoise the noised material structures. The main hyperparameters for training CDVAE are shown in Table S4-6. All main loss functions on the training set and validation set converge well (Figure S46), demonstrating the training of CDVAE was adequate.

Supervised GNN

Six popular supervised GNNs (CGCNN55, SchNet56, DimeNet + +33,34, PaiNN57, GemNet58 and GemNet-OC51) were tested for surface property prediction. As shown in Figure S47, the CGCNN and SchNet, which did not consider the information of interatomic angles, showed a clear performance gap with other GNNs on testing data. The DimeNet + + had comparable performance to PaiNN and outperformed the GemNet and GemNet-OC on testing data. Moreover, the DimeNet + + exhibited faster training speed than PaiNN (1.2x), GemNet (2x) and GemNet-OC (2.5x). Thus, the DimeNet + + was utilized to predict CO and H adsorption energies in this work. The main hyperparameters of training these GNNs are listed in Table S2, 7–11.

Bird swarm algorithm

The BSA algorithm was inspired by the swarm intelligence observed in bird swarms. Birds exhibit three main behaviors: foraging, vigilance, and flight. These social interactions help birds find food and avoid predators, increasing their chances of survival. BSA models these behaviors with five simplified rules (see Supplementary methods S3 and Figure S2), endowing it with good optimization efficiency and the ability to escape local optima. Thus, the BSA is used for global exploration of the chemical space in our framework. Table S3 shows the hyperparameters of performing BSA. We wrote the BSA with python language and the code is available in https://github.com/szl666/CO2RR-inverse-design.

Automated DFT calculations

All the DFT energies in this work were calculated by the VASP package59. The slabs with all kinds of adsorbates were automatically built using the Pymatgen package60. The structure optimization was performed using a plane wave-based group with a 350 eV cutoff energy and the RPBE exchange-correlation function. The energy and force convergence criterion are set to be 5 × 10-4 eV and 0.02 eV·Å-1, respectively. The Gibbs free energy difference ΔG of the adsorbates before and after adsorption on the surface was calculated to consider temperature’s influence. The standard hydrogen electrode approximation was used to bypass electron energy calculation. The free energy was calculated by Eq. (1):

$$G=E+{ZPE}-{TS}$$
(1)

where E is energy, ZPE and S are the zero-vibration energy and entropy, respectively, which can be obtained by VASP vibrational calculation. T is the temperature setting to 300 K.

Material synthesis

All chemicals are of analytical grade and used without further purification. Copper powder, aluminum powder and palladium powder were purchased from Hebei Jiuyue New Material Technology Co. Palladium diacetylacetonate and selenium powder were bought from Aladdin. SnCl2, NaBH4, Polyvinyl pyrrolidone (PVP) and ethylene glycol were bought from Mackli. Ethanol, potassium format, N₂H₄·H₂O and KOH were purchased from Sinopharm. The ion exchange membrane was purchased from Dupont. Carbon paper (CP) was purchased from Avcarb. The detail of the synthesis of CuAl, CuAlSe2, PdAl, Pd15Sn6 and Pd15Sn6 are discussed in Supplemental Methods S4. The EDS results of above-mentioned materials are shown in Table S12.

Material characterization

The phase and crystallinity of samples were characterized by X-ray diffraction (Miniflex6000, Rigaku) at 40 kV and 15 mA using Cu-Kα radiation (λ = 1.54178 Å) at room temperature and scan speed was 15°/min. Morphology of the catalysts was characterized by High resolution field emission scanning electron microscope (FEI Inspect F50) and Thermo Scientific Talos F200X transmission electron microscope (STEM, Talos F200X). X-ray photoelectron spectroscopy (XPS) was performed on Escalab 250Xi. NMR spectra were recorded on a AVANCE III HD 600 MHz. In which 500 μL electrolyte was added with 100 μL D2O and dimethyl sulfoxide (DMSO) was added as the internal standard.

Electrochemical characterization

The electrocatalytic performance of a three-electrode system for CO2RR was investigated on a CHI 760E electrochemical workstation at room temperature. The flow cell (Figure S43) assembly used consists of a gas flow chamber, a cation chamber and an anion chamber (0.5 × 0.5 × 0.5 cm3). Each chamber has an inlet and outlet for electrolytes or gas. A commercial platinum sheet (0.5 × 0.5 cm2) is used as anode and an Ag|AgCl is acted as the reference 1. M KOH (pH = 13.93 ± 0.028) are used as the cathode and anode electrolyte, respectively. The fabrication process for the working electrode involved adding 100 μL of catalyst ink dropwise to the carbon paper (0.5×0.5 cm2) electrode to achieve a loading of approximately 1 mg cm-2. The electrode was then dried under an infrared lamp. The cathode chamber and anode chamber were separated by a piece of ion exchange membrane. Electrolytes were cycled at 20 mL min-1 and the CO2 gas was supplied at rate of 20 sccm.

All potentials in our experiments are converted to reversible hydrogen electrode (RHE) reference scale by using the Nernst function as below,

$$E\,({vs}.{RHE})=E\,({vs}.{Ag}|{AgCl})+0.197V+0.059\,\times {pH}$$

The detail about the products analysis is discussed in Supplementary Methods S5 and Figure S44-45.