Pregnancy entails a U-shaped trajectory in human brain structure linked to hormones and maternal attachment

Abstract

Growing evidence places the gestational period as a unique moment of heightened neuroplasticity in adult life. In this longitudinal study spanning pre, during, and post pregnancy, we unveil a U-shaped trajectory in gray matter (GM) volume, which dips in late pregnancy and partially recovers during postpartum. These changes are most prominent in brain regions associated with the Default Mode and Frontoparietal Network. The U-shaped trajectory is predominantly linked to gestational factors, as it only presents in gestational mothers and correlates with fluctuations in estrogens over time. Finally, the mother’s mental health status mediates the relationship between postpartum GM volume recovery and maternal attachment at 6 months postpartum. This research sheds light on the complex interplay between hormones, brain development, and behavior during the transition to motherhood. It addresses a significant knowledge gap in the neuroscience of human pregnancy and opens new possibilities for interventions aimed at enhancing maternal health and well-being.

Introduction

Each year, nearly 140 million women give birth worldwide¹. Pregnancy represents a transformative journey marked by critical psychological adaptations to motherhood². In humans, neuroimaging studies scanning women before and after pregnancy and around the peripartum suggest that first-time mothers experience a remodeling of brain architecture^3,4,5 that predicts postpartum maternal attachment towards the newborn⁴. Concurrently, murine research suggests that maternal brain changes are driven by gestational hormones, including steroid hormones, and facilitate maternal behavior^6,7,8. A promising hypothesis posits that human brain changes during the maternal transition follow a U-shaped trajectory, with an initial decrease in cortical gray matter (GM) volume during pregnancy, followed by a partial recovery in the postpartum period⁹. Such neural trajectory could be driven by mirroring fluctuations in steroid hormones before and after childbirth¹⁰ and could be further influenced by parenting experience^11,12. Despite these observations, no previous study has charted the complete trajectories of human brain change from pre-conception throughout pregnancy and postpartum, integrating multimodal neuroimaging data, endocrine assessments, and neuropsychological information (see Pritschet et al., for a precision imaging study of a single-subject¹³).

In this prospective study, women completed a Magnetic Resonance Imaging (MRI) scanning protocol, hormonal analyses, and neuropsychological evaluations before, during, and after pregnancy, along with a group of nulliparous women with no plans to become pregnant. The study also included a group of non-gestational mothers, who were partners of the gestational mothers, to discern the effects of pregnancy from those of the parenting experience. This landmark design allowed to uncover the brain trajectory that unfolds during the transition to motherhood, as well as its connection with steroid hormones and maternal attachment, filling a critical void in the human maternal brain literature.

Results

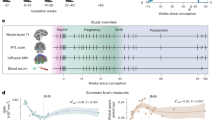
This longitudinal study included 127 women undergoing their first pregnancy, henceforth referred to as gestational mothers. We acquired structural MRI scans at five sessions: before conception, at the second and third trimesters of pregnancy, and during the postpartum, at one and 6 months after birth, as well as resting state MRI scans before conception and at one and 6 months after birth. To distinguish the impact of gestational factors from parenting-related factors, we also collected longitudinal data at similar time intervals from 20 female partners of the women in the gestational mothers’ group, henceforth, non-gestational mothers. Finally, to account for brain changes unrelated to motherhood, we scanned 32 women without children nor plans of going through pregnancy or maternity; henceforth, nulliparous women. For every group and session, structural MRI data was paired with urine samples for endocrine determinations and questionnaires to assess mental health, and maternal attachment toward the infant (see the demographic information in table S1).

Trajectory of structural brain changes across gestation

To unravel the complete trajectory of structural brain changes during pregnancy and postpartum, we analyzed the participants’ global cortical GM volume, thickness, and surface area over the five sessions. There were no pre-existing differences in global cortical GM volume, thickness, and surface area among the three groups of gestational mothers, non-gestational mothers, and nulliparous controls (cortical GM volume: F(2,176) = 0.461, η2 = 0.005, p = 0.631; cortical thickness: F(2,176) = 0.258, η2 = 0.003, p = 0.773; surface area: F(2,176) = 0.583, η2 = 0.007, p = 0.559).

Compared to nulliparous women, gestational mothers displayed a U-shaped quadratic trajectory in global cortical GM volume from before pregnancy to 6 months postpartum, with the inflection point at late pregnancy (Group x Session [Quadratic Term] interaction: B = 207,552.67, 95% CI = [177,360.29, 237,723.63], SE = 15,457.46, t = 666.43, p < 0.001, q < 0.001) (Fig. 1A and table S2). The observed trajectory was statistically significant even after controlling for the effects of the participants’ age, total intracranial volume (eTIV), image quality, and time between sessions (Table S2). Changes in Body Mass Index (BMI) during pregnancy and the postpartum did not yield a statistically significant effect in the results (Table S3). This quadratic model had a significantly better fit than a linear model of the cortical GM volume trajectory over time (Table S4), and adding the eTIV into the interaction term did not improve the fit of the quadratic model either (Table S5). Moreover, a generalized additive model further confirmed the quadratic nature and symmetry of the pattern of GM volume changes (fig. S1).

Fig. 1: Longitudinal cortical gray matter volume trajectory across pregnancy and postpartum (N = 179).

Longitudinal changes were derived from the group x session² fixed effect term of the adjusted linear mixed effect model: Cortical GM Volume ∼ Group + Session + Session² + Group*Session + Group*Session² + eTIV + Age + Euler + Inter-session Interval + (1 ∣ participant ID). A Mean percentage of cortical GM volume change per group and session in relation to the baseline (i.e., Session 1 - Pre-pregnancy Session). Error bars correspond to 95% confidence intervals around the sample’s mean at each experimental group and session, respectively. The gray shading corresponds to the pregnancy period. B Vertex-wise signed effect size maps (η_p²) of the group x session² interaction (q value < 0.05). Indicating larger quadratic effects (red) and smaller quadratic effects (blue) in gestational mothers than in nulliparous or non-gestational mothers. Signed effect size maps were projected to the inflated fsaverage template provided by the FreeSurfer software. Colors were collapsed to ±0.14, which indicated a large effect size. Gest, gestational mothers; nGest, non-gestational mothers; Null, nulliparous women.

The U-shaped trajectory comprised a global 4.9 % GM volume decrease during pregnancy (95% CI = [−5.2, −4.6]) (table S6), followed by a 3.4 % GM volume increase from late pregnancy to 6 months postpartum (95% CI = [3.1, 3.6]). In the second trimester of pregnancy cortical GM volume had already decreased by 2.7% (95% CI = [−3.0, −2.5]) (Table S6). GM volume did not fully return to pre-pregnancy levels at 6 months postpartum (B = −7693.05, 95% CI = [−9371.04, −6010.90], SE = 857.18, t = −8.97, p < 0.001) (Table S7), although the GM volume change between these sessions did not significantly differ compared to nulliparous women (B = 72.22, CI = [−3362.64, 3,520.97], SE = 1768.46, t = 0.04, p = 0.967 (Table S8). Hence, we found support for a U-shape trajectory of cortical GM volume reductions during pregnancy, with a partial recovery at 6 months into postpartum.

A vertex-wise analysis indicated that, compared to nulliparous women, the cortical GM volume quadratic trajectory affected widespread bilateral regions (94% of brain vertices surviving a q < 0.05 False Discovery Rate (FDR) correction) (Fig. 1B). The most prominent GM volume changes, measured as partial eta squared greater than 0.06, were observed in the inferior parietal, superior frontal, supramarginal, precuneus, and superior temporal (Table S9). Similar findings were observed when comparing the quadratic GM volume trajectory in gestational versus non-gestational mothers (Fig. 1B). Moreover when decomposing GM volume into area and thickness, both global and vertex-wise analyses revealed a comparable U-shaped pattern in gestational mothers (Figs. S2 and S3 and Tables S10–S11). The quadratic trajectories observed in GM volume, area, and thickness followed a normal distribution, with no discernible subgroups among gestational mothers showing distinct brain trajectories (Fig. S4). Thus, the observed brain changes were highly consistent, affected both hemispheres and were observed in both cortical surface and thickness measures.

No significant linear or quadratic changes in GM volume, area, or thickness were found in non-gestational mothers (versus nulliparous women) during their transition to motherhood (Tables S2, S10, and S11), suggesting that the observed cortical trajectory was primarily influenced by gestational factors (Fig. 1). Additional supplementary analyses on gestational mothers indicated that type of conception, nor the biological sex of the baby, affected the quadratic trajectory for cortical GM volume (Tables S12–S13). Moreover, the type of parturition and type of breastfeeding did not play a significant role in the cortical GM volume increases occurring during postpartum (Tables S14–S15). Therefore, the observed changes were unique to gestational mothers and were independent of situational factors.

For completeness, changes in cerebral white matter (WM) volume and global cerebrospinal fluid (CSF) were also examined throughout the transition to motherhood, although it should be noted that T1 MRI images are not optimal for analyzing these metrics. Compared to nulliparous women, gestational mothers displayed a U-shaped quadratic trajectory in global WM volume from before pregnancy to 6 months postpartum (Fig. S5A), and an inverse U-shaped trajectory in CSF (Fig S5B), both reaching an inflection point at late pregnancy (WM volume: Group x Session [Quadratic Term] interaction: B = 48,457.14, 95% CI = [37,294.88, 59,623.65], SE = 5,717.89, t = 8.47, p < 0.001, q < 0.001; CSF: Group x Session [Quadratic Term] interaction: B = −477.48, 95% CI = [−699.73, −255.27], SE = 113.82, t = −4.20, p < 0.001, q < 0.001) (Tables S16–S17). These trajectories were statistically significant after controlling for the effects of the participants’ age, eTIV, image quality, and time between sessions (Tables S16–S17). An analysis of variance confirmed that both WM volume and CSF changes were better explained by the quadratic model than by a linear model (Tables S18–S19).

We then examined whether there could be differences in the cortical GM volume trajectory based on the functional location of the changes by parcellating the brain in Yeo’s seven large-scale functional brain networks¹⁴ (Fig. 2A). Pre-post pregnancy changes have been mainly reported in Default Mode and Frontoparietal regions^4,5, which also seem to undergo smaller GM volume increases during early postpartum³. Hence, we hypothesized that there might be two different neuroanatomical trajectories: one for regions belonging to higher-order cognition networks (Default Mode and Frontoparietal) and another including the rest of the networks (Visual, Somatomotor, Dorsal Attention, Ventral Attention, and Limbic).

Fig. 2: Cortical gray matter volume trajectories based on the functional location of the changes in gestational mothers (N = 179).

The different trajectories were assessed by parcellating the brain in Yeo’s seven large-scale functional brain networks¹⁴. A Cortical parcellation of Yeo’s seven large-scale functional brain networks. B Mean percentage of cortical GM volume change per group and session and functional location in relation to the baseline (i.e., Session 1 - Pre-pregnancy Session). The gray shading corresponds to the pregnancy period. C Vertex-wise signed effect size maps (η_p²) of the group x session² interaction (q value < 0.05 and η_p² > 0.06 to capture medium to big effect sizes). Indicating larger quadratic effects (red) and smaller quadratic effects (blue) in gestational mothers than in nulliparous. Signed effect size maps were projected to the inflated fsaverage template provided by the FreeSurfer software. Colors were collapsed to ±0.14, which indicated a large effect size. Gest, gestational mothers; Null, nulliparous women. D Spin test for the signed effect sizes of the vertex-wise Group [gestational mothers vs nulliparous women]*Session² interaction in cortical volume within the seven large-scale functional brain networks. Black horizontal bars represent the observed values and the violin plots reflect the null distributions obtained using 1000 spin-permutations of the maps. The exact one-tailed p values are reported when p < 0.05. No multiple comparisons corrections were applied. The black dot on the center of the boxplot represents the median, the box encloses the lower and upper quartiles, and the whiskers extend to the minimum and maximum values within a range of 1.5 times the interquartile range.

We observed the U-shaped pattern in all networks (Fig. 2B). However, using a model that differentiated the cortical GM volume trajectory occurring in higher-order networks (Default Mode and Frontoparietal) from the remaining networks (Model A—see “Formula Nine” from “Methods”), we observed a steeper curve for the trajectory in higher-order regions (Nested Networks [Default Mode + Frontoparietal] x Session [Quadratic Term] interaction: B = 22893.02, 95% CI = [20,574.91, 25,211.13], SE = 1180.91, t = 19.36, p < 0.001) (Fig. 2B and Table S20). Indeed, this model had a better fit than the one assessing a single trajectory for all networks (Model B—see “Formula Ten” from “Methods” and table S21), therefore outperforming the one-size-fits-all trajectory approach (BIC Model A < BIC Model B: 71395.88 < 72353.42). When evaluating the spatial correspondence between the signed effect size maps of the vertex-wise analysis and Yeo’s networks, we observed a significant above-chance quadratic effect in the Default Mode network (p = 0.006) (Fig. 2C, D). There was also a significant below-chance cortical quadratic effect in the Limbic network (p = 0.012). Hence, we observed U-shaped trajectories with varying magnitudes based on the functional location of the GM volume changes.

Functional connectivity changes across gestation

We next explored whether pregnancy also entails changes in women’s functional connectome. We used Schaefer’s cortical parcellation (400 parcels) mapped to Yeo’s 7 large-scale functional networks^14,15 to evaluate changes in functional network connectivity before and after pregnancy. Specifically, we measured changes in the functional organization and network segregation using whole-brain and within-network modularity, mean participation coefficient, and system segregation graph theory metrics^16,17. Modularity allowed us to capture network compartmentalization. That is the extent to which a specific network is subdivided into communities of strong within-module connectivity and weak between-module connectivity. Using system segregation, we assessed the balance between connections within each Yeo’s network and those spanning different networks. Finally, through the mean participation coefficient we quantified the extent of intermodular connectivity across Yeo’s 7 large-scale functional networks.

No significant shifts in the whole-brain modularity were observed when considering Yeo’s 7-large-scale functional networks as the initial communities (Table S22). Similarly, there were no functional changes in the system segregation, modularity organization or mean participation coefficient of the network’s nodes within each network (Table S23). Overall, no significant alterations in the segregation/integration properties of functional networks were observed during the transition to motherhood.

Relationship between structural brain changes and gestational steroid hormones

Since murine models suggest that gestational steroid hormones are key drivers of neuroplasticity^18,19, we assessed their contribution to the observed cortical trajectory in human pregnancy. Specifically, we tested the association between the longitudinal trajectories of percentage of cortical GM volume change and the levels of a wide array of steroid metabolites, considering data from before pregnancy to the first month postpartum (i.e., sessions 1, 2, 3, and 4). Among the 49 analyzed hormones, 39 of them, including six estrogens, twelve progestogens, fourteen glucocorticoids, and seven androgens, followed a quadratic trajectory during pregnancy and early postpartum (Table S24). We observed two types of trajectories: an inverse U-Shape with either a turning point at early or late pregnancy and a U-Shape with a turning point at early or late pregnancy (Figs. S6–S9).

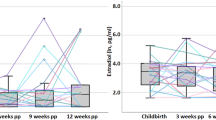
When evaluating the linked evolution between neuroanatomical and hormonal trajectories, only the trajectory of two sulfated estrogens (estriol sulfate and estrone sulfate) showed significant negative correlations with the GM volume trajectory found in gestational mothers, surviving a hierarchical multiple testing correction within each steroid family (estriol sulfate: Spearman’s R = −0.32, p = 0.001, q = 0.006; estrone sulfate: Spearman’s R = −0.24, p = 0.016, q = 0.049; Fig. 3) (see Table S25 for all 49 correlations). Thus, the observed U-shape in cortical GM volume changes in gestational mothers was associated with the mirroring trajectory of sulfated estrogens.

Fig. 3: Longitudinal correlation between estrogens and cortical gray matter (GM) volume in gestational mothers (N = 100).

From our sample of 127 gestational mothers, 100 provided urine samples at sessions 1, 2, 3, and 4 and were therefore included in these analyses. A On the left Y-axis, there is the global percentage of cortical GM volume change in each session in relation to the baseline (i.e., Session 1 - Pre-pregnancy Session). On the right Y-axis, the relative levels in estriol 3-sulfate and estrone sulfate per session relative to the maximum change (% of max) are represented. Mean values are represented as circles and their 95%-confidence intervals as error bars. B Two-sided correlations between the quadratic parameter coefficients of GM volume change (Y-axis, extracted from the adjusted model: cortical GM volume change ∼ Session + Session² + (Session²∣ participant ID)) and the two steroid concentrations (X-axes, extracted from the adjusted model: Steroid concentration ∼ Session + Session² + (Session²∣ participant ID)). P-values were corrected within each metabolite family using FDR. The green lines and the gray shaded area represent the least squares regression lines and the 95% confidence intervals around the smooth line, respectively. Spearman’s R, Spearman’s correlation coefficient; p, uncorrected p-value; and q, hierarchical FDR corrected p-value.

Relationship between structural brain changes and maternal well-being and attachment

In rodents, the brain remodeling during pregnancy orchestrates the onset of maternal behavior at birth⁶. Hence, we next assessed the link between the observed global neuroanatomical changes in gestational mothers and their maternal attachment toward the newborn. With this aim, we divided the cortical GM volume trajectory into two components: the percentage of GM volume decreases from pre-pregnancy to late pregnancy (sessions 1 and 3), and the percentage of GM volume increases from late pregnancy to 6 months postpartum (sessions 3 and 5). Both components of the trajectory - the GM decrease from pre-pregnancy to late pregnancy, and the GM increase from late pregnancy to 6 months postpartum- were positively associated with the mother-to-infant attachment scale at 6 months postpartum. Specifically, smaller GM volume decreases during pregnancy and higher GM volume recovery during postpartum predicted lower levels of hostility towards their baby (Fig. 4A). However, only the latter association remained significant after adjusting for multiple comparisons (Pearson’s R (96) = 0.29, CI = [0.10, 0.46], t = 3.00, p = 0.003, q = 0.028). No other subscales of antenatal or postnatal maternal attachment were correlated with the GM volume changes (Table S26). Thus, a greater recovery of maternal brain changes from late pregnancy to 6 months postpartum was associated with higher levels of attachment with the infant at 6 months postpartum, particularly in terms of reduced hostility.

Fig. 4: Longitudinal correlation between cortical gray matter volume, maternal attachment, and maternal well-being in gestational mothers (N = 98).

From our sample of 127 gestational mothers, 98 completed the MRI session at 6 months postpartum, and were therefore included in these analyses (see Fig. S7 for the dropout scheme). A Two-sided Pearson’s correlation between the percentage of cortical GM volume recovery during postpartum—from the 34th week of pregnancy to 6 months postpartum- (X-axis) and absence of hostility at 6 months postpartum (Y-axis). P-values are corrected for multiple testing, using FDR. The orange line and the gray shaded area represent the least squares regression line and the 95% confidence intervals around the sample’s mean at each experimental session, respectively. Pearson’s R, Pearson’s correlation coefficient; p, uncorrected p-value; and q, False-Discovery-Rate corrected p-value. B Path diagram of the mediation model between the percentage of cortical gray matter volume recovery (% GMV) during postpartum—from the 34th week of pregnancy to 6 months postpartum -, maternal well-being, and absence of hostility at 6 months postpartum. P-values used for the path diagram are uncorrected p-values. Numbers represent the coefficient estimates, asterisks indicate the significance of each pair of associations (*, p < 0.05; **, p < 0.01; ***, p < 0.001), and the positive symbol (+) indicates the positive association between each pair of variables.

Finally, given the impact of mental health on maternal behavior, we sought to investigate whether the relationship between global cortical GM volume recovery from late pregnancy to 6 months postpartum and maternal attachment was mediated by maternal mental health outcomes at 6 months postpartum, including well-being, perceived stress, and postnatal depression. The three measures significantly correlated with absence of hostility at 6 months postpartum in gestational mothers (Well-being: Pearson’s R (96) = 0.55, CI = [0.40, 0.68], t = 6.48, p < 0.001, q < 0.001; Depression: R (95) = −0.31, CI = [−0.48, −0.12], t = −3.22, p = 0.002, q = 0.002; Stress: R = −0.44, CI = [−0.58, −0.26], t = −4.75, p < 0.001, q < 0.001). Moreover, the mother’s well-being mediated 51% of the effect of GM volume recovery on absence of hostility (B = 0.51, 95% CI = [0.22, 1.13], p = 0.003, q = 0.008; Table S27; Fig. 4B). The mother’s lower perceived stress mediated 29% of the effects of GM volume recovery and absence of hostility, however, this result did not survive multiple testing correction (B = 0.29, 95% CI = [0.01 0.71], p = 0.045, q = 0.069, Table S27). Depression scores did not have a significant mediating effect (B = 0.13, 95% CI = [−0.08, 0.39], p = 0.167, q = 167, Table S27). In sum, the positive association between maternal attachment in gestational mothers and cortical GM volume recovery was partly explained by higher levels of maternal well-being.

Discussion

This prospective study uncovered a U-shaped trajectory in cortical GM volume, area, and thickness in first-time gestational mothers during pregnancy and postpartum, peaking in the peripartum period. GM reductions were evident as early as the second trimester, suggesting an early onset of brain remodeling during pregnancy. At 6 months postpartum, GM volume had not returned to pre-pregnancy levels, supporting the notion that maternal brain changes may be a long-lasting phenomenon that persists beyond the postpartum period^4,5,20,21. These findings indicate that gestation and postpartum induce opposite effects on the cortical mantle, resolving a long-debated puzzle for scholars in the field. In particular, our results suggest that previous studies reporting volume increases in cortical GM during postpartum^{21,22,23,24,25} and less pronounced cortical GM decreases before and after pregnancy (−2.7% at 3 months postpartum vs −4.9% at late pregnancy)^4,26, were indeed capturing part of the postpartum recovery process. We also discovered a similar U-shaped pattern in WM volume, alongside an inverse U-shaped pattern in CSF volume, suggesting that at least part of the observed changes could result from a compensatory effect, where increased brain fluid compresses cortical tissue. These patterns, along with specific subcortical changes, warrant further validation via more appropriate MRI sequences, such as diffusion imaging for WM microstructure, arterial spin labeling for cerebral blood flow changes, and T2 high-resolution images for subcortical structures.

External factors related to the parental experience minimally influenced this trajectory, as it solely manifested in women undergoing pregnancy but was absent in non-gestational mothers. This suggests that the U-shaped trajectory observed from before pregnancy to 6 months postpartum is mainly due to gestational factors. Importantly, these findings do not preclude parenting-related brain adaptations in non-gestational mothers nor do they exclude such adaptations as contributing factors of the neuroanatomical changes observed in gestational mothers. The impact of childrearing and environmental factors on the human maternal brain may be less pronounced and more localized than the effects of pregnancy, in line with previous research on the paternal brain^27,28. Given that motherhood is a life-long journey, parenting-related factors may also contribute to brain changes observed beyond the immediate postpartum^4,20,25, and in middle-aged and older mothers²⁹. Lastly, our study did not measure parenting investment or behavior; thus, we cannot determine whether gestational mothers were more engaged in parenting behaviors than non-gestational mothers.

The dynamic neuroanatomic changes observed in gestational mothers were associated with fluctuations in two types of estrogens: estriol and estrone sulfate. Similarly, a previous study reported estradiol levels in the third trimester to be associated with GM volume changes before and after pregnancy in humans⁵. Our study offers a more complete picture, showing that both trajectories evolve together yet in opposite directions. The larger the increase and posterior decrease in estriol and estrone, the larger the decrease and posterior recovery in GM volume change. Estrogen surge during pregnancy is mainly due to placental production³⁰ and consequently plummets after placental expulsion at childbirth. In line with this, we observed a turning point in estrogenic and cortical trajectories around childbirth. These observations suggest that parturition is a critical phase in maternal brain remodeling that deserves more research attention³¹. The brain-hormone associations revealed in our study bridge findings in humans with the mechanistic insights gained from animal models^6,8, reinforcing the idea that estrogens critically influence neuroplasticity processes during human pregnancy. Research should confirm these results using blood samples, which will more closely reflect the circulating free-hormonal levels and their conjugates.

The U-shaped trajectory of GM volume affected numerous regions across the brain’s cortex, encompassing 94% of its surface. Particularly striking changes were observed in higher-order cognitive networks such as the Default Mode and Frontoparietal networks, which exhibited a steeper decrease during gestation, reaching the lowest point at late pregnancy. After childbirth, these networks recovered at a similar rate as the rest of the networks and thus remained at a lower level at 1 and 6 months postpartum. These findings align with previous studies showing that late pregnancy GM decreases affect all networks³ and that reductions in Default Mode and Frontoparietal networks persist longer compared to other networks^3,4,5. However, none of the networks exhibited changes in their functional segregation properties, suggesting that the distinct GM volume trajectories might not be reflected in a functional network reorganization. Of note, the lack of changes observed in these metrics do not preclude the occurrence of numerous other functional changes during this life transition or at later stages of the postpartum period. Using network coherence as their measure of interest, Hoekzema and colleagues reported pre-post-pregnancy increases in network connectivity within a cluster located in the Default Mode Network. Moreover, cross-sectional studies have reported differences in the effective connectivity between key nodes of the parental caregiving network in first-time mothers across the early and late postpartum periods^32,33. Together, a more in-depth analysis of functional changes, including the examination of other network functional properties and even alternative network constructions, is essential to characterize connectomic changes in mothers. Furthermore, future investigations should explore the structural-functional coupling across the perinatal period.

Behaviorally, the percentage of GM volume recovery during the postpartum was associated with a higher absence of hostility towards the infant at 6 months postpartum. This positive association suggests that the brain remodeling experienced by gestational mothers might be adaptive, facilitating facets of maternal behavior. Our results agree with a prior study reporting an association between pre-to-post-pregnancy GM volume changes and higher scores on attachment quality and absence of hostility⁴. Here, we reveal that maternal attachment at 6 months postpartum depends more on the recovery of GM volume during the postpartum period than on the decrease in GM volume during pregnancy. Forthcoming work should incorporate precise assessments of childrearing involvement and parent-infant interactions to further understand the functional meaning of these brain changes. Additionally, studies integrating cognitive and neuroimaging assessments should also explore if this pronounced neural remodeling is linked to the increased cognitive load and subsequent cognitive reserve of new mothers³⁴.

Pregnancy and postpartum are defined as stages with high risk for mental health disorders^35,36. Mental health can, in turn, impact mother-to-infant attachment and the infant’s cognitive development³⁷. We found that even in a sample of healthy mothers, higher well-being, lower perceived stress, and lower depression scores correlate with a higher absence of hostility towards the newborn. Our results further reveal that the mother’s general well-being mediates more than 50% of the relationship between GM volume recovery and attachment at 6 months postpartum. This suggests that the neuroanatomical changes occurring after pregnancy affect the mental well-being in mothers, which in turn facilitates adaptive maternal attachment. Maternal well-being has also been shown to mediate the relationship between improved cognitive performance and reduced top-down corticolimbic inhibition in first-time mothers at one year postpartum³². Together, these findings open the door to identifying specific periods during pregnancy and postpartum when experiences and interventions may have the greatest impact on maternal brain health and psychological well-being. Research should also explore if these neuroanatomical trajectories are disrupted in psychiatric disorders such as perinatal depression.

In sum, our study offers a comprehensive view of the brain’s adaptations to motherhood by linking brain structure, hormonal dynamics, and maternal attachment. Leveraging the largest longitudinal neuroimaging dataset of mothers to date, we unveil a distinctive U-shaped trajectory of cortical changes during pregnancy and the postpartum. Notably, this U-shaped trajectory was associated with dynamic fluctuations in gestational estrogen levels, while the postpartum recovery of GM volume was associated with increased maternal attachment. Along with these widespread neuroanatomical changes, we discerned a more pronounced trajectory within the Default Mode and the Frontoparietal networks. By revealing the dynamic brain changes during pregnancy, the possible hormonal drivers behind these changes, and how their interplay impacts the mother’s psychological well-being, this study marks a crucial advance in maternal brain research.

Methods

This research was approved by the Ethics Committee at the Hospital del Mar Research Institute (Ref: 2017/7450/I), the Hospital Clínic de Barcelona (Ref: HCB/2018/0357), and the Hospital Universitari Quirón Dexeus (Ref: 7/2/2017), in accordance with the Declaration of Helsinki guidelines. All participants signed a consent form before participating in the study and received monetary compensation for their participation.

Study design and participants

For this prospective cohort study, first-time mothers participated in an MRI acquisition protocol before, during, and after their first pregnancy. This longitudinal design allowed us to use each woman’s baseline state as her control. First-time gestational mothers were also compared to a group of non-gestational mothers and nulliparous women. Participants completed a total of five sessions: (1) pre-conception, (2) at 18 weeks of pregnancy (mean ± sd = 18.25 ± 0.94 weeks), (3) at 34 weeks of pregnancy (mean ± sd = 34.20 ± 0.90 weeks), (4) at one month postpartum (mean ± sd = 1.09 ± 0.27 months), and (5) at 6 months postpartum (mean ± sd = 6.05 ± 0.32 months).

Participants were recruited in the Barcelona area through word-of-mouth, local hospitals, and social media ads. We recruited nulliparous women who were planning on becoming pregnant in the near future (i.e., gestational mothers), nulliparous women whose female partners were planning to become pregnant in the near future (i.e., non-gestational mothers), and nulliparous women without any plans of having children soon (i.e., nulliparous women). Exclusion criteria for all participants included being over 45 years old, being pregnant at the pre-conception session, previous pregnancies, current major neurological or psychiatric disorders assessed by the MINI International Neuropsychiatric Interview³⁸, intake of psychiatric medication, and MRI incompatibilities. Gestational mothers and their non-gestational partners who did not achieve pregnancy after the first MRI session were discontinued from the study.

The initial sample at the pre-conception session comprised 317 gestational mothers, 56 non-gestational mothers, and 60 nulliparous women. However, we only included participants who completed at least sessions 1, 3, and 4 (pre-conception, 34 pregnancy weeks, and one month postpartum), met the above-mentioned inclusion criteria, and whose MR images were not affected by artifacts in the structural MRI data analyses. Participants with an artifact or no MRI acquisition at sessions 2 and 5 (18 pregnancy weeks and 6 months postpartum) were included in the analyses, excluding only the session with the affected MRI acquisitions. Our final experimental sample consisted of 127 first-time gestational mothers (mean age ± sd = 33.67 ± 4.04 years), 20 non-gestational mothers (mean age ± sd = 32.15 ± 3.53 years), and 32 nulliparous women (mean age ± sd = 30.38 ± 3.23 years). Of note, except for one, all non-gestational mothers of the final sample were partners of women from the gestational mothers group. For an overview of the group allocation and dropout per group and session, please see Fig. S10.

In the gestational mothers’ group, 45.67% of participants became pregnant via natural conception (58 women), and 54.33% conceived via assisted reproduction methods (69 women). Of those who used assisted reproduction, 23.19% used artificial insemination (16 women), 40.58% used in-vitro fertilization (28 women), and 36.23% used intracytoplasmic sperm injection (25 women). At childbirth, 61.90% of women delivered their babies via vaginal birth (78 women), 11.11% had a scheduled C-Section (14 women), and 26.98% had an unplanned C-Section (34 women). One woman gave birth to monozygotic twins, and one delivered dizygotic twins. Of the total 129 babies delivered, 56.80 % were males and 43.20% were females. Lastly, 84.68% of gestational mothers breastfed exclusively in the first month postpartum, 7.26% mixed breastfeeding and baby formula, and 8.06% did not breastfeed (Table S1).

Gestational mothers and non-gestational mothers did not differ in age (B = −1.52, p = 0.232) nor did non-gestational mothers and nulliparous women (B = 1.77, p = 0.242). However, we did observe significant age differences between gestational mothers and nulliparous women (B = 3.29, p < 0.001). Groups were homogenous in education level (χ2(4, N = 179) = 2.7, p = 0.608). Finally, there were no significant group differences in the time intervals between sessions, except for a difference in the interval between the first and second sessions in gestational and non-gestational mothers when compared to nulliparous women (B = 11.32, p < 0.001 & B = 10.67, p < 0.001). To account for the potential confounding effects of age and time interval between Session 1 and 2, both variables were included as covariates in all analyses involving group comparisons.

All participants in this study self-reported as females and identified as women. As such, sex- and gender-based analyses were not applicable. In the manuscript, we use the term “women” to refer to females whose sex aligns with their gender identity. We acknowledge that this terminology reflects the characteristics of our specific sample and recognize the importance of evolving language to be more inclusive as research in this field expands to encompass gestational individuals of diverse sex characteristics and gender identities. The study sample is broadly representative of the Spanish population of mothers in terms of education level, conception and parturition methods, and the baby’s biological sex. Additionally, the sample is inclusive regarding participants’ sexual orientation, encompassing lesbian mothers—both gestational and non-gestational—as well as heterosexual partners. However, we acknowledge that greater representativity could be achieved, particularly in terms of racial and ethnic diversity, which remains an important goal for future research.

Procedure

Each session consisted of an MRI acquisition, a collection of urine samples for hormonal determinations, and the completion of self-report neuropsychological questionnaires. The neuroimaging sessions before and after pregnancy (sessions 1, 4, and 5) comprised both structural and resting-state functional MRI acquisitions (long protocol). The neuroimaging sessions that took place during pregnancy (i.e., sessions 2 and 3) included only a structural acquisition (short protocol) to ensure the comfort of our participants. We decided to exclude hormonal measurements at 6 months postpartum based on previous literature indicating a plummet in sex steroids after childbirth¹⁰.

Data acquisition and analyses

Anatomical MRI

Data acquisition

We acquired three-dimensional T1-weighted images on a 3 Tesla Philips Ingenia CX with a Head-and-Neck 32-channel coil. We used a Turbo Field Echo (TFE) sequence in sagittal orientation and the following parameters: Voxel size = 0.75 × 0.75 × 1 mm³; field of view (FOV) = 240 × 240 × 180 mm³; echo time (TE) = 4.6 ms; repetition time (TR) = 9.9/2300 ms; prepulse delay = 900 ms; flip angle (FA) = 8°; acceleration factor = 1.9; percent sampling = 78%; acquisition time = 259 s. The MR technician performed an on-site visual inspection of the images, and the acquisition was repeated in case of significant head movement. A technical error in the FOV affected two acquisitions: one during a participant’s second session and one during a participant’s fourth session. We excluded the affected session of the first participant and completely excluded the second participant (Fig. S10).

Image processing

To analyze the structural images, we employed the recon-all longitudinal stream within FreeSurfer, version 7.2.0³⁹. Initially, the individual brain images from each session were processed cross-sectionally. This pipeline extracted outer (pial) and inner (white matter) cortical boundaries to construct the cortical surfaces and the corresponding vertex-wise maps, including volume, cortical thickness, and white matter surface area. The pipeline also computed the Euler number, whose average across hemispheres is an excellent proxy for image quality⁴⁰ (Table S1). Then, we used a longitudinal workflow to process each participant’s brain image at each subsequent session to create a participant-specific unbiased template based on individual native images. This longitudinal workflow ensured uniformity in the number of vertices and faces of cortical surfaces for every participant across sessions, improving intra-participant precision of metrics. The participant-specific templates were used to initialize the reconstruction of the surfaces at each session. Additionally, at the final stage, this workflow allowed us to compute the participants’ estimated intracranial volume (eTIV), which did not differ among groups (F(2,176) = 1.44, p = 0.240).

Cortical metrics were studied at both global and vertex-wise levels. To assess global metrics, cortical maps in the subjects’ anatomical space were employed to compute total cortical gray matter (GM) volume, mean cortical thickness, and total surface area. Additionally, Yeo’s parcellation was projected onto the cortical surfaces obtained during the longitudinal processing to compute the aforementioned cortical metrics within the seven functional networks described by Yeo¹⁴. For the vertex-wise analysis, the subjects’ cortical maps were projected onto the common fsaverage space and then smoothed with a 10 mm full-width-at-half-maximum (FWHM) Gaussian kernel. As a quality control, we identified outliers using non-parametric methods (within each group and session) to detect failures in the hemispheric parcellation process. The parcellation of such outliers was visually inspected, and those participants in which the process failed were excluded (fig. S10).

Statistical Analyses

Quadratic trajectory of the neuroanatomical changes. Data was analyzed using linear mixed effects (LME) models. In both global and vertex-wise analyses, we fitted separate LME models using total cortical volume, mean cortical thickness, and total surface area as dependent variables. Across models, we used group (gestational mother, non-gestational mother, and nulliparous women), a linear and quadratic term for session, and two interactions (i.e., group*linear term for session, group*quadratic term for session) as fixed effects. To account for confounding factors, we also included z-standardized covariates of age at session 1, eTIV, mean Euler number of each session, and time interval between sessions 1 and 2. Moreover, we incorporated a random intercept to control for subject-specific differences (see Formula 1, where cortical metric corresponds to cortical GM volume, thickness, or surface area). In the vertex-wise analysis, we additionally orthogonalized the interaction terms to avoid collinearity with the simple terms of the model. Our contrasts of interest were the following: (1) linear effect of session on gestational mothers (compared to nulliparous women) (2) linear effect of session on non-gestational mothers (compared to nulliparous women) (3) quadratic effect of session on gestational mothers (compared to nulliparous women) (4) quadratic effect of session on non-gestational mothers (compared to nulliparous women) (5) differences between gestational and non-gestational mothers in the linear effect of session, and (6) differences between gestational and non-gestational mothers in the quadratic effect of session.

$${{\rm{Cortical\; Metric}}} \sim \, {{\rm{Group}}}+{{\rm{Session}}}+{{{\rm{Session}}}}^{2}+{{\rm{Group}}} * {{\rm{Session}}} \\ +{{\rm{Group}}} * {{{\rm{Session}}}}^{2}+{{\rm{eTIV}}}+{{\rm{Age}}}+{{\rm{Euler}}} \\ +{{\rm{Inter}}} -{{\rm{session}}}\; {{\rm{Interval}}}+(1{{\rm{| }}}{{\rm{participant}}}\; {{\rm{ID}}})$$

(1)

We explored global differences using the lmer function (lmer library), within the Rstudio software under R version 4.2.1. The quadratic term for session was assessed using the poly function (stats library version 4.3.1). The covariables were standardized to z-scores using the scale function (base library version 4.3.1). We corrected p-values for the three different metrics (volume, thickness, and surface area) using the Benjamini & Hochberg False Discovery Rate (FDR)⁴¹ p.adjust function built on the stats library (version 4.3.1). In this article, corrected p-values using FDR correction are referred to as q-values. Moreover, we confirmed that the above-mentioned quadratic model (Formula 1) provided a better fit than the one only including linear changes over sessions by performing an analysis of variance using the anova function of the R stats library.

To better describe the symmetry of gray matter volume trajectory over pregnancy and postpartum we performed a generalized additive model using the gam function built on the mcgv library (version 1.8.42) (see supplementary text I for methodological details). To visually inspect the intervariability of the U-shaped brain changes within the gestational mothers group, we modeled the quadratic term for Session as a random effect in each cortical metric (gray matter volume, cortical thickness, and surface area, see “Formula 2”). Then, we extracted the conditional means of the random effects in these models using the ranef function and plotted them using an histogram.

$${{\rm{Cortical\; Metric}}} \sim 1+({{\rm{Session}}}+{{{\rm{Session}}}}^{2}| \,{{\rm{participant\; ID}}})$$

(2)

For completeness, we also analyzed the cerebral white matter volume and cerebrospinal fluid changes using the same model as in Formula 1. We corrected p-values for these two supplementary metrics using the Benjamini & Hochberg False Discovery Rate (FDR)⁴¹ p.adjust function built on the stats library (version 4.3.1). We also confirmed that the quadratic model provided a better fit than the one only including linear changes over sessions by performing an analysis of variance using the anova function of the R stats library.

For the vertex-wise analysis, we used MATLAB’s LME vertex-wise tool distributed within FreeSurfer⁴². For each contrast of interest, we corrected vertex-wise p-value maps using an FDR correction across hemispheres and cortical metrics. For all analyses, we considered q-values below a threshold of 0.05 significant. Lastly, for the FDR-corrected vertex-wise maps, we calculated effect sizes as partial eta squared (ηp2), considering the sign of the parameter associated with each contrast. We used the Desikan-Killiany atlas⁴³ to obtain a listing of the anatomical spatial distribution of those GM volume quadratic changes modeled by formula 1 with an effect greater than 0.06 (i.e., moderate effect size). Similarly, we used the Yeo atlas to obtain a listing of the functional spatial distribution¹⁴.

For the sake of simplicity, in the following analyses we focused only on cortical volume.

GM volume recovery at 6 months postpartum. To confirm whether GM volume at 6 months postpartum had returned to pre-pregnancy levels in gestational mothers, we fitted an LME model using cortical volume as the dependent variable, and session as a two-level factor (Session 1 and Session 5) fixed effect. To account for confounding factors, we also included z-standardized covariates of age at session 1, eTIV, mean Euler number of each session, and the time interval between sessions 1 and 2. Moreover, we incorporated a random intercept to control for subject-specific differences (see Formula 3).

$${{\rm{Cortical}}}\; {{\rm{GM}}}\; {{\rm{Volume}}} \sim \, {{\rm{Session}}}+{{\rm{eTIV}}}+{{\rm{Age}}}+{{\rm{Euler}}} \\ +{{\rm{Inter}}} -{{\rm{session}}}\; {{\rm{Interval}}}+(1| {{\rm{participant}}}\; {{\rm{ID}}})$$

(3)

Additionally, to assess group differences in GM volume at 6 months postpartum, we built a similar LME but with group (gestational mothers, non-gestational mothers, and nulliparous women) as another fixed factor (see Formula 4).

$${{\rm{Cortical}}}\; {{\rm{GM}}}\; {{\rm{Volume}}}\sim \, {{\rm{Group}}}+{{\rm{Session}}}+{{\rm{Group}}} * {{\rm{Session}}}+{{\rm{eTIV}}}\\ +{{\rm{Age}}}+{{\rm{Euler}}}+{{\rm{Inter}}}-{{\rm{session}}}\; {{\rm{Interval}}} \\ +(1| {{\rm{participant}}}\; {{\rm{ID}}})$$

(4)

Effect of situational and gestational factors of the GM volume changes. To take into account relevant situational or gestational factors that could be affecting the cortical GM volume trajectory observed in gestational mothers, we built four separate models assessing: the type of conception (natural or assisted), the baby’s biological sex (male or female), the parturition type (vaginal, scheduled c-section, or unplanned c-section) and the type of breastfeeding at one month postpartum (no breastfeeding, exclusive breastfeeding, or mixed breastfeeding). For each variable, we fitted an LME model using total cortical GM volume as the dependent variable. Then, for the models assessing the type of conception and the baby’s biological sex, we used said variables, a linear and quadratic term for session, and two interactions (i.e., conception/baby’s biological sex* linear term for session, conception/baby’s biological sex* linear term for session) as fixed effects. Due to the temporality of childbirth and breastfeeding regarding the quadratic GM volume trajectory, we decided to model the impact of these variables on GM recovery from late pregnancy to 6 months postpartum rather than on the quadratic trajectory. Hence, we used the type of childbirth/breastfeeding type, session (3 to 5), and an interaction between both (i.e., type of childbirth/breastfeeding type * Session (3 to 5)) as fixed effects. Moreover, we incorporated a random intercept to control for subject-specific differences (see formulas 5 to 8).

$${{\rm{Cortical}}}\; {{\rm{GM}}}\; {{\rm{Volume}}}\sim \, {{\rm{Conception}}}+{{\rm{Session}}}+{{{\rm{Session}}}}^{2} \\ +{{\rm{Conception}}} * {{\rm{Session}}}+{{\rm{Conception}}} * {{{\rm{Session}}}}^{2}\\ +(1| {{\rm{participant}}}\; {{\rm{ID}}})$$

(5)

$${{\rm{Cortical}}}\; {{\rm{GM}}}\; {{\rm{Volume}}}\sim \, {{\rm{Baby}}}\hbox{'}{{\rm{s}}}\; {{\rm{biological}}}\; {{\rm{sex}}}+{{\rm{Session}}}+{{{\rm{Session}}}}^{2}\\ +{{\rm{Baby}}}\hbox{'}{{\rm{s}}}\; {{\rm{biological}}}\; {{\rm{sex}}} * {{\rm{Session}}}\\ +{{\rm{Baby}}}\hbox{'}{{\rm{s}}}\; {{\rm{biological}}}\; {{\rm{sex}}} * {{{\rm{Session}}}}^{2}+(1| {{\rm{participant}}}\; {{\rm{ID}}})$$

(6)

$${{\rm{Cortical}}}\; {{\rm{GM}}}\; {{\rm{Volume}}}\sim \, {{\rm{Parturition}}}\; {{\rm{type}}}+{{\rm{Session}}}({\mathrm{3,4}}\,{{\rm{and}}}\,5)\\ +{{\rm{Parturition}}}\; {{\rm{type}}} * {{\rm{Session}}}+(1| {{\rm{participant}}}\; {{\rm{ID}}})$$

(7)

$${{\rm{Cortical}}}\; {{\rm{GM}}}\; {{\rm{Volume}}}\sim \, {{\rm{Breastfeeding}}}\; {{\rm{type}}}+{{\rm{Session}}}({\mathrm{3,4}}\,{{\rm{and}}}\,5)\\ +{{\rm{Breastfeeding}}}\; {{\rm{type}}} * {{\rm{Session}}}+(1| {{\rm{participant}}}\; {{\rm{ID}}})$$

(8)

Spatial correspondence with large-scale functional networks. To assess the spatial distribution of the GM volume trajectory in gestational mothers’ brains, we fitted an LME model using cortical volume as the dependent variable and linear and quadratic term for session as fixed effects. Then, we added Yeo’s 7 large-scale functional networks as a random factor nested within the participant’s random intercept. Additionally, we included standardized covariates for age at the pre-conception session, total intracranial volume, mean Euler number of each session, and the time interval between sessions 1 and 2 as covariables. This model allowed us to fit a unique curve for all networks (see Formula 9). Based on prior literature^3,4,5, we hypothesized that there might be two different trajectories in the brain: one including higher-order cognition networks (Default Mode and Frontoparietal) and another one including the rest of the networks. Hence, we fitted a second LME model with nested networks (Default Mode and Frontoparietal versus others) as an additional fixed factor. That is, we used network group, a linear and quadratic term for session, and the interactions between network group and the linear and quadratic terms for session as fixed effects, and a random factor with the 7 Yeo Networks nested within the participant’s random intercept (see Formula 10). This model allowed us to fit a different curve for each group of networks. Once the models were fitted, we used the Bayesian Information Criteria (BIC) to compare both models and select which model better explained the brain’s GM volume trajectories. The model with a lower BIC was selected as the better-fitted model.

$${{\rm{Cortical}}}\; {{\rm{GM}}}\; {{\rm{Volume}}}\sim \, {{\rm{Session}}}+{{{\rm{Session}}}}^{2}+{{\rm{eTIV}}}+{{\rm{Age}}}+{{\rm{Euler}}}\\ +{{\rm{Inter}}}-{{\rm{session}}}\; {{\rm{Interval}}}\\ +(1| {{\rm{participant}}}\; {{\rm{ID}}}/{{\rm{Yeo}}}\; {{\rm{Networks}}})$$

(9)

$${{\rm{Cortical}}}\; {{\rm{GM}}}\; {{\rm{Volume}}}\sim \, {{\rm{Nested}}}\; {{\rm{Networks}}}+{{\rm{Session}}}+{{{\rm{Session}}}}^{2}\\ +{{\rm{Session}}} * {{\rm{Nested}}}\; {{\rm{Networks}}}+{{{\rm{Session}}}}^{2} * \,{{\rm{Nested}}}\; {{\rm{Networks}}}\\ +{{\rm{eTIV}}}+{{\rm{Age}}}+{{\rm{Euler}}}+{{\rm{Inter}}}-{{\rm{session}}}\; {{\rm{Interval}}}\\ +(1| {{\rm{participant}}}\; {{\rm{ID}}}/{{\rm{Yeo}}}\; {{\rm{Networks}}})$$

(10)

We also calculated the mean signed effect size within each of Yeo’s seven large-scale functional networks and compared them to suitable null distributions to determine which networks exhibited significantly higher or lower spatial correspondence with the observed quadratic GM volume trajectory in gestational mothers compared to nulliparous women (See Group*Session² interaction from Formula 1). To generate null distributions, we used spin-permutations (rotations) of the maps and then recomputed the mean values in each network (which remained unrotated). We performed 1,000 uniformly distributed random rotations of the fsaverage vertex indices using the spin-test toolbox (https://github.com/spin-test/spin-test). Finally, we calculated p-values for each map and network as the proportion of rotations that produced higher or lower values than our original maps. We considered p-values below a threshold of 0.05 significant.

Resting-state functional MRI

Resting-state functional MRI (rs-fMRI) data was collected before and after pregnancy (sessions 1, 4, and 5). The rs-fMRI analyses only included participants who had completed the first (pre-pregnancy) and fourth (1-month postpartum) sessions, and whose MR images were not affected by artifacts. Participants with an artifact or no MRI acquisition at session 5 (6 months postpartum) were included in the analysis, and only the affected session was excluded. The final experimental sample for the functional analyses consisted of 123 gestational mothers, 20 non-gestational mothers, and 40 nulliparous women. For an overview of the group allocation and dropout per session, please see Fig. S11.

Data acquisition

We obtained rs-fMRI images on the same 3 Tesla Philips Ingenia CX with a Head-and-Neck 32-channel coil. We acquired T2*-weighted whole-brain single shot echo-planar images (EPIs, with 225 images, the first three serving as dummy scans to account for T1 saturation effects equilibration) with the following parameters: TR = 1.6 s; TE = 35 ms; Flip Angle = 75°; Field of View = 240 × 240 × 138 mm; voxel size = 3 × 3 mm; 46 slices; and slice thickness = 3 mm. Subsequently, two extra images were acquired to address image distortions induced by the magnetic field. These images were acquired using single-shot spin-echo EPI sequences in opposing phase encoding directions—one with phase encoding in the anterior-posterior direction and the other with phase encoding in the posterior-anterior direction. Each image comprised two volumes with the same spatial resolution and matrix dimensions as the resting-state images and the acquisition parameters were TR = 1600 ms; TE = 35 ms; and a flip angle = 90°.

Image processing

To process the rs-fMRI images, we applied the standard preprocessing procedures for rs-fMRI signals using a Nipype pipeline implemented in Python (version 3.9.7). This procedure involved a fieldmap intensity correction, head motion realignment, spatial co-registration and normalization, 8 mm-FWHM spatial smoothing, and temporal filtering (0.009–0.08 Hz). Then, six head motion parameters, signals from white matter, and cerebrospinal fluid were regressed from the images to control for head motion and physiological noises. All steps were performed using FS^44,45, except the temporal filtering, which was performed using AFNI⁴⁶. Subjects with evident poor image quality (measured as large signal loss or extended hyperintensities) or excessive head motion (mean framewise displacement (FWD) > 0.25 mm) in any of the evaluated sessions were excluded from the analysis (Fig. S11).

Graph construction

The organization of functional brain networks was examined using graph theory, which characterizes the topological properties of large-scale brain networks⁴⁷. Nodes were defined based on Schaefer’s 400-region cortical parcellation¹⁵, which are assigned to one of the networks of Yeo’s original parcellation¹⁴. We calculated a 400 × 400 functional connectivity matrix for each participant and session, which indicated the Pearson correlation coefficients between each pair of nodes. Then, we applied a Fisher z transformation to each correlation matrix and set the diagonal elements and negative connections to 0. We chose Pearson r values to represent functional connectivity between nodes because of their simplicity in interpretation and extended usage in human network neuroscience⁴⁸.

Graph theoretical metrics

Graph theoretical metrics were computed for each participant and session using in-house scripts based on the Brain Connectivity Toolbox¹⁷. Moreover, we calculated each metric over a range of costs (0.05–0.15 at 0.01 intervals, a range and interval widely used in graph theory analyses⁴⁸). All graph metrics reported here are the average values across all costs.

Modularity. We calculated the whole-brain modularity under the Louvain community detection algorithm. As inputs, we used the previously calculated undirected, weighted connectivity matrices and a 1 × 400 vector indicating each column’s correspondence to Yeo’s 7-large-scale functional networks as the initial community affiliation vector. Whole-brain modularity quantified the strength of segregation into Yeo’s 7-large-scale functional networks. In addition, we calculated a within-network modularity index for each of Yeo’s 7-large-scale functional networks, quantifying the modular structure of each network.

Strength of system segregation. System segregation was used to describe the relative strength of within-network connections compared to between-network connections. We calculated the strength of system segregation for each of Yeo’s 7-large-scale functional networks. Following the methodology described by Cohen and D’esposito, 2016⁴⁹, within-network connectivity strength was calculated as the mean connectivity strength between all pairs of nodes within the same network. Between-network connectivity strength was calculated as the mean connectivity strength between all pairs of nodes that connected two networks.

Participation coefficient. Lastly, we used the mean participation coefficient to measure intermodular connections within Yeo’s 7-large-scale functional networks. The participation coefficient was first calculated for each node on the 400×400 weighted connectivity matrices. Then, each node was assigned to one of Yeo’s functional networks, and the participation coefficient values were averaged for each network.

Null model correction

All the graph theory metrics were compared with the same measures computed on a reference network. We randomized the undirected weighted matrices for each subject, session, and cost, preserving the degree distribution. Each edge was rewired approximately 100 times. Then, we calculated the same graph theory metrics on the randomized matrices (i.e., null graph theory metrics). For each subject and session, we used the averaged values across all costs. Finally, we corrected our metrics by subtracting the values obtained from the null graph theory metrics subject-wise. These were the values used in our analyses.

Statistical analyses

To evaluate between-group differences in functional connectivity changes at a whole-brain level, we fitted an LME model using modularity as a dependent variable. We used group (nulliparous women, gestational mother, and non-gestational mother), session (Pre-pregnancy, 1-month postpartum, and 6-month postpartum), and group*session interaction as fixed effects. To account for possible confounding factors, we also included z-standardized covariates of age at session 1, the FWD of each session, and the time interval between sessions 1 and 4. Lastly, to account for subject-specific differences, we incorporated random intercepts into the models (Formula 11).

$${{\rm{Whole}}}-{{\rm{brain}}}\; {{\rm{Modularity}}}\sim \ {{\rm{Group}}}+{{\rm{Session}}}+{{\rm{Group}}} * {{\rm{Session}}}\\ +{{\rm{Age}}}+{{\rm{FWD}}}+{{\rm{Inter}}}-{{\rm{session}}}\; {{\rm{Interval}}}\\ +(1| {{\rm{participant\; ID}}})$$

(11)

To determine changes in the within-network functional connectivity, we built a separate LME model per network using modularity, system segregation, and mean participation coefficient as predictors. In all models, we used session (pre-pregnancy, 1-month pp, and 6-month pp), group (nulliparous women, gestational mother, and non-gestational mother), and a session*group interaction as fixed effects. We also included z-standardized covariates of age at session 1, the FWD of each session, and the time interval between sessions 1 and 4 to account for possible confounding factors. Lastly, to account for subject-specific differences, random intercepts were incorporated into the models (Formula 12). P-values were corrected for all built models using FDR correction (21 models: 3 graph theory measures*7 networks). We considered significant corrected q-values below a threshold of 0.05.

$${{\rm{Functional}}}\; {{\rm{Metric}}}\; {{\rm{for}}}\; {{\rm{Network}}}\sim \, {{\rm{Group}}}+{{\rm{Session}}}+{{\rm{Group}}} * {{\rm{Session}}}\\ +{{\rm{Age}}}+{{\rm{FWD}}}+{{\rm{Inter}}}-{{\rm{session}}}\; {{\rm{Interval}}}\\ +(1| {{\rm{participant\; ID}}})$$

(12)

Steroid hormones data

From the 127 gestational mothers, 20 non-gestational mothers, and 32 nulliparous women who underwent neuroanatomic scans in sessions 1, 2, 3, and 4, 100 gestational mothers, 15 non-gestational mothers, and 29 nulliparous women provided urine samples during these same sessions. One sample was missing from one nulliparous woman in session 2.

Sample preparation and determination

Urinary steroid metabolite levels were measured at sessions from pre-conception to one month postpartum. Each sample of spot urine was collected by the participant the day before the MRI session after 3 pm to avoid the morning cortisol peak concentration⁵⁰. In case the participant forgot to bring the urine sample to the visit, the sample was either taken during the visit if it was after 3 pm or it was collected that same afternoon at home and sent to the laboratory via private courier service. After the visit, the urine samples were aliquoted and stored at −80 °C. On the analysis day, an aliquot of urine samples was thawed at room temperature and proceeded for steroid extraction and concentration using the solid-phase extraction (SPE) method. We used liquid chromatography-tandem mass spectrometry as a targeted approach to analyze urine steroids. To detect and quantify unconjugated steroids we used a previously published methodology by our team⁵¹. Additionally, to detect and quantify conjugated steroids—including monosulfated, monoglucuronidated, bisulfated, and sulfo-glucuronidated steroids - we used a recently developed methodology (see supplementary text IV for methodological details).

Due to sample collection and processing constraints, we processed urine samples in eight batches. Batches one to three included urine samples from the first session, and batches four to eight included urine samples from the first to the fourth session. For each batch, we calculated the corresponding calibration curves using solid phase extraction-stripped urine and a set of quality control samples. Quality control samples were injected at least twice per each batch-analysis.

Data processing

Using targeted metabolomics, we obtained urinary hormonal concentrations from 50 steroid metabolites. Seven steroids belonged to the estrogens family, twelve to the progestogens family, another twelve to the androgens family, and nineteen to the corticoids family (see Table S24). To correct hormonal values below the detection limit, we performed a half-minimum (HM) imputation for each metabolite. Specifically, we replaced undetected levels (noted as zeros) with half of the minimum value detected among the non-zero hormonal concentrations.

As concentration levels for most of these metabolites increase during pregnancy (i.e., at 18 and 34 pregnancy weeks), we excluded one metabolite that was detected in less than 80% of pregnancy samples. After the imputation, we adjusted the steroid metabolites’ concentration in each sample for creatinine levels. Lastly, we applied a logarithmic transformation to our data to account for the typically skewed distributions of hormones. All in all, we used creatinine normalized and logarithmically corrected steroid metabolites’ concentrations in our analyses.

Statistical analysis

Steroidal data was analyzed using LME models. We fitted separate LME models using each steroid metabolite concentration as the dependent variable. For each model, we used group (gestational mother, non-gestational mother, and nulliparous women), a linear and quadratic term for session, and two interactions (i.e., group*linear term for session, group*quadratic term for session) as fixed effects. To account for confounding factors, we also included z-standardized covariates of age at session 1, body mass index (BMI), and the time interval between sessions 1 and 2. Moreover, we incorporated a random intercept to control for subject-specific differences (see Formula 13). We corrected p-values within each steroid family (i.e., estrogens, progestogens, corticoids, and androgens) using FDR.

$${{\rm{Steroid}}}\; {{\rm{concentration}}}\sim \, {{\rm{Group}}}+{{\rm{Session}}}+{{{\rm{Session}}}}^{2}+{{\rm{Group}}} * {{\rm{Session}}}\\ +{{\rm{Group}}} * {{{\rm{Session}}}}^{2}+{{\rm{Age}}}+{{\rm{BMI}}}+{{\rm{Inter}}}-{{\rm{session\; Interval}}}\\ +(1| {{\rm{participant\; ID}}})$$

(13)

Then, to assess the possible joint evolution of GM volume in gestational mothers and the different steroid changes along the transition to motherhood, we computed a Spearman correlation between the quadratic parameter coefficients of GM volume change and steroid concentrations. To conduct this correlation, we first calculated the percentage of GM volume change for each participant session compared to pre-conception. Then, we fitted an LME model using the percentage of GM volume change at each session (i.e., 1,2,3,4) as the dependent variable. This model contained a linear and quadratic term for sessions as fixed effects and a random intercept to account for subject-specific differences. Lastly, we added a random slope for the quadratic term component, which allowed us to extract a coefficient for the quadratic GM volume trajectory of each participant (see Formula 14). Similarly, we fitted an LME model for each metabolite which significantly followed a quadratic trajectory over sessions (Table S24). These models contained a linear and quadratic term for session as fixed effects, a random intercept for each participant, and a random slope for the quadratic time component (See Formula 15). We then computed a two-sided Spearman correlation between the quadratic parameter coefficients of both models. Lastly, within each metabolite family, we corrected p-values using FDR (i.e., hierarchical FDR). We applied a hierarchical FDR correction because, in these analyses, each metabolite is not an isolated feature but a part of a subfamily of the data set⁵².

$$\%{{\rm{GM}}}\; {{\rm{volume}}}\; {{\rm{change}}}\sim {{\rm{Session}}}+{{{\rm{Session}}}}^{2}+({{{\rm{Session}}}}^{2}| \,{{\rm{participant\; ID}}})$$

(14)

$${{\rm{Steroid}}}\; {{\rm{concentration}}}\sim {{\rm{Session}}}+{{{\rm{Session}}}}^{2}+({{{\rm{Session}}}}^{2}| \,{{\rm{participant}}}\; \,{{\rm{ID}}})$$

(15)

Hormonal dense sampling

To confirm the steroidal trajectories correlating with the observed neuroanatomical trajectory, we collected urine samples from five extra gestational mothers at a higher sampling frequency. The hormonal sampling started at the pre-pregnancy session and continued every two weeks during pregnancy up to the first two postpartum weeks (pregnancy weeks: 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40). All women, except one, gave birth before the 40th week of pregnancy. The sample preparation, steroidal determination, and processing were identical to the above-explained methodology (see sample preparation and determination and data processing sections). The steroidal trajectories of both the extra sample and the main sample are depicted in Fig. S12.

Neuropsychological data

Before each MRI session (mean ± sd = −1 ± 5 days), participants completed a series of self-reported questionnaires administered online. Questionnaires administered during pregnancy measured antenatal mother-to-infant attachment (Maternal Antenatal Attachment Scale, MAAS⁵³), while postpartum questionnaires measured postnatal mother-to-infant attachment (Maternal Postnatal Attachment Scale, MPAS⁵⁴) among gestational mothers. Moreover, we obtained sociodemographic, lifestyle, and health information, as well as perceived stress (Perceived Stress Scale, PSS⁵⁵), depressive symptoms (Edinburgh Depression Antenatal Scale, EDAS and Edinburgh Depression Postnatal Scale, EDPS^56,57), and general well-being (Well-being Index, WHO-5⁵⁸) measures across all time points and experimental groups. Two participants (one gestational mother and one non-gestational mother) did not complete these questionnaires at session 4.

Statistical analysis

To assess the potential link between GM volume changes during pregnancy and postpartum and antenatal and postnatal attachment, we used the subscales of MAAS (i.e., intensity of preoccupation, and attachment quality) assessed at 34 pregnancy weeks and MPAS (i.e., absence of hostility, attachment quality, and pleasure in interaction) at 6 months postpartum. Moreover, we divided the GM volume trajectory into two components: the percentage of GM volume change from before pregnancy to late pregnancy (sessions 1 to 3), and the percentage of GM volume change from late pregnancy to 6 months postpartum (sessions 3 to 5). The percentage of GM volume change was calculated as: ((GM volume at session 3—GM volume at session 1)/GM volume at session 1)*100 and ((GM volume at session 5 - GM volume session 3)/GM volume at session 3)*100. Then, we assessed separate two-tailed Pearson’s correlations between each component using the attachment measures and the percentage of GM volume change during pregnancy or postpartum. In total, we had 8 correlation tests (two assessing the effect of GM volume change during pregnancy on antenatal attachment, three assessing the effect of the GM volume change during pregnancy on postnatal attachment, and three assessing the effect of the GM volume change during postpartum on postnatal attachment). For all tests, p-values were corrected by FDR⁵⁹.

Moreover, we analyzed if the relationship between the absence of hostility at 6 months postpartum and the GM volume recovery at postpartum was causally mediated by mental health outcomes. Thus, we built three separate mediation models with mediate R function (mediation library version 4.5.0) using well-being, perceived stress, and depressive symptoms as possible mental health mediators. For each mediation, we modeled the effect of the independent variable and the mediator on the dependent variable (Absence of hostility ~ % GM volume recovery + Mental health mediator) and the effect of the independent variable on the mediator (Mental health mediator ~ % GM volume recovery). We then estimated the average causal mediation effect, the direct effect, the proportion mediated, and the total effect. For each mediation model, we applied nonparametric bootstrapping with 10,000 permutations to estimate the 95% confidence intervals. All p-values were corrected by FDR across the three mediation models.

Software

Statistical analyses were performed in Rstudio (version 2023.06.0 + 421), under R version 4.3.1, with the following libraries: lmer (version 1.1.33) for LME models, including global neuroanatomical, functional connectomics, neuropsychological and hormonal data; emmeans (version 1.8.7) for computing estimated marginal means for assessing contrasts among modeled factors; stats (version 4.3.1) for assessing quadratic effects in neuroanatomical and hormonal data, to apply FDR corrections, and to perform pearson and Spearman correlations between neuroanatomical and neuropsychological or hormonal data; and mediation (version 4.5.0) for the mediation analysis. Vertex-wise FDR-corrected maps were computed using the lme_mass_FDR function included in the MATLAB’s LME vertex-wise tool distributed within FreeSurfer. Figures were plotted using ggplot2 R library. The in-house Rscript also used the following libraries: htmltools (version 0.5.5), tydiverse (version 2.0.0), readxl (version 1.4.3), kableExtra (version 1.3.4.9000), doBy (version 4.6.17), ggpurb (version 0.6.0), corrplot (version 0.92), dyplr (version 1.1.2), MASS (version 7.3.60), flextable (version 0.9.4), officer (version 0.6.3), sjPlot (version 2.8.14). Vertex-wise analyses were plotted using the R library fsbrain (version 0.5.4).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.