Introduction

Dielectric capacitors are widely used in advanced electronics and high-power electrical systems such as microwave communications, hybrid electric vehicles, and distributed power systems1,2,3. The mechanism of dielectric capacitors lies in their exceptional high-power density and rapid charge/discharge capabilities. These capacitors store energy by virtue of the displacement of bound charged elements, distinct from the energy storage mechanisms relying on chemical reactions observed in batteries and solid oxide fuel cells4,5. However, the relatively low recoverable energy storage density (Wrec typically <4 J/cm3) significantly constrains the application scope of ceramic capacitors and impedes their progress toward device miniaturization and intelligence. In conjunction with environmental concerns6, there has been a notable focus on the advancement of lead-free dielectric capacitors with high energy density and storage efficiency (“dual high”)7,8,9,10.

The energy density Wrec is a function of the dielectric polarization (P) when subjected to an external electric field. This relation is quantitatively described by the equation Wrec = \({\int }_{{P}_{r}}^{{P}_{m}}{EdP}\), where Pm and Pr are the maximum polarization after charging and the remnant polarization after discharging, respectively, and E is the electric field4. Consequently, a high Wrec requires a large Pm, a small Pr, and a high breakdown electric field (Eb). To achieve these electrical characteristics simultaneously, dielectric materials should be engineered to exhibit the following features: a dense microstructure, fine grains, heightened polarizability in response to an electric field, and rapid reversion to the nonpolar state11. The most prevalent method for enhancing the polarization characteristics of dielectrics is through chemical composition design, with extensive exploration of numerous Pb-free compounds. The energy storage capacity of these compounds has seen rapid enhancement to above 7 J/cm3 3,12,13,14,15,16.

Benefiting from the nanoscale heterogeneous polar nanoregions (PNRs) structure, relaxor ferroelectrics (RFEs) are considered to be an excellent option for “dual high” dielectric capacitors6,8,17,18,19. High-entropy materials, characterized by multiple elements occupying equivalent lattice sites, have recently been shown to significantly enhance the energy storage performance in bulk RFE (Wrec ~ 10 J/cm3 and η ~ 90%) and RFE thin films (Wrec ~ 182 J/cm3 and η ~ 78%). The configuration entropy (Sconfig) defined as \({S}_{{config}}=-R[{\sum }_{i=1}^{N}\;{x}_{i}{{{\mathrm{ln}}}}\;{x}_{i}+{\sum }_{j=1}^{M}{x}_{j}{{{\mathrm{ln}}}}\;{x}_{j}]\), where R, N(M), and xi(xj) are the ideal gas constant, atomic species and contents at the equivalent cation (anion) sites, respectively, was proposed to evaluate the compositional inhomogeneity20. However, in most high-entropy relaxor ferroelectrics, the effects of multi-elements at the equivalent lattice sites have been regarded as changes in the average structure21,22,23. The chemical order and polarization heterogeneity play a significant role in the microstructure and functional properties of relaxor ferroelectric materials24. However, the relationship between them, as well as their impact on performance in high-entropy ferroelectric materials, has not yet been fully understood. As illustrated in Fig. S1, we have extracted data from the literature regarding configurational entropy and energy storage performance. It is evident that the relationship between performance and entropy is not a simple linear correlation, indicating the presence of other mechanisms that affect performance.

In high-entropy alloys, chemical short-range order (SRO) is common and has a significant impact on the microstructure and macroscopic properties25,26,27,28,29,30. However, in high-entropy relaxor ferroelectrics, there is currently a lack of attention to chemical SRO. Inspired by this, we proposed a chemical SRO strategy, and proved its contribution to modulate the polarization response under external electric field, leading to the breakthrough of the bottleneck of energy storage performances. The phase-field simulations (Fig. S2) were performed to theoretically analyze the effectiveness of this strategy. Specifically, we first consider a high-entropy matrix with elements uniformly distributed. In this scenario, as shown in Fig. S3, the polarization in the high-entropy matrix has the same polarization switching energy barrier. Under the electric field, the polarization has a uniform and poor polarization switching. As illustrated in Fig. 1a, for high-entropy ferroelectrics with chemical SRO, we assume that the chemical SRO region has a lower energy barrier. As shown in Fig. 1b–d, under the electric field, these regions respond more intensively and facilitate a faster response of polarization in the surrounding matrix. Moreover, chemical SRO enhances the local heterogeneity, which is expected to further enrich the polarization configurations. Therefore, this chemical SRO region is expected to elevate the maximum polarization (Pm) and decrease the remnant polarization (Pr), thereby facilitating superior energy storage performances.

Fig. 1: Strategic diagram.
figure 1

a Schematic diagram of phase-field simulations; Polarization field at the b 0th, c 10th, and d 20th-time steps, where the colorbar represents the magnitude of the polarization deviation from the [001] direction, with larger deviation angles indicating a stronger response of the polarization to external fields; Schematic diagram of crystal structures, domain structures, and P-E loops of e pristine BNT, f A-site high-entropy BNT and g A-site high-entropy BNT with B-site chemical SRO.

Full size image

In this study, guided by density functional theory (DFT) calculations, we theoretically proved that niobium (Nb) can implement the above strategy in the Bi0.5Na0.5TiO3 (BNT) system. Based on this, we experimentally designed an Nb-doped high-entropy BNT-based system and achieved ultra-high energy storage density of ~16.4 J/cm3 and efficiency of 90%, surpassing the reported high-entropy energy storage ceramics. These results indicate that a thorough investigation of the microstructure of high-entropy ferroelectric ceramics can effectively enhance their performance in applications. As shown in Fig. 1e, f, through equimolar elements at the A-site, we introduced a high-entropy strategy into the BNT matrix. Multi-elements occupy the A-site, causing heterogeneity in local strain and electric fields. The nanodomains of BNT are broken into PNRs, and the ferroelectric long-range ordered R3c (R) phase is transformed into a coexistence of Cubic (C)- R-Tetragonal (T) phases with significantly improved Eb, resulting in improved energy storage performances. Subsequently, as depicted in Fig. 1g, the incorporation of Nb at the B-site gives rise to chemical SRO regions. As analyzed above, this can further promote polarization response and significantly enhance energy storage performance.

Results

Density functional theory (DFT) calculations

In this work, the Nb was selected to achieve the SRO in high-entropy BNT. The DFT calculations were performed to verify the role of Nb. As shown in Fig. S4a, b, we constructed a 2 × 2 × 2 supercell of P4bm. As shown in Fig. 2a, we considered three configurations, i.e., the body-diagonal distribution, face-diagonal distribution, and nearest-neighbor distribution. The body-diagonal distribution can be regarded as a disordered distribution of Nb, while the nearest-neighbor distribution represents a locally ordered distribution of Nb. As shown in Fig. 2a, it is evident that as the order degree increases, the energy of the configuration decreases, indicating that Nb tends to exhibit a locally ordered distribution within BNT. We employed the energetically favorable nearest-neighbor configuration for further analysis. As shown in Fig. 2b, the local ferroelectric distortion of the B-site ions can be characterized by the differences in the six B-O bond lengths. In the paraelectric phase (PE phase), the bond length difference is zero; as the degree of ferroelectric distortion increases, the bond length difference increases. As shown in Fig. 2c, the difference in the six Ti-O bond lengths is 0.055 Å, while the difference of Nb-O bond lengths is significantly reduced to 0.003 Å, indicating that Nb can lead to a notable decrease in ferroelectric distortion. In ferroelectric materials, a smaller ferroelectric distortion corresponds to a flatter energy barrier, which can be expressed by the energy difference between the ferroelectric phase (FE phase) and paraelectric phase. We further compute the energy of pristine Pm3m BNT and Nb-doped Pm3m BNT (Fig. S4c, d). As shown in Fig. 2d, in the Nb-doped configuration, the energy difference between the weak polar phase (P4bm) and paraelectric phase (Pm3m) (1.758 eV) is lower than that in the undoped configuration (2.062 eV). Therefore, Nb can induce local short-range order within BNT, and the reduced ferroelectric distortion can lead to a flatter energy barrier.

Fig. 2: Density functional theory (DFT) calculation.
figure 2

a Energy of different Nb-doped BNT structures; b Schematic diagram of the relationship between ferroelectric distortion and B-O bond lengths difference; c Six B-O bond lengths of Ti and Nb doping site; d Polarization switching energy barrier of pristine BNT and Nb-doped BNT.

Full size image

Energy storage performances

To experimentally implement our strategy, we designed the composition of pristine Bi0.5Na0.5TiO3, (Bi0.2Na0.2K0.2La0.2Sr0.2)TiO3 and (Bi0.2Na0.2K0.2La0.2Sr0.2)Ti0.95Nb0.05O3, abbreviated as pristine BNT, BNKLST and BNKLSTN5 ceramics. The Sconfig of BNT, BNKLST, and BNKLSTN5 is 1.04, 1.50, and 1.60, respectively, indicating that the BNKLST and BNKLSTN5 is in the high-entropy range (Sconfig ≥ 1.5)31. We tested their polarization-electric field (P-E) loops. As shown in Fig. S5a, pristine BNT exhibits a poor energy density of ~1.37 J/cm³ and an efficiency of ~24%. After introducing the high-entropy strategy, as shown in Fig. S5b, BNKLST ceramic exhibits an enhanced energy storage density of ~7.4 J/cm³ and efficiency of ~84%. Notably, as shown in Fig. S6 and Fig. 3a, BNKLSTN5 ceramic demonstrates slimed P-E loops under various electric fields, revealing an energy storage density of ~16.4 J/cm³ and an efficiency of ~90% under a breakdown electric field strength of 85 kV/mm. Figure 3b compares the performance of BNKLSTN5 with other high-entropy ferroelectric ceramics5,6,22,23,32,33,34,35, indicating that the BNKLSTN5 ceramic has exceptional energy storage performances. As shown in Fig. S7, although ferroelectric materials tend to experience fatigue under bipolar testing, resulting in lower electric field strengths36,37, BNKLSTN5 still exhibits a high breakdown field strength of ~60 kV/mm. As shown in Fig. S8, a comparison of the results between bipolar and unipolar tests reveals that they are nearly identical, indicating the robustness of performance across different testing conditions.

Fig. 3: Comprehensive energy storage performances.
figure 3

a P-E loops of BNKLSTN5 ceramic under 85 kV/mm; b Performances comparison between BNKLSTN5 and other high-entropy ferroelectric ceramics.

Full size image

Additionally, BNKLSTN5 shows outstanding stability in terms of temperature, frequency, and cycling performance. As shown in Fig. S9a, b, under an electric field of 50 kV/mm, the sample exhibits excellent temperature stability in the range of 25 to 155 °C (Wrec ~8.64 ± 0.42 J/cm3 and η ~90.3 ± 3.1%). As shown in Fig. S9c, d, under an electric field of 50 kV/mm, the BNKLSTN5 ceramic demonstrates outstanding frequency stability from 1 to 80 Hz (Wrec ~8.42 ± 0.43 J/cm3 and η ~92 ± 2.5%). Additionally, as shown in Fig. S9e, f, under a 45 kV/mm electric field, the BNKLSTN5 ceramic exhibits excellent stability in energy storage density and efficiency as the number of cycles increases from 1 to 106 (Wrec ~6.5 ± 0.02 J/cm3 and η ~92.7 ± 0.3%).

The charge-discharge performances and thermal stability are also critical performance indicators for dielectric capacitors. We tested the charge-discharge performances of the BNKLSTN5 ceramic under different electric fields and temperatures. As shown in Fig. S10a–c, BNKLSTN5 exhibits high maximum current (Imax), current density (CD), and power density (PD) at 21 kV/mm, with values of 15.4 A, 1962 A/cm2, and 206 MW/cm3, respectively. As illustrated in Fig. S10d–f, at 22 kV/mm, the BNKLSTN5 ceramic achieves a high discharge energy density (WD) of 2.58 J/cm³ within an ultrafast time frame of approximately 20 ns (t0.9 ~ 20 ns, the time required for the discharge density to reach 90% of the total energy density). Moreover, as shown in Fig. S11, under an electric field of 16 kV/mm, the BNKLSTN5 ceramic demonstrated excellent temperature stability in its charge-discharge performance, with WD ≈ 1.55 ± 0.08 J/cm3, t0.9 ≈ 14 ± 2 ns, CD ≈ 1500 ± 90 A/cm3, PD ≈ 120 ± 7 MW/cm3 from 25 to 155 °C.

Structural mechanism analysis

Figure 4a–c illustrate the temperature-dependent dielectric constants and loss of pristine BNT, BNKLST, and BNKLSTN5 ceramics. Consistent with previous reports38, the temperature for dielectric maximum (Tm) of pristine BNT is observed to be ~600 K @ 100 kHz, which is above room temperature and shows no frequency dispersion of △Tm (Tm,500 kHz – Tm,10 kHz) < 1 K. After the introduction of the high-entropy strategy at the A-site, the Tm is reduced to below room temperature, approximately 269 K @ 100 kHz. Similar to pristine BNT, BNKLST does not exhibit significant frequency dispersion of △Tm ~ 3 K. Significantly, for BNKLSTN5, the Tm is further reduced to low temperature, ~222 K @ 100 kHz, and a pronounced frequency dispersion phenomenon is observed (△Tm is ~21 K), exhibiting that Nb promotes the promote relaxor ferroelectric behavior. The decreased Tm and its frequency dispersion indicate that both the phase structure and domain structure of BNKLSTN5 have undergone substantial modifications. The Burns temperature (TB) is defined as the temperature at which the ceramic fully converts to a paraelectric phase. The TB can be calculated from the temperature dependence of the reciprocal of the permittivity curve, which follows the Curie–Weiss law as the temperature is above TB (Fig. S12). The superparaelectric state has been defined as the condition of relaxor ferroelectrics above the Tm temperature and below the TB temperature1,33. Combining the Tm ~222 K and TB ~530 K, the BNKLSTN5 exhibited the superparaelectric state at room temperature (i.e., Tm < T < TB).

Fig. 4: Structural characterization.
figure 4

Temperature-related dielectric constants and loss of a pristine BNT, b BNKLST, and c BNKLSTN5 ceramics; XRD patterns of d pristine BNT, e BNKLST, and f BNKLSTN5 ceramics; g Phase fraction by XRD refinements; h Temperature-related in situ XRD patterns of BNKLSTN5 ceramic; i Temperature dependence of the (111) peak and corresponding contour map; j Temperature dependence of the (200) peak and corresponding contour map; k Temperature-related in situ Raman spectra of BNKLSTN5 ceramic; The variations in wavenumber and FWHM of the peak at l 272 cm−1 and m 543 cm−1.

Full size image

Figure 4d–f show the XRD patterns of pristine BNT, BNKLST, and BNKLSTN5 ceramics. As shown in Fig. 4d, the {111} diffraction peak of BNT exhibits a double-peak structure at 2θ ~38–42°, with a superlattice diffraction peak at 2θ ~38.3° corresponding to 1/2(311), which is a characteristic peak of the R3c structure39. As illustrated in Fig. 4e, f, for the BNKLST and BNKLSTN5 ceramics, the superlattice diffraction peak near 38° weakened, and the split structure of the R3c peak transformed into a single-peak structure. This indicates that the R3c phase transitions to a multiphase coexistence structure. Further XRD refinement results (Fig. S13) reveal that BNKLST ceramics exhibit a coexistence of Pm3m (abbreviated as C phase) of ~39.45%, P4bm (abbreviated as T phase) of ~37.11%, and R phase of ~23.42%, indicating that the A-site high entropy can promote the transformation from R3c to weak polar phase of P4bm and nonpolar phase of Pm3m. For BNKLSTN5 ceramic, the Nb doping leads to a further enhancement of P4bm content (~41%) and Pm3m content (~50%), which is consistent with the temperature-related dielectric constants.

From the perspective of internal contributions, the coexistence of multiple phases can lead to a flat polarization energy barrier, enabling rapid polarization response. Therefore, the stability of functional performance is closely related to the stability of the phase structure33,40,41. As shown in Fig. 4h, we have added temperature-dependent in situ XRD for BNKLSTN5 ceramics, which demonstrates that the phase structure remains stable within the tested temperature range. Specifically, as shown in Fig. 4i, j, the (111) and (200) peaks show no changes, including splitting or merging, indicating that the phase structure is stable. This is consistent with the results shown in Fig. S12c, where the ceramics remain in a superparaelectric state over a wide temperature range. Additionally, in situ Raman spectroscopy provides parallel results, confirming the structural temperature stability of the BNKLSTN5 ceramic. As depicted in Fig. 4k, the deconvolution results reveal that the number of Raman peaks remains unchanged with increasing temperature, suggesting the local symmetry is maintained over a wide temperature range. Moreover, the wavenumbers of the peak at ~272 and ~543 cm−1 decrease, while the full width at half maximum (FWHM) shows a noticeable increase (Fig. 4l, m), demonstrating an increase in structural disorder, which helps suppress the increase of Pr during a rise in temperature42,43.

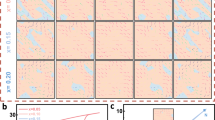
The statistical breakdown strengths (Eb) were calculated through Weibull distribution fitting based on a total of 10 samples for each ceramic (Fig. S14). Pristine BNT ceramic exhibited a poorly calculated Eb of 35 kV/mm. After introducing a high-entropy strategy, the BNKLST ceramic exhibited a higher calculated Eb of 58 kV/mm. After introducing the chemical SRO strategy, the BNKLSTN5 ceramic exhibited the highest calculated Eb of 85.5 kV/mm. These results are very close to the experimental Eb values. Moreover, a high β of ~14.55 for BNKLSTN5 indicated that this high value is not coincidental but can be reproduced reliably. Figure S15 show the scanning electron microscopy (SEM) images of the BNKLST and BNKLSTN5 ceramics. The pristine BNT ceramic exhibits an average grain size of ~7.5 μm44. Following the implementation of the high-entropy strategy, the grain size of BNKLST is reduced to around 0.87 μm. It is well-known that Nb acts as a grain growth inhibitor during sintering45, and BNKLSTN5 demonstrates an even finer grain size of ~0.25 μm. It is widely recognized that a reduction in average grain size (Ga) is correlated with an increase in breakdown strength (Eb), which typically adheres to an exponential decay relationship with respect to grain size (i.e., Eb ∝ Ga⁻¹)46,47. This phenomenon can be attributed to the presence of a depletion layer at the grain boundaries, which facilitates a higher barrier for the mobility of ions and electrons48. Moreover, electron paramagnetic resonance (EPR) tests exhibit that Nb doping suppressed the O vacancy (Fig. S16). The intrinsic breakdown mechanism in dielectrics typically involves electron breakdown, with the bandgap being a decisive factor. As shown in Fig. S17, we conducted UV-Vis testing on the BNKLSTN and BNKLSTN5 samples and analyzed the bandgap using the Tauc plotting method23. The results indicate that the incorporation of Nb leads to an increase in the bandgap from 3.1 to 3.2 eV, which can be attributed to the wider bandgap of Nb2O5 (~3.4 eV)49 compared to TiO2 (~3.09 eV)50. Furthermore, as shown in Fig. S18, BNKLSTN5 exhibits a dense cross-sectional grain structure and a high relative density above 99%. Consequently, the combination of fine and compact grain structure, increased internal bandwidth, and suppressed oxygen vacancies collectively contribute to the enhanced breakdown field strength.

To characterize the response behavior of PNRs under the external field, as shown in Fig. 5a, b, we performed in situ piezoresponse force microscopy (PFM) measurements on the BNKLST and BNKLSTN5 ceramics. In the PFM results, both ceramics lack long-range ordered ferroelectric domains. Upon applying ±10 V to the ceramics, both ceramics exhibited total polarization switching. However, for BNKLST ceramic, after removing the electric field for 5 and 10 min, a considerable portion of the polarization remained difficult to return to its original state. In contrast, for BNKLSTN5 ceramic, after removing the electric field, there are no significant difference from the initial state. This indicates that the PNRs in BNKLSTN5 ceramic have a stronger response to the external electric field, which is beneficial for the high Pm and low Pr, and thus, for excellent energy storage density and efficiency. Due to resolution limitations, it is challenging to discern the size differences of the PNRs in PFM. To further analyze the changes in the microstructure of the ceramics, we conducted TEM observations on BNT, BNKLST, and BNKLSTN5.

Fig. 5: Microstructural characterization.
figure 5

PFM results of a BNKLST and b BNKLSTN5 ceramics; Bright-field TEM observation of c BNT, d BNKLST, and e BNKLSTN5 ceramics; SAED patterns along [110] zone axis of f BNT, g BNKLST, and h BNKLSTN5 ceramics with the normalized pixel intensities; SAED patterns along [001] zone axis of i BNKLST and j BNKLSTN5 ceramics with the normalized pixel intensities.

Full size image

Figure 5c–e display bright-field TEM observations of the BNT, BNKLST, and BNKLSTN5 ceramics. As shown in Fig. 5c, pristine BNT ceramics exhibited large-scale nanodomain structures. In contrast, as shown in Fig. 5d, e, no significant long-range ordered structures were observed in BNKLST and BNKLSTN5 ceramics, indicating that the introduction of the high-entropy strategy leads to polarization refinement from nanodomain to polar nanoregions (PNRs). Figures 5f1, h1, g1 present the Selected area electron diffraction (SAED) images along the [110] zone axes. For the [110] crystallographic zone axis, the R3c phases exhibit superlattice diffraction spots of 1/2{ooo} which is related to the anti-phase a-a-a- type BO6 tilting39. Using the pixel of the brightest transmission spot as a reference, we extracted the pixel intensity of adjacent superlattice diffraction spots, and the results were shown in Figs. 5f2, h2, g2. For pristine BNT, the pixel brightness ratio of the superlattice diffraction spot to the central transmission spot is 0.7. For BNKLST and BNKLSTN5, the above ratio is 0.278 and 0.148, respectively, suggesting a significant reduction in the R3c content. For the [001] crystallographic zone axis51, the superlattice diffraction spots of 1/2{ooe} is related to the in-phase a0a0c+ type BO6 tilting of P4bm symmetry. To further compare the structural changes of the P4bm phase in BNKLST and BNKLSTN5, the SAED images of the two ceramics along the [001] zone axes were conducted, as shown in Fig. 5i, j. For BNKLST, the pixel brightness ratio of the superlattice diffraction spot to the central transmission spot is 0.797, while for BNKLSTN5, it is 0.982, indicating that the incorporation of Nb leads to an enhancement in the weak polar P4bm phase. These results are consistent with the XRD refinement results, indicating that Nb leads to a reduction of the polar R3c phase and an increase in the content of the weak polar phase and nonpolar phase.

To further observe the PNRs of BNT and BNKLSTN5 ceramics and analyze the relationship between chemical order and polarization heterogeneity, we conducted atomic-scale high-angle annular dark-field (HAADF) observations. As shown in Fig. 6a1, in the HADDF observations, a converged electron beam scans across atomic columns and projects onto a plane. As shown in Fig. 6a2, for perovskite ABO3 ferroelectrics, the polarization vector can be obtained by the displacement of B-site ion relative to the central of the A-site sublattice6,52. Moreover, as shown in Fig. 6a3, the pixel intensity is proportional to the square of atomic number (Z2). Variations in atomic contrast can be employed to analyze the chemical composition order24. We compared the compositional differences of BNKLST and BNKLSTN5 along the [001] zone axis. As shown in Fig. 6b-c, for both BNKLST and BNKLSTN5 ceramics, the intensity at the A-site shows a similar compositional inhomogeneity, indicating that Nb doping has no significant effect on the distribution of A-site. In contrast, as shown in Fig. 6d, e, for the B-site, the B-site intensity of BNKLST exhibits a uniform distribution while BNKLSTN5 exhibits significant contrast variations, revealing B-site nanoscale inhomogeneity. Since the atomic number of Ti is 22 and Nb is 41, regions enriched with Nb will exhibit brighter intensity. Therefore, region I can be attributed to the Nb-rich region, while region II can be attributed to the Ti-rich region. As shown in Fig. S19, atomic-scale energy dispersive spectroscopy (EDS) analysis also confirms that Nb exhibits a notable inhomogeneous distribution while Ti has a uniform distribution. These results indicate that Nb exhibits chemical SRO phenomena within the high-entropy matrix. As shown in Fig. 6f, g, Nb doping leads to further reduction of PNRs to the scale of a few unit cells (i.e., polar nanoclusters1,53), with numerous nonpolar regions. Figure S20 show the polarization intensity mapping and distribution of the two ceramics, also showing a decrease in polarization intensity in the BNKLSTN5 ceramic, along with the presence of nonpolar regions. By combining Fig. 6e and g, it is possible to analyze the heterogeneity of the compositions and the heterogeneity of polarization. As shown in Fig.6h, i, the regions with lower polarization lengths correspond precisely to the areas enriched with Nb. This finding is consistent with DFT calculations, revealing that Nb doping can lead to a significant reduction in the ferroelectric distortion. Moreover, in the Nb-rich regions, the size of the PNRs is smaller than 1 nm (Fig. 6h2). Conversely, in areas with lower Nb content, the sample exhibits a longer polarization and larger PNRs ~2 nm. These results indicate that the short-range ordered Nb promotes a further reduction in the size of PNRs. This leads to a more effective response to the external fields and promotes the relaxor ferroelectric behavior, which benefits the overall energy storage performance. It is worth noting that the PNRs/polar nanoclusters of BNKLSTN5 ceramic exhibit greater polarization heterogeneity, indicating the presence of a multiphase coexistence. To further characterize the flexibility of polarization configuration, we conducted observations on BNKLSTN5 along the [110] zone axis, as shown in Fig. 6j. It is evident that within the ultrafine PNRs, there exists a localized coexistence of R, Orthodromic (abbreviated as O), T and C phases. This multiphase coexistence leads to a flatter energy landscape, which is conducive to achieve exceptionally high overall energy storage performances22.

Fig. 6: Atom-scale HADDF observations and in situ TEM observations.
figure 6

a Schematic diagrams of HADDF image analysis: (a1) In the HADDF image, a converged electron beam scans across atomic columns and projects onto a plane; (a2) By analyzing the ionic positions at A and B site, the direction and magnitude of the polarization vector can be determined; (a3) Furthermore, the variations in the brightness of atomic columns can be analyzed to assess compositional changes, where heavier atoms (e.g., Nb) result in increased pixel intensity. A-site intensity of b BNKLST and c BNKLSTN5 ceramics; B-site intensity of d BNKLST and e BNKLSTN5 ceramics; Polarization direction of f BNKLST and g BNKLST5 ceramics along [001] zone axis; h B-site intensity and polarization direction in the region I; i B-site intensity and polarization direction in the region II; j Polarization direction of BNKLSTN5 ceramic along [110] zone axis, exhibiting a R-O-T-C multiphase coexistence; Evolution of polarization of BNKLSTN5 with the applied voltages of (k1) before applying voltage, (k2) 30 V, (k3) 40 V, and (k4) after applying voltage; l Corresponding [001]-oriented SAED patterns measured under different voltages.

Full size image

To gain deeper insights into the microstructure, we employed in situ TEM under an applied voltage to analyze the polarization response to the external field. As shown in Fig. 6k1, prior to the application of the electric field, no significant long-range order is observed, and the sample exhibits fine PNR/polar nanocluster (as evidenced by atomic-scale STEM). Upon applying the electric field, as shown in Fig. 6k2, k3, the sample gradually develops long-range order, which rapidly disappears upon removal of the field (Fig. 6k4), indicating that these PNR/polar nanoclusters exhibit excellent response to the external electric field. Furthermore, as shown in Fig. 6l1–l3, the SAED results during applying voltages revealed that the diffraction spots of the P4bm phase become brighter, indicating a transition from Pm3m to P4bm phase during the formation of long-range order. Upon removal of the electric field, as shown in Fig. 6l4, the P4bm phase quickly reverts to the Pm3m phase, which facilitates a reduced Pr. This is consistent with our hypothesis that SRO exhibits lower barriers, enabling polarization to respond rapidly to the application of an electric field, thereby forming a long-range order under the electric field and quickly reverting to its initial state after removing the electric field. As observed in Fig. S21, the εr and tanδ of BNKLSTN5 ceramic fluctuate weakly with frequency, favoring the realization of frequency-insensitive energy storage performance, also indicating highly active PNRs/Polar nanoclusters. The high activity of the PNRs/polar nanoclusters induced by SRO contributes to superior energy storage performances with excellent stability.

Discussion

In summary, this work proposes a chemical short-range order strategy to modulate energy storage performance in high-entropy relaxor ferroelectrics. The polarization switching barriers at chemical short-range regions are lower, enabling rapid response to external electric fields and enhancing the overall energy storage performances. We validated the effectiveness of this strategy in Nb-doped high-entropy BNKLST ceramics and achieved comprehensive energy storage performances of Wrec ~16.4 J/cm3 and η ~90%. Atomic-scale HADDF observations show that Nb exhibits a short-range ordered structure, with Nb enriched regions displaying smaller polar nanoregions (PNRs) than 1 nm and flexible polarization configurations of R-O-T-C multiphase coexistence, which is conducive to achieving high Pm and low Pr. Moreover, refined and compacted grain, suppressed oxygen vacancies and enhanced bandwidth contribute to a high breakdown field strength. These collective factors result in exceptionally high energy storage density and efficiency. The short-range order strategy is expected to enhance the functional performances in other high-entropy relaxor ferroelectrics.

Methods

Ceramics preparation

The pristine Bi0.5Na0.5TiO3 and the lead-free Bi0.2Na0.2K0.2La0.2Sr0.2Ti1-xNbx (BNKLSTNx, x = 0.0 and 0.05) ceramics were prepared by raw powders of K2CO3 (99.0%), Na2CO3 (99.8%), SrCO3 (99.0%), Bi2O3 (99.0%), TiO2(98.0%), La2O3(99.99%), and Nb2O5(99.9%) through a conventional solid-state reaction. The raw powders were weighed stoichiometrically and then mixed thoroughly using ball-milling with zirconia balls and absolute ethyl alcohol in a polyethylene container for 12 h. After being calcined at 1100 °C for 2 h, the mixture was ball-milled again for 8 h. The dried mixture was pressed into pellets with a diameter of 10 mm under 200 MPa for 30 s. At last, BNKLSTNx ceramics were sintered at 1220 °C in air for 2 h.

The samples are polished into ~0.05−0.07 mm in thickness, then coated with gold electrode for P-E hysteresis loop measurements. Diamond polishing liquid with particle sizes of 3, 2, and 0.5 microns was used for polishing to ensure low surface roughness. Underdamped and over-damped charge/discharge performance is tested by a capacitor charge-discharge system (CFD-003, Gogo Instruments, China). As shown in Figs. S10a,S11a, during the testing process, the left switch is first turned to the left to initiate charging, with a charging time of 500 ns. Subsequently, after charging, the bidirectional switch is turned to the right, allowing the ceramic capacitor to discharge into a load resistor (R) of 300 Ω, while the discharge signal is measured over a duration of 500 ns.

The crystal structures of samples were analyzed using X-ray diffraction (XRD, SMARTLAB, Japan) with Cu Kα-0.1541 nm. The in situ RAMMA spectra were obtained by Raman spectrometer (Horiba LabRAM HR Evolution). Surface morphologies of the samples were examined by a field emission scanning electron microscope (Gemini SEM 500, Carle Zeiss, Germany). The dielectric properties of the samples were measured using an LCR meter (E4980A, Agilent). The P-E hysteresis loops under different electric fields were measured by Precision Premier II from Radiant Technologies, connected to a high voltage amplifier. The focused ion beam (FIB) milling technology was used in this work to prepare the TEM sample. A spherical aberration-corrected transmission electron microscope (Thermo Fisher Spectra 300, USA) was used to acquire the bright field observations and high-angle annular dark-field scanning-transmission electron microscopic (HAADF-STEM) images. The equipped EDS apparatus was used to acquire the elements distribution. Based on the HAADF-STEM images, the polarization vector and atom column intensity were calculated and extracted by the MATLAB scripts54. For the in situ TEM observation, Pt-electrodes were deposited on both sides of the TEM sample and an electrochemically etched tungsten tip was used as a movable electrode44. Piezoresponse force microscopy (PFM) measurements were conducted using Park Systems XE7 AFM. UV-Vis absorption spectra were obtained by a UV-Vis Spectrometer (Shimadzu UV-3600i Plus). The Electron Paramagnetic Resonance (EPR) results were obtained by an EPR Spectrometer (Bruker EMXplus-6/1, Germany).

Phase-field simulations

Phase-field simulations were performed to show the impact of lowered local polarization switching energy on the ferroelectric domain structure evolution and, therefore, on the polarization response. In the phase-field model, the time-dependent Ginzburg-Landau equation was used to describe the evolution of the polarization P(x, t) for the ferroelectric system without and with a lowered local energy barrier, as follows55:

$$\frac{\partial {{{\boldsymbol{P}}}}}{\partial t}=-L\frac{\delta F}{\delta {{{\boldsymbol{P}}}}}\,$$
(1)

where x and t are the space position and time, respectively, L is the kinetic coefficient, and F means the total free energy of the system. The above equation describes that the polarization will evolve over time in the direction of minimizing the free energy of the system. The total free energy can be expressed as follows:

$$F=\int _{V}{f}_{{\!\!bulk}}+{f}_{{\!\!elas}}+{f}_{{\!\!elec}}+{f}_{{\!\!grad}}\;{dV}\,$$
(2)

where V denotes the system volume, \({f}_{{bulk}}\) the Landau bulk free energy density, \({f}_{{elas}}\) the elastic energy density, \({f}_{{elec}}\) the electrostatic energy density and \({f}_{{grad}}\) the gradient energy density. The bulk free energy is expressed as follows:

$$\begin{array}{c}{f}_{{\!\!bulk}}={\alpha }_{1}\left({P}_{1}^{2}+{P}_{2}^{2}+{P}_{3}^{2}\right)+{\alpha }_{11}\left({P}_{1}^{4}+{P}_{2}^{4}+{P}_{3}^{4}\right)+{\alpha }_{12}\left({P}_{1}^{2}{P}_{2}^{2}+{P}_{2}^{2}{P}_{3}^{2}+{{P}_{1}^{2}P}_{3}^{2}\right)+{{\alpha }_{123}P}_{1}^{2}{P}_{2}^{2}{P}_{3}^{2} \\+{\alpha }_{111}\left({P}_{1}^{6}+{P}_{2}^{6}+{P}_{3}^{6}\right)+{\alpha }_{112}\left({P}_{1}^{2}\left({P}_{2}^{4}+{P}_{3}^{4}\right)+{P}_{2}^{2}\left({P}_{1}^{4}+{P}_{3}^{4}\right)+{P}_{3}^{2}\left({P}_{1}^{4}+{P}_{2}^{4}\right)\right)\end{array}$$
(3)

where \({\alpha }_{1}\), \({\alpha }_{11}\), \({\alpha }_{12}\), \({\alpha }_{111}\), \({\alpha }_{112}\) and \({\alpha }_{123}\) are Landau energy coefficients, these values are come from our previous work44. Details for the rest of the contribution to the total free energy can be found in ref. 56.

We adopted a finite element method to numerically solve the above partial differential equations. The triangular elements were used for the space discretization. Specifically, it is performed through the mathematical interface in the COMSOL software due to its powerful solving capabilities in multiphysics problems. The schematic diagram of the phase-field simulation model (Fig. 1a) was created using Visio software.

DFT calculations

DFT calculations were performed by using the Vienna ab initio simulation package (VASP)57. For the exchange-correlation function, the generalized gradient approximation (GGA) of Perdew–Burke–Emzerhof for solid was used58. Electron-ion interactions were described by the projector augmented-wave (PAW) potential with a kinetic energy cut-off of 500 eV. The Na 2p3s, Bi 5d6s6p, Nb 4s4p4d5s, Ti 3d4s, and O 2s2p states were treated as valence electrons. The Brillouin zone integrations were sampled by using 4 × 4 × 4 Monkhorst-Pack grids for all the calculations. Specifically, 2 × 2 × 2 P4bm and Pm3m phase were used as starting configurations. All supercells have a uniform distribution of A-site cations (Bi and Na) along the a, b, and c directions in the calculations, as shown in Fig. S3. The energy convergence criterion was set to be 10−6 eV and the structure was fully relaxed until the force was <0.02 eV/Å. After the calculations were completed, the crystal structure was visualized using Vesta software.