Introduction

Artificial Intelligence algorithms, spurred by the growth of deep neural networks (DNN), have produced the state-of-the-art solutions in several domains ranging from computer vision1, speech recognition2, game playing3 to scientific discovery4, natural language processing (NLP)5, and more. The general trend in all these applications has been increasing the model size by increasing the number of layers and the number of weights in each layer. This trend has, however, caused growing concern in terms of energy efficiency for both edge applications and servers for training; power is scarce due to battery limits in edge devices while the total energy required for training large models in the cloud raises environmental concerns. Edge devices have a further challenge posed by strong latency requirements in applications such as keyword spotting to turn on mobile devices, augmented reality and virtual reality platforms, anti-collision systems in driverless vehicles etc.

The bottleneck for implementing DNNs on current hardware arises due to the frequent memory access necessitated by the von Neumann architecture and the high memory access energy for storing the parameters of a large model6. As a solution to this problem, a new architecture of In-memory Computing (IMC) has become increasingly popular. Instead of reading and writing data from memory in every cycle, IMC allows neuronal weights to remain stationary in memory with inputs being applied to it in parallel and the final output prior to neuronal activation being directly read from memory. Among the IMC techniques explored, analog/mixed-signal IMC using non-volatile memory devices such as memristive7 ones have shown great promise in improving latency, energy and area efficiencies of DNN training8,9,10 and inference11,12,13, combinatorial optimization14,15, hardware security11,16, content addressable memory17, signal processing18,19,20 etc. It should be noted that analog IMC does not refer to the input and output signals being analog; rather, it refers to the storage of multi-bit or analog weights in each memory cell (as opposed to using memristor for 1-bit storage21,22) and using analog computing techniques (such as Ohm’s law, Kirchoff’s law etc.) for processing inputs. Analog weight storage23 enables higher density of weights as well as higher parallelism (by enabling multiple rows simultaneously) compared to digital counterparts.

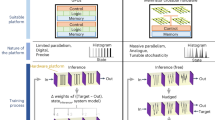
Comparing the energy efficiency and throughput of recently reported DNN accelerators (Fig. 1a) shows the improvements provided by IMC approaches over digital architectures. However, taking a closer look based on DNN architecture exposes an interesting phenomenon–while analog IMC has improved energy efficiency of convolutional and fully connected (FC) layers in DNNs, the same cannot be said for recurrent neural network (RNN) implementations such as long short term memory (LSTM)24,25,26,27,28. Resistive memories store the layer weights in their resistance values, inputs are typically provided as pulse widths or voltage levels, multiplications between input and weight happen in place by Ohm’s law, and summation of the resulting current occurs naturally by Kirchoff’s current law. This enables an efficient implementation of linear operations in vector spaces such as dot products between inputs and weight vectors. Early implementations of LSTM using memristors have focussed on achieving acceptable accuracy in network ouptut in the presence of programming errors. A 128 × 64 1T1R array29 was shown to be able to solve real-life regression and classification problems while 2.5 M phase-change memory devices30 have been programmed to implement LSTM for language modeling. While these were impressive demonstrations, energy efficiency improvements were limited, since RNNs such as LSTMs have a large fraction of nonlinear (NL) operations such as sigmoid and hyperbolic tangent being applied as neuronal activations (Fig. 1b). With the dot products being very efficiently implemented in the analog IMC, the conventional digital implementation of the NL operations now serves as a critical bottleneck.

Fig. 1: Limitation of current In-memory computing (IMC) for Recurrent Neural Networks and our proposed solution.
figure 1

a A survey of DNN accelerators show the improvement in energy efficiency offered by IMC over digital architectures. However, the improvement does not extend to recurrent neural networks (RNN) such as LSTM and there exists a gap in energy efficiency between RNNs and feedforward architectures. Details of the surveyed papers available here66. b Architecture of a LSTM cell showing a large number of nonlinear (NL) activations such as sigmoid and hyperbolic tangent which are absent in feedforward architectures that mostly use simple nonlinearities like rectified linear unit (ReLU). c Digital implementation of the NL operations causes a bottleneck in latency and energy efficiency since the linear operations are highly efficient in time and energy usage due to inherent parallelism of IMC. For a LSTM layer with 512 hidden unit and with k = 32 parallel digital processors for the NL operations, the NL operations still take 2–5X longer time for execution due to the need of multiple clock cycles (Ncyc) per NL activation. d Our proposed solution creates an In-memory analog to digital converter (ADC) that combines NL activation with digitization of the dot product between input and weight vectors.

Full size image

As an example, an RNN transducer was implemented on a 34-tile IMC system with 35 million phase-change memory (PCM) devices and efficient inter-tile communication31. While the system integration and scale of this effort31 is very impressive, the NL operations are performed off-chip using low energy efficiency digital processing reducing the overall system energy efficiency. Another pioneering research23 integrated 64 cores of PCM arrays for IMC operations with on-chip digital processing units for NL operations. However, the serial nature of the digital processor, which is shared across the neurons in 8 cores, reduced both the energy efficiency and throughput of the overall system. This work used look-up tables (LUT), similar to other works32,33,34; alternate techniques using cordic35 or piece wise linear approximations24,36,37,38 or quadratic polynomial approximation39 have also been proposed to reduce overhead and latency (Ncyc) of computing one function. However, it is the big difference in parallelism of crossbars versus serial digital processors which causes this inherent bottleneck. Even in a hypothetical situation with an increased number of parallel digital computing engines for the NL activations (Fig. 1c, Supplementary Note S6), albeit at a large area penalty, the latency of the NL operations still dominates the overall latency due to the extremely fast implementation of vector-matrix-multiplication (VMM) in memristive crossbars.

In this work, we introduce an in-memory analog to digital conversion (ADC) technique for analog IMC systems that can combine nonlinear activation function computations in the data conversion process (Fig. 1d), and experimentally demonstrate its benefits in an analog memristor array. Utilizing the sense amplifiers (SA) as a comparator in ramp ADC, and creating a ramp voltage by integrating the current from an independent column of memristors which are activated row by row in separate clock cycles, an area-efficient in-memory ADC for memristive crossbars is demonstrated. However, instead of generating a linear ramp voltage as in conventional ADCs, we generated a nonlinear ramp voltage by appropriately choosing different values of memristive conductances such that the shape of the ramp waveform matches that of the inverse of the desired NL activation function. Using this method, we demonstrate energy-efficient 5-bit implementations of commonly used NL functions such as sigmoid, hyperbolic tangent, softsign, softplus, elu, selu etc. A one-point calibration scheme is shown to reduce the integral nonlinearity (INL) from 0.948 to 0.886 LSB for various NL functions. Usage of the same IMC cells for ADC and dot-product also gives added robustness to read voltage variations, reducing INL to  ≈0.04 LSB compared to  ≈5.0 LSB for conventional methods. Using this approach combined with hardware aware training40, we experimentally demonstrate a keyword spotting (KWS) task on the Google speech commands dataset (GSCD)41. With a 32 hidden neuron LSTM layer (having 128 nonlinear gating functions) that uses 9216 memristors from the 3 × 64 × 64 memristor array on our chip, we achieve 88.5% accuracy using a 5-bit NL-ADC with a  ≈9.9X and  ≈4.5X improvement of area and energy efficiencies respectively at the system level for the LSTM layer over previous reports. Moreover, compared to a conventional approach using the exact same configuration (input and output bit-widths) as ours, the estimated area and energy efficiency advantages are still retained at c ≈6.2X and  ≈1.46X respectively for system level of evaluation. Finally, we demonstrate the scalability of our system by performing a character prediction task on the Penn Treebank dataset42 using a LSTM model  ≈100X bigger than the one for KWS using experimentally validated nonideality models and achieving software equivalent accuracy. The improvements in area efficiency are estimated to be 6.6X over a conventional approach baseline and 125X over earlier work31 at the system level, with the drastic increase in performance due to the much higher number of nonlinear functions in the larger model.

Results

Nonlinear function approximation by ramp ADC

A conventional ramp ADC operates on an input voltage Vin ∈ {Vmin, Vmax} and produces a binary voltage Vout whose time of transition from low to high, tin ∈ {0, TS}, encodes the value of the input. As shown in Fig. 2a, Vout is produced by a comparator whose positive input is connected to a time-varying ramp signal, Vramp(t) = f(t) and the negative input is connected to Vin. For the conventional case of linearly increasing ramp voltage, and denoting the comparator’s operation by a Heaviside function Θ, we can mathematically express Vout as:

$${V}_{out}=\Theta ({V}_{ramp}(t)-{V}_{in})=\Theta (f(t)-{V}_{in})=\Theta (Kt-{V}_{in})$$
(1)

The threshold crossing time tin can be obtained as \({t}_{in}={f}^{-1}({V}_{in})=\frac{1}{K}{V}_{in}\) by setting Equation (1) equal to zero and solving for ‘t’. The pulse width information in tin may be directly passed to the next layers as pulse-width modulated input31 or can be converted to a digital code using a time-to-digital converter (TDC)43. Now, suppose we want to encode the value of a nonlinear function of Vin, denoted by g(Vin) in tin. Comparing with the earlier equation of tin, we can conclude this is possible if:

$${t}_{in}={f}^{-1}({V}_{in})=g({V}_{in})\ \Rightarrow \ f()={g}^{-1}()$$
(2)

where we assume that the desired nonlinear function g() is bijective and an inverse exists in the defined domain of the function. Supplementary Note S1 shows the required ramp function for six different nonlinear activations. For the case of non-monotonic functions, this method can still be applied by splitting the function into sections where the function is monotonic. Examples of such cases are shown in Supplementary Note S12 for two common non-monotonic activations–Gelu and Swish.

Fig. 2: Overview of in-memory nonlinear ADC.
figure 2

a The concept of traditional ramp-based ADC. b The schematic and timing of in-memory computing circuits with embedded nonlinear activation function generation. c The Inverse of the sigmoid function illustrates the shape of the required ramp voltage. d The value of each step of the ramp voltage Vramp denoted by ΔVk is proportional to memristor conductances Gadc,k used to program the nonlinear ramp voltage. The desired conductances for a 5-bit implementation of a sigmoid nonlinear activation is shown. e Comparison of used cell numbers between 5-bit and 4-bit in-SRAM with 5-bit in-RRAM nonlinear function. The RRAM-based nonlinear function has an approximation error between the two SRAM-based ones due to write noise while using a smaller area due to its compact size.

Full size image

In practical situations, the ramp function is a discrete approximation to the continuous function f(t) mentioned earlier. For a b-bit ADC, the domain of the function Vramp = f(t) is split into P = 2b segments using P + 1 points tk such that \({t}_{0}=0,{t}_{k}=\frac{k{T}_{s}}{P}\) and tP = Ts. The initial voltage of the ramp, f(0) = V0 = Vinit, defines the starting point while the other voltages Vk (k = 1 to P) can be obtained recursively as follows:

$${V}_{k}={V}_{k-1}+\Delta {V}_{k}={V}_{k-1}+({g}^{-1}({t}_{k})-{g}^{-1}({t}_{k-1}))$$
(3)

Here, Vinit may be selected appropriately to maximize the dynamic range of the function represented by the limited b-bits. Supplementary Table S2 demonstrates the choice of (tk, ΔVk) tuples for six different nonlinear functions commonly used in neural networks.

In-memory Implementation of nonlinear ADC and vector-matrix multiply in a crossbar array

Different from traditional IMC systems where the ADCs and nonlinear functions calculation are separated from the memory core, our proposed hardware implements the ADC with nonlinear calculation ability inside the memory along with the computation part. The nonlinear function approximating ADC described earlier is implemented using memristors with the following unique features:

  1. 1.

    We utilize the memristors to generate the ramp voltages directly within the memory array which incurs very low area overhead with high flexibility.

  2. 2.

    By leveraging the multi-level state of memristors, we can generate the nonlinear ramp voltage according to the x-y relationship of the nonlinear function as described in Equation (3).

Take the sigmoid function, (y = g(x) = 1/(1 + e−x)) as an example. To extract the step of the generated ramp voltages, we first take the inverse of the sigmoid function (\(x={g}^{-1}(y)=\ln \frac{y}{1-y}\)) as shown in Fig. 2c. This function is exactly the ramp function that needs to be generated during the conversion process, as described in detail in the earlier section. The figure shows the choice of 32 (x,y) tuples for 5-bit nonlinear conversion. The voltage difference between successive points (Δvk in Equation (3)) is shown in Fig. 2d highlighting the unequal step sizes. Memristors proportional to these step values need to be programmed in order to generate the ramp voltage, as described next. We show our proposed in-memory nonlinear ADC circuits in Fig. 2b. In each memory core, only a single column of memristors will be utilized to generate Vramp(t) = f(t) with very low hardware cost as shown in Fig. 2e. The memory is separated into N columns for the multiplication-and-accumulation (MAC) part and one column for the nonlinear ADC (NL-ADC) part. For the MAC part, the inputs are quantized to b-bit (b = 3–5 in experiments) if necessary and transferred into pulse width modulation (PWM) signals sent to the SL of the array. To adapt to the positive and negative weights or inputs in the neural networks, we encode one weight or input into differential 1T1R pairs and inputs shown in Supplementary Fig. S9. We propose a charge-based approach for sensing the MAC results where the feedback capacitor of an integrator circuit is used to store the charge accumulated on the BL. Denoting the feedback capacitor by Cfb, the voltage on the sample and hold (S&H) for the k-th column is:

$${V}_{mac,k}={V}_{CLP}+\frac{1}{{C}_{fb}}{\sum}_{i}{V}_{read}{G}_{ik}{T}_{in,i}$$

where VCLP is the clamping voltage on the bitline enforced by the integrator, Tin,i denotes the pulse width encoding the i-th input and Gik is the memristive conductance on the i-th row and k-th column.

In the column of the NL-ADC part, we have two sets of memristors. One is the memristors for generating the initial bias voltage (Vinit in the earlier section), and another set of memristors is for generating the nonlinear ramp voltages. The addition of bias memristors is used to set the initial ramp value as well as calibrate the result after programming the NL-ADC memristors due to programming not being accurate. The ‘one point’ calibration will move the ramp function generated by the NL-ADC column to intersect the desired, theoretical ramp function at the zero-point which leads to minimal error. This is described in detail in the next sub-section. As shown in the timing diagram in Fig. 2b, after the MAC results are latched on the S&H, the positive input with one cycle pulse width is first sent into NL-ADC column to generate a bias voltage (corresponding to the most negative voltage at the starting point Vinit) for the ramp function on Vramp. Then for each clock cycle, negative input is sent to the SL of NL-ADC memristors to generate the ramp voltages on Vramp. Since the direction of each step voltage is known, only one memristor is used corresponding to the magnitude of the step while the polarity of the input sets the direction of the ramp voltage. Using less memristors for every step provides the flexibility to use more devices for calibration or error correction if stuck devices are found. The ramp voltage generated at the q-th clock cycle, \({V}_{ramp}^{q}\), is given by the following equation:

$${V}_{ramp}^{q}={V}_{CLP}+{V}_{init}+\frac{1}{{C}_{fb}}{\sum}_{i=1}^{q}{V}_{read}{G}_{adc,i}{T}_{adc}$$

where Tadc are the pulse width of ADC read pulses and \(\frac{{V}_{read}{G}_{adc,k}{T}_{adc}}{{C}_{fb}}\) equals ΔVk from Equation (3). An example of the temporal evolution of the ramp voltage is shown in the Supplementary Note S9. The comparison between the Vramp and MAC result is done by enabling the comparator using the clk_ad signal after each step of the generation of ramp voltages. The conversion continues for P = 2b cycles producing a thermometer code or pulse width proportional to the nonlinear activation applied to the MAC result. The pulse-width can be directly transferred to other layers as the input as done in other works31; else, the thermometer code can be converted to binary code using a ripple counter23.

To prove the effectiveness of this approach, we simulate it at the circuit level and the results are shown in Fig. S2. The fabricated chip does not include the integrators and the comparator which are implemented in software after obtaining the crossbar output. In-memory ramp ADC using SRAM has been demonstrated earlier44 in a different architecture with a much larger (100%) overhead compared to the memory used for MAC operations; however, nonlinear functions have not been integrated with the ADC. Implementing the proposed scheme using SRAM would require many cells for each step due to the different step sizes. Since an SRAM cell can only generate two step sizes (+1 or −1) intrinsically, other step sizes need to be quantized and represented in terms of this unit step size (or LSB). Denoting this unit step by \(min(\Delta {V}_{k}),round(\frac{\Delta {V}_{k}}{min(\Delta {V}_{k})})\) is the number of SRAM cells needed for a single step while the total number of steps needed is given by \({\sum }_{k=1}^{{2}^{n}}round(\frac{\Delta {V}_{k}}{min(\Delta {V}_{k})})\). Figure 2e illustrates this for several common nonlinear functions. However, thanks to the analog tunability of the conductance of memristors, we can encode each step of the ramp function ΔVk into only one memristor Gadc,k which leads to the usage of much lower number of bitcells (1.28X–4.68X) compared with nonlinear SRAM-based ramp function generation (Fig. 2e) for the 5-bit case. However, the write noise in memristors can result in higher approximation error than the SRAM version. Using Monte-Carlo simulations for the SRAM case, we estimate the mean squared error (MSE) for a memristive 5-bit version is generally in between that of the 5-bit and 4-bit SRAM versions (e.g., MSE for sigmoid nonlinearity is  ≈0.0008 and  ≈0.0017 respectively for the 5-bit and 4-bit SRAM versions, while that of the memristive 5-bit version is  ≈0.0014). Hence, we also plot in Fig. 2e the number of SRAM bitcells needed in 4-bit versions as well. However, combined with the inherently smaller (>2X) bitcell size of memristors compared to SRAM, our proposed approach still leads to more compact implementations with very little overhead due to the ramp generator. The approximation accuracy for the memristive implementation is expected to improve in future with better devices45 and programming methods46. Details of the number of SRAM cells needed for six different nonlinear ramp functions are shown in Supplementary Table S2. The topology shown here is restricted to handle inputs limited to the dimension of the crossbar. We show in Supplementary Note S10 how it can be extended to handle input vectors with dimensions larger than the number of rows in the crossbar by using the integrator to store partial sums and splitting the weight across multiple columns.

Calibration procedures for accurate programming of nonlinear functions in crossbars

Mapping the NL-ADC into memristors has many challenges including device-to-device variations, programming errors, etc such that the programmed conductance \({G}_{adc,k}^{{\prime} }\) will deviate from the desired Gadc,k. To tackle these problems, we introduce the adaptive mapping method to calibrate the programming errors. For each nonlinear function, we first extract the steps ΔVk of the function as illustrated in Fig. 2d. Then we normalize them and map them to the conductances with a maximum conductance of 150 μS. Detailed characterization of our memristive devices were presented earlier47. We program the conductances using the iterative-write-and-verify method explained in methods. However, the programming will introduce errors, and hence, we reuse the Ncali (=5 in experiments) bias memristors to calibrate the programming error according to the mapped result. These memristors are also used to create the starting point of the ramp Vinit, which is negative in general (assuming domain of g() spans negative and positive values). Hence, positive voltage pulses are applied to these bias/calibration conductances while negative ones are applied to the Gadc,k for the ramp voltage as shown in Fig. 2a. Based on this, the one-point calibration strategy is to match the zero crossing point of the implemented ramp voltage with the desired theoretical one by changing the value of Vinit to Vinit,new. The total calibration conductance is first found as:

$${G}_{{{{\rm{cali}}}},{{{\rm{tot}}}}}=\mathop{\sum }_{i=1}^{m}{G}_{adc,i}^{{\prime} }\quad \,{{\mbox{where}}}\,\,m\in {\mathbb{N}}\,s.t.\quad {V}_{m}=0$$

Here, m is the index where the function g() = f −1() crosses the zero point of the x-axis. We then represent this calibration term using only a few memristors with the largest conductance on the chip (\({G}_{\max }=150\,{{{\rm{\mu }}}}{{{\rm{S}}}}\)). The number of memristors used for calibration is Ncali = [Gcali,tot/150 μS] + 1 in which Ncali − 1 memristors are 150 μS and the one left is Gcali mod 150 μS. More details about the calibration process including timing diagrams are provided in the Supplementary Note S9.

To demonstrate the effectiveness of our approach, we experimentally programmed two frequently used nonlinear functions in neural network models: sigmoid function and tanh function, with the calibration methods mentioned above, as shown Fig. 3a. We program 64 columns containing the same NL-ADC weights and calibration terms in one block of our memristor chip and set the read voltage to 0.2 V. In the left panel, we compare the transfer function with 3 different cases: (1) Ideal nonlinear function (2) Transfer function without on-chip calibration (3) Transfer function with on-chip calibration. We can find that the curve with calibration matches well with the ideal curve while the one without calibration has some deviation. We also show the programmed conductance map in the right panel for a block of 8 arbitrarily selected columns to showcase different types of programming errors that can be corrected. The first 32 rows are the NL-ADC weights representing 5-bit resolution. The remaining 5 rows are the calibration memristors after reading out the NL-ADC weights to mitigate the program error. In the conductance map on the right, we can also find some devices which are either stuck at OFF or have higher programming error. Fortunately,these errors happening during the NL-ADC weights programming can be compensated by the calibration part as evidenced in the reduced values of average INL. In addition to these two functions, we also show other nonlinear functions with in-memory NL-ADC in Supplementary Fig. S7 which covers nearly all activation functions used in neural networks. Further reductions in the INL may be achieved through redundancy. Briefly, the entire column used to generate the ramp has many unused memristors which may be used to program redundant copies of the activation function. The best out of these may be chosen to further reduce the effect of programming errors. Details of this method along with measured results from two examples of nonlinear activations are shown in Supplementary Note S11.

Fig. 3: Experimentally demonstrated NL-ADC on crossbar arrays.
figure 3

a Calibration process for accurate NL-ADC programming. The left panel shows the ramp function of the ideal case, programming without bias calibration and with bias calibration. The case with bias calibration shows better INL performance. The right panel shows the actual conductance mapping on the crossbar arrays on two blocks of 8 arbitrary selected columns. The lower 5 conductances are for bias calibration while the top 32 are for the ramp generation. We show the cases when mapping of NL-ADC weights doesn’t have stuck-at-OFF devices and low programming error (left block), and the cases which have stuck-at-OFF devices and high programming error (right block). The results show that both cases can be calibrated by the additional 5 memristors. b Robustness of our proposed in-memory NL-ADC under Vread variations. We sweep the Vread from 0.15 V to 0.25 V to simulate noise induced variations in read voltage. Normal ADC has large variations while our in-memory NL-ADC can track the Vread.

Full size image

In a real IMC system, the voltage variations on-chip could harm the performance. This can be a challenge when using traditional ADC due to the lack of ability to track the voltage variation. For example, if the voltage we set for VMM is 0.2 V but the actual voltage sent to SL is 0.25 V (due to supply noise, voltage drop etc.), the final result read out from the ADC will deviate a lot from the real VMM result. Fortunately, our in-memory NL-ADC has the natural ability to track the voltage variations on-chip since the LSB of the ADC is generated using circuits matching those generating the MAC result. Hence, the read voltage is canceled out during the conversion and only the relative values of MAC and ADC conductances will affect the final result. To demonstrate that our proposed in-memory NL-ADC is robust under different read voltages, we run the experiment by setting different read voltages from 0.15 V to 0.25 V and measure the transfer function. From the result shown in Fig. 3b, we can see that the conventional ADC has large variations (maximum INL of 4.12–5.5 LSB) due to Vread variations while our in-memory NL-ADC only experiences a little effect (maximum INL of 0.02–0.44 LSB).

Long-short-term memory experiment for keyword spotting implemented in memristor hardware

After verifying the performance of the nonlinear activations on chip, we proceed to assess the inference accuracy obtained when executing neural networks using NL-ADC model on chip. The GSCD41, a common benchmark for low-power RNNs48,49, is used to train and test for 12-class KWS task. The KWS training network consists of Mel-frequency cepstral coefficient (MFCC), standardization, LSTM layer (9216 weight parameters in a 72 × 128 crossbar) and FC layer; detailed parameters pertaining to the task are provided in “Methods”. Further training with weight noise-aware and NL-ADC noise-aware (Methods) is implemented.

On-chip inference shown in Fig. 4a is performed after training. After feature extraction (MFCC extraction and normalization), a single input audio signal is divided into 49 arrays, each with a feature length of 40. These extracted features, along with the previous 32-dimensional output vector ht from the LSTM, are then sent to the memristor crossbar. The architecture of LSTM layer, along with the direction of data flow, is depicted in Fig. 4b. The equations of the LSTM layer are given by Equation (4) and Equation (5) as below:

$$\left[\begin{array}{c}{h}_{f}^{t}\\ {h}_{a}^{t}\\ {h}_{i}^{t}\\ {h}_{o}^{t}\end{array}\right]=\left[\begin{array}{c}\sigma \\ \tanh \\ \sigma \\ \sigma \end{array}\right]\left[\begin{array}{ll}{x}^{t}&{h}^{t-1}\end{array}\right]\left[\begin{array}{l}W\\ U\end{array}\right]$$
(4)
$${h}_{c}^{t} ={h}_{f}^{t}\odot {h}_{c}^{t-1}+{h}_{i}^{t}\odot {h}_{a}^{t}\\ {h}^{t} ={h}_{o}^{t}\odot \tanh \left({h}_{c}^{t}\right)$$
(5)

where xt represents the input vector at the current step, ht and ht−1 denote hidden state vector also known as output vector of the LSTM cell at the current and previous time steps, and \({h}_{c}^{t}\) represents cell state vector at the current time step. The model parameters, including the weights W and recurrent weights U, are stored for \({h}_{f}^{t},{h}_{i}^{t},{h}_{o}^{t}\) and \({h}_{a}^{t}\) (forget gate, input/update gate, output gate, cell input, respectively). ⊙ denotes element-wise multiplication and σ is the sigmoid function. The parameters (W and U) and functions (σ and tanh) in Equation (4) are programmed in the memristor crossbar (Methods) and the conductance difference map of the memristor crossbar is depicted in Fig. 4b. Therefore, all MAC and nonlinear operations specified in Equation (4) are executed on chip removing the need to transfer weights back and forth. The four vectors outputted by the chip (\({h}_{f}^{t},{h}_{a}^{t},{h}_{i}^{t},{h}_{o}^{t}\)) are all digital, allowing them to be directly read by the off-chip processor without requiring an additional ADC. This approach provides notable benefits, such as a substantial reduction in the latency due to nonlinearity calculation in a digital processor and decreased energy consumption.

Fig. 4: LSTM for KWS task.
figure 4

a Architecture of LSTM network on-chip inference. b Mapping of LSTM network onto the chip. Weights and nonlinearities (Sigmoid and Tanh) of LSTM layer are programmed crossbar arrays as conductance. Input and output (I/O) data of LSTM layer are sent from/to the integrated chip through off-chip circuits. c Weight conductance distribution curve and error. d The measured inference accuracy results obtained on the chip are compared with the software baseline using the ideal model, as well as simulation results under different bit NL-ADC models and hardware-measured weight noise. e Energy efficiency and area efficiency comparison: our LSTM IC, conventional ADC model and recently published LSTM ICs from research papers23,25,26,27,28,31,67,68. Energy efficiency and throughput under 8 bit, 5 bit, 4 bit and 3 bit NL-ADC are calculated based on 16 nm CMOS technology and clock frequency of 1 GHz. Detailed calculations are shown in Supplementary Note S3, Supplementary Note S4 and Tab. S5. Area efficiency of all works are normalized to 1 GHz clock and 16 nm CMOS process. f Energy efficiency comparison (this work, conventional ADC model, a chip for speech recognition using LSTM model31) at various levels: MAC array, NL-processing, full system. Full system includes MAC and NL-processing and other modules that assist MAC and NL-processing.

Full size image

Figure 4d depicts inference accuracy results for 12-class KWS. After adding the NL-ADC model to replace the nonlinear functions in the LSTM cell (Equation (4)), 91.1%, 90%, and 89.4% inference accuracy were obtained in the 5-bit, 4-bit, and 3-bit ADC models respectively which compare favorably with a floating-point baseline of 91.6%. To enhance the model’s robustness against hardware non-ideal factors and minimize the decrease in inference accuracy from software to chip, we injected hardware noise (“Methods”) in the weight crossbar and NL-ADC crossbar conductances during the training process. The noise model data used in this process is obtained from the actual memristor crossbar and follows a normal distribution ≃N(0.5 μS) (Supplementary Fig. S8c). As a result, we attain inference accuracies in software of 89.4%, 88.2%, and 87.1% for the 5-bit, 4-bit, and 3-bit NL-ADC cases models respectively. Note that the drop in accuracy is much less for feedforward models as shown in Supplementary Note S8. Further, the robustness of the classification was verified by conducting 10 runs; the small standard deviation shown in Fig. 4d confirming the robustness. Through noise-aware training, we obtain weights that are robust against write noise inherent in programming memristor conductances. These weights are then mapped to corresponding conductance values through a scaling factor by matching the maximum weight after training to the maximum achievable conductance (Methods). Both the conductance values associated with the weights and the NL-ADC are programmed on the memristor crossbar, facilitating on-chip inference.

Figure 4c shows the performance of weight mapping after programming the memristor conductance using iterative methods. The error between the programmed conductance value and the theoretical value follows a normal distribution. The on-chip, experimentally measured inference accuracies achieved are 88.5%, 86.6%, and 85.2% for the 5-bit, 4-bit, and 3-bit ADC models, respectively where the redundancy techniques in Supplementary Note S11 were used for the 3-bit version. The experimental results indicate that 5-bit and 4-bit NL-ADC models can achieve higher inference accuracy than previous work31,48 (86.14% and 86.03%) based on same dataset and class number and are also within 2% of the software estimates, while that of the 3-bit version is marginally inferior. Nonetheless, it is important to highlight that the LSTM layer with the 3-bit ADC model significantly outperforms the 5-bit NL-ADC models in terms of area efficiency and energy efficiency as shown in Fig. 4e (31.33TOPS/W, 60.09 TOPS/W and 114.40 TOPS/W for 5-bit, 4-bit, and 3-bit NL-ADC models, respectively). The detailed calculation to assess the performance of our chip under different bit precision is done following recent work15,50 and shown in Supplementary Tab. S5. The earlier measurements were limited to the LSTM macro alone and did not consider the digital processor for pointwise multiplications (Eq. S3) and the small FC layer. The whole system level efficiencies are estimated in detail in Supplementary Note S4a for all three bit resolutions.

Table 1 compares the performance of our LSTM implementation with other published work on LSTM showing advantages in terms of energy efficiency, throughput and area efficiency. For a fair comparison of area efficiencies, throughput and area are normalized to a 1 GHz clock and 16 nm process respectively. Figure 4e also graphically compares the energy efficiency and normalized area efficiency of the LSTM layer in our chip for KWS task with other published LSTM hardware. The results demonstrate that our chip with 5-bit NL-ADC exhibits significant advantages in terms of normalized area efficiency ( ≈9.9X) and energy efficiency ( ≈4.5X system level) compared to the closest reported works. It should be noted that comparing the raw throughput is less useful since it can be increased by increasing the number of cores. In order to dig deeper into the reason for the superiority of our chip compared to conventional linear ADC chips51,52, detailed comparisons with a controlled baseline were also done using two models as shown in Fig. S3 where k = 1 digital processor is assumed. While their inputs and outputs remain the same, the key distinction lies in the nonlinear operation component. Utilizing these two architectures, we conducted evaluations on the energy consumption and area of the respective chips (Tab. S10 and Tab. S11) to find the proposed one has  ≈1.5X and  ≈2.4X better metrics at the system level respectively. Figure 4f presents a comprehensive comparison of energy efficiency for its individual subsystems among this work (5-bit NL-ADC), the conventional ADC model, and a reference chip31 using IMC—the MAC array, NL-processing, and the full system comprising the MAC array, NL-processing, and other auxiliary circuits (Tab. S13). Our approach exhibits significant energy efficiency advantages, particularly in NL-processing, with a remarkable 3.6 TOPS/W compared to 0.3 TOPS/W and 0.9 TOPS/W for the other two chips. This substantial improvement in NL-processing energy efficiency is a crucial factor contributing to the superior energy efficiency of our chip, as depicted in Fig. 4e.

Table 1 Comparison of LSTM performance with previous works
Full size table

The improvements in area efficiency also come about due to the improved throughput of the NL-processing. Fig. S4 shows the energy and area breakdown of the main chip components of this work (5-bit NL-ADC) and the conventional model (5-bit ADC). Our work demonstrates superior area efficiency, with a value of 130.82 TOPS/mm2, compared to the conventional ADC model’s 9.56 TOPS/mm2 in Tab. S5. This  ≈13X improvement is attributed mostly to throughput improvement of 4.6X over the digital processor in conventional systems. Table 2 compares our proposed NL-ADC with other ADC used in IMC systems. While some works have used Flash ADCs that require single cycle per conversion, they have a higher level of multiplexing (denoted by # of columns per ADC) since these require exponentially more comparators than our proposed ramp ADC. Hence, the effective AC latency in terms of number of clock cycles for our system is comparable with others. Moreover, since our proposed NL-ADC is the only one with integrated activation function (AF) computation, the latency in data conversion followed by AF computation (denoted by AF latency in the table) is significantly lower for our design. Here, we assume LUT based AF computation using Ncyc = 2 clocks and 1 digital processor per 1024 neurons like other work23. Compared with other ramp converters, the area occupied by our 5-bit NL-ADC is merely 558.03 μm2 due to usage of only one row of memristors, while the traditional 5-bit Ramp-ADC51,52 together with nonlinear processor occupy an area of 4665.47 μm2. This substantial disparity in ADC area due to a capacitive DAC-based ramp generator51,52 leads to a further difference in the area efficiency of the two chips. Using oscillator-based ADCs53,54 instead of ramp-based ones will reduce the area of the ADC in traditional systems, but the throughput, area and energy-efficiency advantages of our proposed method will still remain significant. Also, note that due to the usage of memristors for reference generation, our system is robust to perturbations (such as changes in temperature or read voltage) similar to other designs using replica biasing55. Lastly, for monotonic AF, our design can directly generate pulse width modulated (PWM) output (like other ramp based designs31) which can be passed to the next stage avoiding the need for DAC circuits at the input of the next stage as well as counters in the ADC. This is known to further increase energy efficiencies56, an aspect we have not explored yet.

Table 2 Comparison of ADC performance with previous works
Full size table

Scaling to large RNNs for natural language processing

Although KWS is an excellent benchmark for assessing the performance of small models31,57, our nonlinear function approximation method is also useful in handling significantly larger networks for applications such as character prediction in NLP. To demonstrate the scalability of our method, we conduct simulations using a much larger LSTM model on the Penn Treebank Dataset42 (PTB) for character prediction. There are a total of 50 different characters in PTB. Each character is embedded into a unique random orthogonal vector of 128 dimensions, which are taken from a standard Gaussian distribution. Additionally, at each timestep, a loop of 128 cycles will be executed. The training method is shown in Methods and Fig. 5a illustrates the inference network architecture. The number of neurons and parameters in the PTB character prediction network (6,112,512 weight parameters and 8568 biases in LSTM and projection layers) are  ≈66X and  ≈600X more than the corresponding numbers in the KWS network (Fig. 5b) leading to a much larger number of operations per timestep.

Fig. 5: LSTM for NLP task.
figure 5

a Architecture of LSTM network for on-chip inference in character prediction task. b Comparison in the LSTM layer between the number of neurons and operations per timestep in the NLP model for character prediction and the KWS model. c Simulation results under different bit resolution of NL-ADC models and hardware-measured weight noise compared with software baseline using the ideal model. BPC results follow the “smaller is better” principle, meaning that lower values indicate better performance. d Energy efficiency and area efficiency comparison: our LSTM IC, conventional ADC model and recently published LSTM ICs from research papers23,25,26,27,28,31,67,68. Detailed calculation of energy efficiency and throughput for both macro and system levels are shown in Supplementary Note S3, Supplementary Note S4 and Tab. S9. Area efficiency of all works are normalized to 1 GHz clock and 16 nm CMOS process. e Energy efficiency and throughput comparison: our LSTM IC, conventional ADC model and recently published LSTM ICs from research papers23,25,26,27,28,31,67,68.

Full size image

To map the problem onto memristive arrays, the LSTM layer alone needs a 633 × 8064 prohibitively large crossbar. Instead, we partition the problem and map each section to a 633 × 512 crossbar (similar to recent approaches31) with 16 such crossbars for the entire problem. Within each crossbar, only 256 input lines are enabled at one phase to prevent large voltage drops along the wires, with a total of 3 phases to present the whole input, with the concomitant cost of 3X increase in input presentation time. An architecture for further reduced crossbars of size 256 × 256 is shown in Supplementary Note S10. To assess the impact of on-chip buffers and interconnects in performing data transfer between tiles, Neurosim58 is used to perform system level simulations where the ADC in the tile is replaced by our model (details in Supplementary Note S4(b)). First, the accuracy of the character prediction task is assessed using bits per character (BPC)23, which is a metric that measures the model’s ability to predict samples from the true underlying probability distribution of the dataset, where lower values indicate better performance. Similar to the earlier KWS case, memristor write noise and NL-ADC quantization effects from the earlier hardware measurements are both included in the simulation. The results of inference are displayed in Fig. 5c, with a software baseline of 1.334. BPC results of 1.345, 1.355, and 1.411 are obtained with the 5-bit, 4-bit, and 3-bit ADC models, respectively when considering perfect weights, and exhibits a drop of only 0.011 for the 5-bit NL-ADC model compared to the software baseline. Finally, the write noise of the memristors are included during both the training and testing phases using the same method as the KWS model resulting in BPC values of of 1.349, 1.367, and 1.428 are obtained with the 5-bit, 4-bit, and 3-bit NL-ADC models (with error bars showing standard deviations for 10 runs). Compared to other recent work23 on the same dataset that obtained a BPC of 1.358, our results are promising and show nonlinear function approximation by NL-ADC can be successfully applied to large-scale NLP models. There may be some other applications which are more sensitive to AF variations; for those cases, an iteration of chip-in-the-loop training may be necessary after hardware-aware training.

The throughput, area, and energy efficiencies are estimated next (details in Supplementary Note S3, Tab. S6 at the macro level and in Supplementary Note S4b at the system level) and compared with a conventional architecture (Tab. S7, S8) for two different cases of k = 1 and k = 8 digital processors. These are compared along with current LSTM IC metrics in Fig. 5d and Fig. 5e. Considering the 5-bit NL-ADC, our estimated throughput and energy efficiency of 19.5 TOPS and 47.9 TOPS/W at the system level are  ≈4.0X and 24.4X better for system level than earlier reported metrics23 of 4.9 TOPS and 2 TOPS/W respectively. Lastly, the normalized area efficiency of our NL-ADC based LSTM layer is  ≈86X better at system level than earlier work23 (reporting results on same benchmark) due to the increased throughput and reduced area (we also estimated that an 8-bit version of our system will still be 24X more area efficient and 3.6X more energy efficient). Compared to the conventional IMC architecture baseline for this LSTM layer, we estimate an energy efficiency advantage of 1.1X at the system level similar to the KWS case, but the throughput and area efficiency advantages of  ≈4.8X and  ≈6.6X for system level respectively remain even for k = 8 digital processors.

Discussion

In conclusion, we proposed and experimentally demonstrated a novel paradigm of nonlinear function approximation through a memristive in-memory ramp ADC. By predistorting the ramp waveform to follow the inverse of the desired nonlinear activation, our NL-ADC removes the need for any digital processor to implement nonlinear activations. The analog conductance states of the memristor enable the creation of different programmable voltage steps using a single device, resulting in great area savings over a similar SRAM-based implementation. Moreover, the in-memory ADC is shown to be more robust to voltage fluctuations compared to a conventional ADC with memristor crossbar based MAC. Using this approach, we implemented a LSTM network using 9216 weights programmed in the 72 × 128 memristor chip to solve a 12-class keyword spotting problem using the GSCD. The results for the 5-bit ADC show better accuracy of 88.5% than previous hardware implementations31,49 with significant advantages in terms of normalized area efficiency (≈9.9X) and energy efficiency (≈4.5X) compared to previous LSTM circuits. We further tested the scalability of our system by simulating a much larger network (6,112,512 weights) for NLP using the experimentally validated models. Our network with 5-bit NL-ADC again achieves better performance in terms of BPC than recent reports23 of IMC based LSTM ICs while delivering  ≈86X and  ≈24.4X better area and energy efficiencies at the system level. Our work paves the way for very energy efficient in-memory nonlinear operations that can be used in a wide variety of applications.

Methods

Memristor integration

The memristors are incorporated into a CMOS system manufactured in a commercial foundry using a 180 nm technology node. The integration process starts by eliminating the native oxide from the surface metal through reactive ion etching and a buffered oxide etch dip. Subsequently, chromium and platinum are sputtered and patterned with e-beam lithography to serve as the bottom electrode. This is followed by the application of reactively sputtered 2 nm tantalum oxide as the switching layer and sputtered tantalum metal as the top electrode. The device stack is completed with sputtered platinum for passivation and enhanced electrical conduction.

Memristor programming methods

In this work, we adopt the iterative-write-and-verify programming method to map the weights to the analog conductances of memristors. Before programming, a tolerance value (5 μS) is added to the desired conductance value to allow certain programming errors. The programming will end if the measured device conductance is within the range of 5 μS above or below the target conductance. During programming, successive SET or RESET pulses with 10 μs pulse width are added to each single 1T1R structure in the array. Each SET or RESET pulse is followed by a 20 ns READ pulse. A RESET pulse is added to the device if its conductance is above the tolerated range while a SET pulse will be added if its conductance is below the range. We will gradually increase the amplitude of the SET/RESET voltage and the gate voltage of transistors between adjacent cycles. For SET pulse amplitude, we start from 1 V to 2.5 V with an increment of 0.1 V. For RESET pulse amplitude, we start from 0.5 V to 3.5 V with an increment of 0.05 V.For gate voltage of SET process, we start from 1.0 V to 2.0 V with an increment of 0.1 V. For gate voltage of RESET process, we start from 5.0 V to 5.5 V with an increment of 0.1 V. Detailed programming process is illustrated in Supplementary Fig. S9.

Hardware aware training

Directly mapping weights of the neural network to crossbars will heavily degrade the accuracy. This is mainly due to the programming error of the memristors. To make the network more error-tolerant when mapping on a real crossbar chip, we adopted the defect-aware training proposed in previous work40. During training, we inject the random Gaussian noise into every weight value in the forward parts for gradient calculation. Then the back-propagation happens on the weights after noise injection. Weight updating will occur on the weight before the noise injection. We set the standard deviation to 5 μS which is relatively larger than experimentally measured programming error (2.67 μS shown in Supplementary Fig. S8c) to make the model adapt more errors when mapping to real devices. Detailed defect-aware training used in this work is described in Algorithm 1. In this work, we set σ to 5 μS and \({g}_{\max }\) to 150 μS.

Algorithm 1

Defect-aware training

Data: Weight matrix at training iterationt: \({{{{\bf{W}}}}}_{\mu }^{{{{\bf{t}}}}}\); input data X; learning rate: α; weight-to-conductance ratio gratio; maximum conductance in crossbar \({g}_{\max }\); injected noise σ; loss function L

Result: Weight at time step t + 1: \({{{{\bf{W}}}}}_{\mu }^{{{{\bf{t}}}}+{{{\bf{1}}}}}\)

\({{{{\bf{W}}}}}_{\mu }^{{{{\bf{t}}}}}[{{{{\bf{g}}}}}_{{{{\rm{ratio}}}}}{{{{\bf{W}}}}}_{\mu }^{{{{\bf{t}}}}} \, > \, {g}_{\max }]={g}_{\max }/{g}_{{{{\rm{ratio}}}}}\)

\({{{{\bf{G}}}}}_{\mu }^{{{{\bf{t}}}}}\leftarrow | {{{{\bf{W}}}}}_{\mu }^{{{{\bf{t}}}}}| \cdot {g}_{{{{\rm{ratio}}}}}\) (differential mapping)

Initialize \({{{{\bf{G}}}}}_{\sigma }^{{{{\bf{t}}}}}\): Conductance standard deviation

\({{{{\bf{W}}}}}_{\sigma }^{{{{\bf{t}}}}}\leftarrow {{{{\bf{G}}}}}_{\sigma }^{{{{\bf{t}}}}}/{g}_{{{{\rm{ratio}}}}}\)

\({{{{\bf{W}}}}}^{{{{\bf{t}}}}}\leftarrow {{{{\bf{W}}}}}_{\mu }^{{{{\bf{t}}}}}+\epsilon \cdot {{{{\bf{W}}}}}_{\sigma }^{{{{\bf{t}}}}}\quad \epsilon \sim {{{\mathcal{N}}}}({{{\bf{0}}}},{{{\bf{I}}}})\)

Compute loss L(X, Wt)

Update Wμ through back propagation

\({{{{\bf{W}}}}}_{\mu }^{{{{\bf{t}}}}+{{{\bf{1}}}}}\leftarrow {{{{\bf{W}}}}}_{\mu }^{{{{\bf{t}}}}}-\alpha \cdot \frac{\partial L}{\partial {{{{\bf{W}}}}}_{{{{\boldsymbol{\mu }}}}}}\)

Weight clipping and mapping

We clip weights between −2 and 2 to avoid creating excessively large weights during training. Weights can be mapped to the conductance of the memristors when doing on-chip inference, nearly varying from 0 μS to 150 μS. The clipping method is defined according to Equation (6) and the mapping method is shown in Equation (7).

$$w=\left\{\begin{array}{ll}-2\quad &w < -2\\ w\quad &-2\le w \le 2\\ 2\quad &w \, > \,2\end{array}\right.$$
(6)
$$g=\gamma w\left(\gamma=\frac{{g}_{max}}{| w{| }_{max}}\right)$$
(7)

where w is weights during training, g is the conductance value of memristors and γ is a scaling factor used to connect the weights to g. The maximum conductance of memristors (gmax) is 150 μS and the maximum absolute value of weights (∣w∣max) is 2, therefore, the scaling factor (γ) is equal to 75 μS.

Training for LSTM keyword spotting model

The training comprises of two processes: preprocessing and LSTM model training.

Preprocessing: The GSCD41 is used to train model. It has 65,000 one-second-long utterances of 30 short words and several background noises, by thousands of different people, contributed by members of the public57. We reclassify the original 31 classes into the following 12 classes49: yes, no, up, down, left, right, on, off, stop, go, background noise, unknown. The unknown class contains the other 20 classes. For every one-second-long utterance, the number of sampling points is 16,000. MFCC57 is applied to extract Mel-frequency cepstrum of voice signals. 49 windows are used to divide a one-second-long audio signal and extract 40 feature points per window.

LSTM model training: The custom LSTM layer is the core of this training model. The custom layer is necessary for modifying the parameters, including adding the NL-ADC algorithm to replace the activation function inside, adding weight noise training, quantizing weights, etc. Although the custom LSTM layer will increase the training time of the network, this is acceptable by weighing its advantages and disadvantages. The input length is 40 and the hidden size is 32. The sequence length is 49, which means the LSTM cell will iterate 49 times in one batch size of 256.

A FC layer is added after the LSTM layer to classify the features output by LSTM. The input size of the FC layer is 32 and the output size is 12 (class number). Cross-entropy loss is used to calculate loss. We train the ideal model (without NL-ADC and noise) for 128 epochs and update weights using the Adam optimizer with a learning rate (LR = 0.001). After finishing the ideal model training, NL-ADC-aware training and hardware noise-aware training are added. All models’ performance is evaluated with top-1 accuracy.

Training for LSTM character prediction model

Preprocessing: The PTB42 is a widely used corpus in language model learning, which has 50 different characters. Both characters in the training dataset and the validation dataset of PTB are divided into many small sets. Each set consists of 128 characters and each character is embedded into a random vector (dimension D = 128) obtained from the standard Gaussian distribution and then perform Gram-Schmidt orthogonalization on these vectors.

LSTM model training: We use a one-layer custom LSTM with projection23. The input length is 128 and the hidden size is 2016. The length hidden state and the LSTM output are both 504. The sequence length is 128, which means the LSTM cell will loop 128 times in one batch (batch size = 8).

The FC layer after the LSTM layer will further extract the features output by LSTM and convert them into an output of size 50 (class number). Cross-entropy loss is used to calculate loss. We train the model for 30 epochs and update weights using the Adam59 optimizer with a learning rate (LR = 0.001). The model’s performance is evaluated through the BPC60 metric and the data of BPC is smaller the better. After finishing the ideal model training, we use the same training method to train the model after adding NL-ADC and hardware noise.

Inference with the addition of write noise and read noise

During the inference stage, we performed 10 separate simulations with different write noise following the measured distribution N(0, 2.67 μS) (Fig. S8c) in each case (simulating 10 separate chips). For each of the simulation, read noise following measured read noise distribution N(0,3.5 μS) (Fig. S14b) is included. It is worth noting that in each chip simulation, a consistent write noise was introduced into the inference process applied to the entire test dataset. However, in relation to read noise, the normal distribution N(0,3.5 μS) is employed for each mini-batch to generate distinct random noises. These noises are subsequently incorporated into the simulation. Then we obtain the inference accuracy with the addition of write noise and read noise.