Introduction

Green hydrogen production from water electrolysis has been recognized as an ideal sustainable approach for energy transition from fossil fuels to clean energy and carbon neutrality goals1,2,3. Hydroxide exchange membrane water electrolysis (HEMWE) stands out as a high-performance and low-cost technique for the production of green hydrogen, featuring high current density, fast response, and low cost4,5,6,7. The hydroxide exchange membrane, which selectively transports hydroxide ions and isolates the produced gases from the crossover, is the core component of HEMWE. Nevertheless, most HEMs have relatively low hydroxide conductivity due to the high energy barrier of hydroxide transport that requires rearrangement of the hydrogen bond networks. Moreover, polymeric HEMs generally suffer from inevitable degradation of the main chains and positively-charged functional groups, e.g., quaternary ammonium, due to the electrophilic substitution of hydroxide in hot alkaline solution, leading to a rapid decay of ionic conductivity and mechanical strength8,9,10.

Currently, studies on HEM focus on improving the ionic conductivity of HEM by tuning components, microstructures, and ion transport channels of HEM from molecular chemistry (e.g., polymer backbone, side chain, and cation exchange groups) and microstructure regulation and so on11,12,13,14,15. HEMs with stable backbone and cationic groups, for example, aryl ether-free backbone and piperidinium groups, respectively are discovered, which are generally recognized as state-of-the-art HEMs due to their excellent stability16,17,18,19. However, despite these efforts, the in-situ stability of HEMs during electrolysis remains significantly inferior to their ex-situ stability, which is typically measured in static and stable alkaline solutions. For example, quaternary ammonium functionalized HEM has ex-situ stability for 1200 h but only less than 72 h in the electrolyzer20. HEM with quinine ring cations can stabilize for more than 1800 h in the ex-situ condition but stand only 200 h in the electrolyzer21. Compared with the stable ex-situ condition, the in-situ operation condition of water electrolysis is generally more complex, involving electrode reactions and different components of the electrolyzer and being influenced by a variety of factors22,23. The large discrepancy between in-situ and ex-situ HEM stability has not received enough attention so far, and the approaches to improving the in-situ stability of HEM are rarely investigated although they are vital for the commercialization of HEMWE.

In this work, we unravel that the inferior in-situ stability of HEM originates from inhomogeneous heat accumulation and high localized temperature of HEM during the operation of water electrolysis due to the low thermal conductivity of HEM. Thus, a 3D thermally conductive network in HEM to effectively evacuate heat during electrolysis is developed to reduce localized heat and promote the in-situ stability of HEM. We build a 3D thermally conductive network using a low volume fraction of boron nitride (BN) nanosheets and increase the thermal conductivity of HEM to 13 W m−1 K−1, 32 times that of the pure polymeric HEM. The thermally conductive HEMs efficiently disperse the local temperature and improve the in-situ stability, resulting in good dynamic/static durability for water electrolysis with almost no degradation. The understanding of the effect of the thermal conductivity of HEMs for in-situ stability and the approach of 3D efficient heat diffusion is expected to inspire the rational design of ion-exchange membranes for long-life water electrolysis as well as other energy conversion and storage systems.

Results

Origin of the low in situ stability of HEM

In the water electrolyzer, in addition to the external preheating of the cell, heat is generated from the electrode reaction and Joule heating, following Joule’s law, \(Q={I}^{2}{Rt}\), where Q is the Joule heat, I is the current, R is the internal resistance. We measured the temperature distribution inside a water electrolyzer assembled with commercial HEM, FAAM-40 (Fig. 1a) using an invasive but non-destructive technique based on ultrathin micro-thermocouples (50 µm, Supplementary Fig. 1). The temperature of the electrolyzer elevates upon water electrolysis and further increases with the current densities. For example, the temperature near HEM (Tb) increases by 9 °C during electrolysis at 2 A cm−2 (Fig. 1b). As the polymeric HEM has relatively high resistance and low thermal conductivity (k, <1 W m−1 K−1)24 compared to carbon-based catalytic materials and metallic gas diffusing layer (GDL), the Joule heat tends to generate and accumulate in the membrane electrode area25, causing Tb near HEM to be higher than Ta and Tc near the GDL. By comparing the electrolysis voltage of FAAM-40 under different operating temperatures and fitting the voltage as a function of time (Fig. 1c), we find that the degradation rate of HEM positively increases with the temperature of HEM.

Fig. 1: In-situ stability of HEM affected by localized temperature and thermal conductivity.
figure 1

a Schematic diagram of the setup for the temperature measurement of HEMWE, where the thermocouples are inserted along the GDL layer near the cathode side (Ta), cathode catalyst layer near the HEM (Tb), and GDL layer near the anode side (Tc), respectively. b Temperature (Ta, Tb, Tc) evolution of HEMs operated in a water electrolyzer assembled with commercial HEM of FAAM−40 at various current densities. c Voltage evolution of the water electrolyzer assembled with FAAM−40 operated at different cell temperatures and the corresponding voltage degradation rates. d Schematic diagram of components in HEMWE for the numerical simulation and simulated 2D temperature contour plot of HEMs with k = 0.4 and k = 6.2 W m−1 K−1. e Simulated 1D temperature profile within the HEMWE assembled with HEMs with different thermal conductivities at a current density of 2 A cm−2. Unit of k is W m−1 K−1. HEM is indicated by a red shadow. f Simulated temperature contours of HEMs operated in HEMWE at various current densities assembled with HEMs with different thermal conductivities. The bipolar plate, gas diffusion layer, cathode catalyst layer, and anode catalyst layer are respectively abbreviated as BP, GDL, C-CL, and A-CL in panels (a, d, and e).

Full size image

To systematically understand the role of thermal conductivity for the localized heat in HEM, we performed a numerical simulation based on the finite volume method to uncover the temperature distribution of each component in HEMWE (Fig. 1d), where the heat generation from Ohmic internal resistance is considered, and heat conduction is applied based on the thermal conductivity of each component (Detailed assumption for simplifying the physical model is found in Supplementary Tables 1, 2 and Supplementary Note 1). The resulting two-dimensional (2D) heat contour plot (Fig. 1d) and one-dimensional (1D) thermal profiles (Fig. 1e and Supplementary Fig. 2) show that the temperature distributes unevenly among the various components of the electrolyzer. The temperature of the HEM is much higher than that of the GDL. HEM with high thermal conductivity can greatly reduce its temperature, e.g., from 72.9 °C (k = 0.4 W m−1 K−1) to 63.4 °C (k = 13 W m−1 K−1) at 2 A cm−2 (Fig. 1e). The high thermal conductivity is especially important to reduce the temperature of HEM at high current densities. For example, with an electrolysis current density of 4 A cm−2, the HEM with high thermal conductivity (k = 13 W m−1 K−1) reduces the localized temperature by 13.7 °C compared with the HEM with k = 0.4 W m−1 K−1 (Fig. 1f). Our simulated temperatures of HEM are in the range of the reported values (Supplementary Table 3). Note that ionic conductivity does not affect the temperature of HEM as significantly as the thermal conductivity (Supplementary Fig. 1 and Supplementary Table 4). Thus, highly thermally conductive HEMs are crucial to decrease the localized temperature and enhance the in-situ stability.

Construction of 3D thermally conductive HEMs

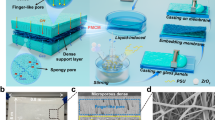
To create highly thermally conductive HEMs, we incorporated 2D BN nanosheets with a large size-thickness ratio (Supplementary Fig. 3) to form a 3D thermally conductive network for HEMWE (Fig. 2a)26. BN is selected due to its high intrinsic thermal conductivity (in-plane: 600 W m−1 K−1, out-of-plane: 30 W m−1 K−1) and high endurance of hot alkaline aqueous solutions. Quaternized chitosan (QCS) is applied as a model HEM to investigate its chemical stability in an alkaline environment. Following a two-step mixing and casting procedure, QCS/BN membranes with a white flexible lamellar structure were prepared (Supplementary Fig. 4). The 2D BN nanosheets facilitate the phonon transport to form thermally conductive pathways while the QCS polymer provides efficient conductivity for hydroxide ions (Fig. 2b), creating a thermally and ionic conductive composite HEM.

Fig. 2: Highly thermally conductive composite HEM.
figure 2

a Schematic diagram of HEMWE in which the BN composite HEM with a 3D thermally conductive network is applied. Composite HEM exhibits fast heat diffusion, thereby potentially reducing the localized temperature and promoting the in-situ stability of HEM in a water electrolyzer. b Design of BN composited HEM, where phonon and hydroxide transport along the 3D network. c, d Side-view SEM image of the QCS/3.8%BN and QCS/10.6%BN membranes, respectively. The structure of QCS/BN membranes is indicated in insets. e Thermal conductivity of QCS/BN membranes with different BN volume fractions. Inset: Photo of pure QCS and QCS/10.6%BN. Data in (e) are presented as mean values  ±  standard deviation based on at least three trials. f Infrared photos of membranes with a square region cooling from 60 °C to 10 °C.

Full size image

The composite membrane exhibits a BN-isolated dispersion in the polymeric matrix with low content of BN (e.g., QCS/3.8%BN, Fig. 2c) and changes to a 3D network in QCS/10.6%BN (Fig. 2d), forming a continuous 3D thermally conductive network. The interlayer distance of BN sheets in QCS/10.6%BN membrane is within the nanoscale size (Supplementary Fig. 5). The microstructure of the composite membranes dramatically influences the thermal conductivity. Specifically, the composite HEM exhibits enhanced thermal conductivity, which rises with the volume fraction of BN. In comparison with the thermal conductivity of 0.4 W m−1 K−1 in the pure QCS without BN, the thermal conductivities of the QCS/BN composite HEMs are 6.2 W m−1 K−1 in QCS/10.6%BN, 11.5 W m−1 K−1 in QCS/13.2%BN, and increase to 13.2 W m−1 K−1 (32 times increase) when 16.1% BN is added (Fig. 2e). Due to the large size-thickness ratio of BN nanosheets, BN can form efficient thermal percolation with a low volume threshold of ~10.6% in the composite HEM.

To further explore the relationship between the microstructure and thermal conductivity of composite HEM, we performed finite element simulation of composite HEMs, whose volume fraction and the arrangement of BN are controlled to mimic the QCS/10.6%BN and QCS/3.8%BN. The simulated thermal conductivity of QCS/10.6%BN reaches 25 W m−1 K−1, significantly higher than that of QCS/3.8%BN (7.6 W m−1 K−1), consistent with the enhancement tendency of thermal conductivity observed in experiments (Fig. 2e and Supplementary Fig. 6). Moreover, the simulated temperature distribution across the membrane (Supplementary Fig. 6) indicates that the 3D BN network effectively increases the heat transfer rate in HEM. We verified the heat dissipation capability of the composite membranes on a macroscopic scale, in which the membranes were heated on a hot plate to 60 °C and then allowed cooling. The QCS/10.6%BN membrane is cooled to around 10 °C within 4 s. In contrast, the temperature of QCS only decreases to 42 °C after 4 s (Fig. 2f), indicating the high thermal conductivity and faster heat dissipation rate of the QCS/BN composite membrane.

High ionic conductivity enabled by 2D nanoconfinement

In addition to the thermal conductivity, the integration of BN nanosheets with suitable ratios also improves the ionic conductivity and mechanical strength of the composite HEM, which are indispensably required for HEMs. Although BN itself is not a hydroxide conductor, the integration of BN nanosheets and QCS anti-empirically raises the hydroxide conductivity from 29.1 mS cm–1 of pure QCS membrane to 64.5 mS cm−1 in QCS/10.6%BN composite (Fig. 3a). Further increasing the ratio of BN beyond 10.6% would reduce the hydroxide conductivity due to the excess BN-induced aggregation disrupting the continuous hydroxide pathways, suggesting that the 10.6% volume ratio of BN is the optimal ratio for the composite HEM. In addition, the QCS/10.6%BN membrane exhibits a tensile strength of 75.8 MPa in the dry state (Fig. 3a). Even in the hydrated state, the tensile strength of QCS/10.6%BN is three times that of pure QCS (Supplementary Fig. 7), showing its promising application in water electrolysis. The similar tendency of ion conductivity and tensile strength with BN fraction increasing is mostly related to the structure of the composite QCS/BN.

Fig. 3: Ionic transport properties of QCS/BN composite HEM.
figure 3

a Ion conductivity in water (room temperature) and tensile stress of QCS/BN membranes with different BN volume fractions. b IEC of QCS/BN membranes. c Arrhenius plots of QCS and QCS/10.6%BN membranes. d Dielectric relaxation spectra and (e) relaxation times of different QCS/BN membranes. f Relationship between relaxation time and temperature. g Schematic diagram of water and hydroxide transport of QCS with open space and QCS/BN composites with different space confinement effects. Data in (a, b) are presented as mean values  ±  standard deviation based on at least three trials.

Full size image

To understand the nonlinear effect of the BN nanosheets on the hydroxide conductivity, we first examined the ion exchange capacity (IEC) of the QCS/BN composite membranes, which positively correlates with the cation exchange groups and the ionic conductivity of QCS. As the ratio of BN in the QCS/BN composite increases, the IEC decreases monotonically (Fig. 3b), diverging from the trend observed in ionic conductivity with the BN content (Fig. 3a). Besides, the QCS/10.6%BN composite has a lower activation energy than the pure QCS membrane (8.20 kJ mol−1 vs. 9.35 kJ mol−1) (Fig. 3c). Thus, we deduce that the 2D BN nanosheets enhance the intrinsic transport rate of hydroxide ions through nanoconfined ionic transport and thereby increasing the ionic conductivity. To gain insight into the confinement-enhanced ionic transport, we applied dielectric relaxation spectroscopy to explore the relaxation dynamics of water dipoles in the composite membranes (Supplementary Fig. 8a). With the increase of BN volume ratio, the relaxation frequency of water dipolar resonance (Peak I) gradually increases from ~ 100 Hz (QCS/1.8%BN) to 104 Hz (QCS/10.6%BN), with the dipolar relaxation time of water decreasing from 2 ms to 0.01 ms (Fig. 3d and e). The faster dipolar relaxation of water indicates that the 2D BN- induced-confinement (moderate confined space) facilitates the exchange of hydroxide ions via the water chains. When the BN content is over 10.6%, a slower relaxation at 10 Hz (Peak II) emerges, indicating that the enhancement of confinement uprises the energy barrier of the intermolecular exchanging process (Fig. 3f and Supplementary Fig. 8d), and results in the decay of ionic conductivity (Fig. 3a). Thus, although the IEC is reduced with the BN ratio, the moderate confined space generated in the QCS/BN promotes fast water and hydroxide ion diffusion, thereby achieving the highest ion conductivity with the optimal ratio of BN (~ 10.6%).

In-situ stability of thermally conductive HEM

The QCS/BN composite HEMs featuring modulated thermal and ionic conductivities were assembled in an alkaline membrane water electrolyzer to test the temperature distribution and performance of water electrolysis. The temperature near HEM, Tb, was recorded during water electrolysis (Fig. 4a and Supplementary Fig. 9). Using HEMs with thermal conductivities increasing from 0.42 (pure polymeric QCS) to 13.0 W m−1 K−1 (QCS/16.1%BN), Tb is reduced from 62.9 to 60.5 °C at a current density of 0.25 A cm−2, and more profoundly reduced by 5 °C at 1 A cm−2. The experimental results comprehensively considering the thermal conductivity and electrolysis current density (Fig. 4b) also demonstrate that the HEMs with high thermal conductivities reduce the localized temperature Tb, especially under high current densities.

Fig. 4: In-situ stability of HEMs for water electrolysis.
figure 4

a Temperature profiles of the cathode catalyst layer near the HEM (Tb). b Tb of the HEMWE with QCS/BN composite HEMs with different thermal conductivities measured at different current densities. c Voltage evolution of HEMs with different thermal conductivities at 1 A cm−2. d Relationship between in-situ voltage degradation rates and temperature vs. thermal conductivity of HEMs. e Possible degradation pathways and (f) the accordingly energy barriers calculated by DFT. g 1H NMR spectrum and (h) the accordingly QA content retention of the HEMs after the in-situ stability test. Peaks of GLU and QA are indicated by the purple shadows in panel (g). The peak at 3.8–4.2 ppm ascribed to the glucosamine (GLU) unit of chitosan is considered a reference peak. The HEM after the stability test was treated by dissolving it in acetic acid solution and centrifugal filtration to remove the catalyst and boron nitride for the 1H NMR test. i Long-term in-situ stability of FAA-3, QCS/10.6%BN, and QCS for water electrolysis. Unit of k is W m−1 K−1.

Full size image

The reduced temperature of HEM is expected to alleviate its degradation rate27, and effectively extend its lifetime, which is also demonstrated by the experimental stability test and theoretical analysis of QCS membranes (Supplementary Fig. 10). Thus, we further assessed the influence of the thermal conductivity of HEMs on the in-situ degradation behavior in the electrolyzer. Operating at a current density of 1 A cm−2, electrolysis voltages of all HEM samples gradually increase (Fig. 4c), indicating the in-situ degradation of HEM. Nevertheless, the voltage degradation rate decreases with the enhanced thermal conductivities of HEMs and increases with the current densities (Fig. 4d and Supplementary Fig. 11a, b). When the thermal conductivity of HEM increases to 13.0 W m−1 K−1, the voltage degradation rate is only 1.13 mV h−1, which is reduced by 11 times compared to that of the HEM with k = 0.4 W m−1 K−1 (12.43 mV h−1) (Fig. 4d).

Generally, the degradation of HEM mainly results from the reactions between cation exchange groups and OH−, including SN2 nucleophilic substitution, Hoffmann elimination, and Ylide reaction under a hot alkaline environment (Fig. 4e). Density functional theory was applied to calculate the energy barrier (ΔG) of the degradation of QCS via potential degradation pathways (Supplementary Fig. 12). The energy barrier of Hoffmann elimination (ΔG = 11.67 kcal mol−1) is lower than those of SN2 (ΔG = 24.23 kcal mol−1) and Ylide reaction (ΔG = 43.28 kcal mol−1) (Fig. 4f), indicating that Hoffmann elimination is the most possible degradation pathway. Our simulated ΔG of the three reactions is in the range of other simulated or experimental values in the reported references, indicating that our simulation method is feasible and our simulated results are reliable (Supplementary Figs. 13, 14 and Supplementary Tables 5–8). To find the main degradation pathway of the QCS/BN membranes, we analyzed the chemistry and structure of the HEMs after the 12 h in-situ stability test in water electrolyzer by Fourier transform infrared spectroscopy (FT-IR) and proton nuclear magnetic resonance (1H NMR). FT-IR shows that the HEM degradation product consists of methyl ketone groups (Supplementary Fig. 11c), indicating that the degradation pathway of Hoffmann elimination exists. 1H NMR Peak at 3.45 ppm is ascribed to the quaternary ammonium (QA) (Fig. 4g), which generally reduces during the degradation reaction. The QA content retention (relative to the initial QA intensity before degradation) gradually increases with the increasing thermal conductivities (Fig. 4h), suggesting that in-situ degradation is reduced by the high thermal conductivities. Therefore, we can conclude that the temperature and degradation rate of HEM in the electrolyzer can be reduced by increasing the thermal conductivity of HEM. With the optimized thermal conductivity and ionic conductivity, QCS/10.6% BN exhibits stability over 120 h with a low voltage degradation of 99 µV h–1, which is 1/33 and 1/45 of commercial HEM (FAA-3) and pure QCS (Fig. 4i), respectively, demonstrating the in-situ stability in a water electrolyzer is promoted by the thermally conductive HEM.

Long-term durability of HEMWE

To further validate the effect of thermal conductivity for in-situ stability of HEMs, we used quaternary ammonium poly(n-methyl-piperidine-co-p-terphenyl) (QAPPT) containing alkali-stable cationic groups of piperidinium and prepared QAPPT/BN composite HEMs (material and structure characterized in Supplementary Fig. 15). Similar to the QCS/BN composite, the QAPPT/8.9%BN composite membrane exhibits optimal ionic conductivity of 68 mS cm−1, compared to 43 mS cm−1 of QAPPT at 25 °C and higher mechanical strength (104 MPa) than QAPPT (Fig. 5a and Supplementary Fig. 16). More importantly, the thermal conductivity of QAPPT/8.9%BN is improved to 11.86 W m−1 K−1, 10 times higher than that of pure polymeric QAPPT (0.95 W m−1 K−1), which is due to the formation of an efficient thermal conductive network. Owing to the high ionic and thermal conductivity of QAPPT/BN HEM, QAPPT/BN-based HEMWE can reach a current density of 1.23 A cm−2 and 1.64 A cm−2 at 2 V for operating at 90 °C and 110 °C, both superior to the HEMWE with pure QAPPT (Fig. 5b). It is worthwhile to note that most HEMs cannot stand the high temperature of 110 °C, further indicating the high thermal endurance of the QAPPT/BN composite HEM.

Fig. 5: Performance of water electrolysis using QAPPT/BN composite HEM.
figure 5

a Ionic conductivity and thermal conductivity of QAPPT and QAPPT/8.9%BN HEMs. The inset shows the chemical structure of QAPPT. b Polarization curves measured in 15% KOH at 90 °C and 110 °C. c Transient in-situ stability test based on transiently oscillated current densities between 1 A cm–2 and 0.1 A cm–2, holding for 2 s and standing for 1 s for each current density every cycle. d Resistance changes of the electrolyzer before and after the transient stability test. e In-situ stability test in 15% KOH at a constant current density of 1 A cm−2. The inset shows the polarization curves of the pristine HEM and the HEM after the in-situ stability test at 90 °C. f Comparison of voltage degradation rate and temperature between the proposed QAPPT/BN composite HEM and reported HEMs11,20,21,36,37,38,39,40,41,42,43,44,45,46,47,48,49,50,51,52,53,54,55,56,57,58,59,60. Testing parameters, including current density and KOH concentration are indicated by bubble size and color contrast, respectively. Lifetime is placed beside the bubbles. The samples in this work are indicated by the blue shadow. g Comparison of ex-situ stability and in-situ stability of the QAPPT/BN composite HEM and reported HEMs in HEMWE11,20,21,36,41,42,43,45,48,49,52,53,57,58,59,60. The reported HEMs are indicated by the blue shadow.

Full size image

To comprehensively evaluate the in-situ stability of QAPPT/BN composite HEM, we employed water electrolysis in transient and static modes to mimic the off-grid and on-grid conditions, respectively. A stressful current density shock, namely transiently oscillated current densities between 1 A cm−2 and 0.1 A cm−2 is employed to determine the response behavior of HEM in the extreme practical condition of an on/off duty cycling. QAPPT/BN HEM exhibits a stable electrolysis cycling with negligible voltage change of 0.77 µV/cycle for 20,000 on/off cycles, much smaller than that of QAPPT (159.28 µV/cycle). In sharp contrast, the voltage of FAA-3 (the commercial benchmark HEM) shows an abrupt increase to over 4 V after ~ 15000 cycles (Fig. 5c). After the accelerated in-situ stability test, the QAPPT/BN has little change in Ohmic resistance (Rohm), in contrast to the increased Rohm of QAPPT and FAA-3 (Fig. 5d), further demonstrating the superior in-situ stability of QAPPT/BN. In a static in-situ stability test at the constant current density of 1 A cm–2, QAPPT/BN HEM can stand for over 1000 h with an ultralow voltage degradation rate of 121 µV h–1, one-sixth of QAPPT measured at 90 °C. Even operated at 110 °C, QAPPT/BN HEM can steadily work for more than 300 h with a low voltage degradation rate of 138 µV h–1. Moreover, the polarization curves of the QAPPT/BN membrane after the stability test for 1000 h at 90 °C remain close to the initial polarization curve, indicating the high in-situ stability of QAPPT/BN (Fig. 5e and Supplementary Fig. 17). The in-situ stability in a water electrolyzer can be promoted by the highly thermal conductive HEMs in a wide range of temperatures (60−110 °C) and KOH concentrations (15−30%) (Supplementary Fig. 18). When assembled with optimized catalysts (the FeOOH/NiFe LDHs@CCH NAs-NF for anode and NiFe LDHs@NiCoS NAs-NF for cathode), the performance of water electrolyzer with QAPPT/8.9%BN can be further improved to 3.85 A cm–2 at 2 V and 90 °C (Supplementary Fig. 19a). The duration of in-situ stability of QAPPT/BN can be at least 900 h with a low degradation rate of 33 µV h–1 operating at constant current of 1 A cm–2. The performance is competitive with the latest literature work in HEMWE (Supplementary Fig. 19b, c and Supplementary Table 9).

Environmental and experimental parameters, including high alkali concentration, temperature, and current density will significantly accelerate the HEM degradation and thus weaken the durability and lifetime of water electrolysis. Notably, our proposed QAPPT/BN HEM exhibits a low voltage degradation rate and long lifetime, a record among the reported and commercial HEMs, demonstrating its significantly promising in-situ stability (Fig. 5f and Supplementary Tables 10, 11). Furthermore, our thermally conductive HEM-based electrolyzer is demonstrated to feasibly operate at extreme low-temperature, which is significantly beneficial for applications in cold regions. Due to the high thermal conductivity, electrolyzer assembled with QAPPT/BN HEM can operate at − 30 °C with a starting time of 3.94 s, much faster than QAPPT (9.59 s) and FAA-3 (17.29 s) (Supplementary Fig. 20). The fast response of the QAPPT/BN HEM is mostly because the heat generated from the Joule heating of composite HEM can rapidly transport to the electrolyte, increase the temperature of the electrolyte, and thereby reduce the duration of cold starting. Therefore, based on the high current density and long lifetime in HEMWE, especially at high temperatures, the highly thermally conductive QAPPT/BN HEM comprehensively exhibits its merits, including the high thermal/ionic conductivity, high mechanical strength, lower degradation rate, and remarkable in-situ stability, which eliminates the discrepancy between the in-situ and ex-situ stability (Fig. 5g, Supplementary Figs. 21, 22, and Supplementary Table 12) and will promote the operational stability of HEM for long-life water electrolysis.

Discussion

In this work, we have revealed that the inferior in-situ stability of HEM in electrolyzers originates from the localized high temperature accumulated near the HEM with low thermal conductivity and thus developed highly thermally conductive HEMs to promote the stability of water electrolysis. We build composite HEMs with BN nanosheets with an effective 3D thermally conductive network, which can accelerate the diffusion of heat generated from Joule heating during electrolysis, decrease the localized temperature of HEM, and thereby reduce the HEM degradation for the durability of water electrolysis. Operating in 15% KOH at 90 °C, a harsh in-situ condition, the water electrolyzer based on optimized BN composited HEM can operate at 1 A cm−2 for at least 1000 h with an ultralow voltage degradation rate of 121 µV h−1, in contrast to the pristine polymeric HEM (786 µV h−1 within 200 h). Our design of thermally conductive HEM with high in-situ stability will inspire the development of various durable ion exchange membranes, such as proton exchange membranes and ion-solvating membranes, to facilitate the development of long-life stable electrochemical reactor devices in water electrolysis and beyond.

Methods

Chemicals and materials

Hexagonal boron nitride (h-BN) was received from Tianyuan Aviation Materials and Shanghai Boronmatrix New Material LLC. Chitosan (high molecular weight, deacetylation degree > 95%) was purchased from Millipore Sigma. Chemicals including glutaraldehyde, ethanolamine, acetic acid, polyvinyl pyrrolidone (PVP), 2,3-epoxypropyl trimethylammonium chloride, 2-propanol, N-methyl-4-piperidone, terphenyl, trifluoroacetic acid (TFA), trifluoromethanesulfonic acid (TFSA), iodomethane, potassium hydroxide (KOH), potassium carbonate (K2CO3), sodium hydroxide (NaOH), Dimethyl sulfoxide (DMSO), ethyl acetate, nickel nitrate hexahydrate (Ni(NO3)2·6H2O), cobalt nitrate hexahydrate (Co(NO3)2·6H2O), ammonium fluoride (NH4F), urea, sodium thiosulfate (Na2S2O3), and Iron (III) nitrate nonahydrate (Fe(NO3)3·9H2O) were purchased from Shanghai Aladdin Biochemical Technology Co., Ltd. All solvents and reagents are commercially available A.R. grade and used without further purification unless otherwise noted. Deionized water was used throughout all experiments.

Preparation for exfoliated boron nitride

Exfoliated boron nitride (ex-BN) was prepared by physical exfoliation with a microfluidic homogenizer (ISA-NKM100). Especially, 0.4 g hexagonal boron nitride, 4 g polyvinylpyrrolidone (PVP) (PVP as a stabilizer to prevent BN reaggregate sterically by adsorbing on the BN surface), and 400 mL ethanolamine as solvent were well-mixed under ultrasound treatment for 1 h. The receiving suspension liquid was treated with the microfluidic homogenizer for 2 h. After cooling to room temperature, the mixed solution was washed with ethanol and dried in the air, receiving the exfoliated boron nitride.

Preparation of quaternized chitosan

Quaternary ammonium modification by grafting 2,3-epoxypropyl trimethylammonium chloride on amino groups of chitosan is applied to introduce more positive charges and enhance the ion conduction of chitosan. Specially, 4 g chitosan dissolving in acetic acid (1 wt.%) was precipitated with NaOH and centrifugated. The regenerated chitosan and 12 g 2,3-epoxypropyl trimethylammonium chloride were dissolved in 400 mL mixed solution (isopropanol and DI water with a volume ratio of 1:1). After reacting at 80 °C for 8 h, washing with ethanol and drying in air, QCS powers were obtained with a surface potential of 63 mV and a quaternized degree of approximately 30.8% determined by the conductometric titration using AgNO3 as the titrant.

Synthesis of QAPPT

QAPPT was synthesized by the Friedel-Crafts Alkylation12. A typical synthesis procedure is as follows: N-methyl-4-piperidone (7 g) and terphenyl (16 g) were dissolved into methylene chloride (75 mL) in a three-necked flask. TFA (5 mL) and TFSA (75 mL) were then added dropwise slowly at 0 °C. The reaction was carried out for 24 hours under stirring. By immersing the obtained viscous liquid in a cold methanol solution, the precipitated white solid was washed with deionized water and immersed in 1 M K2CO3 at 50 °C for 12 h. Finally, the product was washed with water and dried completely at 60 °C under vacuum.

The above sample was dissolved in DMSO and reacted with iodomethane under dark conditions for more than 24 hours at room temperature. The resulting viscous and yellow solution was added dropwise into ethyl acetate followed by washing with ethyl acetate and drying completely under vacuum, resulting in the formation of QAPPT.

Fabrication of composite membranes

Composite membranes were prepared by a drop-casting method. QCS dissolving in acetic acid solution (1 wt. %) and boron nitride (BN) dissolving in ethanol solution (1 wt. %) were mixed, followed by adding glutaraldehyde (1%) and stirring for 1 h. The mixed solution was cast on a plastic petri dish and dried in air, resulting in a dry composite membrane. By controlling the volume ratio of QCS and BN, the composite membranes with different BN contents were prepared, which were defined as QCS/x BN (x referred to the BN volume fraction relative to the composite membrane). The pristine QCS membrane was also prepared through the same drop-casting method.

QAPPT composite membranes were prepared by casting the QAPPT-BN mixture on a clean glass plate and dried at 120 °C for 2 h. The composite mixture is prepared by mixing the QAPPT polymer (1.0 g) in DMSO (30 mL) and BN in DMSO solution. The membranes in iodide form were peeled off from the glass plate. By ion exchanging in 5% KOH solution at 80 °C completely, the membranes in hydroxide form were obtained after washing with deionized water.

The volume fraction (V%) of BN in composite HEM is calculated by the following formula,

$$V \%=\frac{1}{{m}_{P}\times {\rho }_{{BN}}/{m}_{{BN}}\times {\rho }_{P}+1}$$
(1)

where \({m}_{P}\) and \({m}_{{BN}}\) are the applied mass of polymer and BN, respectively. \({\rho }_{P}\), and \({\rho }_{{BN}}\) are the mass density of the polymer and BN, respectively. \(\normalsize \normalsize {\rho }_{{BN}}=2.27\) g cm–3. For QCS and QAPPT, the mass density is calculated from the pure membrane fabricated with the same process but without BN. The calculated value \({\rho }_{{QCS}}\) and \({\rho }_{{QAPPT}}\) is 0.808 and 2.00 g \({\mathrm {cm}}^{-3}\), respectively.

Synthesis of non-precious metal electrodes

The non-precious metal electrodes of NiFe LDHs@NiCoS NAs-NF and FeOOH/NiFe LDHs@CCH NAs-NF were prepared by two hydrothermal synthesis steps, respectively, as reported in the literatures28,29. Briefly, for NiFe LDHs@NiCoS NAs-NF catalyst, a cleaned nickel felt was firstly immersed into a precursor solution containing Ni(NO3)2·6H2O, Co(NO3)2·6H2O, NH4F, urea, Na2S2O3, and deionized water in a Teflon-lined stainless autoclave and was heated at 135 °C for 12 h. After washing with deionized water and drying in a vacuum, the black NiCoS nanorod arrays on Ni felt (named as NiCoS NAs/NF) were obtained. Secondly, the NiCoS NAs/NF was immersed into a precursor solution containing Ni(NO3)2·6H2O, Fe(NO3)3·9H2O, NH4F, urea, Na2S2O3, and deionized water in an autoclave at 120 °C for 8 h. After washing with deionized water and drying in a vacuum, the NiFe LDHs@NiCoS NAs-NF catalyst was obtained. The FeOOH/NiFeLDHs@CCH NAs-NF catalyst was synthesized with similar procedures of two hydrothermal synthesis steps. The first step was related to a precursor solution containing Co(NO3)2, urea, and deionized water and a heating condition of 120 °C for 5 h. The second step was related to a precursor solution containing Fe(NO3)2, NH4F, urea, and deionized water and a heating condition of 120 °C for 5 h. Other procedures, including the washing and drying procedure, were the same as the NiFe LDHs@NiCoS NAs-NF catalyst.

Characterizations

SEM and Energy dispersive spectroscopy (EDS) images were taken with ScientificTM Apreo (Thermo Fisher Scientific, USA) at 10 kV. Scanning transmission electron microscopy (STEM) was performed on a Talos F200X (Thermo Fisher Scientific, USA) with an acceleration voltage of 200 kV. The cross-sectional membrane for STEM was sliced with a Leica EM UC7. Elemental and structural information of the BN was measured by X-ray photoelectron spectroscopy (XPS, Thermo Scientific K-Alpha) with an Al Kα radiation (1486.6 eV). Atomic force microscopy (AFM) was conducted on a Dimension Icon (Bruker, Germany) by tapping mode. FT-IR (Thermo Fisher Scientific Nicolet iS20) was performed with an ATR mode. Visualized temperature profiles were measured by an infrared thermal imager (InfiRay, C200Pro). The thermal conductivity of the composite membranes was obtained by a laser thermal conductivity analyzer (LFA467 HyperFlash). Thermal conductivity of the catalyst (IrO2 or Pt/C), bipolar plates (Titanate), and gas diffusion layer (Stainless steel) for the numerical simulation were measured by the thermal conductivity tester (C-Therm Company) via a transient plane heat source method. Tensile strength tests were performed on the tensile testing machine (ETNALN YTN-D5-PC) with a tensile speed of 6 mm min−1, and average values were obtained from at least three tests. The 1H NMR spectra (JNM-ECZ600R/S1, JEOL, Japan) were used to record the molecular structure of the polymer.

Hydroxide conductivity and ex-situ alkali stability

The hydroxide conductivity of HEM in hydroxide form was measured using a four-electrode cell at temperatures ranging from 25 °C to 90 °C in water. The electrochemical impedance spectroscopy (EIS) was performed on a CHI 660E electrochemical station (Chenhua Instrument, Shanghai, China) with a frequency from 100 kHz to 1 Hz. The hydroxide conductivity, \(\sigma\), was calculated by the following equation

$$\sigma=\frac{L}{{RS}}$$
(2)

where L is the distance between two electrodes, R is the resistance obtained by the EIS tests (the real axis value at the high-frequency intercept), and S is the cross-sectional area of the membrane. Temperature dependence of hydroxide conductivity was fitted by a semiempirical Arrhenius equation of

$$\sigma={\sigma }_{0}\exp \frac{-{E}_{a}}{{RT}}$$
(3)

where\(\,{\sigma }_{0}\) is a preexponential factor, Ea is the activation energy of hydroxide migration, R is the universal gas constant, and T is the absolute temperature.

Ex-situ alkali stability of HEM was recorded by the losses of ion conductivity after alkali treatment by immersing in NaOH solution at 90 °C for certain times.

Ion exchange capacity

To measure the ion exchange capacity (IEC), an accurately weighed membrane was placed in an HCl standard solution at room temperature for 24 h. Subsequently, the above solution was titrated back to neutralization using a KOH standard solution and phenolphthalein as an indicator. The IEC was calculated using the following formula:

$${IEC}=\frac{\left({N}_{{HCl},i}-{N}_{{HCl},f}\right)}{{m}_{{dry}}}$$
(4)

where \({N}_{{HCl},i}\) is the HCl quantity (equivalent) in the initial solution, \({N}_{{HCl},f}\) is the remaining amount of HCl (equivalent) determined by the titration, and \({m}_{{dry}}\) is the mass of the dry membrane.

Dielectric relaxation spectra

Dielectric relaxation spectra were analyzed from the impedance spectra, which were recorded on an Impedance analyzer (MFIA LCR) with a frequency range of 1 M Hz to 0.01 Hz. Membranes were sandwiched between two stainless steel electrodes and stabilized for at least 4 h at temperature- and humidity-controlled box (relative humidity 95%). The \({\varepsilon }^{*}\) data were analyzed with the Havriliak–Negami relaxation model, the complex dielectric permittivity ε(ω) can be written as30,31:

$$\hat{\varepsilon }\left(\omega \right)={\varepsilon }^{{\prime} }-i{\varepsilon }^{{\prime} {\prime} }={\varepsilon }_{{\infty }}+{\sum }_{j=1}^{n}\frac{{\Delta \varepsilon }_{j}}{{\left(1+{\left(i\omega {\tau }_{j}\right)}^{{\alpha }_{j}}\right)}^{{\beta }_{j}}}$$
(5)

where \({\varepsilon }^{{\prime} }\) (dielectric constant) and \({\varepsilon }^{{\prime} {\prime} }\) (dielectric loss factor) is the real and imaginary components of the dielectric permittivity, respectively; \({\varepsilon }_{{\infty }}\) represents the measured \({\varepsilon }^{{\prime} }\) at infinite frequency, and \(\Delta \varepsilon\) is the relaxation strength and gives the difference between \({\varepsilon }^{{\prime} }\) at zero and infinite frequency (\({\varepsilon }_{{\infty }}\)) \((\Delta \varepsilon=\,{\varepsilon }^{{\prime} }-{\varepsilon }_{{\infty }})\); ω is the angular frequency (ω = 2πf); τ is the characteristic relaxation time, and ω equals to the frequency; The parameters α and β is used to describe the skewing and broadening of dielectric function, varying from 0 to 1; j represents the different Havriliak–Negami terms when multiple relaxations are observed.

Temperature dependence of the relaxation times (τ1 and τ2) was described by the Arrhenius equation of \(\tau={\tau }_{{\infty }}{e}^{{E}_{a}/{RT}}\), where Ea is the apparent activation energy.

Thermal conductivity and diffusion behavior simulation

The effect of BN volume content on the thermal conductivity of the QCS/BN composite membrane was investigated by using finite element simulation. The BN nanosheets with an in-plane k of 600 W m–1 K–1 and an out-of-plane k of 30 W m–1 K–1 were simplified into 1 × 1 × 0.05 μm3 flat sheets (based on statistical lateral size and thickness of BN) and randomly distributed in the QCS film, and the rest of them were QCS with k of 0.5 W m–1 K–1. The distribution of nanosheets in the QCS/3.8%BN was sparser, and the nanosheets in QCS/10.6%BN were partially interconnected due to the high volume fraction, corresponding to the SEM results. The top of the composite membrane is heated in the solid heat transfer interface based on Fourier’s law equations and using the Transient Plane Source Method,

$$q=-k\nabla T$$
(6)
$$\rho {C}_{p}\frac{\partial T}{\partial t}=\nabla \cdot \left(k\nabla T\right)+Q$$
(7)

where \(q\) is the conduction heat flux, \(k\) is the thermal conductivity, \(\rho\) is the density, \({C}_{p}\) is the constant pressure heat capacity, \(T\) is the temperature, t is the time, and Q is the heat source. The heating conditions are set as follows: constant temperature T0 = 100 °C as the top boundary heat source, convective heat flux at the lower boundary, and insulation at the remaining boundary.

Electrolytic water thermal model

ANSYS Fluent Software was applied to simulate the temperature distribution and the influence of HEM on the temperature distribution of the electrolyzers under steady state. The heat transfer in the electrolyzer mainly includes the heat conduction between the membranes, the catalytic layer, the gas diffusion layer, and the bipolar plate. The expression of the energy equation for the entire computational domain is as follows:

$$\nabla \left(k\nabla T\right)=Q$$
(8)

where k is the thermal conductivity of the material, and \(Q\) is the heat source in the solid domain. The uniform heat source was used in different regions of the model, and the thermal physical properties in each region were set as shown in Supplementary Table 2. The ambient temperature of the electrolytic cell is 60 °C, so the contact surface between the anode and cathode bipolar plates and the environment was set as the boundary condition of the fixed wall temperature. The model was solved as a steady-state problem, and the algorithm was coupled algorithm. The discrete format of the energy equation is a second-order upwind format, the convergence residual standard is set to \({10}^{-5}\), and the number of iterations is set to 1000.

Density functional theory calculation

All DFT calculations were carried out using Vienna ab initio simulation package (VASP)32 with the Perdew-Burke-Ernzerhof (PBE) generalized gradient approximation (GGA)33 (Validation of this functional are found in Supplementary Fig. 13 and the according discussion). Projector-augmented-wave (PAW) potentials34 were used to take into account the electron-ion interactions. The energy cutoff was set as 500 eV for the plane wave-basis expansion and the convergence criteria of the electron self-consistent loop was set to 10–6 eV. The geometry of initial states (IS) and final states (FS) was put in a 20 Å × 20 Å × 20 Å box and optimized with a conjugate gradient algorithm until the forces acting on the atoms were less than 0.05 eV/Å. Vibrational frequency computation was performed to obtain the thermodynamic parameters, and the convergence tolerance was set as 10–6 eV. The Brillouin zone was sampled on a 1 × 1 × 1 Gamma grid. The transition states (TS) were found using the climbing-image nudged elastic band method (CINEB) with five images interpolating35. The change of Gibbs free energy (∆G) of degradation from IS to FS was calculated by the following equation:

$$\Delta G=\Delta E+\Delta {ZPE}-T\Delta S$$
(9)

where \(\Delta E\), \(\Delta {ZPE}\), and \(\Delta S\) denote the change of energy, zero-point energy, and entropy from IS to FS, respectively. The zero-point energy and entropy were obtained from vibrational frequency computation.

Assembly of electrolyzer and water electrolysis performance test

The membrane electrode assembly (MEA) was prepared by a catalyst-coated membrane (CCM) method. Commercial IrO2 (Sinero, Ir > 85 %) and Pt/C (Johnson Matthey, 60% Pt on AC01) were used as the anode and cathode catalysts, respectively. Catalysts and ion-conducting ionomer of QAPPT (weight ratio of the catalyst and ionomer was 5:1) were added into isopropanol solvent, followed by sonication for 30 min in an ice-water bath, to prepare electrode inks. The catalyst ink was sprayed on both sides of the membrane (30−40 µm thick) to fabricate the catalyst-coated membrane (CCM) with an effective square area of 4 cm2. The loading amount of the anode and cathode catalyst is 2 mgPt cm−2 and 4 mgIr cm−2, respectively. After that, stainless steel foam (260 μm in thickness, Suzhou Sinero Technology Co., Ltd) was added to the cathode and anode side of the CCM, respectively to assemble in a water electrolyzer. Homemade non-platinum group metal (the FeOOH/NiFe LDHs@CCH NAs-NF for anode and NiFe LDHs@NiCoS NAs-NF for cathode.) and commercial non-PGM (W2K2 type for both electrodes, WuZhou HGP Advanced Materials Technology Co., LTD) were applied as the electrode catalyst, respectively, which were further assembled with HEM in a water electrolyzer. The effective area of the electrolyzer assembled with non-PGM electrodes was 4 cm2. The in situ temperature of the electrolytic cell during operation was monitored with a thermometer by inserting thermocouple wires (0.05 mm in diameter, Kaipusen, Type K) in each layer when assembling the electrolyzer cell. 15% KOH solution at 60 °C was applied as the electrolyte.

The performance of a single cell was evaluated on a water electrolyzer at controlled temperatures and electrolytes (15% KOH) with a flow rate of 10 mL min–1. Polarization curves were received by recording the current densities at varied voltages ranging from 1.3 V to 2.0 V. The transient in situ stability is tested based on transiently oscillated current densities between 1 A cm–2 and 0.1 A cm–2 for each cycle. The cycle consisted of holding the current density at 1 A cm–2 for 2 s, standing for 1 s, holding at 0.1 A cm–2 for 2 s, and returning to the current density at 1 A cm–2 for 2 s. The static in situ stability was studied in a galvanostatic mode at different current densities of 0.2, 0.5, and 1 A cm−2. All data were collected on a battery testing system (Neware Technologies CT-4008Tn-5V12A-S1). Transient response time for the cold starting procedure was received by the voltage-time curves, which were recorded after the water electrolyzer was cooling at – 30 °C for 10–60 h.