Introduction

Birds fluttering their wings to soar through the skies, kangaroos springing their legs to leap across the grassland, and fish moving their tails to propel themselves underwater—all demonstrate oscillation, a fundamental motion that enables periodic locomotion and is ubiquitous in the natural world1. These oscillatory motions, actively generated by animals, produce kinetic energy through periodic back-and-forth movements in specific directions2,3. This dynamic process is driven by biological actuation systems, including muscles as actuators, skeletons as supports, the cortex for control logic, and the nervous system as control circuits, which regulate the oscillatory motions through negative feedback loops4. Many efforts have been made to artificially replicate these natural oscillations using various actuation methods such as light5,6, heat7,8, pneumatics9,10,11,12,13,14, magnetism15,16, and electricity17,18,19. These efforts have demonstrated the potential of artificial oscillators to power robotic movements across diverse terrains and environments. However, these systems often rely on electrical power for continuous energy and clock signals, resulting in bulky, complex designs that limit their applications in extreme conditions, such as areas with strong electromagnetic fields or places where electricity is scarce20. Pneumatic actuation, with embedded non-electrical logic gates, emerges as a promising solution to overcome these limitations14,21,22,23,24,25.

Existing pneumatic oscillators operate on a principle that leverages the mechanical instability of elastic materials. Examples include elastic bistable mechanisms22,26, valve structures with fluidic relaxation properties25, tube-balloon mechanisms11,27, piston structure28, and buckling-sheet structures29. These designs transform a constant supply pressure into a periodic output, driving robots to perform various tasks such as crawling, diving, climbing, and walking26,29,30, without relying on electronic systems. Despite these advantages, there still exist significant challenges to improve their capabilities, including frequency, integration, and tunability. For instance, the micro piston valve28 displays a high operational frequency (up to kHz), yet is utilized to facilitate oscillatory airflow. Consequently, external actuators must be integrated to perform their intended function. As for the oscillator with actuation capabilities, the highest frequency achieved by these devices is 15 Hz27, however such design suffers from continuous escape of the airflow, resulting in high energy loss27,29. Although bistable actuation principles are introduced to improve energy efficiency, their maximum frequencies do not exceed 3.3 Hz26. In addition, the number of oscillators in integrated cascaded-loop systems is inherently constrained to an odd value due to the intrinsic limitations of their internal ring architecture23,28, leading to restricted actuation configurations. Furthermore, the phase-frequency characteristics of existing oscillator designs are predominantly non-tunable23,24, severely impeding their versatility in robotic systems for multi-modal motions. Therefore, there is a compelling requirement for high-frequency and versatile oscillators to enhance the functionality of electronics-free robotic systems and expand their potential applications.

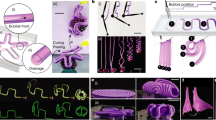
To this end, we introduce a pneumatic hybrid oscillator (PHO) with a soft-elastic-rigid hybrid structure, designed to enhance performance and versatility in robotic applications. This PHO incorporates lightweight fabric-based chambers and tubes, a rotating-based bistable elastic beam, and rigid rocker and structural components that efficiently switch airflow direction, enabling high-frequency motions up to 51 Hz (see Supplementary Movies 1 and 5). PHO’s scalability allows any number of oscillators to form a cascaded-loop (serial connection in a closed loop), with tunable oscillation phases, facilitating various motion modes, such as jumping, crawling, and swimming (Fig. 1a). Notably, even without electronic circuitry, these robots showcase substantial advantages in motion speed and frequency (Fig. 1b). Additionally, PHO’s modular design employs multi-material segments for easy component replacement and maintains performance over an impressive lifespan of 3 million cycles (Fig. 1c). We first investigate the PHO’s working principle, particularly the phase motion of its rotating joint. A circuit equivalent model is then developed to elucidate the relationship between the oscillator’s frequency and design parameters such as supply pressure, stiffness, and the geometric parameters of the elastic beam. Finally, the PHO’s adaptability is showcased through its application in a range of high-speed robotic motions, from land-based to aquatic environments. This design enables robots to execute complex, high-speed tasks autonomously and efficiently without reliance on electronic control.

Fig. 1: Overview of the pneumatic hybrid oscillator (PHO).
figure 1

a Overview of the high frequency, cascade ability, and phase tunable pneumatic hybrid oscillator (PHO) for various robot actuations. b Comparison of the motion speed and frequency of the bionic kangaroo robot designed based on the proposed PHO with the same type of pneumatic robot in the literatures9,14,22,24,25,26,29,30,41,42,43,44,45,46,47,48,49,50,51,52. c The design of PHO.

Full size image

Results

Design and working principle of the PHO

The proposed pneumatic hybrid oscillator (PHO) mainly consists of three primary components: two actuation chambers, a rotating-based bistable beam equipped with active and passive joints, and a switch valve linked to the beam’s joints (Fig. 2a). Each actuation chamber features a soft bellow structure and a fixed hinge (active joint of the bistable beam) that expands when pressurized and contracts when exposed to the ambient atmosphere, akin to the opening and closing of a fan (Supplementary Fig. 1). Unlike many existing bistable beams31,32, we added two revolute joints (i.e., active and passive joints) at either end of our bistable elastic beam, converting traditional pushing-activated snap-through movements into rotating-activated ones (Fig. 2a, Supplementary Fig 2). This enables the snap-through motion to be controlled by rotating the active joint at one end, which triggers instantaneous snap-through rotations at the passive joint (Supplementary Note 2 and Supplementary Fig. 2). The switching valve assembly includes a rigid rocker centered on a revolute joint (passive joint) and connects with four soft pneumatic tubes forming the air inlets and outlets (see Supplementary Movie 1 and Supplementary Fig. 7). As shown in Fig. 2a, the rotation of the rigid rocker, dictated by the passive joint, reliably maintains only two stable positions, corresponding to the dual stable states of the elastic beam. This configuration ensures that at any given time, two tubes remain open while the other two are obstructed, facilitating airflow and control.

Fig. 2: Concept and working principle of the pneumatic hybrid oscillator (PHO).
figure 2

a Design principle of PHO. b Demonstration of the oscillation process of PHO. c The relation between the stored potential energy of the elastic beam and the active joint. d The nonlinear relationship between the rotation angle of the active joint and the passive joint, where \({\theta }_{c}\) and \({\theta }_{p}\) are the critical angle of the active joint and passive joint, respectively. e During the oscillation, the active joint rotates continuously, and the passive joint steps. There is a difference in the phase of their rotation. f Construction of the PHO: the actuation chambers, the rotating-based bistable beam, and the switching valve. g High-speed camera images of one oscillation period with a rotation period of 19 ms.

Full size image

Figure 2b demonstrates the oscillation process when the PHO system is pressurized. Initially, the actuation chamber connected to the open-air tube inflates. This inflation progressively expands, rotating the active joint until the elastic beam snaps to its alternative stable state (Fig. 2b, c, Supplementary Fig. 3 and Supplementary Movie 2). Concurrently, the passive joint undergoes a rapid rotation, releasing energy stored in the elastic beam (Fig. 2c and Supplementary Movie 3), which drives the rocker to snap to its opposite stable position. This action kinks the previously open tube, deflates the expanded chamber, and initiates the inflation of the opposite chamber on the other side of the active joint (Fig. 2b, d and Supplementary Movie 4). This sequence enables the PHO system to maintain continuous oscillation as long as air supply persists. The rapid switching of the 5/2 valve ensures that the inflation of actuation chambers is instantaneously alternated and stably maintained, preventing any counteraction between the opposing chambers (Fig. 2d, e). Moreover, the phase difference between the active and passive joints prevents the elastic beam from becoming jammed during the snap-through process, thereby ensuring the stability and reliability of the oscillation.

The proposed soft-elastic-rigid hybrid PHO structure was constructed as Fig. 2f. The actuation chambers and the switching valve’s tubes were fabricated from a soft yet unstretchable fabric with a thickness of 0.16 mm (see Supplementary Figs. 4, 5 and Supplementary Note 1 for details). This design ensures that the pneumatic input is fully and efficiently utilized for rotating the actuation joint, rather than being wasted on inflating the soft materials33. A lightweight carbon fiber beam serves as the bistable beam; it is 0.3 mm thick, 27 mm in original length, and 26.5 mm in assembly length, giving a normalized length (λ) of 0.98. This configuration allows the beam to achieve rapid, powerful snap-through in just 9 ms (Fig. 2g and Supplementary Movie 5), due to its pure elastic structure without material stretching. The other components of the PHO, including structural supports, are made from 3D-printed rigid materials that enhance motion and force transmission efficiency (see Supplementary Figs. 6, 7 and Supplementary Note 1 for details). This structure enables the oscillator to achieve an unparalleled driving frequency, completing a full motion cycle in 19 ms (equivalent to 51 Hz). The oscillator also exhibits exceptional durability, capable of enduring over 3 million oscillations without significant performance degradation.

Analytical model for PHO

To elucidate the relationship between the PHO’s design parameters and its oscillation frequency, we established an equivalent circuit model that simulates the system’s operational mechanism. The three core components of PHO system, namely the actuation chamber, the elastic beam, and the switch valve, are represented by specific electronic components within a closed-loop system featuring negative feedback (Fig. 3a). Our approach began with the development of kinematic and mechanical models for the elastic beam’s buckling process and the actuation chamber, respectively (see Supplementary Notes 2, 3, Supplementary Figs. 7, 8 and Supplementary Figs. 9, 11).

Fig. 3: Analytical model for pneumatic hybrid oscillator (PHO) to predict oscillation frequency with varying design parameters.
figure 3

a PHO can be modeled using RC analogue electrical circuit. One oscillation period contains two deformation processes with one chamber inflating and the other deflating, shown by flow-indicating diagrams and two snap-through processes. b–d Characteristic values of electronic components including capacitance of chamber, capacitance for elastic beam, and valve blocking factor over design parameters, guiding the optimized design for higher frequency. Rf represents the equivalent resistance of the valve, while the Rall is the maximum value of Rf. e–g Predictions from the analytical RC circuit model (dashed lines) and experiment data points of oscillation frequency for PHOs with distinct normalized length and bending stiffness. Error bars represent the standard deviation of the measured oscillation frequency from 10 measurements.

Full size image

In this circuit model (Supplementary Fig. 12), the actuation chamber functions as an adjustable capacitor Cc, which modulates and transfers the input pneumatic energy to the active joint. Meanwhile, the elastic beam itself is dual functional: it transfers energy and controls the valve via the active joint. These functions are modeled by another capacitor Ceb and a hysteresis comparator, respectively. The hysteresis comparator outputs a signal representing the passive joint’s angle, high when θ > 0° and low otherwise. Based on the energy equivalence principle, the expression of Cc and Ceb are derived in a theoretical manner (Supplementary Note 4).

Furthermore, the capacitance value Cc, as an inherent property to the chamber’s design, changes depending on its expansion angle and is dynamically linked to the elastic beam’s capacitance Ceb (Fig. 3b). Besides, we mapped the capacitance (Ceb) against the bending stiffness (EI) and its characteristic length (λ), showcasing how these physical properties influence the system’s behavior (Fig. 3c). The output from the comparator then modulates two sets of equivalent programmable resistors (Rf,a, Rf,b) of the switch valve34. These resistors toggle between high and low resistance states based on the comparator’s output and exhibit opposite resistance characteristics under the same signal (Fig. 3d). In addition, the resistors Rc, Reb, and Rt are used to simulate the energy loss in the chamber, elastic beam, and tubes, respectively. Here, Rt is obtained by a theoretical expression while Rc and Reb are acquired by integrating measured experimental data into the theoretical model.

Such a configuration leads to the instability of the system. At a constant supply pressure Ps, chambers A and B alternate between two states of inflation and deflation, resulting in sustained oscillations (Supplementary Fig. 3). It is noted that the hysteresis characteristics of the comparator are determined by the critical moment of the elastic beam, which means that the start-up pressure of the oscillation is related to its design parameters. In addition, the switching time of the valve in the high frequency state (>10 Hz) is not negligible, therefore the oscillation period of the system consists of two parts, namely the switching time tb of the valve and the rotation time td of the active joint. The former is an inherent property of the valve and can be measured and fitted experimentally (Supplementary Fig. 13), while the latter can be characterized analytically by:

$${t}_{d}={K}_{d}\cdot {R}_{{BCT}}\cdot {C}_{{BCT}}\cdot {\mathrm{ln}}\left({P}_{{BCT}}\cdot {\left({P}_{{BCT}}{-}{P}_{B{UCK}}\right)}^{-1}\right)$$
(1)

where RBCT and CBCT represent the equalized values of resistance and capacitance, deduced as a function of Rt, Rc, Reb, Ceb, and Cc. RBCT symbolizes the input pressure when the supply pressure passes the soft valve, accounting for the contributions of the kinked and unkinked fabric tubes. PBUCK refers to the snap-through critical pressure determined by the beam, derived from a theoretical model. Kd is the correction factor revising the influence introduced by the equalization assumptions. All the afore mentioned parameters can be tuned by varying the design parameters as λ and EI. Furthermore, we can express the oscillation frequency of the system as:

$${F}_{{PHO}}=1\cdot {\left(2\times \left({t}_{d}+{t}_{b}\right)\right)}^{-1}$$
(2)

We devised nine distinct PHOs with varying parameters, encompassing three characteristic lengths from 0.93 to 0.98 and three bending stiffness values from 0.9 mN·m2 to 2.3 mN·m2. The relationship between their oscillation frequency and pressure was tested and compared with the theoretical model (Fig. 3e–g). The oscillation will not be activated until the supply pressure is high enough to satisfy the condition PBCT > PBUCK. As the supply pressure increases, the oscillation frequency increases logarithmically before about 80 kPa, which complies with the proposed equations. The frequency then grows slower and reaches its peak when the supply pressure is about 120–150 kPa. This phenomenon occurs because the soft valve blocks the airflow partially when the supply pressure is high, resulting in a lower actual input pressure for the chamber. The results show that the characteristic length and bending stiffness together affect the frequency characteristics, that is, low characteristic length and stiffness will reduce the blocking ability of the valve and lead to premature termination of the oscillation at high pressure. Besides, high stiffness will lead to high critical moment and reduce the operating frequency. It is worth noting that the valve showed excellent frequency performance in the frequency experiment as a whole, and the PHO oscillated up to 51 Hz under specific elastic beam parameters (λ = 0.98, EI = 1.6 mN·m2), which is 3.3 times the operating frequency of the existing flexible oscillation valve with pull-down resistors27 and 15 times more than the ring oscillator without pull-down resistors26.

High-speed robotic locomotion

Inspired by the kangaroo’s remarkable efficiency in movement, which achieves a jumping rate of 8 body lengths per second with rapid swinging of its feet35, we have developed a bionic kangaroo robot. This robot incorporates our high-frequency pneumatic oscillator to simulate the dynamic leaping ability of its biological counterpart (Fig. 4a and Supplementary Fig. 14). The robot’s bipedal frame is attached to the oscillator’s active joint. Its feet are designed with backward-angled nails to enhance frictional anisotropy, facilitating controlled grip during the forward and backward swinging motions of the legs (Fig. 4b). A flexible tail is affixed at the rear of the bionic kangaroo to maintain balance throughout the jumping sequence. The locomotion of the bionic kangaroo robot mimics the natural kangaroo’s movement, which is segmented into three phases: pushing, taking off, and landing. (Figs. 4c and S10).

Fig. 4: Kangaroo-inspired high-speed and high-frequency robot.
figure 4

a Mechanical design of the robotic kangaroo. b i: the motion of a kangaroo, which jumps with its rear legs, and uses its tail to maintain balance; ii: the robotic counterpart mimicking this posture; iii: schematic diagram of the kangaroo-inspired robot, where β is the initial angle of the assembled rear leg and ф, half of the rotation range; iv: anisotropy friction of the rear leg. c Similar running gaits between a real kangaroo and the robotic one. d High-speed running with a tunable actuation frequency. e Characterization of the jumping speed under different initial angles. Shaded regions represent 1 standard deviation. f Characterization of the jumping step length under different initial angles. Shaded regions represent 1 standard deviation. g Characterization of the ground duty cycle ratio.

Full size image

To optimize the takeoff velocity while preserving the desired driving frequency, we configured the kangaroo robot with an oscillator featuring an assembled elastic beam length characterized by λ = 0.97. By fine-tuning the input pressure, we effectively controlled the robot’s rapid movement across a range of frequencies (Fig. 4d and Supplementary Movie 6). Impressively, the robot achieves a maximum motion speed of 5.1 body lengths per second (BL·s−1) at a supply pressure of 100 kPa, corresponding to an absolute velocity of 68 cm·s−1 at a frequency of 28 Hz. This velocity notably surpass those of existing pneumatic robots that rely on electromagnetic valves by more than two-fold9 and exceed the capabilities of current pneumatic robots without electronic circuit control by 50 times29 (Fig. 1c).

To further investigate the parameters affecting the robot’s motion speed, we conducted an analysis on the leg mounting angles (i.e., β in Fig. 4b iii). Figure 4e illustrates experimental results conducted with three different initial mounting angles for the same oscillator. At low oscillation frequencies, the speed of the bionic kangaroo is effectively zero due to inefficient leg swing speed and inability to achieve takeoff. At a mounting angle of β = 70°, the robot begins to jump at frequencies below 5 Hz. However, this larger takeoff angle reduces the step length, leading to decreased velocity as shown in Fig. 4f. Conversely, at β = 105°, the smaller takeoff angle diminishes the step length even further, adversely affecting the robot’s overall motion speed. The optimal performance was observed at a leg mounting angle of β = 100°, where the robot achieves its highest speed. While the maximum actuation frequency of the bionic kangaroo can reach 36 Hz, the peak velocity occurs around 28 Hz. Beyond this frequency, the robot experiences prolonged airborne period during excessively high actuation frequencies, which results in several motion cycles occurring mid-air (Fig. 4g). Given that the output frequency of the system has not yet reached its upper limit, we believe that further enhancements in motion speed can be achieved through structural and counterweight optimizations. This lightweight (30 g), high-frequency, and high-speed bionic kangaroo robot demonstrates the significant potential of the PHO to achieve superior performance in robotic applications.

Cascaded-loop enabled crawling

In robotic designs that require multi-degree of freedom (DoF) movement, the integration of multiple actuators is a common approach. These actuators are usually controlled systematically via predefined logic, enabling the robot to perform complex movements25. While microcontrollers and solenoid valves can easily control the sequence of actuator pressures, achieving such coordination without electronic components poses significant challenges. Currently, non-electrical control of multi-actuator systems primarily relies on two designs: the ring oscillator23 and the fluidic relaxation oscillator25. However, these methods have limitations; the ring oscillator can control only an odd number of actuators, and the fluidic relaxation oscillator uses a non-bistable structure that leads to higher energy losses.

To address these issues, we introduce a cascaded-loop oscillator system composed of two PHOs engineered to manage cascaded fluidic logic circuits effectively. Both PHOs, fabricated with similar parameters, are arranged in parallel, and their valve outlets are alternately connected to each chamber inlet. This configuration forms a closed-loop system that remains inherently unstable with a constant pressure input, as shown in Fig. 5ai and Supplementary Fig. 16. In this setup, the pressure inside each chamber of a single PHO is regulated by the opposing PHO’s valve, ensuring that the two oscillators activate alternately. This design results in a consistent sequence of oscillations (Fig. 5aii). Figure 5B demonstrates how the four chambers within the sequence oscillator alternately inflate and deflate under a constant pressure supply. Notably, the inflation phases of chambers within the same PHO are offset by half a cycle, while the inflation phase of chambers on the same side across two PHOs differs by a quarter cycle. This staggered timing ensures that while one chamber in a PHO is pressurized, the other is activated to induce a snap-through, maintaining a dynamic equilibrium and effective control over the multi-DoF movements.

Fig. 5: Cascaded-loop crawling robot.
figure 5

a i: Design principle of the cascaded-loop of two pneumatic hybrid oscillators (PHOs). ii: The inner pressures of the four chambers change periodically over time in the cascade configuration. b Waveforms of chamber pressure, active joint angles, and passive joint angles at a constant supply pressure. c The design of the crawling robot. d The crawling gait of the robot. e The robot crawls forward under constant input pressure. f The speed of the crawling robot varies with frequency. Shaded regions represent 1 standard deviation. g Velocity comparison of the pneumatic crawling robots.36,50,53,54,55,56,57,58,59,60.

Full size image

We further explored the practical applications of the cascaded logic circuit of PHOs by constructing a multi-legged crawling robot, as depicted in Fig. 5c. This robot features a pair of identical feet for each PHO, designed with sharp corners angled backward to optimize frictional interaction with the surface. The design links the active joint of one PHO to the body of the other, while the passive joint of the latter connects to the robot’s front leg. This configuration facilitates a stable gait by harnessing the alternating movements of the active joints. The robot’s motion gait is comprised of four distinct states, determined by the limit angles of the two active joints, as shown in Fig. 5d and Supplementary Movie 7. During transitions between these states, the rotation of each active joint moves its corresponding foot, propelling the robot forward. This movement is facilitated by the anisotropic frictional forces generated by the feet’s design. The robot’s dynamic progression through these states illustrates a well-coordinated, stable forward thrust, showcasing the effective implementation of PHO-driven cascaded logic circuits in robotic movement.

We further tested the crawling speed of the robot, which exhibits high motion performance. Under a supply pressure of 100 kPa, the robot achieved a speed of 0.8 BL·s−1 at a frequency of 4 Hz (Fig. 5e, f). Increasing the pressure to 150 kPa raised the motion frequency to 5 Hz; however, this led to noticeable slipping between the legs and the ground as the robot moved forward, resulting in a reduction of speed. Additionally, the impact from the robot’s movement caused slight bouncing during the crawling process, occasionally altering its direction, and further decreasing its speed. Despite these challenges, the robot generally maintained stable locomotion with only minor angular offsets.

This high-speed, electronics-free crawling robot demonstrates the effective capability and response frequency of the cascaded PHOs under its own weight. Notably, we opted not to use wheels, a common feature in many designs to avoid crawling resistance36, yet our robot still achieved the fastest speed among pneumatic crawlers reported in the literature, surpassing even those equipped with wheels and electric control valves (Fig. 5g). Furthermore, the configuration of the cascade does not necessitate structural modifications to the PHOs but merely a rewiring of the tubes. Theoretically, the number of cascaded PHOs can be arbitrary, and we have successfully demonstrated configurations involving more than two PHOs, as shown in Supplementary Fig. 17 and Supplementary Movie 8.

Phase-tunable untethered swimming

The ability to modulate the phase of robotic oscillators opens up possibilities for more complex motions37, as seen in applications like altering the swimming direction of bionic fish38 or controlling the altitude of flapping-wing aircraft39, which typically rely on microcontrollers. However, non-electric oscillators capable of such phase modulation have been limited. Our design leverages the soft-elastic-rigid hybrid, segmented structure of the PHO to enable phase modulation by differentially adjusting the speed of the active joint’s rotation in clockwise and counterclockwise directions under the same input pressure. Figure 6ai shows the phase-tunable PHO that incorporates an auxiliary beam connected at one end to the passive joint and clamped at a fixed angle γ at the other end. When the main elastic beam deforms, this auxiliary beam applies an additional torque to the passive joint, altering the critical snap-through torque required for movement (Supplementary Note 5, Supplementary Figs. 19, 20, and Supplementary Fig. 18). This setup ensures the positive correlation between the angular displacement of the active joint, chamber pressure, and output torque. By modifying the inflating time of the chambers to reach the critical pressure via adjusted torque, we can effectively influence the rotation speed of the active joint in both directions (Fig. 6Aii, Supplementary Movie 9). Notably, when γ = 90°, the deformation of the auxiliary beam remains symmetric, leading to unbiased oscillations. Conversely, when γ > 90° or γ < 90°, the auxiliary beam exerts different torques on the passive joint as the main beam alternates between upward and downward movements, resulting in an asymmetric oscillation.

Fig. 6: Phase modulation of pneumatic hybrid oscillator (PHO) enables a multi-directional untethered swimming robot.
figure 6

a i: the modulation principle of PHO. ii: the effect of tuning the fixed angle of the auxiliary elastic beam. b Design of the multi-directional swimming robot. A CO2 gas cylinder is integrated to make it untethered. c Direction changing of the swimming robot. d Various motion trajectories under different phase settings.

Full size image

An untethered swimming robot was further designed and fabricated to demonstrate the significance of the phase modulation of the PHO in robotic locomotion (Fig. 6b and Supplementary Fig. 21, Supplementary Movie 10). The robot includes a phase-tunable PHO, a CO2 gas cylinder as the pneumatic source, a fin fixed on the active joint to provide propulsion, and a 3D-printed container to provide buoyancy. Additionally, we enhanced the PHO’s design by incorporating a clamped end on the auxiliary beam, serving as an adjustable knob to fine-tune the robot’s movement direction. Figure 6c illustrates the trajectories of the swimming robot in plane coordinates under five tested cases (γ ranging from \(70^\circ\) to \(110^\circ\)). The swimming robot demonstrated the ability to execute a turn over 180° with a turning radius of only 260 mm (less than 1.5 BL) when γ = 110°, thus demonstrating its capability to navigate tight turns across a complete range from 0° to 180°, showcasing a wide range of multi-directional locomotion. Figure 6d depicts the trajectories of the swimming robot under three different phase modulation conditions. When γ was set to 90°, the robot performs a straight motion while oscillating at a frequency of 2.3 Hz, reaching an average speed of 0.6 BL·s−1, under a pressure of ~50 kPa. The robot then changed its direction to left turn when γ was manually adjusted to 100° and executed a right turn when γ was set to 80°. These two conditions demonstrate oscillation frequencies of 2 Hz, and average swimming speeds of 0.5 BL·s−1. The proposed swimming robot showcases remarkable maneuverability (Supplementary Table 1) and compactness through phase modulation, highlighting the impressive actuation capabilities of the PHO in powering an untethered robotic system.

Discussion

Oscillation is a fundamental actuation method in robotics. The trend towards lightweight, electronics-free, and low-cost pneumatic oscillators is driven by their adaptability and ease of large-scale deployment. Traditional pneumatic oscillators, while diversified, typically suffer from low frequency, limited cascading options, and non-tunable oscillation phases, which restrict their speed and responsiveness.

This work introduces a pneumatic hybrid oscillator (PHO) that addresses these shortcomings (Supplementary Table 2). The PHO features bistable characteristics enabled by a rotating-based beam, with actuation chambers and a switching valve installed at both ends. Its design allows for a wide pressure range (8–180 kPa) and frequency range (0–51 Hz), surpassing previous designs in performance26,29,30,40. This enables the PHO to produce high-speed reciprocal circular motions, making it ideal for robotic systems with jointed movements, achieving over 3 million cycles at stable frequencies. For instance, our bionic kangaroo robot powered by a single PHO reached a speed of 5.1 BL·s−1, setting a new benchmark for pneumatic robot performance9.

Additionally, the PHO’s modular structure facilitates easy adjustment of motion generation and frequency characteristics by modifying the elastic beam without replacing other components. Its capability for sequential cascade oscillation makes it versatile for multi-degree of freedom systems, demonstrated in our serial crawling robots. A feature of the PHO is its phase modulation capability, achieved by incorporating an auxiliary elastic beam, allowing for the actuation of robots with complex motion patterns such as changing swimming trajectories.

The PHO employs a fluid mechanical loop with negative feedback, similar to electronic circuits, allowing us to establish an equivalent circuit model to accurately describe and predict its oscillation characteristics at various pressures. This analogue circuit equivalence helps in understanding the airflow dynamics within the system, facilitating the optimization of its design parameters.

The versatility and performance of the PHO not only enhance robot actuation but also suggest potential applications in digital fluid computation and complex gait control. The PHO can be readily configured as a CMOS-type valve through the pneumatic interface and adapted to form basic logic computing units, capable of performing digital computations at high frequencies. These characteristics underscore the PHO’s potential in advancing the field of fluid-powered high-performance robotics.

Methods

Fabrication of fabric components of PHO

We adopted a split approach to manufacture different components of PHO in terms of the different materials properties. Each actuation chamber was fabricated by a reverse-molding method: first, the polyvinyl alcohol (PVA) mold was 3D printed, where two 3D printed polylactic acid (PLA) rigid plate were attached to its sides; second, the TPU-coated fabric was wrapped around the mold tightly; then, the chamber was formed by welding and the PLA plate was fixed with the fabric surface. The PVA mold was removed by water heating to form an empty inner cavity, and finally, the chamber was further sealed by welding. The fabric tube was fabricated using a hybrid structure with a fabric tube in the middle area and two short PVC tubes with 4 mm outer diameter connected at both ends for the connection with the valve. To reduce the resistance of the valve truncation, the middle diameter of the fabric tube is reduced to form an hourglass shape. The elastic beam is made of carbon fiber material, and the bearings are made of ceramic material. The inner and outer diameters of the silicone tube are 4 mm/3 mm, respectively. The rest of the rigid components were fabricated by UV cured 3D printing, where the diameter of both active and passive joints were 5 mm. Details of the design of each component, along with the schematics of the preparation process and the assembly diagrams are presented in the Supplementary Note 1.

Characterization of the joint motion and oscillation frequency

A high-speed camera (Phantom V1840, Vision Research Inc.) was used to capture the motion of the oscillation of PHO with 1000 FPS. Images were recorded (Supplementary Fig. 22) and processed using the mathematics software MATLAB (2022b). A vision algorithm is developed to identify the characteristic points on both active and passive joints.

Pneumatic measurement and control

The pneumatic system first supplied pressure through an air pump (XD-2J1790X3-100L, HYUNDAI Inc.) and a reducing valve (AW20-02DG-B, SMC Inc.), which was then regulated by a proportional solenoid (ITV1010, SMC Inc.). The actual supply pressure and that at the inlet of the chambers were detected in real-time by two pressure sensors (PSE532, SMC Inc.) and transmitted to a microcontroller (Mega 2560, Arduino Inc.). After the expected pressure was given, PID (proportional, integral, and differential) control was applied to calculate the controlling value which was then processed through a DAC module (DC2376A-A, Analog Devices Inc.) and sent to the solenoid. The pneumatic measurement and control system realizes a rapid and smooth response and keeps a stable pressure during the dynamic oscillation process.

Characterization of the switch valve

A separate valve was fixed to a horizontal optical platform. A motor (DCX16, Maxon Inc.) was connected to the rotating joint of the valve through a coupling. Two pressure sensors (PSE532, SMC Inc.) were used to measure the output pressure of the soft valve. At different input pressures, the angle of the rotating joint is changed to obtain the output pressure of the valve. The input pressure in each test was from 20 to 80 kPa. The effective angle in each test was from −20° to 20°. The motor remained stationary during each test.

Characterization of the fabric chamber

A well-air-tight-chamber was fixed to the optical platform. A force sensor (Mini45, ATI Inc.) fixed upon the end-effector of a six-DoF industrial robot (UR10, Universal Robots Inc.) was used to measure the output force at its distal end. The relationship between the output force and the supply pressure of the chamber under different deployment angles is obtained by adjusting the relative position between the chamber and the force sensor. The supply pressure in each test was from 10 to 60 kPa. The effective angle in each test was from 0° to 80°. The industrial robot remained stationary during each test.

Characterization of the kangaroo-inspired robot

The same high-speed camera (Phantom V1840, Vision Research Inc.) was applied to capture the motion of the kangaroo-inspired robot with 1000 FPS. Images were processed manually to separate different states including pushing, taking off and landing. The moving distance and the velocity of one step, as well as the ground duty cycle ratio were converted and calculated according to the body size of the robot.

Characterization of the cascaded-loop crawling robot

A motion capture system (Prime41, OptiTrack Inc.) was applied to capture the position of the robot. An optical target was glued to the head of the robot. The crawling robot was placed on the horizontal platform coved with curtain fabric to increase the friction, and continued crawling under the constant supply pressure. The supply pressure in each test was from 10 to 120 kPa. The sampling frequency of the system was 120 Hz.

Characterization of the untethered swimming robot

An action camera (GoPro Hero7, GoPro Inc.) was used to capture the motion of the untethered swimming robot in an artificial water tank with 1080 P resolution and 60 FPS. The camera was settled right above the robot, fixed on a cantilever support. A black curtain was laid over the water tank in midair to prevent the reflection of light (Supplementary Fig. 23). The motion trajectories of the swimming robot with different phase modulation were recorded and processed (Fig. 6d and Supplementary Movie 10).