Introduction

The term time crystal refers to a unique state of matter in which a system exhibits spontaneous breaking of its time translation symmetry; this state was initially proposed by Frank Wilczek1. In other words, the time crystal is a phase of matter in which the system’s behavior repeats periodically in time. A time crystal exhibits long-range order in time, whereas conventional crystals exhibit long-range order in space. The state includes discrete and continuous time crystal phases2,3,4,5 that exhibit discrete and continuous time-translation symmetry breaking, respectively. Since the initial proposal, time crystals were first reported in experiments using trapped ions6 and the nitrogen-vacancy centers in diamonds7. There has been considerable progress on both the theoretical8,9,10,11,12,13,14 and experimental fronts in efforts to study and understand time crystals15,16,17,18,19,20,21. Researchers continue to strive to improve the stability22 and the coherence23,24 of time crystals and to probe the equilibrium of quantum matter25. Interestingly, the system comes out of thermal equilibrium dissipation under external driving conditions, and researchers have observed stabilized dissipative time crystals26, prethermal discrete time crystals27,28, and higher-order time crystals29,30.

The large dipole moment of the Rydberg atom provides a good platform for the study of the dynamics of strongly correlated systems. For example, researchers have used Rydberg atoms to probe quantum phase transitions31,32, quantum scars33,34, non-equilibrium phase transitions, and self-organized criticality35,36,37,38,39,40. In traditional equilibrium systems, the second law of thermodynamics dictates that entropy will always increase with time, and this leads to thermal equilibrium and the absence of persistent oscillatory behavior. In the driven and dissipative Rydberg system, however, the external driving force injects energy into the system, while the long-range interactions between the system’s constituents aid in redistributing this energy and thus help to maintain a persistent oscillatory evolution of the Rydberg atom population, and generating dissipative continuous time crystal41. In driven and dissipative Rydberg atoms systems, it is possible to observe some special matter phases, such as ergodic breaking42,43, and the exotic emergence and transition dynamics of distinct continuous time crystals are worthy of study44,45.

In this work, we observe a bifurcation effect for the continuous time crystals in strongly interacting Rydberg atoms under external radio-frequency (RF)-field continuous driving. The bifurcation of time crystals in Rydberg atoms originates from the competition between the excitations of different Floquet sidebands. Coupling between the (multiple) many-body states leads to the formation of distinct time crystals, which subsequently results in the emergence of more complex temporal symmetries beyond the simple discrete-time translation symmetry. We observe the full phase diagram of the system, including multiple distinct time crystal phases with several periodicities and chaotic phases. In addition, we observe phase transitions between the distinct time crystals and the hysteresis loop. Study of the emergence of these distinct time crystals will provide new possibilities for the exploration of the dynamics and control of quantum many-body systems when out of equilibrium.

Results

Physical model and experiment setup

To determine the time translation symmetry-breaking mechanism in driven and dissipative Rydberg atoms, we construct a simplified physical model that considers N interacting two-level atoms with a ground state \(| g\rangle\) and the Rydberg state \(| R\rangle\) (with a decay rate γ) to simulate the observations. A laser couples the atoms with a Rabi frequency Ω and detuning Δ. The Rydberg atoms are affected by the many-body interaction strength V = C6/r6 [where C6 is the van der Waals coefficient and r represents the distance between the Rydberg atoms]. These atoms are exposed to an external RF field with an electric field component ERF and frequency ω. The RF field perturbs the system and induces additional frequencies into the system spectrum, thus leading to the appearance of RF sidebands of the Rydberg states46; see the Supplementary Information for further details. In our model, we consider the  ±1-order sidebands of the Rydberg states as \(| {R}_{1,2}\rangle\) with the corresponding Rabi frequency Ω1,2 and detuning Δ1,2. We use a mean field treatment to simulate multiple periodic oscillations in the Rydberg atom population through master equation in Eq. (1); see the “Methods” section for further details.

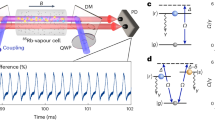
In the experiments, we excite cesium atoms in a thermal vapor to study the features of time crystals. The cesium atom energy level structure and the experimental setup are depicted in Fig. 1a and b, respectively. We use a three-photon electromagnetically induced transparency (EIT) scheme to prepare the Rydberg atoms, as described in the previous study47,48. Specifically, the excitation process involves using an 852 nm probe beam to resonantly drive the transition from state \(| 6{S}_{1/2}\rangle\) to state \(| 6{P}_{3/2}\rangle\) with a Rabi frequency Ωp, a resonant 1470 nm laser with a Rabi frequency Ωd to drive the transition from state \(| 6{P}_{3/2}\rangle\) to state \(| 7{S}_{1/2}\rangle\)), and a 780 nm coupling beam with a Rabi frequency Ωc and detuning Δc to drive the transition from state \(| 7{S}_{1/2}\rangle\) to \(| 49{P}_{3/2}\rangle\). The Rydberg atoms are illuminated by the RF field (the AC stark effect for the atomic state with the low principal quantum number can be ignored in this case). By tuning the system’s parameters, we can observe the distinct continuous time crystals, which exhibit oscillated excitation rates from ground to Rydberg state, as shown in Fig. 1c and d. These are from the limit cycle phase under ergodicity breaking42, manifesting as persistent oscillations in phase space, as described in the physical model section (also predicted in Supplementary Fig. 3f). These oscillations can be persisted for at least a few minutes in the experiment, which is limited by the measurement time of the oscilloscope.

Fig. 1: Energy level diagram and experimental setup for time crystal measurement.
figure 1

a Energy level diagram based on three-photon Rydberg electromagnetically induced transparency (EIT) scheme. γ1, γ2, and γ correspond to the decay rates of states \(\left\vert e\right\rangle\), \(\left\vert m\right\rangle\), and \(\left\vert R\right\rangle\), respectively. The Rydberg state \(\left\vert R\right\rangle\) is divided into Floquet sidebands when atoms are driven by an RF field; three sideband energy levels, \(\left\vert R\right\rangle\), \(\left\vert {R}_{1}\right\rangle\), and \(\left\vert {R}_{2}\right\rangle\) with energy interval ω, are illustrated. b Simplified experimental setup. An RF field is applied to the atoms by two electrodes with a loading frequency ranging from 0 MHz ~ 2π × 30 MHz. c and d Triggered probe transmission within 0.7 ms time interval caused by switching on the RF field [U = 3.8 V], which oscillates with distinct frequencies [f = 2π × 18.1 kHz (c) and f = 2π × 8.3 kHz (d)] obtained by setting Δc = −2π × 24.1 MHz for (c) and Δc = −2π × 32.4 MHz for (d), thus revealing the distinct time crystals. The different colored lines in c and d are from different experimental trials. The dips and peaks of oscillations correspond to the low and high density of excited Rydberg atoms [marked by different numbers of circles in (d)]. e, f Distributions of the Fourier amplitudes with the dominant frequency on the complex plane. In this process, we recorded the probe transmission within the time intervals Δt = 0.7 ms with 300 data points after the RF-field is turned on for e 0.8 ms and f 2.8 ms. The signal in f appears to be noisier than in e because the signal has more low-frequency noise.

Full size image

Figure 1c represents the time crystal of short periodicity (SP) and Fig. 1d represents the time crystal of long periodicity (LP). They are similar time crystals but with different frequencies. The oscillations of the time crystal are at a few to a few tens of kHz. In addition, we present evidence of a random phase distribution in these distinct time crystals. By measuring the dominant frequency peak f in the Fourier spectrum from the repeated trials (see further details in Supplementary Information), we obtain the distribution of the Fourier amplitudes in the complex plane. We performed 45 repeated measurements and a 1 s duration between the nearest measurements. Due to the drift of the peak frequency, we selected the data with the same peak frequency among the 45 sets of data and extracted the phase and amplitude of the oscillations. The phase of the Fourier amplitude A(f) at the dominant frequency f is distributed randomly between 0 and 2π, as shown in Fig. 1e and f, thus indicating spontaneous breaking of the continuous time translation symmetry4.

Phase diagram

To probe the exotic phase in the Rydberg atoms under RF field driving conditions, we measured the system’s phase diagram. The phase diagram provides a comprehensive map of the different phases or states in which the transmission can exist as a function of various parameters, e.g., the coupling detuning Δc, voltage U, and frequency ω of the RF field. We varied the RF field intensity by varying the voltages of the electrodes and measured the probe transmission versus the coupling detuning Δc. Figure 2a shows the color map of the probe transmission when U = 0–10 V and Δc = −2π × 60 MHz–2π × 30 MHz. Figure 2b and c show examples of the probe transmission at U = 5 V and U = 10 V, respectively. We also changed the frequency of the RF field from ω = 0 MHz to ω = 2π × 30 MHz and recorded the probe transmission, with results as shown in Fig. 2d. In the range of oscillation, the oscillation frequency increase versus with ω, which is consistent with the theoretical simulations in Supplementary Fig. 4b. Figure 2e and f show the corresponding results with ω = 2π × 7 MHz and ω = 2π × 28 MHz, respectively.

Fig. 2: Measured phase diagram.
figure 2

Color maps of probe transmission (normalized with respect to their respective maximal values) when scanning Δc and the external RF field voltage U from 0 to 10 V (a), and the external RF field frequency ω from 0 to 2π × 30 MHz (d). Here, the coupling detuning Δc is scanned from Δc = − 2π × 60 MHz to Δc = 2π × 30 MHz. In the oscillating regions in panels a and d, the system is in the time translation symmetry-breaking phase. The color bar ranging from 0 to 1 represents the transmission intensity. b and c correspond to probe transmissions with U = 5 V and U = 10 V, respectively. Here, the RF field is set at ω = 2π × 7.2 MHz. e and f are the probe transmissions with RF field frequencies of ω = 2π  × 7 MHz and ω = 2π × 28 MHz, respectively. The voltage is set U = 2 V. The red arrows shown in e and f indicate sudden jumps in the probe transmission spectrum, which are called non-equilibrium phase transitions. In panels b and e, oscillation behavior occurs in the probe transmission spectrum that corresponds to the non-trivial regime for time translation symmetry breaking.

Full size image

From these results, we found that oscillation effects occurred approximately within the range of U = 0.7 V–U = 9.0 V (Fig. 2a) and ω = 2π × 2 MHz–ω = 2π × 16 MHz (Fig. 2d). These results are also qualitatively predicted by the theories given by Supplementary Fig. 4b and c, in which time crystals appear and then disappear with the increase of parameters δ and Ω1/2. For example, in Fig. 2b, the system response exhibits repetitive back-and-forth motion on probe transmission at around resonance, whereas no oscillation is shown in Fig. 2c. In Fig. 2a, the area of the oscillation covers a large coupling detuning when U = 1 V, but becomes narrower with increasing voltage U. Above U = 9 V, the probe transmission becomes non-oscillatory. The oscillation’s disappearance at high U and high-frequency ω can be attributed to: (i) the high-intensity RF field inducing broadening larger than the shift from the Rydberg atom interactions; and (ii) the RF-field-induced Floquet energy interval (which is proportional to ω) being larger than the shift from the Rydberg atom interactions at high ω. In addition, there are sudden jumps indicated by red arrows in Fig. 2e and f. These jumps are bistability phase transition37, in which the broadening effect induced by the RF field enables facilitated excitation of the Rydberg atoms.

Distinct time crystal phases

To study the characteristics of the time crystal phases in our system, we measured the Fourier spectrum of the oscillated transmission, as shown in Fig. 3a. There are comb-shaped spectra and chaotic spectra distributed in the varied Δc, which are separated within areas A–E. In area A, we see that the first peak (f = f0) of the Fourier spectrum is nearly linear versus the coupling detuning Δc. In area B, the frequency of the time crystal remains stable versus varying Δc; see the peak in Fig. 3b. These dynamics in these two regimes are also predicted qualitatively in Supplementary Fig. 4a in Supplementary Information. Interestingly, the time crystal becomes bifurcated when Δc is increased further. For example, a non-integer multiple of the f0 frequency signals appears in areas C and D. In Fig. 3c and d, there are a series of branches at f = f0/4, f0/2, 3f0/4, 5f0/4, 3f0/2, and 7f0/4 at around f = f0 in the Fourier spectrum. The appearance of multiple time crystals can be also predicted in our theory, they exhibit intertwined trajectories in phase space, see Supplementary Fig. 3 in Supplementary Information.

Fig. 3: Distinct time crystals.
figure 3

a Measured Fourier spectrum versus the coupling detuning Δc. Labels A–E in a indicate the areas that characterize the distinct time crystal phases. The measured responses of several non-integer multiples of f = f0 represent the 'high-order' continuous time crystals relative to the f = f0 time crystal, which are the results of period doubling of f0 peak. The color bar from 0 to 1 represents the Fourier transform intensity. b–e is the corresponding Fourier spectrum at the detuning Δc/2π = −17.4 MHz (b), Δc/2π = −8.9 MHz (c), Δc/2π = −1.3 MHz (d), and Δc/2π = 9.8 MHz (e), respectively. The peaks in Fourier spectra b–d show evidence of distinct periodicity, and e is the measured Fourier spectrum of the chaotic phase. The sideband peaks that appeared close to f0 are from the other small weighted oscillation modes.

Full size image

The emergence of the non-integer multiple of f = f0 frequency signals indicates the transition to a new temporal order. Increasing the coupling detuning from Δc = −2π × 30 MHz to Δc = −2π × 0 MHz adds to the population of Rydberg atoms and thus increases the interactions between the Rydberg atoms. The experimental observation is consistent with the phenomenon of period-doubling bifurcation in classical nonlinear dynamics49. This is due to the fact that the stability of the phase space trajectory changes as the parameter Δc is varied, see Supplementary Fig. 3 in Supplementary Information.

By increasing Δc even further [e.g., to Δc =  2π × 6 MHz], the system enters a chaotic regime in which the time crystals bifurcate further; see the relatively chaotic frequency spectrum in area E. Fig. 3e shows an example of the Fourier spectrum in area E. The bifurcation leads to the formation of additional temporal order patterns and the breakdown of the existing temporal order. This causes the excitation of the Rydberg atoms to be far from synchronized. As a result, the system may show more complex and unpredictable dynamics, along with the emergence of new frequency components and irregular oscillations. By varying the system parameter Δc, we observe the phenomenon of period-doubling bifurcation and the system finally goes to chaos. The phase space trajectory of the system becomes more and more chaotic, which ultimately leads to chaos, i.e., the satisfying of ergodicity. When Δc > 2π × 10 MHz, the system response regains a single frequency oscillation and higher harmonic components as the interactions become weak. In this region, the oscillation frequency varies with respect to the change of Δc, similar to region A.

Phase transition of time crystal

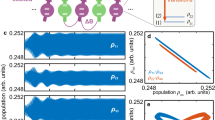
We also measured the response versus the RF field intensity and mapped the phase diagram of the voltage range from 975 to 990 mV (see Fig. 4a), and this diagram illustrates two stable time crystals with different periodicities and the phase transition between them. When the voltage is in the 975 mV < U < 982.5 mV range, the system has a low-frequency time crystal phase. For example, we measured the Fourier spectrum at U = 978.75 mV; there was a low-frequency peak at f = 2π × 19.0 kHz, as shown in Fig. 4b. With increasing voltage U, we found that the onset of the high-frequency time crystal phase appears on exceeding the critical voltage U = 982.5 mV. The low-frequency component in the Fourier spectrum then disappears, and the high-frequency term remains when we increase from U = 975 mV to U = 990 mV; these results are shown in Fig. 4b–d.

Fig. 4: Phase transition between distinct time crystals.
figure 4

a Phase diagram of a voltage range from U = 975 mV to U = 990 mV in a high resolution. The black dashed line represents the modified Heaviside fitting function. The color bar from 0 to 1 represents the Fourier transform intensity. b–d Corresponding Fourier spectra at U = 978.75 mV (b), U = 982.5 mV (c), and U = 986.25 mV (d). The phase diagram includes two temporal periodicities called the LP and the SP, which are separated by the white dashed line. In the SP time-crystal phase, the temporal order is the shorter-range order, which means that the system’s response is repeated periodically over shorter time intervals. In the LP time-crystal phase, however, the system’s response is repeated periodically over longer periods of time.

Full size image

Varying the RF field intensity causes the system’s symmetry to vary, and the probe transmission then shows distinct periodicity. The phase transition represents the system changing from an LP time-crystal into an SP time-crystal. We characterized the scaling of this phase transition using a fitting function; see the dashed line and the description in the caption of Fig. 4a. The modified Heaviside function displays the continuity of the spectrum. This supports a continuous transition from an LP time crystal to an SP time crystal.

Bistability of the time crystal

By scanning the RF field intensity in the forward and backward directions, we observed the bistability of the time crystal; the results are shown in Fig. 5a. Here, in the context of time crystals, bistability refers to the existence of two stable time crystal states or many-body energy levels that the Rydberg system can switch between. The upper panel in Fig. 5a corresponds to the measured phase diagram when the voltage U is increasing, and the lower panel in Fig. 5a shows the phase diagram measured when the voltage U is decreasing. When U is increased gradually, the time crystal phase is stable at a fixed frequency f ~ 2π × 11.64 kHz within the range from U = 3.5 V to U  = 4.2 V. The frequency f corresponds to the largest peak in the spectrum of the system response and represents the dominant frequency component of the system response. Then, the system’s response shows a sudden jump when it crosses the critical point at U = 4.2 V, and the system is then stable in another time crystal phase with a stable frequency of f ~ 2π × 16.93 kHz; see the results shown in Fig. 5b. Similarly, when U is gradually reduced, the time crystal phase switches at another entirely different critical point at U = 3.95 V, as shown by the orange data in Fig. 5b.

Fig. 5: Bistability of time crystal.
figure 5

a Measured phase diagrams with forward scanning from U = 3.5 V to U = 4.5 V and vice versa. b Measured frequency of the dominant peak versus voltage U from (a). The blue data represents the forward scanning case and the orange data corresponds to the backward scanning case. There is a hysteresis loop that indicates the relationship between the voltage U applied to the Rydberg atoms and the resulting dominant peak in the Fourier spectrum of the probe transmission. c Fourier spectra for U = 3.8 V (blue) and U = 4.3 V (orange).

Full size image

The measured critical point voltages U during forward and backward scanning differ because of the dependence of the system on the initial state. This effect is often associated with the presence of non-equilibrium metastable states in the system where the system’s state does not reach a thermodynamic equilibrium. This comes from a non-ergodic effect42 and is also related to the hysteresis effect seen in refs. 36,37. This results in a delayed response in the RF field. This response lag leads to hysteresis and loop formation, as shown in Fig. 5b. Figure 5c illustrates the measured Fourier spectra of these two distinct time crystals.

Discussion

The observed time crystals are characterized using their nontrivial temporal orders, which represent the non-equilibrium persistent oscillations of the excited Rydberg atom population. There are no previous experimental reports observing the bifurcation effect of time crystals. The multiple time crystals and the bistability observed here open up avenues to study non-equilibrium physics with dependence on distinct temporal orders. Furthermore, the existence of multiple stable time crystal phases signifies a rich and diverse landscape for time crystal behavior2,3,4,5. In addition, the RF field-driving technique plays an important role in creating more RF bands for the Rydberg state, thus providing a versatile method to obtain controllable many-body states.

Another interesting point is that the system transits from the time crystal phase to a chaotic phase during scanning of the voltage U, as depicted in area E in Fig. 3a or e. The irregular frequency distribution in Fig. 3e shows disordered properties that correspond to weak time translation symmetry breaking that results from imperfections in the orderly arrangement. We have simulated a nonlinear system using competitive interactions between Rydberg atoms and observed the phenomenon of period-doubling bifurcation. The period-doubling bifurcation that we observe experimentally is a common phenomenon in nonlinear dynamics and an important path to chaos. Further study will allow us to deepen our understanding of complex systems as well as chaotic phenomena. Meanwhile, we can also use Rydberg atoms as a platform for simulating nonlinear dynamics to study nonlinear problems.

The distinct heights of the peaks in the Fourier spectrum (Figs. 3c and 4b) indicate that more than one-time crystal exists under the same physical conditions in the system. This shows that the system could have multiple modes of time crystals. Because of the change in the interactions between the Rydberg atoms caused by Δc, it becomes possible to manipulate the system’s ground state to be the coexistence of multiple time crystals with distinct f. This finding may be helpful in the study of the competition and time-dependence of many-body states.

In summary, we have demonstrated the bifurcation of time crystals in strongly interacting Rydberg atoms driven by an external RF field. Through this RF field-driving approach, we were able to observe the intriguing symmetry-breaking behavior of the time translation in Rydberg atoms. We observed multiple stable time crystals beyond the single time crystal within different coupling detuning ranges. By manipulating the RF field parameters, we observed a continuous phase transition from an LP state to an SP state and discovered the bistability of the time crystal, which manifested as a hysteresis loop. The bifurcation of the time crystal in strongly interacting Rydberg atoms is attributed to the emergence of more complex temporal symmetries beyond the simple discrete time translation symmetry. Our work represents a milestone in understanding of the field of non-equilibrium transitions, and particularly with respect to the progression from a single time crystal phase to multiple distinct phases with different temporal symmetries.

Note: While finishing this manuscript we became aware of a related work of reporting a phase transition from a continuous to a discrete time crystal (ref. 44), and a related work (ref. 45) observing time crystal comb.

Methods

Experimental setup

The experimental details are depicted in Supplementary Fig. 1a. In the experiments, we used the three-photon scheme to excite the Rydberg atoms. The 852 nm external-cavity diode laser (ECDL) was locked by using the saturated absorption spectrum (SAS) as a frequency reference signal. Another ECDL at 1470 nm was locked by using the two-photon spectrum (TPS) as a frequency reference signal. The 780 nm ECDL was amplified using a tapered amplifier (TA) as a coupling laser. The probe laser is divided into two beams, where one beam serves as a reference, and the other beam propagates in the opposite direction to the dressing laser and coupling laser beams. We used the arbitrary function generator (AFG) to generate the RF field and apply it to the electrodes. The probe transmission was recorded using the oscilloscope after the signal passed through the photoelectric detector (PD). To scan the external parameters and thus obtain the phase diagram of the system response, the coupling laser, the oscilloscope, and the AFG were all connected to a computer and controlled together.

The probe light passes through a 7-cm vapor cell in parallel with the reference light, and the dressing light and the coupling light propagate backward from the probe light. The probe light is focused into the cell (1/e2-waist radius of approximately 200 μm) with a probe intensity of 64 μW. The dressing and coupling light are focused into the cell (1/e2-waist radius of approximately 500 μm) and the powers are 16.8 mW and 1.5 W, respectively. The Rabi frequencies of the probe light, dressing light, and coupling light are respectively Ωp = 2π × 35 MHz, Ωd = 2π × 235 MHz and Ωc = 2π × 4.3 MHz. A pair of circular copper plates with a thickness of 3 mm and a diameter of Φ = 120 mm were used in the experiment. The separation between the plates was adjusted to 40 mm and the Cesium cell was placed in the center of the plates.

Mean-field theory description

In our model, we consider N interacting four-level atoms with a ground state ∣g〉 and the Rydberg states ∣R〉, ∣R1〉, and ∣R2〉 (all with an equal decay rate γ). Here, a mean-field treatment was introduced to simulate the results. The system’s master equation is based on the multi Rydberg-state model41:

$${\partial }_{t}\hat{\rho }=i[\hat{H},\hat{\rho }]+{{{{\mathcal{L}}}}}_{R}[\hat{\rho }]+{{{{\mathcal{L}}}}}_{{R}_{1}}[\hat{\rho }]+{{{{\mathcal{L}}}}}_{{R}_{2}}[\hat{\rho }]$$
(1)

where \(\hat{H}\) is the Hamiltonian and \({{{{\mathcal{L}}}}}_{\{R,{R}_{1},{R}_{2}\}}\) is the Lindblad jump operator. The Hamiltonian of the system is

$$\hat{H}= \frac{1}{2}{\sum }_{i}\left(\Omega {\sigma }_{i}^{gR}+{\Omega }_{1}{\sigma }_{i}^{g{R}_{1}}+{\Omega }_{2}{\sigma }_{i}^{g{R}_{2}}+{{h.c.}}\right)\\ -{\sum }_{i}\left(\Delta {n}_{i}^{R}+{\Delta }_{1}{n}_{i}^{{R}_{1}}+{\Delta }_{2}{n}_{i}^{{R}_{2}}\right)\\ +{\sum }_{i\ne j}\left[{V}_{ij}^{R{R}_{1}}{n}_{i}^{R}{n}_{j}^{{R}_{1}}+{V}_{ij}^{R{R}_{2}}{n}_{i}^{R}{n}_{j}^{{R}_{2}}+{V}_{ij}^{{R}_{1}{R}_{2}}{n}_{i}^{{R}_{1}}{n}_{j}^{{R}_{2}}\right.\\ \left.+\frac{1}{2}({V}_{ij}^{RR}{n}_{i}^{R}{n}_{j}^{R}+{V}_{ij}^{{R}_{1}{R}_{1}}{n}_{i}^{{R}_{1}}{n}_{j}^{{R}_{1}}+{V}_{ij}^{{R}_{2}{R}_{2}}{n}_{i}^{{R}_{2}}{n}_{j}^{{R}_{2}})\right]$$
(2)

where \({\sigma }_{i}^{gr}\) (r = R, R1, R2) represents the ith atom transition between the ground state \(| g\rangle\) and the Rydberg state \(| r\rangle\), \({n}_{i}^{R,{R}_{1},{R}_{2}}\) are the population operators of the Rydberg energy levels \(| R\rangle\) and \(| {R}_{1}\rangle\), and \(| {R}_{2}\rangle\), and \({V}_{ij}^{R{R}_{1}}\), \({V}_{ij}^{R{R}_{2}}\), and \({V}_{ij}^{{R}_{1}{R}_{2}}\) are the interactions between the Rydberg atoms in states \(| R\rangle\), \(| {R}_{1}\rangle\), and \(| {R}_{2}\rangle\), respectively.

The Lindblad jump terms are given by

$${{{{\mathcal{L}}}}}_{r}=({\gamma }_{r}/2){\sum}_{i}({\hat{\sigma }}_{i}^{rg}\hat{\rho }{\hat{\sigma }}_{i}^{gr}-\{{\hat{n}}_{i}^{r},\hat{\rho }\}),$$
(3)

which represents the decay process from the Rydberg state \(| r\rangle\) (r = R, R1, R2) to the ground state \(| g\rangle\).

In the mean-field treatment, we obtained the following equations:

$${\dot{\rho }}_{{{{\rm{RR}}}}}=i\frac{\Omega }{2}\left({\rho }_{gR}-{\rho }_{Rg}\right)-\gamma {\rho }_{{{{\rm{RR}}}}},$$
(4)
$${\dot{\rho }}_{{{{{\rm{R}}}}}_{1}{{{{\rm{R}}}}}_{1}}=i\frac{{\Omega }_{1}}{2}\left({\rho }_{g{R}_{1}}-{\rho }_{{R}_{1}g}\right)-\gamma {\rho }_{{{{{\rm{R}}}}}_{1}{{{{\rm{R}}}}}_{1}},$$
(5)
$${\dot{\rho }}_{{{{{\rm{R}}}}}_{2}{{{{\rm{R}}}}}_{2}}=i\frac{{\Omega }_{2}}{2}\left({\rho }_{g{R}_{2}}-{\rho }_{{R}_{2}g}\right)-\gamma {\rho }_{{{{{\rm{R}}}}}_{2}{{{{\rm{R}}}}}_{2}},$$
(6)
$$\begin{array}{rcl}{\dot{\rho }}_{gR}&=&i\frac{\Omega }{2}\left(2{\rho }_{{{{\rm{RR}}}}}+{\rho }_{{{{{\rm{R}}}}}_{1}{{{{\rm{R}}}}}_{1}}+{\rho }_{{{{{\rm{R}}}}}_{2}{{{{\rm{R}}}}}_{2}}-1\right)+i\frac{{\Omega }_{1}}{2}{\rho }_{{R}_{1}R}\\ &&+i\frac{{\Omega }_{2}}{2}{\rho }_{{R}_{2}R}+i\left(\Delta -{\Delta }_{int}+i\frac{\gamma }{2}\right){\rho }_{gR},\end{array}$$
(7)
$$\begin{array}{rcl}{\dot{\rho }}_{g{R}_{1}}&=&i\frac{{\Omega }_{1}}{2}\left(2{\rho }_{{{{{\rm{R}}}}}_{1}{{{{\rm{R}}}}}_{1}}+{\rho }_{{{{\rm{RR}}}}}+{\rho }_{{{{{\rm{R}}}}}_{2}{{{{\rm{R}}}}}_{2}}-1\right)+i\frac{\Omega }{2}{\rho }_{R{R}_{1}}\\ &&+i\frac{{\Omega }_{2}}{2}{\rho }_{{R}_{2}{R}_{1}}+i\left({\Delta }_{1}-{\Delta }_{int}+i\frac{\gamma }{2}\right){\rho }_{g{R}_{1}},\end{array}$$
(8)
$$\begin{array}{rcl}{\dot{\rho }}_{g{R}_{2}}&=&i\frac{{\Omega }_{2}}{2}\left(2{\rho }_{{{{{\rm{R}}}}}_{2}{{{{\rm{R}}}}}_{2}}+{\rho }_{{{{{\rm{R}}}}}_{1}{{{{\rm{R}}}}}_{1}}+{\rho }_{{{{\rm{RR}}}}}-1\right)+i\frac{{\Omega }_{1}}{2}{\rho }_{{R}_{1}{R}_{2}}\\ &&+i\frac{{\Omega }_{1}}{2}{\rho }_{{R}_{1}{R}_{2}}+i\left({\Delta }_{2}-{\Delta }_{int}+i\frac{\gamma }{2}\right){\rho }_{g{R}_{2}},\end{array}$$
(9)
$${\dot{\rho }}_{R{R}_{1}}=i\left(\frac{{\Omega }_{1}}{2}{\rho }_{g{R}_{1}}-\frac{{\Omega }_{1}}{2}{\rho }_{Rg}\right)-i\left(\Delta -{\Delta }_{1}-i\gamma \right){\rho }_{R{R}_{1}},$$
(10)
$${\dot{\rho }}_{R{R}_{2}}=i\left(\frac{{\Omega }_{2}}{2}{\rho }_{g{R}_{2}}-\frac{{\Omega }_{2}}{2}{\rho }_{Rg}\right)-i\left(\Delta -{\Delta }_{2}-i\gamma \right){\rho }_{R{R}_{2}},$$
(11)
$${\dot{\rho }}_{{R}_{1}{R}_{2}}=i\left(\frac{{\Omega }_{1}}{2}{\rho }_{g{R}_{2}}-\frac{{\Omega }_{2}}{2}{\rho }_{{R}_{1}g}\right)-i\left({\Delta }_{1}-{\Delta }_{2}-i\gamma \right){\rho }_{{R}_{1}{R}_{2}},$$
(12)

where Δ1 = Δ−δ, Δ2 = Δ + δ, \({\Delta }_{int}=\xi ({\rho }_{{{{\rm{RR}}}}}+{\rho }_{{{{{\rm{R}}}}}_{1}{{{{\rm{R}}}}}_{1}}+{\rho }_{{{{{\rm{R}}}}}_{2}{{{{\rm{R}}}}}_{2}})\) is the interaction-induced shift, and ξ is the interaction coefficient. The δ is the energy spacing between the Rydberg states in the theoretical model. It corresponds to the frequency of the RF in the experimental system. According to Floquet's theory introduced in the “Methods” section, RF induces equally spaced sidebands in the Rydberg levels, so δ = ω. In this way, we can calculate the system’s dynamics within the limit cycle regime.