Introduction

Quantum spin liquids (QSLs) are exotic topological quantum matter that transcend the traditional framework of Landau’s symmetry-breaking theory. Beyond the absence of zero-temperature order, QSLs are positively characterized by fractionalized degrees of freedom and associated emergent gauge fields that globally constrain the dynamics of these fractionalized particles1,2,3,4,5,6,7,8,9. With the discovery of the exactly solvable QSLs in Kitaev honeycomb model3,10, recent years have seen significant efforts towards theoretically understanding and experimentally searching for novel QSL phases in candidate Kitaev materials due to spin-orbital coupling11. Experimental focus has primarily been on the iridate magnetic insulators A2IrO3 (A = Na, Li and Cu)12,13,14,15,16 and α-RuCl317,18,19,20. Recently, Na3Ni2BiO621, Na2Co2TeO622,23,24,25,26 and YbOCl27,28 have emerged as promising candidates hosting antiferromagnetic Kitaev interactions, thereby broadening the scope of research in the quest for QSLs.

The integrable Kitaev honeycomb model is known to harbor a Dirac QSL in the fractionalized quantum sector of Majorana fermions, which becomes a chiral spin liquid (CSL) under time-reversal-breaking perturbation. Remarkably, beyond the Dirac and CSL phases, recent numerical studies have unveiled a novel gapless phase emerging from antiferromagnetic Kitaev honeycomb model under moderate magnetic field29,30,31, which is experimentally relevant as QSL phases in candidate materials like Na3Ni2BiO6, Na2Co2TeO6 and YbOCl are often stabilized under moderate magnetic fields. Despite lots of numerical efforts to understand this intermediate gapless phase (IGP)30,32,33,34,35,36,37,38,39,40, the mechanism underlying its emergence, as well as the nature of its fractionalization and emergent gauge structure, remain elusive and subject to ongoing debate. Inspired by recent numerical studies revealing the importance of fluctuations of \({{\mathbb{Z}}}_{2}\) fluxes in the formation of the IGP38,40, we develop a mean-field ansatz for the emergence of a Majorana metallic phase from the gapped CSL phase due to the field-induced proliferation of \({{\mathbb{Z}}}_{2}\) fluxes. In contrast to the thermal Majorana metal induced by thermal fluctuations as discussed in previous literature41, in our model, it is the quantum fluctuations stemming from the hybridization of fluxes and Majoranas that leads to the quantum phase transition from a CSL to a quantum Majorana metal. Specifically, we analyze the entanglement between itinerant Majorana fermions and localized \({{\mathbb{Z}}}_{2}\) fluxes in the IGP and show the following: (1) In the background of fluctuating \({{\mathbb{Z}}}_{2}\) fluxes, the massive Majorana fermions of the gapped CSL become metallic in the IGP [Fig. 1], and the low-energy fractionalized Majorana fermions couple to \({{\mathbb{Z}}}_{2}\) gauge fields instead of complex fermions with U(1) gauge fields. (2) The emergent Majorana metal has a finite “Fermi surface” (FS) at zero energy which evolves as a function of the magnetic field in the IGP. (3) The dynamical spectral functions of two- and four-spin correlators decomposed in terms of multi-Majorana correlators in the background of fluctuating fluxes are found to agree well with the results by iPEPS obtained with fine energy-momentum resolution. Although our argument is based on the specific model, it demonstrates a novel and general mechanism for the formation of a \({{\mathbb{Z}}}_{2}\) neutral FS in chiral QSLs. The existence and the nature of the emergent IGP as a \({{\mathbb{Z}}}_{2}\) Majorana metal at zero temperature establish a new class of gapless QSLs alongside those commonly recognized, such as U(1) Dirac QSLs and U(1) spinon Fermi surfaces in prevailing theories. It is hence significant not only theoretically but also in relation to experimental observations of gapless quantum spin liquids.

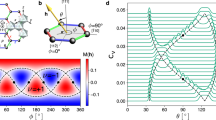
Fig. 1: Emergence of the Majorana metal from the chiral spin liquid (CSL) under moderate magnetic fields at a critical field hc1 = 0.45J.
figure 1

The first row depicts a schematic of the CSL and Majorana metal phases, where the dots in the left plot represent boundary chiral Majorana modes while the Gaussian-like wavepackets in the right plot indicate Majorana zero modes trapped at π-fluxes. The second row shows our results for their respective bulk density of states (DOS) under periodic boundary conditions. The two DOS are calculated from the Majorana-hopping models, one without sign disorder (\({\overline{W}}_{p}=1\), left) and the other with (\({\overline{W}}_{p}=0.05\), right). In both cases we used λ = 0.25J for next neighbor hopping in the Majorana hopping model.

Full size image

Results

Field-induced Majorana metal

We begin with the isotropic Kitaev model on a honeycomb lattice, with a magnetic field applied normal to the honeycomb plane:

$$H={\sum}_{{\langle ij\rangle }_{\alpha }}J{\sigma }_{i}^{\alpha }{\sigma }_{j}^{\alpha }-h{\sum}_{i,\alpha }{\sigma }_{i}^{\alpha },\,\,\alpha \in \{x,y,z\}$$
(1)

where ‹ij›α denotes nearest-neighbor sites on an α-type bond. We show that under a moderate magnetic field normal to the honeycomb plane, the gapped chiral spin liquid (CSL) phase of the Kitaev honeycomb model transitions to the IGP, described as a neutral bulk superconducting Majorana metal with a finite FS at zero energy.

Equation (1) with h = 0 can be exactly solved by fractionalizing the spin into two distinct quantum sectors: the gapless Dirac Majorana fermions and the gapped \({{\mathbb{Z}}}_{2}\) fluxes3. The corresponding ground state has been shown to have no flux and accommodates only the Dirac Majorana fermions42. In the regime of weak magnetic fields, small perturbations do not close the gap (~0.26J) of the \({{\mathbb{Z}}}_{2}\) flux excitation, and thus the \({{\mathbb{Z}}}_{2}\) flux sector is still dominated by the vacuum state \({\left\vert {{{\mathcal{F}}}}\right\rangle }_{0}\) with no flux excitation. A third-order perturbation provides the Hamiltonian \({H}_{{{{\mathcal{M}}}}}=\left\langle {{{{\mathcal{F}}}}}_{0}\right\vert H\left\vert {{{{\mathcal{F}}}}}_{0}\right\rangle\) in the Majorana sector:

$${H}_{{{{\mathcal{M}}}}}={\sum}_{j,k}i{t}_{jk}{c}_{j}{c}_{k}+\,{\mbox{H.c.}}\,,$$
(2)

where tjk = Jujk for nearest-neighbor hoppings; and tjk = λujlulk for anti-clockwise next-nearest-neighbor (NNN) hoppings inside hexagons, with λ ∝ h3 being the leading-order perturbation coefficient. \({u}_{jk}\equiv \left\langle {{{{\mathcal{F}}}}}_{0}\right\vert {\hat{u}}_{ij}\left\vert {{{{\mathcal{F}}}}}_{0}\right\rangle\) in Eq. (2) is the expectation value of the Z2 vector gauge potential \({\hat{u}}_{jk}\) defined on the bond connecting sites j and k. The gauge invariant flux operator corresponding to the flux excitation is the product of six link operators \({\hat{u}}_{jk}\) that belong to a hexagon, i.e., The flux-free vacuum state has \(\left\langle {{{{\mathcal{F}}}}}_{0}\right\vert {\hat{W}}_{p}\left\vert {{{{\mathcal{F}}}}}_{0}\right\rangle=+ 1\) for every hexagon. Since the ground state of the model is flux-free42, and \({\hat{u}}_{jk}\) is a good quantum number in Eq. (2), we can choose the gauge to be ujk = 1 for every bond for the ground state. This Majorana-hopping model captures the gapped CSL phase characterized by a nonzero Chern number in Majorana bands. As the field strength increases to a moderate level, there is a phase transition to an IGP based on our previous simulations29,30, where the simple free Majorana model no longer applies.

We discuss below the mechanism by which the IGP emerges under moderate field, largely from the interplay between flux fluctuations and the Majorana Chern band. We start by establishing a suitable mean-field ansatz that captures the essence of the many-body tensor network representation40 within a quasi-particle picture. Since the Majoranas and Z2 fluxes form a complete basis for the Hilbert space, we can write an ansatz for IGP:

$$\left\vert {\Psi }_{{{{\rm{IGP}}}}}\right\rangle={\sum}_{{{{\mathcal{F}}}}}{\psi }_{{{{\mathcal{F}}}}}\left\vert {{{\mathcal{F}}}}\right\rangle \otimes \left\vert {{{{\mathcal{M}}}}}_{{{{\mathcal{F}}}}}\right\rangle,$$
(3)

where \(\left\vert {{{\mathcal{F}}}}\right\rangle\) denotes a state that corresponds to a disordered flux configuration on the honeycomb lattice; \(\left\vert {{{{\mathcal{M}}}}}_{{{{\mathcal{F}}}}}\right\rangle\) denotes the Majorana state conditioned on the flux configuration; and \({\psi }_{{{{\mathcal{F}}}}}\) a complex scalar conditioned on \({{{\mathcal{F}}}}\). Once we average over all the flux configurations \(\left\vert {{{\mathcal{F}}}}\right\rangle\) we recover a translationally invariant \(\left\vert {\Psi }_{{{{\rm{IGP}}}}}\right\rangle\). This is because all flux patterns obtained by translating \(\left\vert {{{\mathcal{F}}}}\right\rangle\) appear in the linear combinations with the same coefficient. We propose that \(\left\vert {{{{\mathcal{M}}}}}_{{{{\mathcal{F}}}}}\right\rangle\) is the ground state of \({H}_{{{{\mathcal{M}}}}}=\left\langle {{{\mathcal{F}}}}\right\vert H\left\vert {{{\mathcal{F}}}}\right\rangle\), and \({H}_{{{{\mathcal{M}}}}}\) is given by Eq. (2) with sign-disorder in uij. We note that the ansatz in Eq. (3) is distinct from existing microscopic MFTs that attempt to explain the origin of the IGP in moderate fields by solving self-consistent equations of quadratic partons43,44, which fall short in representing the entanglement between the two fractionalized quantum sectors, and in representing a flux as a physical degree of freedom with many-body entanglement among the six \({\hat{u}}_{ij}\)’s of a hexagon. More justifications for our ansatz can be found in Supplementary Information (SI).

To understand the origin of the sign disorder in uij, we trace out the flux sector and get the density matrix of Majorana:

$${\rho }_{{{{\mathcal{M}}}}}={{{{\rm{Tr}}}}}_{{{{\mathcal{F}}}}}\left\vert {\Psi }_{{{{\rm{IGP}}}}}\right\rangle \left\langle {\Psi }_{{{{\rm{IGP}}}}}\right\vert={\sum}_{\{{{{\mathcal{F}}}}\}}| {\psi }_{{{{\mathcal{F}}}}}{| }^{2}\left\vert {{{{\mathcal{M}}}}}_{{{{\mathcal{F}}}}}\right\rangle \left\langle {{{{\mathcal{M}}}}}_{{{{\mathcal{F}}}}}\right\vert .$$
(4)

Unlike the CSL phase, the flux fluctuation is significant in IGP and \(| {\psi }_{{{{\mathcal{F}}}}}{| }^{2}\) is typically nonzero because of the presence of a large number of plaquette fluxes. We assume the flux sector has slow dynamics in the IGP regime according to recent numerical results38, so that for a given flux configuration \(\left\vert {{{\mathcal{F}}}}\right\rangle\), \({H}_{{{{\mathcal{M}}}}}\) is determined by the Eq. (2) with \(\{{u}_{ij}=\left\langle {{{\mathcal{F}}}}\right\vert {\hat{u}}_{ij}\left\vert {{{\mathcal{F}}}}\right\rangle \}\). \({H}_{{{{\mathcal{M}}}}}\)’s conditioned on different flux configurations form an ensemble. We emphasize that configurations {uij} related by gauge transformations are physically equivalent, as they produce identical flux patterns, ensuring that all physical quantities remain unchanged. By sampling the gauge fields uij, we include these slow gauge fluctuations as “flux disorder" seen by the Majorana sector; after averaging over all random flux patterns in the ensemble, translation symmetry is recovered, and we then obtain the momentum-resolved spectral function for the Majorana sector.

The strength of the external field enters \({H}_{{{{\mathcal{M}}}}}\) by determining the strength of NNN hopping λ and affecting the density of the π-fluxes given by {uij}. We define the ensemble average of the flux to be \({\overline{W}}_{p}\equiv {\sum }_{{{{\mathcal{F}}}}}| {\psi }_{{{{\mathcal{F}}}}}{| }^{2}{W}_{p}^{{{{\mathcal{F}}}}}\) with . is the number of hexagons in the system. Since a stronger magnetic field can induce a higher density of π-fluxes, \({\overline{W}}_{p}\) decreases as the external magnetic field increases. Therefore, for stronger magnetic field, we have an ensemble of \({H}_{{{{\mathcal{M}}}}}\) with smaller \({\overline{W}}_{p}\) within the IGP phase. Given the translation symmetry and the three-fold rotation symmetry of our ansatz \(|\Psi_{\rm IGP}\rangle\), the expectation of uij and Wp should be identical on each bond and within each hexagon respectively, i.e., each uij and Wp have the same probability to flip. For this reason, we implement the sign disorder in the gauge fields by randomly flipping each ujk independently with a given probability. Note that similar implementation has been used to study the thermal Majorana metal phase at high temperatures in Kitaev’s honeycomb model, yielding results that align perfectly with quantum Monte Carlo simulations45. In our implementation of sign disorders, \({W}_{p}^{{{{\mathcal{F}}}}}\) of the ensemble \(\{\left\vert {{{\mathcal{F}}}}\right\rangle \}\) follows a Gaussian-like distribution with the mean \({\overline{W}}_{p}\) due to the central limit theorem; for details see SI. Our analysis of the Majorana spectrum from Eq. (2) upon ensemble averaging reveals an entrance into a gapless Majorana metal from a gapped CSL, as illustrated in Fig. 1. While we have utilized a specific scheme to generate the emergent flux disorder, we emphasize that the emergence of the gapless Majorana metal phase does not rely on the specific distribution. Another way to generate flux disorders is discussed in SI to support this point. The underlying mechanism is more general, as we discuss below.

To understand the transition in the MFT, we first remind that Eq. (2) with uij = 1 for all bonds is equivalent to a p + ip topological superconductor, as detailed in SI, in which a π-flux traps a Majorana zero mode (MZM). When the flux density is large enough such that the average separation between two fluxes is comparable to the localization length of the MZMs, then the MZMs can tunnel from one trapped location to the next and form a band around zero energy. Besides the obvious nonzero density of states (DOS) at zero energy shown in Fig. 1, we also obtain the DOS as a function of low energies shown in Fig. 2a, exhibiting a \({{{\rm{\ln }}}}|E|\) scaling as expected for a Majorana metal40,46,47,48. Since a larger gap in the CSL phase results in a smaller localization length for MZMs, we expect that a larger field will be required to enter the IGP, see SI.

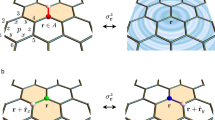
Fig. 2: Nature of intermediate gapless phase (IGP).
figure 2

a The DOS in the Majorana metal shows a logarithmic scaling behavior explaining the origin of states at zero energy. The data are obtained for a system with λ = 0.25, 80 × 80 unit cells, averaging over 20 samples with \({\overline{W}}_{p}=0.05\). b Schematic illustration of a minigap opening due to scattering between Majorana Bloch states induced by fluctuating flux disorder. c The spectral function (averaged over 50 samples) of itinerant Majoranas is shown along a high symmetry cut for the IGP, which matches well with iPEPS results for spin-spin correlations, S1(k, ω), displayed in d. The white dashed lines in c and d are eye-guiding lines that emphasize the shape of the spectra and the presence of the gap.

Full size image

While one can understand the gapless nature of IGP from the flux-induced proliferation of MZM and the \(\ln\!|E|\) scaling of DOS near zero energy, to establish that the IGP is indeed metallic with delocalized states, we analyze the scaling of the inverse participation ratio (IPR). The IPR analysis further reveals the multifractal nature of the zero energy states, and from the behavior at large system size we establish the extended nature of these states, in spite of the presence of flux disorder; see SI.

Our results are consistent with the fact that the random Majorana-hopping models of class D are known to exhibit three distinct phases: a topological insulator, a trivial insulator, and a gapless metal phase dubbed as Majorana metal. The topological insulator phase corresponds to the CSL phase of the Kitaev honeycomb model, where the band of Majorana fermions possesses a nonzero Chern number. In this work, we identify the IGP in the Kitaev honeycomb model under a moderate magnetic field as a quantum Majorana metal phase at zero temperature. The entrance into the Majorana metal phase from the CSL phase can be understood from another useful perspective: The states in the Majorana sector of the CSL phase can be scattered by the fluctuations of the flux configurations between states with different momenta. This results in a mini-gap, as schematically depicted in Fig. 2b around ω ~ 2J, pushing down the states at lower energy and lifting up the states at higher energy, as seen in MFT and also validated by iPEPS data shown in Fig. 2c, d. In the absence of flux disorder, the band bottom is pinned at ω = 2J at the M point for large fields h; see SI. This is because increasing h enhances the second-nearest-neighbor hopping λ ∝ h3 which increases the gap at the K point, leaving the energy unchanged at the M point. Consequently, under a sufficiently strong magnetic field, the band bottom remains at M at ω = 2J, where a minigap forms in the IGP phase. This picture helps us understand the momentum-resolved spectral function and dynamical structures at low energy for the IGP as discussed below.

Spin dynamics

We start by writing the time-dependent spin-spin correlations in terms of the Majorana and flux states,

$$\langle {{{{\boldsymbol{\sigma }}}}}_{i}(t)\cdot {{{{\boldsymbol{\sigma }}}}}_{j}(0)\rangle \sim {\langle \left\langle {{{{\mathcal{M}}}}}_{{{{\mathcal{F}}}}}\right\vert {c}_{i}(t){c}_{j}\left\vert {{{{\mathcal{M}}}}}_{{{{\mathcal{F}}}}}\right\rangle \rangle }_{{{{\mathcal{F}}}}},$$
(5)

of which the Fourier transformation is denoted as S1(k, ω). On the left-hand side \(\langle \bullet \rangle \equiv \left\langle {\Psi }_{{{{\rm{IGP}}}}}\right\vert \bullet \left\vert {\Psi }_{{{{\rm{IGP}}}}}\right\rangle\), on the right side the outer bracket denotes disorder average over flux configurations. We apply the ansatz in Eq. (3) assuming the flux dynamics is much slower than the Majorana dynamics38. Hence the dynamical spin spectrum is determined primarily by Majorana fermions in the diagonal sector (see SI). For i, j belonging to the same sublattice of the honeycomb lattice, the Fourier transform of \({\langle \left\langle {{{{\mathcal{M}}}}}_{{{{\mathcal{F}}}}}\right\vert {c}_{i}(t){c}_{j}\left\vert {{{{\mathcal{M}}}}}_{{{{\mathcal{F}}}}}\right\rangle \rangle }_{{{{\mathcal{F}}}}}\) gives the average of single-particle Majorana spectrum over all flux configurations (see SI), providing distinct features of the emergent Majorana FS.

We now test Eq. (5) by comparing the single-particle Majorana spectrum to the spin-flip dynamics obtained by iPEPS. The Majorana spectral function is computed by:

$$A({{{{\bf{r}}}}}_{1},{{{{\bf{r}}}}}_{2},\omega )={\sum}_{n}{{{{\rm{Tr}}}}}_{{{{\rm{cell}}}}}{\phi }_{n}({{{{\bf{r}}}}}_{1}){\phi }_{n}^{*}({{{{\bf{r}}}}}_{2})\delta (\omega -{E}_{n})$$
(6)

where ϕn(r) = 〈r∣n〉, with \(\left\vert n\right\rangle\) being an eigenstate of \({H}_{{{{\mathcal{M}}}}}\). Note that \({{{{\rm{Tr}}}}}_{{{{\rm{cell}}}}}\) is the trace of intracell degrees of freedom, which corresponds to the sum of intra-sublattice correlations whose momentum-space representation is periodic within the first Brillouin zone (BZ). Since the ground state of IGP is translation invariant, all flux configurations in the ansatz should form a representation of the translation symmetry. Therefore, there is a well-defined momentum resolved spectral function A(k, ω) that is the center-of-mass average of A(r1, r2, ω). This center-of-mass average is equivalent to an average over flux configurations connected by translations, within the average over all flux configurations. As all the Bloch eigenstates in the clean limit form an orthonormal basis, we expand eigenstates of a disordered system into \(\left\vert n\right\rangle={\sum }_{\alpha {{{\bf{k}}}}}{c}_{\alpha {{{\bf{k}}}}}^{n}\left\vert \alpha {{{\bf{k}}}}\right\rangle\), where α is the band index and k the momentum of the Bloch states. Substituting this into Eq. (6) and averaging over center-of-mass R = (r1 + r2)/2, we have

$${\langle A({{{\bf{r}}}},{{{\bf{R}}}},\omega )\rangle }_{{{{\bf{R}}}}}=\frac{1}{N}{\sum}_{n\alpha {{{\bf{k}}}}}{e}^{i{{{\bf{k}}}}\cdot {{{\bf{r}}}}}{\left\vert {c}_{\alpha {{{\bf{k}}}}}^{n}\right\vert }^{2}\delta (\omega -{E}_{n}),$$
(7)

where r = r1 − r2. After a Fourier transformation, one can get the spectral function in momentum space:

$$A({{{\bf{k}}}},\omega )={\sum}_{n\alpha }{\left\vert {c}_{\alpha {{{\bf{k}}}}}^{n}\right\vert }^{2}\delta (\omega -{E}_{n}).$$
(8)

Next, we average Eq. (8) over random flux configurations that are not connected by translations. We show our results of averaged A(k, ω) along high-symmetry lines in Fig. 2c, which captures the gapless feature of the spin-spin correlations around M and K. For comparison we also show numerical evidence from iPEPS for intra-sublattice spin-spin correlations in Fig. 2d; details can be found in SI. Remarkably, our mean field analysis when compared with the unbiased iPEPS results, reproduces the two most salient features in the IGP: (i) The presence of spectral weight at low energies immediately above ω = 0; and (ii) the opening of a gap centered around ω ≃ 2J, which we now understand as a flux-induced gap separating the upper and the lower branches of the Majorana bands.

To gain more information about the gapless modes in the Majorana metal, we further calculate the averaged A(k, ω = 0) over the whole BZ (i.e., the FS) for systems with different \({\overline{W}}_{p}\). The results in Fig. 3 explicitly show the presence of gapless states around M and K in the Majorana sector, which suggests the presence of zero-energy modes with definite momentum or a Majorana FS. It is straightforward to see that when \({\overline{W}}_{p}\) are large (sparse fluxes) for weak magnetic fields, zero energy states are mainly found around the M point. However, when \({\overline{W}}_{p}\) becomes smaller (denser fluxes) for stronger magnetic fields, zero energy states populate mainly around K points. This matches well with our previous iPEPS calculations40. The reason zero energy states first appear near the M point before appearing near the K point is because, in the clean limit, the band edge is at the M point for large enough NNN hopping λ, as depicted in Fig. 2b, and is thus more susceptible to be rendered gapless by fluxes. More information about the band structures for different λ’s can be found in SI. It is important to distinguish the fluctuations of flux configurations that have averaged translation symmetry considered here from quenched bond- or site-vacancy disorder discussed in refs. 49,50. While both types of disorder can lead to gapless states, quenched disorder lacks well-defined momenta for zero-energy modes due to the absence of translation symmetry.

Fig. 3: Fermi surface of quantum Majorana metal.
figure 3

Majorana spectral function at zero energy on the FS, A(k, ω = 0), in the intermediate gapless phase (IGP), sandwiched between the chiral spin liquid (CSL) phase and the polarized phase (PP), for (a) \({\overline{W}}_{p}=0.53\) and (b) \({\overline{W}}_{p}=0.05\), where \({\overline{W}}_{p}\) is the ensemble average of the π-flux density. h represents the strength of the Zeeman field [c.f. Eq. (1)]. The blue dashed contour in (a) marks the boundary of the first BZ and the gray dashed lines represent the cut used in Fig. 2. λ = 0.25J is used for the calculations.

Full size image

We briefly comment on the implications of the Majorana FS on quantum oscillations. There have been previous attempts to attribute the quantum oscillations to a gapless U(1) spin liquid phase characterized by a Fermi surface of complex fermions30,32,33,51. However, as discussed in ref. 52, even if interactions (such as pairing between U(1) fermions) convert the complex fermions into real (Majorana) fermions, the de Haas van Alphen quantum oscillations can still be observed as long as some fraction of Majorana fermions remaining gapless. Similarly, Friedel-type oscillations can also occur due to the presence of an FS of U(1) complex fermions and can persist under \({{\mathbb{Z}}}_{2}\) gauge with fermion pairing53,54,55.

Dimer dynamics

Similar to the spin dynamics, the dimer correlations reflect the dynamics of four-Majorana correlations that can be observed by Resonant Inelastic X-ray Scattering (RIXS) experiments56,57. We denote the dimer by \({{{{\mathcal{D}}}}}_{j}^{\alpha }={\sigma }_{j}^{\alpha }{\sigma }_{j+z}^{\alpha }\). In analogy to the two-spin spectrum, the dimer-dimer spectrum \({S}_{2}({{{\bf{k}}}},\omega )={{{\rm{F.T.}}}}\{\langle{{{{\boldsymbol{{{{\mathcal{D}}}}}}}}}_{i}(t)\cdot {{{{\boldsymbol{{{{\mathcal{D}}}}}}}}}_{j}\rangle\}\) in the IGP can be approximated by:

$$\langle{{{{\boldsymbol{{{{\mathcal{D}}}}}}}}}_{i}(t)\cdot {{{{\boldsymbol{{{{\mathcal{D}}}}}}}}}_{j} \rangle\sim {\langle \left\langle {{{{\mathcal{M}}}}}_{{{{\mathcal{F}}}}}\right\vert {c}_{i}(t){c}_{i+z}(t){c}_{j}{c}_{j+z}\left\vert {{{{\mathcal{M}}}}}_{{{{\mathcal{F}}}}}\right\rangle \rangle }_{{{{\mathcal{F}}}}}$$
(9)

An exact evaluation of the R.H.S. of Eq. (9) using mean-field modes is not entirely justified since the Majorana dispersion is rather broad indicating strong lifetime effects (see Fig. 2c). We therefore attempt to capture the essence using a single-mode approximation (SMA) to describe the excitations of the gapless continuum of the Majorana fermions near low energy. Such a semi-quantitative description of the Majorana FS remarkably shows good agreement with the data obtained by iPEPS.

Informed by the spectral function at the Fermi energy presented in Fig. 3b, we use a low-energy SMA around the soft fermion modes at and near the K and \({{{{\rm{K}}}}}^{{\prime} }\) points, depicting the state deep in the IGP where flux density is near half-filling. It is then straightforward to calculate the dimer-dimer correlation in terms of the effective Majorana band, which in Lehmann spectral representation is:

$${S}_{2}({{{\bf{k}}}},\omega )\simeq {\int}_{{{{\bf{q}}}}\in {{{\rm{BZ}}}}}W({{{\bf{k}}}},{{{\bf{q}}}})\delta [\omega -({E}_{{{{\bf{k}}}}-{{{\bf{q}}}}}+{E}_{{{{\bf{q}}}}})]$$
(10)

up to constants. Here \(W({{{\bf{k}}}},{{{\bf{q}}}})={E}_{{{{\bf{k}}}}-{{{\bf{q}}}}}^{2}/({E}_{{{{\bf{k}}}}-{{{\bf{q}}}}}^{2}-{Q}_{{{{\bf{k}}}}-{{{\bf{q}}}}}^{2})\) is the two-fermion (four-Majorana) spectral weight function given by the approximated single-mode Majorana band Ek, gapless near K and \({{{{\rm{K}}}}}^{{\prime} }\) points in keeping with Fig. 3b; and \({Q}_{{{{\bf{k}}}}} \sim [\sin ({{{\bf{k}}}}\cdot {{{{\bf{n}}}}}_{2})-\sin ({{{\bf{k}}}}\cdot {{{{\bf{n}}}}}_{1})-\sin ({{{\bf{k}}}}\cdot ({{{{\bf{n}}}}}_{2}-{{{{\bf{n}}}}}_{1}))]\), the NNN hopping induced by a time-reversal-breaking perturbation, concomitantly tuned to give the desired soft modes in the aforementioned Ek. The derivation and computational details are relegated to the SI. Results by SMA and iPEPS in Fig. 4 show a strikingly similar spectrum at low energies. At the lowest energies, the strongest intensities for the dimer-dimer spectral functions are observed near the Γ point, followed by slightly weaker signals at K, and negligible signal near M. Minor differences between the Majorana analysis and iPEPS can be attributed to truncation errors of iPEPS and the loss of higher-energy states in the MFT.

Fig. 4: Comparison between the four-Majorana correlation in Eq. (10) (top) and the dimer-dimer correlation in the intermediate gapless phase obtained by iPEPS (bottom) along the momentum cut through high-symmetry points ΓMKΓ.
figure 4

The white dashed lines are eye-guiding lines that enclose the energy-momentum region having the strongest intensities, i.e., those near \({{{\rm{K}}}}({{{{\rm{K}}}}}^{{\prime} })\) and Γ at the lowest energy; while signals around M point are negligible.

Full size image

Discussion

In this work, we shed light on the field-induced IGP in the Kitaev honeycomb model by introducing an effective tight-binding model that describes the interplay between emergent \({{\mathbb{Z}}}_{2}\) flux disorder and Majorana Chern-bands. Within our theory, the IGP is a zero-temperature quantum Majorana metal phase characterized by persistent fermion pairing and a neutral FS. In previous works, the intermediate phase has been either identified as a gapless phase of neutral spinons with a finite Fermi surface and an emergent U(1) gauge structure30,32,33,54 or identified as a gapped topological order with Chern number ± 4 and an emergent \({{\mathbb{Z}}}_{2}\) gauge structure43,44. All of these proposals fail to capture the simultaneous presence of a gapless phase and an emergent \({{\mathbb{Z}}}_{2}\) gauge structure observed in our recent numerical study40. It is by considering the interplay between matter and gauge fields that our work accommodates both the gapless and the \({{\mathbb{Z}}}_{2}\) nature of the IGP.

Recent exact diagonalization studies32,44 claim that the intermediate phase is gapless from the behavior of spin correlations. It is further asserted that the specific heat calculations indicate the proliferation of π-flux at low energy which leads to a \({{\mathbb{Z}}}_{2}\) to U(1) transition in the gauge structure, resulting in a transition from a chiral spin liquid (CSL) to a spinon metal with a spinon Fermi surface. Such statements are difficult to validate since the calculations are based on spin operators on small systems that are not privy to the gauge structure. In addition, it is difficult to understand from a theoretical perspective the \({{\mathbb{Z}}}_{2}\) to U(1) transition in the gauge structure.

In our approach, as discussed above, we have proposed that the \({{\mathbb{Z}}}_{2}\) gauge structure persists under the transition from a gapped CSL to a gapless Majorana metal, and we further present a mechanism for the transition that is supported by features observed in our iPEPS calculations.

Ref. 44 presents a microscopic parton mean field theory (MFT) that provides an explanation of the divergent susceptibility at the transition between the CSL and intermediate phase, consistent with previous DMRG results30,33. However, the MFT also finds that the intermediate phase is gapped with a low-energy ring of gapped excitations around the Γ point in momentum space. This result is however not consistent with our unbiased iPEPS calculations that show a logarithmically divergent density of states at low energy (Fig. 2a and ref. 40) that strongly support a \({{\mathbb{Z}}}_{2}\) gapless Majorana metal.

Our identification of IGP as a zero-temperature Majorana metal suggests novel thermal transport and spin relaxation within this phase48. The understanding gained from the spin-spin and dimer-dimer correlations in terms of multi-Majorana correlations in Fig. 4 provides detailed predictions for observation of fractionalization in Raman scattering and momentum-resolved RIXS experiments. Given that Majorana metal phases can be induced by thermal fluctuations in chiral spin liquids under zero magnetic field as previously reported41,58,59, along with our theory on the gapless IGP as a \({{\mathbb{Z}}}_{2}\) Majorana metal at zero temperature induced by quantum fluctuations, these results are suggestive enough to warrant further investigation into the comprehensive phase diagram parametrized by temperature and magnetic field for the new class of the \({{\mathbb{Z}}}_{2}\) gapless QSLs, and the unusual transport properties therein.

Methods

Average of the spectral function

The center-of-mass averaged spectral function [c.f. Eq. (7)] can be derived from Eq. (6) by decomposing the eigen wave function ϕn(r) into a linear combination of Bloch states:

$${\phi }_{n}({{{\bf{r}}}})=\frac{1}{\sqrt{N}}{\sum}_{\alpha {{{\bf{k}}}}}{c}_{\alpha {{{\bf{k}}}}}^{n}{e}^{i{{{\bf{k}}}}\cdot {{{\bf{r}}}}}{u}_{\alpha {{{\bf{k}}}}}.$$
(11)

where α labels internal degrees of freedom, i.e., the sublattice indices. Substituting Eq. (11) into Eq. (6) and replacing r1 and r2 by r = r1 − r2 and R = (r1 + r2)/2, we can derive

$$ {\langle A({{{{\bf{r}}}}}_{1},{{{{\bf{r}}}}}_{2},\omega )\rangle }_{{{{\bf{R}}}}} \equiv \frac{1}{N}{\sum}_{{{{\bf{R}}}}}A({{{\bf{r}}}},{{{\bf{R}}}},\omega )\\ =\frac{1}{{N}^{2}}{\sum}_{{{{\bf{R}}}}}{\sum}_{n}{\sum}_{\alpha {\alpha }^{{\prime} }}{\sum}_{{{{\bf{k}}}}{{{{\bf{k}}}}}^{{\prime} }}{e}^{i({{{\bf{k}}}}-{{{{\bf{k}}}}}^{{\prime} })\cdot {{{\bf{R}}}}}{e}^{i({{{\bf{k}}}}+{{{{\bf{k}}}}}^{{\prime} })\cdot {{{\bf{r}}}}/2}\\ \times {c}_{\alpha {{{\bf{k}}}}}^{n}{c}_{{\alpha }^{{\prime} }{{{{\bf{k}}}}}^{{\prime} }}^{n\star }{{{{\rm{Tr}}}}}_{{{{\rm{cell}}}}}({u}_{\alpha {{{\bf{k}}}}}{u}_{{\alpha }^{{\prime} }{{{{\bf{k}}}}}^{{\prime} }}^{{{\dagger}} })\delta (\omega -{E}_{n})\\ =\frac{1}{N}{\sum}_{n}{\sum}_{\alpha {\alpha }^{{\prime} }}{\sum}_{{{{\bf{k}}}}{{{{\bf{k}}}}}^{{\prime} }}{\delta }_{{{{\bf{k}}}}{{{{\bf{k}}}}}^{{\prime} }}{e}^{i({{{\bf{k}}}}+{{{{\bf{k}}}}}^{{\prime} })\cdot {{{\bf{r}}}}/2}{c}_{\alpha {{{\bf{k}}}}}^{n}{c}_{{\alpha }^{{\prime} }{{{{\bf{k}}}}}^{{\prime} }}^{n\star }\\ \times {{{{\rm{Tr}}}}}_{{{{\rm{cell}}}}}({u}_{\alpha {{{\bf{k}}}}}{u}_{{\alpha }^{{\prime} }{{{{\bf{k}}}}}^{{\prime} }}^{{{\dagger}} })\delta (\omega -{E}_{n})\\ =\frac{1}{N}{\sum}_{n}{\sum}_{\alpha {\alpha }^{{\prime} }}{\sum}_{{{{\bf{k}}}}}{e}^{i{{{\bf{k}}}}\cdot {{{\bf{r}}}}}{c}_{\alpha {{{\bf{k}}}}}^{n}{c}_{{\alpha }^{{\prime} }{{{\bf{k}}}}}^{n\star }{\delta }_{\alpha {\alpha }^{{\prime} }}\delta (\omega -{E}_{n})\\ =\frac{1}{N}{\sum}_{n\alpha {{{\bf{k}}}}}{e}^{i{{{\bf{k}}}}\cdot {{{\bf{r}}}}}| {c}_{\alpha {{{\bf{k}}}}}^{n}{| }^{2}\delta (\omega -{E}_{n}).$$
(12)

After a Fourier transformation, we can eventually derive Eq. (8) used in our numerical calculations. Specifically, for each flux pattern generated by randomly flipping uij on each bond, we diagonalize the disordered Majorana-hopping model and calculate the spectral function using Eq. (8). We then average the results for different random flux patterns which leads to the plot in Figs. 2 and 3. More details about spectral functions of different phases can be found in SI.

iPEPS calculation

The ground state is described as infinite tensor network with translation invariant local tensor A:

(13)

and tensor A can be derived by minimizing the cost function:

$$L=\frac{\left\langle {\psi }_{0}(A)\right\vert H\left\vert {\psi }_{0}(A)\right\rangle }{\langle {\psi }_{0}(A)| {\psi }_{0}(A)\rangle }$$
(14)

using automatic differentiation60. The single-mode approximation (SMA), introduced in refs. 61,62,63,64,65, is employed to characterize excited states. The SMA uses variational tensors for the excited state as shown below:

(15)

Here, k denotes momentum and \(\left\vert {\Psi }_{{{{\bf{r}}}}}\right\rangle\) signifies the state with an excitation at site r. Under the representation of iPEPS, it’s implemented by replacing the local tensor A of the ground state at site r with a disturbed local tensor B. Note that excited states are required to adhere to the orthogonality constraint in relation to the ground state, depicted as 〈ψ0∣Ψk(B)〉 = 0. Additionally, they must eliminate gauge redundancy to ensure accuracy in calculations64. With these two constraints, we can obtain the B tensor and thus the excited states by minimizing the cost function

$${L}^{{\prime} }=\frac{\left\langle {\Psi }_{{{{\bf{k}}}}}(B)\right\vert H-{E}_{{{{\rm{gs}}}}}\left\vert {\Psi }_{{{{\bf{k}}}}}(B)\right\rangle }{\langle {\Psi }_{{{{\bf{k}}}}}(B)| {\Psi }_{{{{\bf{k}}}}}(B)\rangle }.$$
(16)

With the ground state and the excited states, we can directly calculate the spin-spin and dimer-dimer correlations as detailed in SI.