Introduction

Active metasurfaces, which consist of planar arrays of subwavelength light scatters or antennas (“meta-atoms”), enable dynamic and versatile control over electromagnetic field states and optical responses1,2. Compared to conventional bulk optics, they feature ultra-compact, lightweight, and energy-efficient systems, which are particularly promising for applications constrained by a lean size, weight, or power budget, such as aerospace remote sensing, free-space communication, and point-of-care and wearable health monitoring3,4,5. The high-density meta-atoms capitalizing great amounts of degrees of freedom also facilitate real-time beam shaping and steering for devices including light detection and ranging (LiDAR) in autonomous vehicles and light-field display in augmented/virtual reality (AR/VR) modules6,7,8,9,10. However, compared with their passive counterparts, the extra complexity for post-fabrication tunability introduced in active metasurfaces poses notable technical challenges for implementing these advanced functions2,11, particularly in the mid-infrared regime due to the dearth of rational materials and device designs. For instance, subwavelength-scaled arrays of narrow-bandgap semiconductors suffer from costly crystal growth and require external cooling, impeding the miniaturized device integration12,13. The dynamic switching of phase-change metasurfaces is typically limited to a dichotomy between metallic and dielectric states14,15,16, while multistate phase transition encounters a narrow working window to attain critical temperatures17.

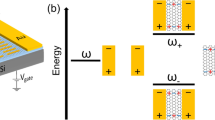
Recent advances in thermal photonics reveal an alternative route for achieving dynamic light control in the mid-infrared range18,19,20,21,22. The metasurface-augmented polaritonic and photonic modes, including surface plasmon polaritons from plasmonic metals23,24, surface phonon polaritons from polar dielectrics25,26,27, photonic crystals and their twisted bilayers28,29, show strong temporal, spatial, or polarized coherence (i.e., narrowband, directional, or polarized emission). These modes can be unified to engineer the photonic density of states \({DOS}\) for the thermal infrared emission intensity formulated as:

$$I=E\left(\omega,T\right)\cdot {DOS}\left(\omega,\hat{n},\hat{p}\right)$$
(1)

where \(\omega\) is the frequency, \(E\) is the average energy per photon \(\hslash \omega /\left({e}^{\hslash \omega /{k}_{B}T}-1\right)\) at temperature \(T\), \(\hat{n}\) is the normal vector of direction, and \(\hat{p}\) is the polarization vector18,19,20. Based on Eq. (1), one can identify two modulation schemes: the first involves the average photon energy \(E\), which can be controlled by temperature \(T\), whereas the second pertains to the photonic density of states \({DOS}\), which corresponds to emissivity, a far-field term normalized to an ideal blackbody commonly employed in radiometry.

To date, various methods have been employed to actively excite thermal infrared metasurfaces, such as thermal hot plate30,31, mechanical actuation32, and optical laser pulse33. However, the realization of electrically programmable on-chip integration for large-area pixelated 2D arrays remains a significant challenge. Single-pixel active metasurfaces, by electrically modulated refractive indices of materials like graphene34,35,36,37,38 and transparent conductive oxides (indium silicon oxide39, indium tin oxide40,41), typically yields limited infrared emissivity contrast. Joule heating in an incandescent metasurface with a fixed resistance restricts the pixel modulation to binary on/off states and imposes constraints on the available design parameters for coherent characteristics due to the overlap of electrodes with optically active regions42,43,44. Although state-of-the-art research has predominantly featured in-plane fan-out writing designs for 1D arrays6,7,45,46,47, electrically driven 2D pixelated metasurfaces have rarely been demonstrated due to the complexities of electrical addressing.

Due to the carbon nature and strong covalent bonding, graphene is stable at elevated temperatures and durable in long working cycles48,49, and can function as a robust, transparent, high-speed, and tunable microheater. The atomically thin single-layer graphene makes it as a broadband transparent electrode from visible to far-infrared50,51, whose time constant for Joule heating can reach picoseconds52,53. More importantly, the semi-metallic nature of graphene allows a fine-tuning of its carrier density by electrostatic gating, allowing for tunable microscale localized heating54,55,56. Based on this spatial temperature modulation, we develop an integrated emissivity-temperature scheme to create an electrically programmable 2D-pixelated mid-infrared metasurface, where emissivity control and temperature regulation are achieved by tuning heating position and strength, respectively.

In this work, we experimentally demonstrate the pixelated modulation of coherent thermal emission from an electrical-programmable plasmonic metasurface integrated with a graphene field-effect transistor (Gr-FET). The broadband transparency of single-layer graphene enables customized control over plasmonic meta-atoms fulfilling the design space for controlling mid-infrared coherent states across a wide range of wavelengths, directions, and polarizations. The spatial temperature modulation generated by the Gr-FET is effectively synergized with the emissivity control by the localized surface plasmon polaritons (LSPs) and quasi-bound states in the continuum (QBICs) from gold nanoantennas. This integrated temperature-emissivity modulation is systematically extended to form a pixelated 2D array with low crosstalk, signifying an advanced approach toward scalable 2D electrical wiring for densely packed, individually addressable pixels. Specifically, a \(3\times 3\) sweeping pixel array demonstrates diverse alphanumeric displays, supported by an explicit analytical model detailing the control mechanism. The small thermal mass from the ultrathin graphene film further enables rapid modulation, achieving a 3-dB bandwidth of \(146\,{{{\rm{kHz}}}}\) in a total \(95{{\upmu }}{{{\rm{m}}}}\times 95\,{{\upmu }}{{{\rm{m}}}}\) device. A dual-gate pixel architecture incorporating pull-up transistors is also developed to significantly reduce crosstalk, overcoming the fundamental limitation imposed by zero-bandgap graphene. Our method offers superior potential in large-area scalability: to independently control \(N\times N\) pixel arrays, only \(2N+1\) electrical pins (or \(3N+1\) for the dual-gate case) rather than \({N}^{2}\) pins are required. In conjunction with CMOS-compatible fabrication and high-temperature resilience of large-area graphene grown by chemical vapor deposition (CVD), our device represents a significant stride in the development of next-generation mid-infrared active metadevices.

Results and discussion

Integrated emissivity-temperature active metasurfaces

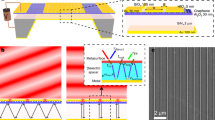
We design and fabricate pixelated active metasurfaces electrically driven by Gr-FETs, as shown in Fig. 1a. Each pixel comprises an array of gold (Au) plasmonic nanoantennas that either directly interfaces with a single-layer graphene channel or is separated from it by an Al2O3 dielectric layer (the schematic shows the direct-contact case). The graphene layer is patterned and fabricated into Gr-FETs with source and drain contacts made of Au. Beneath lies an aluminum oxide (Al2O3) layer, which functions as the gate dielectric of the Gr-FET. The plasmonic nanoantennas and the Au bottom gate electrode of the Gr-FET serve as the meta-atoms and mirror of the metal-insulator-metal (MIM) metasurface, respectively. The Al2O3 layer is also co-optimized as the spacer of the MIM metasurface to achieve critical coupling. The Gr-FET structure provides a tunable and programmable Joule heating channel to modulate the spatial temperature distribution of metasurfaces. The source/drain and bottom gate electrodes of Gr-FETs are further patterned to allow for spatial temperature modulation in an addressable pixelated mode. In Fig. 1b, the active pixelated metadevice is fabricated using hybrid optical and electron lithography processes (detailed design parameters and fabrication procedures in the “Methods” section). The zoom-in image in Fig. 1b shows a typical Au nanosquares based MIM metasurface, in which the LSP mode supports the narrowband emission at the wavelength around \(2.9\,{{\upmu }}{{{\rm{m}}}}\) (as depicted in Supplementary Note 2). The emission states can be finely tuned by engineering the geometries of the meta-atoms, as illustrated by the finite-difference time-domain (FDTD) simulations. As shown in Fig. 1c, the resonance wavelength can be tuned across a range of \(2.9\,{{\upmu }}{{{\rm{m}}}}\) to \(4.8\,{{\upmu }}{{{\rm{m}}}}\) as the side length of nanosquares changes from \(500\,{{{\rm{nm}}}}\) to \(750\,{{{\rm{nm}}}}\).

Fig. 1: Mechanism of a pixelated electrical-programmable graphene-integrated plasmonic metasurface.
figure 1

a Schematic of a \(3\times 3\) pixelated MIM active metasurface driven by graphene field-effect transistors (Gr-FETs). Each pixel contains an upper layer of an Au nanoantenna array for coherent mid-infrared emission (with wavelengths \({\uplambda}_{1},{\uplambda}_{2}\)). The beneath layers of Al2O3 and Au serve as the gate dielectric and spacer, and the gate electrode and mirror for the Gr-FET and metal-insulator-metal (MIM) metasurface, respectively. Inset: Addressable pixelated mode under a source-drain voltage \({V}_{d}\) with a patterned gate electrode assigning one gate voltage (\({V}_{g1}\), \({V}_{g2}\), or \({V}_{g3}\)) to each pixel. b Scanning electron microscope (SEM) image (scale bar: \(35\,{{\upmu }}{{{\rm{m}}}}\)) of the fabricated active metadevice with its zoom-in image (scale bar: \(800\,{{{\rm{nm}}}}\)) revealing the nanosquare meta-atoms with an edge length of \(500\,{{{\rm{nm}}}}\). c Finite-difference time-domain (FDTD) simulations of resonant spectra as nanosquare sizes vary between \(500\,{{{\rm{nm}}}}\) and \(750\,{{{\rm{nm}}}}\). The mid-infrared transparency of graphene permits customized meta-atom designs for versatile coherent emission.

Full size image

As described in Eq. (1), thermal emission of a metasurface is generally controlled by its emissivity and local temperature. Here, by integrating pixelated plasmonic metasurfaces with Gr-FETs, we introduce an integrated emissivity-temperature scheme to actively modulate coherent thermal emission from metasurfaces in the mid-infrared range. Specifically, the Gr-FETs precisely shift the heating position to the target pixel metasurface with a designated emissivity. Other than the size-dependent tuning of resonant wavelength in Fig. 1c, the emissivity engineering of the customized meta-atoms, facilitated by the graphene infrared transparency, can be further demonstrated by tuning the polarization of the Au nanorods array. Figure 2a illustrates two pixels composed of perpendicular Au nanorods with distinct lengths fabricated directly on a single graphene channel. In Fig. 2b, their measured length-dependent resonant spectra depict one emission peak at \(3.9\,{{\upmu }}{{{\rm{m}}}}\) along polarization angle \(\varphi=0^\circ\) (blue curve) and the other at \(5.3\,{{\upmu }}{{{\rm{m}}}}\) along \(\varphi=90^\circ\) (red curve). As shown by the polar plot in Fig. 2c, the emission peaks of the two pixels are measured across a range of polarization angles from \(0^\circ\) to \(180^\circ\), where two orthogonal polarization states are clearly observed. The direct contact between the Au nanoantennas and graphene also enables tunable emissivity directly through an electrostatic gating (instead of switching the heating position) on the active metasurface, where the gating-induced carrier doping in graphene alters the dielectric environment for the LSPs from the Au nanoantennas. However, due to the limited carrier mobility of the CVD graphene, the resonance peak of the metasurface only undergoes a ~ \(0.5\,{{\upmu }}{{{\rm{m}}}}\) blue shift from a gate voltage reaching the Dirac point of the graphene to considerably far from the Dirac point (Supplementary Note 3), which is consistent with previous studies34,35,36,37,38.

Fig. 2: Simulation and experiment of single-pixel metasurface based on localized surface plasmon (LSP).
figure 2

a SEM image (scale bar: \(50\,{{\upmu }}{{{\rm{m}}}}\)) of two pixels comprised of perpendicular Au nanorods with distinct lengths on a single graphene channel. The zoom-in images (scale bar: \(1\,{{\upmu }}{{{\rm{m}}}}\)) illustrate the upper pixel (red rectangle) with a longitudinal edge of \(1\,{{\upmu }}{{{\rm{m}}}}\) along the \(x\)-axis and the lower pixel (blue rectangle) with a longitudinal edge of \(700\,{{{\rm{nm}}}}\) along the \(y\)-axis. The polarization angle \(\varphi\) is defined with respect to \(y\)-axis. b Measured emissivity spectra of the upper pixel at \(5.3\,{{\upmu }}{{{\rm{m}}}}\) (red line) with a polarization angle of \(\varphi=90^\circ\) and the lower pixel at \(3.9\,{{\upmu }}{{{\rm{m}}}}\) (blue line) with \(\varphi=0^\circ\). c Measured polar plots of the emissivity peaks across the polarization angles from \(0^\circ\) to \(180^\circ\). Two distinct orthogonal polarization states are evident for the two pixels.

Full size image

While the design based on LSP exhibits low temporal coherence due to strong non-radiative loss and low spatial coherence due to its local mode nature, we also demonstrate plasmonic quasi-bound state in the continuum (P-QBIC) to improve both aspects (with design parameters given in Supplementary Note 5). Due to the stationary and ergodic thermal fluctuations in equilibrium and quasi-homogeneous pixel emitter25,57, temporal and spatial power spectral densities can be defined through the Wiener-Khinchin theorem (WKT) for the temporal and spatial coherences, respectively22,58,59. While the temporal WKT directly connects the temporal coherence with the spectral bandwidth, under the far-field approximation, the spatial power spectral density can be expressed as the angular radiance distribution, which is thus related to the spatial coherence. Specifically, we can quantify the coherence time and (transverse) coherence length for the metasurface thermal emitter based on the uncertainty principle. A quasi-monochromatic source with bandwidth \(\Delta \omega\) has a coherence time approximately equal to \({\tau }_{c}=2\pi /\Delta \omega\), and a quasi-parallel beam with a spatial frequency bandwidth \(|\Delta {{{{\boldsymbol{k}}}}}_{\parallel }|\) has a transverse coherence length of \({L}_{c}=2\pi /|\Delta {{{{\boldsymbol{k}}}}}_{\parallel }|\), where \(\parallel\) denotes the wavevectors in-plane.

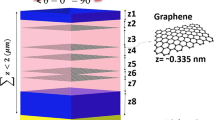
The P-QBIC mode originates from an ideal BIC mode generated by two counter-propagating Rayleigh anomalies or in-plane diffraction orders60,61, based on two elliptical scatterers, and is then perturbed by a small tilt angle to achieve far-field emission in the normal direction. Two primary factors contribute to the enhancement of coherence: (1) the BIC nature of the mode suppresses radiative channels, substantially increasing the radiative quality factor and, consequently, improving temporal coherence; (2) the mode’s nonlocal character narrows the in-plane wavevector distribution, resulting in higher spatial coherence. As shown in Fig. 3a, the P-QBIC design still follows an MIM structure and thus is well compatible with our pixelated array design and graphene tunable heaters. Figure 3b demonstrates that the P-QBIC mode exhibits substantially reduced spectral bandwidth relative to the LSP mode (corresponding to the lower pixel in Fig. 2a), indicating enhanced temporal coherence. The Fourier-transform infrared spectroscopy (FTIR) measurements agree well with the FDTD simulations for both modes, as illustrated in Fig. 3c. The FTIR spectra reveal a tiny emission peak at \(4.2\,{{\upmu }}{{{\rm{m}}}}\) attributed to atmospheric CO2 absorption, which can be mitigated through N2 purging during measurements. The FDTD simulations of the P-QBIC mode reveal a spurious peak at \(3.9\,{{\upmu }}{{{\rm{m}}}}\) from higher-order in-plane diffraction requiring perfect periodicity, which is absent in experimental FTIR spectra due to fabrication imperfection.

Fig. 3: Simulation and experiment of single-pixel metasurface based on plasmonic quasi-bound state in the continuum (P-QBIC).
figure 3

a SEM image of the P-QBIC pixel (scale bar: 30 μm) with the inset showing its elliptical meta-atom array (scale bar: 5 μm). b Non-polarized Fourier-transform infrared spectroscopy (FTIR) spectra of the P-QBIC and LSP modes. c Non-polarized FDTD spectra of the P-QBIC and LSP modes. d Simulated emissivity mapping of wavelength and polar angle \({\theta }_{x}\) with its inserting lines in (e) showing the angular distribution with fixed wavelengths \(\lambda=3.36\,{{\upmu }}{{{\rm{m}}}}\) and \(3.43\,{{\upmu }}{{{\rm{m}}}}\), and the spectral distribution with fixed \({\theta }_{x}=0^\circ\) and \(45^\circ\). f Simulated emissivity mapping in direction cosines \(\left({u}_{x},{u}_{y}\right)\) for the resonant wavelengths λ = 3.36 μm of the P-QBIC mode and λ = 3.87 μm of the LSP mode in (c), respectively.

Full size image

To further quantify the coherence, we analyze the dispersion relation of the P-QBIC mode in the far field for the \(x\)-polarization, as shown in Fig. 3d. Through emissivity mapping as a function of wavelength and polar angle along the \(x\)-axis \({\theta }_{x}\) from \(0^\circ\) to \(80^\circ\) (with fixed azimuthal angle \(\phi=0^\circ\)), we observe a parabolic photonic band structure. While the temporal and spatial coherences are linked and governed by the dispersion relation, we analyze them separately to characterize their respective parameters, coherence time \({\tau }_{c}\) and coherence length \({L}_{c}\), by examining the fixed wavelength or \({\theta }_{x}\) spectra in Fig. 3e. Here, we demonstrate the angular distributions for resonant wavelengths \(3.36\,{{\upmu }}{{{\rm{m}}}}\) and \(3.43\,{{\upmu }}{{{\rm{m}}}}\), corresponding to the green-dash and yellow-dash-dot lines in Fig. 3d. The emissivity exhibits resonances at \({\theta }_{x}\,=\,0^\circ\) (normal) and \(\pm 45^\circ\), with an angular spreading of \(\Delta {\theta }_{x}\,=\,61^\circ\) and \(32^\circ\), resulting in coherent lengths of \({L}_{c}\,=\,3.33\,{{\upmu }}{{{\rm{m}}}}\) and \(8.79\,{{\upmu }}{{{\rm{m}}}}\), respectively. Because the coherence lengths are comparable to and larger than the resonant wavelengths, our metasurface thermal sources hold partially local coherence57. Then, we plot the spectral distributions given the polar angles \({\theta }_{x}\,=\,0^\circ\) and \(45^\circ\), corresponding to the green and yellow dots in Fig. 3d. The bandwidth analysis reveals coherence times of \({\tau }_{c}\,=\,597\,{{{\rm{fs}}}}\) and \(448\,{{{\rm{fs}}}}\) for \(45^\circ\) and \(0^\circ\) angles, respectively. These coherence times represent a substantial improvement compared to the 136 fs coherence time for the LSP mode. Finally, we extend the angular spreading investigation to encompass the full range of propagation angles at the resonant wavelength of \(3.36\,{{\upmu }}{{{\rm{m}}}}\), including \(\theta \,\in \,\left[{{\mathrm{0,80}}}\right]^\circ\) and \(\phi \,\in \,\left[-{{\mathrm{180,180}}}\right]^\circ\), effectively covering nearly the entire positive \(z\)-hemisphere. By introducing the direction cosines \({u}_{x}=\,\sin \theta \,\cos \phi\) and \({u}_{y}=\,\sin \theta \,\sin \phi\), we can construct the k-space (\({u}_{x}={k}_{x}\,/{k}_{0}\), \({u}_{y}={k}_{y}/{k}_{0}\)) plot presented in Fig. 3f. This k-space representation facilitates a direct comparison between the P-QBIC and LSP modes, highlighting the significantly stronger spatial coherence of the P-QBIC mode, as confirmed by its considerably narrower angular spreading. Yet, we do observe four spokes extending \(({u}_{x},{u}_{y})\) from \(({{\mathrm{0,0}}})\) to \((\pm 0.6,\pm 0.5)\), which exhibit relatively large angular spreading, indicating reduced spatial coherence. This phenomenon is dependent on the impedance matching between the emitter and the far field, governed by the dispersion relation. Achieving high spatial coherence across all propagation angles necessitates advanced dispersion engineering techniques22.

Additionally, a minor broad peak appears near \(4.4\,{{\upmu }}{{{\rm{m}}}}\) for the green line (P-QBIC mode) in Fig. 3b, corresponding to an additional LSP mode in the polarization orthogonal to the P-QBIC mode. The polarization-dependent FTIR spectra in Fig. 4a confirm this observation. Along the \(y\)-polarization, the long axis of the elliptical scatterer functions as a conventional LSP antenna, albeit slightly tilted. Its low emissivity stems from the large spacer thickness (\(200\,{{{\rm{nm}}}}\)) in the MIM structure, which optimizes the P-QBIC mode’s impedance matching to the far field while leaving the LSP mode unmatched. This insight enables selective optimization of either the P-QBIC or LSP mode for narrowband or broadband applications, respectively. As demonstrated in Fig. 4b, with a 200 nm Al2O3 spacer, both polarized spectra align well with FTIR measurements, with the P-QBIC mode being dominant. Reducing the thickness to 50 nm causes the LSP mode to exceed the P-QBIC mode.

Fig. 4: Simulation and experiment of single-pixel metasurface switching between LSP and P-QBIC.
figure 4

a Polarized FTIR spectra of the P-QBIC and LSP modes. b Polarized FDTD spectra of the P-QBIC and LSP modes with different thicknesses of Al2O3 spacer.

Full size image

The Gr-FETs allow for programmable spatial temperature modulation because the semi-metallic nature of graphene enables fine tuning of its carrier density and channel resistivity through electrostatic gating. In contrast with traditional metal-based heating with a fixed resistance, the graphene-based tunable heaters can be more straightforwardly scaled up to a large-area on-chip 2D array with densely packed, independently controlled pixels, and potentially achieve a high speed due to the near-zero thermal mass of single-layer graphene. For a Gr-FET with a sole bottom gate electrode, the Joule heating reaches its maximum and generates a “hot-spot” at the position where the local resistivity of graphene is the highest. The local resistivity \(\rho \left(x\right)\) along the graphene channel can be expressed as (detailed derivations in Supplementary Note 1):

$$\rho \left(x\right)=\sqrt{\frac{W}{2I{C}_{{ox}}\mu }}\cdot \frac{1}{\sqrt{{{{\mathrm{sgn}}}}\left(x-{x}_{0}\right)\cdot \left(x-{x}_{0}\right)}}$$
(2)

where \(W\) is the width of the graphene channel, \(I\) is the steady channel current and is kept as constant along the graphene channel, \({C}_{{ox}}\) is the gate dielectric capacitance per unit area, and \(\mu\) is the carrier mobility that is approximated as constant56. \({x}_{0}\) is the position reaching the Dirac point, and \({{\mathrm{sgn}}}\) is the sign function. For the spatial temperature modulation from \(x=0\) to \(L\), we have:

$$\frac{{{{\mathrm{sgn}}}}\left({x}_{0}-L\right)}{{{{\mathrm{sgn}}}}\left({x}_{0}\right)}\sqrt{\frac{{{{\mathrm{sgn}}}}\left({{L}}-{x}_{0}\right)\left(L-{x}_{0}\right)}{{{{\mathrm{sgn}}}}\left(-{x}_{0}\right)\left(-{x}_{0}\right)}}=\frac{{V}_{{{{\rm{Dirac}}}}}-{V}_{g}}{{V}_{{{{\rm{Dirac}}}}}-{V}_{g}+{V}_{d}}$$
(3)

where \({V}_{g}\) is the gate voltage, \({V}_{d}\) is the drain voltage, L is the channel length, and the source electrode is grounded. \({V}_{{\rm{Dirac}}}\) is the Dirac voltage corresponding to the neutrality point of graphene depending on its intrinsic doping and substrate. Hence, the hot spot on the Gr-FET can be controlled and continuously shifted in a programmable way by tuning \({V}_{g}\) and \({V}_{d}\). As shown in Fig. 5a, a preliminary sweep of source-drain current versus gate voltage \({I}_{d}\)-\({V}_{g}\) is conducted for the Gr-FET under a low drain voltage \({V}_{d}=50\,{{{\rm{mV}}}}\) (with the source electrode grounded) to determine the Dirac voltage \({V}_{{{{\rm{Dirac}}}}}=-2\,{{{\rm{V}}}}\). By substituting Eq. (3) into Eq. (2) with the graphene channel length \(L=120\,{{\upmu }}{{{\rm{m}}}}\), and setting \(W/(2I{C}_{{ox}}\mu )=1\) for simplicity, we plot the local resistivity (in arbitrary units) as a function of gate voltage to demonstrate the shifting of the Dirac point, as shown in Fig. 5b. The observed Dirac point positions \({x}_{0}\) correlate well with the thermal mapping results, as indicated by the dash lines in Fig. 5d–f. Figure 5c shows a metadevice composed of two pixels with identical resonant emission wavelengths along the graphene channel under a source-drain bias of \({V}_{d}=30\,{{{\rm{V}}}}\). When the gate voltage is \({V}_{g}=30\,{{{\rm{V}}}}\), the Dirac point position would lie outside the graphene channel region (i.e., \({x}_{0} < 0\)), thus resulting in a stronger illumination in the upper pixel (Fig. 5d). For \({V}_{g}=16\,{{{\rm{V}}}}\), the Dirac point lies in the gap between two pixels, and therefore the two pixels exhibit comparable but notably weaker thermal emission (Fig. 5e) compared to the scenarios at \({V}_{g}=8\,{{{\rm{V}}}}\) and \({V}_{g}=30\,{{{\rm{V}}}}\) due to its larger overall resistance of the Gr-FET. Finally, at \({V}_{g}=8\,{{{\rm{V}}}}\), the Gr-FET is expected to show the Dirac point at the position \({x}_{0}=0.8L\), and thus the lower pixel exhibits stronger thermal infrared emission, as shown in Fig. 5f.

Fig. 5: Experimental demonstration of spatial temperature modulation of a Gr-FET.
figure 5

a Preliminary sweep of drain current versus gate voltage \({I}_{d}\) -\({V}_{g}\) under a drain voltage \({V}_{d}=50\,{{{\rm{mV}}}}\), where the source electrode is grounded. The low \({V}_{d}\) confirms almost equal potential between the source and drain electrodes, allowing the determination of the Dirac voltage \({V}_{{{{\rm{Dirac}}}}}=-2\,{{{\rm{V}}}}\) for the Gr-FET. b Local resistivity \(\rho\) along the graphene channel \(L=120\,{{\upmu }}{{{\rm{m}}}}\) under different gate voltages. The vertical dash lines represent the positions of maximum local resistivity. The gray shaded areas represent regions outside the graphene channel. c SEM image (scale bar: \(50\,{{\upmu }}{{{\rm{m}}}}\)) showing two pixels with the same resonant emissivity on a single bottom gate electrode. d–f Continuous spatial temperature modulation under \({V}_{d}=30\,{{{\rm{V}}}}\). Thermal mapping images (scale bars: \(50\,{{\upmu }}{{{\rm{m}}}}\)) exhibit the hot spot control by aligning \({V}_{g}\). The dash lines indicate the Dirac point positions \({x}_{0}\).

Full size image

Pixelated 2D array dynamics with regulated emission

Here, we introduce addressable pixelated active metasurfaces with separated local gate electrodes for each pixel. Figure 6a shows an active metadevice integrated with a custom-designed printed circuit broad (PCB). In the zoom-in view in Fig. 6b, the bottom gate electrode is distinctly partitioned into three segments, each specifically associated with one individual pixel. The control of each gate voltage is demonstrated in the sweep mapping of \({I}_{d2}\)-\(({V}_{g1},{V}_{g2})\) under \({V}_{d2}=50\,{{{\rm{mV}}}}\) in Fig. 6c, where the gate electrode 3 is grounded (i.e., \({V}_{g3}\)). For each value of the gate 1 voltage \({V}_{g1}\), the sweep of \({I}_{d2}\) - \({V}_{g2}\) for the gate 2 maintains the bipolar transport characteristic curve of the Gr-FET (Fig. 5a). When \({V}_{g2}\) is tuned for the \({V}_{{{{\rm{Dirac}}}}}\) alignment for the pixel on/off, \({V}_{g1}\) can be set to be away from \({V}_{{{{\rm{Dirac}}}}}\) (as depicted by point A) to increase the overall current along the graphene channel for an enhanced pixel brightness. By symmetry, this strategy applies to the sweep of \({I}_{d2}\)- \({V}_{g1}\) under the control by \({V}_{g2}\), as labeled by point B. Through this methodology, we have the capability not only to adjust the position of the heated pixel but also to regulate its heating intensity, which also indicates the pixel’s brightness. The coupling between pixels can be described as 3 Gr-FETs in series whose Dirac point positions \({x}_{01},{x}_{02},{x}_{03}\) are given by (detailed derivations in Supplementary Note 1):

$$\left\{\begin{array}{c}{V}_{g1}-{V}_{g2}=- {{{\mathrm{sgn}}}} \left(\frac{L}{3}-{x}_{02}\right)\sqrt {{{{\mathrm{sgn}}}}\left(\frac{L}{3}-{x}_{02}\right)C\left(\frac{L}{3}-{x}_{02}\right)}+{{{\mathrm{sgn}}}}\left(\frac{L}{3}-{x}_{01}\right)\sqrt {{{{\mathrm{sgn}}}} \left(\frac{L}{3}-{x}_{01}\right)C\left(\frac{L}{3}-{x}_{01}\right)}\\ \begin{array}{c}{V}_{g2}-{V}_{g3}=- {{{\mathrm{sgn}}}}\left(\frac{2L}{3}-{x}_{03}\right)\sqrt {{{{\mathrm{sgn}}}} \left(\frac{2L}{3}-{x}_{03}\right)C\left(\frac{2L}{3}-{x}_{03}\right)}+{{{\mathrm{sgn}}}} \left(\frac{2L}{3}-{x}_{02}\right)\sqrt {{{{\mathrm{sgn}}}} \left(\frac{2L}{3}-{x}_{02}\right)C\left(\frac{2L}{3}-{x}_{02}\right)}\\ {V}_{{{{\rm{Dirac}}}}}-\left[{V}_{g1}-{V}_{d}\right]=- {{{\mathrm{sgn}}}} \left(0-{x}_{01}\right)\sqrt{{{{\mathrm{sgn}}}}\left(0-{x}_{01}\right)C\left(0-{x}_{01}\right)}\\ {V}_{{{{\rm{Dirac}}}}}-\left[{V}_{g3}-0\right]=- {{{\mathrm{sgn}}}}\left(L-{x}_{03}\right)\sqrt {{{{\mathrm{sgn}}}} \left(L-{x}_{03}\right)C\left(L-{x}_{03}\right)}\\ C=\frac{2I}{\mu W{C}_{{ox}} }\end{array}\end{array}\right.$$
(4)
Fig. 6: Experimental demonstration of the addressable pixelated mode for a 2D array display.
figure 6

a Picture (scale bar: \(5\,{{{\rm{cm}}}}\)) of the custom-designed printed circuit board (PCB)-integrated active metasurface system. b Magnified image (scale bar: \(25\,{{\upmu }}{{{\rm{m}}}}\)) of the \(3\times 3\) pixelated 2D metasurface array, accompanied by a schematic depiction of wire bonding. c Sweep mapping of \({{I}}_{d2}\) -\(\,\left({V}_{g1},{V}_{g2}\right)\) under \({V}_{d2}=50\,{{{\rm{mV}}}}\) where the 3rd gate is grounded. For each \({V}_{g1}\) value, sweeping \({I}_{d2}\) -\(\,{V}_{g2}\) maintains the bipolar transport curve of the Gr-FET. Tuning \({V}_{g2}\) enables control over the \({V}_{{{{\rm{Dirac}}}}}\) alignment for pixel on/off. Setting apart from \({V}_{{{{\rm{Dirac}}}}}\) (Point A) boosts the overall current for pixel brightness. Symmetrically, this approach applies to \({I}_{d2}\)- \({V}_{g1}\) sweep under \({V}_{g2}\) control, represented by Point B. d Thermal mapping image (scale bar: \(25\,{{\upmu }}{{{\rm{m}}}}\)) under three gate voltages \(\left[{V}_{g1},{V}_{g2},{V}_{g3}\right]\) in \(\left[-2,\,2,\,-2\right]\,{{{\rm{V}}}}\). The discrete adjustment of gate electrodes under \({V}_{d}=5\,{{{\rm{V}}}}\) results in pixel resistances \(\left[{R}_{1},{R}_{2},{R}_{3}\right]=[529,\,1877,\,1023]\,\Omega\) lighting up the central pixel. e Thermal mapping images (scale bar: \(25\,{{\upmu }}{{{\rm{m}}}}\)) of individual frames displaying the letter “L”.

Full size image

The resistance \({R}_{i}\) for each pixel \(i={{\mathrm{1,2,3}}}\) can then be derived by integrating the local resistivity Eq. (2) using the inputs \({x}_{01},{x}_{02},{x}_{03}\) for each segment. At \({V}_{d2}=5\,{{{\rm{V}}}}\), Fig. 6d employs \([{V}_{g1},{V}_{g2},{V}_{g3}]=[-2,\,2,\,-2]\,{{{\rm{V}}}}\) to light up the central pixel with the computed resistances as \(\left[{R}_{1},{R}_{2},{R}_{3}\right]=[529,\,1877,\,1023]\,\Omega\). The addressable pixelated operation can be readily scaled up to a large-area 2D array for real-world applications. Figure 6e demonstrates a \(3\times 3\) pixelated display showing letter “L” by electrically programming individual frames. Various letter or number patterns can be generated using distinct pixel sweep schemes (demonstration videos available in Supplementary Movie 1). These display demonstrations by independent pixel control use only \(7\) electrical pins (total “\(2N+1\)” pins with 3 gate electrodes, 3 drain electrodes, and 1 grounded source electrode), fewer than \(9\) pins (corresponding to “\({N}^{2}\)” pins) conventionally installed. This advantage becomes more pronounced as the number of pixels increases.

Transient thermal mapping of pixel modulation

To quantitatively understand the response speed of an individual pixel on the 2D array displaying dynamic infrared patterns via pixel sweeping, thermal transient simulations are performed on a single pixel device, where transient responses of temperature change (\(\Delta T\)) due to voltage modulations are collected. Such responses are then verified by the reflectivity change (\(\Delta R/R\)) measured via time-domain thermoreflectance temperature mapping on a fabricated single pixel device (details in the “Methods” section). Here two modulation schemes are demonstrated: (1) gate-voltage modulation using a single gate voltage pulse \({V}_{g}=4\,{{{\rm{V}}}}\) with constant drain voltage \({V}_{d}=6\,{{{\rm{V}}}}\) and grounded source electrode to change the relative brightness of each pixel, and (2) source-drain-voltage on/off modulation using a single drain voltage pulse \({V}_{d}=8\,{{{\rm{V}}}}\) with constant grounded \({V}_{g}\) to activate and deactivate each pixel row. The pulse width of both modulations is set as \(7.5\,{{\upmu }}{{{\rm{s}}}}\), and the monolayer graphene is measured to have the Dirac point about \({V}_{{Dirac}}=1.4\,{{{\rm{V}}}}\) (device setup and electrical measurements in Supplementary Note 4). Figure 7a, b shows the simulated and experimental transient response curve of the two modulations, capturing each time frame of the surface temperature and reflectivity changes by averaging the whole nanoantenna array area, as indicated by the dash-line box in Fig. 7c.

Fig. 7: Simulation and experiment of transient single-pixel modulation.
figure 7

a Gate-voltage modulation with respective thermoreflectance mapping frames at \(t=\left[0,\,2.1\,,6.9\,,9.6\right]{{\upmu }}{{{\rm{s}}}}\) shown in (c)–(f) (scale bar: \(25\,{{\upmu }}{{{\rm{m}}}}\)), with \(\Delta T\) for temperature change and \(\Delta R/R\) for reflectance difference. The upper electrode is the drain electrode, and the lower electrode is the source electrode. Five enlarged Au pads are deposited at the four corners and the center of the array, acting as transducers for the local reflectance measurement and alignment. Local reflectance measurements of three labeled pads A, B and C are given in Supplementary Fig. 7. b Source-drain-voltage on/off modulation with respective thermoreflectance mapping frames at \(t=\left[0\,,\,2.1\,,6.9\,,9.6\right]{{\upmu }}{{{\rm{s}}}}\) shown in (g)–(j). The gate-voltage modulation shows a cutoff frequency \({f}_{c1}=146\,{{{\rm{kHz}}}}\), while the source-drain-voltage on/off modulation has its cutoff frequency \({f}_{c2}=184\,{{{\rm{kHz}}}}\).

Full size image

For the gate-voltage modulation shown in Fig. 7a, initial \({V}_{g}=-2\,{{{\rm{V}}}}\) is provided at time \(t=0\,{{\upmu }}{{{\rm{s}}}}\). Applying boundary conditions of \(V\left(0\right)={V}_{d}\) and \(V\left(L\right)={V}_{s}\), analytical calculation (Supplementary Note 1) gives the Dirac point location \({x}_{0} > L\) and electrical current \(I=8.7\,{{{\rm{mA}}}}\), indicating that the whole graphene channel is at the hole dominant region resulting in a relatively low total resistance (Fig. 7c). When \(t\) reaches \(1.5\,{{\upmu }}{{{\rm{s}}}}\), \({V}_{g}\) is set to \(4\,{{{\rm{V}}}}\). As a result, \({x}_{0}=0.63L\) and \(I=2.1\,{{{\rm{mA}}}}\), hence such reduced current causes a reduction of heat generation and a drop in the average temperature. The ongoing increases of reflectance difference \(\Delta R/R\) with \({V}_{g}=4\,{{{\rm{V}}}}\) at \(t=2.1\,{{\upmu }}{{{\rm{s}}}}\) and \(t=6.9\,{{\upmu }}{{{\rm{s}}}}\) are captured on mapping photos in Fig. 7d, e, corresponding to temperature decreases across the channel. These thermoreflectance mappings also depict the spatial temperature modulation, where the location of the Dirac point \({x}_{0}=0.63L\) near the source (bottom) electrode is implied by a smaller \(\Delta R/R\) value and verified by simulation. Finally, at \(t=9\,{{\upmu }}{{{\rm{s}}}}\), \({V}_{g}\) switches back to \(-2\,{{{\rm{V}}}}\), which brings heat generation pattern back to the initial condition. The surface temperature rises again while magnitude of \(\Delta R/R\) decays, as shown by the overall fainted red color in Fig. 7f. In the full cycle of temperature falling and rising, the 10 to 90% fall time and rise time are measured to be \({t}_{f1}=2.3\,{{\upmu }}{{{\rm{s}}}}\) and \({t}_{r1}=2.4\,{{\upmu }}{{{\rm{s}}}}\), respectively (see Supplementary Movie 2). Similar procedures are followed for source-drain voltage on/off modulation as shown in Fig. 7b where \({V}_{g}\) and the source electrode are kept grounded, \({V}_{d}\) is set to \(0\,{{{\rm{V}}}}\) at \(t=0\,{{\upmu }}{{{\rm{s}}}}\), up to \(8\,{{{\rm{V}}}}\) at \(t=1.5\,{{\upmu }}{{{\rm{s}}}}\), and back to \(0\,{{{\rm{V}}}}\) at \(t=9\,{{\upmu }}{{{\rm{s}}}}\). The temperature rising and falling profile and reflectivity change are captured to have satisfactory match of each other, with \({t}_{r2}=1.9\,{{\upmu }}{{{\rm{s}}}}\) and \({t}_{f2}=2.3\,{{\upmu }}{{{\rm{s}}}}\). Figure 7g–j shows typical mapping photos at the same time frames as Fig. 7c–f. It is worth noting that at \(t=6.9\,{{\upmu }}{{{\rm{s}}}}\), Fig. 7i depicts a hot spot near the source (bottom) electrode as an intensified blue color, which is also verified by simulation and analytical modeling (Supplementary Note 1). The response speed of the electrothermally driven metasurface is limited by its speed of thermal dissipation to the substrate (heat conduction down to the graphene layer, gate oxide, and silicon base). We apply a lumped-capacitance thermal circuit model, which is related to the 10 to 90% rise time \({\tau }_{r}\) by \({f}_{c}=0.35/{\tau }_{r}\)43, to obtain the 3-dB cutoff frequencies for the gate-voltage modulation as \({f}_{c1}=146\,{{{\rm{kHz}}}}\) and for the source-drain-voltage on/off modulation as \({f}_{c2}=184\,{{{\rm{kHz}}}}\). The device speed can potentially reach \({{{\rm{MHz}}}}\)-level by optimizing the substrate design and the size of metasurface for heat transfer44,62.

Dual-gate pixelated array for low crosstalk

Although we successfully demonstrate the feasibility of 2D temperature tuning using Gr-FET arrays, thermal crosstalk occurs by heat generation in the device because the graphene pixel transistors cannot be turned off completely. On the one hand, graphene generates significant heat due to its semimetallic nature, exhibiting higher conductivity compared to other 2D semiconductors such as MoS2, which can also be synthesized through CVD growth63. On the other hand, achieving a sufficient on/off ratio in transistors requires a material with an adequate bandgap. In principle, bandgap engineering in graphene can be achieved through bilayer stacking or quantum-scale patterning to modify its electronic band structure64. However, these techniques present significant technical difficulties and stability issues, particularly when implemented at large scales.

To address such limitations, we develop a pull-up (PU) transistor configuration as a dual-gate pixelated array for low crosstalk. As illustrated in Fig. 8a, each individual pixel consists of a center heating Gr-FET (heater) with metasurfaces deposited on the top, and four “L” shaped PU Gr-FETs encircling the heater. The 4 PUs are connected in parallel to the drain line (\({V}_{D}\)) and controlled by a shared gate electrode (\({V}_{G2}\)) to form a unified PU transistor, which is then connected in series to the drain electrode of the heater controlled by a separate gate electrode (\({V}_{G1}\)), whose source electrode is connected to the source line (\({V}_{S}\)), as shown in Fig. 8b. Such design allows pixels to be arranged into 2-D arrays by sharing common source lines and drain lines in parallel in the same row and control gates in the same column. The separation of PU transistors with their geometry design optimizes the uniformity of substrate temperature distribution and keeps residual heat generated by the PUs away from the heater, hence minimizes their thermal influence. The on/off operation of one pixel is realized by varying \({V}_{G1}\) and \({V}_{G2}\) while keeping the \({V}_{S}\) and \({V}_{D}\) constant so that adjacent pixels on the same row will not be affected. As illustrated by Fig. 8c, when the pixel is at off state, the PU transistors, which are geometrically designed to have larger intrinsic channel resistance, are further charge-depleted by varying \({V}_{G2}\), hence moving the Fermi level \({E}_{F}\) to the Dirac point so that their resistance maximum is reached, and the channel current \({I}_{{DS}}\) is reduced. On the contrary, the heater is negatively gated towards hole-doped direction and its channel resistance is further decreased. Such operation enlarges the channel resistance contrast between the PUs and the heater, hence minimizes the voltage drop and power distribution on the heater. On the other hand, when the pixel is turned on, the channel resistance contrast between the PUs and the heater is reversed, with the PUs change to low-resistance state, pulling up the drain voltage for the heater, and the heater changes to its high-resistance state which is more resistive than that of the PUs, maximizing its power dissipation and therefore leading to big temperature rise. Finally, the metasurface emitter is selectively placed only in the pixel area, while the PUs maintain low emissivity from graphene. This spatial emissivity contrast, combined with the temperature contrast discussed above, enhances the overall IR emission contrast.

Fig. 8: Experimental demonstration of low-crosstalk dual-gate pixelated array.
figure 8

a Schematic of dual-gate controlled Gr-FET pixels. Pixels are connected in parallel with shared source line (\({V}_{S}\)) and drain line (\({V}_{D}\)). Four L-shaped pull-up (PU) transistors are located at the four corners and the square-shaped heating Gr-FET (heater) is located at the pixel center. b Simplified circuit diagram. c Operating scheme of a dual-gate pixel with PUs having larger intrinsic resistance than the heater. The yellow and blue shaded dash circles with their respective cross marks indicate the local gate value \({V}_{{GS}}\) of the PUs and heater when a pixel is turned on (Fermi level \({E}_{F}\) (dot line) of the PUs decreases to the valence band) or off (\({E}_{F}\) of the heater decreases to the valence band). d Optical microscope image (scale bar: 20 μm) of a one-by-two array. e–h Temperature distributions measured via IR thermal mapping under different on/off \({V}_{{GS}}\) combinations with constant \({V}_{{DS}}=5\,{{{\rm{V}}}}\) (scale bar: 20 μm). Black-line squares represent the pixels in the off state.

Full size image

To validate such an on/off operation, a one-by-two pixel array is fabricated, as shown by the optical microscope image in Fig. 8d. Each pixel has a side length of 120 \({{\upmu }}{{{\rm{m}}}}\), and the center heater has a size of 20 \({{\upmu }}{{{\rm{m}}}}\times\) 20 \({{\upmu }}{{{\rm{m}}}}\). During operation, the source line is grounded (\({V}_{S}=0\,{{{\rm{V}}}}\)) and the drain line is applied a constant \({V}_{D}=5\,{{{\rm{V}}}}\). When \({V}_{G1}=-9\,{{{\rm{V}}}}\) and \({V}_{G2}=3\,{{{\rm{V}}}}\) for both pixels, dual off states are obtained and measured via thermal mapping (Fig. 8e). Since metasurfaces are only deposited on top of the heater, IR emission noise from the PU transistors with bare graphene is suppressed and becomes approximately invisible to an IR camera. Compared with the substrate temperature, the heater is measured to have only around \(0.6\,{{{\rm{K}}}}\) temperature rise, making it nearly indistinguishable from the surroundings. To turn on the left pixel, the gate voltages of the left pixel is changed to \({V}_{G1}=1.5\,{{{\rm{V}}}}\) and \({V}_{G2}=6\,{{{\rm{V}}}}\). It can then be monitored that the temperature of the left heater rises by more than \(5\,{{{\rm{K}}}}\), while the right pixel remains unaffected (Fig. 8f). Similarly, by switching the gate voltage combinations, both on (Fig. 8g) or right-on/left-off (Fig. 8h) configurations can be achieved. It can be observed that such a design improves the temperature contrast between on and off states by adding PU transistors to redistribute the power on each pixel. The dual-gate pixel design holds the number of pins as \(3N+1\) (including \(2N\) gate electrodes, \(N\) drain electrodes, and \(1\) grounded source electrode), and it is still far fewer than \({N}^{2}\) number in the conventional design.

We also include additional measurements (Supplementary Fig. 8) demonstrating enhanced on/off temperature contrast (\( > 30\,{{{\rm{K}}}}\)) with increased source-drain voltages. Voltage scaling for higher temperatures is primarily limited by the gate dielectric, with a threshold voltage of approximately \(\pm 20\,{{{\rm{V}}}}\) for our current oxide thickness of \(40\,{{{\rm{nm}}}}\). Increasing the dielectric thickness requires co-optimization with MIM metasurfaces to maintain critical coupling for emissivity, but significant design flexibility remains. Operation at more elevated temperatures (\( > 500\,{{{\rm{K}}}}\)) is primarily limited by Au meta-atom deformation due to its relatively low melting point. Previous studies demonstrate that protective Al2O3 coatings for Au can withstand temperatures of over \(1100\,{{{\rm{K}}}}\)65 or refractory plasmonic materials such as tungsten (W) and molybdenum (Mo) can significantly extend this temperature range66. Additionally, our design architecture is compatible with dielectric metasurfaces, which can also hold high temperatures. Finally, the dual-gate pixel with PU transistors utilizes an identical substrate configuration to the single-pixel case. Due to similar heat transfer dynamics, it exhibits comparable response speeds, maintaining them at the \({10}^{2}\)-\({{{\rm{kHz}}}}\) level (Supplementary Note 6).

In summary, we demonstrate a pixelated electrically driven plasmonic metasurface integrated with the Gr-FET for dynamic coherent mid-infrared emission. The customized design of plasmonic nanoantennas, including LSP and P-QBIC, in combination with the ultrabroad infrared transparency of graphene enables tuning of different coherent states, including resonant wavelengths, directions, and polarizations. The 2D pixelated high-speed dynamics is achieved by integrating the emissivity control with the spatial temperature tunning by the Gr-FET, with the bandwidth of about 146 kHz in low crosstalk. With the highly dynamic control of electromagnetic responses in the infrared range, our implementation of graphene-integrated active metasurfaces has important implications in infrared lab-on-a-chip, chemical and biological sensing, personalized health monitoring, and portable real-time beam shaping and steering.

Methods

Device fabrication

Monolayer graphene is synthesized via low-pressure chemical vapor deposition (LPCVD) on a 99.9% pure Cu foil. The Cu foil is polished via electrochemical polishing in 85% phosphoric acid for \(2.5\) h. It is then cleaned by deionized water and moved into an LPCVD quartz tube furnace. Four-hour hydrogen annealing is performed with \(140\) standard-cubic-centimeter per minute (\({{{\rm{sccm}}}}\)) hydrogen flow until a pressure of \(4\,{{{\rm{torr}}}}\) is stabilized. \(3\,{{{\rm{sccm}}}}\) methane and \(137\,{{{\rm{sccm}}}}\) hydrogen mixing gas is then used to grow monolayer graphene on the Cu substrate for \(30\) min, while the pressure is kept the same. Finally, the furnace is opened for a rapid cooling with \(140\,{{{\rm{sccm}}}}\) hydrogen gas purging until room temperature is reached.

The Gr-FET is fabricated on a Si/1µm-SiO2 wafer diced into \(9\,{{{\rm{mm}}}}\times 9\,{{{\rm{mm}}}}\) chips. The bottom gate electrodes are patterned using lift-off method: firstly, photolithography is performed with AZ P4110 photoresist; then the gate metal is deposited via e-beam evaporation of \(50\,{{{\rm{nm}}}}\) thick Au with \(2\,{{{\rm{nm}}}}\) Ti adhesion layer; lastly, Microposit remover 1165 is used to remove the photoresist. After the Al2O3 layer is deposited via thermal atomic-layer deposition (ALD) under \(250\,^\circ {{{\rm{C}}}}\), the CVD-synthesized monolayer graphene is transferred using the PMMA-assisted wet transfer method and patterned to a desired shape via reactive-ion etching (RIE). Au metasurfaces with various thicknesses are patterned on top of the graphene layer via e-beam lithography using PMMA as the e-beam resist followed by e-beam evaporation of Au with a \(2\,{{{\rm{nm}}}}\) Ti adhesion layer. The thicknesses \({{{{\rm{t}}}}}_{1}\) for the gate dielectric separating the gate electrode (also underneath mirror) and graphene layer and \({{{{\rm{t}}}}}_{2}\) for the separation between the graphene layer and the Au metasurface are summarized for each device: \(({{{{\rm{t}}}}}_{1}=20\,{{{\rm{nm}}}},\,{{{{\rm{t}}}}}_{2}=10\,{{{\rm{nm}}}})\) for Figs. 1b, 6, 7 and Supplementary Figs. 2, 6, 7; \(({{{{\rm{t}}}}}_{1}=20\,{{{\rm{nm}}}},\,{{{{\rm{t}}}}}_{2}=0\,{{{\rm{nm}}}})\) for Fig. 2; \(({{{{\rm{t}}}}}_{1}=150\,{{{\rm{nm}}}},\,{{{{\rm{t}}}}}_{2}=50\,{{{\rm{nm}}}})\) for Figs. 3 and 4; \(({{{{\rm{t}}}}}_{1}=100\,{{{\rm{nm}}}},\,{{{{\rm{t}}}}}_{2}=10\,{{{\rm{nm}}}})\) for Fig. 5; \(({{{{\rm{t}}}}}_{1}=40\,{{{\rm{nm}}}},{{{{\rm{t}}}}}_{2}=10\,{{{\rm{nm}}}})\) for Fig. 8 and Supplementary Fig. 8; \(({{{{\rm{t}}}}}_{1}=100\,{{{\rm{nm}}}},\,{{{{\rm{t}}}}}_{2}=0\,{{{\rm{nm}}}})\) for Supplementary Figs. 3–5. Finally, the source and drain electrodes are patterned using the same method as the gate electrodes.

Thermal and optical simulation

The transient electrothermal simulation is conducted via time-domain finite-element analysis in COMSOL Multiphysics. The single pixel Gr-FET device in Fig. 7 is reconstructed in a COMSOL model, with the constant temperature boundary condition applied to the bottom surface of the simulated device. The electrical properties and setups of graphene applied in simulation are obtained from experimental designs and measurements in Supplementary Information. Material properties of Si, SiO2, Au and Al2O3 are obtained from COMSOL material database.

The optical simulation is based on the Ansys Lumerical FDTD. A single period of the MIM metasurface is illuminated by a plane wave source with periodic boundary conditions. A reflective power monitor is placed above the source to capture the reflective energy, which provides information about the emissivity based on Kirchhoff’s law, revealing coherent features of the thermal infrared emission. For angle-dependent simulations, we change the periodic boundary conditions to Bloch boundary conditions to properly account for the phase correction.

Spectroscopy and thermal mapping measurements

All the spectra are measured by the Thermo Fisher Nicolet iS50 Fourier transform infrared spectrometer. A microscope with an adjustable aperture focuses infrared illumination on the active area of the MIM metasurface. The reflectance \(R\) is measured under different polarization angles based on a polarization filter. By the principle of energy conservation, we can obtain the absorptance as \(1-R\). Since all devices are reciprocal and in thermal equilibrium, Kirchhoff’s law, which states that emissivity equals absorptance, can be applied. The current-voltage sweeps are measured by the Keysight A1500A semiconductor device analyzer. The custom-designed PCB testing system consists of software codes and control circuits. During testing, control commands (codes) are first compiled by Arduino software and then sent to an ATmega-2560 micro-controller unit (MCU) development board. For the gate control, \(16\) bits digital signals/data are sent to \(3\) digital-to-analog converters (DACs) that are simply made by digital potential meters, respectively, from the MCU. Then, 3 OPAMP amplifiers map the \(0\sim 5\,{{{\rm{V}}}}\) analog voltages from the DACs to \(-5\,\sim \,5\,{{{\rm{V}}}}\) gate control. For graphene device source and drain controls, each of its source pads is connected to an N-MOSFET. By wiring an output port of the MCU to the gate of the N-MOSFET, each source and drain can be turned on or off individually. The static and dynamic thermal mapping images are then captured by the QFI InfraScope system. In the time-domain thermoreflectance measurements, a 530-nm monochrome incident LED lights up the pixel area before being reflected and captured by a CCD camera. The reflectivity change is linearly proportional to the surface temperature change: \(\Delta R/R={C}_{{TR}}\Delta T\), where \({C}_{{TR}}\) is the thermoreflectance coefficient depending on surface material and beam wavelength. Au has a local minimum of negative \({C}_{{TR}}\) under \(530\)-\({{{\rm{nm}}}}\) incident wavelength, hence \(\Delta R/R\) will decrease with increase of temperature change, and vis versa. All of the measurements are taken at room temperature.