Strain release by 3D atomic misfit in fivefold twinned icosahedral nanoparticles with amorphization and dislocations

Abstract

Multiple twinning to form fivefold twinned nanoparticles in crystal growth is common and has attracted broad attention ranging from crystallography research to physical chemistry and materials science. Lattice-misfit strain and defects in multiple twinned nanoparticles (MTP) are key to understand and tailor their electronic properties. However, the structural defects and related strain distributions in MTPs are poorly understood in three dimensions (3D). Here, we show the 3D atomic misfit and strain relief mechanism in fivefold twinned icosahedral nanoparticles with amorphization and dislocations by using atomic resolution electron tomography. We discover a two-sided heterogeneity in variety of structural characteristics. A nearly ideal crystallographic fivefold face is always found opposite to a less ordered face, forming Janus-like icosahedral nanoparticles with two distinct hemispheres. The disordered amorphous domains release a large amount of strain. Molecular dynamics simulations further reveal the Janus-like icosahedral nanoparticles are prevalent in the MTPs formed in liquid-solid phase transition. This work provides insights on the atomistic models for the modelling of formation mechanisms of fivefold twinned structures and computational simulations of lattice distortions and defects. We anticipate it will inspire future studies on fundamental problems such as twin boundary migration and kinetics of structures in 3D at atomic level.

Introduction

Twinning of tetrahedra to form decahedra or icosahedra with fivefold symmetry is common in multiply twinned particles (MTPs). Fivefold twinned structures in nanoparticles have attracted continuous attention in the field not only of crystal growth^1,2,3,4, but also of cluster physics^5,6,7,8,9,10, crystallography^11,12,13,14, physical chemistry^15,16, surface science^17,18, and materials^19,20. For example, Wu et al. reported that the icosahedral Pt alloy catalysts have superior activity toward oxygen reduction reaction compared to single-crystalline octahedra, which may arise from strain-induced electronic effects¹⁶. Han et al. found that Au icosahedral particles show more efficient surface-enhanced Raman scattering properties compared to spherical particles with similar sizes¹⁸. The distinct physical and chemical properties of MTPs are largely due to their chemical sites and associated lattice-misfit strain, which makes the knowledge of their full atomic structures essential. Face-centered cubic (fcc) crystals, having co-planar twin planes enclosing an angle of 70.53° (close to 360°/5), can form fivefold twinned structures including decahedron and icosahedron. To fill the concomitant space gaps between two adjacent (111) faces of the fcc regular tetrahedron with an angle of 70.53°, internal distortion needs to be incorporated to form decahedral or icosahedral MTPs^21,22,23,24. Different competing strain models including homogeneous and inhomogeneous strain models have been proposed mostly based on elastic theory to explain the internal distortion and space-filling mechanism. Homogeneous strain model²⁵ suggests the existence of simple linear displacement in crystal lattice. On the other hand, inhomogeneous strain distributions have been observed with evidence of dislocations^26,27,28 and disclinations^20,29. In addition to the internal strain, the final crystallographic symmetry is further determined by a subtle balance between surface and volume contributions to the total energy of the MTPs^30,31. The elastic strain energy resulting from the atomic distortion can be compensated by reducing surface energy through optimal surface atomic arrangements³¹. Ino and Marks proposed extra crystal planes on the classical decahedron models to reduce surface energy. They achieved the energy balance either by exposing more (100) faces³² or introducing re-entrant planes on the twin boundaries³³. Both models have been recently confirmed in core-shell decahedral MTPs, where extra high-index crystal planes at the corners or edges further reduce the surface energy¹⁴. During the growth of icosahedra, faulted islands and grooves have been observed^1,3. These structures form curved surfaces that lower the surface energy and relieve strain³¹.

Despite a number of experimental and computational studies have been done on the formation mechanisms^34,35, stability^23,24,36,37 and lattice defects^20,21,22 of fivefold twinned structures, the 3D atomic structures and associated local strain of icosahedra are still long-standing problems because the embedded internal structures including distribution of dislocations or disclinations remain unclear due to their structural complexity and limitation of conventional projection imaging techniques. The high-resolution electron microscopy images of atomic columns or lattice fringes from the fivefold directions are commonly employed to elucidate the atomic structures of MTPs. Johnson et al. confirmed the presence of disclinations and inhomogeneous strain distribution with shear gradients through geometric phase analysis based on two-dimensional (2D) projection images²⁰. Narayan et al. found the boundaries of fivefold diamond microcrystallites contain coherent twins with occasional presence of dislocations to accommodate the misfit³⁸. Li et al. proposed oriented attachment of small crystal domains induces fivefold twins using in situ electron microscopy⁴. While these experimental observations are predominantly based on 2D projections, the internal structures were not obtained. Recent advances in the atomic resolution electron tomography (AET)^39,40,41,42 offer a method to visualize the internal atomic structures of nanomaterials in 3D and even in 4D. Chen et al. observed the 3D core structure of edge and screw dislocations releasing strain in Pt decahedral MTP¹¹. More recently, Peltz et al. studied the transient 3D structures of a Pd MTP, in which a large number of defects have been revealed qualitatively including disordered regions present mostly on the particle surface¹³. However, although experimental studies show that the strains are inhomogeneous in fivefold MTPs, quantitative measurements of 3D inherent atomic misfit and strain were not obtained, further precluding a thorough understanding of the phenomenon.

Here, by determining the 3D atomic coordinates of gold-palladium MTPs, we show that the 3D angular deficiency in fivefold twinned icosahedral nanoparticles (ICNPs) is compensated by the insertion of edge dislocations and amorphization of several tetrahedra. A geometrically fivefold face (C5 side) consistently corresponds to a less-ordered face (C5′ side), forming two structurally distinct hemispheres. The solid angles of disordered amorphous domains are significantly larger than those of the ideal fcc domains, relaxing a large amount of strain and filling up the angular defects. We also discover a two-sided heterogeneity in a variety of structural characteristics including local bond orientation order (BOO), bond length, distribution of dislocations, and solid angle and size of tetrahedra. The observations of Janus-like structural heterogeneity are corroborated with molecular dynamics (MD) simulations of the atomic structures of Au nanoparticles after annealing in liquid–solid phase transitions. Our research has unveiled a strain model in which some tetrahedra on one side of the ICNP are transformed to disordered structures to release the intrinsic strain, while the rest of tetrahedra on the other side remain almost ideal fcc. This work provides insight into atomistic models for understanding the formation mechanisms of fivefold and icosahedral twinned structures.

Results

Two-sided distribution of local ordering in Janus-like ICNPs

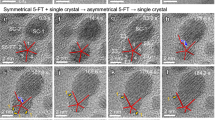
When twinning single-crystalline fcc tetrahedron to form icosahedron, the space-filling is not complete and there is an inherent spatial gap of 7.35° between two adjoining tetrahedra in every fivefold direction (Fig. 1a). Gold MTPs, coated with a thin shell of palladium, were synthesized⁴³ and deposited on thin Si₃N₄ film for high-resolution imaging (“Methods”). As the gold atoms are mobile under the electron beam^44,45, we have deposited a thin layer (2–3 layers) of palladium shell on the gold particle epitaxially to immobilize the surface atoms for better image quality. It was concluded that small MTPs can exhibit many configurations according to local minima in potential energy⁴⁶. Our scanning transmission electron microscopy (STEM) images reveal that the MTPs have similar diameters but exhibit various crystalline structures. We have analyzed over 100 nanoparticles using 2D high-resolution STEM images and found 61 icosahedra (IH), 21 polycrystals (PC), 13 crystals with stacking fault (SF), and 5 decahedra (DH) structures (Supplementary Fig. 1). These findings agree with refs. ^13,47 in which IH configuration could dominate the final crystalline structures in MTPs under certain synthesis conditions. To study the internal structures of MTPs to a large extent, we randomly selected 13 Au@Pd nanoparticles and obtained their atomic coordinates and chemical species using AET with the following procedures. The tomographic tilt series were acquired with aberration-corrected STEM in annular dark-field mode (Supplementary Table 1, “Methods”). Two representative tilt series of ICNPs with I_h center and without I_h center are shown in Supplementary Figs. 2 and 3, respectively. After drift correction and denoising of the raw images, we reconstructed the tomographic tilt series using an iterative reconstruction algorithm⁴⁰ (“Methods”) and obtained the 3D intensity volume (Fig. 1b and Supplementary Fig. 4); we then traced the 3D atomic coordinates and classified the chemical species (Supplementary Fig. 5) of all individual atoms (Supplementary Table 2, “Methods”). Due to the missing wedge effect and noise, some surface atoms (≈5%) were identified as non-atoms due to their weak intensity or the atoms were misclassified due to irregular distribution of atomic intensities. To improve the atom tracing and classification, we performed local re-classification^14,40 and manual correction⁴⁰ to get the final atomic models (“Methods”). The total corrected atoms are less than 10% of the total atoms in the whole particle (Supplementary Fig. 6). Most of the manually corrected atoms are distributed on the surface of some regular tetrahedra from the missing wedge direction (Supplementary Figs. 6 and 7). These atoms have little impact on the overall structure and some key internal structural features such as grain boundary and dislocations (Supplementary Fig. 8). Eight out of 13 particles are ICNPs (ICNPs 1–8) and seven of those (ICNPs 1–7) have an I_h center atom. We also found one DH particle which has only one fivefold axis, three PC particles, and one SF particle among the 3D structures of 13 particles (Supplementary Table 2). We focus on the ICNPs in this work. As all the ICNPs share similar structural characteristics, we select one of the seven ICNPs (ICNP-1) with I_h center to show the detailed structures. From the reconstructed slices (Fig. 1c, d) and isosurface rendering of atoms in a tetrahedral domain (Fig. 1e), the atom positions are clearly resolved. The five hexagonal close-packed (hcp) boundaries converge to form fivefold axes, exhibiting perfect fivefold coordination environment (Fig. 1c), dislocation insertion and grain boundaries slipping (Fig. 1d). We calculated the BOO parameters of all atoms in all ICNPs to distinguish between the disordered, fcc and hcp structures (Supplementary Fig. 9). For a better comparison, we built a geometrically perfect icosahedron with layer-by-layer homogeneous expansion of all atoms and calculated its BOO (Fig. 1f). Instead of forming a geometrically perfect icosahedron with homogeneous expansion, the ICNPs exhibit two-sided distribution of BOO in two hemispheres with distinct Janus-like faces (Fig. 1g, h, Supplementary Fig. 9). This ICNP-1 has one hemisphere featuring six ideal fivefold axes labeled as C5. The opposite hemisphere exhibits six pseudo-fivefold axes labeled as C5′. As illustrated by the BOO parameters (Fig. 1g, h), one face has higher order than the other. The C5 side exhibits a geometrically nearly-perfect icosahedral face with 10 tetrahedra (Fig. 1i, k, and Supplementary Fig. 10a). The C5′ side contains stacking faults and edge dislocations at the twin boundaries, achieved through grain boundary slipping and edge dislocation insertion (Fig. 1j, l, Supplementary Figs. 10b and 11, and Supplementary Movie 1). The adjoining tetrahedral domains share an hcp twin boundary, and five domains share a common edge (Fig. 1i, j, Supplementary Fig. 9). Out of 20 tetrahedra in ICNP-1, 18 have fcc single-crystal structures with varied sizes (Supplementary Table 3), except for two small domains on the C5′ side. The normalized local BOO parameters of the atoms are around 0.5 within the two domains (Fig. 1j, Supplementary Fig. 9), indicating their amorphous nature (“Methods”). The pair distribution function of each domain indexed from 1 to 20 exhibits the transition from crystalline fcc structure to amorphous structure (Supplementary Fig. 12a). It is notable that all the other ICNPs exhibit similar Janus-like morphology with two-sided distribution of BOO (Supplementary Fig. 9) despite each of them has different specific defects.

Fig. 1: 3D atomic structures of ICNP-1.

a Schematic shows the spatial gap of fivefold twinned structures in 2D (upper) and 3D (lower). b–d Volume rendering of the reconstruction of ICNP-1 (b). Two 3-Å-thick slices of the 3D reconstruction in [110] directions from (b) show the fivefold coordination environment (c, with red frame), and dislocation insertion and grain boundaries slipping coordination environment (d, with blue frame). The red, blue, and purple dots in (c, d) highlight the atom positions in fcc domain, hcp grain boundary, and fivefold structures, respectively. Scale bar: 1 nm. e Volume isosurface rendering of the atoms in one tetrahedral crystalline domain. f Distribution of the BOO parameter in the geometrically perfect icosahedral particle where six fivefold axes go through the I_h center. The BOO parameters uniformly distributed in the surfaces: fcc atoms have a high BOO (red), hcp boundary atoms exhibit a lower BOO (pink), the atoms in fivefold axis and their coordination atoms have a much lower BOO (white and blue). g Distribution of the BOO parameter in ICNP-1; the dashed line separates the C5 and C5′ faces. h Unwrapped surfaces of 20 domains (each tetrahedral domain has been assigned a number) of ICNP-1 with averaged normalized BOO parameters separated from the C5 and C5′ side. i, j 3D atomic structure of ICNP-1 viewed from two distinct angles. Local atomic coordination environments are colored by the legend at the bottom. Scale bar: 1 nm. k, l The schematic of the grain boundary frame in ICNP-1 viewed from two distinct angles with hcp in blue and fcc in yellow. The red and green dots represent the ending atoms in fivefold and sixfold axis, respectively. The blue, yellow, and purple dots are atoms with hcp, fcc, and D_h symmetry, respectively. The balls in the atomic model with yellow, blue, light purple, dark purple, and white color represent the atoms with fcc, hcp, D_h, I_h, and amorphous structures, respectively. The balls in the atomic model with red and green color represent the ending atoms in fivefold and sixfold axis, respectively. Source data are provided as a Source Data file.

Coordination environment of fivefold axis

In ICNP-1, the 12 axes—comprising six C5 and six C5′ axes—converge precisely at one center atom, forming the intersection (Fig. 2a). The center atom, exhibiting I_h symmetry, is shared by two intersecting decahedra. The 12 coordinated D_h atoms collectively form a distorted icosahedron (Fig. 2b). The C5′ axes are noticeably curved, bending away from the central direction, contrasting with the straight extension of the C5 axes (Fig. 2c, d, Supplementary Fig. 13, and Supplementary Movie 2). We observed three types of distortions near the axes to fill the inherent spatial gap. One is homogeneous expansion in the C5 axes (Fig. 2e), and the other two are pure edge dislocations (Fig. 2f), and edge dislocation accompanied with one-atom-distance shift of the fivefold axes in the C5′ axes (Fig. 2g). Two types of atom columns composed of one C5 axis and one C5′ axis are shown in Fig. 2c, d; and their corresponding slices are shown in Supplementary Fig. 14. The six C5 axes share a similar expansion pattern (Fig. 2e), characterized by a local twelve-coordination environment, forming two decahedra like the fivefold axes in decahedral nanoparticles¹⁴. Conversely, the other side of the particle features edge dislocations, which expand the angles of fivefold axes to form pseudo-fivefold C5′ axes (Supplementary Fig. 11). These C5′ axes exhibit a deviation from the regular decahedral configuration, forming a distorted coordination polyhedron with varied coordination numbers (Fig. 2f, g). Additionally, the edge dislocation squeezes into the neighboring crystal domains, resulting in a significant increase in the distance between two atoms in the same layer (connected with dashed red line in Fig. 2f, g); these two atoms are no longer bonded. In three of the six C5′ axes (axis-1, 3, 6 in Supplementary Fig. 13), an extra atomic column is inserted into the decahedra, resulting in 13-coordination environment (Fig. 2f). The remaining three C5′ axes demonstrate further distortion (axis-2, 4, 5 in Supplementary Fig. 13), where the edge dislocation disrupts the original axes, forming a new parallel fivefold atomic column comprised of D_h atoms (Fig. 2d, g). The hcp atom in the original C5′ axes direction shares a vertex (as marked in Fig. 2g) with the D_h atoms located at the parallel column of C5′ axis (Fig. 2g). Similar Janus structure is observed in ICNPs 2–7, possessing 12 axes and a geometrically perfect I_h center (Supplementary Fig. 15). In this type of ICNPs, it is interesting that a simple expansion on the C5 side is invariably paired with a complex C5′ side containing edge dislocations. Edge dislocations alter the coordination of the axial atoms, resulting in the change of bond lengths in the coordination polyhedra to accommodate the angular expansion accordingly.

Fig. 2: The two-sided coordination environment and bond length distribution in the fivefold axes.

a Twelve axes of ICNP-1, consisting of six C5 and six C5′ axes, with ending atoms marked as red and green, respectively. b Front and top views, and atomic slices through the raw reconstruction of the central icosahedron, enlarged from the black box in (a). Scale bar: 1 nm. c, d Two types of atom columns composed of one C5 axis and one C5′ axis. The edge dislocations change the coordination of axial atoms either to become 13-coordinated pseudo-D_h atoms (c), or to slip into the adjacent parallel column to form a new axis (d). e–g Front and top views, and atomic slices through the raw reconstruction of the repeating coordination units, enlarged from the blue, green and purple box in (c, d), respectively. The gray shadows highlight the coordination planes above and below the center atom. Scale bar: 1 nm. h An ideal decahedron consisting of three types of atomic bonds. The α, β, and γ represent the capping, capping-ring, and ring atom bonds, respectively. i The deviations of averaged bond lengths of α (yellow), β (dark green), and γ (light green) from the outer surface of C5′ axes to the outer surface of C5 axes, by subtracting the standard Au–Au bond length (2.88 Å). The distance between two neighboring D_h atoms, α, is more and more compressed from C5 axes to C5′ axes. β remains compressed in C5 axes but becomes stretched in C5′ axes. The γ bonds are stretched in both C5 and C5′ axes. The error of averaged bond length of α, β, and γ bonds are estimated using the standard deviation of the bond length (Supplementary Note 2). The confidence interval in (i) is 95%. The balls in the atomic model with yellow, blue, light purple, and dark purple color represent the atoms with fcc, hcp, D_h, and I_h structure, respectively. The balls in the atomic model with red and green color represent the ending atoms in fivefold and sixfold axis, respectively. Source data are provided as a Source Data file.

To quantitatively compare the differences between the two faces of the Janus ICNPs, we analyze the distortion in the twelve axes of each crystal domain. We quantified the deviations in three specific bond lengths (“Methods”, Fig. 2h) within the decahedron in 12 axes relative to the standard Au–Au bond length. The deviations of all three bond lengths are less pronounced in the C5 axes compared to the C5′ axes (two-sided distribution). The deviation maps show that the capping atom bond α is compressed while the ring atom bond γ is stretched to fill the gap on the C5′ side (Fig. 2i, and Supplementary Fig. 16). The capping-ring atom bond β remains compressed in C5 axes but becomes stretched in C5′ axes due to the bending of the atom columns of C5′ axes. The γ bonds are stretched in both C5 and C5′ axes. The stretching of γ is particularly severe due to the insertion of edge dislocations in C5′ axes, with a 9% increase from the center to the surface of the C5′ axes (Fig. 2i). The expansion of γ fills up the angular and spatial gap in the axes. Janus ICNPs 2–7 have a similar coordination environment in the fivefold axis and two-sided distributions in bond length (Supplementary Fig. 17a–e).

We have determined the precisions (evaluated by root mean square deviation (RMSD)) of AET measurements of all the 13 MTPs and 10 atomic models obtained from MD by comparing the experimental models with the simulated models obtained from multi-slice simulation (Supplementary Note 1, Supplementary Tables 5 and 6). The RMSD numbers are below 15 pm which is slightly lower than reported in ref. ¹⁴ (Supplementary Fig. 18). We also calculated all the standard deviations of measured bond length in the experimentally measured nanoparticles (Supplementary Table 5). We found the significant difference in the bond lengths between C5 and C5′ sides using the Mann–Whitney U test (Supplementary Notes 2 and 3, Supplementary Tables 7 and 8), indicating the structures are different in C5 and C5′ sides.

Solid angle distribution and space-filling mechanism

To investigate the space-filling mechanism in icosahedra-like MTPs, we determined the solid angles of all 20 tetrahedra within ICNP-1 (Fig. 3a–c, “Methods”). We assigned numbers to all the 20 tetrahedra and connected adjacent ones, constructing a dodecahedral framework (Fig. 3b). Domains 1 and 20, located at the central positions on the C5 and C5′ sides, respectively, are symmetrically distributed within ICNP-1. On the C5 side, the solid angles of most crystal domains are close to 31.6° which corresponds to the angle in the standard fcc lattice. However, the solid angles of domains on the C5′ side are predominantly larger than 36°, corresponding to the angle in geometrically perfect icosahedron (Fig. 3a). It’s notable that the solid angles follow a hierarchical distribution (Fig. 3c, Supplementary Table 9). The central domain 20 has the largest value of 50.6° while its three adjacent domains (domains 17, 18, and 19) are in the group with the second largest solid angles (39.6°, 40.5°, and 39.6°, respectively). The number of atoms vs. solid angles of all 20 tetrahedra show different trends for C5 and C5′ sides. A 3D rendering of all 20 tetrahedral domains visualizes their two-sided distribution in size (Fig. 3d). The tetrahedra on the C5 side pack closely with the standard fcc structure, containing more atoms, whereas those on the C5′ side have fewer atoms but exhibit larger solid angles (Fig. 3e). Rather than uniformly expanding to fill the inherent angular gap, several tetrahedral domains adopt solid angles larger than 36° to compensate for the 3D angular deficiency. We calculated the atomic packing efficiency (PE) of all tetrahedra in ICNP-1. Although all of them are smaller than the PE of perfect fcc packing, the averaged PE shows a two-sided distribution and drops about 5% from the C5 side to the C5′ side (Supplementary Table 11). The PEs of domains 19 and 20 are lower than random close packing (64%)^48,49, indicating the atoms are loosely packed in these two domains to form amorphous structures. ICNPs 2–4 have a similar two-sided distribution in number of atoms (size), solid angles of tetrahedral domains and PE too (Supplementary Fig. 17f, Supplementary Tables 4, 10 and 12). We found that almost all the ICNPs exhibit similar trends in solid angle and atom numbers of tetrahedral domains from the C5 side to the C5′ side: the solid angle increases (Fig. 3f), while the atom number decreases (Fig. 3g).

Fig. 3: The distinct structural characteristics distinguishing the C5 side and C5′ side.

a The schematic of the solid angle of an ideal tetrahedron in a regular icosahedron. b The solid angle distribution of 20 crystal domains in ICNP-1. The dodecahedral framework is constructed by connecting adjacent tetrahedra. The color and size of the vertices represent the magnitude of solid angles. c Unwrapped surfaces of 20 domains of ICNP-1 with solid angles in both C5 and C5′ sides. d 3D rendering of 20 tetrahedral domains from C5 side to C5′ side, divided into 6 groups based on their relative distance to domain 1 and connectivity including 1 (domain 1, color red), 3 (domain 2–4, color orange), 6 (domain 5–10, color pink), 6 (domain 11–16, color gray), 3 (domain 17–19, color light blue) and 1 (domain 20, color blue) domains, respectively. e Number of atoms in each domain of four ICNPs plotted against the solid angle. f The general increasing distribution of solid angle from C5 to C5′ side drawn with four ICNPs. g The general decreasing distribution of number of atoms from C5 to C5′ side drawn with four ICNPs. In (e, f), we counted the statistics in ICNPs 1-4 in which all 20 tetrahedra can be easily recognized. In the other four ICNPs, some of the tetrahedra merge and grow into big domains, which we excluded from our statistics for comparison. The confidence interval in (e–g) is 95%. Source data are provided as a Source Data file.

Strain tensor distributions in the C5 and C5′ sides

Strain tensor maps were measured based on the 3D coordinates of ICNPs. We employed the Green-Lagrange strain tensor to estimate the strain of this nanoparticle (“Methods”). To improve signal-to-noise ratio, we applied a Gaussian smoothing on the strain tensor with a kernel size of ≈3 Å. We estimated the error of strain measurement using the accuracy of AET reconstruction. For most of our measured MTPs, the error of strain is ≈5% (“Methods”, Supplementary Fig. 19). The local strains between the C5 and C5′ sides of the whole icosahedron were compared. All six components of the full strain tensor in ICNP-1 exhibit block-like distribution, each corresponding to an individual tetrahedron (Fig. 4a, b). Generally, the strain magnitudes are larger on the C5′ side. Additionally, the distributions of shear strains ε_yz and ε_xz on the C5′ side exhibit a bimodal pattern (Fig. 4c), indicative of the expansion of the small crystal domains. Beyond edge dislocations, the distortion of the fcc lattice on the C5′ side crucially addresses angular mismatch due to packing fcc tetrahedra into an icosahedron. While the overall strain configuration and dislocations present in ICNP-1 can account for most of the concomitant space gaps, two tetrahedra on the C5′ side become amorphous to bridge the remaining space gap. ICNPs 2–7 exhibit similar strain tensor distributions (Supplementary Fig. 20). Amorphization of several tetrahedral domains is observed in ICNPs 2–7 (Supplementary Figs. 9 and 15). Our strain analysis indicates that the internal stress on the C5′ side is significant enough to introduce amorphization in one or more of the tetrahedra-like domains.

Fig. 4: The full strain tensor distributions of ICNP-1.

a Atoms in ICNP-1 used to determine the 3D strain tensor, where the atoms in white from the amorphous domains and the surfaces are excluded for strain measurement. The balls in the atomic model with yellow, blue, and dark purple color represent the atoms with fcc, hcp, and I_h structure, respectively. The Z-axis is determined parallel to the perpendicular direction of the {111} planes in domain 1 and domain 20 (Supplementary Fig. 21). Scale bar: 2 nm. b Maps of the six components of the full strain tensor, with the same block-like distribution as crystal domains in (a). The white atoms show where the strain tensor cannot be determined due to the lack of reference lattice. The dashed line highlights the hcp grain boundaries. c The histogram of six components of the full strain tensor on both C5 (red) and C5′ sides (blue), the strain tensor is mostly larger on the C5′ side. d Scatter plot of six components of the full strain tensor vs. distance from core to surface. Source data are provided as a Source Data file.

We further investigate the expansion of all the tetrahedra. The radial distributions of strain tensor in ICNP-1 exhibit more scattered from the core to the surface (Fig. 4d); and it agrees with the distribution of all bond lengths in radial direction, which is asymmetrically distributed along Au–Au bond length of 2.88 Å (Supplementary Fig. 22), showing nearly half of the bond lengths are stretching and the other half is compressing. A gradual increase of strain (both tensile and compressive strain) is observed within the particle from core to surface, which is needed to preserve geometric configuration during growth. To explore how the atoms expand, we analyzed the principal strain relative to the different crystallographic orientations of tetrahedron (Fig. 5a). We found that the direction of the tensile strain is along the tangential direction of the tetrahedral crystal region ((111) face) while the direction of the compressive strain is along the radial direction of the tetrahedral crystal region (<111> face) (Fig. 5b, c). From one atomic slice from the whole particle, it is clear that the expansion in the (111) crystallographic planes and the compression in the <111> family of crystallographic directions (Fig. 5d, e). We also calculated the distribution of these two strains for all 13 particles (Supplementary Fig. 23); the tensile strain and the compressive strain in ICNPs exhibit a bimodal distribution (Fig. 5f, Supplementary Fig. 23). In the DH MTPs, the bimodal distributions are less pronounced; in the SF and PC MTPs, there is almost no difference between the two types of strain. (Fig. 5g, Supplementary Fig. 23). The directional increase of tensile and compress strain at the surface is a property specific to the icosahedron. Our results show the dilation of the tetrahedron almost happens in the (111) direction, and the compression is in the <111> direction.

Fig. 5: The direction of principal strains.

a The 2D (upper) and 3D (lower) schematic diagram of (111) face and <111> face in the tetrahedron, marked by red and blue arrows, respectively. The direction of tensile strain (b), and compressive strain (c) in a tetrahedral domain, and the tensile strain is along the tangential direction of the tetrahedral crystal region ((111) face) while the direction of the compressive strain is along the radial direction of the tetrahedral crystal region (<111> face). The distribution of tensile strain (d) and the compressive strain (e) in a slice with thickness of 3 Å. The inset shows the position of the slice in ICNP-1. The histogram of tensile strain (pink) and compressive strain (light purple) along the tangential direction (e_θ) and radial direction (e_r) in ICNP-1 (f) and SF configuration (g). The deep purple part shows the overlapping of tensile strain and compressive strain. Source data are provided as a Source Data file.

Janus ICNP without I_h center atom

We discovered another type of Janus ICNP without an I_h center atom (Fig. 6a, b). ICNP-8 is a Janus particle with eight axes, including three fivefold (C5) axes, three pseudo-fivefold (C5′) axes, and two sets of twin axes (Supplementary Fig. 24). Notably, these axes do not converge into a single common I_h atom. In ICNP-8, we designate the two faces, A and B. Unlike ICNPs 1–7, ICNP-8 lacks symmetrically distributed C5 side and C5′ side. Face A exhibits an icosahedra-like structure, composed of 10 fcc tetrahedra with three C5 axes and two sets of twin axes (Fig. 6a), contrasting with the six C5 axes in ICNPs with I_h center. Face B consists of four distorted tetrahedra and three large fcc domains; each large domain is made of two tetrahedra-like grains without hcp grain boundaries (Fig. 6b). Three small tetrahedra-like grains have amorphous structures (Fig. 6b, and Supplementary Fig. 9). The hcp grain boundaries, combined with specific fcc atoms coordinated to the C5′ axes, construct an icosahedra-like framework (Supplementary Fig. 24c). Instead of one-atom-distance, the hcp grain boundaries slip two-atom-distance in this particle, breaking the fivefold axes to form a morphology of splitting “3 hcp + 2 hcp” grain boundaries around the twin axes (Supplementary Fig. 24a, b). In C5 + C5′ twin axes, one column composed of D_h atoms and the other column composed of pseudo-D_h atoms are split by two columns of fcc atoms (Fig. 6c, e, and Supplementary Fig. 24a). The twin axes of C5′ + C5′ are composed of two columns of pseudo-D_h atoms. One column is 12-coordinated with seven atoms forming a top ring and five atoms forming a bottom ring (left blue boxes in Fig. 6f); the other column possesses the same 13-coordinated environment cluster (right orange box in Fig. 6f) as shown in Fig. 2f. In addition, two hcp atomic layers slip by one-atom-distance (Supplementary Fig. 24b). The twin axes end in a disordered boundary domain composed of D_h atoms and hcp atoms (Supplementary Fig. 24e) and then continue to connect with a large grain in which most atoms have an fcc structure. The disordered boundaries are composed of fivefold and sixfold skeletons, marked as red and green, respectively (Fig. 6c, d, and Supplementary Fig. 24). Compared to ICNPs 1–7, ICNP-8 has a less-ordered side with completely different morphology, suggesting multiple pathways can occur during the growth of icosahedra-like MTPs.

Fig. 6: 3D atomic structure of the ICNP-8 without an I_h center atom.

a, b The two distinct faces of the icosahedra-like particle with eight axes, including three fivefold axes, three pseudo-fivefold axes, and two sets of twin axes. In Face B, each of four distorted tetrahedra is marked with a small red triangle. Three large fcc domains are marked with black lines; the black dash lines illustrate the two tetrahedra-like grains without clear hcp grain boundaries. Scale bar: 1 nm. The atomic structures of two sets of twin axes, C5 + C5′ (c) and C5′ + C5′ (d). The bonds in five-atom rings and six-atom rings are marked red and green, respectively. e, f The front view and top view of the repeated coordination unit of (c) and (d), respectively. The dashed line box in (f) highlight the coordinated atoms of the center pseudo-D_h atom. The balls in the atomic model with yellow, blue, light purple, dark purple, and white color represent the atoms with fcc, hcp, D_h, I_h, and amorphous structures, respectively. The balls in the atomic model with red and green color represent the ending atoms in fivefold and sixfold axis, respectively.

Janus-like ICNPs corroborated with MD simulation

Our analysis of the ICNPs reveals the two-sided heterogeneity in a variety of structural characteristics, making the ICNPs Janus-like particles. Figure 7a and Supplementary Movie 3 show the C5 and C5′ sides of ICNPs 3–7. All the ICNPs exhibit Janus-like morphology, accompanied by various degrees of amorphization. In addition, we show the atomic structures of all the rest 10 MTPs for better comparison (Fig. 7a). To corroborate our experimental observations, especially to verify the structural variety in IH configurations, we performed MD simulations on the liquid–solid phase transition of gold nanoparticles using the large-scale atomic/molecular massively parallel simulator (LAMMPS). By annealing gold nanoparticles with a similar size to ICNP-1 from 1500 to 300 K, 100 times, we obtained 100 different structural configurations, comprising IH, DH, SF, and PC structures (Fig. 7b, c, and Supplementary Fig. 25). We find that the IH configuration exhibits Janus-like morphology with two distinct faces. A geometrically more icosahedra-like hemisphere consistently contrasts with the other corresponding hemisphere that displays disordered morphology (Fig. 6c). This observation corroborates with our experimental Janus-like ICNPs. We also calculated the potential energy of different configurations and found that IH configurations are comparable to PC configurations. However, it is larger than the energy observed in both DH and SF configurations. We have compared the averaged BOO parameter of all atoms with the potential energy of all 100 configurations, finding that the more fcc-ordered particles possess a lower potential energy (Fig. 7d). It has been reported that small particles do not necessarily correspond to a single stable structure⁴⁶; the experimental Janus-like IH structures we obtained are one of the possible multitude configurations according to local minima in potential energy. The particle configurations fluctuate with the annealing conditions. The predominance of icosahedral configurations has been reported under certain synthesis conditions^13,47. Although IH structure has a higher calculated potential energy, we obtained a higher probability of IH particles under our synthesis conditions, which may result from multiple factors such as kinetic trapping effect, kinetic competition between different structures, and low kinetic barriers of surface nucleation^50,51,52.

Fig. 7: Experimental 3D reconstruction results of Au@Pd nanoparticles (ICNPs 3–7 and particles 9–13) and MD simulation of liquid–solid transition of gold nanoparticles.

a 3D atomic structures of Au@Pd nanoparticles with different morphologies. All the ICNPs exhibit Janus-like morphology; the rest particles include five MTPs, with one DH particle having a single fivefold axis, three PC particles with more than one fivefold axis, and one SF particle with a stacking fault. Scale bar: 2 nm. b The schematic of the annealing process of gold nanoparticles from 1500 to 300 K. c The four major types of morphologies in annealed gold nanoparticles with 3580 atoms. The icosahedra-like particle has two distinct faces like experimental ICNPs. Scale bar: 2 nm. d The normalized potential energy plots against the averaged BOO parameter of each simulated particle. The orange, light purple, magenta, and green dots represent particles with DH, IH, PC, and SF configuration, respectively. The balls in the atomic model with yellow, blue, light purple, dark purple, and white color represent the atoms with fcc, hcp, D_h, I_h, and amorphous structures, respectively. The balls in the atomic model with red and green color represent the ending atoms in fivefold and sixfold axis, respectively. Source data are provided as a Source Data file.

Discussion

We resolved the 3D atomic misfit and the angular compensation of fivefold icosahedral MTPs with Janus-like morphology using AET. A geometrically near-ideal fivefold face is consistently paired with a less-ordered face, forming two hemispheres in the ICNPs. Many structural characteristics are two-sided distributed in the two hemispheres of the ICNPs. Our findings reveal two mechanisms that compensate for the inherent atomic misfit and angular deficiency in icosahedra-like MTPs. These are: (i) Inserting an edge dislocation in the C5′ axes to alter the original axial atomic coordination. (ii) Sacrificing several tetrahedra-like crystal domains to become amorphous, thereby releasing the strain.

Our observations show that the two-sided heterogeneity in a variety of structural characteristics and the amorphization of certain small crystalline domains play a crucial role in strain relaxation and angular filling. This phenomenon could further support and supplement the successive twinning growth mechanism of icosahedral MTPs^1,2,4. During the growth process of the icosahedron, first nearly-perfect tetrahedral domains twin with (111) facets, forming a geometrically ideal face corresponding to the ordered C5 faces we observed in the ICNPs. Subsequently, when further twinning introduces more tetrahedral domains, the inherent spatial gap results in the formation of dislocations or stacking faults, such as those in C5′ faces. Furthermore, the newly attached tetrahedral domains deviate from a regular tetrahedron increasingly more, adapting their solid angles to accommodate the dilated angle. When the distortion and internal strain increase beyond a certain point, amorphization of tetrahedra occurs, further filling the remaining grooves and releasing the strain. This work has unveiled how the spatial gap of the icosahedron is compensated at the 3D atomic scale and provides clear experimental 3D atomistic models for future modeling of formation mechanisms of fivefold symmetry and computational simulations of defects in multiple twinned structures.

Methods

Sample preparation

The gold seeds are synthesized following ref. ⁴³. 82.3 mg (0.2 mmol) HAuCl₄·3H₂O (99%) was dissolved in 7 mL cyclohexane (99.7%) and 7 mL oleylamine (90%), stirred for 15 min at room temperature. 34.8 mg (0.4 mmol) TBAB (99%) was dissolved in 1 mL cyclohexane (99.7%) and 1 mL oleylamine (90%), sonicated for 5 min to accelerate the dissolution, injected into HAuCl₄ solution quickly, stirred for 1 h at room temperature to obtain 4 nm Au seeds. The Au seeds solution was centrifuged at 16,100 × g for 10 min and then re-dissolved in 4 mL cyclohexane (99.7%). We added 15 mL oleylamine (90%) to the above obtained Au seed solution and heated it to 150 °C. 182.9 mg (0.6 mmol) Pd(acac)₂ (98%) was dissolved in 1 mL oleylamine (90%) and quickly injected into the pre-heated Au seed solution, stirred for 2 h, centrifuged at 16,100 × g for 10 min and washed with ethanol (99.7%) 7 times. The final MTPs were re-dissolved in cyclohexane (99.7%).

Data acquisition

After depositing on thin Si₃N₄ film, we performed plasma cleaning on the particles to avoid any possible contamination during the data acquisition. The tilt series of each particle was acquired using an aberration-corrected FEI Titan Themis G2 300 electron microscope with an electron acceleration voltage of 300 keV. To obtain high-quality STEM images and to reduce damage to the sample, a fiducial particle nearby was used to adjust the residual aberration and focus. The electron dose used for the ICNPs was at ≈10⁵ e⁻ Å⁻², which has been demonstrated as a safe electron dose to prevent the damage to bimetallic nanoparticles^14,40,41. To minimize sample drift, we acquired three sequential images at each angle with a dwell time of 2 μs.

Image pre-processing and tomographic reconstruction

The three sequential images acquired at each angle were registered by cross-correlation and then averaged to one image so that the linear stage drift introduced during the scanning process could be corrected¹⁴. To eliminate the effects of Poisson noise and Gaussian noise, the registered images are denoised by the block-matching and 3D filtering (BM3D) algorithm⁵³. We tested different denoise parameters, selected the parameters that can remove most of the noise and do not obliterate the lattice details information, and applied it to the drift-corrected images.

The pre-processed images were reconstructed using the real space iterative reconstruction (RESIRE) algorithm⁴¹. The R factors converged after 200 iterations. Angular refinement and spatial re-alignment were employed to minimize the angular errors due to sample holder rotation and stage instability. After no further angular correction and reconstruction quality improvement, the final reconstructions were computed.

Determination of 3D atomic coordinates and chemical species classification

The local maxima in the 3D reconstruction were obtained and the peak positions were determined using polynomial fitting performed on a 7 × 7 × 7-voxel volume around each local maximum⁵⁴. The possible atomic positions were determined with the constraints of the minimum inter-atomic distance of 3.45 Å. A 3D polynomial fitting is then performed on the possible atomic positions to determine the exact atomic coordinates. The automatic tracing atoms procedure may encounter fitting failures, particularly when dealing with connected intensity blobs representing multiple atoms. The traced positions may deviate from the actual center position of the atom. For atoms with fitting failure either due to their physical proximity or the absence of an associated atom within a blob, the incorrect traced positions are removed and re-traced again, which we call manual correction. The manual correction is a manually-assisted auto-tracing process, following the same principle as auto-tracing, with the assistance of algorithms. The total corrected atoms are less than 10% of the total atoms in the whole particle. Most of the manually corrected atoms are distributed on the surface of some regular tetrahedra from the missing wedge direction. These atoms have little impact on the overall structure and some key internal structural features such as grain boundary and dislocations. The tracing code is available from Zenodo⁵⁵.

All atoms are classified into Au and Pd by K-means clustering, based on the integrated intensity within the surrounding 7 × 7 × 7 voxels centered at each atom⁵⁶. Due to the effect of missing wedge and noise, some surface atoms were identified as non-atoms due to their weak intensity or the particles were misclassified due to irregular distribution of atomic intensities inside the particles⁴¹. We performed local re-classification and manual correction of the initially classified model to get the final results⁴⁰. The total number of atoms and the classification of the particles are shown in Supplementary Table 2.

BOO calculation

The averaged local BOO parameters, such as Q₄ and Q₆, as well as the normalized BOO parameters for the ideal fcc, and hcp models were calculated using the procedure published elsewhere^41,42. The first nearest-neighbor (NN) shell distance of 3.45 Å was used as a constraint.

Crystal structure determination

The number of NN atoms around each atom, the distance, and relative coordinates to the NN atoms are calculated first, and the ideal fcc, hcp, D_h, and I_h models containing 12 coordinated atoms are built. We do a dictionary lookup between ideal polyhedra at different orientations, and then the iterative closest point (ICP) algorithm^57,58 is used to search for the best transformations between the coordinated polyhedra of each atom and the ideal model. If the distance between the coordinated atom and its nearest model atom is less than the radius of the atom, the coordinated atom will be paired with the center atom. A similarity score will be given to the center atom based on the similarity between the coordinated polyhedra and the ideal model, where the score for each class of polyhedra is an order parameter defined as

$${s}_{k}={\sum }_{j=1}^{12}\max (1-\frac{|{{{{\bf{r}}}}}_{j}-{{{{\bf{r}}}}}_{k}-{{{\bf{m}}}}{{{{\bf{p}}}}}_{j}|}{{d}_{\max }},0)$$

(1)

where s_k is an order parameter for each polyhedron at each site, r_j is the position of the j_th neighboring coordinate to site k at position r_k, m is the rotation matrix for the best transformations, p_j is the polyhedra with 12 vertices, and d_max is the maximum allowed distance of a site from an ideal position.

To compare the scores of different crystallographic textures, the similarity score of the center atom is normalized by the total number of NN-coordinated atoms. The model with the highest similarity score will be assigned as the crystal type of the center atom. If the highest similarity score of possible crystal type is lower than a score threshold of 0.5, the atom will be classified as undefined. We further checked those undefined atoms based on their local crystallographic texture.

Bond length calculation

The atoms categorized as D_h crystal type in the Polyhedron Template Matching (PTM) classification are selected for the calculation of α, β, and γ, in which those with less than 12 coordination numbers are further removed. The coordination polyhedra of each central atom are rearranged in the order of five atoms in the upper plane, five atoms in the lower plane, one atom in the upper vertex, and one atom in the lower vertex by the ICP algorithm. The α, β, and γ of the upper and lower decahedron are calculated for each atom. Each central atom possesses two α bonds, 20 β bonds, and 10 γ bonds, the averaged bond length of α, β, and γ is assigned to the central atom, respectively.

Solid angle and packing efficiency calculation

The categorization of atoms into a specific crystal region is dictated by the directional vectors of three edges, originating from the center icosahedral atom in this region. The representative direction for each edge is determined using principal component analysis⁵⁹. After we obtain the directions of three edges represented by the normalized basis $[{{{{\bf{e}}}}}_{{{{\boldsymbol{1}}}}}{{{{\bf{e}}}}}_{{{{\boldsymbol{2}}}}}{{{{\bf{e}}}}}_{{{{\boldsymbol{3}}}}}]$, the transformed position of every atom relative to the center I_h atom can be written as

$${{{{\bf{p}}}}}^{{\prime} }={[{{{{\bf{e}}}}}_{{{{\bf{1}}}}}{{{{\bf{e}}}}}_{{{{\bf{2}}}}}{{{{\bf{e}}}}}_{{{{\bf{3}}}}}]}^{-1}{{{\bf{p}}}}$$

(2)

where p is the position relative to the I_h atom, and p' is the transformed position. If the elements of p' are all positive with 1/6 distortion tolerance, the atom is in this current region with basis $[{{{{\bf{e}}}}}_{{{{\boldsymbol{1}}}}}{{{{\bf{e}}}}}_{{{{\boldsymbol{2}}}}}{{{{\bf{e}}}}}_{{{{\boldsymbol{3}}}}}]$. Two crystal regions share one common face can be called connected regions. With this connection definition, we can create a graph to represent the connection of 20 crystal regions. The solid angle Ω of each region can be obtained by the basis vectors as follows

$$\varOmega=\frac{|{{{{\bf{e}}}}}_{{{{\bf{1}}}}}^{{{{\rm{T}}}}}\cdot ({{{{\bf{e}}}}}_{{{{\bf{2}}}}}\times {{{{\bf{e}}}}}_{{{{\bf{3}}}}})|}{|{{{{\bf{e}}}}}_{{{{\bf{1}}}}}||{{{{\bf{e}}}}}_{{{{\bf{2}}}}}||{{{{\bf{e}}}}}_{{{{\bf{3}}}}}|+|{{{{\bf{e}}}}}_{{{{\bf{3}}}}}|({{{{\bf{e}}}}}_{{{{\bf{1}}}}}^{{{{\rm{T}}}}}\cdot {{{{\bf{e}}}}}_{{{{\bf{2}}}}})+|{{{{\bf{e}}}}}_{{{{\bf{2}}}}}|({{{{\bf{e}}}}}_{{{{\bf{1}}}}}^{{{{\rm{T}}}}}\cdot {{{{\bf{e}}}}}_{{{{\bf{3}}}}})+|{{{{\bf{e}}}}}_{{{{\bf{1}}}}}|({{{{\bf{e}}}}}_{{{{\bf{2}}}}}^{{{{\rm{T}}}}}\cdot {{{{\bf{e}}}}}_{{{{\bf{3}}}}})}$$

(3)

PE of a crystal region can be calculated by the volume occupied by atoms within the alpha-shaped region. The value of alpha can be set by the first valley of RDF curve. The occupation volume is hard to be calculated directly. As a result, Monte Carlo has been carried out to estimate the PE. The implementation of the Monte Carlo method is as follows: For each grain within the particle, an encompassing envelope is constructed using the alpha-shape method to represent the total volume. Points are randomly and uniformly selected within the space defined by the alpha shape, and the probability of these points falling within the Au atoms is calculated relative to the total number of points. This probability provides the value of PE.

Strain calculation

We employed the similar methods of strain calculation described in ref. ⁶⁰. We employed the Green-Lagrange strain to estimate the strain of this nanoparticle. The strain tensor E can be calculated from the elastic deformation gradient F as follows

$${{{\bf{E}}}}=\frac{1}{2}({{{{\bf{F}}}}}^{{{{\rm{T}}}}}{{{\bf{F}}}}-{{{\bf{I}}}})$$

(4)

The elastic deformation gradient can be directly obtained from PTM. It should be noticed that only the strain tensor of crystalline part can be obtained according to the principle of infinite strain theory in our system. It is not feasible to find a reference lattice for the disordered part. Then, we used the Nadaraya–Watson kernel regression to smooth the strain tensor. The smoothed strain $\hat{{{{\boldsymbol{\varepsilon }}}}}$ was calculated as follow

$$\hat{{{{\boldsymbol{\varepsilon }}}}}({{{{\bf{x}}}}}_{0})=\frac{{\sum }_{i}{{{\boldsymbol{\varepsilon }}}}({{{{\bf{x}}}}}_{i})\cdot {{{\rm{K}}}}({\|{{{{\bf{x}}}}}_{0}-{{{{\bf{x}}}}}_{i}\|}_{2})}{{\sum }_{i}{{{\rm{K}}}}({\|{{{{\bf{x}}}}}_{0}-{{{{\bf{x}}}}}_{i}\|}_{2})}$$

(5)

where ${{{\rm{K}}}}(\cdot )$ is the Gaussian kernel function with the standard deviation σ = 2.884 Å; x₀ and x_i are the positions of one atom, and the ith atoms, respectively; ||⋅||₂ is the L2 norm.

We calculated the magnitude and direction of principal strain by performing the eigen decomposition on the smoothed strain tensor. Then, we calculated the angles θ between the principal strain direction e_s and the radial direction e_r as follows,

$$\theta=\arccos \frac{{{{{\bf{e}}}}}_{{{{\rm{r}}}}}\cdot {{{{\bf{e}}}}}_{{{{\rm{s}}}}}}{|{{{{\bf{e}}}}}_{{{{\rm{r}}}}}|\cdot |{{{{\bf{e}}}}}_{{{{\rm{s}}}}}|}$$

(6)

Error analysis of strain measurements

To estimate the error of strain measurement, we have investigated the relationship between the accuracy of AET reconstruction (evaluated by RMSD), and the accuracy of strain measurement (evaluated by normalized mean absolute error (NMAE)).

The deviations of atomic positions were added to the ground-truth models to simulate the influence of AET reconstruction error on the strain calculation. First, we added a known displacement field onto a ground-truth model to get a ground-truth strain tensor measurement. Since the RMSD analysis from either experiment or simulation models (Supplementary Table 5) shows RMSD ≤ 0.15 Å, we added some random deviations in atomic position from 0.04 to 0.36 Å to the ground-truth models and then calculated the strain. Then we compared the strain differences between ground-truth and error-added models. Using ε_yy as an example, scatters in Supplementary Fig. 19 show the relationship between the ground-truth strain value and the error-added strain. The dashed line shows the location of y = x. The closer the scattered points attach to the dashed line, the more accurate the strain measurement is. With the decrease of AET reconstruction accuracy (i.e., the increase of RMSD), the strain measurement becomes less accurate. We quantify the strain accuracy by NMAE, which is determined by

$${{{\rm{NMAE}}}}({{{\boldsymbol{\varepsilon }}}},\hat{{{{\boldsymbol{\varepsilon }}}}})=\frac{{{{\rm{MAE}}}}({{{\boldsymbol{\varepsilon }}}},\hat{{{{\boldsymbol{\varepsilon }}}}})}{\frac{1}{n}{\sum }_{i=1}^{n}|{\varepsilon }_{i}|}=\frac{{\sum }_{i=1}^{n}|{\varepsilon }_{i}-{\hat{\varepsilon }}_{i}|}{{\sum }_{i=1}^{n}|{\varepsilon }_{i}|}$$

(7)

where ε is the ground-truth strain; $\hat{{{{\boldsymbol{\varepsilon }}}}}$ is the strain measurement with AET reconstruction error; n is the number of atoms; i denotes the ith atom. Supplementary Fig. 19 shows the relationship between the NMAE of strain measurement, and the AET reconstruction accuracy (RMSD of reconstruction). The relative error of strain measurement is 5.2 ± 0.4% when the AET reconstruction accuracy is 0.12 Å.

MD simulation

MD simulations were performed using the LAMMPS. Au nanoparticles, about 5 nm in diameter, consisting of 3580 atoms were annealed from an initial temperature of 1500–300 K, beginning in a liquid state. We employed the many-body embedded-atom method inter-atomic potential for Au atoms. Periodic boundary condition was used with an NVT ensemble. Each simulation was repeated 100 times to ensure accuracy and reproducibility. At first, we took 1 × 10⁵ MD steps (100 ps) at 1500 K to obtain the melted nanoparticle. From 1500 to 300 K, we took 1 × 10⁵ MD steps (100 ps) for every 100 K dropped, and finally, 1 × 10⁶ MD steps (1 ns) were taken at 300 K. The timestep was 1 fs. The final structural configurations are analyzed using the same method as the experimental ICNPs.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.