Abstract
Half-Heuslers emerged as promising candidates for medium- and high-temperature thermoelectric power generation. However, polycrystalline half-Heuslers inevitably suffer from the defect-dominated scattering of electrons that greatly limits the optimization of their electronic properties. Herein, high-quality TiCoSb-based single-crystals with a dimension above 1 cm have been obtained. Benefitting from the improved electron mobility, an average power factor of ~37 μW cm−1 K−2 in the temperature range between 307 and 973 K has been realized in the n-type single-crystalline Ti1-xNbxCoSb. In addition, Hf alloying results in the expansion of the weighted scattering phase space and enhances the anharmonic scattering rate, thereby effectively suppressing the lattice thermal conductivity. Eventually, co-doping of Nb/Ta and alloying of Hf effectively elevate the thermoelectric performance of TiCoSb single crystal, and a peak zT above 1.0 has been realized, which outperforms the previously reported polycrystalline (Ti, Zr, Hf)CoSb-based and ZrCoBi-based materials. Importantly, a single leg of TiCoSb-based single crystals exhibits a heat-to-electricity energy conversive efficiency of ~10.2% at a temperature difference of 700 K. Here, our findings reveal the promise of TiCoSb-based single crystals for thermoelectric power generation, and can potentially guide the future explorations of other single-crystalline half-Heuslers.
Similar content being viewed by others
Introduction
Thermoelectric materials can realize a direct conversion of heat into electricity and vice versa, offering a sustainable solution to energy harvesting and cooling applications1,2. The performance of thermoelectric materials is quantified by the dimensionless figure of merit (zT), zT = S2σT/κ, where S is the Seebeck coefficient, σ is the electrical conductivity, к is the thermal conductivity, and T is the absolute temperature3,4,5,6,7. Half-Heusler materials, with excellent mechanical properties8,9, superior chemical and thermal stability10,11, and reasonably high zTs, have been considered as promising candidates for mid- and high-temperature power generation and their thermoelectric properties have been extensively studied12,13,14,15,16,17,18.
However, polycrystalline half-Hesulers often suffer from the existence of non-equilibrium synthesis-related defects (e.g., point defects, dislocations, and grain boundaries) and secondary phases, which greatly impact the thermoelectric transport properties19,20,21,22,23,24. As an example, the anomalous temperature-dependent electrical conductivity around room temperature in the polycrystalline half-Hesulers indicates the defects play a pivotal role in the electron scattering mechanism25. To reduce the concentration of defects and secondary phases, a time-consuming annealing process is always needed26,27,28,29. Therefore, it would be highly meaningful to study the thermoelectric properties of high-quality single crystals. This not only enables the understanding of the electron and phonon transport mechanism in half-Hesulers but also can potentially improve thermoelectric performance by minimizing undesirable electron scattering from defects.
Challenges in growing the half-Heusler single crystals stem from the high melting points of the constituent elements, the competition from the stable binary phases that prevent the formation of the ternary half-Heusler phase, and the difficulties in minimizing the defects and impurities5,7,19. To date, the flux method has been utilized to obtain half-Heusler single crystals, such as TiNiSn30, ZrNiSn31, TiCoSb32, and other compounds33,34,35. The flux method requires careful control of the dilution ratio, cooling rates, choice of containers, and temperature gradients, to minimize the defects and achieve uniformity in the crystal36,37. While this technique has enabled the growth of half-Heusler single crystals, the size of the obtained crystals is usually less than 3 mm, which precludes the characterization of the thermoelectric properties at elevated temperatures. In addition, systematic studies in the optimization of the thermoelectric performance of single-crystalline half-Heuslers are still lacking.
Herein, high-quality single-crystalline TiCoSb-based half-Heuslers with a dimension above 1 cm have been obtained. Our results demonstrate that Nb and Ta doping in TiCoSb single crystal can effectively optimize the electron concentration. In addition, Hf alloying can greatly intensify the phonon scattering by enhancing the anharmonic scattering rate and significantly reducing the lattice thermal conductivity. Eventually, an average power factor of ~37 μW cm−1 K−2 and average zT of ~0.64 in the temperature range between 307 and 973 K have been realized in the TiCoSb-based single crystals, and outperform the previously reported n-type (Ti, Zr, Hf)CoSb-based and ZrCoBi-based half-Heuslers16,38,39,40,41,42,43. More importantly, a single leg of the single-crystalline TiCoSb-based materials exhibits a heat-to-electricity conversion efficiency of ~10.2% at a temperature difference of 700 K.
Results
Crystal growth of single-crystalline TiCoSb-based half-Heuslers
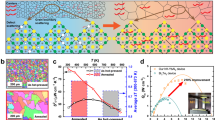
The TiCoSb-based single crystals were synthesized by the flux method. Initially, a slow cooling rate of 0.3 K h−1 was employed to minimize the number of nucleation sites, and it was also essential to avoid unstable growth patterns caused by large supersaturation gradients. Then, a relatively faster cooling rate of 1 K h−1 was employed from 1273 K to 1223 K to balance growth quality and time efficiency. Afterward, an accelerated cooling rate of 2-4 K h−1 was applied until centrifugation to remove the excess Sb flux at 1173 K. This carefully controlled cooling process helped to ensure the formation of high-quality single crystals with minimal defects. The picture of the pristine TiCoSb is shown in Fig. 1a, and the obtained single crystal with shiny surfaces can be as large as 1 cm in one dimension. The pyramid-shaped tetrahedral morphology of the TiCoSb single crystal corresponds to the typical half-Heusler structure, as shown in the inset of Fig. 1a. X-ray diffraction (XRD) pattern obtained on the shiny surfaces of crystals orientated parallel to the (111) planes (Fig. 1b). Scanning electron microscopy (SEM) and energy dispersive spectroscopy (EDS) characterizations confirm the homogeneity in the composition of the TiCoSb single crystal (Supplementary Fig. 1). In addition, single-crystal X-ray diffraction measurements have also been conducted. The single-crystal diffraction pattern of TiCoSb along the [00 l] direction is shown in Fig. 1d. The detailed crystallographic data has been provided in Supplementary Table 1, with the lattice constant determined to be 5.878(2) Å, and the space group identified as \(F\bar{4}3m\). Furthermore, all the atomic site occupancies are in good agreement with the ideal structure. To verify the quality of the single crystal, the rocking curve measurement has been performed by using high-resolution X-ray diffraction. As shown in Fig. 1c, the rocking curve of the (111) peak exhibits an exceptionally narrow full width at half maximum (FWHM) of only ~0.015°, indicating the very low mosaicity and high quality of the TiCoSb crystal. The calculated band structure indicates that TiCoSb is an indirect bandgap semiconductor (Fig. 1e), with the conduction band minimum located at the X point and the valence band maximum situated at the Γ point in the Brillouin zone. The experimentally measured optical bandgap is ~1.20 eV (Fig. 1f), and it is in good agreement with the calculated bandgap, indicating there are no in-gap states in the single crystal. Therefore, the obtained TiCoSb single crystals are of high crystalline quality, and with very low concentrations of impurities and defects.
a Picture of the pristine TiCoSb single crystal and the inset shows the crystal structure of half-Heusler, b XRD measurement on the surface, i.e. the (111) plane, of the TiCoSb single crystal, c the rocking curve measurement performed by the high-resolution X-ray diffraction, d diffraction pattern of the single-crystalline TiCoSb along the [00 l] direction, e electronic band structure of TiCoSb and the partial density of states (PDOS), f optical absorption spectrum of TiCoSb single crystal.
Superior electronic properties of the TiCoSb-based single-crystals
To effectively tune the thermoelectric properties of TiCoSb-based half-Heuslers, the Ti1-xNbxCoSb (x = 0 − 0.12, nominal compositions) single crystals were prepared. The sample of Ti0.97Nb0.04CoSb single crystal is highly uniform (Supplementary Fig. 2) and single phase (Supplementary Fig. 3b). The electrical properties were measured using the four-probe method, and the experimental details were provided in the Methods. The measured electrical properties along (111) of the TiCoSb-based single crystals are shown in Fig. 2. The Nb-doped samples show lower electrical resistivity (ρ) compared to the undoped TiCoSb, and the resistivity decreases with the increasing Nb concentration (Fig. 2a). The room-temperature electrical resistivity of the pristine TiCoSb is as high as ~1 × 10−3 Ω m and the Hall carrier concentration is only ~3 × 1018 cm−3. As the temperature rises from 307 K to 973 K, the resistivity of the undoped TiCoSb shows an initially gradual increase followed by a dramatic decrease, which results from the intrinsic excitation4,44,45. Intrinsic excitation in TiCoSb occurs due to the thermally excited electrons from the valence band to the conduction band, inducing electron-hole pairs that dramatically increase carrier concentration and decrease the resistivity. According to the Hall measurements, the Hall carrier concentration (nH) increases monotonically with the Nb concentration (Supplementary Table 2), which indicates that Nb is an efficient donor for supplying electrons to TiCoSb, similar to the previous report on polycrystalline TiCoSb39,45,46. Accordingly, the Seebeck coefficient of Ti1-xNbxCoSb decreases with the increase of Nb concentration (Fig. 2b). Since band structure remains nearly identical after Nb doping (Supplementary Fig. 4), the increased carrier concentration due to Nb doping effectively elevates the Fermi energy, and resulting in a reduction of Seebeck coefficient (Supplementary Fig. 5). Due to the high quality of TiCoSb single crystals, the power factor (S2σ) has been significantly improved, and a peak power factor as high as ~50 μW cm−1 K−2 can be realized in Ti0.988Nb0.038CoSb (the composition was determined by the electron probe microanalysis, EPMA) at room temperature (Fig. 2c). The power factor gradually decreases with the elevation of temperature, primarily attributed to the deteriorated carrier mobility due to the intensified electron-phonon interaction at higher temperatures47,48,49,50. It is noted that the power factor of the single-crystalline Ti1-xNbxCoSb is much higher than that of polycrystalline (Zr, Hf)CoSb-based half-Heuslers (dashed line in Fig. 2c)16. By minimizing defect-induced electron scattering, materials can achieve higher mobility and it is essential for improving the thermoelectric performance of the half-Heuslers materials. As shown in Fig. 2d, the Hall mobility (µH) of the single-crystalline Ti1-xNbxCoSb samples is around 2-3 times higher than polycrystalline counterparts16,38,40,41, indicating its superior electronic transport properties. It’s the improvement of the Hall mobility of Ti1-xNbxCoSb that results in the superior power factor (Fig. 2e). Therefore, as shown in Fig. 2f, the average power factor (PFavg) of the Ti0.971Nb0.043CoSb single crystals, at ~37 μW cm−1 K−2, is much higher than all of the n-type (Ti, Zr, Hf)CoSb-based and ZrCoBi-based n-type half-Heusler polycrystals16,38,39,41,43,51,52.
Temperature-dependent a electrical resistivity, b Seebeck coefficient, c power factor of the Ti1-xNbxCoSb single crystals. The dashed line in Fig. 2c is the data of the polycrystalline (Zr0.8Hf0.2)0.88Nb0.12CoSb16. Comparison of d the Hall carrier concentration vs. the Hall mobility, e the power factor vs. the Hall mobility between the single-crystalline Ti1-xNbxCoSb and polycrystalline MCoSb-based (M = Ti, Zr, Hf) and ZrCoBi-based samples. (The red-shaded region is single crystals prepared in this work, and the light-gray-shaded region is the previously reported polycrystals16,38,40,41), and f the comparison of the average power factor PFavg (from 307 K to 973 K) among the n-type single-crystalline Ti0.971Nb0.043CoSb (the composition is determined by EPMA), polycrystalline MCoSb-based (M = Ti, Zr, Hf) and ZrCoBi-based half-Heuslers16,38,39,41,43,51,52.
Since thermoelectric properties can be different along different crystallographic planes, it is meaningful to evaluate the thermoelectric anisotropy for single-crystalline TiCoSb-based materials. To this end, the Nb-doped TiCoSb single crystals along different crystallographic planes have been obtained from one crystal (Supplementary Fig. 6). Thermoelectric properties along (110) and (111) planes in the temperature range between 300 and 380 K were characterized by the thermal transport option of the physical property measurement system. A temperature gradient and electrical current were applied to the sample to simultaneously measure the electrical resistivity, Seebeck coefficient, and thermal conductivity (Methods). As shown in Supplementary Fig. 7, the thermoelectric transport properties along (110) and (111) planes are highly comparable, which can be reasonably understood by the nearly isotropic Fermi surfaces (Supplementary Fig. 8) and the cubic structure of TiCoSb (Fig. 1a). In addition, calculations by the BoltzTrap2 also confirm the similar electric and thermal properties in single-crystalline TiCoSb along (111) and (110) crystallographic planes (Supplementary Fig. 9), indicating the compound is thermoelectrically isotropic between (111) and (110) planes.
The lattice thermal conductivity (κlat) reduces with increasing temperature in all TiCoSb-based materials, which can be attributed to the Umklapp processes, as shown in Supplementary Fig. 10c. The total thermal conductivity (κ) is dominated by the lattice thermal conductivity, and there is a significant increase in electronic thermal conductivity (κe) with the increase of Nb content (Supplementary Fig. 10b). The zT increases with temperature for all the samples, and niobium doping can effectively optimize the thermoelectric performance (Supplementary Fig. 10d). To verify the uniformity of the samples, thermoelectric properties (in the temperature range between 250 to 350 K) have been characterized for multiple samples from the same batch. The electrical resistivity, Seebeck coefficient, total thermal conductivity, and dimensionless figure of merit are quite similar for four different samples, indicating the good homogeneity of the single crystals (Supplementary Fig. 11).
The actual chemical compositions of the Ti1-xNbxCoSb single crystals have been determined by EPMA, as shown in Supplementary Table 3 and Supplementary Fig. 12. It is noted that the measured Nb content in Ti1-xNbxCoSb significantly deviates from the linear relationship with the nominal contents, especially when the Nb nominal doping concentration is higher than 12 at.%, due to the significant appearance of a second phase NbSb2 (Supplementary Fig. 13). To avoid the formation of NbSb2, Ta doping was introduced to the Ti1-xNbxCoSb single crystal to partially substitute Nb to achieve the optimal carrier concentration of ~1021 cm−3 11,50,53. As shown in Supplementary Fig. 14 and Table 2, Ta is also a highly efficient dopant for TiCoSb single crystals, and only ~5 at.% doping concentration of Ta is required to reach that carrier concentration. The EDS (Supplementary Fig. 15) and backscattered electron imaging in SEM (Supplementary Fig. 3c) results indicate that Ti0.9Ta0.1CoSb exhibits good uniformity. Therefore, co-doping of Nb and Ta has been employed to optimize the carrier concentration of TiCoSb single crystal for the following studies.
Intensified phonon scattering in the Ti1-xHfxCoSb-based single-crystals
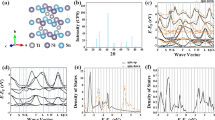
To further enhance the thermoelectric performance of the TiCoSb-based single crystals, it is of great significance to suppress their lattice thermal conductivity. Experimentally, alloying has been proven to be quite effective in reducing the thermal conductivity of the polycrystalline half-Heuslers54,55,56,57. To this end, Hf-alloyed TiCoSb-based single crystals have been prepared (Supplementary Fig. 16). Similar to the Ta-doped samples, the nominal and actual compositions of Hf in the Ti1-zHfzCoSb single crystals also exhibit a linear relationship (Supplementary Table 3 and Supplementary Fig. 12). This unambiguously demonstrates that doping and alloying can both be realized in single-crystalline TiCoSb-based materials, which allows for high degrees of freedom in optimizing the thermoelectric transport properties. As shown in Supplementary Fig. 17 and Fig. 3a, with the increase of Hf content, there is a significant suppression in the thermal conductivity, particularly in the lattice thermal conductivity (κlat). The thermal diffusivity was measured using the laser flash method, and experimental details were provided in the Methods. The room-temperature thermal conductivity of the pristine TiCoSb is as high as ~20.4 W m−1 K−1 and it is only ~ 3.7 W m−1 K−1 after 22 at.% Hf alloying, a reduction of ~82%. Figure 3b shows the unfolded phonon dispersion relation for Ti0.8125Hf0.1875CoSb (in blue), compared to the pristine TiCoSb phonon spectrum (dashed line) calculated. As shown in Supplementary Fig. 18, the Raman-active peaks of the pristine TiCoSb single crystal are comparable with the theoretical peak positions, which indicates the reliability of calculations. The broadening of the phonon spectrum is particularly pronounced in Hf-alloyed TiCoSb (Fig. 3b and Supplementary Fig. 19), which can be ascribed to the strong anharmonicity introduced by Hf alloying58. This can explain the substantial reduction in lattice thermal conductivity in the Ti1-xHfxCoSb-based single crystals. At a given temperature, the lattice thermal conductivity can be expressed as the sum of the contributions from each phonon mode λ, and characterized by the branch p and wave vector q59
where N is the number of q points uniformly sampled in the phonon Brillouin zone, V is the unit-cell volume, Cλ is the phonon mode heat capacity, \({\upsilon }_{\lambda }^{\alpha }\) is the phonon group velocity along the α direction, and \({\tau }_{\lambda }\) is the phonon lifetime. The ratio of the calculated heat capacity between TiCoSb and Ti0.8125Hf0.1875CoSb is about 98.7%, indicating a negligible influence of heat capacity between the two materials (Supplementary Table 4). Furthermore, the differences in the experimentally measured or calculated sound velocity between TiCoSb and Ti0.8125Hf0.1875CoSb are less than ~4% (Supplementary Tables 5 and 6). The similar sound velocities of TiCoSb and Ti0.8125Hf0.1875CoSb can also be understood from the nearly unchanged phonon dispersion around the Γ point. A comparison of the measured sound velocities among the TiCoSb-based single crystals indicates doping and alloying only slightly reduce the sound velocities. Therefore, it’s the phonon lifetime \({\tau }_{\lambda }\) that plays a vital role in suppressing the lattice thermal conductivity of Ti0.8125Hf0.1875CoSb. Based on the relaxation time approximation, the overall phonon lifetime is primarily determined by the anharmonic scattering rate, which is calculated from the sum of the three-phonon transition probabilities \({\varGamma }_{\lambda \lambda {\prime} \lambda {\prime\prime} }^{\pm }\) over all phonon modes, and it can be expressed as60
where \({f}_{\lambda }\) is the Bose-Einstein distribution function, \({\omega }_{\lambda }\) is the phonon angular frequency, and \({V}_{\lambda \lambda ^{\prime} \lambda ^{\prime\prime} }^{\pm }\) is the scattering matrix elements. Compared with TiCoSb, an overall increase in the three-phonon transition probabilities of Ti0.8125Hf0.1875CoSb can be observed, along with a broader distribution of phonon frequencies, consistent with the calculated phonon spectrum (Fig. 3c).
a Temperature-dependent thermal conductivity of TiCoSb-based single crystals. b comparison of the calculated phonon dispersion, c the comparison of the anharmonic scattering rates, d comparison of the weighted phased space in the absorption and emission processes, e comparison of the scattering matrix elements, and f the difference of the third-order anharmonic interatomic force constants between TiCoSb and Ti0.8125Hf0.1875CoSb.
Moreover, the weighted scattering phase space is characterized by the summation of frequency-dependent components that appear in the calculation of three-phonon transition probabilities \({W}_{\lambda }^{\pm }\), denoted as61,62
As shown in Fig. 3d and Supplementary Figs. 20–21, there is a noticeable increase in the anharmonic scattering rate and weighted scattering phase space for both absorption and emission processes of the Ti0.8125Hf0.1875CoSb compared to the pristine TiCoSb. The increase in weighted scattering phase space across all frequencies, especially the pronounced enhancement for low-frequency acoustic phonons, suggests that these low-frequency phonons may play a dominant role in reducing the lattice thermal conductivity in Ti0.8125Hf0.1875CoSb, which is consistent with the normalized cumulative lattice thermal conductivity (Supplementary Fig. 22). Furthermore, the scattering matrix elements \({V}_{\lambda \lambda ^{\prime} \lambda ^{\prime\prime} }^{\pm }\) can be determined using the normalized eigenvectors ep,q of the three interacting phonons and the mass factor Mi,j,k along with the anharmonic interatomic force constants \({\Phi }_{ijk}^{\alpha \beta \gamma }\) (IFCs)63,64,65,66
In both emission and absorption processes, the scattering matrix elements of the Ti0.8125Hf0.1875CoSb show a significant increase in both frequency distribution and intensity (Fig. 3e and Supplementary Fig. 23). Furthermore, Fig. 3f shows the anharmonic third-order interatomic force constants (IFCs3rd) of Ti0.8125Hf0.1875CoSb after subtracting those of pristine TiCoSb. The difference reveals the emergence of numerous new anharmonic third-order interatomic force constants that are absent in the pristine TiCoSb. Along with the noticeable enhancement in the magnitude of the existing force constants, Hf alloying induces significant changes in anharmonic interactions. As shown in Supplementary Fig. 24-26, at the same concentration of doping or alloying, Hf-alloyed TiCoSb not only exhibits a significant number of new anharmonic third-order interatomic force constants compared to Nb- and Ta-doped TiCoSb, but also shows a notable increase in the magnitude of the existing anharmonic force constants. Therefore, the enhanced scattering matrix elements after Hf alloying result in the increased anharmonic scattering rate, leading to shorter phonon lifetimes and thus greatly suppressing the lattice thermal conductivity of the Ti1-zHfzCoSb single crystals.
To synergistically enhance the electric and thermal properties, co-doping of Nb and Ta, and alloying of Hf were employed in the TiCoSb single crystal. The elements are uniformly distributed in Ti0.76Nb0.03Ta0.05Hf0.19CoSb, with no noticeable enrichment or segregation (Supplementary Fig. 3e and 27). The lattice thermal conductivity of single-crystalline Ti0.76Nb0.03Ta0.05Hf0.19CoSb is ~4.0 W m−1 K−1 at 300 K and ~1.8 W m−1 K−1 at 973 K. As shown in Supplementary Fig. 28, with the increase of Hf, there was no deterioration in the power factor of Ti1-x-y-zNbxTayHfzCoSb single crystal. The TiCoSb-based single crystals exhibit a similar density-of-state effective mass at room temperature (Supplementary Fig. 29 and Table 2), and calculations indicate that Nb and Ta doping and Hf alloying do not affect the band structure appreciably (Supplementary Fig. 4). It can explain why the power factors remain comparable after tuning the compositions.
Heat-to-electricity energy conversion of single-crystalline TiCoSb-based single leg
The temperature-dependent zT of the TiCoSb-based single crystal is shown in Fig. 4a. The zT is significantly improved through the simultaneous enhancement of power factor and suppression of thermal conductivity, and the peak zT is ~1.03 in Ti0.76Nb0.03Ta0.05Hf0.19CoSb at 973 K. The average zT between 307 and 973 K can reach ~0.64 in Ti0.76Nb0.03Ta0.05Hf0.19CoSb, which is higher than all the previously reported polycrystalline n-type (Ti, Zr, Hf)CoSb-based and ZrCoBi-based half-Heuslers16,38,39,40,41,42,43 (Fig. 4b). Additionally, as shown in Supplementary Fig. 30, the z values of Ti1-x-y-zNbxTayHfzCoSb increase with temperature, exhibiting a linear trend above 600 K in Ti0.76Nb0.03Ta0.05Hf0.19CoSb, suggesting the potential for further zT improvement at higher temperatures. It should be noted that the reproducibility and cycle stability of the Ti0.76Nb0.03Ta0.05Hf0.19CoSb have been verified, and their thermoelectric properties are comparable (Supplementary Figs. 31-33).
a Temperature-dependent zT, b the comparison of the average zT (zTavg) between this single crystalline TiCoSb-based materials and the other polycrystalline MCoSb-based (M = Ti, Zr, Hf) and ZrCoBi-based half-Heuslers16,38,39,40,41,42,43. c The current-dependent output voltage, d output power, and e energy conversion efficiency of the Ti0.76Nb0.03Ta0.05Hf0.19CoSb single leg. f Comparison of the energy conversion efficiency between the Ti0.76Nb0.03Ta0.05Hf0.19CoSb single leg and other half-Heusler-based single legs41,42.
To further evaluate the potential of the TiCoSb-based single crystal for thermoelectric power generation, a Ti0.76Nb0.03Ta0.05Hf0.19CoSb single leg was prepared. The Cu/Ti0.76Nb0.03Ta0.05Hf0.19CoSb/Cu joint was prepared with Ag-Cu-Zn soldering (Supplementary Fig. 34). The contact resistance of the single leg is ~5.6 µΩ cm2 (Supplementary Fig. 35), ensuring a negligible electrical parasitic loss. The heat-to-electricity energy conversion efficiency was characterized in homemade equipment (Supplementary Fig. 36a). The surface of the single leg was coated with white aerogel to minimize the influence of thermal radiation on the measurement of output heat flow. The electrical-current-dependent output voltage exhibits a good linear relationship and is in good agreement with calculations, as shown in Fig. 4c. In each voltage-current curve, the intercept of the vertical axis represents the open-circuit voltage (Voc), and the slope denotes the internal resistance (Rin) of the single-leg (Supplementary Fig. 36b-c). The observed increase in open-circuit voltage and internal resistance with a rise in temperature difference (ΔT) is attributed to the enhanced Seebeck coefficient and increased electrical resistivity of the Ti0.76Nb0.03Ta0.05Hf0.19CoSb single crystal with temperature. Figure 4d shows the output power versus the electrical current of the single leg, displaying a parabolic relationship where output power peaks at an optimal current. Overall, the measured output voltage and power are in good agreement with the theoretical predictions. As shown in Fig. 4e, the measured conversion efficiency of the single leg rises with an increase in the hot-side temperature and is slightly lower than the theoretical predictions at elevated temperatures. The slight disparity between the predicted and experimental efficiency should be mainly attributed to the effect of thermal radiation, which is particularly notable at elevated temperatures (Supplementary Fig. 37). As a result, the measured conversion efficiency of the Ti0.76Nb0.03Ta0.05Hf0.19CoSb single leg peaks at ~10.2% at a hot-side temperature of 998 K (Fig. 4f), which noticeably outperforms the previously reported ZrCo0.9Ni0.1Bi0.85Sb0.1541 and Nb0.6Ta0.23CoSb42 single legs.
Discussion
To sum up, high-quality single-crystalline TiCoSb-based half-Heuslers with a dimension of approximately 1 cm have been obtained by the flux method. The electron concentration of the TiCoSb-based single crystals can be effectively tuned by co-doping of Nb and Ta. In addition, Hf alloying intensifies anharmonic scattering, significantly reducing the phonon lifetimes and effectively decreasing the lattice thermal conductivity. As a result, an average power factor of ~37 μW cm−1 K−2 and average zT of ~0.64 in the temperature range between 307 and 973 K have been realized in the n-type TiCoSb-based single crystals, which outperform the previously reported polycrystalline (Ti, Zr, Hf)CoSb-based and ZrCoBi-based half-Heuslers. Moreover, a single leg of the single-crystalline Ti0.76Nb0.03Ta0.05Hf0.19CoSb has been fabricated and demonstrated a conversion efficiency of ~10.2% at a temperature difference of 700 K.
Methods
Crystal growth
The TiCoSb-based single crystals with the nominal compositions of Ti1-xNbxCoSb, Ti1-yTayCoSb, Ti1-zHfzCoSb, and Ti1-x-y-zNbxTayHfzCoSb were synthesized using the flux method by employing Sb as the flux30,31,32,33. Raw elements Ti (Alfa Aesar, 99.8%, ingots), Co (Alfa Aesar, 99.5%, ingots), Sb (Afla Aesar, 99.999%, ingots), Nb (Alfa Aesar, 99.8%, ingots), Ta (Alfa Aesar, 99.8%, ingots) and Hf (Alfa Aesar, 99.8%, ingots) were used. The starting materials of Ti, Nb, Ta, Hf, Co, and Sb were weighted according to the molar ratio of 1: x: y: z: 1: 25 (x = 0 – 0.17, y = 0 – 0.1, z = 0 – 0.3). Then, the elements were loaded into corundum crucibles and then sealed in a quartz tube in a vacuum. The sealed tubes were heated up to 1373 K in 2 h, kept at 1373 K for 12 h, followed by a cooling process to 1273 K at a rate of 0.3 K h−1, and subsequently cooled down to 1223 K at a rate of 1 K h−1. Finally, the quartz tubes were cooled down to 1173 K at a rate of 2–4 K h−1 and then removed from the furnace at 1173 K and quickly centrifuged to remove the liquid excess Sb flux. However, a small amount of Sb may remain on the surface even after centrifugation. Prior to all measurements, the surfaces were polished to remove any visible Sb residue. In some cases, to ensure complete removal of Sb, the samples were sealed in Nb tubes under an Ar atmosphere and annealed at 1173 K for 2 hours.
The HfCoSb single crystal was also synthesized using the flux method by employing Sb as the flux, and the starting materials of Hf, Co, and Sb were weighted according to the molar ratio of 1: 1: 25. The elements were then loaded into corundum crucibles, sealed in a quartz tube in a vacuum, and placed in the furnace with the identical heat and cooling process as mentioned-above.
Composition and microstructure characterization
The phase composition and crystal structure of the TiCoSb-based and HfCoSb single crystals were examined by X-ray diffraction with Cu Kα radiation (D/Max-2500 PC, Rigaku), and no secondary phases were observed (Supplementary Fig. 38). The orientation of the crystal was examined by XRD, and the patterns were indexed by the Jana2006 program. The X-ray 2θ-ω linear scan and rocking curve were obtained by high-resolution X-ray diffraction (Rigaku, SmartLab 9 KW). Single crystal structural analysis was conducted using a Siemens SMART platform diffractometer, which was equipped with an Apex (II) area detector and operated with monochromatic Mo Kα radiation. The structure was solved by direct method and refined by full-matrix least-squares calculations. Computational tasks were performed using Bruker Apex (II) software package and WinGX Program system with SHELXL-2014 Programs. The morphologies and compositions of the TiCoSb-based and HfCoSb single crystals were analyzed using scanning electron microscopy (SEM560, Gemini), energy-dispersive X-ray spectroscopy (EDS) mapping and backscattering electron (BSE) microscopy, respectively, as shown in Supplementary Fig. 1, 2–3, 15–16, 27, and 39. The chemical compositions of the TiCoSb-based and HfCoSb single crystals were obtained by electron probe microanalysis (JXA-8100, JOEL). For the accuracy of the electron probe microanalysis results, three distinct regions were selected for each sample, with three points measured in each region. The composition values from all nine points were averaged to obtain a representative composition for each sample.
Characterization of thermoelectric properties
The electrical resistivity and the Seebeck coefficient were simultaneously measured by a commercial system (ZEM-3 ULVAC). Rectangular bar-shaped samples with dimensions ranging from 1.5 × 1.5 × 6 mm3 to 2 × 2 × 9 mm3 were used. The thermal conductivity (κ) was obtained by \(\kappa=DaC_{\rm {p}}\), where D is the volumetric density measured by the Archimedean method, a is the thermal diffusivity determined by a laser flash apparatus (LFA 457, Netzsch), and Cp is the specific heat obtained using Dulong-Petit law. Thermal conductivity measurements were performed on square slices with a cross-sectional area between 5 × 5 mm2 and 7 × 7 mm2. The Hall coefficient (RH) was obtained from the magnetic field-dependent Hall resistivities via the electrical transport option in the physical property measurement system (PPMS Dynacool, Quantum Design). The Hall carrier concentration (nH) and the Hall mobility (μH) were calculated by \({n}_{\rm H}=1/e{R}_{\rm {H}}\) and \({\mu }_{\rm {H}}=\sigma /{n}_{\rm {H}}e\), respectively. The isotropy and uniformity of the Nb-doped TiCoSb single crystal are characterized by the physical property measurement system with the thermal transport option. The Raman scattering measurements were performed at room temperature in the back-scattering geometry on the single crystal with the triple Raman spectrometer (inVia, Renishaw) equipped with a microscope and liquid nitrogen-cooled charge-coupled device detector.
To determine the bandgap of the pristine TiCoSb single crystal, a spectroscopic ellipsometer (J. A. Woollam Co., Inc) was employed by incorporating specular reflectance methodology to gather spectral data. This technique facilitates the precise acquisition of the material’s optical constants by measuring the change in polarization as light reflects off the sample. The extinction coefficient (k) was extracted from the ellipsometric data according to \(\alpha=4{\uppi} k/\lambda\), where α is the absorption coefficient and λ is the wavelength of excitation light (from 210-2500 nm). The bandgap was obtained from the absorption coefficient using the Tauc plot \({(\alpha hv)}^{1/n}=B(hv-E_{\rm {g}})\), where h is Planck’s constant, v is the incident photon frequency, and B is the proportional constant. The value of n is related to the type of semiconductor material, when the semiconductor material is a direct band gap, n = 1/2; When the semiconductor material is an indirect bandgap, n = 267,68.
First-principles calculation
Density functional theory (DFT) calculations were carried out using the plane-wave pseudopotential approach, as implemented in the Vienna Ab initio Simulation Package (VASP)69,70. The electron-ion interactions were described using the projected augmented-wave (PAW) method71, where the explicitly treated valence electrons included 3 s, 3p, 3 d and 4 s (Ti), 4 s, 4p, 4 d and 5 s (Nb), 5p, 5 d and 6 s (Ta), 5p, 5 d and 6 s (Hf), 3 d and 4 s (Co), 5 s and 5p (Sb). The exchange-correlation effects were accounted for using the generalized gradient approximation (GGA)72. The kinetic energy cutoffs for the plane-wave basis set were set to 440 eV. The k-point meshes with a grid spacing of 2π × 0.03 Å−1 were used for electronic Brillouin zone integration. Special quasi-random structures (SQSs) of 2 × 2 × 2 supercells (96 atoms) for Ti0.9375Nb0.0625CoSb, Ti0.9375Ta0.0625CoSb, Ti0.9375Hf0.0625CoSb, and Ti0.8125Hf0.1875CoSb were generated to model disordered solid solutions using the Integrated Cluster Expansion Toolkit73,74. Structural optimization was done through total energy minimization with the residual forces on the atoms converged to below 10−3 eV Å−1.
Spin-orbit coupling (SOC) was included due to the heavy element Sb. A 6 × 6 × 6 k-point mesh was used to sample the Brillouin zone (BZ) in the self-consistent calculations. The unfolded electronic structures of four TiCoSb-based alloys were calculated by utilizing the BandUp code75,76. The maximally localized Wannier function method was employed to generate the Fermi surface as implemented in the Wannier90 code77,78,79. The Fermi surface was visualized using the XCrySDen software80. The resulting electronic structures were used to obtain electrical transport properties. This was done using semiclassical Boltzmann theory81 and the BoltzTraP282 code with first-principles electronic structures evaluated on approximately 1400,000 k pints for [110] direction and 640,000 for [111] direction in the irreducible BZ of TiCoSb.
The lattice thermal conductivities of materials depend on phonon dispersions and anharmonic couplings. We used the temperature-dependent effective potential (TDEP) method83,84,85,86 to extract the harmonic and anharmonic interatomic force constants (IFCs). The TDEP calculations were based on Ab-initio Born-Oppenheimer molecular dynamics with the PAW method71, utilizing a Nose-Hoover thermostat87 at 300 K. In these calculations, the electronic degrees of freedom are fully relaxed for each time step, e.g., for each set of nuclear positions, the nuclear dynamics are governed by the resulting energy and its gradients from the electronic structure calculations with the residual forces on the atoms converged to below 10−3 eV Å−1. We used 96-atom SQSs alloy structures with a simulation time of 50 ps, a time step of 1 fs, and a plane wave cutoff of 440 eV. We used the on-the-fly machine learning potential88,89,90 to accelerate molecular dynamics simulations as implemented in VASP code. The thermal conductivities were determined from the temperature-dependent second and third-order IFCs using the ShengBTE code60. We employed a well-converged phonon momentum q mesh of 7 × 7 × 7 in the calculations. The unfolded phonon dispersions of TiCoSb-based alloys were calculated by using the UPHO code91.
Single leg fabrication and performance characterization
The dimensions of the Ti0.76Nb0.03Ta0.05Hf0.19CoSb single crystal leg is 3.98 × 3.99 × 5.88 mm3. The hot and cold side of the leg was directly brazed (Ag-Cu-Zn solder) with copper electrodes. The contact resistance of this single leg is characterized by our homemade setup. The interface of the single leg was characterized by SEM and EDS, as shown in Supplementary Fig. 34. The conversion efficiency of the module was measured with homemade equipment. The experiments were performed under a high vacuum (below 10−6 mbar) to reduce the heat convection. The cold-side temperature was maintained between 293−295 K by using the water circulation system and the hot-side temperature of the single leg was controlled by PID. The conversion efficiency can be obtained using the following equation (without radiation thermal loss):
where P is the measured output power and Qout is the heat flow. The output voltage (V) and output current (I) were directly measured using a Keithley SourceMeter under different temperature gradients across the single leg. Multiple measurements were conducted under steady-state conditions at each temperature gradient. The output power (P) was then calculated using the equation:
The heat flow was estimated according to the one-dimensional Fourier law, using the equation:
where \({\kappa }_{{{{\rm{Cu}}}}}\), \({A}_{{{{\rm{Cu}}}}}\), \({L}_{{{{\rm{Cu}}}}}\) and \(\varDelta {T}_{{{{\rm{Cu}}}}}\) are the thermal conductivity, cross-sectional area, vertical distance, and temperature difference of the Cu block, respectively. A copper block with a known thermal conductivity (κCu) was used as the heat flow meter. Four K-type thermocouple probes (0.5 mm diameter) with equal spacing were embedded in the heat flow meter to measure the temperature drop (ΔTCu).
Considering the heat radiation not only emits in all directions but also reflects back onto the leg, this would lead to an increased heat flow of the cold side, leading to the overestimation of Qout. This resulted in more conservative efficiency values, particularly at high temperatures, where heat radiation became intense.
Finite element analysis
Finite element analysis was performed using COMSOL Multiphysics to evaluate the output voltage, output power, output heat flow and conversion efficiency of the single leg. The physical properties of the thermoelectric materials were based on the data in Supplementary Fig. 28. The contact resistances of ~5.56 μΩ cm2 at the interfaces were characterized and integrated into the simulation. The boundary conditions were set based on the actual temperatures of the hot and cold sides (Fig. 4c-f). The cold-side temperature was fixed at 293 K, while the hot-side temperature was varied with the interval of 100 K, ranging from 398 K to 998 K. By altering the boundary conditions, the corresponding internal resistance, output voltage, output power, heat flow, and conversion efficiency under different current conditions were determined. These results were used to evaluate the thermoelectric performance under realistic conditions.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
The data generated in this study are provided in the Supplementary Information and Source Data file or from the corresponding authors. Source data are provided with this paper.
References
Bell, L. E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science 321, 1457–1461 (2008).
DiSalvo, F. J. Thermoelectric cooling and power generation. Science 285, 703–706 (1999).
Ioffe, A. F. Semiconductor Thermoelements and Thermoelectric Cooling. (Infosearch, 1957).
Goldsmid, H. J. Introduction to Thermoelectricity. (Springer, 2016).
Snyder, G. J. & Toberer, E. S. Complex thermoelectric materials. Nat. Mater. 7, 105–114 (2008).
Mao, J. et al. Advances in thermoelectrics. Adv. Phys. 67, 69–147 (2018).
He, J. & Tritt, T. M. Advances in thermoelectric materials research: Looking back and moving forward. Science 357, eaak9997 (2017).
Rogl, G. et al. Mechanical properties of half-Heusler alloys. Acta Mater. 107, 178–195 (2016).
Rogl, G. & Rogl, P. F. How severe plastic deformation changes the mechanical properties of thermoelectric skutterudites and half Heusler alloys. Front. Mater. 7, 600261 (2020).
Zhu, H. T. et al. Discovery of ZrCoBi based half Heuslers with high thermoelectric conversion efficiency. Nat. Commun. 9, 2497 (2018).
Fu, C. G. et al. Realizing high figure of merit in heavy-band p-type half-Heusler thermoelectric materials. Nat. Commun. 6, 8144 (2015).
Zhu, T. J. et al. Compromise and synergy in high-efficiency thermoelectric materials. Adv. Mater. 29, 1605884 (2017).
Li, W. J., Ghosh, S., Liu, N. & Poudel, B. Half-Heusler thermoelectrics: advances from materials fundamental to device engineering. Joule 8, 1274–1311 (2024).
Zhu, T. J., Fu, C. G., Xie, H. H., Liu, Y. T. & Zhao, X. B. High efficiency half-Heusler thermoelectric materials for energy harvesting. Adv. Energy Mater. 5, 1500588 (2015).
He, R. et al. Achieving high power factor and output power density in p-type half-Heuslers Nb1-xTixFeSb. Proc. Natl Acad. Sci. USA 113, 13576–13581 (2016).
Liu, Y. T. et al. Lanthanide contraction as a design factor for high-performance half-Heusler thermoelectric materials. Adv. Mater. 30, 1800881 (2018).
Yu, J. J. et al. Unique role of refractory Ta alloying in enhancing the figure of merit of NbFeSb thermoelectric materials. Adv. Energy Mater. 8, 1701313 (2018).
Fu, C. G. et al. Enhancing the figure of merit of heavy-band thermoelectric materials through hierarchical phonon scattering. Adv. Sci. 3, 1600035 (2016).
Zeier, W. G. et al. Engineering half-Heusler thermoelectric materials using Zintl chemistry. Nat. Rev. Mater. 1, 16032 (2016).
Ai, X. et al. Enhancing the thermoelectric properties via modulation of defects in P-type MNiSn-based (M = Hf, Zr, Ti) half-Heusler materials. Adv. Funct. Mater. 33, 2305582 (2023).
Chen, R. C. et al. Entropy-driven multiscale defects enhance the thermoelectric properties of ZrCoSb-based half-Heusler alloys. Chem. Eng. J. 455, 140676 (2023).
Xie, H. H. et al. Beneficial contribution of alloy disorder to electron and phonon transport in half-Heusler thermoelectric materials. Adv. Funct. Mater. 23, 5123–5130 (2013).
Kim, K. S. et al. Direct observation of inherent atomic-scale defect disorders responsible for high-performance Ti1-xHfxNiSn1-ySby half-Heusler thermoelectric alloys. Adv. Mater. 29, 1702091 (2017).
He, R. et al. Unveiling the phonon scattering mechanisms in half-Heusler thermoelectric compounds. Energy Environ. Sci. 13, 5165–5176 (2020).
Hu, C. L., Xia, K. Y., Fu, C. G., Zhao, X. B. & Zhu, T. J. Carrier grain boundary scattering in thermoelectric materials. Energy Environ. Sci. 15, 1406–1422 (2022).
Shi, X., Chen, L. & Uher, C. Recent advances in high-performance bulk thermoelectric materials. Int. Mater. Rev. 61, 379–415 (2016).
Fang, T., Zhao, X. B. & Zhu, T. J. Band structures and transport properties of high-performance half-Heusler thermoelectric materials by first principles. Materials 11, 847 (2018).
Zhu, H. T. et al. Half-Heusler alloys as emerging high power density thermoelectric cooling materials. Nat. Commun. 14, 3300 (2023).
Lee, H. J. et al. Critical role of atomic-scale defect disorders for high-performance nanostructured half-Heusler thermoelectric alloys and their thermal stability. Acta Mater. 180, 97–104 (2019).
Zilber, T., Cohen, S., Fuks, D. & Gelbstein, Y. TiNiSn half-Heusler crystals grown from metallic flux for thermoelectric applications. J. Alloy. Compd. 781, 1132–1138 (2019).
Fu, C. G. et al. Revealing the intrinsic electronic structure of 3D half-Heusler thermoelectric materials by angle-resolved photoemission spectroscopy. Adv. Sci. 7, 1902409 (2020).
Pan, Y. et al. Electronic structure and low-temperature thermoelectric transport of TiCoSb single crystals. Nanoscale 14, 10067–10074 (2022).
Pan, Y., He, B. & Felser, C. Thermoelectric transport properties of single-crystalline ZrCoBi half-Heusler. Mater. Lab 2, 230016 (2023).
Pavlosiuk, O., Kaczorowski, D., Fabreges, X., Gukasov, A. & Wiśniewski, P. Antiferromagnetism and superconductivity in the half-Heusler semimetal HoPdBi. Sci. Rep. 6, 18797 (2016).
Hou, Z. P. et al. Large low-field positive magnetoresistance in nonmagnetic half-Heusler ScPtBi single crystal. Appl. Phys. Lett. 107, 202103 (2015).
Porter, D. A., Easterling, K. E. & Sherif, M. Y. Phase Transformations in Metals and Alloys. (CRC Press, Boca Raton, FL, 2009).
Elwell, D., Scheel, H. J. & Kaldis, E. Crystal Growth from High Temperature Solutions. (Rarcourt, 1976).
He, R. et al. Improved thermoelectric performance of n-type half-Heusler MCo1-xNixSb (M = Hf, Zr). Mater. Today Phys. 1, 24–30 (2017).
Vishwakarma, A. et al. Compositional modulation is driven by aliovalent doping in n-type TiCoSb based half-Heuslers for tuning thermoelectric transport. Intermetallics 125, 106914 (2020).
Wang, R. F. et al. Enhanced thermoelectric performance of n-type TiCoSb half-Heusler by Ta doping and Hf alloying. Rare Met. 40, 40–47 (2021).
Zhu, H. T. et al. Understanding the asymmetrical thermoelectric performance for discovering promising thermoelectric materials. Sci. Adv. 5, eaav5813 (2019).
Gao, Z. H. et al. Selective scatterings of phonons and electrons in defective half-Heusler Nb1-δCoSb for the figure of merit zT > 1. Small 19, 2302457 (2023).
Qiu, P. F., Huang, X. Y., Chen, X. H. & Chen, L. D. Enhanced thermoelectric performance by the combination of alloying and doping in TiCoSb-based half-Heusler compounds. J. Appl. Phys. 106, 103703 (2009).
Ashcroft, N. W. & Mermin, N. D. Solid State Physics. (Cengage Learning, 1976).
CRC Handbook of Thermoelectrics. (CRC Press, Boca Raton, FL, 1995).
Zhang, R. P. et al. Enhanced thermoelectric properties of Nb-doped Ti(FeCoNi)Sb pseudo-ternary half-Heusler alloys prepared using the microwave method. Materials 16, 5528 (2023).
Zhou, J. W. et al. Large thermoelectric power factor from crystal symmetry-protected non-bonding orbital in half-Heuslers. Nat. Commun. 9, 1721 (2018).
Xi, J. Y., Zhu, Z. Y., Xi, L. L. & Yang, J. Perspective of the electron-phonon interaction on the electrical transport in thermoelectric/electronic materials. Appl. Phys. Lett. 120, 190503 (2022).
Wang, R. Y. et al. Strong electron-phonon coupling and high lattice thermal conductivity in half-Heusler thermoelectric materials. Phys. Chem. Chem. Phys. 26, 8932–8937 (2024).
Ren, Q. Y. et al. Establishing the carrier scattering phase diagram for ZrNiSn-based half-Heusler thermoelectric materials. Nat. Commun. 11, 3142 (2020).
Zhou, M., Chen, L. D., Feng, C. D., Wang, D. L. & Li, J. F. Moderate-temperature thermoelectric properties of TiCoSb-based half-Heusler compounds Ti1-xTaxCoSb. J. Appl. Phys. 101, 113714 (2007).
Zhou, M., Feng, C. D. & Chen, L. D. Effects of partial substitution of Co by Ni on the high-temperature thermoelectric properties of TiCoSb-based half-Heusler compounds. J. Alloy Compd. 391, 194–197 (2005).
Quinn, R. J. & Bos, J.-W. G. Advances in half-Heusler alloys for thermoelectric power generation. Mater. Adv. 2, 6246–6266 (2021).
Barczak, S. A. et al. Suppression of thermal conductivity without impeding electron mobility in n-type XNiSn half-Heusler thermoelectrics. J. Mater. Chem. A 7, 27124–27134 (2019).
Zhang, X. L. et al. Ultralow lattice thermal conductivity and improved thermoelectric performance in a Hf-free half-Heusler compound modulated by entropy engineering. J. Mater. Chem. A 11, 8150–8161 (2023).
Tranås, R., Løvvik, O. M., Tomic, O. & Berland, K. Lattice thermal conductivity of half-Heuslers with density functional theory and machine learning: Enhancing predictivity by active sampling with principal component analysis. Comp. Mater. Sci. 202, 110938 (2022).
Bao, X. et al. Multiscale phonon scattering for ultra-low thermal conductivity in Co-doped ZrCoBi half-Heusler. Adv. Funct. Mater. 33, 2404279 (2024).
Simoncelli, M., Marzari, N. & Mauri, F. Unified theory of thermal transport in crystals and glasses. Nat. Phys. 15, 809–813 (2019).
Ziman, J. M. Electrons and Phonons: The Theory of Transport Phenomena in Solids. (Oxford University Press, 2007).
Li, W., Carrete, J., Katcho, N. A. & Mingo, N. ShengBTE: A solver of the Boltzmann transport equation for phonons. Comput. Phys. 185, 1747–1758 (2014).
Li, W. & Mingo, N. Thermal conductivity of fully filled skutterudites: Role of the filler. Phys. Rev. B 89, 184304 (2014).
Li, W. & Mingo, N. Ultralow lattice thermal conductivity of the fully filled skutterudite YbFe4Sb12 due to the flat avoided-crossing filler modes. Phys. Rev. B 91, 144304 (2015).
Broido, D. A., Malorny, M., Birner, G., Mingo, N. & Stewart, D. A. Intrinsic lattice thermal conductivity of semiconductors from first principles. Appl. Phys. Lett. 91, 231922 (2007).
Ward, A., Broido, D. A., Stewart, D. A. & Deinzer, G. Ab initio theory of the lattice thermal conductivity in diamond. Phys. Rev. B 80, 125203 (2009).
Li, W., Lindsay, L., Broido, D. A., Stewart, D. A. & Mingo, N. Thermal conductivity of bulk and nanowire Mg2SixSn1-x alloys from first principles. Phys. Rev. B 86, 174307 (2012).
Fu, Y., Singh, D. J., Li, W. & Zhang, L. Intrinsic ultralow lattice thermal conductivity of the unfilled skutterudite FeSb3. Phys. Rev. B 94, 075122 (2016).
Smith, R. A. Semiconductors. (Cambridge Univ. Press, Cambridge, 1987).
Wooten, F. Optical Properties of Solids. (Elsevier, New York, 1972).
Kresse, G. & Furthmüller, J. Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set. Phys. Rev. B 54, 11169–11186 (1996).
Kresse, G. & Furthmüller, J. Efficiency of ab-initio total energy calculations for metals and semiconductors using a plane-wave basis set. Comp. Mater. Sci. 6, 15–50 (1996).
Blöchl, P. E. Projector augmented-wave method. Phys. Rev. B 50, 17953–17979 (1994).
Perdew, J. P., Burke, K. & Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 77, 3865–3868 (1996).
Ångqvist, M. et al. ICET - A python library for constructing and sampling alloy cluster expansions. Adv. Theor. Simul. 2, 1900015 (2019).
Zunger, A., Wei, S.-H., Ferreira, L. G. & Bernard, J. E. Special quasirandom structures. Phys. Rev. Lett. 65, 353–356 (1990).
Medeiros, P. V. C., Stafström, S. & Björk, J. Effects of extrinsic and intrinsic perturbations on the electronic structure of graphene: Retaining an effective primitive cell band structure by band unfolding. Phys. Rev. B 89, 041407 (2014).
Medeiros, P. V. C., Tsirkin, S. S., Stafström, S. & Björk, J. Unfolding spinor wave functions and expectation values of general operators: Introducing the unfolding-density operator. Phys. Rev. B 91, 041116 (2015).
Yates, J. R., Wang, X., Vanderbilt, D. & Souza, I. Spectral and Fermi surface properties from Wannier interpolation. Phys. Rev. B 75, 195121 (2007).
Mostofi, A. A. et al. wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 178, 685–699 (2008).
Mostofi, A. A. et al. An updated version of wannier90: A tool for obtaining maximally-localised Wannier functions. Comput. Phys. Commun. 185, 2309–2310 (2014).
Kokalj, A. XCrySDen-a new program for displaying crystalline structures and electron densities. J. Mol. Graph. Model. 17, 176–179 (1999).
Jin, Y. et al. High-throughput deformation potential and electrical transport calculations. Npj Comput. Mater. 9, 190 (2023).
Madsen, G. K. H., Carrete, J. & Verstraete, M. J. BoltzTraP2, a program for interpolating band structures and calculating semi-classical transport coefficients. Comput. Phys. Commun. 231, 140–145 (2018).
Hellman, O., Abrikosov, I. A. & Simak, S. I. Lattice dynamics of anharmonic solids from first principles. Phys. Rev. B 84, 180301 (2011).
Hellman, O., Steneteg, P., Abrikosov, I. A. & Simak, S. I. Temperature dependent effective potential method for accurate free energy calculations of solids. Phys. Rev. B 87, 104111 (2013).
Hellman, O. & Abrikosov, I. A. Temperature-dependent effective third-order interatomic force constants from first principles. Phys. Rev. B 88, 144301 (2013).
Knoop, F. et al. TDEP: Temperature dependent effective potentials. J. Open Source Softw. 9, 6150 (2024).
Nosé, S. A molecular dynamics method for simulations in the canonical ensemble. Mol. Phys. 52, 255–268 (1984).
Jinnouchi, R., Lahnsteiner, J., Karsai, F., Kresse, G. & Bokdam, M. Phase transitions of hybrid perovskites simulated by machine-learning force fields trained on the fly with Bayesian inference. Phys. Rev. Lett. 122, 225701 (2019).
Jinnouchi, R., Karsai, F. & Kresse, G. On-the-fly machine learning force field generation: application to melting points. Phys. Rev. B 100, 014105 (2019).
Jinnouchi, R., Karsai, F., Verdi, C., Asahi, R. & Kresse, G. Descriptors representing two- and three-body atomic distributions and their effects on the accuracy of machine-learned inter-atomic potentials. J. Chem. Phys. 152, 234102 (2020).
Körmann, F., Ikeda, Y., Grabowski, B. & Sluiter, M. H. F. Phonon broadening in high entropy alloys. Npj Comput. Mater. 3, 36 (2017).
Acknowledgements
This work was supported by the National Natural Science Foundation of China for Distinguished Young Scholars (52425108), the National Key Research and Development Program of China (2023YFB3809400), and the GuangDong Basic and Applied Basic Research Foundation (2024B1515040022). J.M. acknowledges the financial support from the National Natural Science Foundation of China (52473298), Shenzhen Science and Technology Program (RCJC20221008092725020), the Shenzhen Stable Support Plan for Higher Education Institutions (GXWD20220818151757003), the Fundamental Research Funds for the Central Universities (2024FRFK03013), and the GuangDong Basic and Applied Basic Research Foundation (2023A1515011711). Q.Z. acknowledges the financial support from the National Natural Science Foundation of China (52172194, 52425108), and the Shenzhen Science and Technology Program (RCJC20210609103733073, JCYJ20241202123659001). F.C. acknowledges the financial support from the National Natural Science Foundation of China (52472196). Y.F. acknowledges the financial support from the National Natural Science Foundation of China (62474081 and 22090044).
Author information
Authors and Affiliations
Contributions
J.M., Q.Z., and S.Y. conceived the idea, J.M. and S.Y. designed the research, S.Y., S.Z.Z., J.M.Q., and Y.F.Z. prepared the single crystals, S.Y., S.C.D., and P.Z. characterized the thermoelectric properties of single crystals, S.Y., X.J.M., S.Q.C., Z.X.W., Z.H.C., F.C., and F. J. characterized the quality of the single crystals, S.Y., X.B., X.H.Z, L.Y, and C.H.L. fabricated the single leg, S.Y., X.B., and J.X.C. characterized the heat-to-electricity energy conversion efficiency of the single leg, Y.H.F. performed the first-principles calculations, J.M., S.Y., and Y.H.F. analyzed the data, J.M. and S.Y. wrote and edited the manuscript. All the authors reviewed the manuscript and contributed helpful discussion to this work.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks Nagendra Chauhan, Sergio Gonzalez-Munoz, Kishor Kumar Johari and Sylvain le Tonquesse for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Ye, S., Zhi, S., Ma, X. et al. Superior electron transport in the single-crystalline TiCoSb-based half-Heuslers. Nat Commun 16, 1812 (2025). https://doi.org/10.1038/s41467-025-56961-0
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-56961-0
This article is cited by
-
Miniaturized Mg3Bi2-based thermoelectric cooler for localized electronic thermal management
Nature Communications (2025)