Introduction

Ocean island basalts (OIBs) are volcanic rocks that may originate from rising plumes in the Earth’s deep mantle, potentially sampling the materials near the core-mantle boundary (CMB)1. The isotopic analyses of OIBs reveal significant chemical heterogeneities in the Earth’s deep interior that have long provided key insights into the evolution of our planet1. Recent studies have identified intriguing 182W deficits in some OIBs with μ182W (defined as the deviation of 182W/184W from terrestrial standards in parts per million) as low as  −23 ± 4.52,3,4,5,6, while μ182W is around 0 in the modern upper mantle. The negative μ182W anomalies were produced by the depletion of the now extinct 182Hf with a half-life of 8.9 Myr7.

Various mechanisms have been proposed to account for the μ182W anomalies in OIBs. The element fractionation during the crystallization of putative magma oceans may lead to the formation of enriched deep mantle reservoirs or early protocrust with a low Hf/W ratio2,8,9, subsequently causing lower μ182W. However, subducted, early-formed crust may not possess sufficiently negative μ182W to account for OIBs5. In addition, the enriched deep mantle reservoirs and the protocrust would also be enriched in other incompatible elements, including U and Th. This enrichment leads to more radiogenic 4He and lower 3He/4He ratio (3He is primordial), which is inconsistent with the observed negative correlation between μ182W and 3He/4He2,5.

As a moderately siderophile element, W primarily partitions into the core during core-mantle differentiation, while Hf remains in the mantle due to its lithophile nature. The early core formation during the first  ~30 Myr of solar system history, when 182Hf was still extant, resulted in the terrestrial mantle exhibiting a higher 182W/184W ratio compared to bulk chondrites and the complementary reservoir, the core10,11,12. Therefore, the assimilation of the Earth’s core materials or chondritic materials after core formation may significantly modify the μ182W characteristics of OIB source reservoirs. For example, it has been proposed that iron-rich liquids from the core may penetrate into the oxides in the lowermost mantle due to morphological instability13 or capillarity phenomenon14. Since the core is believed to host a substantial amount of 3He15,16, it may also be a source of high 3He/4He in OIBs17,18,19,20, simultaneously explaining the 182W depletion and 3He enrichment. However, the direct incorporation of outer core metal or late-accreted materials could lead to significant enrichment of highly siderophile elements (HSEs), which contradicts the observed absence of HSEs enrichments of OIB samples4,5. In addition, the extreme lithophile behavior of Ne under high pressures predicted by ab initio calculations likely results in a high 3He/22Ne ratio of core materials, which is not observed in OIBs either21.

It is suggested that atomic diffusion of some siderophile elements along grain boundaries (GBs) may be an efficient mechanism for core-mantle interaction22. Recent experimental results also indicate high GB diffusivities of W in lower mantle phases with a strong temperature dependence23. Therefore, diffusive isotopic exchange at the CMB has been considered a viable mechanism to explain the 182W deficits in OIBs4,5,18,23. However, those experiments have puzzling aspects: First, W and Au exhibit diffusivity three orders of magnitude higher than other siderophile elements, despite having similar atomic masses, radii, and chemical properties22 (Fig. 1). Second, extrapolating the W diffusivity to the CMB temperatures according to the experimentally determined temperature dependence yields unreasonably high results23 (see Results and Discussion). Recently, a theoretical prediction suggests that the GB transport in MgO is considerably less efficient at CMB conditions than has been extrapolated from experimental results at lower pressures and temperatures24. Our recent findings also favor sluggish Fe diffusion along ferropericalse GBs, questioning the feasibility of GB diffusion as an effective core-mantle interaction mechanism25. Therefore, it is important to further quantify the efficiency of GB diffusion in exchanging W isotopes, especially at the temperature and pressure conditions of the CMB.

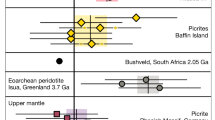
Fig. 1: Comparisons of experimental and theoretical results under 0–2.5 GPa.
figure 1

a Diffusivities of siderophile elements along (Mg0.9Fe0.1)O grain boundaries (blue) and in supercooled (Mg0.2Fe0.8)O liquid (green) obtained from molecular dynamics simulations under 2.5 GPa and 1873 K compared with previous experimental results (HW200722) of grain boundary diffusivity in MgO under the same condition. b Diffusivities of W in different systems obtained from molecular dynamics simulations compared with experimental diffusivities in MgO grain boundaries (HW200722), basaltic melt (J200633), and granitoid melt (HPG8 + 20 wt% Na2O, M199932) under 0–2.5 GPa and 1873 K. The compositions of the simulated systems were made consistent with those of the experimental samples. The molecular dynamics simulations of the grain boundary systems and liquids were performed using machine learning potentials and ab initio calculations, respectively. Error bars indicate the standard deviations across different simulation runs. Source data are provided as a Source Data file.

Full size image

Performing diffusion experiments under high temperature and pressure is challenging26, and obtaining the GB diffusivity requires separating the contributions of lattice and GB diffusion to the bulk diffusion profiles (e.g., Yoshino et al.23), introducing additional errors. In this study, we examine the self-diffusion of W in ferropericlase GBs and (Mg,Fe)O liquid using molecular dynamics (MD) simulations under various pressure and temperature conditions. The recently developed machine learning potential (MLP) method27,28 enables the simulations of large GB systems with high efficiency while maintaining ab initio accuracy. Considering the isotopic exchange process via GB diffusion, we evaluate the μ182W anomalies of the plume-source mantle that might have arisen over the past 4.54 billion years. Our findings imply that GB diffusion across the CMB cannot explain W isotope anomalies in the plume-source mantle, and other mechanisms are desired to resolve the puzzle of μ182W anomalies in mantle-derived rocks.

Results and Discussion

Grain boundary diffusion of W and Pt in ferropericlase

We developed an MLP for Mg-Fe-O-W system by training an artificial neural network model with the ab initio data (see Methods). In addition, a separate MLP for Mg-Fe-O-Pt system was also trained to compare the diffusion behaviors of different siderophile elements under the CMB conditions, since Pt is a representative and well-studied HSE (e.g., Médard et al.29). The MLPs target temperatures up to 8000 K and pressures up to 200 GPa. We evaluated the reliability of the MLPs by comparing the energies, atomic forces, and stresses with those obtained from ab initio simulations based on density functional theory (DFT), for configurations not present in the training set (Methods; Supplementary Fig. 1). The diffusion coefficients were directly obtained from atomic trajectories of MD simulations (Eq. (2), Methods). The diffusion coefficients of Mg, Fe, O, and W calculated using MLPs align well with the DFT results for (Mg,Fe)O liquids (Supplementary Fig. 2). In addition, our DFT results show excellent consistency with experimentally measured W diffusivities in silicate melts, further validating the reliability of our methods (Fig. 1b). As shown in Supplementary Information, we also carefully investigated the factors affecting the diffusion of W including the exchange-correlation functional used in DFT calculations (Supplementary Fig. 3), system size (Supplementary Fig. 4), GB structure (Supplementary Fig. 5), vacancy concentration (Supplementary Fig. 6), valence state of W (Supplementary Fig. 7), and distribution of elements and vacancies (Supplementary Fig. 8), to ensure that diffusivity results are converged and robust25,30.

Figure 1 a presents our results for the diffusion coefficients of W and Pt in periclase at 2.5 GPa and 1873 K. These two siderophile elements show similar diffusion behavior along GBs and exhibit similar diffusion coefficients (Fig. 1a). The GB diffusivity for W is approximately two orders of magnitude lower than its diffusivity in supercooled (Mg,Fe)O liquid, which aligns with previous findings of GB diffusion in olivine31. A previous experimental study, also plotted in Fig. 1a for comparison, reported GB diffusivities for multiple siderophile elements in MgO periclase under the same condition22. For Pt, our theoretical prediction closely matched the experimental result. However, experimental results indicated strong variations in GB diffusivities for different siderophile elements, spanning up to four orders of magnitude, with notably higher diffusivities for W and Au compared to other elements. This is perplexing considering the similarities of these two elements with other siderophile elements shown in Fig. 1a in terms of atomic mass and siderophility22. Furthermore, the experimental diffusivity for W is an order of magnitude higher than those in supercooled (Fe,Mg)O liquid, and over two orders of magnitude higher than W diffusivities in silicate melts under similar temperature and pressure conditions32,33 (Fig. 1b). Admittedly, the GB features a relatively disordered atomic environment and exhibits higher diffusivities than the lattice counterpart34,35. However, regardless of the GB structure, GB diffusivity is always lower than that in a fully disordered liquid with the same chemical composition36,37. Therefore, the notably faster GB diffusion for W compared to liquid diffusion is unreasonable, suggesting that contributions to the large flux of W in the experiment may come from additional sources other than GB diffusion.

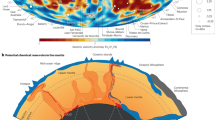
The high-pressure GB diffusion coefficients in (Mg0.9Fe0.1)O are shown in Fig. 2. The temperature dependence of the GB diffusivities can be fitted using the Arrhenius equation (Eq. (3), Methods), denoted as the activation enthalpy (ΔH), which is proportional to the slope of the fitted lines. A recent experimental study reported the GB diffusivity of W in a post-spinel (bridgmanite + ferropericlase) phase at 25 GPa23, indicating that W exhibits fast and strongly temperature-dependent GB diffusion, with an activation enthalpy of 493 kJ mol−1. To directly compare with these experimental results, we performed simulations at multiple temperatures under a pressure of 25 GPa and calculated the GB diffusivities of W (Fig. 2a). We observe a lower diffusivity and weaker temperature dependence of diffusivities compared to Yoshino et al.23, and the activation enthalpy is found to vary as a function of temperature (ΔH = 322 kJ mol−1 for 2000–2750 K; ΔH = 218 kJ mol−1 for 2750–3500 K). Note that our calculations pertain to self-diffusion without a W concentration gradient, which is different from the chemical diffusion measured in the experiments, even though the two are similar at very low W concentrations (Supporting Information). Moreover, W may oxidize to WO3 in experiments23, resulting in a significant drop in its melting point. This allowed the oxide melt to mechanically penetrate GBs due to surface tension, with a penetration rate likely exceeding the GB diffusion rate, potentially providing another mechanism for core-mantle interaction. This process, however, was absent in our simulations because we set a low W concentration to mimic the extremely low W content in Earth’s mantle38 (Methods), while previous experiments used metallic W foils as the diffusion source22,23 and the W concentrations reached several tens of wt% in sink particles23. Additionally, the much lower valence state of Pt29 compared to W39,40 in silicate melts suggests Pt may be less likely to form oxides and migrate via a similar mechanism. This difference likely explains the significantly lower flux of Pt compared to W observed by Hayden & Watson22.

Fig. 2: Diffusion coefficients of W and Pt under high pressures.
figure 2

a Diffusion coefficients of W in (Mg0.9Fe0.1)O grain boundary (GB) and (Mg0.8Fe0.2)O liquid as a function of reciprocal temperature under 25 GPa. Previous experimental results for the post-spinel phase are shown for comparison23. b Diffusion coefficients of W and Pt as a function of reciprocal temperature under 140 GPa. The shading area represents the extrapolation of experimental results23 assuming an activation volume of 0–2 cm3 mol−1 (Eq. (4), Methods). Dashed and dotted blue lines are fitted Arrhenius equations (Eq. (3), Methods) over 2000–2750 K and 2750–3500 K, respectively. Other dashed lines are fitted Arrhenius equations from the data points with the same color. Error bars indicate the standard deviations across different simulation runs. Source data are provided as a Source Data file.

Full size image

The low and temperature-dependent ΔH reported in this study can be justified from a microscopic perspective. ΔH is defined as the energy difference between the system when the diffusing atom occupies the most energetically favorable positions (energy minima) and when it traverses the saddle point (energy barrier) connecting the energy minima41,42,43. For lattice diffusion, W atoms face a strong steric effect when migrating between lattice sites (deep energy minima) by passing through interstitial sites (high energy barrier), and thus show high activation enthalpy. The high ΔH may be contributed by the increased strain energy caused by the distorted crystal lattice when W transitions at the saddle point43. In liquids, due to the disordered nature of the medium, W is likely to have a more flexible diffusion pathway that may be coupled with the free movements of neighboring atoms in the absence of lattice strain. Additionally, the larger volume and thus larger interatomic distances in liquids compared to solids may facilitate W migration, resulting in low ΔH. GBs, as solid-solid interfaces, exhibit characteristics of an amorphous state and should therefore display diffusion behaviors that are intermediate between those of solids and liquids, which is supported by the observations that GB atoms do not have fixed lattice sites, yet there remains a significant steric effect on diffusion24,25. Thus, the ΔH for GB diffusion of W should lie between the ΔH for W diffusion in liquids (118 kJ mol−1, green data in Fig. 2a) and in the single crystal (365 kJ mol−1 for olivine)40.

As the temperature increases, the disorder in the GB structure intensifies, and may trigger premelting (i.e., the GB transitions into a liquid-like, thermodynamically stable nanoscale film below melting temperature)44, as observed in ferropericlase25 and many other materials45,46,47. The incorporation of W6+ may reduce the melting point of ferropericlase and facilitate this premelting process. This order-disorder transition of GB structures results in the temperature-dependent activation enthalpy, represented by solid-like and high ΔH at low temperature and liquid-like and low ΔH at high temperature, which has been observed in GB diffusion in MgO24. Consequently, GB diffusivities gradually increase towards liquid diffusivities with increasing temperature (Fig. 2a).

Previous studies have attempted to extrapolate the experimentally measured GB diffusivities23 to high pressure and high temperature conditions, in order to explain the W isotope anomalies in the plume-source mantle18,23. Due to the temperature-dependent activation enthalpy described above, such extrapolation is likely unreliable. We now evaluate the feasibility of these extrapolations. At 25 GPa, the extrapolated W diffusivity at 3000 K is 6 × 10−4 m2 s−1, over two orders of magnitude higher than the W diffusivity in (Mg0.9Fe0.1)O liquid under corresponding conditions calculated in this study (Fig. 2a). It is also orders of magnitude greater than the diffusivities for almost all elements in all kinds of silicate melts measured under ambient pressure, if we extrapolate those results to 3000 K48. Note that we have not considered the diminishing effect of pressure on diffusion in silicate melts; otherwise, the gap would be even more significant. In addition, if we assume an activation volume of 2 cm3 mol−118,23 to incorporate the pressure effect (Eq. (4), Methods), the extrapolated value under CMB conditions also reaches 10−6 m2 s−1, about three orders of magnitude higher than the (Mg0.9Fe0.1)O liquid. Therefore, extrapolating the GB diffusivities to CMB conditions using the previously reported low-temperature activation enthalpy is unreasonable, and we believe that the GB diffusivities and ΔH may have been significantly overestimated in experiments, potentially indicating additional physical/chemical mechanisms beyond GB diffusion (e.g., melting and mechanical penetration of W oxides) that have transported a significant amount of W under those experimental conditions.

Under the CMB pressure, we reported the GB diffusivities of W and Pt at temperatures from 4000 to 5000 K (Fig. 2b), which covers the upper limit of the estimated CMB temperatures throughout the Earth’s thermal evolution49. Similar to low-pressure results (Fig. 1), W and Pt exhibit very close GB diffusivities, which are essentially identical within the uncertainties. Additionally, due to the enhancement effect of pressure on activation enthalpy, the GB diffusivities at 140 GPa show a higher temperature dependence than those at 25 GPa, characterized by ΔH = 371 kJ mol−1 for W. The activation enthalpy of GB diffusion for W in ferropericlase is similar to that of Fe (328 kJ mol−1)25 at 140 GPa, which may be related to the similar ionic radii of W6+ and Fe2+ (W6+: 74 pm; Fe2+: 75 pm)50. Although W6+ has a slightly lower mass and a much smaller radius than Pt0 (135 pm)50, its significantly lower electronegativity51 and higher valence state29,39,40 compared to Pt0 under high pressure may cause W to form strong chemical bonds with undercoordinated O atoms in ferropericlase GBs24,25, leading to similar diffusion behaviors for W and Pt. Our diffusivity results are more than four orders of magnitude lower than the extrapolated experimental results (Fig. 2b), leading to markedly different geochemical implications.

Geochemical Implications

As a potentially significant reservoir of W (with low μ182W) and He (with high 3He/4He), the core has been proposed to be a source of the negative correlation between μ182W and 3He/4He anomalies in OIBs4,5,18,19. The isotopic exchange between the core and the mantle through GB diffusion has been proposed to be the underlying mechanism18,23. Here, we used the diffusion coefficients of W, directly obtained under the high temperature and pressure conditions of the CMB without any extrapolation, to reassess the reliability of this mechanism.

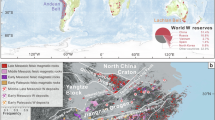
Due to its siderophile nature, W is abundant in the Earth’s core ( ~500 ppb)52 and depleted in the mantle (27–31 ppb)38, which enables a continuous supply of core-like W across the CMB, maintaining a constant, core-equilibrated μ182W value of about  −220 at the very bottom of the mantle. Subsequently, the core-derived W may undergo isotopic exchange with the ambient background mantle (μ182W ≈ 0), mediated by self-diffusion in mantle rocks, gradually modifying the W isotopic characteristics of the lowermost mantle. Given that the cation diffusion in ferropericlase is significantly faster than that in bridgmanite and post-perovskite23,42,53,54, we calculated the effective diffusion coefficient of W (DW, Eq. (5), Methods) using its GB diffusivity in ferropericlase to constrain the upper limit of this isotopic exchange efficiency. We first consider a diffusion distance, \(L=\sqrt{{D}_{{{\rm{W}}}}t}\), to assess the characteristic spatial scale L over which this mechanism can impact within a certain time scale t. We find that even if this diffusive isotope exchange remains undisturbed over the age of the Earth (4.54 Gyr)55, the maximum diffusion distance is only about 30 meters (Fig. 3a), far lower than the values obtained by extrapolating low-temperature experimental results18,23.

Fig. 3: The efficiency of grain boundary diffusion in transporting W isotope signals across the core-mantle boundary.
figure 3

a The effective diffusion distance of W as a function of grain size over 4.54 Gyr, calculated from effective diffusivities under 4000–5000 K and 140 GPa. The orange shading corresponds to the grain size predicted for the average lower mantle94. b The μ182W value of OIB samples as a function of the height of the plume generation zone after the diffusive isotopic exchange over 4.54 Gyr. The blue shading represents the values calculated from effective diffusion coefficients (5.0 × 10−16 m2 s−1 to 6.2 × 10−15 m2 s−1, calculated from Eq. (5) in Methods) under 4000–5000 K and 140 GPa. The green curve is calculated from the effective diffusion coefficient (7.1 × 10−14 m2 s−1) assuming W diffusivity in (Mg,Fe)O liquid at 5000 K is the upper bound of grain boundary diffusivity. The grain size of 0.1 mm is considered. The lowest height of observable ultra-low velocity zones (ULVZs) is shown for reference62. The histogram showing the frequency distribution of previously reported μ182W measured in OIB natural samples5 is shown for comparison. Source data are provided as a Source Data file.

Full size image

Furthermore, we modeled the possible μ182W anomalies in OIBs that result from this diffusive isotopic exchange based on the diffusion coefficients derived above. OIBs with W or He isotope anomalies may originate from deep-rooted mantle plumes56. Seismic observations suggest a geographical correlation between the generation zones of deep-rooted mantle plumes and the large low-shear velocity provinces (LLSVPs), indicating that these plumes are likely generated at the thin margins of LLSVPs57,58. Specifically, OIBs with low μ182W values and high 3He/4He ratios usually lie above ultra-low velocity zones (ULVZs) at the margins of LLSVPs2,59,60. Therefore, LLSVPs5,18,61 and ULVZs2,5,23 may be the potential source reservoirs for those isotopic anomalies. Using the effective diffusion coefficients, we calculated the vertical composition profile of W isotopes above the CMB after 4.54 Gyr of diffusive isotopic exchange (Eq. (7), Methods; Supplementary Fig. 9). We then calculated the μ182W composition of a plume generation zone (PGZ) based on the average composition of the mantle between the CMB and the top of PGZ (Eq. (8), Methods). We consider the degree of entrainment—the ratio of dense material carried by the hot plume to the total upwelling material—to calculate the final μ182W value of OIBs reaching the Earth’s surface18 (see Methods). The results are shown in Fig. 3b. If we use the observed minimum height of ULVZs ( ~5 km, limited by the seismic resolution)62 as the lower limit for the height of PGZ, our results indicate that the 182W deficit caused by GB diffusion would be within 0.2 in μ182W towards negative. Even if we use the W diffusivity in super-cooled (Mg,Fe)O liquid at 5000 K instead of GB diffusivity to calculate the effective diffusion coefficient, which constrains the maximum possible effect on mantle W isotopic composition by GB diffusion, the change in μ182W is still within 0.55 towards negative. This value is around an order of magnitude smaller than those of many OIB samples (Fig. 3b)5. Therefore, we conclude that diffusive isotopic exchange cannot be the source of W isotope anomalies in OIBs or any other mantle-derived rocks. Note that even if we further reduce the height of the PGZ to 1 km, this mechanism still cannot explain the significant μ182W anomalies observed in a large number of natural samples. The model discussed above addresses the isotopic exchange in the absence of a concentration gradient of W in the mantle. We also modeled the chemical diffusion of W from the core to the mantle considering a net mass flux of W given the possible enhanced lithophility of W at the CMB conditions. The results show that chemical diffusion fails to explain the observed 182W anomalies in OIBs (see Supplementary Information). Although small-scale convection within LLSVPs may enhance the transport of core-affected material within the mantle63, the amount of core-derived W sufficient for the observed μ182W in OIBs requires a W diffusion coefficient of over 10−11 m2 s−163, which is several orders of magnitude higher than the effective diffusion coefficient calculated in this study (see caption of Fig. 3).

Although diffusion in solids is excessively sluggish, our results indicate that the diffusivity for W in (Mg,Fe)O liquid can reach 2.19 × 10−9 m2 s−1 at 5000 K and 140 GPa, corresponding to a diffusion distance of  ~18 km over a time scale of 4.5 Gyr. Therefore, partial melts, if present in the lowermost mantle64,65,66, may accelerate the equilibration process of W isotopes between the plume source and core5. However, the temporal and spatial extent of these partial melts remains highly uncertain. In addition, the expected downward percolation of dense partial melts can cause drainage and accumulation, forming a melt-rich layer at the CMB, which may be inconsistent with geophysical constraints67. Although the melts may remain in suspension within ULVZs due to the viscous stirring, numerical simulations suggest that the bottom of ULVZs is relatively depleted in liquids68, which limits the efficiency of the diffusive isotopic equilibration. Therefore, atomic diffusion, especially the GB diffusion alone, is unlikely to be a viable mechanism to modify the μ182W values of the plume-source mantle. Other mechanisms, such as the addition of core-exsolved oxides that are potentially enriched in W during the secular cooling (e.g., Rizo et al.4, Deng & Du19), are necessary to transport the core-like signature into the Earth’s mantle.

Methods

Development of Machine Learning Potentials

Recently, we developed an MLP for Mg-O-Fe system covering a wide compositional range of various Mg:O:Fe ratios at pressure up to 200 GPa and temperature up to 8000 K69. Here, we further extended the compositional space of this MLP to include one more element X (X is either Pt or W) following the same procedure outlined at Peng & Deng30. Two MLPs were built with training sets inherited from the Mg-O-Fe MLP69 and additional ones that entail Mg-O-Fe-X mixtures. Specifically, we added configuration with bulk compositions including 32MgO + aX with a = 2–16, 64Fe + bX with b = 2–16, cMgO + dFe + eX + fO with c = 32–64, d = 48–144, e = 2–8, f = 0–48.

To briefly summarize the training process, configurations (structures of a given atomic arrangement) of training and test sets were drawn from multithermal and multibaric simulations70, which were used to efficiently sample the multi-phase configurational space. We used the structure factor of B1 MgO as the collective variable to drive the sampling. High-accuracy ab initio calculations were performed on the selected configurations to derive the corresponding energies, atomic forces, and stresses. The DeePMD approach was employed to train an MLP that takes a configuration and predicts its energy, atomic forces, and stresses without iterating through the time-consuming self-consistent field calculation27,28. The loss function is defined as

$$L\left({p}_{\epsilon },{p}_{f},{p}_{\xi }\right)={p}_{\epsilon }\Delta {\epsilon }^{2}+\frac{{p}_{f}}{3N}\mathop{\sum}\limits_{i}\left\vert \Delta {{{\bf{F}}}}_{i}\right\vert+\frac{{p}_{\xi }}{9}\, \parallel \Delta \xi {\parallel }^{2},$$
(1)

where pϵ, pf, pξ are tunable prefactors for the difference between the MLP prediction and training data. ϵ is the energy per atom; Fi is the atomic force of atom i; ξ is the virial tensor divided by N; N is the number of atoms. We adopted the conventional setting of increasing both pϵ and pξ from 0.02 to 1 while decreasing pf from 1000 to 1 over the course of training. A three-layer fitting network with 240 nodes in each layer was used to determine the form of the potential energy surface following our previous studies30,69,71.

An iterative training scheme71 was employed throughout the training process. Principal component analysis was used to identify the most representative frames from MD trajectories for high-accuracy DFT recalculations. These recalculated results were compared with the predictions of the current model to identify frames that were poorly described by the MLP, which were then added to the training set. This iterative approach ensures that the training set remains concise and well-balanced. The final training sets consist of 6245 and 7557 configurations for Mg-O-Fe-W and Mg-O-Fe-Pt systems, respectively. We compared the energies, atomic forces, and stresses from MLPs to those from DFT calculations for 16579 and 16956 configurations of test sets that are not included in the training set for Mg-O-Fe-W and Mg-O-Fe-Pt systems, respectively (Supplementary Fig. 1). For Mg-O-Fe-W system, the root-mean-square errors (RMSEs) of the energies, atomic forces, and stresses are 6.76 meV atom-1, 0.32 eV Å-1, and 0.53 GPa, respectively. For Mg-O-Fe-Pt, RMSEs are 6.69 meV atom-1, 0.30 eV Å-1, and 0.51 GPa, respectively. The RMSEs of energy falls below the commonly accepted threshold of 10 meV/atom; the RMSEs of stress is at least an order of magnitude lower than the discrepancies between the MgO equation of state obtained from DFT calculations and experimental measurements72.

Ab Initio Calculations

Ab initio calculations were performed using Vienna Ab Initio Simulation Package (VASP)73. We used the projector augmented wave (PAW) method74 as implemented in VASP73 and PBEsol approximation75. PAW potentials are widely utilized in DFT calculations for planetary interior conditions and, when combined with the PBEsol approximation, demonstrate excellent agreement with experimental measurements of the physical properties of silicates and oxides9,76,77. The core radii are O: 0.820 Å (2s22p4), Mg: 1.058 Å (2p63s2), Fe: 1.164 Å (3p63d74s1), W: 1.455 Å (5p66s25d4), Pt: 1.455 Å (6s15d9). High-precision ab initio calculations were performed for training and test configurations used to construct MLPs with an energy cutoff of 800 eV, energy tolerance of 10−6 eV and 2 × 2 × 2 Monkhorst-Pack mesh.

Construction of the Grain Boundary Structure

The GBs of ferropericlase are symmetric tilt GBs constructed with Atomsk78 in our previous study25. MgO bicrystals with two misorientation angles were considered: α = 36.8° where the two crystals meet with {310} planes, and α = 29.5° where the GB plane does not correspond to any high-symmetry crystal plane (see Supplementary Information). The compact GB structures at energy minima favored under mantle pressures were identified79, which can further interact with vacancy defects and transform the atomic configuration80. Various amounts of Mg-O vacancy pairs were randomly introduced within a 1-nm-wide region at the GB, and the convergence of GB diffusivities as a function of the vacancy concentration was tested25 (see Supplementary Information). Then, the structures of (Mg0.9Fe0.1)O ferropericlase were generated by the random substitution of Mg with 10 mol% of Fe in the MgO bicrystals. We tested the potential impact of these random factors on the W diffusivities (see Supplementary Information). Ferropericlase bicrystals contain over 50,000 atoms, of which  ~2000 are located within the 1-nm-wide GB regions, resulting in an average distance of over 20 nm between the centers of adjacent grains. Twenty W or Pt atoms were randomly introduced into the GB region. Based on previous experimental results, we set the valence state of W to +623,39,40 and that of Pt to 029 for both GB and liquid systems. The valence states were controlled by removing Mg atoms near W. The effects of the valence state on the W diffusivity were tested (see Supplementary Information).

Molecular Dynamics Simulations

Ab initio MD simulations were performed using VASP73 under the canonical ensemble (NVT) with the Nosé-Hoover thermostat81. Our ab initio MD simulations run for 10–40 ps, sampling the Brillouin zone at the Γ point with energy cutoffs of 500 eV and an energy tolerance of 10−4 eV. MD simulations driven by MLPs were conducted by LAMMPS82 and DeePMD-kit28. The GB systems were first equilibrated in isothermal-isobaric conditions (NPT) for 100 ps under the target temperatures and pressures. The resulting structures were then used as the initial configurations to set up the MD simulations for 2 ns under an NVT ensemble, in order to evolve the GB structure to reach a steady state. Subsequently, we performed long NVT simulations for 2 ns, from which the GB diffusivity is calculated. (Mg,Fe)O liquids with different Fe contents were obtained by melting ferropericlase at high temperatures and gradually cooling, followed by NPT equilibration for 10 ps. The diffusivity was obtained from NVT simulations for 40 ps. The timestep of all MD simulations is 1 fs. All NVT simulations were repeated 4–20 times to report the standard deviation (error bars in all figures) of the diffusion coefficients.

Diffusion Coefficients

Diffusion coefficients were calculated as the slope of mean square displacements (MSDs) by,

$$D={\lim }_{t\to \infty }\frac{{{\rm{MSD}}}}{6t}={\lim }_{t\to \infty }\frac{{\left\langle {\left[\overrightarrow{r}\left(t+{t}_{0}\right)-\overrightarrow{r}\left({t}_{0}\right)\right]}^{2}\right\rangle }_{{{\rm{H}}}}}{6t},$$
(2)

where \(\overrightarrow{r}(t)\) is the particle trajectories in Cartesian space, and 〈⋯〉 represents an average over all atoms of the target element and over time with different origins83. The diffusivity as a function of temperature obtained from our simulations was fitted by the Arrhenius equation,

$$D={D}_{0}\exp \left(-\frac{\Delta H}{RT}\right),$$
(3)

where D0 is the pre-exponential factor, R is the ideal gas constant, T is the temperature in K, and ΔH is the activation enthalpy. Extrapolating experimental results to higher pressures requires an additional parameter to describe the pressure dependence of the diffusivity, then the Arrhenius equation becomes

$$D={D}_{0}\exp \left(-\frac{\Delta E+P\Delta V}{RT}\right),$$
(4)

where ΔE is the activation energy and ΔV is the activation volume.

The effective diffusion coefficient of W (DW) can be estimated by the combination of lattice diffusivity (\({D}_{{{\rm{W}}}}^{{{\rm{lattice}}}}\)) and GB diffusivity (\({D}_{{{\rm{W}}}}^{{{\rm{GB}}}}\))18,23,84:

$${D}_{{{\rm{W}}}}={D}_{{{\rm{W}}}}^{{{\rm{lattice}}}}+\frac{3\delta }{d}{D}_{{{\rm{W}}}}^{{{\rm{GB}}}},$$
(5)

where δ is the GB width (~1 nm) and d is the grain size (0.1–10 mm in the lower mantle)85. Since there is no available \({D}_{{{\rm{W}}}}^{{{\rm{lattice}}}}\) data in lower mantle minerals, we assume the lattice diffusivity of W is the same as that of Si86 following Yoshino et al.23 due to their similarly high valence state23,40. Since the available experimental data are limited to 25 GPa86, a small activation volume of 1 cm3 mol−1 is assumed to estimate the upper bound of the effective diffusion coefficient.

Modeling μ182W anomalies in OIBs

We calculated the vertical composition profile of W isotopes above CMB (Supplementary Fig. 9) considering Fick’s second law of diffusion

$$\frac{\partial C}{\partial t}=-{D}_{{{\rm{W}}}}{\nabla }^{2}C$$
(6)

Since the bottom of the mantle may have a fixed μ182W value of  −220 and the diffusion distance of W is within 1% of the core radius, the solution to Eq. (6) can be well approximated by the diffusion in a half-space with a constant surface concentration87:

$$C={C}_{\infty }+({C}_{0}-{C}_{\infty }){{\rm{erfc}}}\left(\frac{y}{\sqrt{4Dt}}\right)$$
(7)

where C0 is the core-equilibrated 182W/184W (μ182W = −220), C∞ is the 182W/184W in the ambient mantle (μ182W = 0), y is the vertical distance above the CMB, t is the diffusion time of 4.54 Gyr, and erfc is the complementary error function. The 182W/184W of the PGZ is taken as the integral average of Eq. (7):

$${C}_{{{\rm{PGZ}}}}=\frac{1}{h}\int_{0}^{h}C(y)\,{{\rm{d}}}y$$
(8)

where h is the height of the PGZ.

The mixing ratio between PGZ material and background mantle material in OIBs is characterized by the degree of entrainment of dense material neighboring hot upwelling mantle18,88

$${R}_{\max }={\left(\frac{\Delta {\rho }_{{{\rm{T}}}}}{\Delta {\rho }_{{{\rm{Ch}}}}}\right)}^{2}$$
(9)

where ΔρT is the thermal density anomaly in the hot mantle plume, ΔρCh is the chemical density anomaly in the PGZ, and \({R}_{\max }\) is the maximum ratio of entrained dense material to total material. Considering that the estimated density anomaly of ULVZs is greater than that of LLSVPs89,90,91, we took the ΔρCh of LLSVPs following Ferrick & Korenaga18 to constrain the maximum proportion of plume-source material in OIBs. All parameters and the \({R}_{\max }\) result (11%) are consistent with those reported in Ferrick & Korenaga18. The μ182W in OIBs as a function of the height of PGZ was obtained by mixing the plume source (Eq. (8)) and the background mantle (μ182W = 0) with a mixing ratio of 1:8.