Abstract
Gravimeter measures gravitational acceleration, which is valuable for geophysical applications such as hazard forecasting and prospecting. Gravimeters have historically been large and expensive instruments. Micro-Electro-Mechanical-System gravimeters feature small size and low cost through scaling and integration, which may allow large-scale deployment. However, current Micro-Electro-Mechanical-System gravimeters face challenges in achieving ultra-high sensitivity under fabrication tolerance and limited size. Here, we demonstrate a μGal-level Micro-Opto-Electro-Mechanical-System gravimeter by combining a freeform anti-spring design and an optical readout. A multi-stage algorithmic design approach is proposed to achieve high acceleration sensitivity without making high-aspect ratio springs. An optical grating-based readout is integrated, offering pm-level displacement sensitivity. Measurements reveal that the chip-scale sensing unit achieves a resonant frequency of 1.71 Hz and acceleration-displacement sensitivity of over 95 μm/Gal with an etching aspect ratio of smaller than 400:30. The benchmark with a commercial gravimeter PET demonstrates a self-noise of 1.1 μGal Hz−1/2 at 0.5 Hz, sub-1 μGal Hz−1/2 at 0.45 Hz, and a drift rate down to 153 μGal/day. The high performance and small size of the Micro-Opto-Electro-Mechanical-System gravimeter suggest potential applications in industrial, defense, and geophysics.
Similar content being viewed by others
Introduction
Constantly emerging applications, such as resource exploration, hazard forecasting, and geophysical research1,2,3,4,5 pose demanding needs for precise measurement of local gravitational acceleration. Compared with absolute gravimeters that measure the acceleration of a freely falling mass6,7, relative gravimeters measure the gravity variation via the displacement of a mass suspended by springs, thus incorporating relatively smaller size, lighter weight, and poorer stability8,9. However, conventional relative gravimeters, such as Scintrex CG6 (https://scintrexltd.com/wp-content/uploads/2019/01/CG-6-Brochure_R5.pdf) and Microg LaCoste PET (https://microglacoste.com/wp-content/uploads/2017/03/MgL_gPhoneX-Brochure.pdf), are still large and expensive instruments. Micro-Electro-Mechanical-System (MEMS) gravimeter10,11,12,13,14,15,16 is an emerging field with potential applications in terms of their further miniaturization, mass production, and cost reduction. MEMS gravimeters with various strategies, such as lowering the spring constant10,11,13, enlarging the mass17, and applying highly sensitive readout18,19 have been published to achieve precise gravity variation measurement. However, MEMS gravimeters still face challenges compared with large-size competitors with μGal Hz-1/2-level sensitivity and corrected long-term stability of around 20 μGal/day(https://scintrexltd.com/wp-content/uploads/2019/01/CG-6-Brochure_R5.pdf), (https://microglacoste.com/wp-content/uploads/2017/03/MgL_gPhoneX-Brochure.pdf). The first challenge is to achieve high acceleration sensitivity with an easily fabricated chip-scale structure. Achieving high sensitivity (or low resonant frequency) in a small size usually requires slender springs with a high aspect ratio and always brings the maximum stress dangerously close to the tolerable limit. Finding the optimal spring design requires a large parameter space and an efficient design approach. The second challenge is to integrate a readout with better displacement sensitivity without compromising the miniaturization and process compatibility. Although optical shadow sensors10,11, optical grating sensors20,21,22, and capacitive sensors23,24 with nm or sub-nm sensitivity have been subsequently introduced to MEMS gravimeters, the acceleration sensitivity could be pushed further via picometer- or femtometer-level displacement methodology25,26,27,28,29,30.
As an effective way to improve sensitivity, the anti-spring mechanism31,32 has been recently introduced into MEMS accelerometers33,34 and gravimeters10,11. For example, Middlemiss et al. developed a MEMS gravimeter with a resonant frequency of 2.3 Hz and sensitivity of 40 μGal Hz−1/2 based on an asymmetric arc-shaped anti-spring structure10,35. Tang et al. combined a pair of cosine-shaped negative stiffness springs with a pair of folded positive stiffness springs11, achieving a resonant frequency of 2.9 Hz, a sensitivity of 8 μGal Hz−1/2, and a dynamic range of 8 Gal. Boom et al. designed a MEMS accelerometer with a resonant frequency of 28.1 Hz based on arc-shaped anti-springs33. However, the limited degrees of freedom of these anti-spring mechanisms result in a small design parameter space, making it difficult to find a solution that balances ultra-high sensitivity, fabrication tolerance, and stress robustness. More specifically, the lowest reported resonant frequencies are always around 2~3 Hz, and the required etching aspect ratio is larger than 16, even exceeding 4010,36,37. The introduction of freeform geometries38,39,40 opens a path to address this issue owing to its larger design parameter space. Some researchers have explored the design of MEMS freeform structures. For example, Wang et al. used polynomial and Bézier curves to achieve global optimization of beams41,42, while the lack of local adjustability made these curves challenging to perform fine-tuning. Anti-springs undergo dramatic changes in stiffness during the loading process34. The optimal design of such freeform anti-springs (F-ASs) requires multiple iterations to tune the mechanical response. Therefore, although F-AS can provide a larger design parameter space, the vast parameter space makes it tough to find an optimal design in a single-stage optimization with conventional metaheuristic algorithms43,44,45. The local adjustability of freeform geometry and feasible algorithm are both necessary to decompose the expensive optimization problem46 of F-ASs.
In this paper, we demonstrate a Micro-Opto-Electro-Mechanical-System (MOEMS) gravimeter based on optimized locally adjustable F-ASs and a highly integrated optical grating-based readout. A multi-stage algorithmic approach is developed to spring design, providing a larger parameter space and feasible optimization. The first-stage optimization is performed to obtain a global design of the anti-spring geometry, and the second-stage optimization performs local fine-tuning of the geometry to meet multiple design requirements. A chip-scale spring-mass system is optimized to achieve high acceleration-displacement sensitivity over 95 μm/Gal (resonant frequency lower than 2 Hz) without making high-aspect ratio springs. The optical grating-based readout allows displacement measurement with 1.2 pm Hz−1/2 sensitivity and shows high integration and compatibility with the process. Designated manufacturing and packaging are implemented to minimize the impact of internal stress and external temperature and pressure, thereby enhancing long-term stability. The prototype of the MOEMS gravimeter is tested to have a noise level of 1.1 μGal Hz−1/2 at 0.5 Hz and a drift rate of 153 μGal/day. Co-site Earth tide and seismic measurements using the prototype and a commercial gravimeter are conducted to confirm the sensitivity and long-term stability. Such a small-size and high-performance MOEMS gravimeter could provide portable and precise measurements and platforms for geophysics and potential applications in prospecting and hazard forecasting. In addition, the algorithm-enabled multi-stage design approach of locally adjustable F-ASs opens a pathway toward the optimal design of complex structures with a large degree of freedom.
Results
Sensing unit of the MOEMS gravimeter with F-ASs and optical readout
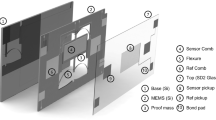
Figure 1a illustrates the packaged sensing unit of the MOEMS gravimeter, including the grating, mechanical sensing unit, supporting layer, adhesive layer, and silicon substrate with patterned Pt resistors. The mechanical sensing unit converts the gravitational acceleration into the displacement of the proof mass suspended by springs. The displacement of the proof mass is measured by the optical grating-based readout, which comprises a pair of gold grid lines patterned on the fixed glass substrate and the proof mass. The supporting layer and adhesive layer are used to support and bond the device. The integrated Pt resistors are used to measure and control temperature.
a Schematic diagram of the packaged sensing unit of the MOEMS gravimeter. b Layout of the mechanical sensing unit, including (I) the proof mass, (II) connecting rods, (III) freeform anti-springs (F-ASs), and (IV) compression mechanisms, with motion in the y-axis direction. c Schematic diagram illustrating the construction of a F-AS.
The mechanical sensing unit is shown in Fig. 1b. It includes (I) the proof mass with metal grid lines at the surface center, (II) connecting rods, (III) F-ASs, and (IV) compression mechanisms. The sensitive direction is the y-axis, and the proof mass is connected to four F-ASs through two connecting rods. The four F-ASs have the same geometry and are symmetrically distributed on both sides of the proof mass to reduce cross-axis sensitivity in the x-direction. The other end of the F-AS is connected to the compression mechanism (Supplementary Fig. 17). This mechanism is used to actively compress the anti-spring with a certain distance to lower the stiffness along the y-axis. The working principle and semi-analytical calculation of the stiffness of the anti-springs, as well as its force-displacement relationship, can be found in Supplementary Note 1.
The F-ASs are constructed using B-spline curves due to their convex hull property and the local adjustment ability47, as shown in Fig. 1c. Control points P1, P2,…, Pn-1, Pn form a freeform curve, and the freeform curve is offset on both sides to form a closed area with connecting line segments. It is noted that the F-AS can be constructed by two separate B-spline curves, while the parameter space may be too large in actual trial designs for numerical computing-based optimization.
Multi-stage design of highly sensitive anti-springs with fabrication tolerance
This paper proposes a multi-stage algorithmic approach to design F-ASs to achieve high performance with constraints of stress and fabrication tolerance. The design flow is depicted in Fig. 2a, containing three main steps: (1) Initialization: Construct F-ASs and analytically predict the mechanical performance. (2) Multi-stage directional optimization: Conduct global optimization on the F-ASs, followed by local fine-tuning of the first-stage optimization results. (3) Evaluation: Evaluate the optimization results; perform local fine-tuning or global optimization if they do not meet the requirements; conduct a robustness analysis of the design if they meet the requirements.
a Multi-stage design flowchart, mainly including three steps: initialization, multi-stage directional optimization, and evaluation. b Convergence graph of the objective function for global optimization of the F-AS. The figure of merit (FOM) continues to decrease, with the final FOM being 1.5673 × 10−3. c Global optimization results of the freeform anti-springs (F-AS) illustrate the deformation and stress distribution, with the displacement to acceleration response inset (black solid line represents the simulation result, red solid line represents the fitting curve). The sensitivity and resonant frequency are 79.3501 μm/Gal and 1.03 Hz, respectively, with a linearity of 0.9179 and a maximum stress of 313.7 MPa. d Schematic diagram of local adjustment of the F-AS, adjusting control points P6 and P7 to change the shape of the compression end without affecting the overall shape of the anti-spring. e Local optimization results of the F-AS, including the deformation and stress distribution, with the acceleration-frequency and acceleration-displacement response insets. The sensitivity and resonant frequency are 72.3056 μm/Gal and 1.46 Hz, respectively, with a linearity of 0.9826 and a maximum stress of 299.7 MPa.
Seven control points (P1 ~ P7) were chosen to define the F-AS, considering the balance between the degree of freedom and computational expense. Table 1 lists ten variable structural parameters of the sensing unit and their upper and lower limits. The sensing unit has a total of 23 important structural parameters, which are listed in Supplementary Table 1. The thickness of the proof mass and springs was set to be the same as the thickness of a readily accessible wafer, taking advantage of the whole thickness of a wafer to construct a big mass. The freeform curve was a third-order quadratic B-spline curve. The control points P1 and P2 were overlapped and fixed to ensure a smooth connection between the anti-springs and the connecting rods. The x-coordinates of control points P6 and P7 were fixed to ensure that the length of the anti-springs in the x-axis direction remains unchanged. The coordinate ranges of the remaining control points were determined by the footprint of the unit. The lower limit of the spring width was determined by the etching aspect ratio.
Regarding the objective function of the optimization, we focused on the static response of the spring-mass system under nominal operating conditions because of the low-frequency characteristic of the gravitational acceleration10,11,12. Ultra-high acceleration-displacement sensitivity is the primary property of the sensing unit and serves as the first factor of the objective function. The linear range of acceleration-displacement response and the R-squared value within the range of 10 Gal are considered the second and third factors because the anti-spring structure usually exhibits highly nonlinear behavior34. The range of 10 Gal was selected considering the local gravitational acceleration variation at different locations48,49 and anti-spring-based competitors10,11. The optimization objective function for the F-AS is as follows:
where S represents the acceleration-displacement sensitivity, G represents the linear range, R2 is the R-squared value of the linear fit of the acceleration-displacement curve within the range of 10 Gal, and k1 to k3 are corresponding weight factors. Our purpose is to minimize the figure of merit (FOM). In the initialization step, we employed a semi-analytical method to predict the stiffness of the F-AS (Supplementary Note 1). In the multi-stage optimization, we used the Finite Element Method (FEM) to precisely evaluate the nonlinear performance of the F-AS (Methods).
For expensive optimization problems, it is beneficial to distribute the initial value of parameters covering the entire parameter space in the early stage of the optimization, and it is preferred to improve the convergence speed in the later stage. In this paper, both the first and second stages of optimization were conducted using the Adaptive Elite Learning Particle Swarm Optimization (AELPSO) algorithm, a self-built algorithm based on complementary sub-strategies for multimodal expensive problems (Methods).
The primary goal of the first-stage optimization is to pursue the three aforementioned objectives. The maximum stress value and spring width serve as soft constraints. The iteration number of the first-stage optimization was set to 200. Figure 2b illustrates the convergence graph, and the FOM can be observed to continue to decrease in the optimization. The global optimal results for the variable parameters are presented in Table 1. The geometry of the F-AS obtained by global optimization is shown in Fig. 2c, along with its compression and loading state. The simulation result and the fitting curve of the displacement to the applied acceleration response are depicted in black and red in the inset. The resonant frequency of the anti-spring was as low as 1.03 Hz, the acceleration-displacement sensitivity within the range of 10 Gal was 79.3501 μm/Gal, and the linearity was 0.9179. The sensitivity is lower than the frequency-calculated value by the relationship a = ω² × d because the sensitivity is the slope of the fitted straight line of the curve within a relatively large range, more likely an average slope. The sensing unit exhibited exceptionally high sensitivity and a moderate linearity that could be further improved. In addition, the maximum stress in the structure was 313.7 MPa, slightly exceeding the safe stress limit, which was set as 300 Mpa50,51.
The second-stage design was performed to adjust the anti-springs locally to address the issue of relatively low linearity and high local stress. The maximum stress and spring width are strictly constrained to be within 300 MPa and larger than 30 μm, respectively. As shown in Fig. 2c inset, the region with the maximum stress is located at the compression end of the F-AS. Adjusting control points P6 and P7, as illustrated in Fig. 2d, allows for the adjustment of local shape near the compression end without affecting the overall shape of the anti-spring based on the characteristics of the third-order quadratic B-spline curve. Table 1 lists the upper and lower limits of the local fine-tuning parameters. The iteration number of the second-stage optimization was set to 50, considering the smaller number of parameters. The local fine-tuning results are presented in Table 1. The geometry of the optimized F-AS and its compression state are shown in Fig. 2e, where the insets depict the simulation result of the acceleration-displacement response. The resonant frequency of the anti-spring was 1.46 Hz, the mechanical sensitivity of the spring-mass system was 72.3056 μm/Gal, and the linearity was 0.9826. The maximum stress was reduced to 299.7 MPa, within the safe stress limit. It is noted that the linearity and maximum stress were modified without sacrificing much sensitivity and resonant frequency. The MEMS sensing unit still has one of the lowest reported resonant frequencies and the highest acceleration-displacement sensitivity. The modal analysis results of the optimized structure indicate that the cross-axis sensitivity is small (Supplementary Note 2).
Finally, a robustness analysis was conducted to confirm the feasibility. Supplementary Table 2 lists the parameters and parameter ranges of the sensing unit for the robustness analysis. We considered errors in both manufacturing processes and material properties. Errors arising from manufacturing processes include fillet radius, variations in the width of the anti-spring and the proof mass, and the compression distance. Errors arising from material properties include variations in Young’s modulus, density, and Poisson’s ratio. Single-parameter and multi-parameter robustness analysis results indicate that even in the worst case, the design can achieve a resonant frequency of 1.89 Hz, a sensitivity of 56.3262 µm/Gal, and linearity of 0.9762, respectively (single- and multi-parameter robustness analysis results see Supplementary Note 3). It demonstrates that the F-AS obtained by multi-stage design had excellent performance and fabrication tolerance. Note that the stress limit is safe enough to further reduce the width of the spring, and it is easy to obtain an F-AS-based structure with a resonant frequency below 1 Hz by setting a more tolerant constraint
Experiment results
Displacement sensitivity measurement of the optical grating-based readout
The sensing unit of the MOEMS gravimeter was composed of the designated F-AS-based mechanical structure and an integrated optical grating cavity, as shown in Fig. 3a. The optical grating cavity allows pm-level displacement sensitivity and shows high integration. It comprises a pair of gold grid lines patterned on a fixed glass substrate and the proof mass, termed G1 and G2, respectively. Two gratings had the same period of 3 µm. A laser beam emitted from a source illuminated the optical cavity, generating a series of interferometric diffraction beams. For a certain cavity length, the light intensity of the first-order diffraction beam is related to the in-plane displacement of the proof mass along the y-axis but is insensitive to the x-axis displacement. The details can be found in Supplementary Note 4. The inset of Fig. 3a shows the simulation results of the light intensity as a function of the displacement. The intensity was detected by a photodetector, enabling the measurement of the displacement of the proof mass.
a Schematic of the displacement measurement via an optical grating cavity, which comprises a pair of gold grid lines. The displacement of the proof mass along the y-axis results in the variation in the light intensity of the interferometric diffraction beam, as shown in the inset. The period of the light intensity versus displacement is equal to the period of the metal gratings. b Photograph and schematic of the optical displacement measurement setup based on a piezoelectric ceramic. c Static results of the output voltage versus the input displacement. d Noise performance of the optical displacement measurement unit.
The displacement sensitivity of the readout was experimentally evaluated through the setup shown in Fig. 3b. A dissociated proof mass with grating G2 was bonded to a quartz plate, which was then bonded and fixed onto a piezoelectric ceramic (Model PA25LEW, Thorlabs Inc.). Grating G1 was mounted on a five-dimensional adjustment stage to facilitate the alignment of the cavity. Both gratings were mounted perpendicular to the ground, with their grid lines parallel to the x-direction. The expansion and contraction direction of the piezoelectric ceramic is the y-direction. First, the grating G2 was driven by a piezoelectric ceramic to test sensitivity and noise level. Figure 3c plots the experimental results of output voltage versus the input displacement, where each point corresponds to the average value of the static measurement result in 5 min. The response resembles the simulation results and has a sensitivity of 1.22 V/µm, with the standard deviations from 1 to 12 mV. The standard deviation error primarily arises from environmental vibrations and disturbances, which are transmitted through structural components to the cavity. At certain positions, specifically those with a larger slope, the response becomes noisier because a larger slope indicates higher sensitivity to the disturbances. The standard deviations correspond to acceleration errors from 8.2 to 98.3 μGal, combining the optical displacement sensitivity and the acceleration-displacement sensitivity of around 100 μm/Gal. The experimental result is not a perfectly linear response but rather resembles the typical response of such an optical cavity. Figure 3d shows the spectral density of the displacement measurement. It indicates that the noise level of the optical cavity is 1.2 pm Hz−1/2 at 1 Hz and below 5 pm Hz−1/2 within the frequency range of 0.5–1 Hz.
Acceleration sensitivity and resonant frequency measurement of the mechanical sensing unit
The fabricated sensing unit is shown in Fig. 4a. The shape of the proof mass was adjusted to avoid collisions with anti-springs. The adjustment did not change the center of the proof mass, nor did it affect the device’s modes and mechanical properties (Supplementary Note 5). In addition, we designed a sensing unit with single-convex freeform anti-springs (SF-ASs) using the same design approach to make a comparison with a smaller parameter space. The non-optimized structural parameters, the number of control points, the objective function, and design constraints remained unchanged for a fair comparison. The resonant frequency, sensitivity, and linearity of the sensing unit with SF-ASs were 2.08 Hz, 43.2631μm/Gal, and 0.9822, respectively (optimization results see Supplementary Note 6). The fabricated structure is shown in Fig. 4b. This comparison demonstrates that the complete F-AS performs better than the SF-AS with a general layout.
a Processed sensing unit based on the complete F-ASs. b Processed sensing unit based on the single-convex freeform anti-springs (SF-ASs). c Schematic diagram of the turntable experiment of the sensing unit, with the gravitational acceleration along the sensitive axis as gcosθ. d Acceleration (or angle)-frequency responses of both ASs. The frequency of the complete F-AS-based structure at 90° is 1.61 and 1.71 Hz for simulation and experimental results, and the minimum resonant frequency of the SF-AS-based structure at 90° is 2.77 and 2.45 Hz for simulation and experimental results. e Results of the turntable tilt experiment, with red and blue series representing the results of the complete F-AS-based and the SF-AS-based sensing units, respectively. The scatter represents the experimental results, and the solid lines represent the linear fitting of the experimental results, respectively. The time-domain data for some input acceleration points in one minute are shown in the insets. The measured acceleration-displacement sensitivity of the complete F-AS and the SF-AS-based units are 95.3674 µm/Gal and 40.5394 µm/Gal, respectively.
Figure 4c illustrates the turntable experiment setup for the mechanical sensing unit. The mechanical sensing units were packaged using wafer-level manufacturing and bonding techniques (Supplementary Note 7). The manufacturing and packaging process is presented in Methods. The gravimeter prototype was fixed on the high-precision turntable (Model DP300, Dantsin-RPI Inc.). The sensitive axis of the gravimeter was parallel to the turntable, and the turntable surface was perpendicular to the ground. By rotating the turntable, the angle θ between the sensitive axis of the gravimeter and the gravitational acceleration g, pointing downward, could be finely changed. This variation in θ led to a change in the acceleration variation gcosθ along the sensitive axis. More specifically, a change of the angle of 0.0004° corresponds to the variation of the gravitational acceleration component applied to the sensitive axis of g*(sin(0.0004°) – 0) ≈ 7 mGal at the angle of 0° and g*(1 – cos(0 – 0.0004°)) ≈ 24 nGal at 90°. Herein, the turntable was first fast rotated around the z-axis to scan and then finely adjusted to locate the point with high sensitivity. As shown in Fig. 4d, the resonant frequency of the mechanical sensing units with complete F-ASs and SF-ASs were measured as 1.71 Hz and 2.45 Hz at the angle of 90°, close to the simulated results of 1.61 Hz and 2.77 Hz, considering the fabrication errors. The tiny deviation between the experiment and simulation is mainly due to the unobservable fabrication errors, as presented in Supplementary Fig. 18a. The resonant frequency could be lowered to 1 Hz or even below in consideration of the over etch, and it was realized in practice (see Supplementary Fig. 18b).
Subsequently, a fine scan was conducted within the dynamic range with a step size of 1.44 arc seconds. The system was paused at each angle for one minute to acquire the static response. Figure 4e presents the static response of the displacement versus the gravitational variation, where the red and blue colors represent the responses of sensing units based on the complete F-ASs and SF-ASs, respectively. The scattered points represent experimental data, and the solid lines represent the linear fitting. The time-domain data for some input acceleration points in one minute are shown in the insets. Within the last 30 s, the time-domain output curves at each acceleration point are highly stable after 30-s stabilization, with standard deviations from 4 nm to 14 nm, indicating virtually no drift. The fitted acceleration-displacement sensitivity of these two units is measured to be 95.3674 µm/Gal and 40.5394 µm/Gal, respectively, with linearity of 0.9985 and 0.9919. The linearity of 0.9985 demonstrates that the linearity is significantly enhanced via local fine-tuning. The experimental results indicate that the optimized F-AS-based structures exhibit low resonant frequency, high acceleration-displacement sensitivity of more than 95 µm/Gal, and reasonable linearity, which further demonstrate the superiority of multi-stage design.
Noise level measurement and comparison of gravimeters
The noise level of the MOEMS gravimeter was evaluated in a cave laboratory, where the MOEMS gravimeter and a reference commercial gravimeter, Microg LaCoste PET, were placed side by side, as shown in Fig. 5a. The reference gravitational acceleration obtained from the cave laboratory is 9.7944 m/s2. The temperature variation in the cave was within 100 mK per day, and the temperature variation was further decreased to within 5 mK by temperature control (Supplementary Note 8). The two instruments were positioned within 10 meters, detecting nearly identical gravitational signals. The output of the gravimeters had been recorded without vibration isolation or vacuum maintenance. Several teleseismic signals were recorded according to the benchmark with the reference gravimeter. Figure 5b shows the seismic signal generated by a magnitude 4.4 earthquake in Guangdong, China, on 4th November 2023. The P-waves and S-waves can be clearly distinguished. The acceleration power spectral density of the MOEMS gravimeter is shown in Fig. 5c. Data were recorded by a fast sampling rate of 10 Hz and a slow sampling rate of 0.1 Hz in order to observe the responses of Earth tremor peaks and tides. The noise floor of the prototype reaches down to 1.1 μGal Hz−1/2 at 0.5 Hz, and the ultimate noise floor can be smaller than 0.3 μGal Hz−1/2 at around 0.45 Hz; the diurnal and semi-diurnal components of the Earth tides are visible at 10−5 Hz; the Earth tremor peak can be observed at around 0.2 Hz and around 2-3 Hz. The noise bump around 0.1 Hz could be due to insufficiently precise temperature control. Finer temperature control and temperature compensation are expected to suppress the noise level in this frequency range. Supplementary Fig. 19 depicts the acceleration noise floor of the optical readout and the mechanism in the power spectral density plot. It demonstrates that, apart from the bump caused by thermal control, the optical readout noise is close to the self-noise floor, which can be considered the main limiting factor. Two pale red and deep red lines in Fig. 5d depict the data recorded by the MOEMS gravimeter from 11th to 17th June 2024 over five days, corresponding to the raw time series and data removing the linear drift. The prototype achieved reasonably good long-term stability, with a drift of 153 μGal/day. The drift is comparable to other MEMS gravimeters, which is around 100–300 μGal/day. According to the Allan deviation results shown in Fig. 5e, a bias instability of 6 μGal can be obtained with an integration time of 600 s. Comparing the data obtained from the reference gravimeter (in blue) shows a strong correlation coefficient of 0.9218, as shown in Fig. 5f, indicating that the MOEMS gravimeter has successfully observed Earth tides.
a Setup of the MOEMS gravimeter and the reference gravimeter in the cave laboratory. b Teleseismic signals caused by the earthquake in Guangdong, China, on 4th November 2023 with a data sampling frequency of 1 Hz. c Acceleration spectral density plot of the MOEMS gravimeter and the reference gravimeter. The red and blue lines represent the noise plot of the MOEMS gravimeter and the reference gravimeter, respectively, and the orange line represents the self-noise floor of the MOEMS gravimeter. The red and the orange series were recorded at a sampling rate of 10 Hz. The pink series represent data that were recorded at a sampling rate of 0.1 Hz. At 10−5 Hz, the diurnal and semi-diurnal components of the Earth tides are visible; the Earth tremor peak can be observed at around 0.2 Hz; and the resonant peak of the device is located at around 1.6 Hz. d Data of the tide measurement with a sampling rate of 0.1 Hz. The pale red line represents the raw data, and the deep red line represents the data removing the linear drift. e Allan deviation of the data in d. f Comparison of Earth tides measured by the MOEMS gravimeter and the reference gravimeter. The red line is obtained from the MOEMS gravimeter, and the blue line is obtained from the reference gravimeter. The correlation coefficient between these two sets of data is 0.9218. g Allan deviation of the data of the MOEMS gravimeter in f.
Table 2 compares the proposed MOEMS gravimeter and the reported MEMS and commercial gravimeters. Thanks to the multi-stage design of locally adjustable F-AS, the mechanical sensing unit achieves a resonant frequency of 1.71 Hz under nominal operating conditions, acceleration-displacement sensitivity of over 95 µm/Gal, and a dynamic range of over 10 Gal, which outperforms its previously reported counterparts. In addition, the highly integrated optical grating cavity enables the pm-level displacement measurement, further allowing the gravitational acceleration measurement with a noise level of 1.1 μGal Hz−1/2 at 0.5 Hz. The compact MOEMS gravimeter with ultra-high sensitivity, reasonable robustness, and high stability shows promise for portable and precise relative gravity measurement worldwide.
Discussion
This paper introduces a multi-stage algorithmic approach for freeform spring design. The approach provides a larger parameter space and allows highly efficient optimization via global optimization and local fine-tuning. A chip-scale spring-mass system with high acceleration-displacement sensitivity of over 95 μm/Gal (resonant frequency of 1.71 Hz) was achieved without making high-aspect ratio springs. It pushed forward the acceleration sensitivity to μGal-level or even below, combining the integrated optical readout with pm-level sensitivity. The F-AS-based mechanical sensing unit and the optical cavity were packaged using wafer-level manufacturing and bonding techniques. High-precision real-time temperature control was implemented to further enhance the long-term stability of the device. The performances of the MOEMS gravimeter were experimentally confirmed by the long-period test. The comparison between the commercial large-size gravimeter indicates that the drift rate of the MOEMS gravimeter reaches 153 μGal/day, the noise level is 1.1 μGal Hz-1/2 at 0.5 Hz, and the ultimate noise floor of the device can be smaller than 0.3 μGal Hz−1/2 at 0.45 Hz. The diurnal and semi-diurnal components of the Earth tides are visible, and the correlation coefficient between the data of the MOEMS gravimeter and the reference gravimeter is 0.9218.
This on-chip mechanical sensing unit realizes the resonant frequency of around 1 Hz in MEMS devices with reasonable fabrication tolerance and robustness. The multi-stage design of F-ASs provides a solution to problems with a large degree of freedom and ultra-high targets, i.e., sub-μGal sensitivity combining fabrication tolerance. The MOEMS gravimeter, owing to its high performance, small size, and mass production, proves to be a potential candidate in industrial, defense, civil, and scientific applications. It is possible to construct a gravity monitoring network to capture time-dependent images of the gravitational field in a region, facilitating geophysics exploration and hazard forecasting.
Methods
Finite element simulation
Besides using semi-analytical analysis to roughly predict the stiffness of the F-ASs, we used FEM to precisely simulate the nonlinear behavior of the F-ASs. The mechanical model was simplified as a 2D finite element model to reduce the computing costs because of the identical thickness of the die. More specifically, 3D simulation of the F-AS response requires a time of around two hours, and 2D simulation only requires less than one minute. The validity of the 2D FEM results was confirmed by the thorough comparison with the 3D FEM results (Supplementary Fig. 20). The 2D model was further simplified to half of the unit due to the symmetry. Thousands of elements and a mapped method were used to mesh the 2D model. The modulus tensor of single-crystal silicon was set according to reference52. In addition, the density of single-crystal silicon was set to 2329 kg/m3. The boundary condition was that the displacement of the proof mass in the x-direction was zero due to structural simplification, a specified displacement was applied at the compression end of the F-ASs, and an inertial force was applied to the proof mass. The equilibrium equations for the F-ASs were established in the deformed state and updated with deformation. The solution was path-dependent, so the gravitational acceleration was increased gradually to achieve a slow growth in the load, ensuring good convergence.
Optimization algorithm
A self-built Particle Swarm Optimization algorithm53,54, AELPSO, was proposed to solve the expensive optimization problem. AELPSO employs four sub-swarms with complementary ‘CODA’ strategies that are adaptively fused via the adaptive elite learning (AEL) method to balance exploration and exploitation. The letters ‘C’, ‘O’, ‘D’, and ‘A’ stand for four learning exemplars generation strategies of Cross-, Ortho-, Dynamic-, All-, in which “C” and “A” use binomial crossing method and weighted average method to generate learning examples respectively, which excel in exploration, while “O” and “D” use updated orthogonal and dynamic (adaptive learning) strategies, which excel in exploitation. In the AEL method, better particles are selected to execute more strategies to escape local optima quickly; the number of particles executing all strategies is adaptively increased to prevent premature convergence from the exploratory to the exploitative state; finally, each time when the adaptive elite learning method is performed, a certain number of particles with the same subscript are selected from the population for elimination to avoid the risk of premature convergence and elimination of the best particles. Promising particles in AELPSO explore the search space in multiple ways and are more likely to find better solutions in a limited iteration number (typically 200) when faced with such an expensive optimization problem. A thorough benchmark with six state-of-the-art optimization algorithms was conducted, demonstrating the superiority of AELPSO in optimization performance and convergence speed (Supplementary Note 9).
Manufacturing and packaging process
The manufacturing and packaging process is illustrated in Fig. 6. As shown in Fig. 6c, wafer 1 of grating G1 was made of a 400-μm-thick glass wafer with thermal expansion coefficients comparable to single-crystal silicon wafers, and the grating fabrication process on its surface was the same as the process used for the surface of the proof mass. The wafer 2 of mechanical sensing unit was based on a 400-μm-thick single-crystal silicon wafer with a crystal orientation of <100>, as illustrated in Fig. 6d. First, a 100-nm-thick layer of gold was deposited on the top surface of the silicon using magnetron sputtering. The gold layer was then patterned by a standard photolithography and peeling process, obtaining 3-μm-period grid lines. Next, a 10-μm-thick layer of AZ4620 photoresist was spin-coated on the top surface of the sample wafer and placed on a hot plate at 90 °C for 90 s. The mask of the mechanical sensing unit’s was aligned and exposed using cross marks, followed by a positive development in TMAH for approximately 3 min, forming the patterned photoresist (Supplementary Fig. 21). Due to the large area to be etched, halo masking technology was used to design the mask (Supplementary Fig. 22). The mask was designed with a 200-μm-width halo, which was used to etch away the contour of the structure rather than all unwanted areas55. Paraffin was used as the mounting adhesive to affix the sample to a carrier wafer (with the photoresist side upward). The sample was then loaded into an SPTS dry-etching machine to run a deep reactive ion etching (DRIE) process for approximately 120 min until the wafer was etched through. The etched sample was soaked in acetone to remove the photoresist, and a plasma stripper was used to remove the residual photoresist. The sample was inverted in a dish, and alcohol and deionized water were used to detach the sample from the carrier silicon wafer. As shown in Fig. 6e, wafer 3 of the supporting layer was manufactured by deep wet etching of the thinned glass wafer with a relatively large thickness. Figure 6f shows that wafer 4 was made of a 400-μm-thick single-crystal silicon. Platinum resistors were first patterned on the backside of the silicon wafer. Then, a confinement trench was etched by the DRIE process. These four wafers were bonded by a low-stress bonding technique (Supplementary Note 7) sequentially to finish the packaging, as shown in Fig. 6g–i. This packaging offers reasonable shock resistance (Supplementary Note 10).
a Schematic diagram and b Photograph of the packaged device. c–i Schematic diagram of the manufacturing and packaging process. c1 A glass wafer. c2 Metal patterning of the grating on the glass wafer. d1 A silicon wafer of the mechanical sensing unit. d2 Metal patterning of the grating on the silicon wafer. d3 Lithography patterning of the mechanical sensing unit. d4 Deep reactive ion etching of the mechanical sensing unit. d5 Release of the mechanical sensing unit. d6 Processed mechanical sensing unit. e1 A glass wafer. e2 Deep wet etching of the glass wafer. f1 A silicon wafer of the substrate. f2 Platinum patterning on the silicon wafer. f3 Deep reactive ion etching of the confinement trench. g Low-stress bonding of wafer 2 and wafer 4. h Low-stress bonding of wafer 3 and the bonded wafer 2 + 4. i Low-stress bonding of wafer 1 and the bonded wafer 2 + 3 + 4.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.
Data availability
Source data are provided with this paper.
Code availability
The code used in this study is available on CodeOcean under the following link: https://codeocean.com/capsule/1049332/tree/v2.
References
Sandwell, D. T. et al. New global marine gravity model from CryoSat-2 and Jason-1 reveals buried tectonic structure. Science 346, 65–67 (2014).
Wang, W. et al. Seismological observation of Earth’s oscillating inner core. Sci. Adv., 8, eabm9916 (2022).
Carbone, D. et al. The added value of time-variable microgravimetry to the understanding of how volcanoes work. Earth Sci. Rev. 169, 146–179 (2017).
van Dam, T. et al. Using GPS and absolute gravity observations to separate the effects of present-day and pleistocene ice-mass changes in South East Greenland. Earth Planet. Sci. Lett. 459, 127–135 (2017).
Han, S. C. et al. Postseismic gravity change after the 2006-2007 great earthquake doublet and constraints on the asthenosphere structure in the central Kuril Islands: gravity change of the Kuril Earthquakes. Geophys. Res. Lett. 43, 3169–3177 (2016).
Menoret, V. et al. Gravity measurements below 10-9 g with a transportable absolute quantum gravimeter. Sci. Rep., 8, 12300 (2018).
Bidel, Y. et al. Absolute marine gravimetry with matter-wave interferometry. Nat. Commun. 9, 627 (2018).
Francis, O. Performance assessment of the relative gravimeter Scintrex CG-6. J. Geod. 95, 116 (2021).
Fores, B. et al. Impact of ambient temperature on spring-based relative gravimeter measurements. Geod. 91, 269–277 (2017).
Middlemiss, R. P. et al. Measurement of the Earth tides with a MEMS gravimeter. Nature 531, 614–617 (2016).
Tang, S. et al. A high-sensitivity MEMS gravimeter with a large dynamic range. Microsyst. Nanoeng. 5, 45 (2019).
Prasad, A. et al. A 19 day earth tide measurement with a MEMS gravimeter. Sci. Rep. 12, 13091 (2022).
Middlemiss, R. P. et al. Microelectromechanical system gravimeters as a new tool for gravity imaging. Philos. T. R. Soc. A. 376, 20170291 (2018).
Middlemiss, R. P. et al. Field tests of a portable MEMS gravimeter. Sensors 17, 2571 (2017).
Prasad, A. et al. A portable MEMS gravimeter for the detection of the Earth tides. In 17th IEEE Sensors Conference, New Delhi, India, (IEEE, 2018).
Yang, L. et al. A highly stable and sensitive MEMS-based gravimeter for long-term Earth tides observations. IEEE Trans. Instrum. Meas. 71, 1–9 (2022).
Pike, W. T. et al. A compact MEMS gravimeter with sub ng performance (Copernicus Meetings, 2024).
Qu, Z. et al. 2.4 ng/√Hz low-noise fiber-optic MEMS seismic accelerometer. Opt. Lett. 47, 718–721 (2022).
Mustafazade, A. et al. A vibrating beam MEMS accelerometer for gravity and seismic measurements. Sci. Rep. 10, 10415 (2020).
Williams, R. P. et al. Optically read displacement detection using phase-modulated diffraction gratings with reduced zeroth-order reflections. Appl. Phys. Lett. 110, 151104 (2017).
Xin, C. et al. Ultra-compact displacement and vibration sensor with a sub-nanometric resolution based on Talbot effect of optical microgratings. Opt. Express 30, 40009–40017 (2022).
Hu, P. et al. Displacement measuring grating interferometer: a review. Front. Inform. Tech. El. 20, 631–654 (2019).
Mansouri, B. E. et al. High-resolution MEMS inertial sensor combining large-displacement buckling behaviour with integrated capacitive readout. Microsyst. Nanoeng. 5, 60 (2019).
Kavitha, S. et al. Design and analysis of MEMS comb drive capacitive accelerometer for SHM and seismic applications. Measurement 93, 327–339 (2016).
Hou, Y. et al. A low 1/f noise tunnel magnetoresistance accelerometer. IEEE Trans. Instrum. Meas. 71, 9502511(2022).
Eichenfield, M. et al. A picogram- and nanometre-scale photonic-crystal optomechanical cavity. Nature 459, 550–579 (2009).
Krause, A. G. et al. A high-resolution microchip optomechanical accelerometer. Nat. Photonics 6, 768–772 (2012).
Lu, Q. et al. Inverse design and realization of an optical cavity-based displacement transducer with arbitrary responses. Optoelectron. Adv. 6, 220018 (2023).
Liu, T. et al. Integrated nano-optomechanical displacement sensor with ultrawide optical bandwidth. Nat. Commun. 11, 4579 (2020).
Hortschitz, W. et al. Robust precision position detection with an optical MEMS hybrid device. IEEE Trans. Ind. Electron. 59, 4855–4862 (2012).
Ghavidelnia, N. et al. Curly beam with programmable bistability. Mater. Des. 230, 111988 (2023).
Gan, J. et al. Design of a compliant adjustable constant-force gripper based on circular beams. Mech. Mach. Theory 173, 104843 (2022).
Boom, B. A. et al. Nano-G accelerometer using geometric anti-springs. In: 30th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), Las Vegas, NV, (IEEE, 2017).
Hussein, H. et al. Near-zero stiffness accelerometer with buckling of tunable electrothermal microbeams. Microsyst. Nanoeng. 10, 43 (2024).
Rymer, H. Gravity measurements on chips. Nature 531, 585–586 (2016).
Standley, I. M. et al. Short period seismometer for the lunar farside seismic suite mission. In: IEEE Aerospace Conference (IEEE, 2023).
Liu, D. et al. In-situ compensation on temperature coefficient of the scale factor for a single-axis nano-g force-balance MEMS accelerometer. IEEE Sens. J. 21, 19872–19880 (2021).
Elgarisi, M. et al. Fabrication of freeform optical components by fluidic shaping. Optica 8, 1501–1506 (2021).
Meng, X. et al. A direct approach to achieving efficient free-form shells with embedded geometrical patterns. Thin-Walled Struct. 185, 110559 (2023).
Ai, S. et al. Analysis of negative stiffness structures with B-spline curved beams. Thin-Walled Struct. 195, 111418 (2024).
Wang, C. et al. Design of freeform geometries in a MEMS accelerometer with a mechanical motion preamplifier based on a genetic algorithm. Microsyst. Nanoeng. 6, 104 (2020).
Wang, C. et al. Genetic Algorithm for the design of freeform geometries in a large-range rotary microgripper. In: 34th IEEE International Conference on Micro Electro Mechanical Systems (MEMS), (IEEE, 2021).
Jutte, C. V. et al. Design of nonlinear springs for prescribed load-displacement functions. In: ASME International Design Engineering Technical Conferences, Las Vegas, NV, (ASME, 2008).
Foli, K. et al. Optimization of micro heat exchanger: CFD, analytical approach and multi-objective evolutionary algorithms. Int. J. Heat Mass Transfer 49, 1090–1099 (2006).
Melnyk, M. et al. Application of a genetic algorithm for dimension optimization of the MEMS-based accelerometer. In 20th International Conference Mixed Design of Integrated Circuits and Systems, Gdynia, Poland, (IEEE, 2013).
Zhang, H. M. et al. Mode-localized accelerometer in the nonlinear Duffing regime with 75 ng bias instability and 95 ng/√Hz noise floor. Microsyst. Nanoeng. 8, 17 (2022).
Gordon, W. J. et al. B-spline curves and surfaces (Academic Press, 1974).
Van Camp, M. et al. Geophysics from terrestrial time-variable gravity measurements. Rev. Geophys. 55, 938–992 (2017).
Hirt, C. et al. New ultrahigh-resolution picture of Earth’s gravity field. Geophys. Res. Lett. 40, 4279–4283 (2013).
Petersen, K. E. Silicon as a mechanical material. Proc. IEEE 70, 420–457 (1982).
Kamp, P. Towards an ultra sensitive seismic accelerometer (University of Twente, 2016).
Hopcroft, M. A. et al. What is the Young’s modulus of silicon? J. Microelectromech. Syst. 19, 229–238 (2010).
Zen, N. et al. A dynamic neighborhood-based switching particle swarm optimization algorithm. IEEE Trans. Cybern. 52, 9290–9301 (2022).
Cao, Y. et al. Comprehensive learning particle swarm optimization algorithm with local search for multimodal functions. IEEE Trans. Evol. Comput. 23, 718–731 (2019).
Pike, W. T. et al. Analysis of sidewall quality in through-wafer deep reactive-ion etching. Microelectron. Eng. 73, 340–345 (2004).
Acknowledgements
The authors gratefully acknowledge financial support from the National Natural Science Foundation of China (62004166), the Natural Science Foundation of Zhejiang Province (LY23F040002), the Natural Science Foundation of Ningbo (202003N4062), the National Postdoctoral Program for Innovative Talents (BX20200279), Natural Science Basic Research Program of Shaanxi Province (2020JQ−199), National Key Research and Development Program of China (2022YFB3403800), Aeronautical Science Foundation of China (20230008053003). We would like to thank the Xi’an LeadMEMS Co., Ltd. for microfabrication.
Author information
Authors and Affiliations
Contributions
S.W. and W.Y. contributed equally to this work. Q.L., X.W., and W.H. conceived and supervised the project. Q.L. designed the optimization scheme and experiments. S.W. and W.Y. completed the optimal design of the mechanical sensing units. S.W., W.Y., X.Y., Y.Y., Q.Z., and G.Y. conducted the experiments. Q.L., W.Y., Z.Y., and C.J. completed the manufacturing and packaging, Q.X. carried out the optical simulation. Z.W. and J.S. completed the optimization algorithm. Q.L., S.W., W.Y., and P.L. analyzed the simulation and experimental results. Q.L., S.W., and W.Y. wrote the paper. Q.L., X.W., and W.H. revised the paper. All authors discussed the results and commented on the manuscript.
Corresponding authors
Ethics declarations
Competing interests
The authors declare no competing interests.
Peer review
Peer review information
Nature Communications thanks the anonymous reviewers for their contribution to the peer review of this work. A peer review file is available.
Additional information
Publisher’s note Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Supplementary information
Source data
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License, which permits any non-commercial use, sharing, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if you modified the licensed material. You do not have permission under this licence to share adapted material derived from this article or parts of it. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by-nc-nd/4.0/.
About this article
Cite this article
Wu, S., Yan, W., Wang, X. et al. A μGal MOEMS gravimeter designed with free-form anti-springs. Nat Commun 16, 1786 (2025). https://doi.org/10.1038/s41467-025-57176-z
Received:
Accepted:
Published:
DOI: https://doi.org/10.1038/s41467-025-57176-z